Learning-Based Online QoE Optimization in Multi-Agent Video Streaming

Abstract

Video streaming has become a major usage scenario for the Internet. The growing popularity of new applications, such as 4K and 360-degree videos, mandates that network resources must be carefully apportioned among different users in order to achieve the optimal Quality of Experience (QoE) and fairness objectives. This results in a challenging online optimization problem, as networks grow increasingly complex and the relevant QoE objectives are often nonlinear functions. Recently, data-driven approaches, deep Reinforcement Learning (RL) in particular, have been successfully applied to network optimization problems by modeling them as Markov decision processes. However, existing RL algorithms involving multiple agents fail to address nonlinear objective functions on different agents’ rewards. To this end, we leverage MAPG-finite, a policy gradient algorithm designed for multi-agent learning problems with nonlinear objectives. It allows us to optimize bandwidth distributions among multiple agents and to maximize QoE and fairness objectives on video streaming rewards. Implementing the proposed algorithm, we compare the MAPG-finite strategy with a number of baselines, including static, adaptive, and single-agent learning policies. The numerical results show that MAPG-finite significantly outperforms the baseline strategies with respect to different objective functions and in various settings, including both constant and adaptive bitrate videos. Specifically, our MAPG-finite algorithm maximizes QoE by $15.27\%$ and maximizes fairness by $22.47\%$ compared to the standard SARSA algorithm for a 2000 KB/s link.

1. Introduction

Video streaming has become a major usage scenario for Internet users, accounting for over 60% of downstream traffic on the Internet [1]. The growing popularity of new applications and video formats, such as 4K and 360-degree videos, mandates that network resources must be apportioned among different users in an optimal and fair manner in order to deliver a satisfactory Quality of Experience (QoE). There are many factors impacting the quality of experience of the video streaming service; for example, the peak signal-to-noise ratio (PSNR) of the received video [2] or the structural similarity of the image (SSIM) [3]. In particular, the stall time during streaming is a critical performance objective, especially for services that require a low response time and highly rely on customer experience, e.g., online video streaming and autonomous vehicle networks [4]. Further, the streaming device impacts the bitrate and, in turn, affects the QoE parameter (see [5] and the citations within). The online optimization of stall time and QoE in a dynamic network environment is a very challenging problem that can be analyzed as an optimization problem [6] or learning problem [7]. Traditional optimization-based approaches often rely on precise models to crystalize the network system and the underlying optimization problems. For instance, the authors in [8] construct the QoE-aware utility functions using a two-term power series model, while the authors in [9] leverage both “bSoft probe” and “Demokritos probe” to model the QoE measurement by analyzing the weight factors and exponents of all video-streaming service parameters, as well as quantifying the “Decodable Frame Rate” of three different types of frames. However, these model-based approaches cannot solve the online QoE optimization with incomplete or little knowledge about future system dynamics.

Recently, Reinforcement Learning (RL) has been proven as an effective strategy in solving many online network optimization problems that may not yield a straightforward analytical structure, such as Wireless Sensor Network (WSN) routing [10], vehicle networks spectrum sharing [11], data caching [7], and network service placement [12]. In particular, deep RL employs neural networks to estimate a decision-making policy, which self-improves based on collected experiential data to maximize the rewards. Compared with traditional model-based decision-making strategies, deep RL has a number of benefits: (i) it does not require a complete mathematical model or analytical formulation that may not be available in many complex practical problems; (ii) the use of deep neural networks as function approximators makes the RL algorithms easily extensible to problems with large state spaces; and (iii) it is capable of achieving a fast convergence in online decision making and dynamic environments that evolve over time.

The goal of this paper is to develop a new family of multi-agent reinforcement learning algorithms to apportion download bandwidth on the fly among different users and to optimize QoE and fairness objectives in video streaming. We note that existing RL algorithms often focus on maximizing the sum of future (discounted) rewards across all agents and fail to address inter-agent utility optimization, aiming at balancing the discounted reward received by each individual agent. Such inter-agent utility optimizations are widely considered in video streaming problems, e.g., to optimize the fairness of network resource allocation and to maximize a non-linear QoE function of individual agent’s performance metrics. More precisely, in a dynamic setting, the problem being solved must be modeled as an MDP, where agents take actions based on some policy $\pi$ and observed system states, causing the system to transition to a new state. A reward $r_k$ is fetched for each agent k. The transition probability to the new state is dependent only on the previous state and the action taken in the previous state. RL algorithms aim to find an optimal policy $\pi$ to maximize the sum of (discounted) rewards ${\sum }_{t=1}^{\infty }{\gamma }^t{\sum }_k{r}_k\left(t\right)$ for all users. However, when QoE and fairness objectives are concerned, a nonlinear function f, such as the fairness utility [13] and sigmoid QoE function reported by [14], must be applied to the rewards received by different agents, resulting in the optimization of a new objective $f({\overline{r}}_1,{\overline{r}}_2,\dots )$, where ${\overline{r}}_k=\frac{1}{T}{\sum }_{t=1}^T{\gamma }^t{r}_k\left(t\right)$ is the average discounted reward for each agent k in a finite time T. It is easy to see that such nonlinear functions will potentially violate the memoryless rule of MDP which is required for RL since the optimization objective now depends on all past rewards/states. In this paper, we will develop a new family of multi-agent reinforcement learning algorithms to optimize such nonlinear objectives for QoE and fairness maximization in video streaming.

We propose Multi-agent Policy Gradient for Finite Time Horizon (MAPG-finite) for the optimization of nonlinear objective functions of cumulative rewards of multiple agents with a finite time horizon. We employ MAPG-finite in online video streaming with the goal of maximizing QoE and fairness objectives by adjusting the download bandwidth distribution. To this end, we quantify the stall time for online video streaming with multiple agents under a shared network link and dynamic video switching by the agents. At the end of the time horizon, a nonlinear function $f(·)$ of the agents’ individual cumulative rewards is calculated. The choice of $f(·)$ is able to capture different notions of fairness—e.g., the well-known $\alpha$-fairness utility [13] that incorporates proportional fairness and max–min fairness as special cases, and the sigmoid-like QoE function reported by [14] that indicates that users with a mediocre waiting time tend to be more sensitive than the rest—and thus balances the performance received by different agents in online video streaming. We leverage the RL algorithm proposed in [15] to develop a model-free multi-agent reinforcement learning algorithm to cope with the inter-agent fairness reward for multiple users. In particular, this RL algorithm modifies the traditional policy gradient to find a proper ascending direction for the nonlinear objective function using random sampling. We improve the convergence of the proposed algorithm to at least a local optimal of the target optimization problem. The proposed multi-agent algorithm is model-free and shown to efficiently solve the QoE and fairness optimization in online video streaming.

To demonstrate the challenge associated with optimizing nonlinear objective functions, consider the example shown in Figure 1. Two users, A and B, share a download link for video streaming. Due to the bandwidth constraint, the link is only able to stream one high-definition (HD) video and one low-definition (LD) video at a time. In each time slot t, the two users’ QoE, denoted by $r_A\left(t\right)$ and $r_B\left(t\right)$, are measured by a simple policy that multiplies the quality of the content (from one to five stars) and the resolution of the video (1 for LD and 2 for HD). The service provider is interested in optimizing a logarithmic utility of the users’ aggregate QoE, i.e., $u=ln\left({\sum }_t{r}_A\left(t\right)\right)+ln\left({\sum }_t{r}_B\left(t\right)\right)$ (which corresponds to the notion of maximum proportional fairness [13,16]), for the two time slots $t=\{1,2\}$. It is easy to see that, in Case 1, user A received $r_A\left(1\right)=6$ in time slot 1 and user B $r_B\left(1\right)=4$. If we stream HD to user A and LD to user B in the next time slot, then the total received utility becomes $ln(6+6)+ln(4+4)\approx 4.56$, whereas the opposite assignment achieves a higher utility $ln(6+3)+ln(4+8)\approx 4.68$. However, in Case 2, choosing user A in time slot 2 to receive HD and user B LD gives the highest utility of $ln(2+6)+ln(5+4)\approx 4.28$. Thus, the optimal decision in time slot 2 depends on the reward received in all past time slots (while we have only shown the rewards in time slot 1 for simplicity in this example). In general, the dependence of the utility objective on all past rewards implies a violation of the Markovian property, as the actions should only be affected by the currently observed system state in MDP. This mandates a new family of RL algorithms that are able to cope with nonlinear objective functions, which is the motivation of this paper.

We note that, in video streaming optimization, the action space for learning-based algorithms can still be prohibitively large, since the bandwidth assignment decisions are continuous (or at least fine-grained if we sample the continuous decision space), whereas the action space suitable for RL algorithms should be small as the output layer sizes of neural networks are limited. The action space for bandwidth assignment increases undesirably with both the growing number of users and the increasing amount of network resources in the video streaming system.

To overcome this challenge, we propose an adaptive bandwidth adjustment process. It leverages two separate reinforcement learning modules running in parallel, each tasked to select a target user to increase or decrease their current bandwidth by one unit. This effectively reduces the action space of each RL module to exactly the number of users in the system, while both learning modules can be trained in parallel with the same set of data through backpropagation. This technique significantly reduces the action spaces in MAPG-finite and makes the optimization problem tractable.

To evaluate the proposed algorithm, we develop a modularized testbed for the event-driven simulation of video streaming with a multi-agent bandwidth assignment. In particular, a bandwidth assigner is developed to observe the agent states, obtain an optimized distribution from the activated action executor, and then adjust the bandwidth of each agent on the fly. We implement this distribution-generating solution along with the model-free multi-agent deep policy gradient algorithm, and compare the performance with static and dynamic baseline strategies, including “Even” (which guarantees balanced bandwidths for all users), “Adaptive” (which assigns more bandwidth to users consuming higher bitrates), and SARSA (which is a standard single-agent RL-driven policy that fails to consider inter-agent utility optimization). By simulating various network environments, as well as both constant and adaptive bitrate policies, we validate that the proposed MAPG-finite outperforms all other tested algorithms. With Constant Bitrate (CBR) streaming, MAPG-finite is able to improve the achieved QoE by up to $169.66\%$, and the fairness by up to $8.28\%$ compared with baseline strategies. Further, with the Adaptive Bitrate (ABR) streaming, up to a $41.25\%$ QoE improvement can be obtained.

We conclude that the key contributions of this work are:

• We model the bandwidth assignment problem for optimizing QoE and fairness objectives in multi-user online video streaming. The stall time is quantified for general cases under system dynamics.
• Due to the nature of the inter-agent fairness problem, we propose a multi-agent learning algorithm that is proven to converge and leverages two reinforcement learning modules running in parallel to effectively reduce the action space size.
• The proposed algorithm is implemented and evaluated on our testbed, which is able to simulate various configurations, including different reward functions, network conditions, and user behavior settings.
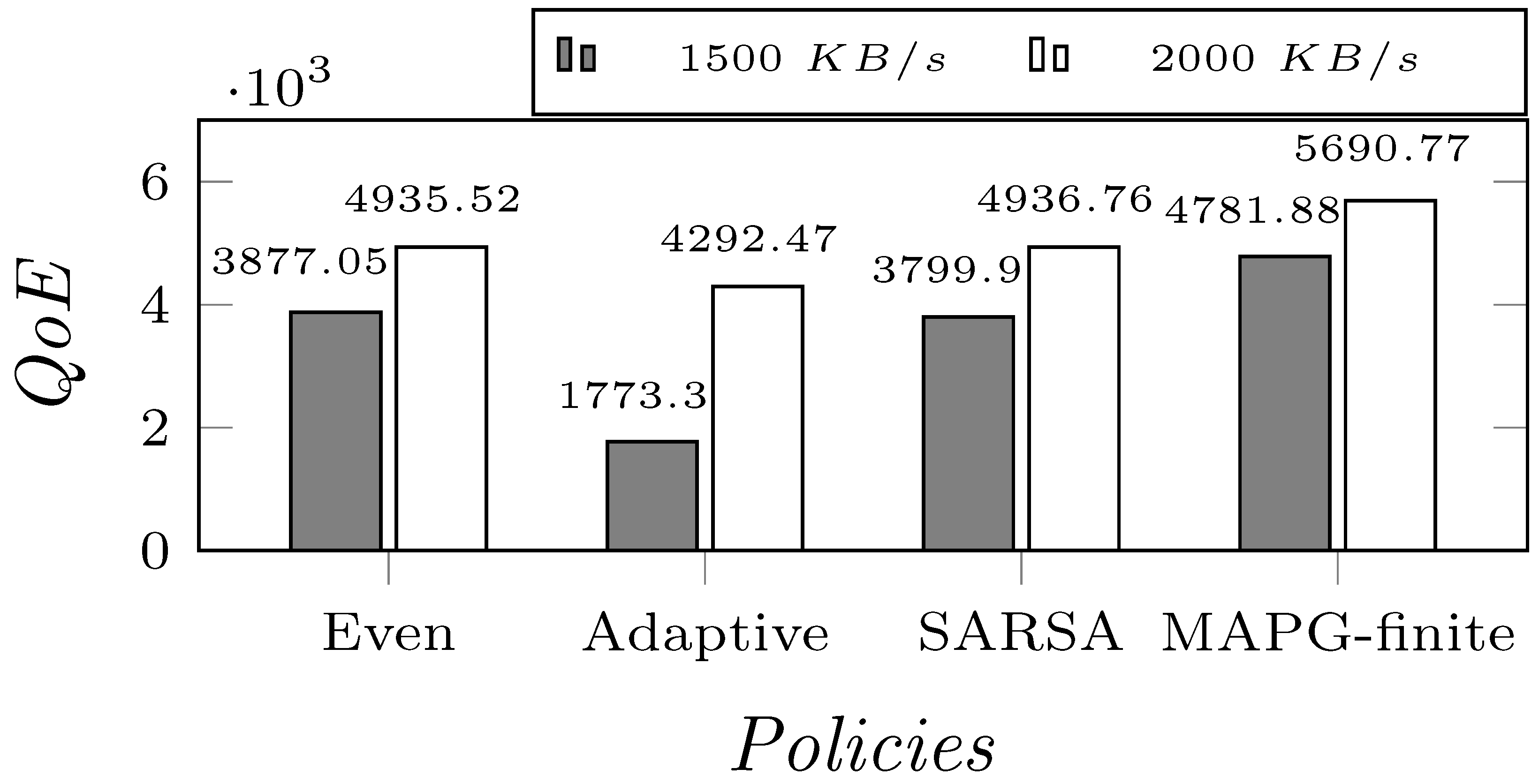
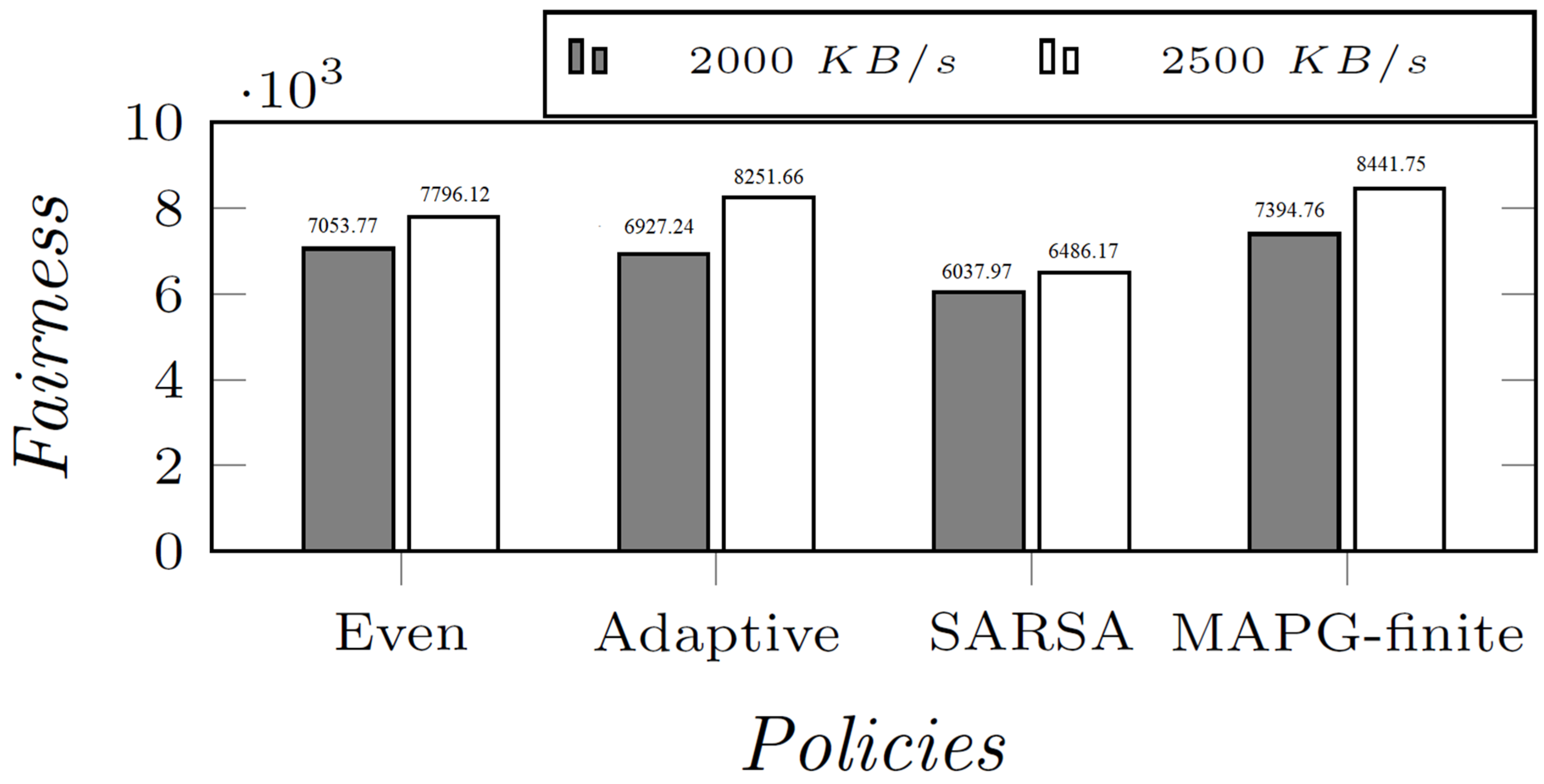
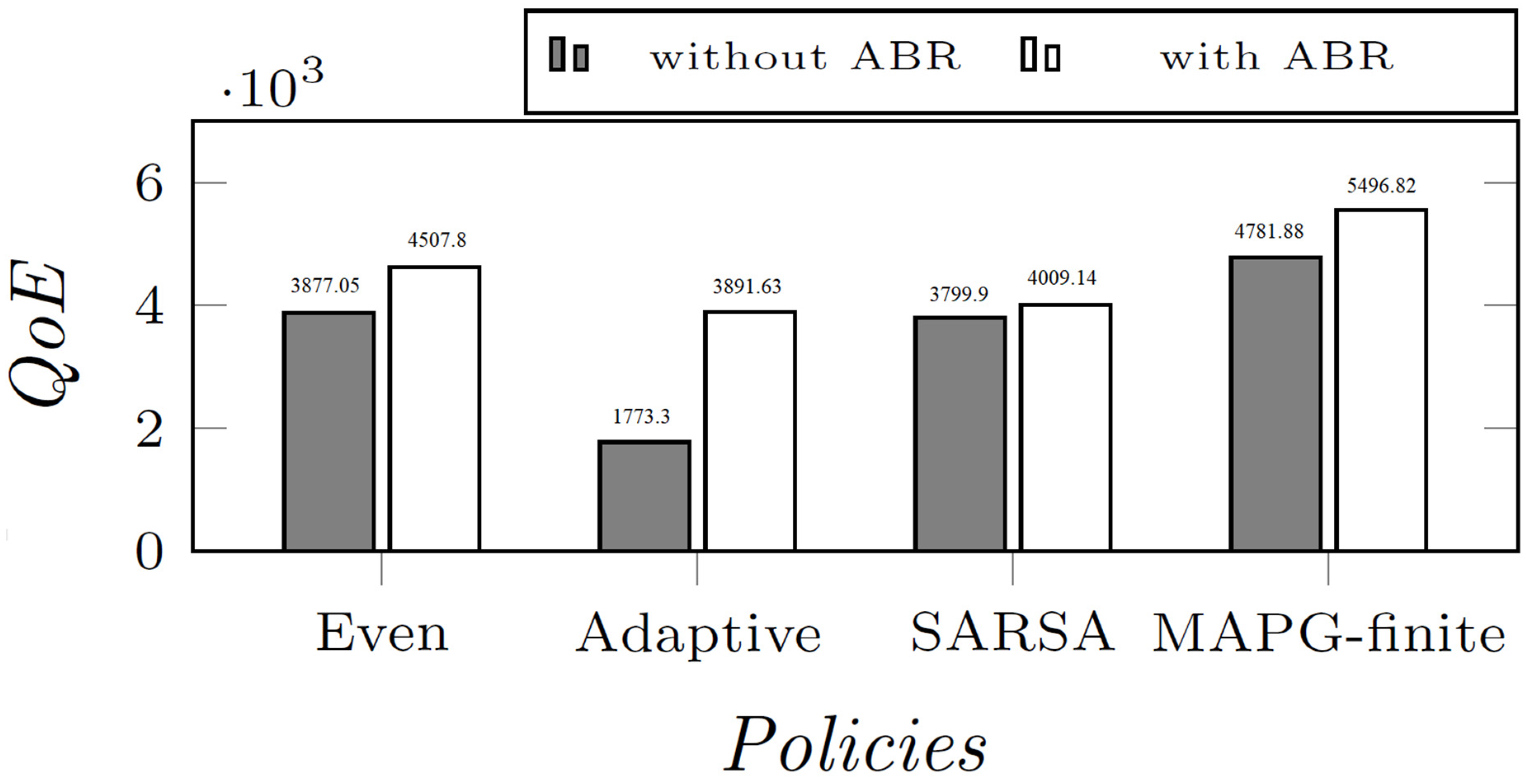
• The numerical results show that MAPG-finite outperforms a number of baselines, including “Even”, “Adaptive”, and single-agent learning policies. With CBR, MAPG-finite achieves up to a $169.66\%$ improvement in the achieved QoE, and a $8.28\%$ improvement in the logarithmic fairness; with ABR, MAPG-finite achieves up to a $41.25\%$ WoE improvement.

2. Related Work

Multi-Agent Reinforcement Learning: In the past, the Multi-agent Reinforcement Learning (MARL) technique [17] has been discussed for scenarios where all of the agents make decisions individually to achieve a global optimal. Existing works include coordinated reinforcement learning [18], which coordinates both the action selections and the parameter updates between users; sparse cooperative Q-learning [19], which allows agents to jointly solve a problem when the global coordination requirements are available; ref. [20], which uses the max-plus algorithm as the elimination algorithm of the coordination graph; ref. [21], which compares multiple known structural abstractions to improve the scalability; and ref. [22], which automatically expands an agent’s state space when the convergence is lacking. Apart from the standard Q-learning [23] and policy gradient [24] algorithms, there is rich literature on meta-heuristic algorithms for reinforcement learning. In [25], an ant-colony optimization method for swarm reinforcement learning is provided, which improves empirically over the Q-learning-based methods by using parallel learning inspired by ant swarms. Building on biological inspired algorithms, ref. [26] provides a genetic algorithm to search for parameters for deep-reinforcement learning. In addition, the authors of [27] study a modification of ant colony optimization by considering $ϵ$-greedy policies combined with Levy flight for random exploration in order to search for possible global optima. In addition, the authors of [28] consider a multi-period optimization using an ant-colony-optimization-inspired algorithm relaxation-induced neighborhood search algorithm for performing a search in large neighborhoods.

Recently, along with the development of neural networks and deep learning, the deep-MARL [29] is proposed to resolve real-world problems with larger state spaces. With various aspects of deep-MARL researched, such as investigating the representational power of network architectures [30], applying deep-MARL with discrete-continuous hybrid action spaces [31], enhancing the experience selection mechanism [32], etc., real-world applications can be solved, including wireless sensor networks (WSN) routing [10], vehicle networks spectrum sharing [11], online ride-sourcing (driver–passenger paring) services [33,34], video game playing [35], and linguist problems [29]. Comparing with existing work, our proposed solution in this paper focuses on optimizing inter-agent fairness objectives in reinforcement learning.

Video Streaming Optimization: In order to improve the performance of data streaming, various techniques have been proposed. The mostly discussed method is Adaptive Bitrate (ABR) [36] streaming, which dynamically adjusts the streaming bitrate to reduce the stall time. The different algorithms include BBA [37], Bola [38], FastMPC [39], LBP [40], FastScan [36], and Pensieve [41]. In addition to ABR and bandwidth allocation considered in this paper, caching is also a popular technique to reduce the stall time and further improve QoE. Inspired by the LRU cache replacement policy, ref. [42] analyzes an alternative gLRU designed for video streaming application, and DeepChunk [7] proposes a Q-learning-based cache replacement policy to jointly optimize the hit ratio and stall time. Within an edge network environment, the placement of calculations will also affect the streaming performance, thus work [12] breaks the hierarchical service placement problem into sub-trees, and further solves it using Q-learning.

For video streaming services still using Constant Bitrate (CBR) systems, ref. [43] proposed QUVE, which estimates the future network quality and controls video-encoding accordingly. The study in [44] considers maximizing QoE by optimizing the cache content in edge servers. This is different from our setup, where we consider caching chunks at client devices. Similar to us, ref. [45] also provides a bandwidth allocation strategy to maximize QoE. However, they use model-predictive control, whereas we pose it as a learning problem and use reinforcement learning. The study in [46] considers a multi-user encoding strategy where the encoding schemes for each user vary depending on their network condition. However, the study uses a Markovian model and does not take the possible future network conditions into account. In [47], a future dependent adaptive strategy is considered, where the TCP throughput and success probability of a chunk download are estimated. Similar to us, the authors of [48] consider a reinforcement learning protocol to maximize the QoE for multiple clients. However, they use average client QoE at time t as a reward for time t and use deterministic policies learned from Q-learning [23]. We show that our formulation outperforms standard Q-learning algorithms by considering stochastic policies and rewards as a function of the QoE of the clients.

Our work, by using a model-free deep-RL policy [15], aims to maximize the overall quality of experience of multiple agents. To measure the QoE, ref. [14] considers the web page loading time as a factor, ref. [49] tracks graphic settings, and [50] focuses on mobile networks, such that the signal-to-noise ratio, load, and handovers matter. More mapping methodologies can be found in the survey [51].

3. System Model

We consider a server with a total bandwidth of B stream videos to users in set $\left[K\right]=\{1,2,\cdots ,K\}$, in which, all of the users are consuming videos continuously. We consider a streaming session to be divided into nonidentical logical slots. In each time slot, all of the users will maintain requesting/playing chunks from the same videos. Once any user $k\in \left[K\right]$ starts a request for a new video in the current time slot l, the slot counter increments, thus the new slot $l+1$ starts for all users in $\left[K\right]$, even if the video does not change for users $k^{\prime }\in \left[K\right]/\left\{k\right\}$. Using the logical time slot setting described above, at time slot $l\in \left[L\right]=\{1,\cdots ,L\}$, a user $k\in \left[K\right]$ consumes downloading rate $d_k\left(l\right)\ge 0$ to fetch video $v_k$, which is coded with bitrate $r_k\left(l\right)$. The downloading speed is limited by ${\sum }_{k\in K}{d}_k\left(l\right)=B,\forall l\in \left[L\right]$, and may update for all users when the time slot increments in the system. The video server continuously sends video chunks to the user with downloading speed $d_k\left(l\right)$, and the user plays the video with bitrate $r_k\left(l\right)$, which is defined by the property of the video. For Adaptive Bitrate (ABR) videos, we update the bitrate of the chunk on starting a new slot only. Thus, all of the chunks sent in slot l are of bitrate $r_k\left(l\right)$. For Constant Bitrate (CBR) videos, $r_k\left(l\right)$ may remain constant across time slots $l\in \left[L\right]$ if multiple slots span the video $v_k$. A list of the key variables used in this paper can be seen in

Table 1. List of the key variables used in this paper.

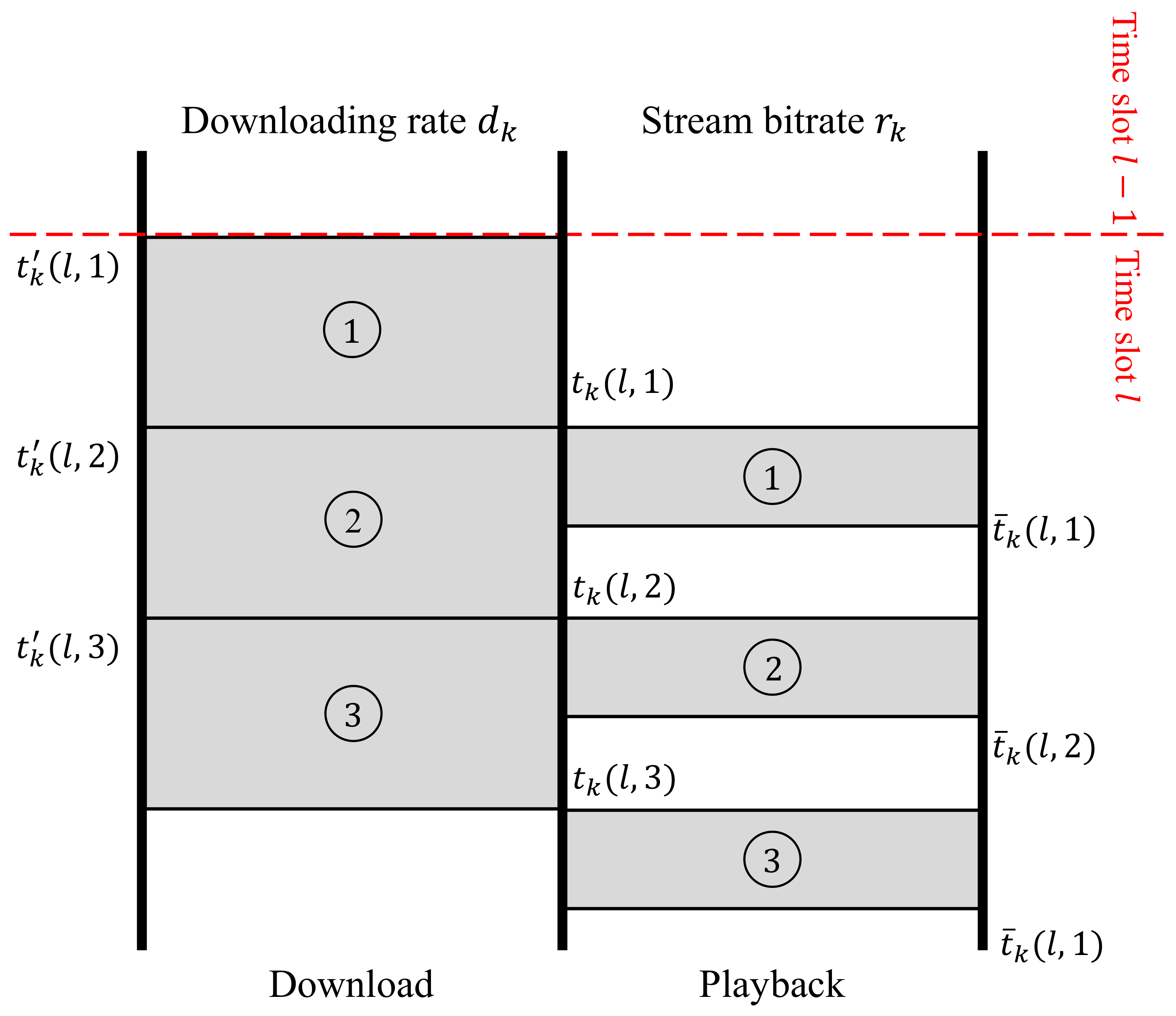
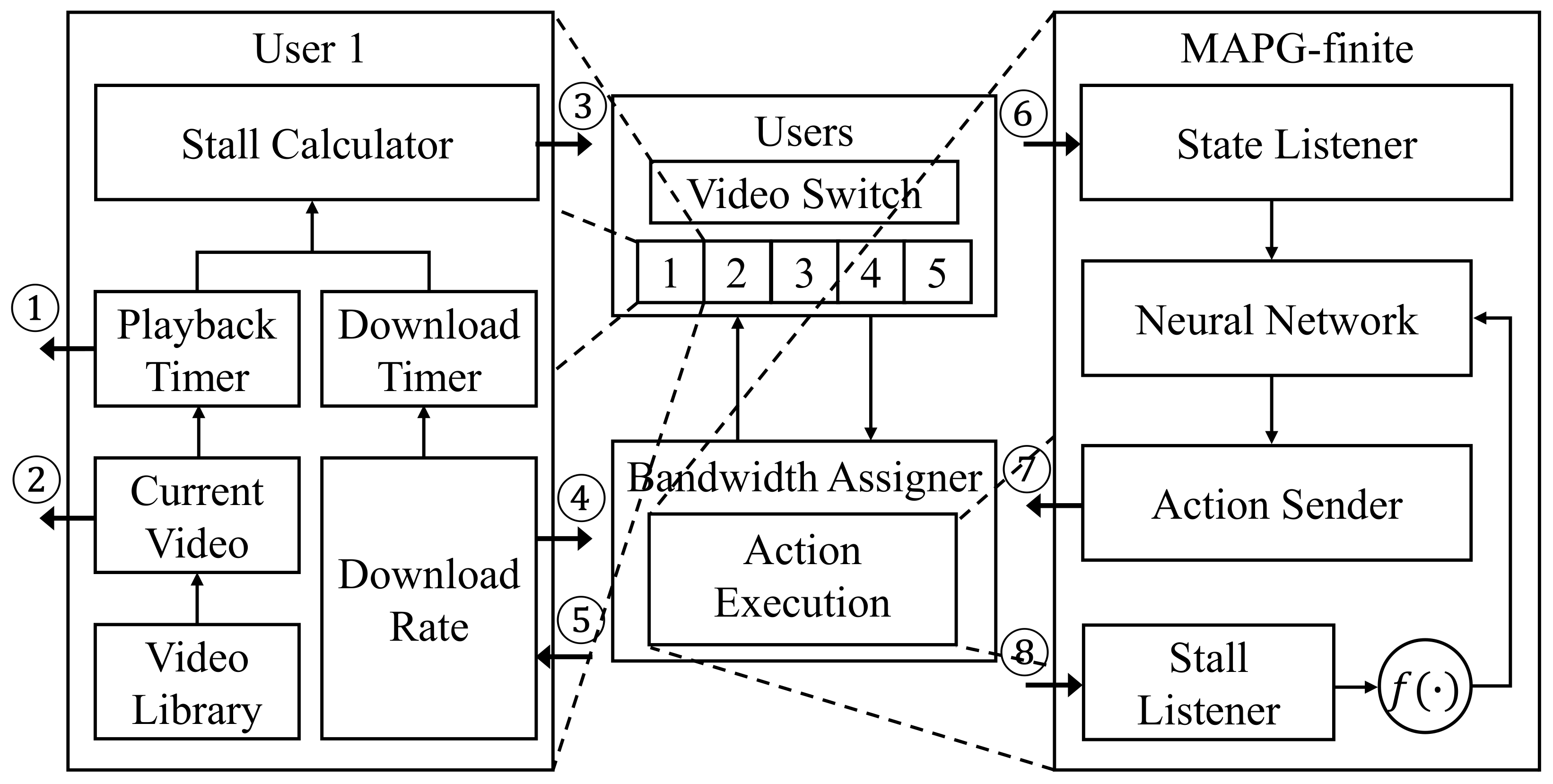
Variable	Description
K	number of clients in the system
k	index for agents, runs from 1 to K
B	total bandwidth of the system
l	slot index
L	total slots considered
$d_k\left(l\right)$	download rate for user k in slot l
$r_k\left(l\right)$	bitrate of chunk sent to user k in slot l
$v_k\left(l\right)$	index of video streamed by user k in slot l
m	chunk index of the video $v_k\left(l\right)$
$t_k(l,m)$	time at which user k starts playing chunk m for video $v_k\left(l\right)$
$t_k^{\prime }(l,m)$	time at which server starts sending chunk m for video $v_k\left(l\right)$
${\overline{t}}_k(l,m)$	time at which user k finishes playing chunk m for video $v_k\left(l\right)$

.

     In each slot, we reset the clock to zero. We use $t_k^{\prime }(l,m)$ to denote the time when the server starts to send the m-th chunk of video $v_k$ in the time slot l, $t_k(l,m)$ to denote the time when the user starts to play video chunk m, and ${\overline{t}}_k(l,m)$ to denote the moment that chunk m is finished playing. For analysis, we consider that the size of each chunk is normalized to 1 unit.

With our formulation, there will be two classes of users in a time slot l. The first class is of users who requested a new video and triggered the increment of the time slot to l. Since the user has requested a new video, it can purge the already downloaded chunks for the previous video. Users in this class may observe a new downloading rate $d_k\left(l\right)$ and video bit rate $r_k\left(l\right)$. The second class of users are those who do not request a new video, but a new streaming rate $d_k\left(l\right)$ is assigned to them because some other user $k^{\prime }\in \left[K\right]$ has requested a new video and triggered a slot change. For these users, the video bitrates will remain the same from the previous slot $l-1$, or be adjusted solely by the ABR streaming policy when CBR or ABR policies are activated, whereas, for the downloading rate $d_k\left(l\right)$, it is updated by the bandwidth distribution policy. Note that a resource allocation scheme may still allocate bandwidth to the user such that $d_k\left(l\right)=d_k(l-1)$; however, this may not be always true.

Next, we calculate the stall time in a slot l for both classes of users.

3.1. Class 1: User Requests a New Video

We first calculate the stall durations for user k that has requested a video change. As shown in Figure 2, user k starts to fetch a video from the beginning of the slot l. We assume that the chunk m is played in time-slot l; if not, the calculations for the stall duration for those chunks will be studied in Case 2. With the given downloading speed and bitrate, we can observe the relationships between $t^{\prime }(l,m)$, $t(l,m)$, and $\overline{t}(l,m)$:

$$\begin{array}{c}\hfill t_k^{\prime }(l,m)=\left\{\begin{array}{cc}{t}_k^{\prime }(l,m-1)+\frac{1}{d_k\left(l\right)},\hfill & m>1,\hfill \\ 0,\hfill & m=1,\hfill \end{array}\right.\end{array}$$

(1)

$$\begin{array}{c}\hfill t_k(l,m)=\left\{\begin{array}{cc}\max (t_k^{\prime }(l,m),{\overline{t}}_k(l,m-1)),\hfill & m>1,\hfill \\ t_k^{\prime }(l,m),\hfill & m=1,\hfill \end{array}\right.\end{array}$$

(2)

$${\overline{t}}_k(l,m)=t_k(l,m)+\frac{1}{r_k\left(l\right)},m\ge 1.$$

(3)

Since we will be limiting the analysis for user k in slot l, we drop the subscript k and the argument l from $t_k(l,m),t_k^{\prime }(l,m)$, and ${\overline{t}}_k(l,m)$ for brevity. Let T denote the time elapsed in time slot l, and let $T_s(l,T,k)$ denote the stall time in slot l till elapsed time T for user k. Clearly, when the video downloading speed is equal to or higher than the video bitrate ($d_k\left(l\right)\ge r_k\left(l\right)$), the user only has to wait for the first chunk to arrive, and then experience a stall-free video playback. Otherwise, for $d_k\left(l\right)<r_k\left(l\right)$, three conditions need to be considered for T. If T is smaller than or equal to $t\left(1\right)$, no video chunk has been played and the stall time is exactly the time elapsed T in the time slot. Otherwise, if T lands in an interval in which a video chunk m is being played, the stall time of T is equal to the stall time of $t\left(m\right)$, and if T lands in an interval where the user is waiting for the chunk $m+1$ to be downloaded, the stall time needs an additional wait after the m-th chunk is played. Hence, the stall time until the end of the slot l, $T_s(l,T,k)$, can be defined as a recursive conditional function,

$$\begin{array}{c}\hfill T_s(l,T,k)=\left\{\begin{array}{cc}{T}_s(l,t\left(m\right),k),\hfill & t\left(m\right)<T\le \overline{t}\left(m\right),\hfill \\ & d_k\left(l\right)<r_k\left(l\right),m\ge 1,\hfill \\ T-\overline{t}\left(m\right)+\hfill & \overline{t}\left(m\right)<T\le t(m+1),\hfill \\ T_s(l,t\left(m\right),k),\hfill & d_k\left(l\right)<r_k\left(l\right),m\ge 1,\hfill \\ \min (T,t(1\left)\right),\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(4)

In the condition of $d_k\left(l\right)<r_k\left(l\right)$, the stall time before the m-th chunk is downloaded is the key to obtaining the stall time of T. The stall time of $t\left(m\right)$ fits the second condition of Equation (4). Thus, we have:

$$T_s(l,t\left(m\right),k)=T_s(l,t(m-1),k)+t\left(m\right)-\overline{t}(m-1),m>1.$$

(5)

According to Equations (1)–(3), the difference between $t\left(m\right)$ and $\overline{t}(m-1)$ can be calculated. Thus, Equation (5) can be written in a recursive form:

$$\begin{array}{c}\hfill T_s(l,t\left(m\right),k)=\left\{\begin{array}{cc}{T}_s(l,t(m-1),k)+\frac{1}{d_k\left(l\right)}-\frac{1}{r_k\left(l\right)},\hfill & m>1,\hfill \\ \frac{1}{d_k\left(l\right)},\hfill & m=1,\hfill \end{array}\right.\end{array}$$

(6)

and further solved as:

$$T_s(l,t\left(m\right),k)=\frac{m}{d_k\left(l\right)}-\frac{m-1}{r_k\left(l\right)},m\ge 1.$$

(7)

Finally, substitute $T_s\left(t_k(l,m)\right)$ into Equation (4); the stall time of time slot length T is

$$\begin{array}{c}\hfill T_s(l,T,k)=\left\{\begin{array}{cc}\frac{m}{d_k\left(l\right)}-\frac{m-1}{r_k\left(l\right)},\hfill & t\left(m\right)<T\le \overline{t}\left(m\right),\hfill \\ & d_k\left(l\right)<r_k\left(l\right),m\ge 1,\hfill \\ T-\frac{m}{r_k\left(l\right)},\hfill & \overline{t}\left(m\right)<T\le t(m+1),\hfill \\ & d_k\left(l\right)<r_k\left(l\right),m\ge 1,\hfill \\ \min (T,t(1\left)\right),\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(8)

Note that, if some other user $k^{\prime }\ne k$ requests a new video triggering an increment in the time slot from l to $l+1$, the stall duration analysis will fall to the second class of users. We discuss the stall duration for the second class of users in the next section.

3.2. Class 2: Users Continuing with the Old Video

We now discuss the stall time model for users who continue the video from time slot $l-1$ to time slot l (Figure 3).

Assume that, in the previous time slot $l-1$, the total slot duration is $T^{\prime }$. At the moment of $T^{\prime }$, a chunk—denoted by 0—is being downloaded. As a result of the chunks that were continuously downloaded, by evaluating $T^{\prime }$ and the download speed $d_k(l-1)$, we can calculate the length or ratio of chunk 0, which has not been downloaded by

$$l_0=1-d_k(l-1)·\left(T^{\prime }mod\frac{1}{d_k(l-1)}\right).$$

(9)

Note that, since the length of the chunks are normalized, we have: $l_m=1,\forall m\ne 0$.

Downloaded with speed $d_k\left(l\right)$, the leftover chunk 0 with length $l_0$ needs time $l_0/d_k\left(l\right)$ to be ready for the user to play it. Following the continuous downloading rule, in time slot l, we have $t^{\prime }\left(1\right)=l_0/d_k\left(l\right)$. Then, similar to Equation (1), the rest of the $t^{\prime }\left(m\right)$ can be recursively obtained.

$$\begin{array}{c}\hfill t^{\prime }\left(m\right)=\left\{\begin{array}{cc}{t}^{\prime }(m-1)+\frac{1}{d_k\left(l\right)},\hfill & m>1,\hfill \\ \frac{l_0}{d_k\left(l\right)},\hfill & m=1,\hfill \\ 0,\hfill & m=0.\hfill \end{array}\right.\end{array}$$

(10)

We denote the last chunk being played in time slot $l-1$ as chunk $-n$, which is the video chunk ahead of chunk 0 by n, and we denote its finish time calculated in the previous time slot by ${\overline{t}}^{\prime }(-n)$. If $n=1$ and ${\overline{t}}^{\prime }(-1)\le T^{\prime }$, we know that all chunks before chunk 0 have finished playing in slot $l-1$. Otherwise, chunk $-n$ is being played half-way at the moment of the time slot transition. For the latter case, user k will continue the play of video chunk $-n$ at the beginning of time slot l. Then, in the new time slot l, because the video bitrate is not changed, chunk $-n$ will be finished at $\overline{t}(-n)={\overline{t}}^{\prime }(-n)-T^{\prime }$. Since, at the beginning of slot l, chunk 0 is being downloaded, we know that chunks in interval $\{-n,\cdots ,-1\}$ in t are all ready to be played. Therefore, we can derive the play finish time of chunks $\{-n,\cdots ,-1\}$ in slot l as:

$$\begin{array}{c}\hfill \overline{t}\left(m\right)=\left\{\begin{array}{cc}\overline{t}(m-1)+\frac{1}{r_k(l-1)},\hfill & -n<m\le -1,\hfill \\ {\overline{t}}^{\prime }\left(m\right)-T^{\prime },\hfill & m=-n.\hfill \end{array}\right.\end{array}$$

(11)

As the download finish time $t^{\prime }\left(1\right)$ and play finish time $\overline{t}(-1)$ are defined, the leftover video chunk 0 is played at time $t\left(0\right)=\max (t^{\prime }\left(1\right),\overline{t}(-1))$ and finished at $\overline{t}\left(0\right)=t\left(0\right)+1/r_k\left(l\right)$.

With all of the leftover chunk issues tackled, we finally obtain the chunk time equations for time slot l:

$$\begin{array}{c}\hfill t^{\prime }\left(m\right)=\left\{\begin{array}{cc}{t}^{\prime }(m-1)+\frac{1}{d_k\left(l\right)},\hfill & m>1,\hfill \\ \frac{l_0}{d_k\left(l\right)},\hfill & m=1,\hfill \end{array}\right.\end{array}$$

(12)

$$t\left(m\right)=\max (t^{\prime }(m+1),\overline{t}(m-1)),m\ge 0,$$

(13)

$$\begin{array}{c}\hfill \overline{t}\left(m\right)=\left\{\begin{array}{cc}t\left(m\right)+\frac{1}{r_k\left(l\right)},\hfill & m>0,\hfill \\ t\left(m\right)+\frac{1}{r_k(l-1)},\hfill & 0\ge m>-n,\hfill \\ {\overline{t}}^{\prime }\left(m\right)-T^{\prime },\hfill & m=-n.\hfill \end{array}\right.\end{array}$$

(14)

With all of the time equations obtained, we can now calculate the stall time using the similar procedure shown in the previous sub-section. Since, for $m<0$, all of the chunks are being played stall-free, if the slot ends at time $T<\overline{t}(-1)$, the stall time will be zero. From chunk $m>0$, it is possible that the stall appears between the gap where chunk $m-1$ is finished, while chunk m is not downloaded yet ($\overline{t}\left(m-1\right)<t\left(m\right)=t^{\prime }(m+1)$). If T happens to be in this gap, the stall time $T_s\left(T\right)$ will be the accumulated waiting time of chunks $[0,m-1]$ (denoted as $T_s\left(t\left(m-1\right)\right)$) plus the additional time between T and $\overline{t}\left(m-1\right)$. Otherwise, if T happens to be during when a chunk m is being played, then the stall time $T_s\left(T\right)$ should be the accumulated stall time for chunks $\{0,\cdots ,m\}$, which can be denoted as $T_s(l,t\left(m\right),k)$.

$$\begin{array}{c}\hfill T_s(l,T,k)=\left\{\begin{array}{cc}{T}_s(l,t\left(m\right),k),\hfill & t\left(m\right)<T<\overline{t}\left(m\right),\hfill \\ & m\ge 0,\hfill \\ T_s(l,t\left(m\right),k)+\hfill & \overline{t}\left(m\right)\le T\le t\left(m+1\right),\hfill \\ T-\overline{t}\left(m\right),\hfill & m\ge -1,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(15)

3.3. Quality of Experience

The goal of this work is to maximize the inter-agent QoE utility for all users. In this paper, we consider the fairness utility functions in [13] and optimize the inter-agent fairness with two existing evaluations—the sigmoid-like QoE function and the logarithmic fairness function. By analyzing real-world user rating statistics, a sigmoid-like relationship between the web page loading time and the user QoE was reported in [14]. Inspired by that, we draw a similar nonlinear, sigmoid-like QoE curve to map the streaming stall time ratio, and verify that (i) reducing the stall time for users who already have a very low stall time or (ii) increasing the stall time for users who already suffer from a high stall time does not impact the QoE values, while (iii) users with a mediocre QoE are more sensitive to stall time changes:

$$f\left(x\right)=\frac{1}{1+e^{10(x-0.35)}}.$$

(16)

We also consider a logarithmic utility function that achieves the well-known proportional fairness [13] among the users:

$$f\left(x\right)={log}_2(-x+2).$$

(17)

It is easy to see that, with the unit stall time decrease, this utility function provides (i) a larger QoE increment for users experiencing a higher stall time and (ii) a smaller increment for users already enjoying a good performance with a low stall time.

In both Equations (16) and (17), x represents the stall time ratio for playing a video. It is defined by

$$x(L_v,k)=\sum _{l\in L_v}\frac{T_s(l,T_l,k)}{T_l},$$

(18)

where $L_v$ denotes the time slots that video v has been played in, and $T_s(l,T_l,k)$ denotes the stall time for user k in time slot l with slot length $T_l$.

We note that (16) is only one representative QoE function, while other functions may be used. Suppose that, in L time slots, $V_k\left(L\right)$ is the set of videos played by user k. Then, the total QoE of the L time slots obtained by user k is given as:

$$Q_k=\sum _{v\in V_k\left(L\right)}f\left(x(L_v,k)\right),$$

(19)

and, for all users, the total QoE is

$$Q\left(L\right)=\sum _{k\in K}{Q}_k.$$

(20)

Substituting (19) and (18) in (20), we have

$$Q\left(L\right)=\sum _{k\in \left[K\right]}\sum _{v\in V_k\left(L\right)}f\left(\sum _{l\in L_v}\frac{T_s(l,T_l,k)}{T_l}\right).$$

(21)

Note that the QoE function defined in Equation (19) assigns a higher quality of experience to a lower stall time. The QoE metric remains constant for small stall times. If the stall times are lower than a certain value and are not noticeable, the QoE does not vary, as obtained in the sigmoid-like function of Equation (19). In addition, the QoE decreases rapidly with increasing stall times and remains zero if the stall times exceed a certain value, therefore ruining the viewing experience.

4. Problem Formulation

In this section, we propose a slice assignment system to distribute the download link bandwidth to users. Let $\overline{\pi }\left(l\right)=({\pi }_1\left(l\right),\cdots ,{\pi }_K\left(l\right))$ be a vector in ${[0,1]}^K$ such that ${\sum }_{k\in K}{\pi }_k\left(l\right)=1$. Each element ${\pi }_k\left(l\right)$ denotes the portion of the total bandwidth that user k is assigned to. By this definition, user k’s downloading bandwidth $d_k\left(l\right)$ under policy $\overline{\pi }\left(l\right)$ can be calculated as ${\pi }_k\left(l\right)B$.

The Multi-Agent Video Streaming (MA-Stream) optimization problem is defined as the following:

$$\begin{array}{ccc}& & \mathrm{Problem}\mathrm{MA-Stream}:\hfill \end{array}$$

$$\begin{array}{ccc}& \max & \sum _{k\in \left[K\right]}\sum _{v\in V_k\left(L\right)}f\left(\sum _{l\in L_v}\frac{T_s(l,T_l,k)}{T_l}\right),\hfill \end{array}$$

(22)

$$\begin{array}{ccc}& \mathrm{s}.\mathrm{t}.& \sum _{k\in \left[K\right]}{d}_k\left(l\right)=B\forall l\in \{1,\cdots ,L\},\hfill \end{array}$$

(23)

$$\begin{array}{ccc}& \mathrm{var}.& \overline{\pi }.\hfill \end{array}$$

(24)

We now discuss the MA-Stream optimization problem described in Equations (22)–(24). Equation (22) denotes the sum of the quality of experience for each user $k\in \left[K\right]$ across each video played in L time slots. The control variable is the policy $\pi$ (in Equation (24)), which directly controls the bandwidth allocation. This gives the constraint in Equation (23) where the sum of allocated bandwidths, $d_k\left(l\right)$, to each user $k\in \left[K\right]$ can be, at most, the total bandwidth of the system for all slots $l\in \left[L\right]$. Moreover, the QoE for any video is a non-linear function of the cumulative stall durations over each chunk in the video played.

We utilize the deep reinforcement learning technique to optimize the bandwidth distribution $\overline{\pi }\left(l\right)$. In the following sub-sections, we define the state, action, and objective for the decision making.

4.1. State

At time slot l, the observed state is defined by a $4K$ dimensional vector $s\left(l\right)=(v_1\left(l\right),\cdots ,v_K\left(l\right),d_1\left(l\right),\cdots ,d_K\left(l\right),$$z_1\left(l\right),\cdots ,z_K\left(l\right),c_1\left(l\right),\cdots ,c_K\left(l\right))$, where $v_k\left(l\right)$ denotes the video bitrates, $d_k\left(l\right)$ represents the currently assigned download speeds, $z_k\left(l\right)$ tracks the accumulated stall time for the current playing video until slot l, and $c_k\left(l\right)$ counts the number of chunks that are downloaded but not yet played for user $k\in \left[K\right]$. For brevity, we use the notation $s\left(l\right)=(\overline{v}\left(l\right),\overline{d}\left(l\right),\overline{z}\left(l\right),\overline{c}\left(l\right))$, where $\overline{v}\left(l\right)=(v_1\left(l\right),\cdots ,v_K\left(l\right)),\overline{d}\left(l\right)=(d_1\left(l\right),\cdots ,d_K\left(l\right)),$$\overline{z}\left(l\right)=(z_1\left(l\right),\cdots ,z_K\left(l\right)),\overline{c}\left(l\right)=(c_1\left(l\right),\cdots ,c_K\left(l\right))$. We will expand the corresponding vector when necessary. By considering the variables $v_k\left(l\right)$ and $d_k\left(l\right)$, the learning model should be able to estimate the downloaded and played video chunk information in the current time slot l, while $z_k\left(l\right)$ and $c_k\left(l\right)$ provide the objective-related history information.

4.2. Action and State Transition

At the beginning of time slot l, in order to find the optimal download speed distribution, multiple decisions are needed to adjust the observed speed distribution. We utilize two decision processes to obtain the optimal distribution $\overline{\pi }\left(l\right)$ while maintaining the constraint shown in Equation (23). One of the processes is a decreasing process that decides for which user the download speed will be decreased by one unit of rate, and the other process is an increasing process that decides the user that will obtain the released one unit of download speed.

The download speed distribution is iteratively adjusted to a final distribution by recursively running the decreasing and increasing decision processes. A distribution will not be assigned to the system until the final decision is concluded, and the system will not transit into the next time slot. Assuming, at time slot l, with the observed state $s\left(l\right)=(\overline{v}\left(l\right),\overline{d}\left(l\right),\overline{z}\left(l\right),\overline{c}\left(l\right))$, actions $a_{-},a_{+},a_{-}\ne a_{+}$ are made by the decreasing and increasing processes. The intermediate state $s\left({\tau }^{\prime }\right)$ can be derived by

$$\begin{array}{cc}\hfill s\left({\tau }^{\prime }\right)=& (\overline{v}\left(l\right),d_1\left(l\right),\cdots ,d_{a_{-}}\left(l\right)-1,\cdots ,\hfill \\ \hfill & d_{a_{+}}\left(l\right)+1,\cdots ,d_K\left(l\right),\overline{z}\left(l\right),\overline{c}\left(l\right)).\hfill \end{array}$$

(25)

Now, this intermediate state $s\left({\tau }^{\prime }\right)$ is used in the decision making for both processes. New actions will be made to push the distribution towards the final state. Finally, at state $s\left(\tau \right)$, when both the increasing and decreasing processes give the same action $a_{+}=a_{-}$, the distribution $\overline{\pi }$ is obtained as $\overline{\pi }\left(l\right)=(d_1\left(\tau \right),d_2\left(\tau \right),...,d_K\left(\tau \right))/B$.

According to $\overline{\pi }\left(l\right)$, the system distributes the bandwidth to each user for the time slot l. The next time slot $l+1$ will be triggered when a user switches its playing video. We assume that the new content request for all users follows Poisson arrival processes with arrival rate ${\lambda }_k$ for user k, so the mean value of slot duration $T_l$ can be derived by $1/{\sum }_{k\in K}{\lambda }_k$, and the probability that user k triggers the state transition is ${\lambda }_k/{\sum }_{\kappa \in K}{\lambda }_{\kappa }$. For time slot $l+1$, the initial system state $s(l+1)=(\overline{v}(t+1),\overline{d}(t+1),\overline{z}(t+1),\overline{c}(t+1))$ should have video bitrates $v_{\kappa }(l+1)=v_{\kappa }\left(l\right),(\forall \kappa \in K,\kappa \ne k)$ if CBR is activated as the bitrate policy, and downloading speeds $d(l+1)=\overline{\pi }\left(l\right)B$ calculated in the previous time slot.

The accumulated stalls $\overline{z}\left(l\right)$ can be calculated using Equations (4) and (15). Let $v_k\left(l\right)$ be the video played by the user k in time slot l, and let $l_{v_k\left(l\right),0}$ be the time slot where user k starts playing video $v_k\left(l\right)$. Let $T_{l^{\prime }}$ denote the length of time slot $l^{\prime }$; we have

$$z_k\left(l\right)=\sum _{l^{\prime }=l_{v_k\left(l\right),0}}^{l-1}{T}_s(l^{\prime },T_{l^{\prime }},k).$$

(26)

The number of remaining chunks $\overline{c}\left(l\right)$ can easily be tracked during the downloading/playing procedures, and observed whenever the information is needed. Both the downloading and playing processes can be monitored. For the downloading process, let $c_d\left(l\right)=h_d\left(l\right)+{\rho }_d\left(l\right)$, where $h_d\left(l\right)\in \mathbb{N}$ denotes the chunk of the video being played at the beginning of time slot l being downloaded, and ${\rho }_d\left(l\right)\in [0,1)$ denotes the ratio or percentage of chunk $h_d\left(l\right)$ that has been completed. The similar mechanism holds for the playing process, $c_p\left(l\right)=h_p\left(l\right)+{\rho }_p\left(l\right)$. Using both of the processes, the remaining chunks $c\left(l\right)$ can be calculated by $c\left(l\right)=c_d\left(l\right)-c_p\left(l\right)$ in any time slot l.

4.3. Feedback

As pointed out in Equation (22), the goal of the controller is to maximize the average QoE. For our RL algorithm to learn an optimal policy to maximize the objective, every slot provides a feedback of the value of the objective calculated from the average stall times for all users.

In Section 4.2, we mention, that when the decreasing and increasing processes take decisions $a_{-}\left({\tau }^{\prime }\right)\ne a_{+}\left({\tau }^{\prime }\right)$, the state transition only happens in a logic domain instead of the realistic time domain. During this intermediate state transition, no real stall time calculations exist and we assign zero rewards for actions $a_{-}\left({\tau }^{\prime }\right)\ne a_{+}\left({\tau }^{\prime }\right)$ in the intermediate state before converging to $\overline{\pi }\left(l\right)B$. When the final distribution is achieved ($a_{+}=a_{-}$), the slot duration $T_l$ can be obtained and, hence, stall times $T_s(l,T_l,k)$ can be calculated for all users. We can also obtain rewards from the calculated stall times using Equation (21).

The complete schema is presented in Algorithm 1.

Algorithm 1 Proposed MA-Stream Algorithm

1: Input: Set of users $\left[K\right]$, maximum bandwidth B

2: for slot $l\ge 0$  do

3:   Observe state $s\left(l\right)$ as described in Section 4.1

4:   Compute bandwidth allocations $d_k\left(l\right)$ for all $k\in \left[K\right]$ using RL engine

5:   while No user switches video do

6:     Continue streaming with $d_k\left(l\right)$ for all $k\in \left[K\right]$

7:     Store Stall duration, $T_s(l,T_l,k)$ for slot l for all $k\in \left[K\right]$

8:   end while

9: end for

5. Policy Gradient for MA-Stream

In the previous section, we define the network streaming problem MA-Stream for multiple users. Note that the objective defined in Section 4.3 is a nonlinear function (Equation (19)) of the total stall duration until the current time instant. At any time slot l, the reward not only depends on the stall times observed by the users in the slot l, but also on the stall times observed by users in the previous time slots. Hence, the decision-making module needs to track not only the current state but also the history of the decision and the rewards obtained to select the current action. Hence, we are not able to utilize standard RL algorithms that require modeling the problems into MDP. To this end, we leverage Multi-agent Policy Gradient for Finite Time Horizon (MAPG-finite) [15], a novel multi-agent policy gradient RL algorithm that aims to solve optimization problems without the requirements of MDP modeling. In the following Section 5.2, we give a short description of this algorithm.

5.1. Standard RL Algorithms

Standard RL problems consider an agent that interacts with a Markov decision process $\mathcal{M}$. The agent, at time t, observes the state $s_t$ of the environment and plays action $a_t$ to obtain a reward $r_t$, causing the environment to transition to state $s_{t+1}$ [52]. Let the next state transition probability be ${\mathcal{P}}_{s{s}^{\prime }}^a=P(s_{t+1}=s^{\prime }|s_t=s,a_t=a)$ and the expected reward of playing action a in state s be ${\mathcal{R}}_s^a=\mathbb{E}\left[r_t\right|s_t=s,a_t=a]$. The goal of the agent is to find a policy $\pi (s,a;\theta )=P(a_t=a|s_t=s,\theta )$ parameterized on $\theta$ that maximizes the discounted cumulative reward

$$V_{\pi }\left(s_0\right)={\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }{\gamma }^t{r}_t|s_0\right],$$

(27)

where $s_0$ is the initial state, and $\gamma <1$ is a discounted factor. Using the linearity of cumulative rewards in Equation (27), the state action value function $Q_{\pi }(s,a)$ for policy $\pi$ is defined as

$$Q_{\pi }(s,a)={\mathcal{R}}_s^a+\gamma \sum _{s^{\prime }}\sum _a{\mathcal{P}}_{s{s}^{\prime }}^a\pi (s,a;\theta )V_{\pi }\left(s^{\prime }\right).$$

(28)

Based on Equation (28), many algorithms have been proposed, e.g., SARSA [53,54,55], Q-learning [23], policy gradient [24], etc. Based on these fundamental algorithms, many deep-learning-based implementations are also proposed [52].

In many network optimization problems, the reward metrics are nonlinear when multiple subjects are jointly optimized. One typical example is resource fairness among agents/users in one network [13,56]. With a nonlinear reward function, the decision-making engine must be aware of the historical decisions and states in the past. To demonstrate the requirement of policies that require history, we take the following example. Suppose that there are $K=2$ users who share the network resource and we want to allocate this network resource fairly between the two users. If we use proportional fairness, the fairness for the two users can be calculated as the sum of the logarithms of the QoE indicators of the two users. We call the users 1 and 2, and we assume that both users 1 and 2 start with the same video. In slot 1, the bandwidth allocated to user 1 is higher than user 2 ($d_1\left(1\right)>d_2\left(1\right)$). This results in higher stall times for user 2 compared to user 1.

Now, in the next time slot 2, user 2 switches the video with a video bitrate that is the same as the previous video, and user 1 continues with the old video. Then, since the video bitrates remain the same, allocating a higher download rate to user 2 ($d_2\left(2\right)>d_1\left(1\right)$) will result in lower stall times for user 2 and, hence, the fairness can be maximized. This requires the controller to ensure that the decisions at time slot 2 are made taking into account the decision made in time slot 1. However, the state defined in Section 4.1 does not store the cumulative stall duration of the previous video for the user triggering the current time slot. The algorithm used in this paper to deal with such a nonlinear problem is explained in the next subsection.

We further note that one possible way to tackle the non-Markovian nature is to introduce a high-order Markov model by including the objective value until time slot $l-1$ in the state. This approach, however, potentially increases the state space dramatically to ${\left(SA\right)}^L$, where S is the number of states and A is the number of actions that the controller can take. Hence, we consider a multi-agent learning algorithm in the next session, which does not require the use of high-order Markov models and allows an individual agent to improve its policy.

5.2. Model-Free Multi-Agent Policy Gradient Algorithm

In [15], a novel model-free algorithm is proposed in order to solve the nonlinear (in time) optimization problems in a finite time horizon scenario. Like the traditional deep policy gradient RL algorithm, the MAPG-finite algorithm utilizes the observed system state $s\left(t\right)$ as the input of a neural network that is parameterized by $\theta$, then takes the output of the neural network to be the decision policy ${\pi }_{\theta }$, which indicates the action probabilities. Finally, according to the policy $\pi$, an action is randomly chosen to interact with the environment.

With a proper training process, the neural network is improved by the reward feedback. Expectedly, the neural network parameter $\theta$ should evolve to stage ${\theta }^{*}$, which maximizes the objective function f:

$${\theta }^{*}=arg\underset{\theta }{\max }f\left((1-\gamma )J_{{\pi }_{\theta }}^1,...,(1-\gamma )J_{{\pi }_{\theta }}^K\right),$$

(29)

where $J_k^{{\pi }_{\theta }}$ denotes the long term reward obtained by agent k running policy ${\pi }_{\theta }$:

$$\begin{array}{c}\hfill J_{\pi }^k={\mathbb{E}}_{s_0,a_0,s_1,a_1,...}\left[\underset{L\to \infty }{\lim }\sum _{l=0}^L{\gamma }^{l}f\left(T_s(l,T_l,k)\right)\right],\end{array}$$

(30)

$$\begin{array}{c}\hfill s_0\sim {\rho }_0\left(s_0\right),a_l\sim \pi \left(a_l\right|s_l),s_{l+1}\sim P\left(s_{l+1}\right|s_l,a_l).\end{array}$$

(31)

Since the objective function f is differentiable (refer to Equation (16)), the gradient estimation for Equation (29) can be obtained by:

$$\begin{array}{c}\hfill {▿}_{\theta }f=\sum _{k\in \left[K\right]}\frac{\partial f}{\partial (1-\gamma )J_k^{\pi }}{▿}_{\theta }{J}_k^{\pi }\\ \hfill =(1-\gamma ){({▿}_{(1-\gamma ){\overline{J}}^{\pi }}f)}^T({▿}_{\theta }{\overline{J}}^{\pi }),\end{array}$$

where ${\overline{J}}^{\pi }={(J_1^{\pi },...,J_K^{\pi })}^T$, in which, ${\overline{J}}_k^{\pi }$ denotes the expected cumulative reward, and is further estimated as

$${\widehat{J}}_k^{\pi }=\frac{1}{N}\sum _{n=1}^N\sum _{l=0}^L{T}_s(l,T_l,k).$$

(32)

In each episode n, time slots l runs from 0 to L. Finally, with learning rate $\beta$, the step parameter update can be shown as:

$${\theta }_{i+1}={\theta }_i+\beta (1-\gamma ){\left({▿}_{(1-\gamma ){\overline{J}}^{\pi }}f(\widehat{\overline{J}})\right)}^T\left({\widehat{▿}}_{\theta }{\overline{J}}^{\pi }\right),$$

(33)

and further utilized for gradient ascent in the neural network.

We now state a formal result of convergence to a stationary point from the gradient ascent steps.

Lemma 1.

For a policy function parameterized with a neural network with softmax activations, and function f with continuous gradients, Equation (33) converges to a stationary point.

Proof. 

Since we use softmax activations, the gradient of policy $\pi$, ${\nabla }_{\theta }\pi$ is also continuous in $\theta$, and, obtaining the continuity of ${\nabla }_{\pi }{J}_k^{\pi }$ from Theorem 2 in [24] with respect to parameter $\theta$, we have the continuity of ${\nabla }_{\theta }{J}_k^{\pi }$. Using the continuity of gradient $\frac{\partial f}{\partial J_k^{\pi }}$ from the definition of f, the continuity of ${\nabla }_{\theta }{J}_k^{\pi }$, and Proposition 3.4 in [57], we have the convergence of policy to a stationary point. □

6. Evaluation

We conduct a hybrid simulation on a network containing five users over a shared downloading link, and evaluate the performance of the proposed learning algorithm. In particular, three users prefer to watch HD videos (with desired bitrates at 8 Mbps and 5 Mbps), whereas the other two users watch videos at a lower resolution (with desired bitrates at 2.5 Mbps and 1 Mbps). The video durations of all users follow an exponential distribution with an identical 120 s average. We run the simulation on both channels with different bandwidths, i.e., 1500 KB/s and 2000 KB/s channels. In both settings, our proposed algorithm is shown to substantially outperform the baseline policies (relying on heuristics and single-agent learning) in terms of the QoE reward and fairness.

6.1. Evaluation Setup

6.1.1. Evaluated Policies

We evaluate our model-free MAPG-finite algorithm along with three baselines, which are denoted by “Even”, “Adaptive”, and SARSA policies, as follows.

Policy MAPG-finite: Our proposed algorithm leverages a model-free, multi-agent policy gradient to optimize the download bandwidth distribution among agents. Recall that, in the algorithm, multiple decisions/actions are made to either increase or decrease the download speed of specific users by one unit. During the training process, the two decision-making processes (to increase and decrease download speeds) need to perform a random exploration in a non-cognitive fashion, which often leads to a long exploration time and, thus, a slow convergence in the optimal policy. Suppose that the bandwidth distribution at time t is ${\pi }_t$. To mitigate this problem during training, we suspend the exploration process if the same bandwidth distribution is observed again in the future, i.e., ${\pi }_{t+x}={\pi }_t$ for some $x\in {\mathbb{N}}^{+}$.

Policy “Even”: The downloading bandwidth is evenly distributed to all users in the system. For instance, when the total bandwidth is 1500 KB/s, each of the five users will receive 300 KB/s for its downloading speed, regardless of its demand and preference. This one-size-fits-all policy equally distributes bandwidth among the users.

Policy “Adaptive”: The download bandwidth is split between the users in proportion to their desired video bitrates. This policy guarantees that users with a high data rate demand (i.e., those watching the high-resolution video) receive a higher downloading speed, whereas users with a low data rate demand receive a lower speed. Specifically, user k will be assigned a bandwidth of $d_k=v_{k}B/{\sum }_{\kappa \in K}{v}_{\kappa }$, where $v_{\kappa }$ is the desired video bit rate of user $\kappa$.

Policy SARSA: This policy leverages single-agent learning, SARSA [53,54,55], to distribute the download bandwidth to the users. It uses a standard policy gradient strategy with the same state/action definition of our proposed MAPG-finite. Without considering the nonlinear reward function feature, this policy simply utilizes the sum of the step reward as its immediate reward for learning. Note that we make the same state variables, including reward-related history information $\overline{z}\left(l\right)$, known to the SARSA policy to boost the performance of this baseline.

6.1.2. Reward Functions

Our proposed MAPG-finite algorithm allows for the maximization of any nonlinear reward in a finite time period. We consider two reward functions in the evaluation, namely QoE and fairness, to compare the performances achieved by different policies.

For the QoE reward, we use a sigmoid-like function to measure the reward with respect to the stall time. In particular, we choose parameters in Equation (16) to match a stall-to-QoE curve reported by [14]. We plot our fitted reward function in Figure 4a, which matches well with the reported stall-to-QoE curve in [14]. In addition, for the fairness objective, we choose a logarithmic utility function shown in Equation (17) and Figure 4b of the users’ received stall time. By maximizing the logarithmic function, the proportional-fair QoE assignment between the users [13] is obtained.

Naturally, our proposed multi-agent learning algorithm is able to learn and optimize any reward functions, linear or nonlinear. We note that, even when the exact function is unknown, the model-free algorithm can still be trained and evaluated using the real-world user traces.

6.1.3. Users and Videos

We implement a network with five users and both high- and low-resolution videos. In particular, three users prefer to watch high-resolution videos with bitrates of 8 Mbps (1080p) and 5 Mbps (720p) (similar to Youtube videos [58]), whereas the other two users consume 2.5 Mbps (480p) and 1 Mbps (360p) videos randomly.

The video durations for all users follow an independent, identical exponential distribution with an average of 2 min. Thus, the combined video switching rate for all five users is once every 24 s. When a user elects to switch video, a random video is selected and starts streaming. Note that the new video may have the same or different bitrate to the previous video. For example, when user 1 finished watching a video, the new video will have a bitrate of 8 Mbps or 5 Mbps with the same $50\%$ probabilities. The user preferences and their corresponding probabilities are shown in

Table 2. Simulated user preferences.

User	Resolutions	Bitrates	Probabilities
1	1080p 720p	8 Mbps 5 Mbps	0.5 0.5
2	1080p 720p	8 Mbps 5 Mbps	0.5 0.5
3	1080p 720p	8 Mbps 5 Mbps	0.5 0.5
4	480p 360p	2.5 Mbps 1 Mbps	0.5 0.5
5	480p 360p	2.5 Mbps 1 Mbps	0.5 0.5

.

6.1.4. Implementation

We implement a testbed using Python 3.5. The workflow of the testbed is depicted in Figure 5. First, at the beginning of a new cycle, according to the video switching rates (which result from the known video duration distributions), the video switch module randomly schedules a user who will be the next candidate to change their video. The users then start downloading video chunks continuously, and their download timers record the timestamp when each chunk is successfully downloaded (i.e., $t_{m+1}^{\prime }$ in Figure 3). Next, based on the download timestamps and the bitrate of the current video, the playback timer schedules the playback and further obtains $t_m$ and $\overline{t_m}$. With all timestamps confirmed, the stall calculator is able to calculate the stall time for the user/videos. Such a stall time is transferred to the distribution module for training and evaluation. Finally, the chosen user randomly picks a new video from its video library at the end of the current cycle.

Recall that, from Section 4, the state variables utilized for MAPG-finite decision making include video bitrates, downloading speeds, accumulated stall time, and residue video chunks, which can be reported through output paths ②, ④, ③, and ①, respectively, in Figure 5. The state variables are then collected by the state listener through input path ⑥. Further, utilizing the neural network, a bandwidth distribution—as the action—is decided and sent by the action sender to all of the users via ⑦. For training and evaluation purpose, a copy of the stall ratio is also sent from ③ to ⑧. It is processed by the reward function $f(·)$ to calculate either the QoE (Equation (16)) or the fairness (Equation (17)) reward. Finally, the reward is delivered to the neural network for policy backpropagation, and also logged for experiment evaluation. By input path ⑤ of each user, the users adjust their download rates according to the bandwidth decision from ⑦. At this point, the testbed completes one workflow cycle and prepares to initiate the next cycle, starting with the video switch.

Using the modularized testbed implemented in this project, we are able to evaluate different policies under various environment configurations, including with different reward functions, network conditions, and user behavior settings. We note that, with some minor logic adjustments, we can even test the streaming performance in a discrete time domain, while this paper focuses on continuous time evaluations.

6.2. Evaluation Results

The numerical results for the QoE reward function (Equation (16)) is depicted in Figure 6. It is shown that our proposed MAPG-finite algorithm outperforms the static “Even” and dynamic “Adaptive” strategies by $23.34\%$ and $169.66\%$ (in terms of achieved QoE) with the shared download link of 1500 KB/s. With the 2000 KB/s download link, MAPG-finite still obtains a $15.30\%$ and $32.58\%$ higher QoE reward than the “Even” and “Adaptive” policies, while the improvement becomes smaller because of a smaller marginal QoE improvement when the stall time is already small under a higher bandwidth. As for the SARSA policy, it is unable to cope with the nonlinear utility function and fails to achieve much improvement over its initial decision policy—“Even”. Since the QoE reward function is nonlinear to the assigned bandwidth, we also observe that the “Adaptive” policy (allocating bandwidth proportional to desired video bitrate) performs worse than “Even” in both cases.

These can be further seen from

Table 3. Reward breakdown for QoE function on 1500 KB/s download link.

Policy	Total Reward	User Average
		User	Stall Ratio	Reward
“Even”	3877.05	1, 2, 3 (HD) 4, 5 (LD)	0.64 0.13	0.07 0.86
“Adaptive”	1773.30	1, 2, 3 (HD) 4, 5 (LD)	0.51 0.59	0.20 0.14
MAPG-finite	4781.88	1 2 3 4 5	0.34 0.50 0.39 0.07 0.08	0.52 0.27 0.44 0.91 0.91

, which shows the stall time and reward breakdown of different policies. Apparently, the “Adaptive” policy achieves a similar stall time for both HD and LD users, whereas the “Even” policy sacrifices the performance of HD users, and, in return, significantly reduces the stall time of LD users, leading to a higher overall QoE. More precisely, according to the QoE reward curve shown in Figure 4a, the reward boost for the LD users is much greater than the loss suffered by the HD users, which finally results in the overall QoE improvement in the “Even” policy.

As a learning-based algorithm, MAPG-finite can achieve a substantially better performance, since it is aware of the current network conditions and system states, in order to optimize the bandwidth distribution between the users. For example, when a user has enough cached chunks for future playback, its bandwidth can be temporarily turned over to the other users, who recently started playing a new video or are suffering from a stall. Thus, all users are able to obtain increased QoE rewards under the MAPG-finite strategy, compared with the baselines.

Results for the fairness reward function are shown in Figure 7. We note that, due to the use of the logarithmic fairness function, the improvement appears to be smaller when measured by the fairness reward than by the QoE reward, while the gains should be interpreted in the “multiplicative” sense. Our proposed MAPG-finite still outperforms the “Even” and “Adaptive” strategies (in terms of the logarithmic fairness reward) by $4.83\%$ and $6.75\%$ for the 2000 KB/s downloading link, and $8.28\%$ and $2.30\%$ for the 2500 KB/s link.

With the 2500 KB/s downlink,

Table 4. Reward breakdown for fairness function on 2500 KB/s download link.

Policy	Total Reward	User Average
		Users	Stall Ratio	Reward
“Even”	7796.12	1, 2, 3 (HD) 4, 5 (LD)	0.39 0.08	0.67 0.93
“Adaptive”	8251.66	1, 2, 3 (HD) 4, 5 (LD)	0.18 0.28	0.86 0.77
MAPG-finite	8441.75	1, 2, 3 (HD) 4, 5 (LD)	0.24 0.11	0.80 0.91
“Low Dev”	8263.49	1, 2, 3 (HD) 4, 5 (LD)	0.22 0.20	0.82 0.84

shows that the dynamic “Adaptive” strategy achieves similar performances for all users, leading to a better fairness reward than the “Even” policy, which creates more difference between the HD and LD users that have significantly different bitrate requirements. On the other hand, our MAPG-finite strategy reduces the average stall ratio of HD users by $38.46\%$, with a cost of a $37.50\%$ higher stall ratio for LD users compared to the “Even” policy. This way, it is able to reduce the stall ratio deviation of all users from $0.1698$ to $0.0712$, and improves the fairness reward. Comparing with the “Adaptive” policy, MAPG-finite has an approximately $30\%$ higher stall ratio deviation. However, the optimization object, known as the proportional fairness utility [13], is not solely about “equalizing” different users’ performances. (To illustrate this, we construct a “Low Dev” policy in Table 4 that has a close-to-zero stall ratio deviation but a low fairness reward.) The use of a proportional fairness reward function indeed balances two important objectives—efficiency (i.e., assigning more bandwidth to users that can achieve a higher reward per unit bandwidth) and fairness (i.e., balancing different users’ performances). MAPG-finite is able to attain the highest reward under the choice of proportional fairness utilities, demonstrating its ability to achieve complex optimization objectives.

The evaluation results show that the “Even”, “Adaptive”, and SARSA policies fail to perform consistently under different application scenarios and network conditions, whereas our learning-based MAPG-finite policy is able to achieve the highest reward. Figure 8 depicts the average download rate distribution decided by the MAPG-finite policy. The gray bars represent the average video bitrates requested by the users.

The white bars represent the average download rate achieved by our MAPG-finite policy (for presentation purposes, the unit of download rates is converted from KB/s to Mbps). It is can be seen that, in order to maximize the fairness reward, MAPG-finite ensures that (i) for users with the same HD preference (e.g., users 1, 2, and 3), the same average downloading bandwidth is assigned to obtain a similar stall time for these users, and (ii) for users watching videos with lower desired bitrates, less bandwidth is assigned to balance the stall time, since video chunks are consumed at a slower pace. According to Figure 7, the “Adaptive” policy achieves a lower fairness reward than “Even” under the total download link of 2000 KB/s, which indicates that proportionally adjusting the download bandwidth does not always achieve a better result when fairness is concerned. Through the exploration and training of RL, MAPG-finite is able to self-teach, improve, and finally converge to an optimal policy, making the model-free suitable for bandwidth allocation with complex networks and objectives that often do not have a straightforward mathematical formulation.

To further illustrate the agility of our proposed MAPG-finite algorithm, we perform another evaluation on a 1500 KB/s downlink, with an ABR streaming algorithm implemented. Figure 9 depicts the QoE performances for this evaluation. We utilize a basic buffer-based ABR algorithm proposed in [37]. Each time a video chunk is requested, if the last chunk downloaded is already being played, the bitrate is adjusted to $80\%$ of the max bitrate of the video to avoid a high stall time. When the number of residue cached chunks is more than three, the agent starts to request for the max bitrate, and, thus, a better display quality is obtained. Comparing Figure 9 with Figure 6, all policies receive higher rewards under ABR due to the benefits of bitrate adaptation. We note that MAPG-finite still outperforms the “Even” policy by $21.94\%$, the “Adaptive” policy by $41.25\%$, and the SARSA policy by $37.11\%$. In this evaluation, we choose the buffer-based strategy for ABR due to its efficiency for implementation. According to the numerical results, our proposed MAPG-finite is able to adapt well to a dynamic bitrate environment. We are aware that new ABR policies—some are engined by RL algorithms themselves—have been proposed and evaluated [36,38,39,40,41] to improve the streaming quality. The key aim of the evaluation was to show that the proposed framework can work on ARB streaming strategies, not to compare the different streaming strategies. Thus, any streaming algorithm can be used in our evaluations and our results show that an efficient bandwidth distribution among multiple agents can be achieved with the proposed algorithms, where each agent uses any of the ABR/CBR streaming algorithms.

7. Conclusions

In this paper, we model the MA-Stream problem, which apportions bandwidth to multiple users in a video streaming network, to maximize nonlinear, non-convex objectives such as QoE and fairness objectives. We propose a novel multi-agent reinforcement learning algorithm MAPG-finite that is able to work with nonlinear objective functions to solve this optimization problem.

Using our testbed implemented in Python, we verify that our proposed solution outperforms existing baseline policies (including “Even”, “Adaptive”, and single-agent SARSA) measured by both QoE and fairness. Our algorithm improves QoE by $15.27\%$ and fairness by $22.47\%$ for the 2000 KB/s link data link. Further, it is able to adapt well in collaboration with the existing Adaptive Bitrate (ABR) streaming algorithm by improving the QoE by more than $30\%$ over the adaptive algorithm. The interaction between the bandwidth distribution and ABR policies could be considered in future work to further improve the performance of video streaming. Another interesting future work is to perform large-scale experiments with network scale users.