Quantum Computing Approaches for Mission Covering Optimization
Abstract
:1. Introduction
1.1. Quantum Solutions to MCO
1.1.1. Quantum Annealing (QA)
1.1.2. Quantum Alternating Operator Ansatz (QAOA)
1.1.3. Quantum Alternating Operator Ansatz with Constraint Hamiltonian (QAOAH)
1.2. Paper Outline
2. Formalism for Mission Covering Optimization
- is the set of missions,
- is the set of resources,
- is the set of qualifications,
- is the capability function,
- is the mission’s requirements function,
- is the resource’s requirements function,
- is the objective function that scores problem solutions.
2.1. Missions
2.2. Resources
2.3. Qualifications
2.4. Capabilities
2.5. Mission’s Requirements
2.6. Resource’s Requirements
2.7. Solutions and Solution Score
3. MCO Scenarios
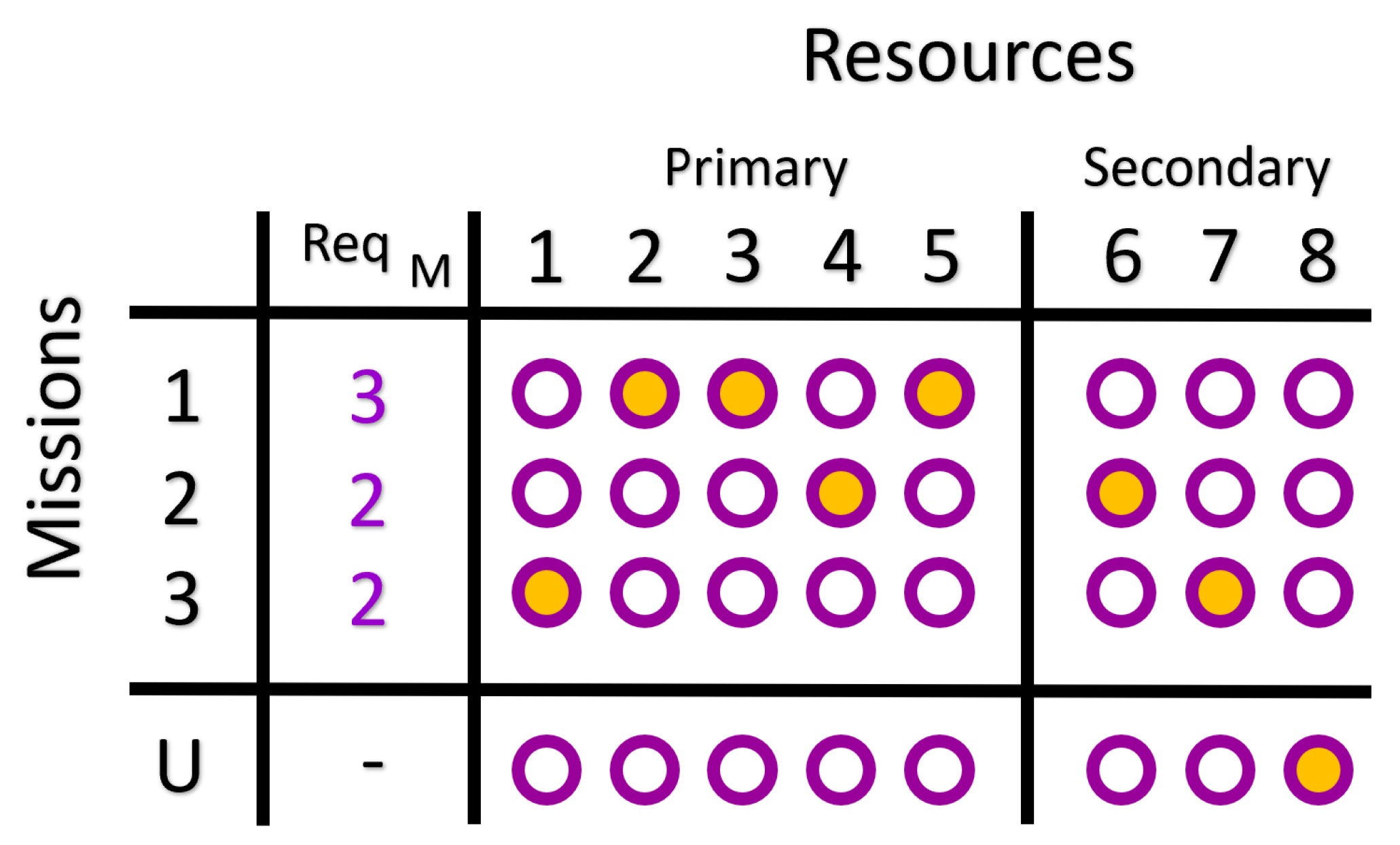
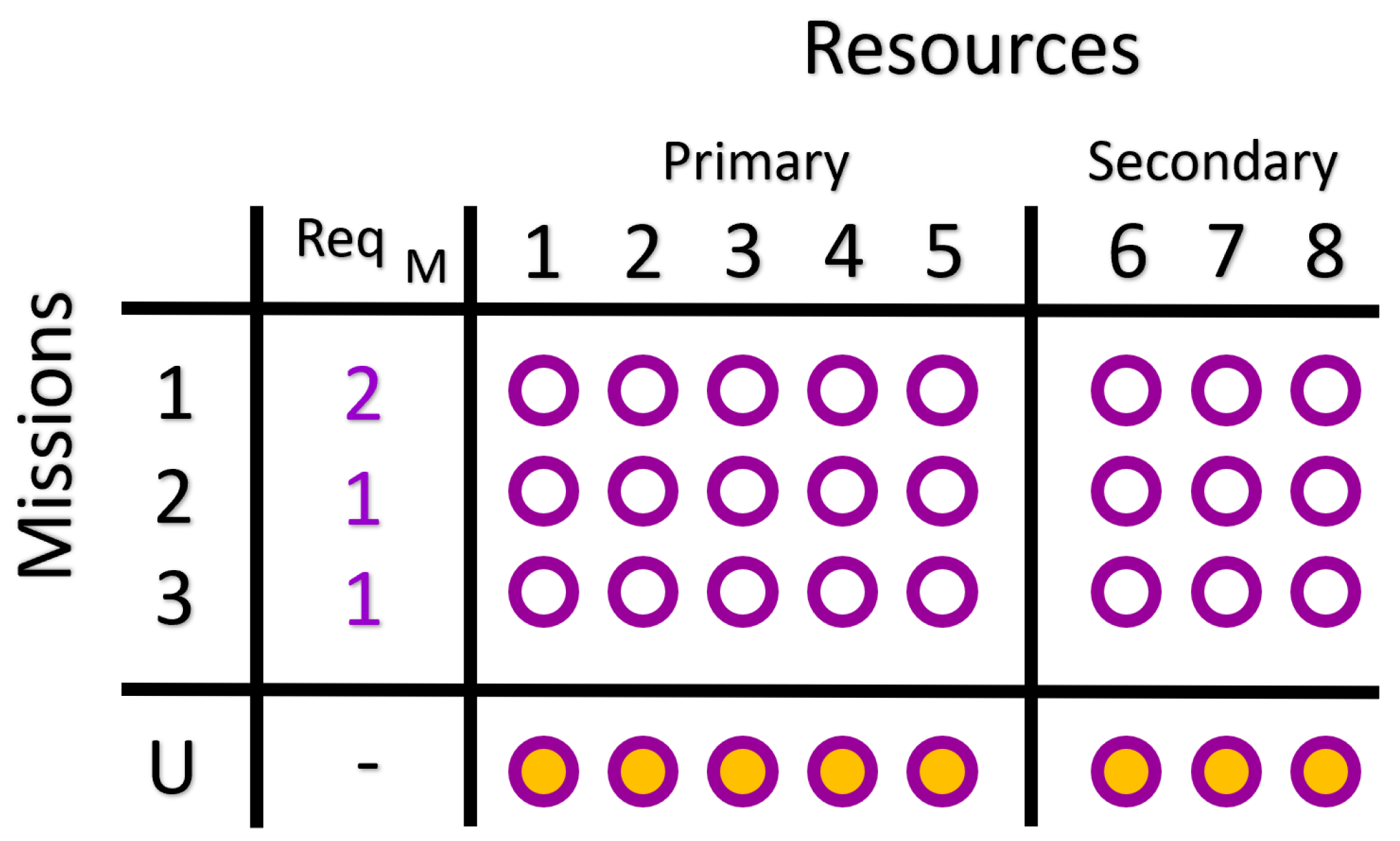
3.1. Scenario 1: Primary and Secondary Resources
- The set of missions in the problem is .
- The set of resources is .
- There only exists one qualification, which is the ability to fly a plane, .
- Resources can have a capability of 1 or 2. Therefore, the capability function is then . This is a way to represent how ready the resource is to be allocated to a mission. It can be thought of as an ordering for the allocation of resources; resources with capability 2 should be allocated before ones with 1. Resources that have capability 2 are referred to as primary resources, which are assigned to missions first. Resources that have capability 1 are referred to as secondary resources, which are assigned to missions only if primary resources become unavailable.
- is the mission’s requirement. For example:
- .
- .
- .
- There are no resource requirements. Therefore, the resource requirement function is
- is the function used to score the different problem solutions in terms of cost The mission cost includes two parts:
- The mission cost represents how many of the mission’s requirements are not met. It is a penalty introduced every time a mission is not able to accomplish its goal due to a lack of resources.
- The precedence cost measures how well each solution allocates resources with higher capabilities before others to missions. In the specific example, it means that it is desirable that primary pilots are allocated to missions before secondary pilots.
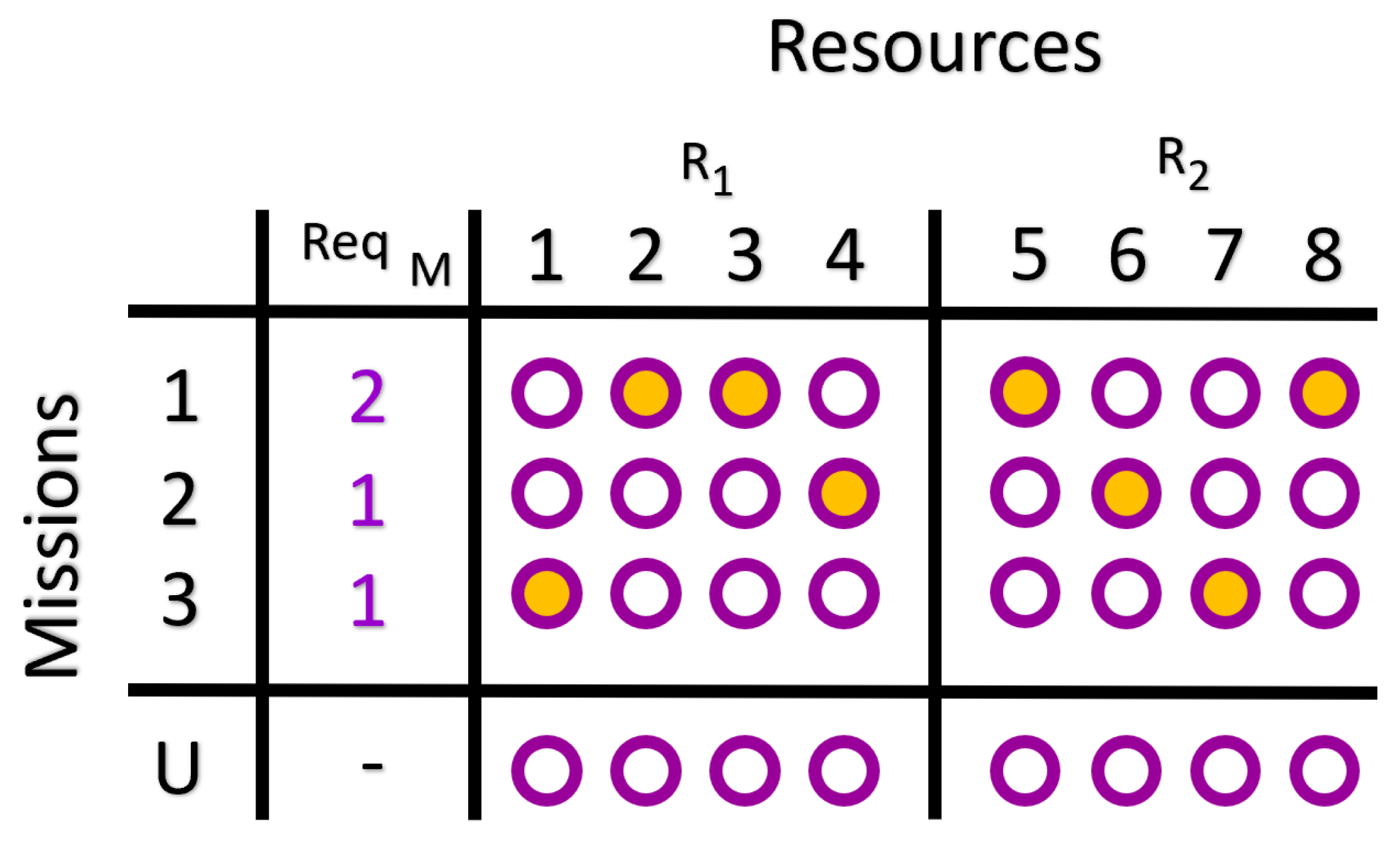
3.2. Scenario 2: The Buddy System
- Column constraint: a resource can be assigned at most to one mission. This is the hard constraint of the problem.
- Row constraint: if a type of resource is chosen, then a resource of the second type must also be chosen. We call it the buddy constraint. This is the additional constraint added in this scenario.
- The set of missions in the problem is .
- The set of resources is .
- There are two qualifications , which means that resources are divided in two groups: and .
- Resource’s capability is , which means that all resources that are qualified have the same capability. Resources have only one qualification:
- The set of all resources that have capability 1 for qualification is notated as .
- The set of all resources that have capability 1 for qualification is notated as .
- The sets and do not contain the same resource: .
- The sets and contain all resources: .
- The number of resources in and is the same .
- Missions require resources with qualification and not . Therefore, the mission require function can be formally described as: .
- The resource’s requirement is called the buddy requirement. Every resource when allocated requires another resource with the opposite qualification.
- As in the previous scenario, the objective function measures the total mission cost.
4. Algorithm Implementation
- Quantum Annealing (QA) [21]
- Quantum Alternating Operator Ansatz (QAOA) [17]. It implements constraints by means of a Lagrange multiplier embedded into a cost function Hamiltonian.
- QAOAH, which is a version of QAOA with a constrained mixer. It is denoted as QAOAH as it was developed by Hadfield et al. [20]. It engineers the constraints to remain within a constraint space during the entire solution process.
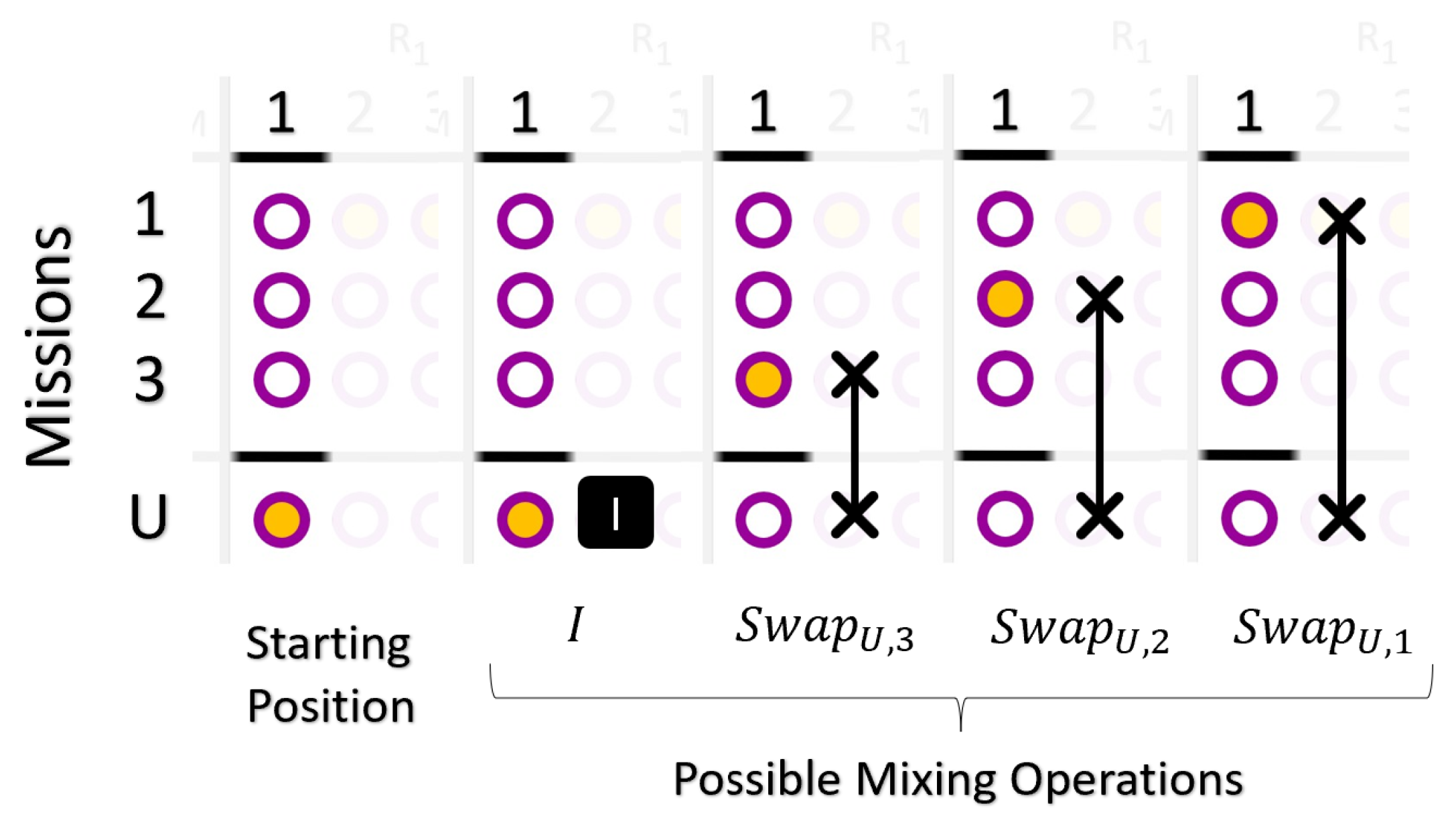
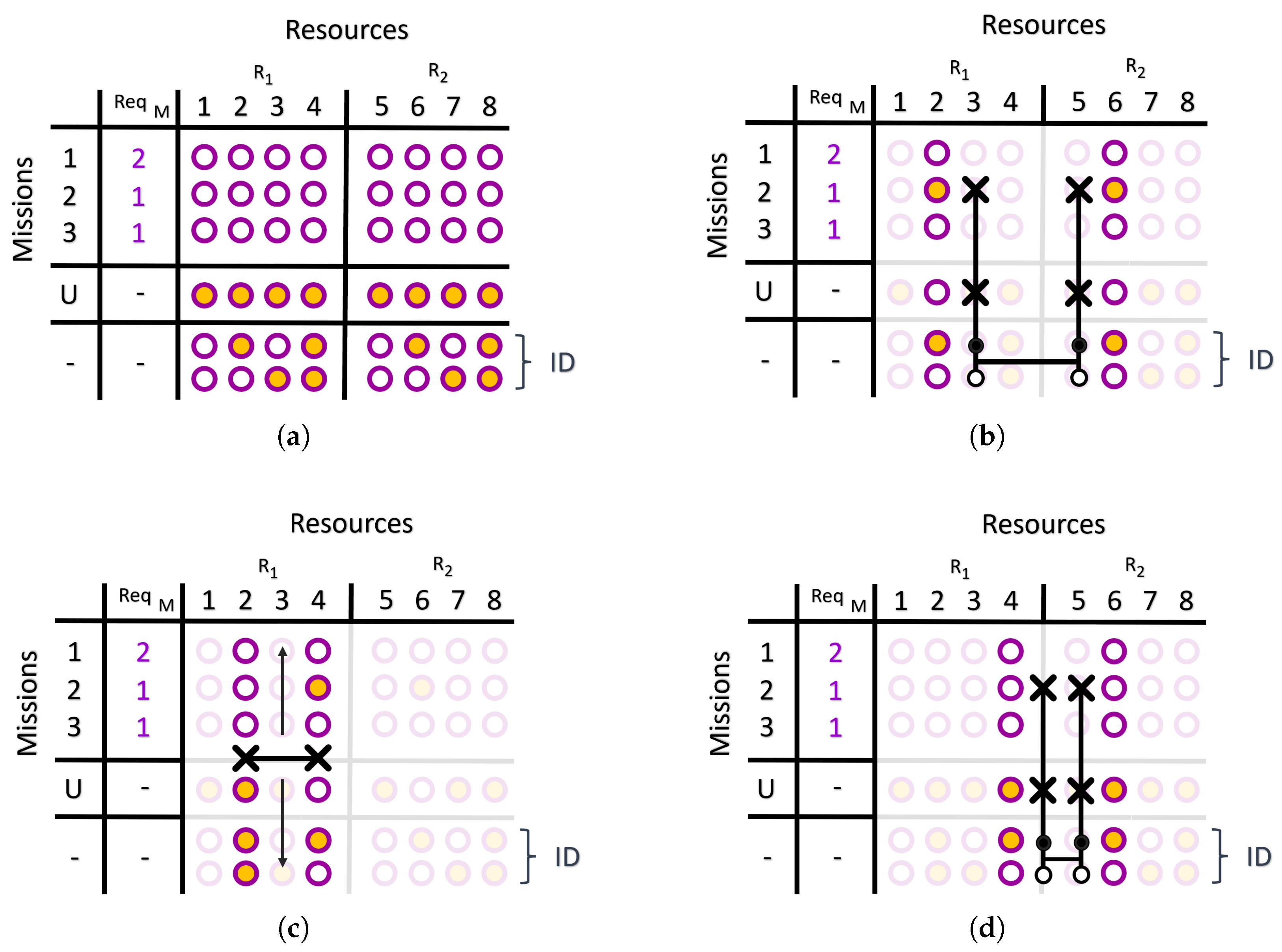
4.1. Scenario 1 (One Constraint)
4.1.1. QA and QAOA
4.1.2. QAOAH
4.2. Scenario 2 (Two Constraints)
4.2.1. QA and QAOA
4.2.2. QAOAH
- If a mixing operator allowed a resource in to move from an unallocated state to an allocated state by pairing it with a mission, then it must also move a resource from to the same mission.
- The mixing operator must operate such that it is possible after multiple applications to visit every classical state from the starting quantum state. These two obstacles require a slightly different mixing operator and more qubits.
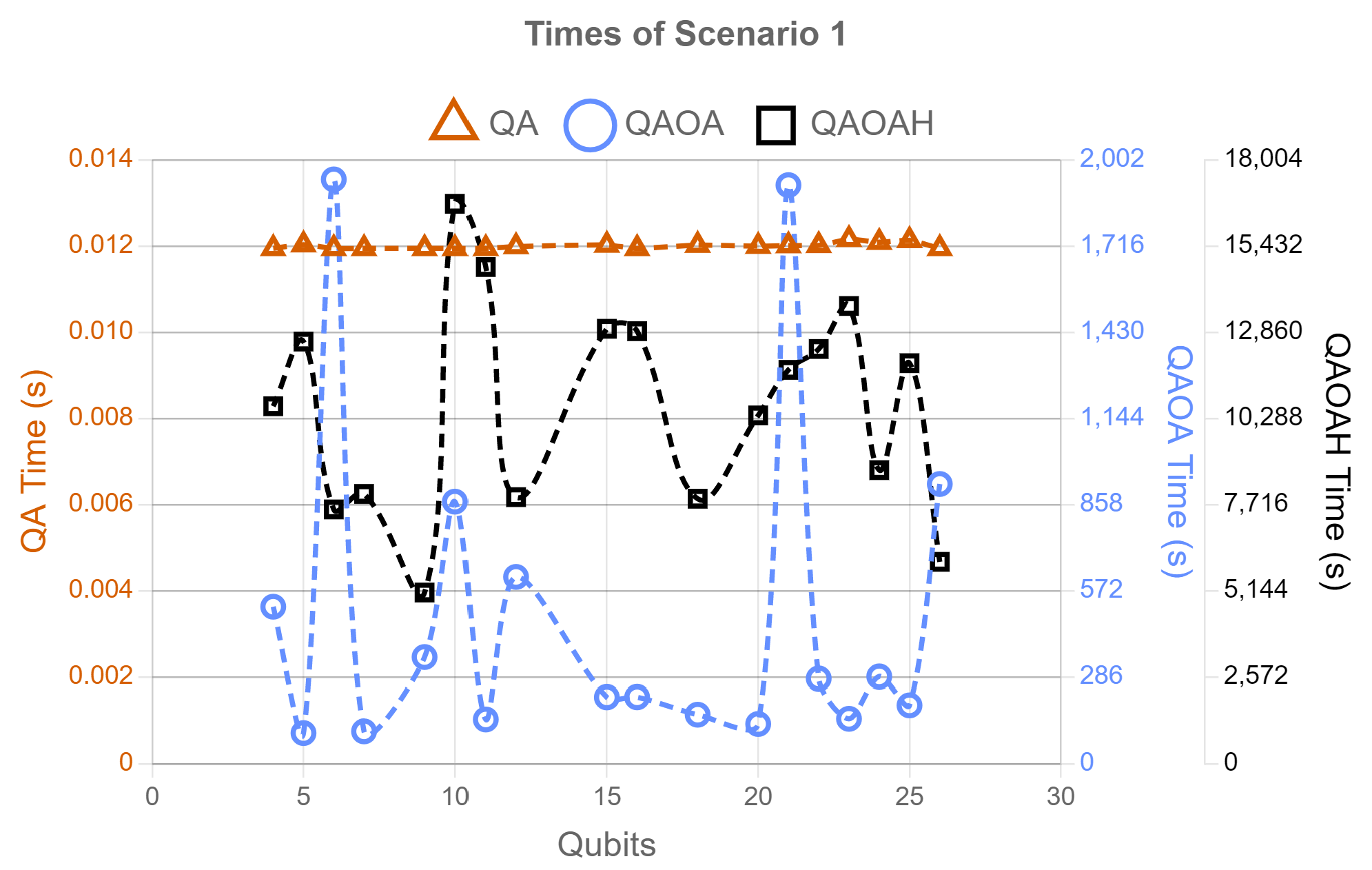
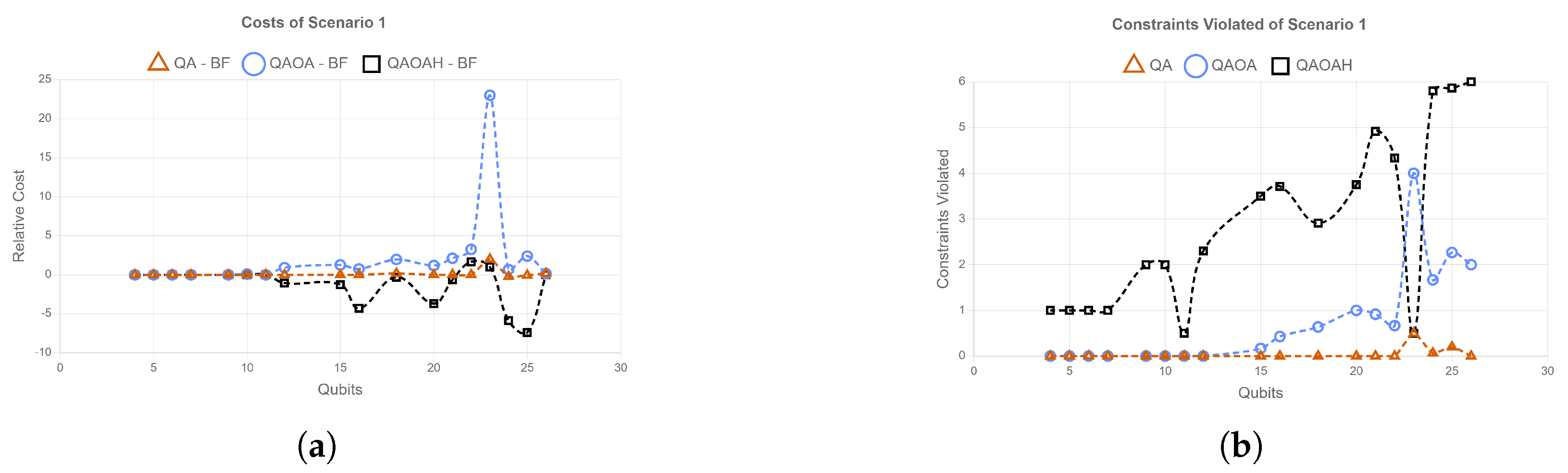
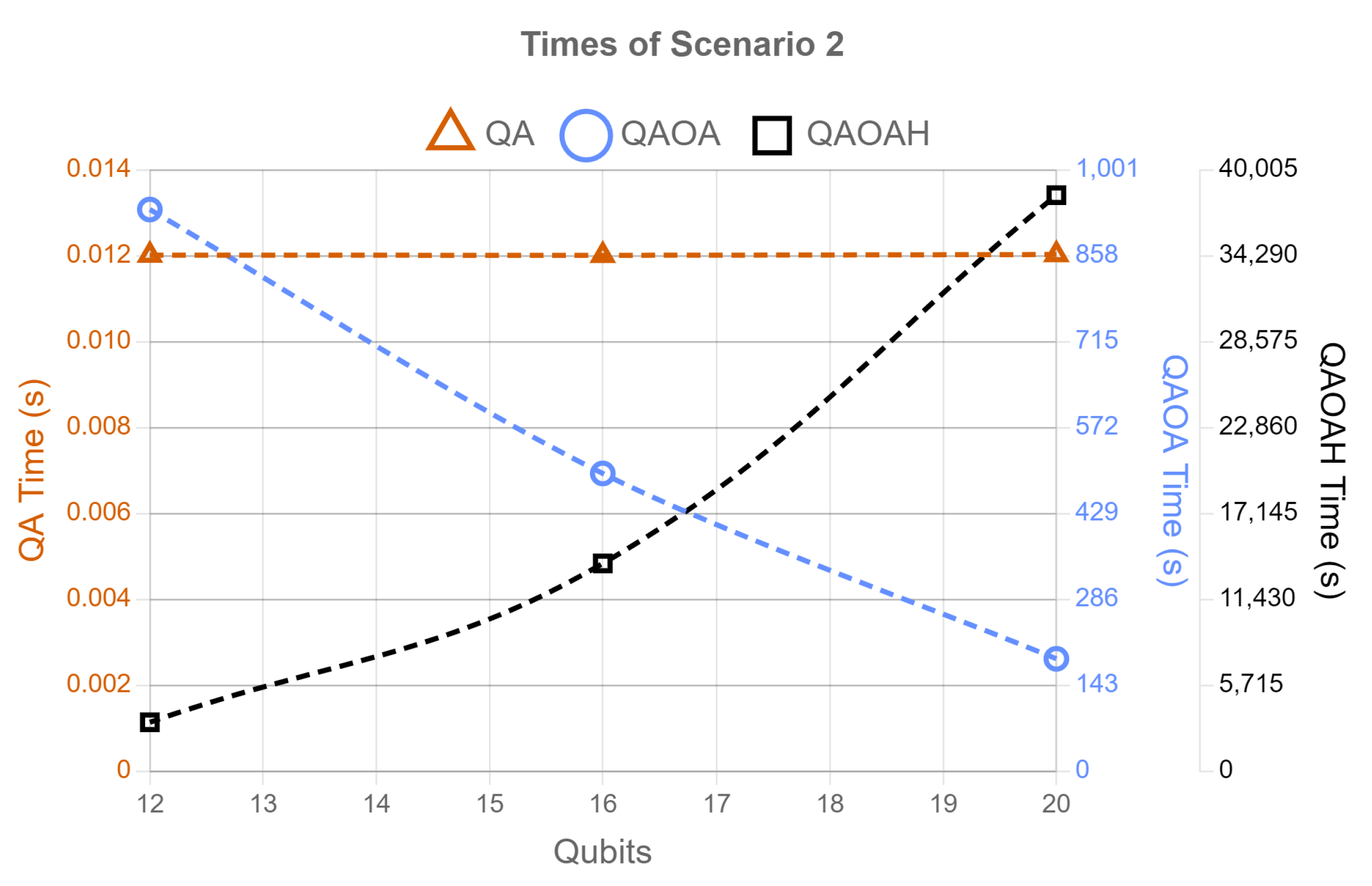
5. Analyses of Results
- Number of qubits,
- Quantum processor time,
- Cost,
- Number of constraints violated.
5.1. Scenario 1
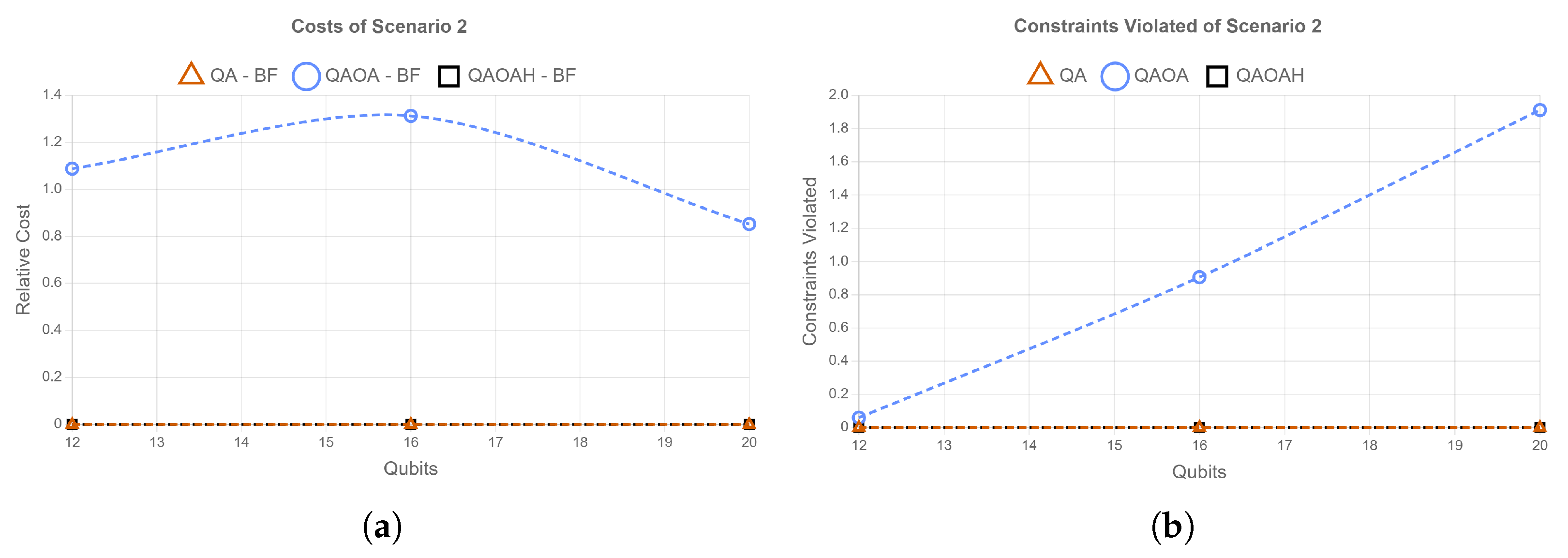
5.2. Scenario 2
6. Summary and Conclusions
7. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- de Leon, N.P.; Itoh, K.M.; Kim, D.; Mehta, K.K.; Northup, T.E.; Paik, H.; Palmer, B.; Samarth, N.; Sangtawesin, S.; Steuerman, D. Materials Challenges and Opportunities for Quantum Computing Hardware. Science 2021, 372, eabb2823. [Google Scholar] [CrossRef]
- Weidenfeller, J.; Valor, L.C.; Gacon, J.; Tornow, C.; Bello, L.; Woerner, S.; Egger, D.J. Scaling of the Quantum Approximate Optimization Algorithm on Superconducting Qubit based Hardware. arXiv 2022, arXiv:2202.03459. [Google Scholar]
- Bhaskar, M.K.; Hadfield, S.; Papageorgiou, A.; Petras, I. Quantum Algorithms and Circuits for Scientific Computing. Quantum Inf. Comput. 2021, 16, 197–236. [Google Scholar] [CrossRef]
- Andersson, M.P.; Jones, M.N.; Mikkelsen, K.V.; You, F.; Mansouri, S.S. Quantum Computing for Chemical and Biomolecular Product Design. Curr. Opin. Chem. Eng. 2022, 36, 100754. [Google Scholar] [CrossRef]
- Gao, P.; Perkowski, M.; Li, Y.; Song, X. Novel Quantum Algorithms to Minimize Switching Functions Based on Graph Partitions. Comput. Mater. Contin. 2022, 70, 4545–4561. [Google Scholar] [CrossRef]
- Phillipson, F.; Chiscop, I. ultimodal Container Planning: A QUBO Formulation and Implementation on a Quantum Annealer. In InInternational Conference on Computational Science 2021; Springer: Cham, Switzerland, 2021; pp. 30–44. [Google Scholar]
- Çaliş, B.; Bulkan, S. A research survey: Review of AI solution strategies of job shop scheduling problem. J. Intell. Manuf. 2013, 26, 961–973. [Google Scholar] [CrossRef]
- Venturelli, D.; Marchand, D.J.J.; Rojo, G.H. Job Shop Scheduling Solver Based on Quantum Annealing; Association for the Advancement of Artificial Intelligence Constraint Satisfaction techniques for planning and Scheduling (COPLAS): London, UK, 2016. [Google Scholar]
- Özbakira, L.; Baykasoğlu, A.; Tapkan, P. Bees Algorithm for Generalized Assignment Problem. Appl. Math. Comput. 2010, 215, 3782–3795. [Google Scholar] [CrossRef]
- Öncan, T. A Survey of the Generalized Assignment Problem and Its Applications. Inf. Syst. Oper. Res. 2007, 45, 123–141. [Google Scholar] [CrossRef]
- Yu, Y.; Argüello, M.; Song, G.; McCowan, S.M.; White, A. A New Era for Crew Recovery at Continental Airlines. Interfaces 2003, 33, 5–22. [Google Scholar] [CrossRef]
- Schnore, G. Quantum Annealing for Asset Sustainment. 2019. Available online: https://www.dwavesys.com/media/prsl42qn/ge-research-asset-sustainment-2019-qubits-europe_0.pdf (accessed on 31 March 2022).
- Ng, X.W. Complex Optimization Problems. In Concise Guide to Optimization Models and Methods: A Problem-Based Test Prep for Students; Springer: Cham, Switzerland, 2022; pp. 69–120. [Google Scholar]
- Das, A.; Chakrabarti, B.K. Quantum Annealing and Related Optimization Methods; Springer: Cham, Switzerland, 2005. [Google Scholar]
- Kochenberger, G.; Hao, J.K. The Unconstrained Binary Quadratic Programming Problem: A Survey. J. Comb. Optim. 2014, 28, 58–81. [Google Scholar] [CrossRef] [Green Version]
- Glover, F.; Kochenberger, G. A Tutorial on Formulating and Using QUBO Models. arXiv 2019, arXiv:1811.11538. [Google Scholar]
- Farhi, E.; Goldstone, J.; Gutmann, S. A Quantum Approximate Optimization Algorithm. arXiv 2019, arXiv:1411.4028. [Google Scholar]
- Community, T.J.B. Solving Combinatorial Optimization Problems Using QAOA. Available online: https://qiskit.org/textbook/ch-applications/qaoa.html (accessed on 7 June 2022).
- Hen, I.; Spedalieri, F.M. Quantum Annealing for Constrained Optimization. Phys. Rev. Appl. 2016, 5, 034007. [Google Scholar] [CrossRef] [Green Version]
- Hadfield, S.; Wang, Z.; O’Gorman, B.; Rieffel, E.G.; Biswas, R.; Venturelli, D. From the Quantum Approximate Optimization Algorithm to a Quantum Alternating Operator Ansatz. Algorithms 2019, 12, 34. [Google Scholar] [CrossRef] [Green Version]
- Kadowaki, T.; Nishimori, H. Quantum Annealing in the Transverse Ising model. Phys. Rev. E 1998, 58, 5355. [Google Scholar] [CrossRef] [Green Version]
- Streif, M.; Leib, M.; Wudarski, F.; Rieffel, E.; Wang, Z. Quantum Algorithms with Local Particle-Number Conservation: Noise effects and Error Correction. Phys. Rev. A 2021, 103, 042412. [Google Scholar] [CrossRef]
- Gilliam, A.; Woerner, S.; Gonciulea, C. Grover Adaptive Search for Constrained Polynomial Binary Optimization. Quantum 2021, 5, 428. [Google Scholar] [CrossRef]
- Amaro, D.; Modica, C.; Rosenkranz, M.; Fiorentini, M.; Benedetti1, M.; Lubasch, M. Filtering Variational Quantum Algorithms for Combinatorial optimization. Quantum Sci. Technol. 2022, 7, 015021. [Google Scholar] [CrossRef]
- Bapat, A.; Jordan, S. Bang-bang Control as a Design Principle for Classical and Quantum Optimization Algorithms. Quantum Inf. Comput. 2019, 19, 424–446. [Google Scholar] [CrossRef]
| Results | Execution Environment | Average Violated Constraints | ||||
|---|---|---|---|---|---|---|
| Machine | D-Wave | IBMQ | D-Wave | IBMQ | ||
| Algorithm | QA | QAOA | QAOAH | QA | QAOA | QAOAH |
| S1 Hardware | ✓ | ✓ | ✓ | 0.05 | 0.97 | 3.89 |
| S1 Simulation | - | - | - | - | - | - |
| S2 Hardware | ✓ | ✓ | - | 0.0 | 0.96 | - |
| S2 Simulation | - | - | ✓ | - | - | 0.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cutugno, M.; Giani, A.; Alsing, P.M.; Wessing, L.; Schnore, A. Quantum Computing Approaches for Mission Covering Optimization. Algorithms 2022, 15, 224. https://doi.org/10.3390/a15070224
Cutugno M, Giani A, Alsing PM, Wessing L, Schnore A. Quantum Computing Approaches for Mission Covering Optimization. Algorithms. 2022; 15(7):224. https://doi.org/10.3390/a15070224
Chicago/Turabian StyleCutugno, Massimiliano, Annarita Giani, Paul M. Alsing, Laura Wessing, and Austar Schnore. 2022. "Quantum Computing Approaches for Mission Covering Optimization" Algorithms 15, no. 7: 224. https://doi.org/10.3390/a15070224
APA StyleCutugno, M., Giani, A., Alsing, P. M., Wessing, L., & Schnore, A. (2022). Quantum Computing Approaches for Mission Covering Optimization. Algorithms, 15(7), 224. https://doi.org/10.3390/a15070224







