Abstract
The Jump Point Search (JPS) algorithm ignores the possibility of any-angle walking, so the paths found by the JPS algorithm under the discrete grid map still have a gap with the real paths. To address the above problems, this paper improves the path optimization strategy of the JPS algorithm by combining the viewable angle of the Angle-Propagation Theta* (AP Theta*) algorithm, and it proposes the AP-JPS algorithm based on an any-angle pathfinding strategy. First, based on the JPS algorithm, this paper proposes a vision triangle judgment method to optimize the generated path by selecting the successor search point. Secondly, the idea of the node viewable angle in the AP Theta* algorithm is introduced to modify the line of sight (LOS) reachability detection between two nodes. Finally, the paths are optimized using a seventh-order polynomial based on minimum snap, so that the AP-JPS algorithm generates paths that better match the actual robot motion. The feasibility and effectiveness of this method are proved by simulation experiments and comparison with other algorithms. The results show that the path planning algorithm in this paper obtains paths with good smoothness in environments with different obstacle densities and different map sizes. In the algorithm comparison experiments, it can be seen that the AP-JPS algorithm reduces the path by 1.61–4.68% and the total turning angle of the path by 58.71–84.67% compared with the JPS algorithm. The AP-JPS algorithm reduces the computing time by 98.59–99.22% compared with the AP-Theta* algorithm.
1. Introduction
1.1. Research Background
Initially, the use of mobile robots was limited to manufacturing. However, with the development of technology and innovation, mobile robots are now commonly used in various industries such as medical [1], mining, rescue, military, education, agriculture [2] and service industries [3].
From the perspective of mobile robots, the real point is to move from a designed starting point to another target point and the need to smoothly avoid obstacles in a path-optimal manner [4]. Therefore, the navigation of mobile robots is crucial for mobile robots [5]. Sarif and Buniyamin pointed out that path planning is the main problem of mobile robots and an important component of navigation [6]. The result of path planning will intuitively have an impact on how well the robot completes the task in real time and how well the result is achieved.
From the present point of view, path planning algorithms are favored by many researchers with the rise of mobile robots, UAVs [7,8,9], the unmanned field [10,11], and the video game field [12]. However, the study of path planning for mobile robots, especially the trajectory optimization of generated paths, remains a great challenge. For example, Figure 1 shows a robot and its target location. The solid path is a path consisting of straight lines and sharp turns at points A, B, C, and D. It is also the path generated for the discrete map state due to the fixed pathfinding direction. This path is not ideal for the movement of a mobile robot. First, mobile robots cannot make sudden sharp turns and need to slow down. For example, for driverless cars, sudden turns between path nodes and discontinuities in speed and acceleration are very dangerous behaviors for passengers [13,14]. For intelligent wheelchair robots, there are interruptions and sharp turns among the paths, which may cause secondary injuries for the patient [15,16]. Second, fixing the robot’s search direction is not suitable for finding the shortest or optimal path, which makes many possible paths in the map ignored by the robot. As shown by the dashed line in Figure 1, a shorter path means higher efficiency and less energy consumption while ensuring the safety of the mobile robot. For example, in unmanned warehousing as well as in the workshop transportation process, the efficiency of the transport robot will directly affect the overall operational efficiency of the warehouse and workshop [17].
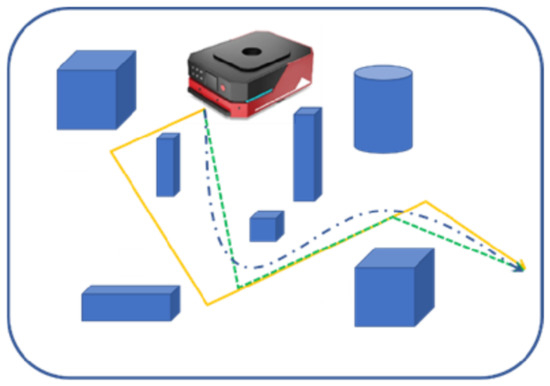
Figure 1.
Non-smooth path for mobile robots.
To solve these problems, any-angle path planning [18] and path smoothing techniques [19] need to be introduced. Path smoothing is an important issue in path finding for mobile robots. Smooth paths need to satisfy the constraints of continuity such as path position, robot movement speed, and acceleration. At the same time, in order to ensure that the mobile robot finds the shortest path in the path finding process, the any-angle path planning is needed to no longer restrict the search direction of the mobile robot.
1.2. Related Work
Path planning for mobile robots is actually the selection of a shortest obstacle avoidance path in the task area that can be connected from the starting point to the end point. The essence of this is the problem of optimal solution of the path [20]. The path planning should fully take into account the feasibility constraints that arise during the practical application of the robot [21]. More precisely, the path generated by the path planning algorithm of the mobile robot should satisfy the shortest and most efficient path with continuous and smooth transition of the path node states (position, velocity, acceleration and other information).
Various path optimization methods have been developed in previous studies. Among the most intuitive methods for path smoothness optimization are Bessel curves [22] and B spline curve optimization [23]. This approach allows curve fitting using trajectory control points in the path generation phase to achieve path smoothing. Usually, the initial number of control points obtained by the global path planning algorithm is low fitting, and the fitted paths are prone to re-collide with obstacles. To increase the curve fit, the path control points are usually added. However, a single increase in the number of control points can lead to a significant decrease in the efficiency of the algorithm [24]. In the paper [13], a polynomial interpolation-based method is proposed to improve the continuity problem in the automatic parking process. Polynomial interpolation is a simple functional approach [25]. This method is solved by finding a polynomial containing all path nodes and adding continuity constraints for node positions, velocities, accelerations, etc. In addition, the polynomial interpolation method can be used to construct a Safe Flight Corridor (SFC) by generating collision avoidance linear constraints using the convex packet property of Bernstein polynomials as a further solution to the safety of mobile robots during operation [26].
The JPS method using heuristic search methods has been proposed in recent years driven by the efficiency of path planning for mobile robots. The classical JPS algorithm is built on the basis of the evaluation function of the A* algorithm, which improves the search efficiency of the A* algorithm by ignoring useless nodes and retaining only key nodes, thus greatly reducing the time consumption in the search process [27]. However, on the other hand, the JPS algorithm still cannot escape the limitation of the search direction imposed by the discretized grid map [28]. When planning a grid map, JPS usually plans from the center of each grid cell and only allows transitions to the center of adjacent grid cells. This will cause the JPS algorithm path direction variation to be limited to a multiple of , resulting in a suboptimal path, as shown in Figure 2.
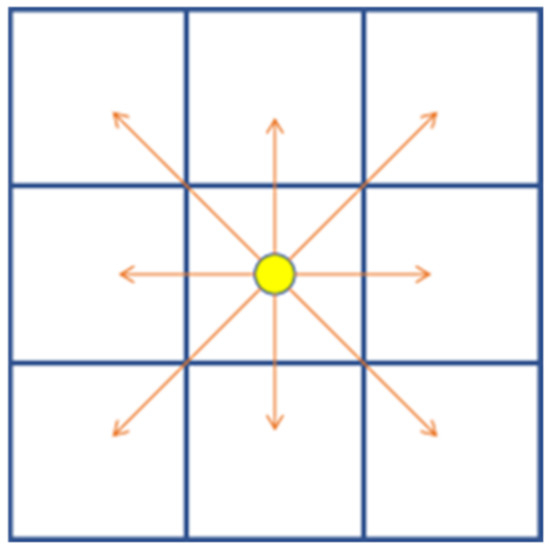
Figure 2.
Limitations of search angle.
The article [29] proposes an improved version of Field D* based on the D* algorithm. The algorithm generates smoother paths by linearly interpolating the grid so that the path points are not limited to endpoints and the planning direction is no longer limited to integer multiples of . However, from the experimental results of the Field D* algorithm, the paths are not optimal, and there are still optimizable sections in the overall path. The Theta* family of algorithms is a good choice, where the Basic Theta* and AP-Theta* algorithms avoid the limitation of the angular direction of the search by passing information along the edges of the grid during the pathfinding process [30]. Among them, the AP-Theta* algorithm further solves the problem of insufficient operational efficiency of the Basic Theta* algorithm through the propagation of angular information. However, since the Theta* family of algorithms is designed based on the A* algorithm framework [31], it still suffers from the A* algorithm in terms of operational efficiency.
Some of the problems in the commonly used path planning algorithms, path smoothing techniques and any-angle path planning techniques for mobile robots are shown in Table 1.

Table 1.
Map information selected for the dataset.
Based on the above problems, an AP-JPS algorithm is proposed in this paper based on the JPS algorithm. The AP-JPS algorithm uses the any-angle path planning rule in AP-Theta* to improve the drawback that the original JPS algorithm cannot be multi-angle pathfinding. Meanwhile, this paper uses a seven-segment polynomial optimization method based on minimum snap, incorporating flight corridor inequality constraints, so that the smoothness and continuity of the resultant path generated by the AP-JPS algorithm can be guaranteed while satisfying safety. For the overall structure of the article, first, this paper proposes a vision triangle judgment to optimize the generation path of JPS by selecting inherited search points. Second, the LOS reachability detection between two nodes of the generated path is modified using the viewable angle in the AP Theta* algorithm. Finally, the paths are optimized for smoothness using a seventh-order polynomial based on minimum snap.
2. JPS Algorithm
The JPS algorithm is a pathfinding algorithm that uses pruned neighbor rules as the search direction of nodes and the position of forced neighbors as the judgment of jump points. The JPS algorithm extends the jump points by iterative computation and by selecting the least costly node among the candidate jump points as the subsequent path. The JPS algorithm’s method of determining the current jump point x consists of the following three parts:
- If node is a start point or a target point, then node is a jump point.
- If node has at least one forced neighbor, then node is a jump point.
- If the search direction from the parent node of node to is diagonal and there is a point in the horizontal or vertical direction of that satisfies condition 1 and 2, then is a jump point.
JPS Algorithm for Pruned Neighbor Rule and Forced Neighbors
In the JPS algorithm, the neighboring nodes in each direction need to be considered when searching from the starting node. When the JPS algorithm determines a specific search direction, it expands in that direction and does not need to calculate the generation value of nodes in that direction until it meets an obstacle or jump point. If a path is blocked, all nodes along that direction will be pruned without further consideration.
While JPS is extending a path in a particular direction, it identifies a set of natural neighbors for a node under evaluation. When the extension direction is a straight line, the natural neighbor of the current point is defined as the next node in the same direction. That is, JPS will continue to search along the direction of the current natural neighbor. When the extension direction is diagonal, the natural neighbors of the current point include three nodes, which are the next node along the extension diagonal, and the next vertical and horizontal nodes in the extension direction, as shown in Figure 3a,b. That is, JPS will start expanding in the direction of vertical and horizontal natural neighbors first until they are blocked or jump points are found before considering the search in the diagonal direction.
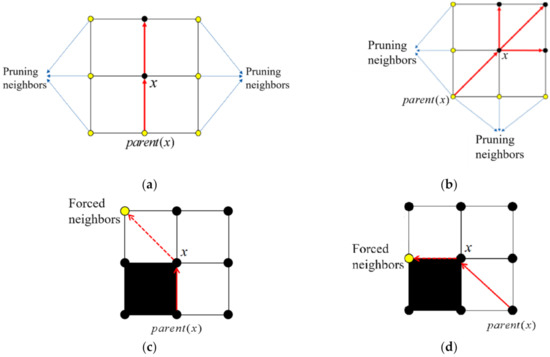
Figure 3.
JPS algorithm for natural neighbors and forced neighbors. (a) pruning rule of JPS algorithm, (b) pruning rule of JPS algorithm, (c) the way to determine the forced neighbor nodes, (d) the way to determine the forced neighbor nodes.
In the JPS algorithm, the current node has obstacles among its eight neighbors, and is a non-obstacle, non-search direction neighbor node of the current node. Then, the distance cost of ’s parent node to reach n through is smaller than the distance cost of any path to reach without going through . Then, is said to be a forced neighbor of . If the current node is found to have forced neighbors, the node is identified as a jump point, and the expansion in the direction of forced neighbors must be considered, as shown in Figure 3c,d.
3. JPS Path Optimization Based on Angle-Propagation Theta* Algorithm
As shown in Figure 3, the JPS algorithm differs from the A* algorithm in the way it selects successor nodes, and the jump search method can avoid the calculation of a large number of redundant nodes in the A* algorithm. The JPS algorithm is undoubtedly an excellent path planning algorithm. However, because the search direction of the JPS algorithm is fixed in the pathfinding process, this will cause the JPS algorithm to miss some important path turning points in the search process, resulting in the JPS algorithm’s result path and the shortest realistic path still exists. A common optimization method is the LOS optimization method. The LOS optimization method can only eliminate the redundant points on the path in some cases, while it cannot obtain the judgment due to the existence of obstacles between two nodes, as shown in Figure 4.
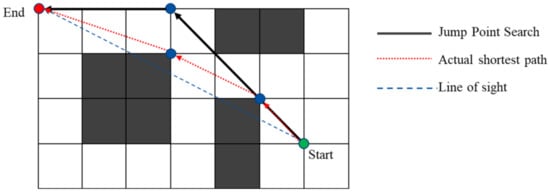
Figure 4.
Unoptimized case based on line of sight.
Based on the disadvantages of the LOS optimization method, this paper proposes a vision triangle judgment rule and introduces the Angle-Propagation Theta* algorithm of the viewable angle for further optimization of the above problem.
3.1. The Method of Judging the Field of Vision Triangle
This paper propose a vision triangle to determine whether there are possible turning points in the path within the coverage of this triangle and compare the generation value (the actual path length between two nodes) between all possible turning points and the current search point in order to select the optimal turning point.
As shown in Figure 3, first, all the passing nodes on the JPS result path are discretized and put into a list, which is called . Next, we need to set the path starting node as the first search node and determine the LOS reachability of the search nodes one by one according to the order of the nodes stored in until we find the first node that does not have reachability. Here, the LOS reachability of two nodes is expressed, as the two nodes can be reached through a straight line between them with no obstacle in the intermediate path.
This method uses the flag to denote the first node that does not have LOS reachability to the search point and the flag to denote the previous node of this node. LOS reachability detection is generally accomplished using the Bresenham’s line algorithm [36], and in subsequent work, LOS reachability detection will be replaced by the viewable angle of the AP Theta* algorithm. Finally, call the triangle formed by , and the search point the field of vision triangle. In the view triangle, all contained obstacle vertices (possible turning points of the path) are detected, their generation value to the search point is calculated, and the obstacle vertex with the smallest generation value is selected as the optimal turning point of the path and the next search point.
The process of how to find the optimal turning point (successor search point) among the view triangles is illustrated in Figure 5. The dots represent the path discrete points and the information of the points present in the list. The triangle nodes represent optimal turning points and successor search points.
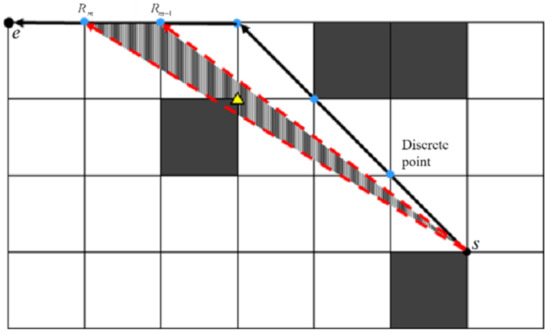
Figure 5.
Unoptimized case based on line of sight.
3.2. Angle-Propagation Theta* Algorithm
In this paper, based on the LOS reachability detection between two nodes proposed in the above optimization process, the Angle-Propagation Theta* algorithm is introduced to determine whether there is LOS reachability between two nodes by calculating the viewable range of the nodes in the section to be optimized. As shown in Figure 6, AP Theta* calculates the viewable angle range when expanding outward from a grid and determines whether the new node is reachable based on whether the angle at which it is located is included in the viewable angle range. Because the time to compute the angle is essentially constant, the consumption of AP Theta* in scaling is not linearly related to the number of grids, and the optimization efficiency of the JPS shortest path is further improved.
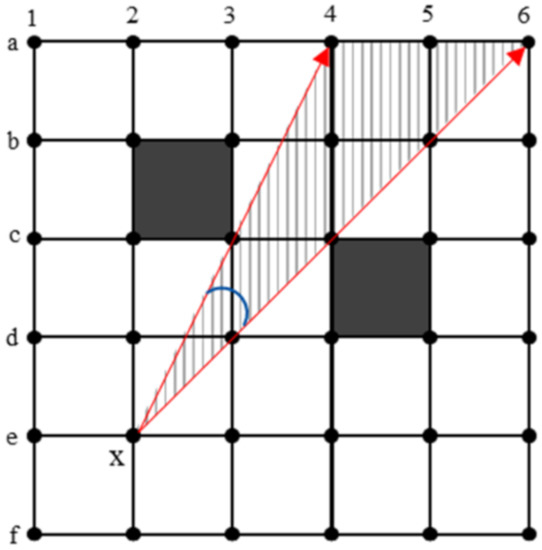
Figure 6.
Visual angle of x node in AP theta*.
3.2.1. Definition of Angle-Propagation Theta* Algorithm Viewable Angle
In the AP Theta* algorithm, any node has two variables that represent the viewable angle, namely the upper angle region and the lower angle region . The viewable angle of the node is denoted as . The meaning of is the visible range angle of from to from the parent node of the current node , and the ray angle of to reach is 0.
For the neighbor node ’ of the current node , if the angle between the ray arriving at ’ from and the ray arriving at from is in the range , it means that ’ must be LOS reachable with , as shown in Figure 7.
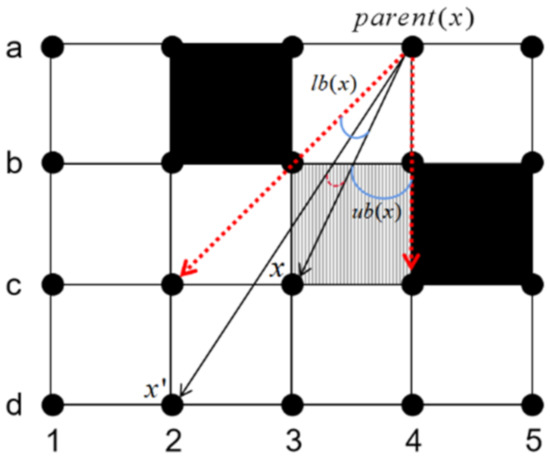
Figure 7.
The viewable angle range of node .
3.2.2. AP-Theta* Algorithm for Visual Angle Constraint
The AP Theta* algorithm sets the viewable angle of the current node to when expanding from the current node to other nodes, and then, it constrains and by the viewable angle constraints. We set the current node as , the parent of the current node as , the path start point as , and the end point as . The specific constraints are as follows:
- If the current node is a vertex of the obstacle grid and all other vertices of the current obstacle grid satisfy one of the following conditions, the lower angle region of the current node’s viewable angle area is equal to 0.If the current node is a vertex of the obstacle grid and all other vertices of the current obstacle grid satisfy one of the following conditions, the upper angle region of the current node’s viewable angle area is equal to 0.
- For a neighbor node ′ of the current node , if satisfies all of the following conditions.
If is satisfied between node and node , then:
If is satisfied between node and node , then:
- 3.
- For a neighbor node of the current node , if satisfies all of the following conditions.
If the viewable angle satisfies then:
If the viewable angle satisfies then:
where denotes the angle between the ray formed from to and the ray formed from to . . When the ray consisting of to is in the clockwise direction of the ray consisting of parent (x) to , then takes a positive value, and vice versa, it takes a negative value. The function represents the value of the generation between two nodes , . For example, denotes the generation value from node to node, which is the actual path length of node to node. indicates the list of nodes that have been searched.
After the angle constraint is completed, the LOS reachability of and can be determined by checking whether is satisfied when expanding from the current node to the neighboring node . The pseudo code for visual angle constraint is shown below.
| Algorithm 1: Visual Angle Constraint. |
 |
3.3. JPS Path Optimization Process with Viewable Angle Based on AP Theta *
In this paper, we improve the path optimization strategy for the JPS algorithm based on the idea of using angles to find the shortest path in the AP Theta* algorithm. The complete optimization path process is shown in the following example.
- First, the starting point (f,2) is taken as the first search point, and we judge whether there is an LOS reachable between the search point and the end point. If the LOS is reachable, the algorithm ends; if the LOS is not reachable, the path is discretized and loaded into the list. Set the child node (e,3) of the start point to the current node . Then, set the viewable range of to . Next, the constraint calculation of the viewable angle of is needed to obtain its viewable angle as [0,45]. Set the (d,4) node to in the order of the nodes in the list. The LOS reachability between all discrete points and the search point is checked in turn until the first node (a,8) is found that does not have LOS reachability, as shown in Figure 8 (1).
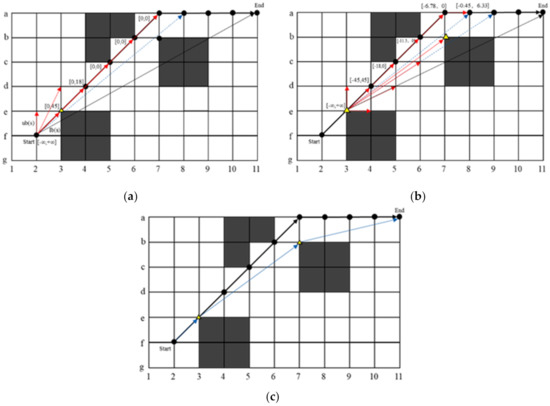 Figure 8. Example of the pathing process. (a) (e,3) is selected as the next search point, (b) (b,7) succeeds (e,3) as the next search point, (c) comparison of paths before and after optimization.
Figure 8. Example of the pathing process. (a) (e,3) is selected as the next search point, (b) (b,7) succeeds (e,3) as the next search point, (c) comparison of paths before and after optimization. - Set (a,8) to flag and (a,7) to flag . The obstacle vertices within the triangular region of the field of view consisting of , and the search points are searched. The optimal turning angle (e,3) is found by calculating and comparing the cost of each vertex to the search point, as identified by the triangle in Figure 8 (1).
- Set the node (e,3) as the next search point and its path sub-node (d,4) as the current node . Continue the search by the method provided in step 1 until the next search point is found, as shown in Figure 8 (2).
- If the current search point is found to have LOS reachable with the end of the path by detection, the search is ended, as shown in Figure 8 (3). The final generated path is (f,2), (e,3), (b,7), and (a,11).
4. Trajectory Optimization
It is well known that the fold path generated by the JPS algorithm is not conducive to the robot’s motion in real work scenarios. Therefore, this paper uses polynomials for trajectory optimization based on the AP-JPS algorithm. The derivatives of each order of the polynomial are used as the position, velocity, acceleration, jerk, and snap of the trajectory. Since it is difficult to adapt single segment polynomials to more complex scenarios, and considering the continuity of position, velocity, acceleration and rate of change of acceleration at the junction between two moving trajectories of the robot, the snap function is used as the minimization objective in this paper, and the path is smoothed using the minimum snap objective function to solve the seventh-order polynomial minimally.
4.1. Seventh-Order Polynomial Optimization Based on Minimum Snap
First, the trajectory is segmented according to the path nodes, and assuming that the path is divided into segments in total and each segment is fitted as a polynomial curve, the expression of the th segment path is shown in Equation (17).
where means the th path polynomial coefficient and means time. For the overall path, then the following expression (18) is given.
where … denote the times of the path interruption points. From Equation (19), the position, velocity, acceleration, jerk function, and snap function at any moment can be obtained by deriving the equation as shown below.
Combined with the characteristics of smooth robot moving path, this paper uses deterministic values for the position (), velocity () and acceleration () of the start and end points of the path to constrain, and it adds the position information of the middle trajectory points of the path to constrain at the same time. Finally, we construct the cost function as the integral that minimizes the snap square; the formula is shown in Equations (21) and (23) below.
where expanding it for yields the expression (22).
The constraints for polynomial optimization are shown in Equation (24).
Since the polynomial optimized trajectory has the possibility of re-collision with obstacles, this paper adds a safety corridor to the overall optimized path by establishing inequality constraints. The corridor width is set to half of the grid to ensure sufficient safety distance, and the formula is shown below.
where denotes the corridor width.
4.2. Time Allocation
The time allocation in polynomial optimization has a direct impact on the generated trajectories. In this paper, the total time is calculated based on the preset velocity and the total length of the initial trajectory generated according to the AP-JPS algorithm. In general, the allocation time of each trajectory is evenly distributed in proportion to the path length, but in order to weaken the degree of influence of the trajectory length on the allocation time and make the robot travel faster in the longer path and relatively slower in the trajectory with more inflection points to increase the safety of robot motion, the time allocation strategy used in this paper is shown in Equation (26).
where denotes the time allocated to the th trajectory, denotes the time allocation coefficient, and is the length of the th trajectory. Once the time allocation is determined, the velocity, acceleration, jerk and other parameters of the trajectory can be obtained by calculation, and if the parameters do not satisfy the constraints, the time allocated to the segment is adjusted in a fixed proportion until the constraints are satisfied.
5. Simulation
In this paper, three sets of experiments were conducted on the AP-JPS algorithm proposed in the paper and the original JPS algorithm using Matlab 2020b simulation software based on the i5-1135G7 small mobile computer.
In Experiment 1, randomized obstacle distribution experiments were conducted for maps with different sizes and different obstacle percentages, given the path start and end points.
In Experiment 2, this paper uses two 256 × 256 grid maps of part of Shanghai and part of New York City to compare the A* algorithm, RRT algorithm, AP-Theta* algorithm, JPS algorithm, AP-JPS algorithm and polynomially optimized AP-JPS algorithm.
In Experiment 3, this paper uses the datasets distributed freely from Moving AI Lab, and four groups of indoor small map (80 × 80), outdoor medium map (512 × 512) and outdoor large map (768 × 768) are used for dataset experiments; this is used to verify the reliability of the AP-JPS algorithm proposed in this paper in approximating real environment maps.
5.1. Randomness Map Test
The first set of experiments was conducted using 10 sets of grid maps ranging from 10 × 10 to 100 × 100, with each set of map obstacles set from 10% to 55%, respectively, for the JPS algorithm, the AP-JPS algorithm, and the polynomially optimized AP-JPS algorithm for 100 sets of randomness experiments. To better distinguish the resultant path from the obstacle grid, this experiment places the starting point of the path planning at the middle point of the grid. The distance calculation in the heuristic function of the JPS algorithm and AP-JPS algorithm in the simulation uses the Euclidean distance formula, and the actual results are the average of 10 experiments. In this paper, the polynomially optimized AP-JPS algorithm is referred to as Op-AP-JPS to facilitate the presentation of experimental results. The results of the simulation experiment were selected from 20 × 20, 40 × 40 and 80 × 80 size raster maps, and the obstacles were selected from 10%, 30% and 50% for display.
As can be seen in Figure 9, the JPS algorithm searches in a fixed number of eight directions during the path search. If the JPS algorithm encounters an obstacle during the search process, it will reselect the path according to other fixed directions, resulting in a large path turning angle and long search path edges, thus making it difficult to approach the actual optimal solution. The AP-JPS algorithm shown in Figure 8 reselects the path nodes by means of optimization in this paper to obtain a shorter path. Meanwhile, the AP-JPS algorithm has better path smoothing after trajectory optimization by minimum snap seventh-order polynomial interpolation. The specific 100 experimental comparisons are shown in Figure 10, where the total turning angle change rate is the reduction rate of the total turning angle of the path of the AP-JPS algorithm compared to the JPS algorithm.
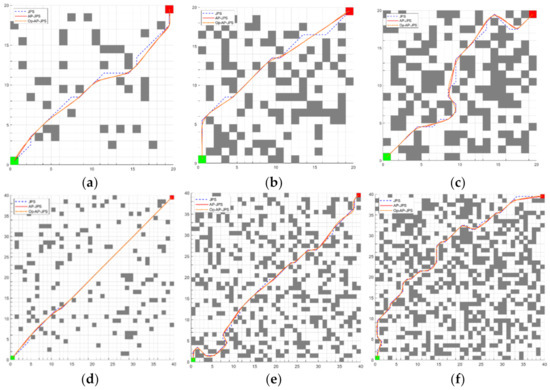
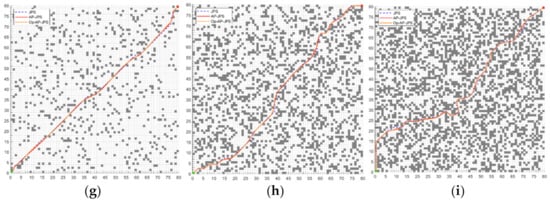
Figure 9.
Comparison of JPS algorithm, AP-JPS algorithm and polynomial optimized AP-JPS algorithm under three size maps. (a) 10% obstacles, (b) 30% obstacles, (c) 50% obstacles, (d) 10% obstacles, (e) 30% obstacles, (f) 50% obstacles, (g) 10% obstacles, (h) 30% obstacles, (i) 50% obstacles.
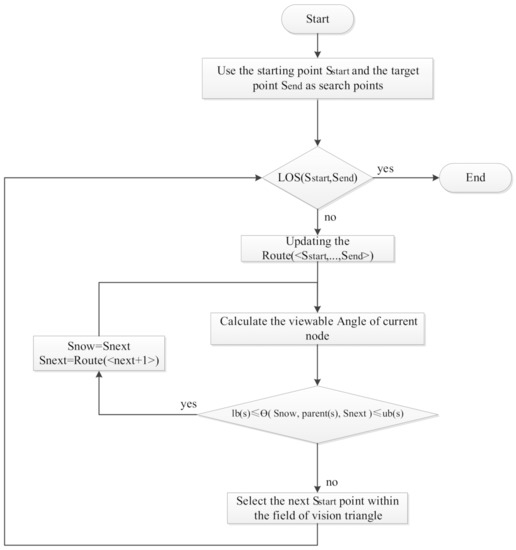
Figure 10.
AP Theta* Main Flow Chart.
From Figure 11a–c, it can be seen that as the number of grids and the percentage of obstacles increase, the total turning angle of the path and the difference of the total turning angle between the JPS algorithm and the AP-JPS algorithm are on an increasing trend, with the largest angle difference for 100 × 100 grids and the percentage of obstacles reaching 55%. Figure 11d shows that the rate of change of the total turning angle for both algorithms shows a decreasing trend with the increase in the obstacle percentage. Among them, the 90 × 90 grid map has the highest ratio at 10% obstacle percentage, and the total path turning angle of the AP-JPS algorithm is 88.4% lower than that of the JPS algorithm. The 40 × 40 grid map, with the lowest ratio at 50% obstacle share, shows a 13.7% reduction in total path turning angle for the AP-JPS algorithm compared to the JPS algorithm.
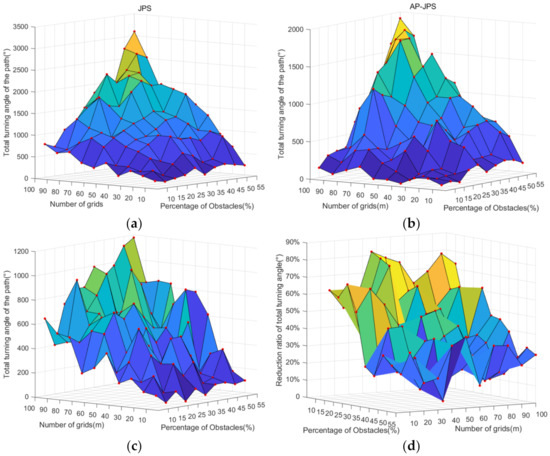
Figure 11.
Comparison of JPS algorithm and AP-JPS algorithm path total turning angle parameters. (a) JPS algorithm path total turning angle, (b) AP-JPS algorithm path total turning angle, (c) Total Turning Angle Difference, (d) Total Turning Angle Change Rate.
From Figure 12a–c, it can be seen that the path length and path length difference of both the AP-JPS algorithm and JPS algorithm show an increasing trend as the raster size and obstacle percentage increase. In the case of the 100 × 100 grid map with a 50% obstacle ratio, the path length difference is the largest, and the AP-JPS algorithm generates a path length 5.27 m shorter than the JPS algorithm. In addition, in the case of a 10 × 10 grid map with a 20% obstacle ratio, the path length difference is the smallest, and the generated path length of the AP-JPS algorithm is 0.41 m shorter than that of the JPS algorithm. It can be seen in Figure 12d that the rate of change of path length shows a decreasing trend with the growth of the number of grids. The path variation rate is highest in the case of the 10 × 10 grid with an obstacle percentage up to 10%, and the generated path length of the AP-JPS algorithm is 5.2% shorter than that of JPS. The path variation rate is lowest in the 100 × 100 raster map with 15% obstacle percentage, and the generated path length of the AP-JPS algorithm is 1.1% shorter than that of JPS.
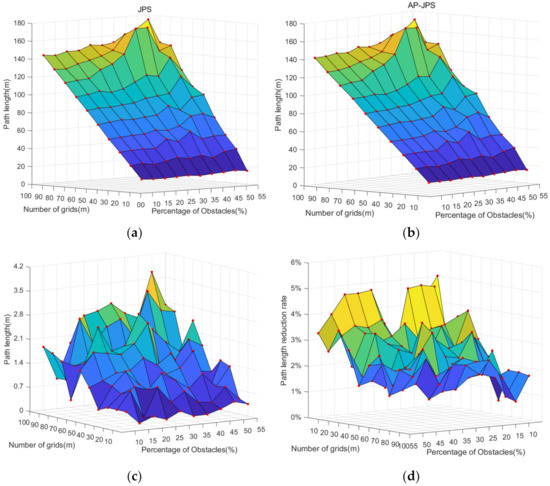
Figure 12.
Comparison of JPS algorithm and AP-JPS algorithm to generate path length parameters. (a) JPS algorithm path length, (b) AP-JPS algorithm path length, (c) Path length difference, (d) Path length change rate.
The first randomness experiment shows that the total path turning angle generated by the AP-JPS algorithm is 13.7% to 88.4% lower than the total path turning angle generated by the JPS algorithm, the generated path length is 1.1% to 5.2% lower than that of the JPS algorithm, and the path smoothing is better than that of the JPS algorithm.
5.2. Algorithm Comparison Experiment
This experiment uses the AP-JPS algorithm, A* algorithm, RRT algorithm, JPS algorithm and AP-Theta* algorithm to conduct comparative experiments in terms of algorithm running time, algorithm memory usage, path length and total path turning angle using maps of downtown Shanghai, downtown New York and downtown Boston extracted from public datasets. The experiments were conducted. The experimental procedure is shown in Figure 13. The comparative results are shown in Table 2.
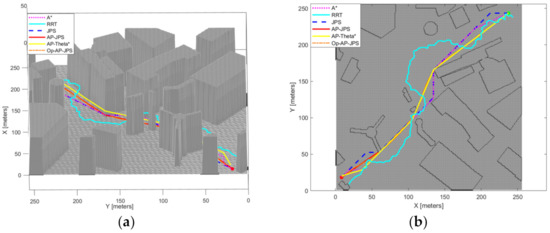
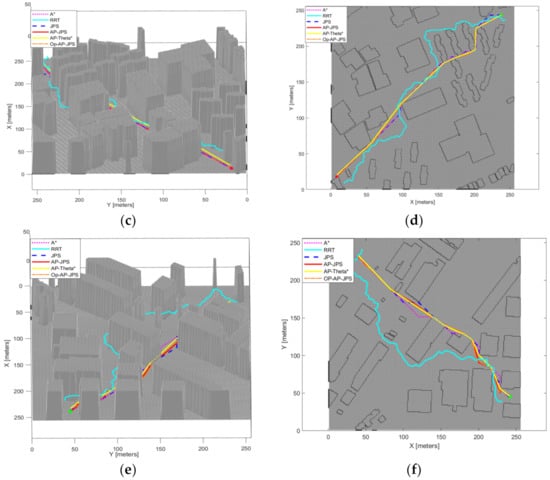
Figure 13.
Experimental procedure of algorithm comparison. (a) Shanghai, (b) Shanghai, (c) New York, (d) New York, (e) Boston, (f) Boston.

Table 2.
Map information selected for the dataset.
The following information can be derived from Table 2. From the experiments of the three maps, the AP-JPS algorithm has the smallest total path turning angle and the best path smoothness, and the RRT algorithm has the largest total path turning angle and the worst path smoothness. Among them, the AP-JPS algorithm is effective in reducing the total path turning angle by 58.71% to 84.67% compared with the original JPS. From the resultant path length of each algorithm, the AP-JPS algorithm has the shortest path length and the RRT algorithm has the longest path length, where the resultant path length of the AP-JPS algorithm is 1.61% to 4.68% less than the resultant path length of the original JPS algorithm. Analyzing the space complexity of these algorithms, it can be seen that the RRT algorithm has the lowest memory footprint and the AP-Theta* algorithm has the highest memory footprint. The AP-JPS algorithm has an increased memory footprint compared to the JPS algorithm and a reduced memory footprint compared to the AP-Theta* algorithm. The memory footprint of the AP-JPS algorithm increased by 14.71% to 22.66% and decreased by 43.72% to 55.32% over the memory footprint of the JPS algorithm and the AP-Theta* algorithm. Finally, from the running time point of view, we can find that the JPS algorithm has the shortest computation time and the RRT algorithm has the longest computation time. The computation time of the AP-JPS algorithm is increased compared to the JPS algorithm, and the computation time of the AP-JPS algorithm is increased from 73.35% to 86.01% compared to JPS. However, at the same time, the AP-JPS algorithm has a significant decrease in computing time compared to the AP-Theta* algorithm. The AP-JPS algorithm reduces the running time by 98.59% to 99.22% compared to the AP-Theta* algorithm.
The following conclusions can be seen from the results of this comparison experiment. The AP-JPS algorithm proposed in this paper has a smaller total path turning angle, shorter path and better overall result path smoothing compared to the JPS algorithm, A* algorithm, RRT algorithm and AP-Theta* algorithm. Meanwhile, the AP-JPS algorithm has reduced algorithmic time complexity and space complexity compared to JPS, but it has substantially improved compared to the AP-Theta* algorithm based on multi-angle pathfinding. That is, the AP-JPS algorithm substantially improves the quality of the resultant path while ensuring the efficiency of the algorithm, making it more consistent with the motion process of the mobile robot in real situations.
5.3. Data Set Map Experiment
The experiments were conducted using a public dataset freely distributed by Moving AI Lab. Four sets of maps of 80 × 80, 512 × 512, and 768 × 768 sizes are used for the dataset maps. The specific map information is shown in Table 3.

Table 3.
Map information selected for the dataset.
In this experiment, A*, JPS, AP-JPS and AP-JPS after polynomial optimization are selected for experimental comparison. The experimental data and results are the average of ten experiments, and the results are shown in Figure 14.

Figure 14.
Data set experiment. (a) AR0310SR, (b) AR0513SR, (c) AR0709SR, (d) AR0709SR, (e) divideandconquer, (f) plunderisle, (g) moonglade, (h) harvestmoon, (i) BlastFurnace, (j) Crossroads, (k) Hellfire, (l) SapphireIsles.
The generated path lengths, total path turning angles, and actual data of the three algorithms were recorded in the twelve sets of experiments as shown in Table 4, Table 5 and Table 6.

Table 4.
The 80 × 80 grid map experiment.

Table 5.
The 512 × 512 grid map experiment.

Table 6.
The 768 × 768 grid map experiment.
From the dataset experiments, it can be seen that the total path turning angle of the AP-JPS algorithm is much smaller than that of the A* algorithm and JPS algorithm, and the total path turning angle of the AP-JPS algorithm is reduced by 43.90% to 89.51% compared with JPS. The path length of the AP-JPS algorithm is 0.57% to 5.36% shorter than the JPS algorithm and 0.51% to 5.36% shorter than the A* algorithm. The AP-JPS algorithm has better path smoothing and better paths compared to the path smoothing. The shortest path expressiveness in an approximate real environment is closer to the actual situation.
6. Conclusions
- This paper proposes a smoothed JPS path planning method, combining the improved JPS algorithm with the smoothing method in this paper, adding angle indicators to the paths to exchange a smaller time sacrifice for a smoother path.
- This paper combines the AP-JPS algorithm with the seventh-order polynomial optimization based on minimum snap while introducing a safety corridor to solve the safety problem of AP-JPS optimized paths by inequality constraints.
- In this paper, we verify the path optimization effect of the AP-JPS algorithm in different complex map situations by three sets of experiments. First, the AP-JPS algorithm is tested by performing the AP-JPS algorithm under different sizes of random obstacle maps. From the test results, the AP-JPS algorithm shortens the total turn angle of the path by 13.7% to 88.4% and the path length by 1.1% to 5.2% compared with the JPS algorithm. Secondly, this paper uses some map data of three cities for algorithm comparison experiments. From the experimental results, the AP-JPS algorithm has shorter and smoother paths compared to the JPS algorithm. At the same time, the time complexity and space complexity of the AP-JPS algorithm are much smaller than that of the AP-Theta* algorithm. Finally, this paper simulates real indoor and outdoor scenes by using large maps with public datasets for path planning tests. From the experimental results, the AP-JPS algorithm can complete the task with better paths, and its generated paths are more consistent with the actual motion requirements of mobile robots than other algorithms.
- The AP-JPS algorithm still has some drawbacks, as it sacrifices more computing time compared to the JPS algorithm, and the complexity of the algorithm is still high. As the size and complexity of the grid map increase, the efficiency of the algorithm decreases. In future work, we need to further optimize the computational efficiency and memory usage of AP-JPS algorithm, and we hope to apply AP-JPS 3D to UAV path planning [7].
Author Contributions
Author Contributions: software, J.L.; validation, Y.L. (Yanyu Liu); investigation, Y.L. (Yanyu Liu); resources, Y.L. (Yuan Luo); data curation, Q.Q.; writing—original draft preparation, J.L.; writing—review and editing, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, G.; Liu, Y.; Zhao, J.; Zhu, L. Path planning for a new mine rescue robot base on visual tangent graphs. Jilin Daxue Xuebao 2011, 41, 1107–1112. [Google Scholar]
- Yang, C.; Liu, Y.; Wang, Y.; Xiong, L.; Xu, H.; Zhao, W. Research and Experiment on Recognition and Location System for Citrus Picking Robot in Natural Environment. Nongye Jixie Xuebao 2019, 50, 14–22+72. [Google Scholar]
- Oh, J.S.; Choi, Y.H.; Park, J.B.; Zheng, Y.F. Complete coverage navigation of cleaning robots using triangular-cell-based map. IEEE Trans. Ind. Electron. 2004, 51, 718–726. [Google Scholar] [CrossRef]
- Atiyah, A.N.; Adzhar, N.; Jaini, N.I. An overview: On path planning optimization criteria and mobile robot navigation. J. Phys. Conf. Ser. 2021, 1988, 012036. [Google Scholar] [CrossRef]
- Babunski, D.; Berisha, J.; Zaev, E.; Bajrami, X. Application of Fuzzy Logic and PID Controller for Mobile Robot Navigation. In Proceedings of the 9th Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 8–11 June 2020; pp. 21–36. [Google Scholar]
- Sariff, N.; Buniyamin, N. An overview of autonomous mobile robot path planning algorithms. In Proceedings of the 4th Student Conference on Research and Development, Shah Alam, Malaysia, 27–28 June 2006; pp. 183–188. [Google Scholar]
- Zhang, N.; Zhang, M.; Low, K.H. 3D path planning and real-time collision resolution of multirotor drone operations in complex urban low-altitude airspace. Transp. Res. Part C Emerg. Technol. 2021, 129, 103123. [Google Scholar] [CrossRef]
- Ivić, S.; Crnković, B.; Grbčić, L.; Matleković, L. Multi-UAV trajectory planning for 3D visual inspection of complex structures. arXiv 2022, arXiv:math/2204.10070. [Google Scholar] [CrossRef]
- Pehlivanoglu, Y.V. A new vibrational genetic algorithm enhanced with a Voronoi diagram for path planning of autonomous UAV. Aerosp. Sci. Technol. 2012, 16, 47–55. [Google Scholar] [CrossRef]
- Ayawli, B.B.K.; Chellali, R.; Appiah, A.Y.; Kyeremeh, F. An Overview of Nature-Inspired, Conventional, and Hybrid Methods of Autonomous Vehicle Path Planning. J. Adv. Transp. 2018, 2018, 8269698. [Google Scholar]
- Zhou, K.; Yu, L.; Long, Z.; Mo, S. Local path planning of driverless car navigation based on jump point search method under urban environment. Futue Internet 2017, 9, 51. [Google Scholar] [CrossRef] [Green Version]
- Foderaro, G.; Swingler, A.; Ferrari, S. A model-based cell decomposition approach to on-line pursuit-evasion path planning and the video game Ms. Pac-Man. In Proceedings of the IEEE Conference on Computational Intelligence and Games (CIG), Granada, Spain, 11–14 September 2012; pp. 281–287. [Google Scholar]
- Hu, Q.; Wang, J.; Zhang, X. Optimized Parallel Parking Path Planning Based on Quintic Polynomial. Comput. Eng. Appl. 2022, 1–9. Available online: http://kns.cnki.net/kcms/detail/11.2127.TP.20210325.1007.008.html (accessed on 21 May 2022).
- Leiyan, Y.; Xianyu, W.; Zeyu, H.; Zaiyou, D.; Yufeng, Z.; Zhaoyang, M. Path Planning Optimization for Driverless Vehicle in Parallel Parking Integrating Radial Basis Function Neural Network. Appl. Sci. 2021, 11, 8178. [Google Scholar]
- Chen, L.; Wang, S.; Hu, H.; McDonald-Maier, K.; Fei, M. Novel path curvature optimization algorithm for intelligent wheelchair to smoothly pass a narrow space. Zidonghua Xuebao Acta Autom. Sin. 2016, 42, 1874–1885. [Google Scholar]
- Sahin, H.; Kavsaoglu, A. Indoor path finding and simulation for smart wheelchairs. In Proceedings of the 29th Signal Processing and Communications Applications Conference (SIU), Istanbul, Turkey, 9–11 June 2021; pp. 1–4. [Google Scholar]
- Hu, M.; Cao, J.; Chen, X.; Peng, F. Path planning of intelligent factory based on improved ant colony algorithm. In Proceedings of the Asia-Pacific Conference on Communications Technology and Computer Science (ACCTCS), Shenyang, China, 22–24 January 2021; pp. 1–4. [Google Scholar]
- Firmansyah, E.; Masruroh, S.; Fahrianto, F. Comparative analysis Of A and basic theta algorithm in android-based pathfmding games. In Proceedings of the 6th International Conference on Information and Communication Technology for The Muslim World (ICT4M), Jakarta, Indonesia, 22–24 November 2016; pp. 275–280. [Google Scholar]
- Geng, S.; Peng, S.; Han, Y. Research on motion planning of snake-like robot based on the interpolation function. In Proceedings of the 8th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 27–28 August 2016; pp. 81–84. [Google Scholar]
- Huo, F.; Chi, J.; Huang, Z.; Ren, L.; Sun, Q.; Chen, J. Review of Path Planning for Mobile Robots. Jilin Daxue Xuebao 2018, 36, 639–647. [Google Scholar]
- Ravankar, A.; Ravankar, A.; Kobayashi, Y.; Hoshino, Y.; Peng, C. Path smoothing techniques in robot navigation: State-of-the-art, current and future challenges. Sensors 2018, 18, 3170. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Su, Y.; Bu, C.; Fan, X. A mobile robot path planning algorithm based on improved A*. J. Phys. Conf. Ser. 2020, 1468, 032018. [Google Scholar] [CrossRef]
- Foo, J.L.; Knutzon, J.; Kalivarapu, V.; Oliver, J.; Winer, E. Path planning of unmanned aerial vehicles using B-splines and particle swarm optimization. J. Aerosp. Comput. Inf. Commun. 2009, 6, 271–290. [Google Scholar] [CrossRef]
- Elbanhawi, M.; Simic, M.; Jazar, R.N. Continuous Path Smoothing for Car-Like Robots Using B-Spline Curves. J. Intell. Robot. Syst. Theor. Appl. 2015, 80, 23–56. [Google Scholar] [CrossRef]
- Huh, U.-Y.; Chang, S.A. G2 continuous path-smoothing algorithm using modified quadratic polynomial interpolation. Int. J. Adv. Rob. Syst. 2014, 11, 25. [Google Scholar] [CrossRef]
- Liu, S.; Watterson, M.; Mohta, K.; Sun, K.; Bhattacharya, S.; Taylor, C.J.; Kumar, V. Planning dynamically feasible trajectories for quadrotors using safe flight corridors in 3-D complex environments. IEEE Robot. Autom. 2017, 2, 1688–1695. [Google Scholar] [CrossRef]
- Harabor, D.; Grastien, A. Online graph pruning for pathfinding on grid maps. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 7–11 August 2011; Volume 25, pp. 1114–1119. [Google Scholar]
- Huang, J.; Wu, Y.; Lin, X. Smooth JPS Path Planning and Trajectory Optimization Method of Mobile Robot. Nongye Jixie Xuebao 2021, 52, 21–29+121. [Google Scholar]
- Dave, F.; Anthony, S. Field D*: An Interpolation-Based Path Planner and Replanner; Robotics Research; Springer: Berlin/Heidelberg, Germany, 2007; pp. 239–253. [Google Scholar]
- Daniel, K.; Nash, A.; Koenig, S.; Felner, A. Theta*: Any-Angle Path Planning on Grids. JAIR 2010, 39, 533–579. [Google Scholar] [CrossRef] [Green Version]
- Sinyukov, D.A.; Padir, T. CWave: Theory and Practice of a Fast Single-source Any-angle Path Planning Algorithm. Robotica 2020, 38, 207–234. [Google Scholar] [CrossRef]
- Jayasree, K.; Jayasree, P.; Vivek, A. Smoothed RRT techniques for trajectory planning. In Proceedings of the International Conference on Technological Advancements in Power and Energy (TAP Energy), Kollam, India, 21–23 December 2017; Volume 1, pp. 1–8. [Google Scholar]
- Chen, L.; Shan, Y.; Tian, W.; Li, B.; Cao, D. A Fast and Efficient Double-Tree RRT*-Like Sampling-Based Planner Applying on Mobile Robotic Systems. IEEE ASME Trans. Mechatron. 2018, 23, 2568–2578. [Google Scholar] [CrossRef]
- Gammel, J.; Srinivasa, S.; Barfoot, T. Informed RRT*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar]
- Yao, Q.; Zheng, Z.; Qi, L.; Yuan, H.; Guo, X.; Zhao, M.; Liu, Z.; Yang, T. Path Planning Method with Improved Artificial Potential Field–A Reinforcement Learning Perspective. IEEE Access 2020, 8, 135513–135523. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, L.; Xiang, Q.; Qian, T.; Lou, Z.; Xue, W. Research on USV trajectory tracking method based on LOS algorithm. In Proceedings of the 14th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 11–12 December 2021; Volume 1, pp. 408–411. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).