A Tailored Pricing Strategy for Different Types of Users in Hybrid Carsharing Systems
Abstract
:1. Introduction
- In a hybrid carsharing system with both the service of CSCs and the service of SAVs, users’ choice behaviors for different service modes are modeled by considering the rental costs and walking costs of the two service modes.
- Based on the different characteristics of each user cluster, a bi-objective nonlinear programming model is built up to determine the optimal fleet size and prices for different service modes. The TPS is proposed to improve the operator’s profit and the system’s service level. Results show the proposed TPS can enhance the operator’s profit and lower users’ costs.
2. Literature Review
2.1. Pricing Strategy in Conventional Carsharing Systems
2.2. SAVs
3. Model Formulation
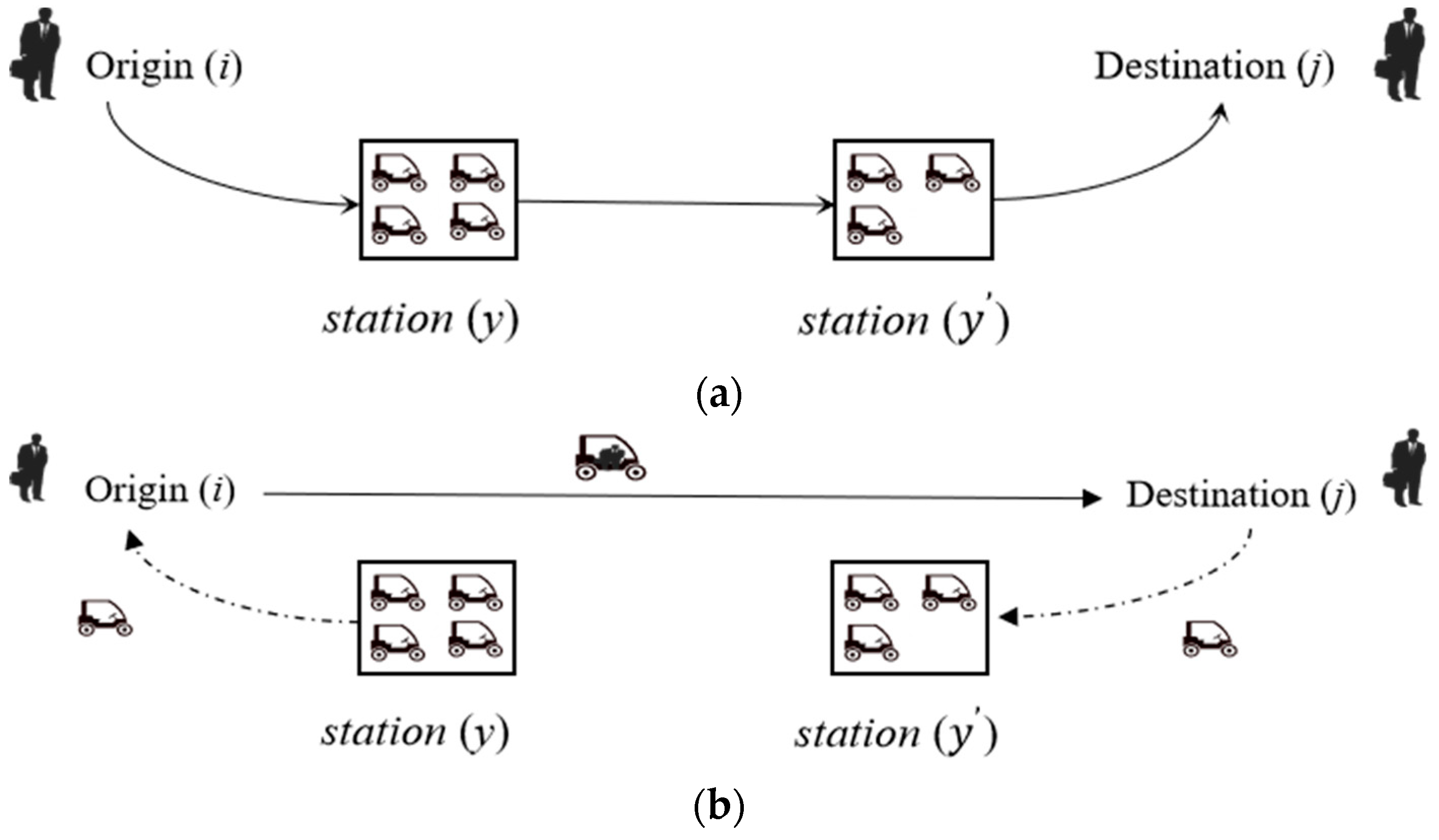
3.1. The Hybrid Carsharing System
3.2. Notations
| Set | |
| Set of service modes, . and separately represent the service of CSCs and the service of SAVs. | |
| is the maximum cluster. | |
| is the maximum time step of the studied period. | |
| are commonly used indices. | |
| Carsharing stations for the service of both CSCs and SAVs, Commonly used indices are and . | |
| Time-space nodes set combines the nodes and time steps, and means node at time step . | |
| Parameters | |
| Travel demands of user cluster between nodes and node , the departing time step is , and the arriving time step is The demands can be satisfied either by CSCs or SAVs, is dependent on the service mode the user cluster chooses, . | |
| Walking time for user cluster who choose service , between origin and station , departing from time step , . | |
| Walking time for user cluster choosing service , between station and destination , and the departing time step is , . | |
| Waiting time for user cluster choosing service , between station and origin , departing from time step , . | |
| Walking cost per minute for user cluster who choose service . | |
| Waiting cost per minute for user cluster who choose service , . | |
| The initial number of trips for user cluster who choose service , departing from node at time step and arriving at node at time step is different when users choose different service modes. | |
| The initial or the highest price can be set between node and for user cluster who choose service , . | |
| The number of parking places of CSC station , . | |
| The maintenance cost for a parking place per day under service , . | |
| The depreciation cost per car per day under service , . | |
| The driving cost, the operator, should pay for a car per time step under service , . | |
| Travel cost for user cluster who chooses service , departing from node at time step and arriving at node at | |
| Decision variables | |
| The number of trips for user cluster who choose service , departing from node at time step and arriving at node at , is dependent on the service mode users choose. | |
| Rental price per time step between nodes and for user cluster choosing service , and the departing time step is , . | |
| The number of parking places for SAV station , . | |
| Auxiliary variables | |
| The probability of carsharing users who would potentially choose SAVs between nodes and , and the departing time step is . | |
| Demand variation between nodes and for user cluster who choose service , . | |
| Price variation between nodes and for each user cluster under service , and the departing time step is , . | |
3.3. User Clusters and Price Elasticity
3.4. Bi-Objective Nonlinear Programming Model
3.4.1. Service Choices of Users
3.4.2. Model Formulation
- (1)
- Objective Functions
- (2)
- Constraints
- Flow conservation
- Constraints about demands
- Constraints about the fleet size
- Domain of decision variables
3.5. Solution Approach
4. Case Studies: Lanzhou, China
4.1. Setting Up the Case Studies
4.2. Experiments and Results
4.2.1. Performance of the Hybrid Carsharing System
4.2.2. Efficiency of the TPS
4.2.3. Performance of the Hybrid Carsharing System
5. Conclusions
- (1)
- Considering that not all demands can be satisfied by the hybrid carsharing system. A penalty coefficient is defined to reflect the potential effect of unsatisfied demands for each cluster on the profit. It is incorporated into the objective function. It combines travel potential, consumption potential, travel efficiency, and average revenue. The penalty coefficient for loyal users is the highest. It shows the importance of loyal users on the profit.
- (2)
- Differential prices are offered to different users by considering the unique characteristic of each user cluster. The price elasticity combines the price variations and demand variations, and it is used to distinguish different clusters. The carsharing operator can get 14.48% more profit at less extra costs. The loyal users contribute the most to the carsharing operator’s profit and the number of trips, while they pay the highest prices, especially during peak hours. The numbers of carsharing trips for the other two clusters are nearly the same. Compared with the losing users, the potential users can make more profit. The carsharing operator should pay the most attention to loyal users, then the potential users.
- (3)
- Compared with the carsharing system only with conventional cars, the performance of the hybrid carsharing system is explored. It reveals that the adoption of the SAVs benefits the operator and the users, especially the loyal users. Therefore, the conventional carsharing operator should embrace the new technology (referring to AVs in this study).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jorge, D.; Correia, G. Carsharing systems demand estimation and defined operations: A literature review. Eur. J. Transp. Infrast. 2013, 13, 201–220. [Google Scholar]
- Sai, Q.; Bi, J.; Chai, J. Optimal model for carsharing station location based on multi-factor constraints. Algorithms 2020, 13, 43. [Google Scholar] [CrossRef] [Green Version]
- Hu, P.S.; Reuscher, T. Summary of Travel Trends: 2001 National Household Travel Survey. 2004. Available online: https://rosap.ntl.bts.gov/view/dot/58882 (accessed on 1 May 2005).
- Li, M.; Zeng, Z.; Wang, Y. An innovative car sharing technological paradigm towards sustainable mobility. J. Clean. Prod. 2020, 288, 125626. [Google Scholar] [CrossRef]
- Shaheen, S.A.; Chan, N.D.; Micheaux, H. One-way carsharing’s evolution and operator perspectives from the Americas. Transportation 2015, 42, 519–536. [Google Scholar] [CrossRef]
- Gibbs, S. Google sibling waymo launches fully autonomous ride-hailing service. The Guardian, 7 November 2017. [Google Scholar]
- Launching Our Self-Driving Robotaxi in Germany. 2021. Available online: https://www.mobileye.com/blog/self-driving-robotaxi-sixt-germany-iaa/ (accessed on 5 March 2022).
- Darwesh, A.; Woods, G.; Saripalli, S. Systems integration, simulation, and control for autonomous trucking. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 1486–1491. [Google Scholar]
- Jian, S.; Rey, D.; Dixit, V. An Integrated supply-demand approach to solving optimal relocations in station-based carsharing systems. Netw. Spat. Econ. 2018, 19, 611–632. [Google Scholar] [CrossRef]
- Wood, N.; Jones-Meyer, S.N. Integrating automated toll discounts into a real-time ridesharing program. Transp. Res. Rec. 2016, 2597, 20–27. [Google Scholar] [CrossRef]
- Jorge, D.; Molnar, G.; Correia, G.H.D.A. Trip pricing of one-way station-based carsharing networks with zone and time of day price variations. Transp. Res. Part B Methodol. 2015, 81, 461–482. [Google Scholar] [CrossRef]
- Wu, C.; Le Vine, S.; Sivakumar, A.; Polak, J. Dynamic pricing of free-floating carsharing networks with sensitivity to travellers’ attitudes towards risk. Transportation 2021, 49, 679–702. [Google Scholar] [CrossRef]
- Habib, K.M.N.; Morency, C.; Islam, M.T.; Grasset, V. Modelling users’ behaviour of a carsharing program: Application of a joint hazard and zero inflated dynamic ordered probability model. Transp. Res. Part A Policy Pract. 2012, 46, 241–254. [Google Scholar] [CrossRef]
- De Luca, S.; Di Pace, R. Modelling users’ behaviour in inter-urban carsharing program: A stated preference approach. Transp. Res. Part A Policy Pract. 2015, 71, 59–76. [Google Scholar] [CrossRef]
- Habib, K.N.; Morency, C.; Zaman, M.H. Modelling activity persistency and usage of car sharing in Montreal. In Proceedings of the 88th Annual Meeting of Transportation Research Board, Washington, DC, USA, 1–15 January 2009. [Google Scholar]
- Xu, M.; Meng, Q.; Liu, Z. Electric vehicle fleet size and trip pricing for one-way carsharing services considering vehicle relocation and personnel assignment. Transp. Res. Part B Methodol. 2018, 111, 60–82. [Google Scholar] [CrossRef]
- Khalid, M.; Yue, C.; Aslam, N.; Suthaputchakun, C.; Khalid, W. Optimized pricing & scheduling model for long range autonomous valet parking. In Proceedings of the 2018 International Conference on Frontiers of Information Technology (FIT), Islamabad, Pakistan, 17–19 December 2018. [Google Scholar]
- Huang, K.; Correia, G.H.D.A.; An, K. Solving the station-based one-way carsharing network planning problem with relocations and non-linear demand. Transp. Res. Part C Emerg. Technol. 2018, 90, 1–17. [Google Scholar] [CrossRef]
- Duan, L.; Wei, Y.; Zhang, J.; Xia, Y. Centralized and decentralized autonomous dispatching strategy for dynamic autonomous taxi operation in hybrid request mode. Transp. Res. Part C Emerg. Technol. 2020, 111, 397–420. [Google Scholar] [CrossRef]
- Lu, R.; Correia, G.H.D.A.; Zhao, X.; Liang, X.; Lv, Y. Performance of one-way carsharing systems under combined strategy of pricing and relocations. Transp. B Transp. Dyn. 2020, 9, 134–152. [Google Scholar] [CrossRef]
- Schulte, F.; Vo, S. Decision support for environmental-friendly vehicle relocations in free-floating car sharing systems: The case of Car2go. Procedia CIRP 2015, 30, 275–280. [Google Scholar] [CrossRef]
- Angelopoulos, A.; Gavalas, D.; Konstantopoulos, C.; Kypriadis, D.; Pantziou, G. Incentivized vehicle relocation in vehicle sharing systems. Transp. Res. Part C Emerg. Technol. 2018, 97, 175–193. [Google Scholar] [CrossRef]
- Vasconcelos, A.; Martinez, L.M.; Correia, G.; Guimarães, D.C.; Farias, T. Environmental and financial impacts of adopting alternative vehicle technologies and relocation strategies in station-based one-way carsharing: An application in the city of Lisbon, Portugal. Transp. Res. Part D Transp. Environ. 2017, 57, 350–362. [Google Scholar] [CrossRef]
- Fagnant, D.J.; Kockelman, K.M. Dynamic ride-sharing and fleet sizing for a system of shared autonomous vehicles in Austin, Texas. Transportation 2018, 45, 143–158. [Google Scholar] [CrossRef]
- Hyland, M.; Mahmassani, H.S. Dynamic autonomous vehicle fleet operations: Optimization-based strategies to assign AVs to immediate traveler demand requests. Transp. Res. Part C Emerg. Technol. 2018, 92, 278–297. [Google Scholar] [CrossRef]
- Wang, S.; Correia, G.H.D.A.; Lin, H.X. Exploring the performance of different on-demand transit services provided by a fleet of shared automated vehicles: An agent-based model. J. Adv. Transp. 2019, 2019, 7878042. [Google Scholar] [CrossRef] [Green Version]
- Hanna, J.P.; Albert, M.; Chen, D.; Stone, P. Minimum cost matching for autonomous carsharing. IFAC-PapersOnLine 2016, 49, 254–259. [Google Scholar] [CrossRef]
- Li, M.; Zheng, N.; Wu, X.; Li, W.; Wu, J. An Efficient solving method to vehicle and passenger matching problem for sharing autonomous vehicle system. J. Adv. Transp. 2020, 2020, 3271608. [Google Scholar] [CrossRef]
- Karamanis, R.; Angeloudis, P.; Sivakumar, A.; Stettler, M. Dynamic pricing in one-sided autonomous ride-sourcing markets. In Proceedings of the International Conference on Intelligent Transportation Systems, Maui, HI, USA, 4–7 November 2018. [Google Scholar]
- Mehr, N.; Horowitz, R. Pricing traffic networks with mixed vehicle autonomy. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Miao, F.; Wu, J.; Niu, Y.; Wang, C.; Lownes, N.E. Dynamic Pricing for autonomous vehicle e-hailing services reliability and performance improvement. In Proceedings of the 2019 IEEE 15th International Conference on Automation Science and Engineering (CASE), Vancouver, BC, Canada, 22–26 August 2019; pp. 948–953. [Google Scholar] [CrossRef]
- Schaller, B. Can sharing a ride make for less traffic? Evidence from Uber and Lyft and implications for cities. Transp. Policy 2021, 102, 1–10. [Google Scholar] [CrossRef]
- Shokoohyar, S. Ride-sharing platforms from drivers’ perspective: Evidence from Uber and Lyft drivers. Int. J. Data Netw. Sci. 2018, 2, 89–98. [Google Scholar] [CrossRef]
- Shokoohyar, S.; Sobhani, A.; Sobhani, A. Impacts of trip characteristics and weather condition on ride-sourcing network: Evidence from Uber and Lyft. Res. Transp. Econ. 2020, 80, 100820. [Google Scholar] [CrossRef]
- Morency, C.; Trepanier, M.; Agard, B.; Martin, B.; Quashie, J. Car sharing system: What transaction datasets reveal on users’ behaviors. In Proceedings of the 2007 IEEE Intelligent Transportation Systems Conference, Bellevue, WA, USA, 30 September–3 October 2007; pp. 284–289. [Google Scholar] [CrossRef]
- Zhou, C.; Zhao, X.; Liu, E.; Zhao, J. Differential pricing strategies based on user clustering in a one-way carsharing system. Int. J. Sustain. Transp. 2022. [Google Scholar]
- Gambella, C.; Malaguti, E.; Masini, F.; Vigo, D. Optimizing relocation operations in electric car-sharing. Omega 2018, 81, 234–245. [Google Scholar] [CrossRef]
- Liang, X.; Correia, G.; An, K.; van Arem, B. Automated taxis’ dial-a-ride problem with ride-sharing considering congestion-based dynamic travel times. Transp. Res. Part C Emerg. Technol. 2020, 112, 260–281. [Google Scholar] [CrossRef]







| Indicators | Cluster 1 | Cluster 2 | Cluster 3 |
|---|---|---|---|
| Proportion (%) | 36.63 | 34.55 | 28.82 |
| Using frequency monthly | 6.41 | 1.01 | 3.38 |
| Time of the first use | 181.58 | 169.95 | 51.81 |
| Time of the last use | 19.95 | 147.93 | 31.71 |
| Using duration | 161.63 | 22.02 | 20.1 |
| Consumption potential (¥/day) | 921.87 | 206.5 | 223.16 |
| Travel potential | 42.53 | 6.5 | 7.46 |
| Travel efficiency (min/km) | 4.90 | 5.29 | 5.92 |
| Average revenue (¥/trip) | 21.67 | 31.75 | 29.89 |
| Penalty coefficient | 11.113 | 0.554 | 0.651 |
| Clustering | No Clustering | |||
|---|---|---|---|---|
| Cluster 1 | Cluster 2 | Cluster 3 | ||
| 1.3 | 1.4 | 1.5 | 1.5 | |
| CSCs | SAVs | |
|---|---|---|
| Step 1: Initialization |
| , , . |
| Step 2: Get the value of the objective function , . |
| Step 3: Update the maximum of the objective function . |
| Step 4: Stop criteria If m = M, stop. Otherwise, proceed to Step 5. |
| Step5: Crossover and mutation |
| Step 5.1: Crossover , then crossover is performed. The procedure of the crossover is as below: , then the new values are taken as the new generations for the next iteration. |
| Step 5.2: Mutation . |
| Step 6: Update the number of iterations Set m = m + 1, and go back to Step 2. |
| Parameters | (¥/min) | ||
|---|---|---|---|
| CSCs | 2 | 7 | 0.007 |
| SAVs | 5 | 7 | 0.050 |
| Indicators | TPS (¥) | No TPS (¥) | ||
|---|---|---|---|---|
| Carsharing operator | Revenue | 88,602.79 | 77,392.83 | |
| Profit | 85,378.79 | 74,428.83 | ||
| Depreciation cost of sharing cars | 768 | 588 | ||
| Maintenance cost of the parking places | 2456 | 2376 | ||
| Number of parking spaces for SAVs | 410 | 392 | ||
| Fleet size | CSC | 132 | 124 | |
| SAV | 154 | 121 | ||
| Users | Rental fee | CSC | 39,873.56 | 36,854.75 |
| SAV | 51,695.78 | 43,952.23 | ||
| Walking cost of CSC users | 3100.23 | 3049.56 | ||
| Waiting cost of SAV users | 2056.63 | 2049.56 | ||
| All Users’ costs | 96,726.2 | 85,906.1 | ||
| Cluster | Revenue | Walking Cost (CSCs) | Waiting Cost (SAVs) | |
|---|---|---|---|---|
| CSCs | SAVs | |||
| 1 | 22,634.25 | 28,693.23 | 1213.25 | 809.25 |
| 2 | 7681.31 | 10,466.79 | 948.67 | 658.67 |
| 3 | 8237.67 | 10,889.54 | 881.64 | 581.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, R.; Zhao, X.; Wang, Y. A Tailored Pricing Strategy for Different Types of Users in Hybrid Carsharing Systems. Algorithms 2022, 15, 172. https://doi.org/10.3390/a15050172
Lu R, Zhao X, Wang Y. A Tailored Pricing Strategy for Different Types of Users in Hybrid Carsharing Systems. Algorithms. 2022; 15(5):172. https://doi.org/10.3390/a15050172
Chicago/Turabian StyleLu, Rongqin, Xiaomei Zhao, and Yingqi Wang. 2022. "A Tailored Pricing Strategy for Different Types of Users in Hybrid Carsharing Systems" Algorithms 15, no. 5: 172. https://doi.org/10.3390/a15050172
APA StyleLu, R., Zhao, X., & Wang, Y. (2022). A Tailored Pricing Strategy for Different Types of Users in Hybrid Carsharing Systems. Algorithms, 15(5), 172. https://doi.org/10.3390/a15050172






