Performance of Parallel K-Means Algorithms in Java
Abstract
:1. Introduction
2. Background on K-Means
2.1. About the Initialization Methods
- exclude outlier points;
- be located in regions of high density of local data points;
- be far from each other so as to avoid, e.g., (since K is fixed) splitting a homogeneous dense cluster, thus degrading the clustering accuracy.
3. Parallel K-Means in Java
3.1. Supporting K-Means by Streams
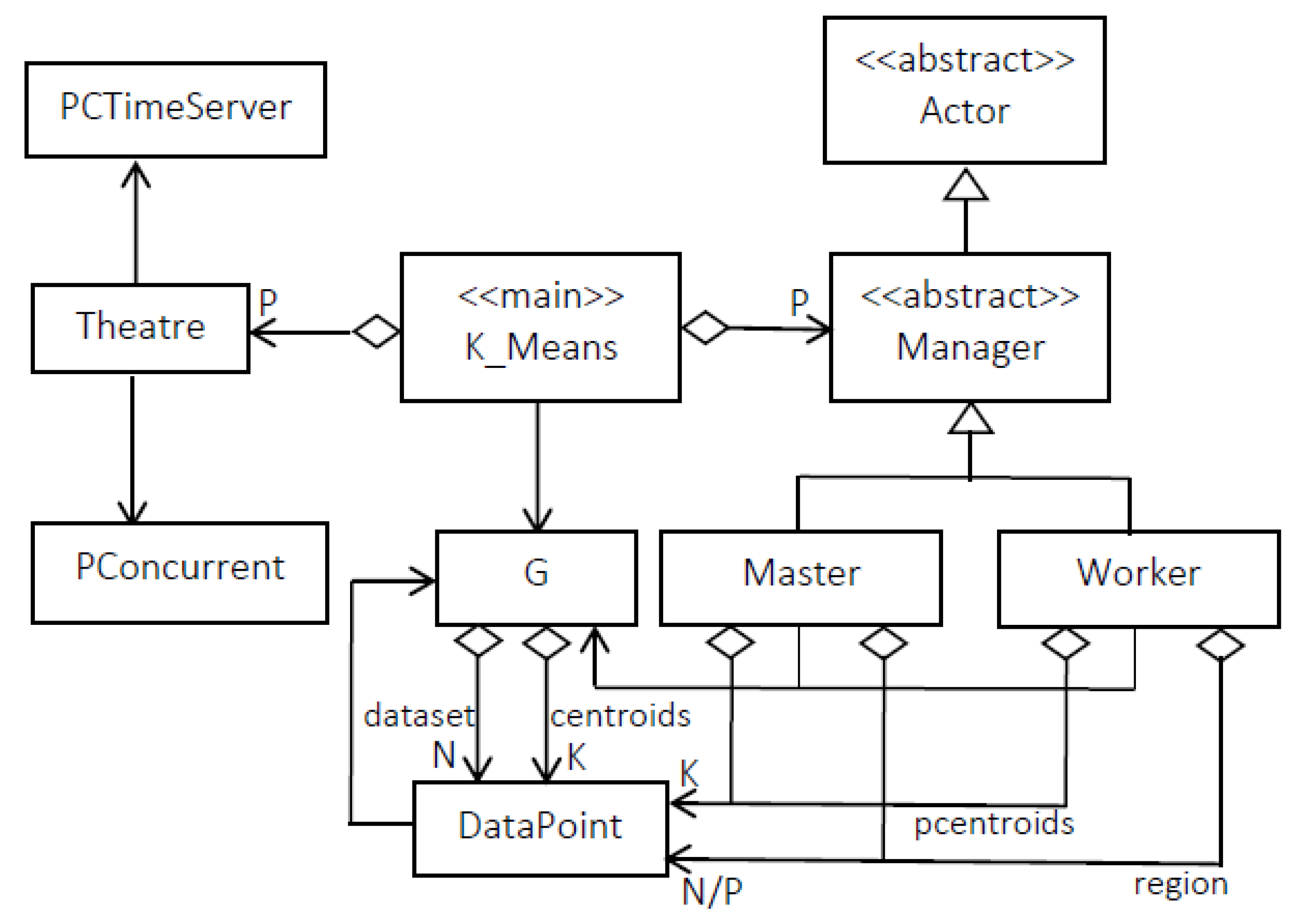
3.2. Actor-Based K-Means Using Theatre
3.2.1. The Parallel Programming Model of Theatre
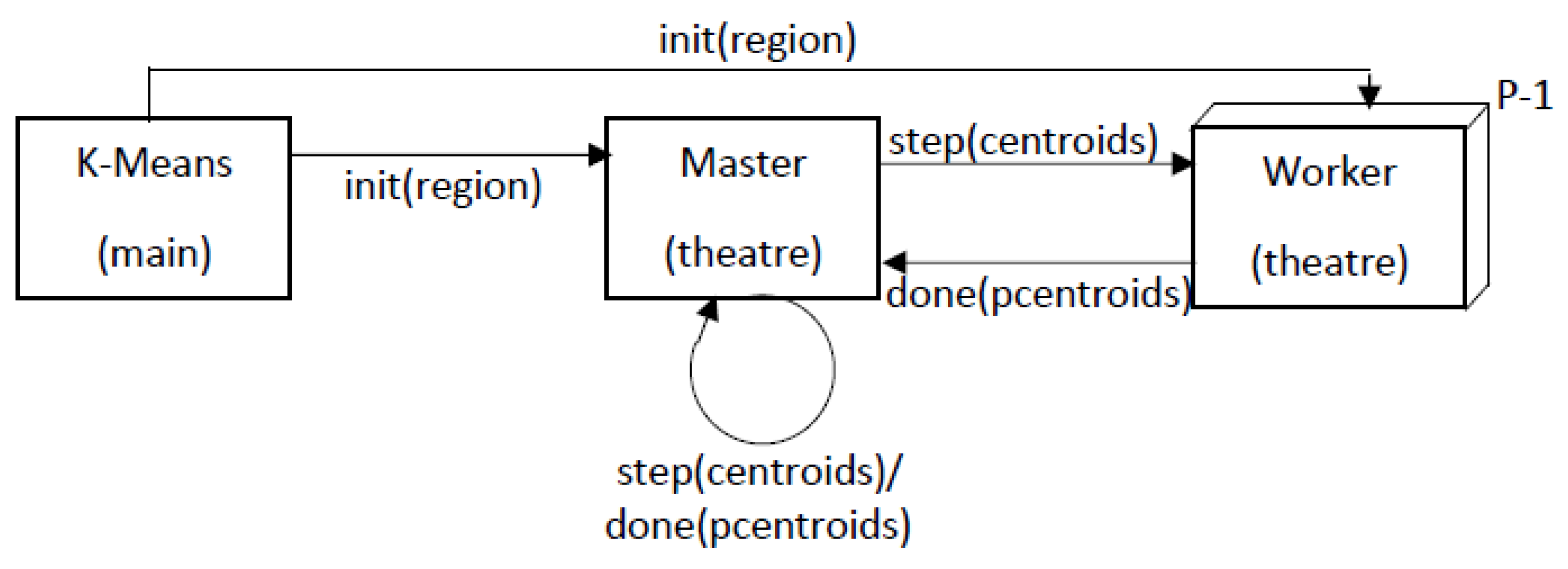
3.2.2. Mapping Parallel K-Means on Theatre
4. Experimental Results
5. Conclusions
- Adapting the approach for studying variations of the K-Means clustering [3].
- Porting the parallel Theatre-based version of K-Means to a distributed context, so as to cope with very large datasets.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1965 and 27 December 1965–7 January 1966; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond k-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Vouros, A.; Langdell, S.; Croucher, M.; Vasilaki, E. An empirical comparison between stochastic and deterministic centroid initialisation for K-means variations. Mach. Learn. 2021, 110, 1975–2003. [Google Scholar] [CrossRef]
- Qiu, X.; Fox, G.C.; Yuan, H.; Bae, S.H.; Chrysanthakopoulos, G.; Nielsen, H.F. Parallel clustering and dimensional scaling on multicore systems. In Proceedings of the High Performance Computing & Simulation (HPCS 2008), Nicosia, Cyprus, 3–6 June 2008; p. 67. [Google Scholar]
- Zhang, J.; Wu, G.; Hu, X.; Li, S.; Hao, S. A parallel k-means clustering algorithm with MPI. In Proceedings of the IEEE Fourth International Symposium on Parallel Architectures, Algorithms and Programming, NW Washington, DC, USA, 9–11 December 2011; pp. 60–64. [Google Scholar]
- Kantabutra, S.; Couch, A.L. Parallel K-means clustering algorithm on NOWs. NECTEC Tech. J. 2000, 1, 243–247. [Google Scholar]
- Zhao, W.; Ma, H.; He, Q. Parallel K-Means clustering based on MapReduce. In Proceedings of the IEEE International Conference on Cloud Computing, NW Washington, DC, USA, 21–25 September 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 674–679. [Google Scholar]
- Bodoia, M. MapReduce Algorithms for k-Means Clustering. Available online: https://stanford.edu/~rezab/classes/cme323/S16/projects_reports/bodoia.pdf (accessed on 1 January 2022).
- Naik, D.S.B.; Kumar, S.D.; Ramakrishna, S.V. Parallel processing of enhanced K-Means using OpenMP. In Proceedings of the IEEE International Conference on Computational Intelligence and Computing Research, Madurai, India, 26–28 December 2013; pp. 1–4. [Google Scholar]
- Cuomo, S.; De Angelis, V.; Farina, G.; Marcellino, L.; Toraldo, G. A GPU-accelerated parallel K-means algorithm. Comput. Electr. Eng. 2019, 75, 262–274. [Google Scholar] [CrossRef]
- Bloch, J. Effective Java, 3rd ed.; Addison Wesley: Boston, MA, USA, 2018. [Google Scholar]
- Subramaniam, V. Functional Programming in Java—Harnessing the Power of Java 8 Lambda Expressions; The Pragmatic Programmers, LLC: Raleigh, NC, USA, 2014. [Google Scholar]
- Nigro, L. Parallel Theatre: A Java actor-framework for high-performance computing. Simul. Model. Pract. Theory 2021, 106, 102189. [Google Scholar] [CrossRef]
- Lloyd, S.P. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef] [Green Version]
- Franti, P.; Sieranoja, S. K-means properties on six clustering benchmark datasets. Appl. Intell. 2018, 48, 4743–4759. [Google Scholar] [CrossRef]
- Al Hasan, M.; Chaoji, V.; Salem, S.; Zaki, M.J. Robust partitional clustering by outlier and density insensitive seeding. Pattern Recognit. Lett. 2009, 30, 994–1002. [Google Scholar] [CrossRef]
- Celebi, M.E.; Kingravi, H.A.; Vela, P.A. A comparative study of efficient initialization methods for the k-means clustering algorithm. Expert Syst. Appl. 2013, 40, 200–210. [Google Scholar] [CrossRef] [Green Version]
- Franti, P.; Sieranoja, S. How much can k-means be improved by using better initialization and repeats? Pattern Recognit. 2019, 93, 95–112. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.-P.; Ng, R.T.; Sander, J. LOF: Identifying Density-Based Local Outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000. [Google Scholar]
- Nigro, L.; Sciammarella, P.F. Qualitative and quantitative model checking of distributed probabilistic timed actors. Simul. Model. Pract. Theory 2018, 87, 343–368. [Google Scholar] [CrossRef]
- Cicirelli, F.; Nigro, L. A development methodology for cyber-physical systems based on deterministic Theatre with hybrid actors. TASK Q. Spec. Issue Cyber-Phys. Syst. 2021, 25, 233–261. [Google Scholar]
- Agha, G. Actors: A Model of Concurrent Computation in Distributed Systems. Ph.D. Thesis, MIT Artificial Intelligence Laboratory, Cambridge, MA, USA, 1986. [Google Scholar]
- Karmani, R.K.; Agha, G. Actors; Springer: Boston, MA, USA, 2011; pp. 1–11. [Google Scholar] [CrossRef]
- UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/ml/datasets (accessed on 1 January 2022).
- Gusev, M.; Ristov, S. A superlinear speedup region for matrix multiplication. Concurr. Comput. Pract. Exp. 2014, 26, 1847–1868. [Google Scholar] [CrossRef]
- Gergel, V. Parallel methods for matrix multiplication. In Proceedings of the 2021 Summer School on Concurrency, Saint Petersburg, Russia, 22–29 August 2012; pp. 1–50. [Google Scholar]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, J.; Wang, Y.K.; Yao, X.; Lin, C.T. Adaptive initialization method for K-means algorithm. Front. Artif. Intell. 2021, 4, 740817. [Google Scholar] [CrossRef] [PubMed]
- Lan, X.; Li, Q.; Zheng, Y. Density K-means: A new algorithm for centers initialization for K-means. In Proceedings of the 6th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 23–25 September 2015. [Google Scholar]
- Deshpande, A.; Kacham, P.; Pratap, R. Robust K-means++. In Proceedings of the Conference on Uncertainty in Artificial Intelligence, PMLR, Virtual, 3–6 August 2020; pp. 799–808. [Google Scholar]
- Ahmed, A.H.; Ashour, W.M. An initialization method for the K-means algorithm using RNN and coupling degree. Int. J. Comput. Appl. 2011, 25, 1–6. [Google Scholar]
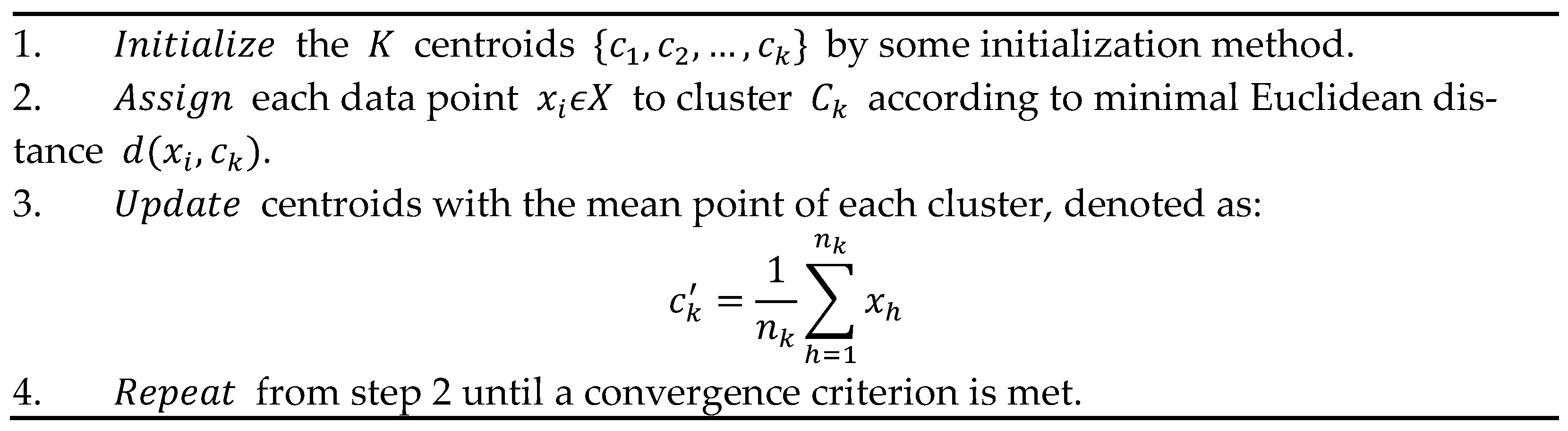

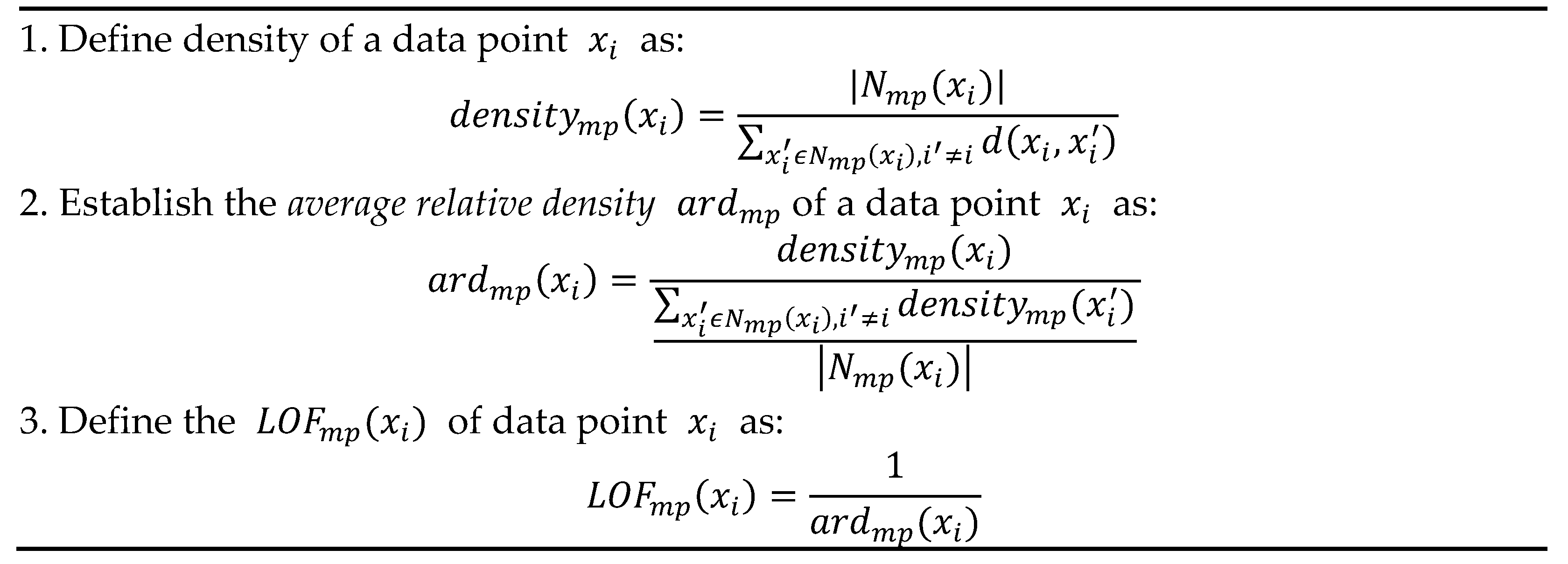



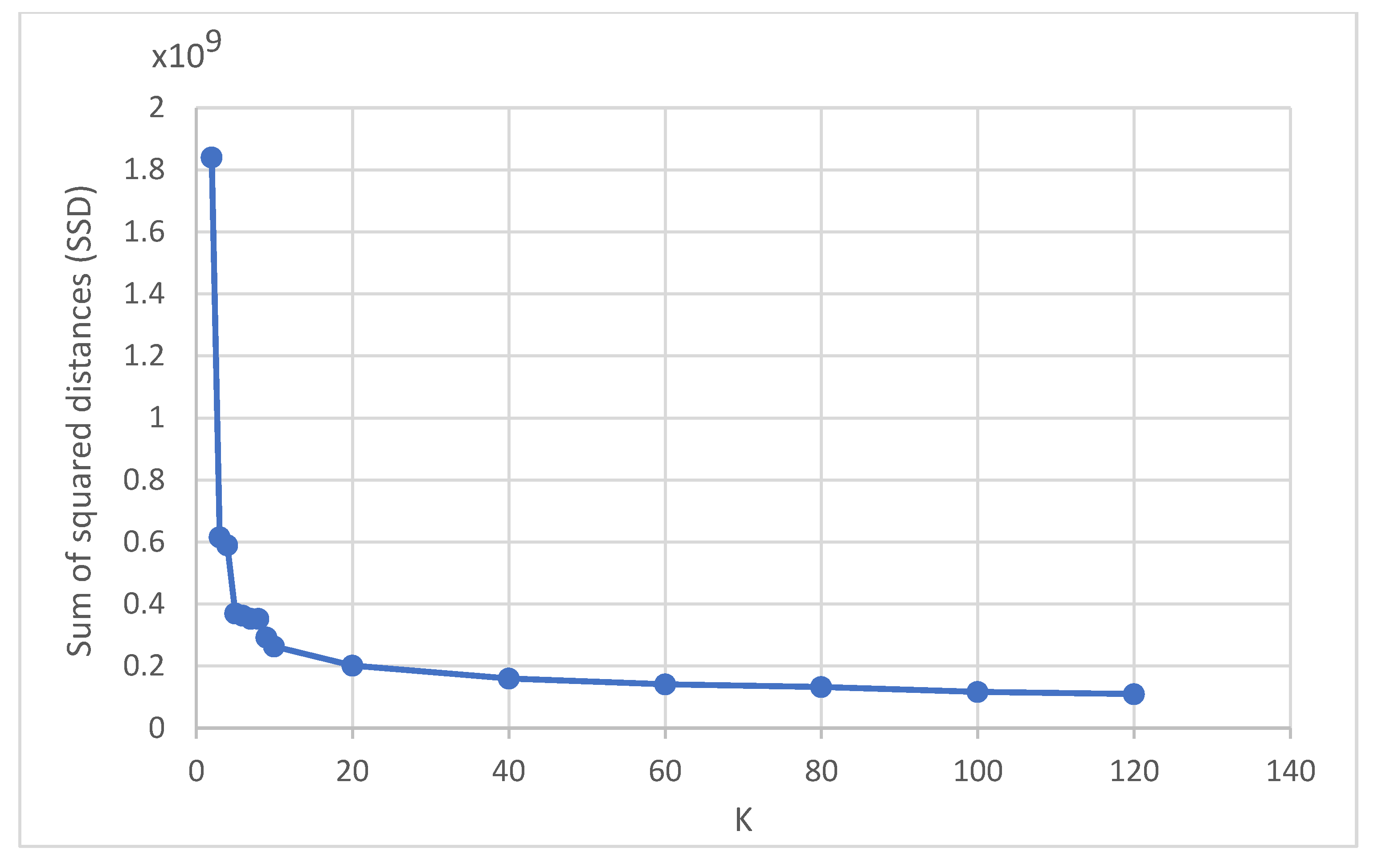
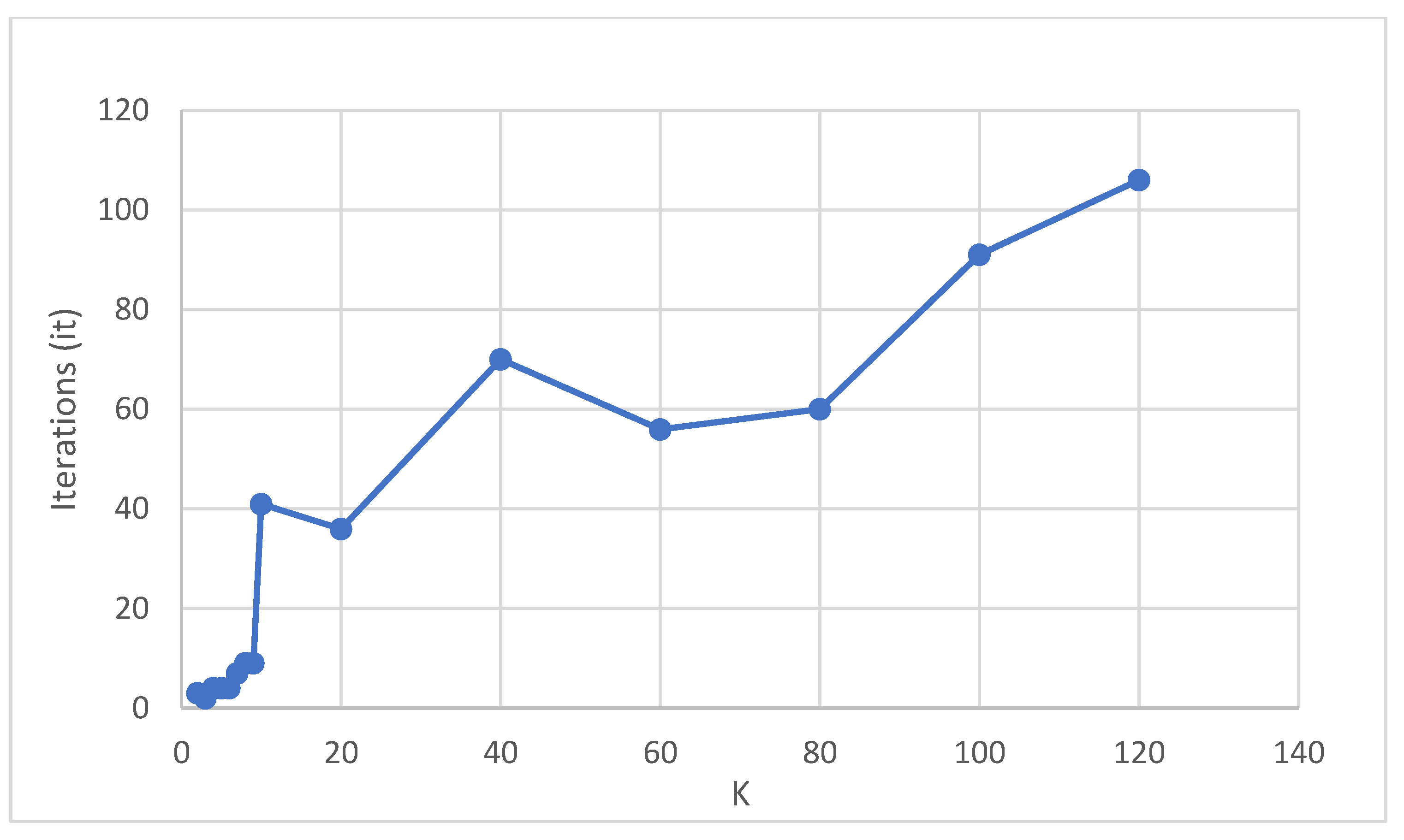
| Parameter | Value | Meaning |
|---|---|---|
| P | 16 | Number of used underlying threads |
| N | 2,458,285 | Size of the Census1990 data set |
| D | 68 | Dimensions of the dataset records |
| K | e.g., 80 | Number of assumed centroids |
| T | 1000 | Maximum number of iterations |
| THR | 1 × 10−10 | Threshold for assessing convergence |
| INIT_METHOD | ROBIN | The centroid initialization method |
| E | 0.05 | Tolerance in the Local Outlier Factor (LOF) detection (ROBIN) |
| MP | e.g., 15 | Size of the MP-neighborhood of data points (ROBIN) |
| 70,566 | 9233 | 7.64 | 59,671 | 7620 | 7.83 | |
| 114,743 | 12,061 | 9.51 | 96,891 | 11,221 | 8.63 | |
| 428,389 | 44,877 | 9.55 | 357,731 | 38,535 | 9.28 | |
| 510,496 | 53,798 | 9.49 | 420,934 | 45,217 | 9.31 | |
| 769,109 | 68,158 | 11.28 | 597,489 | 63,497 | 9.41 | |
| 1,407,401 | 145,346 | 9.68 | 1,117,578 | 111,956 | 9.98 | |
| 1,920,530 | 199,335 | 9.63 | 1,552,306 | 146,059 | 10.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nigro, L. Performance of Parallel K-Means Algorithms in Java. Algorithms 2022, 15, 117. https://doi.org/10.3390/a15040117
Nigro L. Performance of Parallel K-Means Algorithms in Java. Algorithms. 2022; 15(4):117. https://doi.org/10.3390/a15040117
Chicago/Turabian StyleNigro, Libero. 2022. "Performance of Parallel K-Means Algorithms in Java" Algorithms 15, no. 4: 117. https://doi.org/10.3390/a15040117
APA StyleNigro, L. (2022). Performance of Parallel K-Means Algorithms in Java. Algorithms, 15(4), 117. https://doi.org/10.3390/a15040117






