Abstract
The high efficiency, flexibility, and low cost of robots provide huge opportunities for the application and development of intelligent logistics. Especially during the COVID-19 pandemic, the non-contact nature of robots effectively helped with preventing the spread of the epidemic. Task allocation and path planning according to actual problems is one of the most important problems faced by robots in intelligent logistics. In the distribution, the robots have the fundamental characteristics of battery capacity limitation, limited load capacity, and load affecting transportation capacity. So, a smart community logistics service framework is proposed based on control system, automatic replenishment platform, network communication method, and coordinated distribution optimization technology, and a Mixed Integer Linear Programming (MILP) model is developed for the collaborative and persistent delivery of a multiple-depot vehicle routing problem with time window (MDVRPTW) of swarm robots. In order to solve this problem, a hybrid algorithm of genetically improved set-based particle swarm optimization (S-GAIPSO) is designed and tested with numerical cases. Experimental results show that, Compared to CPLEX, S-GAIPSO has achieved gaps of 0.157%, 1.097%, and 2.077% on average, respectively, when there are 5, 10, and 20 tasks. S-GAIPSO can obtain the optimal or near-optimal solution in less than 0.35 s, and the required CPU time slowly increases as the scale increases. Thus, it provides utility for real-time use by handling a large-scale problem in a short time.
1. Introduction
Since the global outbreak of the new crown pneumonia epidemic in winter 2019, robots replaced manual distribution which, used in drugs and goods delivery and supply chains, contributed a lot to the prevention and control of the epidemic. The autonomous mobile robot Phollower100 delivery robot, developed by a Slovakian company, is deployed in hospitals and other healthcare centers for distributing medicines, laundry, and other material to different stations [1]. Keenon Robotics provided many hospitals in the COVID-19 affected areas of China with delivery robots for delivering medical supplies, food, personal protective equipment (PPE), clean linens, and other supplies to people without human contact [2,3]. In a smart community, the joining of e-health, smart home, supply chain management, transportation, and other system technologies can help with proactive prevention and control and the mitigation of COVID-19 and similar epidemics [4]. On the other hand, with the rapid increase in the number and types of logistics orders, the delivery of the last mile is almost impossible to be completed by manual delivery. Through using various intelligent and reliable robotic technologies, logistics can be more automated. The application of robots and drones to intelligent logistics for distribution has received extensive attention and rapid improvement [5]. When robots are widely used in logistics, it is estimated that up to 40% of robots can provide cost reduction [6]. In fact, the self-organizing intelligent Swarm Robots (SR) system composed of lots of robots can be regarded as the prototype of future intelligent management and service systems, and it may greatly promote changes in our daily life.
However, currently used robotic solutions have advantages in the world, as new challenges and requirements emerge. The performing of task allocation and path planning according to actual task requirements is one of the most important tasks faced by robots in intelligent logistics and the future smart community, and not just for the hardware circuits control system of robots [7]. Wen, L. et al. [8] designed a system to accurately locate goods on the entire route, allowing the tracking of products or packages and obtaining a predictable timetable. The use of a path planning algorithm in intelligent delivery ensures the minimization of global routing transit times and reducing average waiting times, thereby improving customer service levels. Regarding the task time and the consumption of the robot as a utility function, there are still few studies on the development of models based on battery limitations [9,10]. Therefore, reducing customer waiting time and improving customer satisfaction is still a key issue. In addition, these researches are based on the actual delivery background of SR, using robots, unmanned aerial vehicles, and trucks for collaborative delivery. However, they did not consider how to achieve persistent coordinated distribution and the uniqueness of robots from other vehicles such as electric vehicles in the distribution:
- (1)
- The power and load-bearing capacity of the robot itself, not like heavy-duty tool trucks, and their speed and travel time will be affected by the weight of the load.
- (2)
- Each robot needs to be charged at intervals and cannot work continuously for a long time.
- (3)
- The charging of the robot takes a certain amount of time, and the charging time is related to the power loss. The longer the travel time, the more the power loss, the longer the charging time.
- (4)
- Each robot should be placed in a service station instead of stopping outside when it completes a task or is not performing the task in order to avoid the loss of the robot.
For the real application of robots, these problems need to be solved. This article is based on the basic characteristics of the robot; a combined smart community logistics service framework consisting of a control system, automatic replenishment platform, network communication method, and coordinated distribution optimization technology is proposed, in real-time dynamic collaborative and persistent delivery. Based on the characteristics of the robots, the MILP model for SR in the context of smart communities is developed.
The contributions of this paper are threefold. First, we propose a smart community logistics service framework, and provide detailed ideas on how to design an intelligent distribution system, including a path planning solution for SR to achieve dynamic and persistent delivery and reduce customer waiting time. Second, corresponding functions are developed for the different customer-oriented needs and the transportation characteristics of the robot itself, including the impact of the weight of the loaded product on the transportation time and the behavior of the robot during idle time, we developed the MILP model. Third, we designed a specific S-GAIPSO algorithm. Compared to CPLEX, S-GAIPSO achieved a gap of 0.157%, 1.097%, and 2.077% on average, respectively, when there were 5, 10, and 20 tasks. S-GAIPSO can obtain the optimal or close-to-optimal solution in less than 0.35 s CPU time, and when the number of tasks reaches 30, it can still provide an excellent solution relatively quickly.
The rest of the paper is organized as follows: Section 2 mainly conducts a literature review on the application of SR, robot task allocation, and path planning. Section 3 describes the system and develops related functions for the characteristics of SR and logistics problems, and establishes the MILP, then designs a set-based particle swarm algorithm for a problem and uses a genetic algorithm improved by the PSO algorithm. Section 4 numerically testes the proposed model and algorithm and compares and evaluates the solutions proposed in this paper based on MATLAB-based S-GAIPSO and the latest solver CPLEX. The last section summarizes this article; our study is applied to SR logistics, has great practical significance, and puts forward the prospect and improvement goals for the future. Finally, acknowledgments and references are stated at the end of the paper.
2. Related Works
Li, J. and Yang, F. et al. [11,12] found that the task assignment problem under the above background is essentially the traveling salesman problem (TSP), which is almost the beginning of path planning-related problems. The vehicle routing problem (VRP) is the core of the current logistics practice, and it is derived from TSP and its variants such as probabilistic TSP and fuzzy TSP. With the development of VRP research, some complex variants have also been derived. For example, R. J. et al. [13] explored this cooperation by developing a model for the vehicle routing problem with drones that considers the presence of customer time windows (VRPTW). The concept of time windows is introduced into VRP by Christofifides, who proposed a branch and bound algorithm for small-scale problems [14]. İLhan, İ. [15] designed an improved simulated annealing algorithm with a crossover operator for the capacitated vehicle routing problem (CVRP). Combining multi-depot and integrated delivery to expand the VRPTW makes the MDVRPTW more scientific and reasonable, and the complexity of the solution is increased accordingly. Bae, H. and Moon, I. et al. [16,17] presented an improved genetic algorithm for solving the MILP considering specific practical issues and related factors.
Now we turn our attention to the SR literature. A recognized definition of SR was proposed by Sahin, E. in 2005 [18]. Foton [19] developed the first cellular robot system, which is a distributed system composed of many autonomous robots. Nedjah, N. and Silva, L. J. [20] discussed and analyzed the urgent need for standardization in many aspects of SR, including hardware and software, so that SR can be applied in real-world APPL. Senanayake, M. et al. [21] summarized the advantages of robot systems and carried out investigations on the search and tracking algorithms of SR. Miljkovicl and Xin W. J. [22] proposed an intelligent logistics scheduling system based on the Internet of Things, which realizes dynamic coordination between customers, sorting robots, and cloud technology, and then used an ant colony algorithm to avoid obstacles in scheduling. Milford M. and Wyeth, G. [23,24] mainly carried out the integrated system research of SR system generation, execution, and monitoring, providing an advanced multi-task planning solution. Eijyne, T. et.al. [25] proposed a task-oriented, auction-based task allocation framework, which is implemented in a multi-robot system, allowing tasks to be dynamically allocated to robots when a given task is completed. These literatures adopt different methods for the research goals to obtain the task allocation table and then update the execution according to the system framework. Boysen, N. et.al. [26] developed a scheduling program for determining truck routes and robot launch locations based on the last mile problem, and then determined that the number of weighted delayed customer deliveries was minimized. Deng P. et al. [27] studied the vehicle path problem of an unmanned aerial vehicle, sidewalk robot, or walking machine movement synchronization.
From the above, robots have high-efficiency communication capabilities, adaptability to different tasks, and low-cost characteristics. These features provide huge opportunities for their application and development in intelligent logistics. Robotics is an important part of intelligent logistics and future logistics. Through the review and analysis of the existing literature, it is found that many documents mainly study the control system and hardware structure of robots, but the effective use of robots is also an important concept to strengthen the development of robotics in addition to the development of service components. So far, the research on the potential of supporting robot delivery is still insufficient, and these documents on robot VRP in logistics delivery did not consider the battery capacity limitations of the robot, the limited load capacity, and the impact of the load on the transportation capacity. They also did not consider the realization of coordinated and persistent delivery specific methods. Thus, through the research and analysis above of all the characteristics of SR in the actual logistics distribution, we developed the SR MILP, which includes load weight and service station charging functions. SR shares a community service station to supplement power and, according to the requirements of different customers, perform corresponding tasks from the service station. Besides, from our knowledge, ours is the first applied to achieve collaborative and durable delivery in the context of large community cities considering customer-oriented needs and the transport characteristics of robots themselves.
Lenstra, J. K. et.al. [28] showed that VRP is NP-hard. Solutions to the problem are mainly divided into two categories: precise algorithms and heuristic algorithms. Although the precise algorithm can find the optimal solution of the problem, the efficiency is low, and the scale of the solution is limited. Therefore, many scholars favor the application of efficient heuristic algorithms to solve the vehicle routing problem, such as a genetic algorithm [29], ant colony algorithm [30], particle swarm algorithm [31], and other intelligent algorithms. Calvet, L. et al. [32] combined statistical learning with metaheuristics for the multi-depot vehicle routing problem with market segmentation. Ting, C. J. et al. [33] proposed a particle swarm optimization approach to solve the discrete and dynamic berth allocation problem (BAP), which assigns ships to discrete berth positions and minimizes the total waiting times and handling times for all ships. Compared with intelligent optimization algorithms such as ant colony optimization, the neural network algorithm, and artificial immune algorithm, PSO algorithm retains a population-based global search strategy, without crossover and mutation individuals, and has a simple structure, easy implementation, and strong robustness. PSO is widely used to solve combinatorial optimization problems, but it is limited to continuous space. Since many optimization problems are defined in the discrete space, many related variants of the PSO algorithm have been proposed and used [34,35]. Yan et al. [36] designed a PSO for the leak source localization problem, combining particles into a “minimal number of low-fitness particles removed from the current group and reset their positions to help the global optimal particle optimization group” to enhance the understanding of the search for the global best particle. In order to plan the smooth path of the mobile robot, in the improved PSO algorithm, an adaptive fractional velocity is introduced, and a certain disturbance is applied to the particle swarm according to the evolution state of the particle swarm, thereby enhancing its ability to jump out of the local minimum value and more thoroughly explore the search space [37]. Stage I grouped the tasks into clusters using the dynamic distributed particle swarm optimization (D2PSO) algorithm, and stage II allocated the robots to the clusters. The assignment of robots to the clusters is represented as multiple traveling salesman problems (MTSP) [38]. Kwa et al. [39,40] presented a fully decentralized swarming strategy achieved by combining adaptive inter-agent repulsion and an adjustable network PSO-based strategy. They studied the search and tracking problem of dynamic targets for swarm robotic systems, based on an adjustable network of PSO-based dynamics. However, most of these methods have similarities in the application of PSO. Particles search in continuous space and convert real-valued positions into integer values to represent routes. These PSO algorithms cannot fully reflect the characteristics of the discrete problem space of VRP, and their operating efficiency is not satisfactory. Zhang Jun et al. [41] proposed a new set-based PSO method, which treats the search space as a general set, and each candidate solution represented by the position of each particle is regarded as a clear subset of the general set. We proposed the S-GAIPSO hybrid algorithm, which can well represent the problem space of MDVRPTW for the cooperative and persistent delivery of SR, retain the advantages of fast local search of particle swarm optimization, and improve the global optimization speed and optimization ability of particles.
3. Materials and Methods
3.1. Problem Description
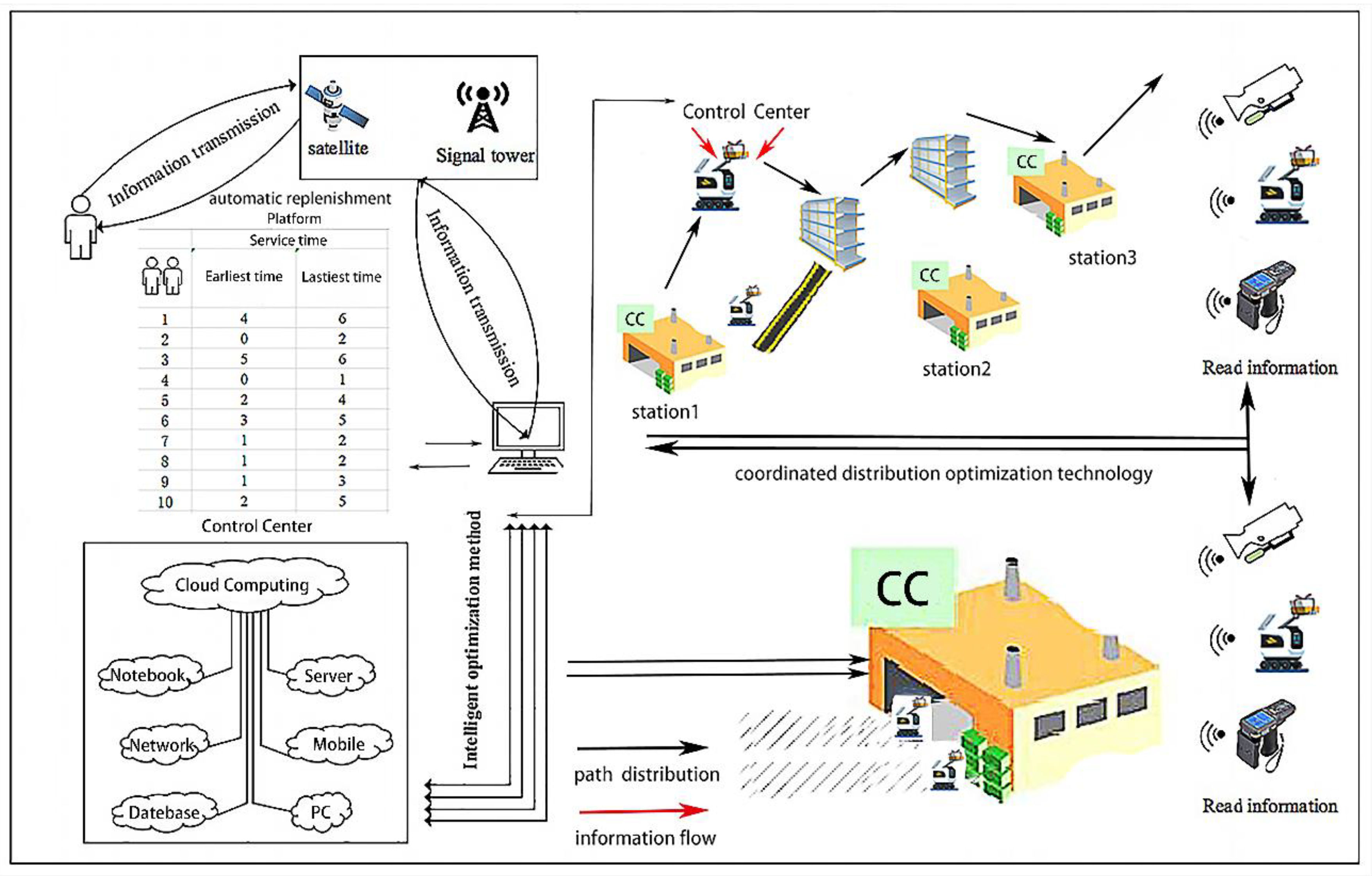
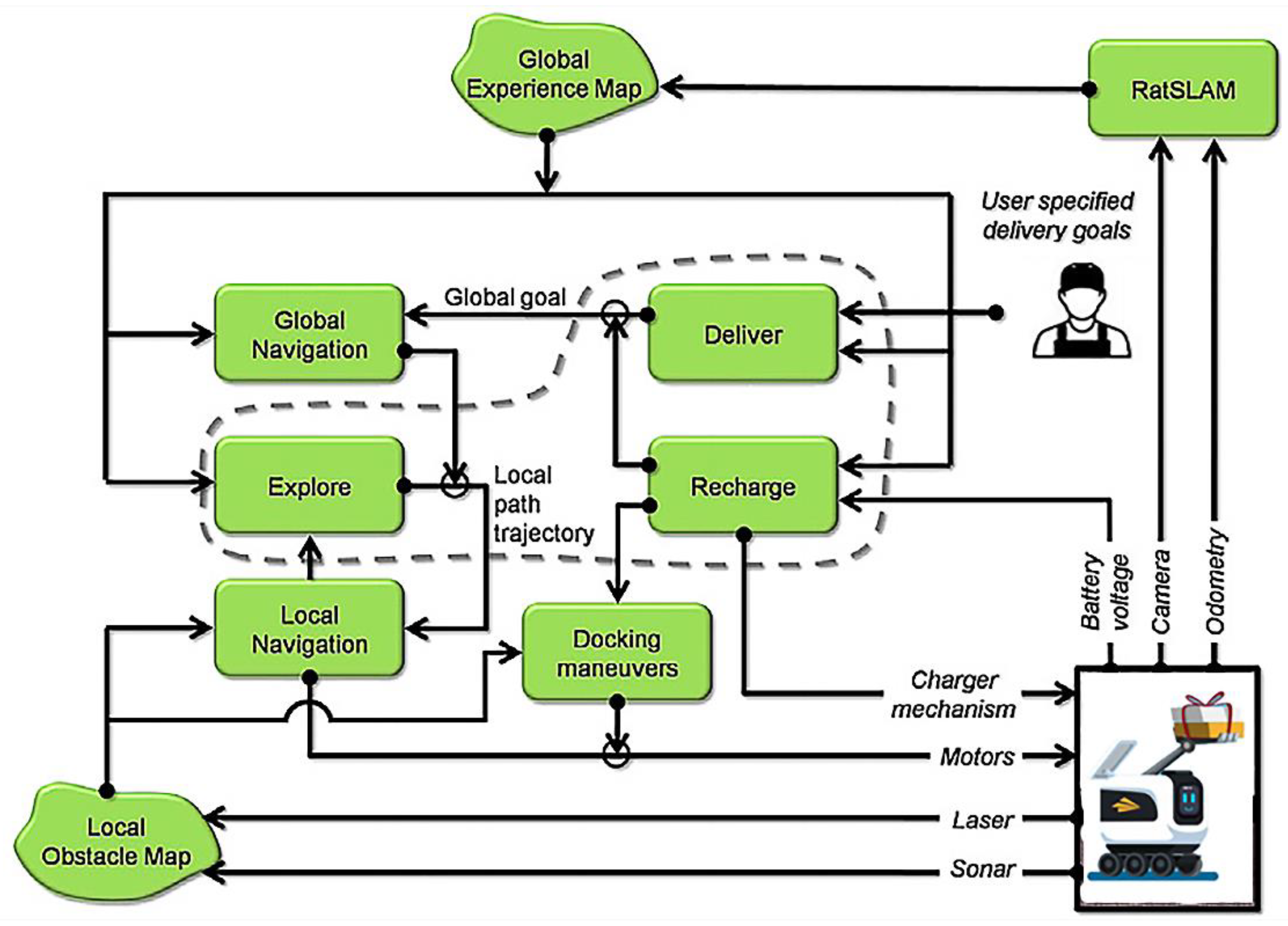
In order to solve all the above problems, enable the continuous execution of robot tasks, and reduce the waiting time of customers, this paper proposes a smart community logistics service framework. As shown in Figure 1, it includes the control system of the robot system, the automatic replenishment platform, the network communication technology, and the component activities of the coordinated distribution optimization technology. The control center of the system receives the deterministic customer location (GPS coordinates) from the service requester, and it is responsible for coordinating the robot tasks allocation plan. Then the control center receives the mission planning schedule through the communication network and executes the order at the time specified by the customer. Each robot sends and continuously updates visual and geographic positioning information to its controller based on the communication network and replenishes charges through the service station. For example, in a large-scale smart community, after robot 1 starts from service station (distribution center with charging) 1 and completes the task requirements for customer 1, it continues to perform the task or returns to one of the service stations for charging. When returning to one service station, this service station serves as a new departure station to perform the following tasks. Figure 2 is the composition structure of the control center system, which is mainly responsible for the function of allocating orders and analyzing and processing the returned data. It realizes path planning and serves customers by coordinating and assigning tasks to SR. Most of the control modules in this control unit operate continuously, but not all modules actively control the robot all the time. Through the task distribution and delivery table, which is obtained by developing a model in this article, a map is generated for the generated task table. Ltd., G. B. et al. [42] saved the task distribution path output to a json file and then uploaded the json file. Each robot obtains the relevant instructions to execute and maintains real-time communication and positioning updates throughout the process to complete dynamic and complex tasks.
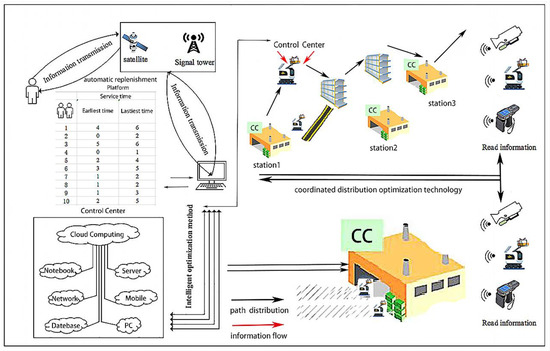
Figure 1.
Smart community logistics distribution service system.
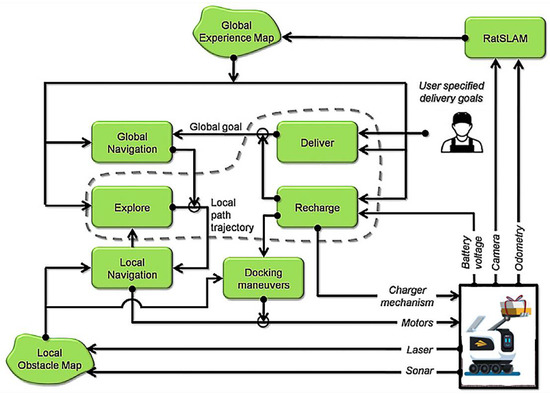
Figure 2.
The composition of the control center system.
3.2. Mathematical Formulation
3.2.1. Model Parameters
The MILP was developed to support SR delivery logistics. In this section, we introduced the developed SR-MILP. The parameters and variables that may be involved in the following model are described as follows:
,: Index of task
: Index of robot
s: Index of station
: Index of transportation frequency
: Set of tasks
: Set of robots
: Set of transportation times
: Set of robots starting station
: Set of robots ending station
:
: Time from zero to full power
: Maximum working power of the robot
: Initial power level
: Decision variable, representing the power consumption in the first transportation
: Task processing time
: Task demand
: The maximum transportation capacity of the robot
: The speed of robot k
: The distance between two tasks
: Binary decision variable, during the first transportation, if the robot processes the task or returns to the service station to charge after the task; otherwise it is 0
: Binary decision variable, if the task is assigned to the robot in the first transportation; otherwise it is 0
: A non-negative real number decision variable, which is the time when the robot starts its transportation task for the first time or charging at the service station
: A non-negative integer decision variable, the amount of product the robot loads after completing the task.
3.2.2. Load Weight Influence Function
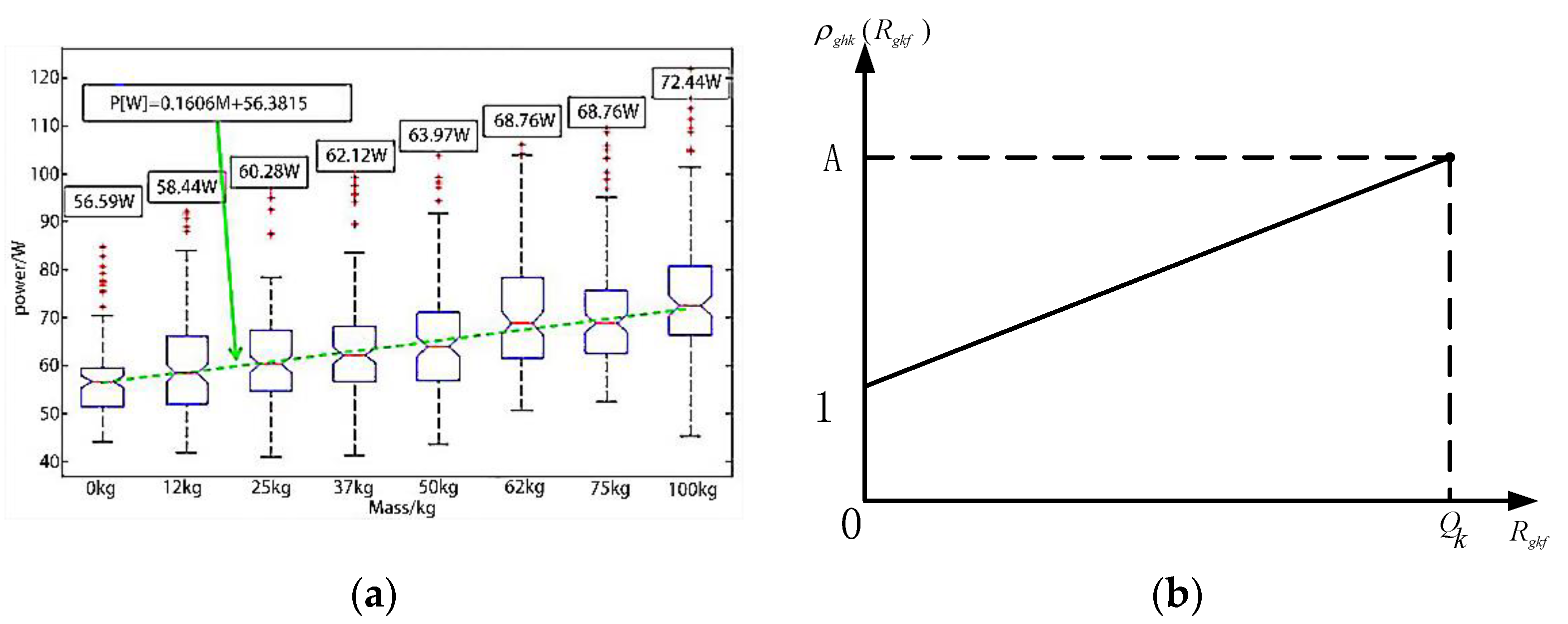
As shown on the left of Figure 3, Hector Montes and Lisbeth Mena found that the power consumption of the robot is significantly affected by the load weight, which means that its transportation time is related to the load weight [43]. On this basis, we developed a function where load weight affects running time, as shown in the right side of Figure 3 and the Equation (1). Where the transport influence coefficient is positively correlated with the load, represents the maximum load of the robot; A is the upper limit of the load weight; and A ≥ 1:
where is .
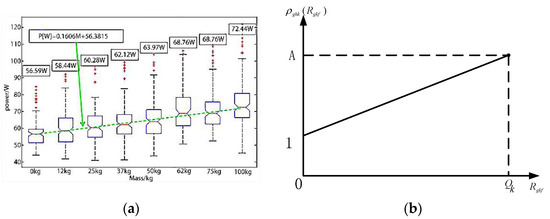
Figure 3.
Study on the influence of load weight. (a) Relationship between power and load; (b) Relationship between transport capacity factor and load.
3.2.3. Service Station Charging Function
In the real world, the robot may be at any initial service station and power level, which has an impact on the charging time of the robot at the service station. In this study, the charging time in the shared service station depends on the remaining battery power of the robot. In addition, since we did not know the remaining power level of the initial working robot, we developed a SGN function as Equation (2) to describe:
It can be seen from Figure 3 that the value of is different when , which is in line with the real situation. These variables need to enforce constraints as show in Equation (3).
3.2.4. The Model
From the above analysis of the proposed intelligent logistics distribution service system, it is obvious that the optimization analysis of the distribution path of the swarm robots is the focus of our study. The purpose of the mission is to minimize the distribution cost while improving the service level. In this part, The MILP is proposed to support the delivery of robots described by the system. Equation (4) is the objective function. The objective of the objective function is to minimize the weighted sum of two objectives, the total travel distance during the completion of the service to the customer, and the delivery of the service within the time window, where Ogkf is the penalty cost where the robot exceeds the customer service time in the transportation; the weighting factor a1 is used to provide a balanced solution between two goals; and a2 represents the penalty coefficient for exceeding the service time.
The relationship between decision variables , is defined in Equation (5):
The robot may end the work after completing the task as show in Equation (6).
Equations (7) and (8) ensure that each robot starts the first transport from its initial service station, where Sbk represents the initial service station. In the same manner, Equation (9) indicates that each time the robot enters a service station, it means that the transportation is completed.
All service tasks need to be completed. An idle robot must stay at a station to reduce unnecessary travel distance, and each task can be served by at most one robot, as follows:
Equation (11) links previous and next shipments. With this constraint, if the robot completes its transportation at the service station s, its transportation starts from the service station s-1:
In addition, because each station has two indexes as the starting station and the ending station, respectively, in order to avoid the robot from completing the transportation at the starting station, as show in Equation (12):
A penalty cost function is used to represent the time window limit of each task, and each robot must perform the task within the allowable range of its power level, where M is a large positive number. The completion time of the of the robot is the start time of , and :
When the task is not assigned to robot k during the transportation, the value of is set to 0 as show in Equation (14):
Each robot’s total time from the starting station to the ending station includes the processing task time and the transportation time and considers the second section, where the transportation time is affected by the load weight. The time that the robot completes the task must be within the allowable range of its power level, as show in Equation (15).
Equation (16) means that when index from represents a service station, means the quantity of products each robot needs to transport each time, and the quantity of each transport should be equal to the customer demand and cannot exceed the load capacity. As each task is delivered, the number of load product gradually decreases, as shown in Equation (17):
3.3. Solving Algorithm
In order to solve the problem better, the above model proposed above is simplified here. Only a single and multitasking transportation of each robot is considered: , and each robot returns to its departure warehouse for charging when it completes its task. Through the above literature review and analysis, the S-PSO can well represent the problem space of discrete combinatorial optimization problems including VRP; in other words, the problem space of VRP is a directed complete graph, and each candidate solution is a generated subgraph of the complete graph. Therefore, PSO can naturally solve VRP by using a set-based method. In this paper, a set-based particle swarm algorithm is designed for the above-mentioned SR distribution model.
3.3.1. S-PSO Algorithm
PSO is a population-based stochastic optimization algorithm proposed by J. Kennedy and R. C. Eberhart in 1995 [44]. The algorithm was first inspired by the social interaction behavior of a bird community and fish education. In order to provide the best solution, each so-called “particle” updates its flight speed and current position iteratively according to its own flight experience and the flight experience of other particles. The speed and position update methods of traditional particle swarms are defined in Formulas (18) and (19).
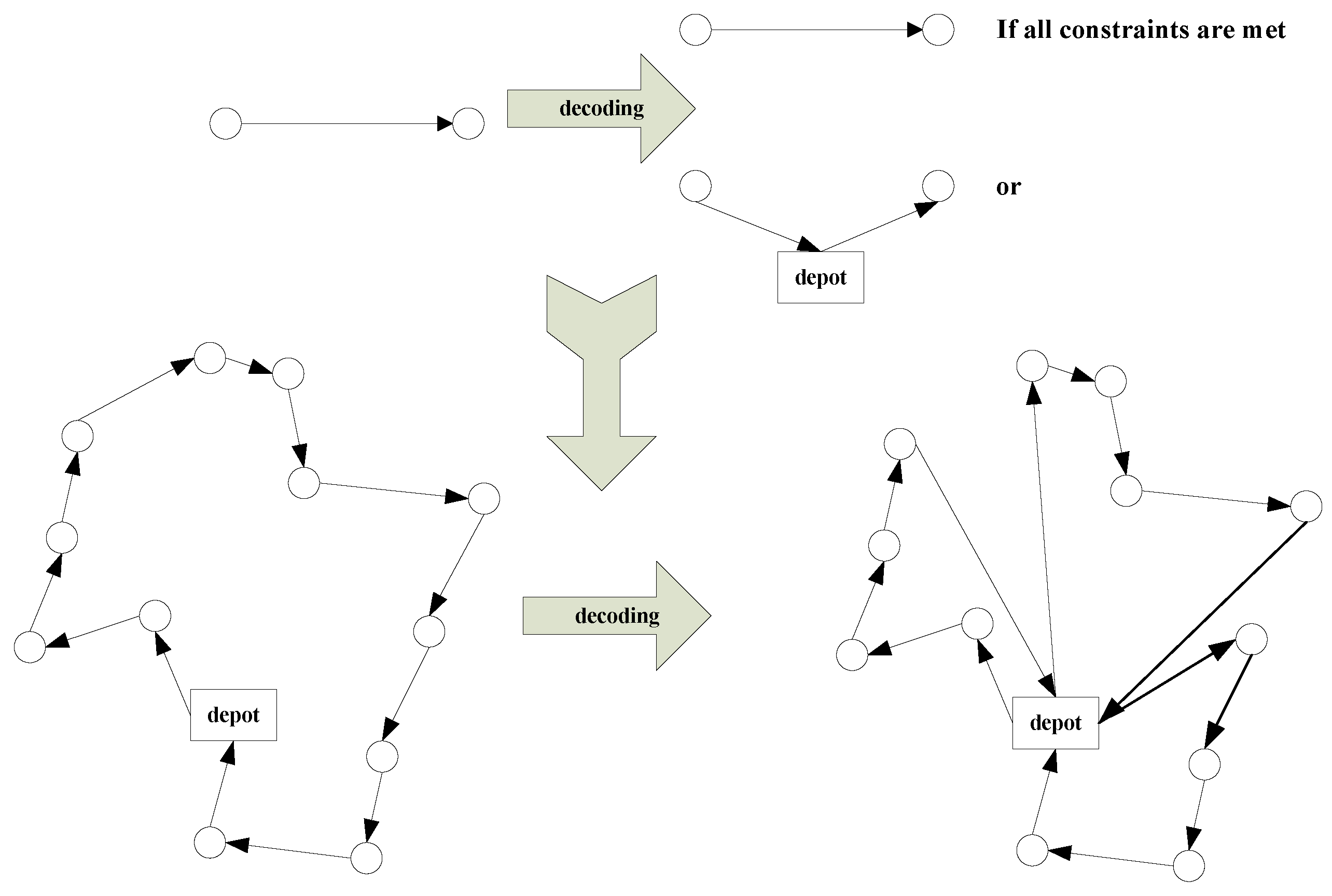
The method used in this paper is the set-based particle swarm optimization (S-PSO), which is a discrete particle swarm optimization algorithm designed specifically for solving the MDVRPTW. represents the position of the particle, and represents the velocity is represented by . If the number of particles in the swarm is N, represents each particle in the swarm,. represents the current number of iterations. The position of the particle in VRPTW is expressed as , and the position of each particle in the m-dimension is expressed as . Therefore, the position of the particles can be expressed as Equation (20). The position of each particle represents a directed Hamilton circle in the complete graph, and the Hamilton circle can be converted into a specific solution for a set of vehicle routes using the constraint-based decoder in this paper. As shown in Figure 4, starting from the outer arc of the warehouse, if an arc in the Hamilton circle satisfies all the constraints in the model, it will be retained; otherwise, the warehouse will be inserted between two nodes and the arc replaced by two new arcs. Through the definition of particle position and a constraint-based decoder, each particle represents a feasible solution to the model of the collaborative and persistent delivery problem of SR in the algorithm.
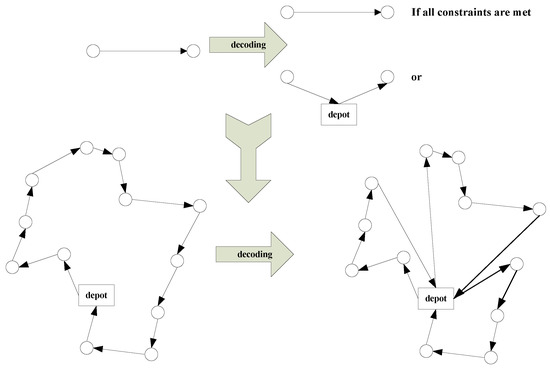
Figure 4.
Decoder method based on model constraints.
The position of the particle in each dimension is composed of two arcs adjacent to node d., as show in Equation (21), represents the current dimension; is the previous customer point; and is the next customer point. among them, , nb1 ≠ nb2.
The velocity of a particle is the probability of a set of arc lengths being selected. represents the speed of the particle in the m-dimensional space. The speed in the m-dimensional space is defined in Equation (22).
represents the probability of edge being selected for particle position update, . If , it means that side will not be selected. When the particle position is updated, the velocity u is converted into an edge, and the edge selection is shown in Equation (24).
The update of the particle position adopts a constructed method; Ω is used to represent the vehicle load and service time window. At the beginning, is an empty collection and repeats the steps. Assume that the customer point currently being delivered is ; the next delivery customer point j is selected, and there are 3 forms, given below as shown in Equations (25)–(27).
Assuming that the current delivery customer point is , the next delivery customer point is selected; there are the following three forms, according to the priority order from top to bottom. If there is no customer point that can be selected, or Ω is not satisfied, a path is generated.
When updating the speed of particles, speed × speed is defined in Equations (28) and (29).
Speed + speed is defined in Equation (30).
Location—location is defined in Equation (31).
From the above equation the Equations (32) and (33) can be obtained as follows:
Speed update equation of S-PSO algorithm is defined in (34), and the speed update according to this operation can obtain .
3.3.2. GA Improved S-PSO Algorithm
Considering that the particle swarm algorithm easily falls into the problem of local extremum, and it takes a long time to solve larger-scale problems [45], this paper proposes the genetics-improved S-PSO (S-GAIPSO) algorithm. When updating particles, it considers the local extremum and global extremum in the traditional particle swarm algorithm. It also combines the crossover operation and mutation operation operator of the genetic algorithm to cross the individual current extreme value with the overall extreme value of the particle swarm, then follows a certain probability of mutation to increase the diversity of particles. The improved algorithm based on the SR distribution model retains the fast local search advantage of the particle swarm algorithm and has the global optimization performance of the genetic algorithm at the same time. The crossover operators of the particle’s velocity and position are defined in Equations (35)–(38).
where represents the offspring of the particle; represents the parent of the particle; and represents the crossover probability. is a random number. Based on multiple experiments, we set the value of to 0.2. The two parents are combined to produce two new offspring. If the fitness of offspring is more than the fitness of the parents, the offspring will be selected to replace the parents; otherwise, the offspring are discarded.
4. Experimental Evaluation
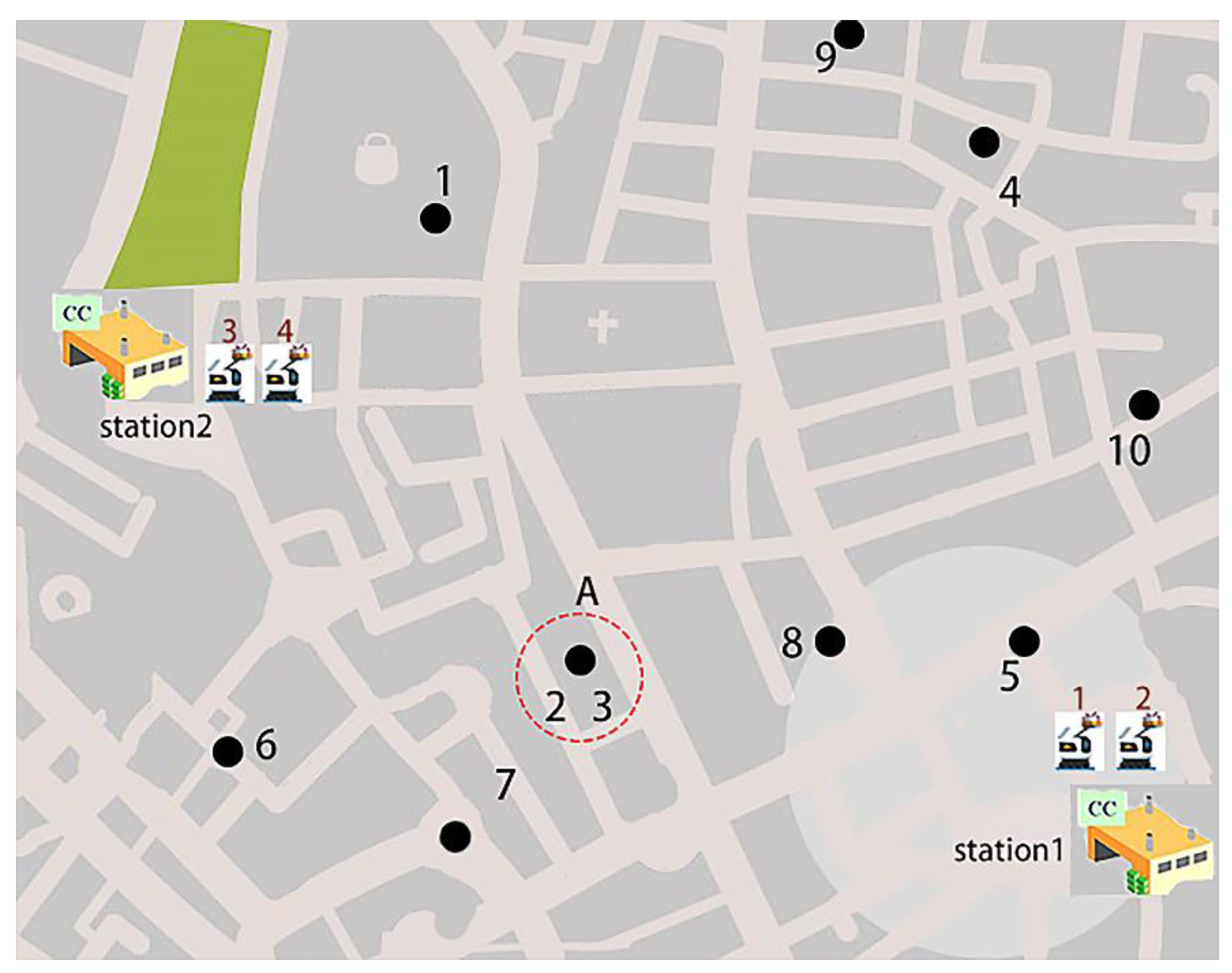
In this example, we tested the proposed MILP and S-GAIPSO algorithm. All experiments were performed on a personal computer using Intel(R) Core (TM) i7-8565U CPU @1.99 GHz and 8.00 GB RAM. We used a CPLEX solver based on MATLAB to call the YAMLIP toolkit and MATLAB R2016a to implement the S-GAIPSO algorithm, which are compared and discussed in terms of the solution gap and computational power with various sizes of randomly generated problems; a1 and a2 are set to 10 and 100, respectively. The following cases were simulated and tested based on real large-scale community distribution. In this case, Figure 5 is a planning map of a community, with two service stations where robots can charge and load goods. A set of randomly generated data is used to represent the service information of customer, including the X/Y coordinates, time window, and service time. The position of the customer is represented by the two-dimensional coordinates of each point, and the distribution path between the two tasks is represented by calculating the Euclidean distance of the two points. Each customer has a serviceable time window, and the robot needs to complete the delivery for it during this time period. The speed of robot is 1.0–1.5 m/s under light load conditions. Some new small robots such as ABB, KUKA, FANUC, etc. can basically reach 5–6 m/s. We take the robot’s speed as 4 m/s. During the transportation process, the robot does not consider the problem of congestion. It is only related to its load weight and drives at a constant speed between the two tasks. In delivery services, an effective delivery schedule achieved by minimizing the total travel distance is very important. In addition, our study considered the time window of customer service, that is, to provide service to each customer in the earliest and latest time period.
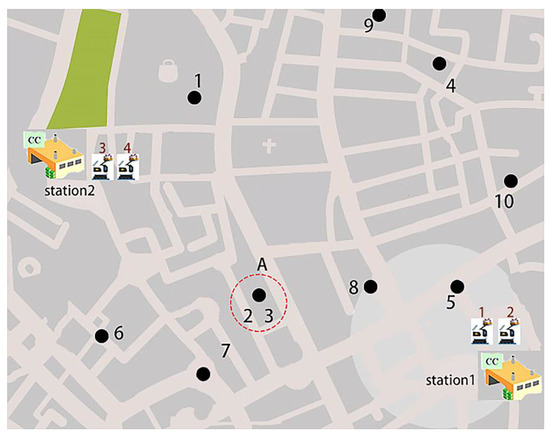
Figure 5.
System layout of smart community delivery service using SR.
4.1. Example Background
The system layout of the smart community is shown in Figure 5. We supposed that there are two service stations, located at (104, 32), (16, 69). Service station 1 has two robots, 1 and 2, and service station 2 has two robots, 3 and 4. The loadable capacity of these robots is 3, and their maximum distance is 300. Table 1 describes the 10 task requests in the delivery service area, and in this table, the serial number of the first column represents service customers. The second and third columns represent the X and Y coordinates of the service customers. The fourth column and the fifth column, respectively, represent the service time window required by the customer; the sixth column represents the time required for service at the customer point. For example, task 1 is located at coordinates (31, 82); it should start between time 0 and 2, and the execution of this task requires 0.5 s of service time. The charging time of the service station is supplemented according to the power loss of the robot during transportation. Since the simplified model considers that each robot is only transported once, it will return to the originating station to recharge or load the product after completing the task. As always, the robot has strict restrictions on the products that can be loaded. However, it is possible that a certain task is too heavy, so we divided this task into two tasks sharing the same location and time constraint, such as task A in the table. In our follow-up algorithm application, the distance between the two tasks is calculated according to the position of each task on the map. The specific calculation is shown in the following formula:

Table 1.
Task delivery information of the robot.
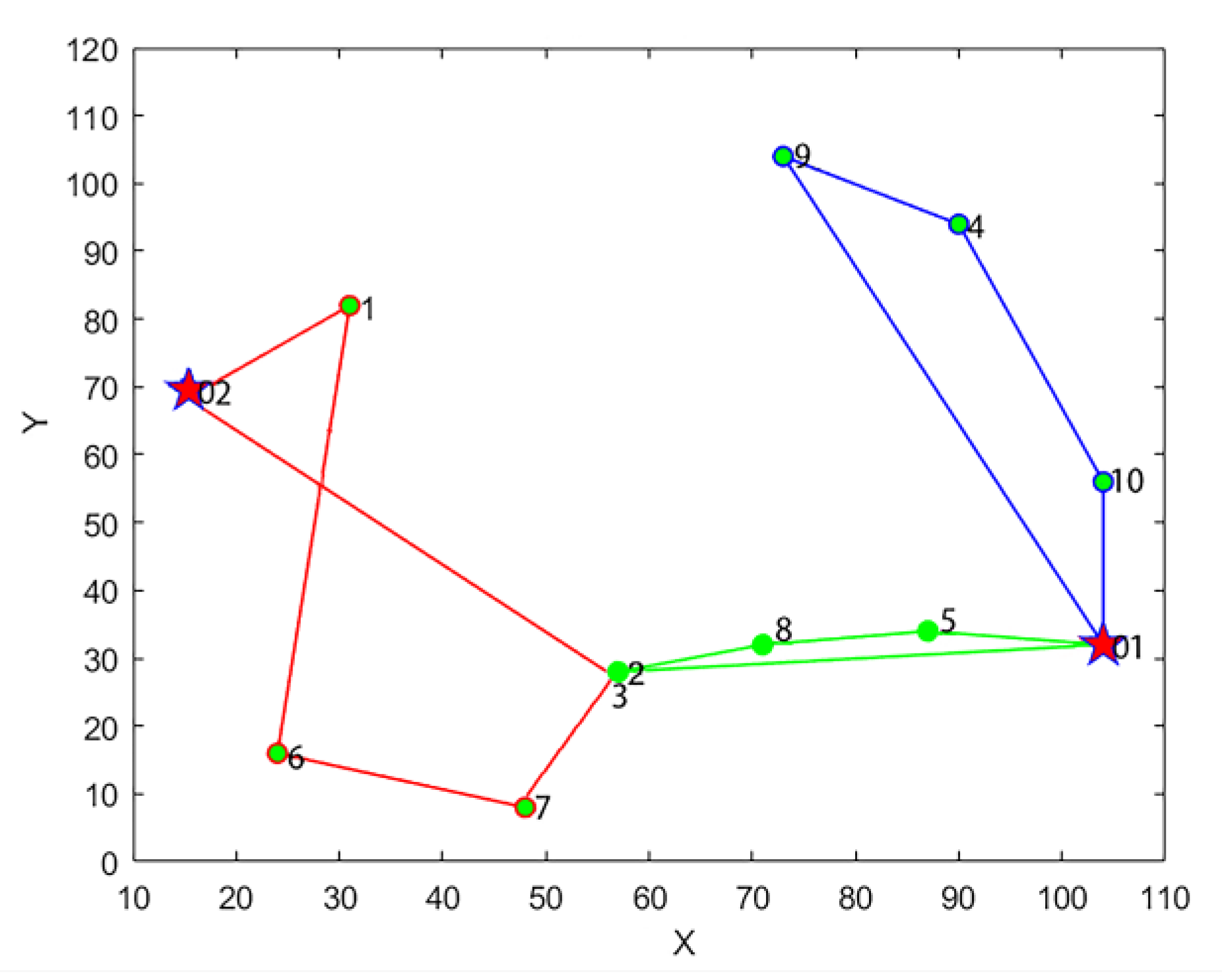
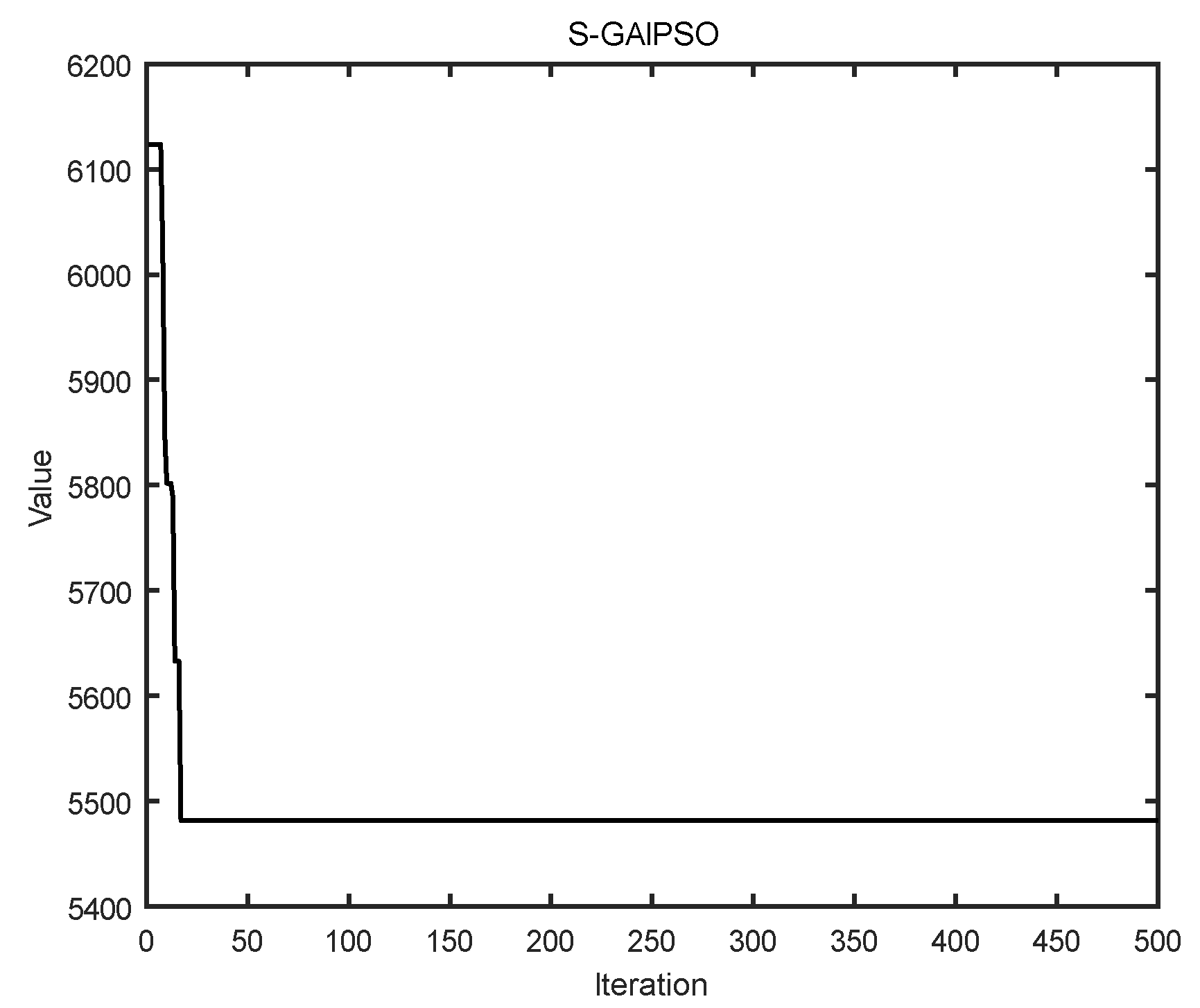
Using the proposed algorithm, we obtained the best solution where the objective function value is 5496.2. As shown in Figure 6, it is the final assignment route of the 10 tasks. The optimal value iteration curve obtained by the algorithm is shown in Figure 7, and the specific task plan is shown in Table 2. Robot 1 leaves station 1 and returns to station 1 after performing tasks 2, 8, and 5. Robot 2 leaves station 1, performs tasks 10, 4, and 9, and then returns to station 1. Robot 3 leaves stations 2 and returns to station 2 after performing task 3, task 7, task 6, and task 1. It can be seen robot 4 is not used. Task A is finished by the robot 1 and 3 together.
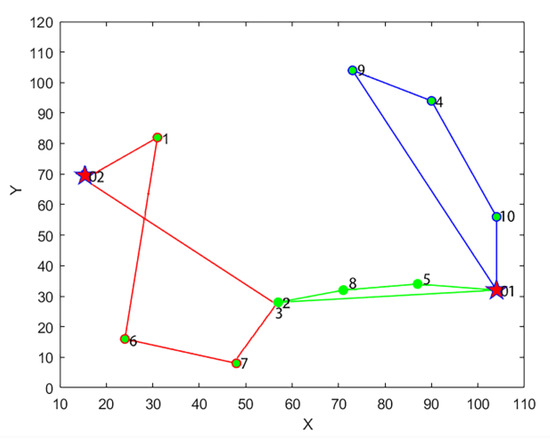
Figure 6.
Final roadmap for 10 missions.
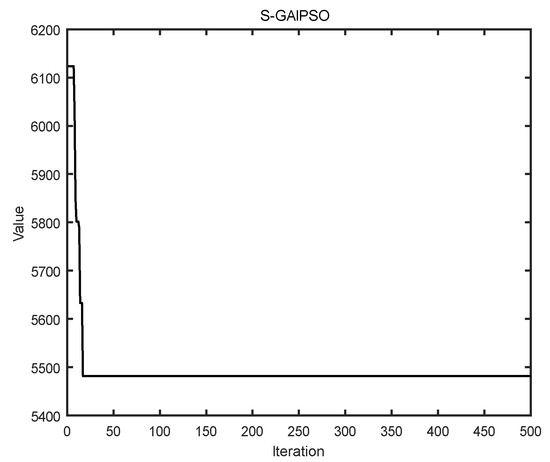
Figure 7.
Schematic illustrations of the search process.

Table 2.
Optimal schedule of SR.
4.2. Performance Evaluation of CPLEX and S-GAIPSO
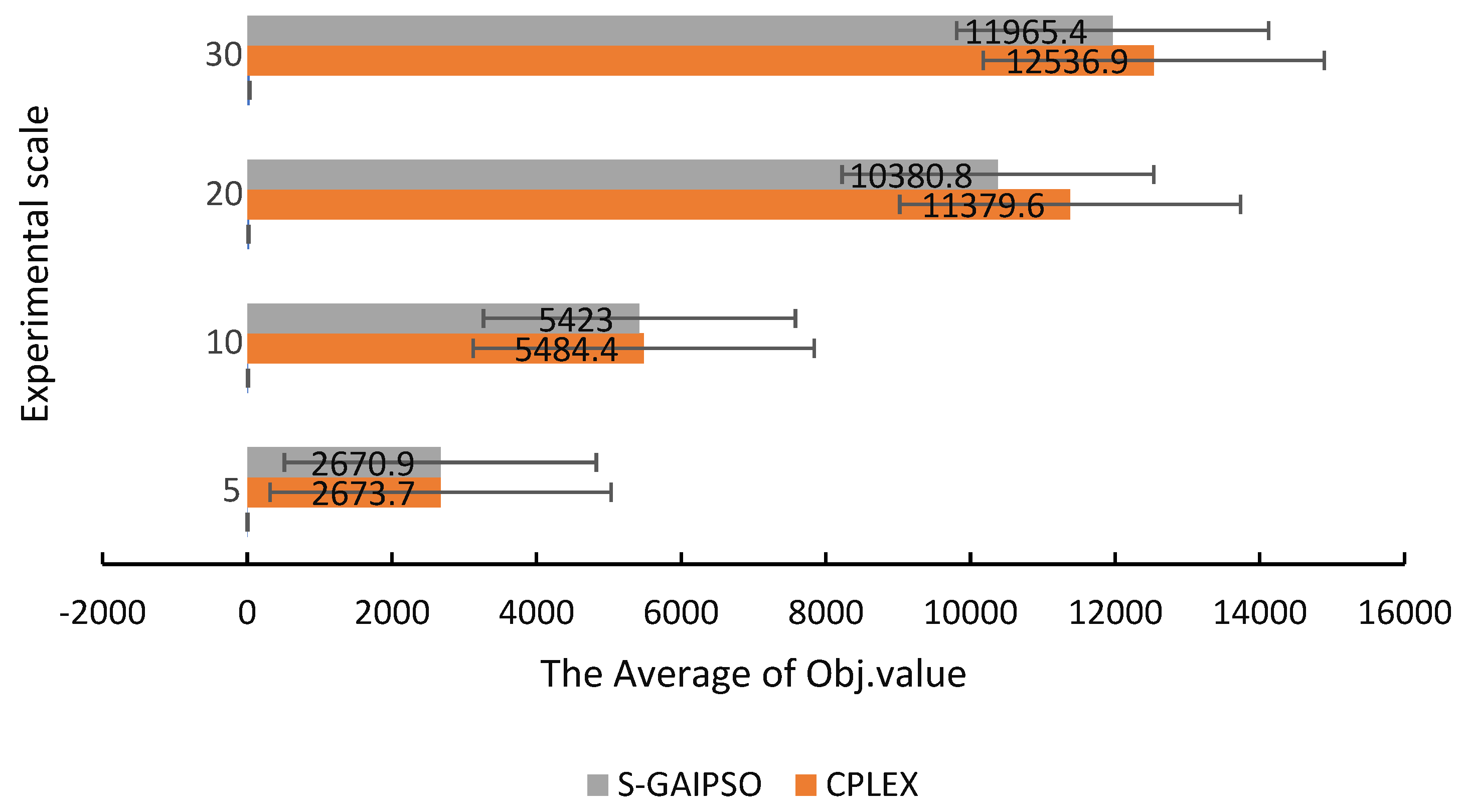
In general, as the scale of the problem increases, its complexity will increase. As an advanced solver CPLEX can solve VRP models of general complexity, the S-GAIPSO proposed in this paper can obtain the optimal solution in a short time. In order to test the calculation and optimization capabilities of the proposed S-GAIPSO algorithm, we conducted experiments on numerical cases with tasks of 5, 10, 20, and 30 in different scales. Table 3 shows the corresponding results and compares the calculation time and optimized gap value of CPLEX and S-GAIPSO. Figure 8 compares the average target values for different scale tasks in the form of a bar graph. As the number of tasks increases, the difference between the function values (the total travel cost of the robot used and the penalty cost of exceeding the customer’s service time) obtained by the algorithm and CPLEX becomes larger and larger. The calculation time of the SR MILP increases rapidly with the increase of the number of tasks. In the experiment to solve a scale of 20 tasks, it appeared that CPLEX could not generate the best solution for 2 cases. As the scale of the experiment continues to increase, for example, and each case has 30 tasks, CPLEX can no longer be used to provide a feasible solution, and our proposed algorithm also shows strong computing power and requires less than 0.35 s CPU time to obtain the optimal or close-to-optimal solution. Compared with CPLEX solvable solutions, S-GAIPSO achieved a gap of 0.157%, 1.097%, and 2.077%, respectively, when there were 5, 10, and 20 tasks on average. The optimality gap is determined by the Formula (40) calculations.

Table 3.
Result comparison of CPLEX and S-GAIPSO.
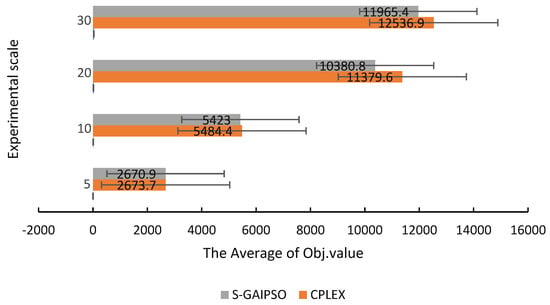
Figure 8.
Comparison chart of the average target value under different task scales.
5. Conclusions and Future Work
A combined intelligent logistics service framework is proposed based on the Internet of Things technology, network communication technology, and coordinated delivery optimization technology in this paper. This study not only focuses on how to realize intelligent logistics services, but also is directly related to reducing customer waiting time, improving customer satisfaction, and the efficiency of completing tasks. The research significance of this article is mainly reflected in two aspects. (a) This article provides detailed ideas on how to design an intelligent distribution system, including how to realize the start-up time and path planning solutions of customers and corresponding robots. (b) This article uses the proposed methods to obtain the corresponding solutions in the form of a case study, which helps the operator to obtain a better reference in practice.
At the departure service station, SR replenish their consumables, including battery charging and loading delivery products. In this way, through solving the problem of being unable to operate remotely for a long time due to the limitation of the power level and load capacity of the robot, we realize the cooperative and persistent delivery service of SR. Corresponding functions are developed for the different customer-oriented needs and the transportation characteristics of the robot itself, including the load weight effects, transportation time, and the behavior of the robot during the idle state. The constructed SR MILP is advanced and applied to the delivery service of large-scale smart communities. The S-GAIPSO algorithm and the solver CPLEX are tested with numerical examples of different scales, and the superiority of the proposed algorithm is proved by the comparison of optimality loss and CPU time. We hope that this research will contribute to existing and emerging robotic applications, improving customer satisfaction by shortening the time customers wait for payment.
Although this article uses model data instead of the actual case data to verify the methods and algorithms we designed, the speed of the robot is based on the existing data, and all task data are based on realistic simulations. Therefore, it does not affect the theoretical and practical value of this paper. Due to the limitation of practical conditions, in the future, the SR of large smart communities can be considered for the experiment of logistics distribution. Our next goal is to consider the collision of obstacles in the driving path of the robot. The dynamic vehicle path optimization problem with changes in customer demand and time window will be more in line with the actual situation of future distribution. In addition, there may be more optimized and comprehensive algorithms for model resolution.
Author Contributions
Conceptualization, M.Z. and B.Y.; methodology, M.Z. and B.Y.; software, M.Z.; validation, M.Z. and B.Y.; formal analysis, M.Z.; investigation, M.Z. and B.Y.; resources, M.Z.; data curation, M.Z.; writing—original draft preparation, M.Z. and B.Y.; writing—review and editing, M.Z. and B.Y.; visualization, M.Z.; supervision, B.Y.; project administration, B.Y.; funding acquisition, B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under grant number 71871136, and the Science and Technology Innovation Action Plan Project of Shanghai under grant number 19DZ1209600.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this study are included within the article.
Conflicts of Interest
The authors declare that they do not have any commercial or associative interests that represents any conflict of interest in connection with the work submitted.
References
- Bačík, J.; Tkáč, P.; Hric, L. Phollower-The Universal Autonomous Mobile Robot for Industry and Civil Environments with COVID-19 Germicide Addon Meeting Safety Requirements. Appl. Sci. 2020, 10, 7682. [Google Scholar] [CrossRef]
- Keenon Robot. 2021. Available online: https://www.keenonrobot.com/GoogleScholar (accessed on 20 March 2021).
- Swayamsiddha, S.; Mohanty, C. Application of cognitive Internet of Medical Things for COVID-19 pandemic. Diabetes Metab. Syndr. Clin. Res. Rev. 2020, 14, 911–915. [Google Scholar] [CrossRef] [PubMed]
- Guptaeepti, D.; Bhatt, S.; Gupta, M. Future Smart Connected Communities to Fight COVID-19 Outbreak. Internet Things 2021, 13, 100342. [Google Scholar] [CrossRef]
- Perdoch, M.; Bradley, D.; Jonathan, K.C. Leader Tracking for a Walking Logistics Robot. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 2994–3001. [Google Scholar] [CrossRef]
- Didier, B. Impacts of Robotization on the Logistics. Available online: https://www.rolandberger.com/zh/Publications/pubofrobotsandmen.html (accessed on 15 December 2021).
- Zhang, R.; Pavone, M. Control of robotic mobility-on-demand systems: A queueing-theoretical perspective. Int. J. Robot. Res. 2014, 35, 186–203. [Google Scholar] [CrossRef]
- Wen, L.; Zhu, F. Swarm Robotics Control and Communications: Imminent Challenges for Next Generation Smart Logistics. IEEE Commun. Mag. 2018, 56, 102–107. [Google Scholar] [CrossRef]
- Xue, F.; Tang, H.; Su, Q. Task Allocation of Intelligent Warehouse Picking System based on Multi-robot Coalition. KSII Trans. Internet Inf. Syst. 2019, 13, 3566–3582. [Google Scholar] [CrossRef] [Green Version]
- Song, B.D.; Kim, J.; Morrison, J.R. Rolling Horizon Path Planning of an Autonomous System of UAVs for Persistent Cooperative Service: MILP Formulation and Efficient Heuristics. J. Intell. Robot Syst. 2016, 84, 241–258. [Google Scholar] [CrossRef]
- Li, J.; Yang, F. Task assignment strategy for multi-robot based on improved Grey Wolf Optimizer. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 6319–6335. Available online: https://link.springer.com/article/10.1007/s12652-020-02224-3 (accessed on 20 October 2021). [CrossRef]
- Pramanik, P.; Maiti, M.K. An inventory model for deteriorating items with inflation induced variable demand under two level partial trade credit: A hybrid ABC-GA approach. Eng. Appl. Artif. Intell. 2019, 85, 194–207. [Google Scholar] [CrossRef]
- Kuo, R.J.; Lu, S.H.; Lai, P.Y.; Mara, S.T.W. Vehicle Routing Problem with Drones Considering Time Windows. Expert Syst. Appl. 2021, 191, 116264. [Google Scholar] [CrossRef]
- Christofifides, J.; Mingozzi, N.A. State-space relaxation procedures for the computation of bounds to routing problems. Networks 1981, 11, 145–164. [Google Scholar] [CrossRef]
- İLhan, İ. An improved simulated annealing algorithm with crossover operator for capacitated vehicle routing problem. Swarm Evol. Comput. 2021, 64, 100911. [Google Scholar] [CrossRef]
- Karakatič, S. Optimizing nonlinear charging times of electric vehicle routing with genetic algorithm. Expert Syst. Appl. 2021, 164, 114039. [Google Scholar] [CrossRef]
- Bae, H.; Moon, I. Multi-depot vehicle routing problem with time windows considering delivery and installation vehicles. Appl. Math. Model. 2016, 40, 6536–6549. [Google Scholar] [CrossRef]
- Sahin, E. Swarm robotics: From sources of inspiration to domains of application, in Swarm Robotics. Lect. Notes Comput. Sci. 2005, 334, 10–20. [Google Scholar] [CrossRef]
- Fukuda, T.; Kawauchi, Y. Cellular robotic system (cebot) as one of the realizations of self-organizing intelligent universal manipulator. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; pp. 662–667. [Google Scholar] [CrossRef]
- Nedjah, N.; Silva, L.J. Review of methodologies and tasks in swarm robotics towards standardization. Swarm Evol. Comput. 2019, 50, 100565. [Google Scholar] [CrossRef]
- Senanayake, M.; Ilankaikone, S.; Carlo, B.J. Search and tracking algorithms for swarms of robots: A survey. Robot. Auton. Syst. 2016, 75, 422–434. [Google Scholar] [CrossRef]
- Wang, J.; Lim, M.K.; Zhan, Y.; Wang, X. An intelligent logistics service system for enhancing dispatching operations in an IoT environment. Transp. Res. Part E Logist. Transp. Rev. 2020, 135, 101886. [Google Scholar] [CrossRef]
- Leofante, F.; Abraham, E.; Niemueller, T. Integrated Synthesis and Execution of Optimal Plans for Multi-Robot Systems in Logistics. Inf. Syst. Front. 2019, 21, 87–107. Available online: https://link.springer.com/article/10.1007/s10796-018-9858-3 (accessed on 23 October 2021). [CrossRef] [Green Version]
- Milford, M.; Wyeth, G. Hybrid robot control and SLAM for persistent navigation and mapping. Robot. Auton. Syst. 2010, 58, 1096–1104. [Google Scholar] [CrossRef]
- Eijyne, T.; Rishwaraj, G.; Ponnambalam, G.S. Development of a task-oriented, auction-based task allocation framework for a heterogeneous multirobot system. Sadhana-Acad. Proc. Eng. Sci. 2020, 45. [Google Scholar] [CrossRef]
- Boysen, N.; Schwerdfeger, S.; Weidinger, F. Scheduling last-mile deliveries with truck-based autonomous robots. Eur. J. Oper. Res. 2018, 271, 1085–1099. [Google Scholar] [CrossRef]
- Puyuan, D.; Amirjamshidi, G.; Roorda, M. A vehicle routing problem with movement synchronization of drones, sidewalk robots, or foot-walkers. Transp. Res. Procedia 2020, 46, 29–36. [Google Scholar] [CrossRef]
- Lenstra, J.K.; Kan, A.H.G.R. Complexity of vehicle routing and scheduling problems. Networks 1981, 11, 221–227. [Google Scholar] [CrossRef] [Green Version]
- Vaziri, S.; Etebari, F.; Vahdani, B. Development and optimization of a horizontal carrier collaboration vehicle routing model with multi-commodity request allocation. J. Clean. Prod. 2019, 224, 492–505. [Google Scholar] [CrossRef]
- Bimgshan, M.A.; Dawei, H.; Xiqiong, C. An Optimization of Pure Electric Vehicle Routing Problem on Half-open Multi-distribution Center. J. Transp. Syst. Eng. Inf. Technol. 2019, 19, 199–205. [Google Scholar] [CrossRef]
- Liang, J.; Qin, K.; Suganthan, P.N. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2016, 10, 281–295. [Google Scholar] [CrossRef]
- Calvet, L.; Ferrer, A.; Gomes, M. Combining statistical learning with metaheuristics for the Multi-Depot Vehicle Routing Problem with market segmentation. Comput. Ind. Eng. 2016, 94, 93–104. [Google Scholar] [CrossRef] [Green Version]
- Ting, C.J.; Wu, K.C.; Chou, H. Particle swarm optimization algorithm for the berth allocation problem. Expert Syst. Appl. 2014, 41, 1543–1550. [Google Scholar] [CrossRef]
- Zhen, T.; Ge, H.; Che, Y.; Jiang, Y. Research on particle swarm optimization for grain logistics vehicle routing problem. In Proceedings of the 2009 IITA International Conference on Services Science, Management and Engineering, Zhangjiajie, China, 11–12 July 2009; pp. 274–277. [Google Scholar] [CrossRef]
- Amini, S.; Javanshir, H.; Tavakkoli-Moghaddam, R. A PSO approach for solving VRPTW with real case study. Int. J. Res. Rev. Appl. Sci. 2010, 4, 118–126. [Google Scholar]
- Yan, Y.; Zhang, R.; Wang, J.; Li, J. Modified PSO algorithms with “Request and Reset” for leak source localization using multiple robots. Neurocomputing 2018, 292, 82–90. [Google Scholar] [CrossRef]
- Song, B.; Wang, Z.; Zou, L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Appl. Soft Comput. 2021, 100, 106960. [Google Scholar] [CrossRef]
- Asma, A.; Sadok, B. PSO-based Dynamic Distributed Algorithm for Automatic Task Clustering in a Robotic Swarm. Procedia Comput. Sci. 2019, 159, 1103–1112. [Google Scholar] [CrossRef]
- Kwa, H.; Kit, J.L.; Bouffanais, R. Optimal swarm strategy for dynamic target search and tracking. In Proceedings of the 19th International Conference on Autonomous Agents and Multi Agent Systems, Singapore, 9–13 May 2020; pp. 672–680. [Google Scholar]
- Kwa, H.L.; Kit, J.L.; Bouffanais, R. Tracking Multiple Fast Targets with Swarms: Interplay Between Social Interaction and Agent Memory. In Proceedings of the 2021 Conference on Artificial Life, Virtual, Czech Republic, 19–23 July 2021. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, J.; Chung, H.S.H.; Zhong, W.; Wu, W.; Shi, Y. A Novel Set-Based Particle Swarm Optimization Method for Discrete Optimization Problems. IEEE Trans. Evol. Comput. 2010, 14, 278–300. [Google Scholar] [CrossRef]
- Liangru, W.U.; Yang, K.; Zheng, Z.; Ding, H. Map Creation Method for Mobile Robot and Path Planning Method Based on The Map. U.S. Patent 16/712,977, 2020. [Google Scholar]
- Montes, H.; Mena, L.; Armada, M. Energy-efficiency hexapod walking robot for humanitarian demining. Ind. Robot.-Int. J. 2017, 44, 457–466. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Yang, J.; Cui, X.; Li, J.; Li, S.; Liu, J.; Chen, H. Particle filter algorithm optimized by genetic algorithm combined with particle swarm optimization. Procedia Comput. Sci. 2021, 187, 206–211. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).