Abstract
In this paper, we introduce a linear program (LP)-based formulation of a rendezvous game with markers on the infinite line and solve it. In this game one player moves at unit speed while the second player moves at a speed bounded by . We observe that in this setting, a slow-moving player may have interest to remain still instead of moving. This shows that in some conditions the wait-for-mummy strategy is optimal. We observe as well that the strategies are completely different if the player that holds the marker is the fast or slow one. Interestingly, the marker is not useful when the player without marker moves slowly, i.e., the fast-moving player holds the marker.
1. Introduction
The problem that we discuss in this article revolves around the problem faced by two parachutists dropped from an airplane on an island and who need to rendezvous. In order to reduce the dimension of the search space, the two can move to the coastline and restrict their search by moving along the coastline. The two parachutists facing the sea can move to right or to the left. However, going to the right or the left is not a common sense of direction. In an island, depending on where the parachutists are located (north or south) a motion to the right can lead to go eastward or westward, and the two cannot agree on a common direction, for instance, by observing where the sea is flowing (as it would be possible if they were moving along a river). The distance separating them initially may not be known. To formalize the problem, the distance may be assumed a random variable or, this is the approach taken here, the distance is assumed to be bounded and an upper bound on the rendezvous time are searched for. Two novel parameters are considered for this problem. We assume that the two parachutists may move at different speeds and we assume that the parachutists can drop off a marker at the position they are and it may be subsequently found by the other as they pass by the same position. Finding the marker is very useful since it indicates in which direction to go to rendezvous with the other.
More formally, we introduce a variation of the asymmetric rendezvous problem on the line that was introduced by Alpern and Gal [1]. In the original setup, two players are placed on a line at a known distance D and move on the line to rendezvous. The player’s strategies may be different and start at the same time, and both players move at the same speed . At the start and while moving, the players look in a fixed direction, say, right or left. The directions are chosen randomly each with probability . It results that players move either in the direction they look to or the other one, i.e., forward or backward. A strategy is a succession of forward and backward moves. The optimal solution of this problem is shown to be . Many variations have been proposed showing that even a simple topology such as the infinite line leads to interesting problems. Among the hardest seems to be the symmetric rendezvous on the line where the two players have to play the same strategy. Partial solutions of this problem were obtained. In [2], a strategy was proposed that ensured the rendezvous time satisfied . Subsequent strategies were proposed in [3,4] that used the same technique as in [2] and reduced the rendezvous time to and , respectively. Ref. [5] generalized the technique and improved the bound to . The best known bound is given in [6].
Some papers deal with the problem where the initial distance between the players is unknown, see for instance [7,8,9,10]. Usually, the distance is characterized by a probability function. Note that if the players use strategies tailored for a known distance D with rendezvous time R to a problem where it is only known that the distance is bounded by D, then the rendezvous time for this problem is bounded by R.
The way time enters the game leads to relevant variations as well. The constraint that the players start at the same time may be relaxed and this leads to asynchronous rendezvous problems [11,12]. Asynchronous rendezvous problems may assume that an adversary chooses the starting delay or the clocks are assumed to drift with different speeds. There are relations between problems where clocks drift at different speeds and ones where players move at different speed [12].
A problem where players move on the line and share similarities with the rendezvous problem is the group search problem on the line [13]. This problem is motivated by the evacuation problem where players must simultaneously gather at some point. One may imagine that people need to leave a building and are helped with a line drawn on the floor but do not know the right direction to follow. When players move at different speeds, interesting strategies can be found where a fast player move to help slower players.
Problems where players move on a circle share similarities with problems on the line [14,15,16,17,18]. Compared to the infinite line, the ring is a compact topology, but symmetry breaking has to be solved as well to ensure rendezvous. Tokens may be left by players [19,20,21]. For rendezvous problems on the line, Refs. [22,23] present results where markers are used by players. With a more robotic and computer science flavor some problems encompass faulty agents [24,25].
Rendezvous problems are far from being limited to the infinite line or a ring. Problems may be stated for agents moving on a plane, on graphs, on a torus, on networks and so on, see for instance [26,27,28]. These problems are different from the ones considered in this paper.
Markers can have different effects. For instance, the game may end at the time the marker is found, i.e., rendezvous occurs or the marker is found. This would be the case if a phone number is written on the marker. With such a marker, the game would be close to a version of a search-and-rescue game [29]. This may be seen as a mix of rendezvous and search games, see for instance [30,31,32] for search games on graphs and [26,33,34] for general references.
2. Our Contributions
In this paper, we consider the (synchronous) rendezvous problem on the line with known initial distance D where players move at different speeds and where a marker can be left by one of the players. Without loss of generality, we assume that one player moves at speed 1 while the second player moves at speed . We show that investigations can be conducted with linear programming techniques to identify optimal strategies. This is not the conventional approach in the literature where the results are usually guessed and optimality is subsequently proved. The reduction of rendezvous search game to another formalism to be solved appears in the literature, see for instance [35]. Here, the reduction to parametric linear programming has the further advantage that the same method can be applied to compute different measures of optimality. For instance, the optimization of the last rendezvous time. Actually, any linear combination of the rendezvous times can be optimized.
In [23,36], a similar problem with markers is considered. The parametric linear programming approach of this article leads to more precise results than the ad hoc approach of [23]. Moreover, here we accommodate to players with different speeds, extending the results of [23,36].
3. Problem Formulation
We begin by presenting the formalization of the problem as given in [1]. Two players, I and II, are placed at distance (although the results depend linearly on the initial distance and are stated for a general D). apart on the real line, and faced in random directions which they call “forward”. Their common aim is to minimize the expected amount of time required to meet. They each know the distance 1 but not the direction the other player is facing. It is not a restriction to assume that player I’s starting point is located at position 0 of the line and their speed is bounded by . Their position is given by a function , where
for some T sufficiently large so that the rendezvous will have taken place.
What are unknown are the initial position of player II that may be and the forward direction of player II that may point to the positive or negative side of the infinite line. Again, without restriction of generality, we assume that the speed of player II is bounded by 1. Hence, depending on the initial conditions of player II their position at time t is given by with .
The rendezvous times are defined by:
when player II is originally located at and their forward direction points to the positive side of the line.
when player II is originally located at and their forward direction points to the negative side of the line.
when player II is originally located at and their forward direction points to the positive side of the line.
when player II is originally located at and their forward direction points to the negative side of the line.
It is common in the literature to speak of four agents (of player II) located at positions and with forward direction and moving concurrently. Player I needs to rendezvous with the four agents to end the game [26]. Concretely,
- Agent 1 is located at with forward direction and its rendezvous time is ,
- Agent 2 is located at with forward direction and its rendezvous time is ,
- Agent 3 is located at with forward direction and its rendezvous time is ,
- Agent 4 is located at with forward direction and its rendezvous time is .
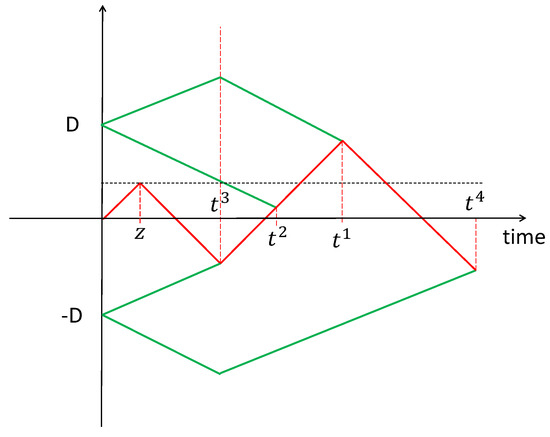
We show in Figure 1 the configurations of the four agents and the optimal solution of the problem without marker. We observe on this figure that the speeds of both players are always maximal (equal to 1). Then, a complete description of the optimal strategy is provided by the order with which player I rendezvous with the agents, i.e., agent and finally 4.
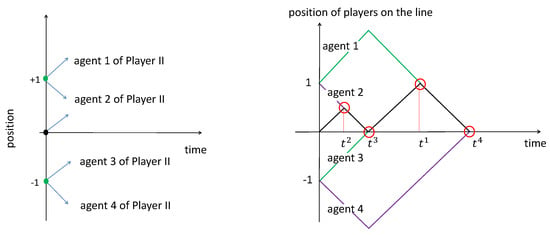
Figure 1.
(On the left): the four agents of player II. Each one corresponds to a particular initial position and direction of the forward move. (On the right): the optimal solution of the game without marker. Player I goes forward for time , then backward for time , then forward for time 1 and backward for time 1. Player II goes forward for time 1, then backward for time 3. The rendezvous occur successively with agents and 4 at times , , and .
Definition 1.
We introduce the notation to denote the rendezvous times in the order they occur, denotes the agent with origin and forward direction . The order of the rendezvous times is given by the index i, is the rendezvous with agent , is the rendezvous with agent , is the rendezvous with agent and is the rendezvous with agent . When necessary, we use the convention .
For instance, for the solution in Figure 1 it holds that , and .
We do not make any assumptions on how the functions and are computed. A different formalism than what we are proposing here may be possible. For instance, as in differential games [37,38,39], and may be bound to be solutions of ordinary differential equation. Our approach here is different. We first show that the functions and that may be optimal have the restricting feature of being of constant derivative between two rendezvous. Then, we enumerate all possible solutions. Notice that pursuit–evasion games are usually modeled as differential games. Compared to pursuit–evasion, our rendezvous game is cooperative and this makes possible the enumeration of all efficient strategies (player I rendezvous with the four agents and what is to be discovered is the order leading to the shorter average of the rendezvous times).
The rendezvous value is defined to be the average value
Finally, the rendezvous value of the game is defined by
A first remark that simplifies the problem is that the functional spaces and may be reduced to consider only functions and lwhose speed is constant between the rendezvous times. Indeed, if the speed is not constant, moving at the average speed between rendezvous times leads to the same rendezvous value. Moreover, similarly to Lemma 5.1 of [1], Theorem 16.10 of [26] or Proposition 3 of [23], we have the following result for .
Proposition 1.
If , then, for the optimal strategies, the function is of constant slope equal to between the rendezvous, i.e., the speed of the fast player is always maximal.
Proof.
Let us assume that player II, whose position is given by function and initial position is known, does not move at maximal speed between rendezvous times . This means that player II can reach the rendezvous position at a time with . By moving faster, it may happen that player II rendezvous with player I before time , reducing the rendezvous time . If not, we modify the trajectory of player II in the following way. After reaching the rendezvous point at time , player II continues in the same direction for a period and then goes the other way for a period , back to the rendezvous position at time . At time , player I must be at a distance less than from the rendezvous position and because player II is at a distance and , the rendezvous must occur before time . To summarize, by moving at full speed, player II always reduces the rendezvous time . After time player II follows the original strategy and the remaining rendezvous times are not changed. In total, the modified strategy reduces the rendezvous value showing that the original strategy is not optimal. We emphasize that the fast-moving player moves at maximal speed while the slow-moving player can move at any speed in . □
Corollary 1.
We assume here that the speed of player I is bounded by and the speed of player II by 1, i.e., and . The sets of optimal strategies for players I and II, respectively, are given by
where , and are the rendezvous times.
Proposition 1 and Corollary 1 are not new and are constantly used in the literature, see for instance Chapter 17.1 of [26]. We stress that player I having the smallest speed bound may move at a slower speed than the maximal one. Indeed, we will observe that for v small, the optimal strategy for player I is to not move before . The “wait for mummy” strategy is then optimal for starting the game.
We consider that player I has at their disposal a marker that may be left at a chosen time. The marker helps player II, who stops following the strategy after finding the marker and continues in the same direction at maximal speed until rendezvousing with player I. The same arguments as the ones in Proposition 1 and Corollary 1 or Proposition 3 of [23], which show that player I move at a constant velocity before and after dropping the marker. There are four different cases to consider for the formulation of the problem depending on which interval, player I drops off the marker at. This leads to the following proposition that characterizes the optimal strategies.
Corollary 2.
When player I has a marker that can be dropped off at chosen time z, the set of optimal strategies f for player I are given by
if .
if .
if .
if . The optimal strategies for player II are still of the form of Equation (8). In any cases, the parameters are constrained to () and , and are the rendezvous times.
Corollaries 1 and 2 are very useful in making the rendezvous value of the game given by Equation (6) computable. Indeed, the set of functions to be considered is finite. Notice that for the problem with marker, the set is finite provided that v is fixed.
It is crucial to point out that in Corollary 2, the optimal strategy of player II is of the form of Equation (8), but if the marker is found at some time, player II no longer follows the strategy but continues in the same direction thereafter. For instance, if the marker is found in the interval at time we must have and the condition
must be satisfied, where o is the original starting point of player II () and b is the forward direction of player II (). Indeed, the condition states that player II starting at position o at time 0 is at the marker’s position at time , i.e., the marker is found. The coefficient is given by the strategy followed by player II and is the effective motion depending on the forward direction b. Thereafter, player II does not follow the strategy but continues in the same direction, i.e., we substitute for in Equation (8). Hence, if the rendezvous does not occur in , player II’s motion is given by
If no rendezvous occurs in the next time interval , the motion of player II is given by
(compare with the second line of Equation (8)). The same reasoning applies for the next time intervals, and .
4. Solution of the Problem without Marker
The optimal strategies of the problem without marker are given in Corollary 1. There are eight unknowns and , the rendezvous time being a consequence of these variables. To reduce the problem to a family of linear programs we rewrite the strategies to remove the products by introducing new variables with the bounds , where v is the maximal speed of player I. To take into account that the speed of player I may be negative (when player I is going backward), we introduce new variables and the motion is computed relatively to . Notice that is a parameter that is fixed before calling the LP-solver (hence, the problem is still linear).
To define the meeting times , we need to specify in which order they occur. Ordering the meeting times amounts to choosing a permutation of such that where are defined by Equations (2)–(5). For this, we introduce new variables with and to refer to specific agents of player II. Concretely,
- Agent 1 is referred by and the rendezvous time is defined by (2),
- Agent 2 is referred by and the rendezvous time is defined by (3),
- Agent 3 is referred by and the rendezvous time is defined by (4),
- Agent 4 is referred by and the rendezvous time is defined by (5).
The rendezvous always occur in the order , , , . The values of and are given by:
For the computation of the solution, we use the variables as parameters. For each set of values, we solve the corresponding linear program. The number of linear programs solved was 1536, which was solved in a few seconds using the Python Gurobi library [40]. Notice that by symmetry, we fixed and .
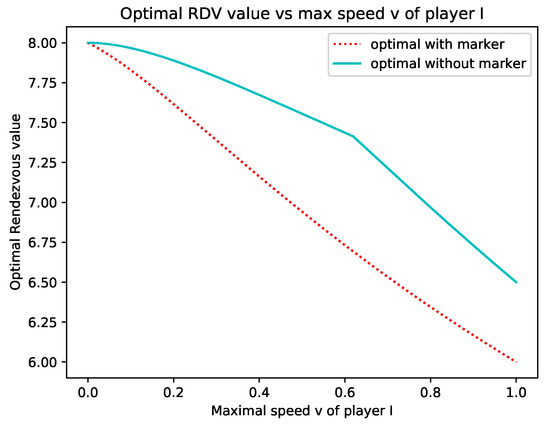
The plot of the results are shown in Figure 2, where the optimal rendezvous value is plotted versus the maximal speed of player I for discrete values , .
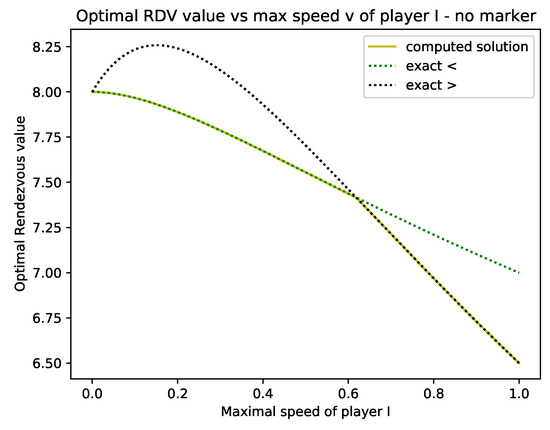
Besides the computation of the optimal rendezvous values, we recorded the corresponding optimal strategy. We observe that for the optimal strategy is (, , and ) for player I and for player II as illustrated in Figure 3. In terms of the optimal strategy of Corollary 1, the speeds of player I are , , and . Notice that player I can play the symmetric strategy as well, which is not illustrated.
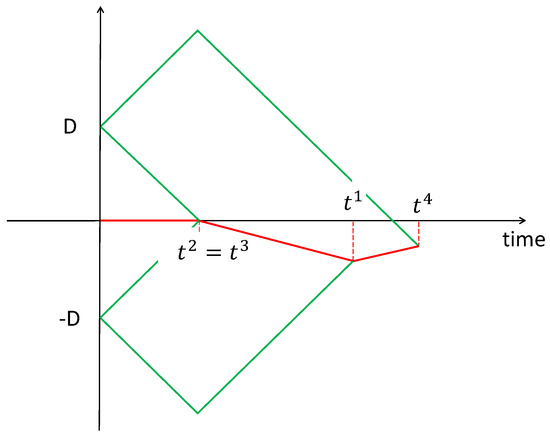
Figure 3.
Optimal strategy for .
It is relevant to observe that until the wait-for-mummy strategy is the optimal strategy for player I, as motion starts only after. For this strategy the expressions for the rendezvous times and the rendezvous value of the game are given by:
Since the optimal strategy is a switch to and for player I and and . In terms of the optimal strategy of Corollary 1 the speeds of player I are , , and . The speed of player I is large enough to allow the improvement of the rendezvous value by moving from the start. The expressions for the rendezvous times and rendezvous value of the game are given by:
It is stated in [26], Chapter 17.1, that the optimal solution is given by (13) for and by (14) for . With our linear programming approach we first conclude that (13) is optimal for and by (14) for , (discrete values).
However, we can say more. Let us denote the function that returns the optimal value of the game when the speed of player I is bounded by v and the function that returns the next-to-optimal value of the game when the speed of player I is bounded by v. These two functions are decreasing since a strategy for v is always a strategy for . Hence, if we have that and the strategy at is the same as that at , it must be that this strategy is optimal in the interval . By computing and , , we detect that the condition stated above is satisfied for and for . To summarize, we have proved the following theorem.
Theorem 1
([26], Chapter 17.1). For , the rendezvous value of the game is given by (13) and the optimal strategy is plotted in Figure 3 and for the rendezvous value of the game is given by (14) and the optimal strategy is plotted in Figure 4.

Figure 4.
Optimal strategy for .
The interval in which Theorem 1 is stated to be true may be enlarged by computing the numerical solutions on a finer mesh, i.e., increasing the number values of n for which we solve the LP.
5. Solution of the Problem with a Marker Held by the Slow Player
The marker is held by one of the players and may be dropped off at any given time. Once dropped off, the marker is to be found by the other player when is passes at the location. Once found, the player stops following the original strategy and continues in the same direction until rendezvous occurs. We first assume that the marker is held by player I, who moves with the lowest speed bounded by , and denote z as the dropping time. There are four possibilities, and , each one leading to a family of linear programs to solve. It happens that only the first case is relevant. For all other cases the optimal solutions do not make use of the marker and are given in Section 4.
The strategy of player I is now given by where indicates whether is positive or negative, i.e., the speed are always assumed positive and the motions are depending on the product . With respect to Section 4, the only novelty is the introduction of , see Equation (9) (compare with (7) with no marker).
Agents of player II can find the marker or not. Hence, for each agent we must generate two linear programs each one assuming the agent finds the marker or not. Actually, for the first agent rendezvousing (agent ), we do not need to differentiate whether the marker is found or not, as the equations are the same. We use the new variable to indicate that agent finds the marker or not (), in the interval . Again if the marker is found by in the interval , the equations do not change. The variable indicate that agent finds the marker in the interval or , respectively. Finally, the variables and indicate that agent finds the marker in the interval , or , respectively.
This leads to the family of linear programs shown in Equations (15)–(17) (we denote and the time at which the marker is found by ).
In this set of equations, the first one is the minimization problem to be solved. Notice that we minimize the sum of the rendezvous time while the number given in the Introduction and Results sections are the average of the rendezvous times. There are four sets of equations, (*), (**), (***) and (****). Equation (*) is the constraint that player I rendezvous with agent at time . Agent may find the marker before time . However, in this case, the optimal solution is to continue in the same direction, i.e., the equation would be
where if player II does not find the marker and else, and is the time at which player II finds the marker. This equation reduces to (*). In (*), if a player finds the marker in the interval the optimal strategy is to continue in the same direction and the marker is useless, and so on for (***) and (****) if the marker is found in the interval and , respectively.
The three remaining sets of equations (**), (***) and (****) are composed of two equations. The first one accounts for the rendezvous of agent with player I and the second one is valid only if the marker is used ( equal 1) and we define the times when the marker is found as .
The next set of equations is composed of the speed constraints. The variable is the product of the speed of player I and the time z at which the marker is dropped; this product is bounded by since the speed of player I is bounded by v. In the results, we observed that the speed of player I is v (maximal) or 0 but we obtaind no solution with v in between.
The family of linear programs was generated by assigning values to the parameters of Equations (15)–(17). These values must satisfy the constraints (the constraints were included in all linear programs)
The families of linear programs were solved for a maximal speed of player I ranging from 0 to 1 with a step size of , i.e., the optimal solutions were computed for , . The result was that the same strategy was used, see Figure 5. The speed of player I was maximal along the trajectory and the best solution was obtained for . With respect to the notation of Corollary 2 the speeds of player I were . The marker reduced the rendezvous value even when the speed of player I was very slow.
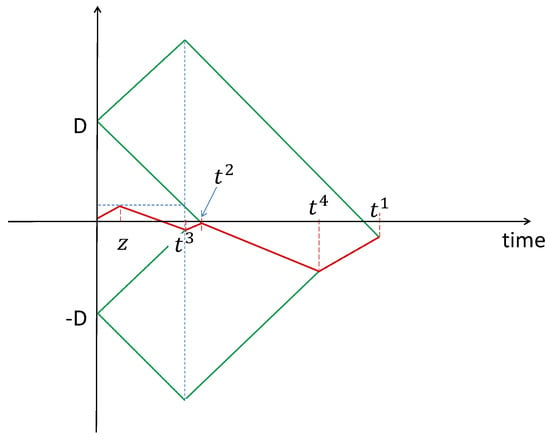
Figure 5.
Optimal strategy when player I holds the marker and is the slower player.
The rendezvous times are given by:
The optimal solution function is decreasing because a strategy for v is a strategy for as well. Hence, if the value of the next-to-optimal strategy for a speed is larger than , the strategy that leads to is optimal for speeds in . With our mesh size of , we numerically observed that this occurred since . Hence, we have a computer-assisted proof summarized in the following Theorem.
Theorem 2.
For , the rendezvous value of the game is given by (18). The optimal strategy is plotted in Figure 5 and the optimal rendezvous values in Figure 6.

Figure 6.
Optimal solutions with (18) and without marker. The slow player holds the marker.
The interval in which the Theorem is stated to be true may be enlarged by computing the numerical solutions on a finer mesh. It is relevant to point out that for the optimal strategy, the time at which the marker is found is , i.e., the same time as the first rendezvous occurs.
6. Solution of the Problem with Marker Held by the Fast Player
The family of linear programs to be solved when the marker is held by the fast player (I) is very similar to the one defined by Equations (15)–(17). The changes are that the coefficients are no longer multiplied by the maximal speed v, as are now the coefficients . The system of equations is not reproduced here to save some space.
The results are plotted in Figure 7. We observe that for speeds slower than the marker is not useful and the optimal solution is given by the optimal solutions without marker stated in Theorem 1. For speeds faster than , the marker starts to be useful and the strategy is similar to the optimal one when the marker is held by the slow player, see Figure 5. When the fast player holds the marker, we obtain that the rendezvous times are given by:
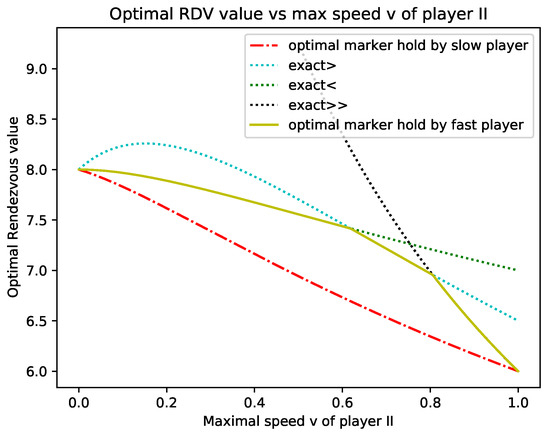
The optimal rendezvous value is decreasing with the maximal speed v because a strategy for maximal speed v is a strategy for maximal speed . Moreover, if we denote the optimal rendezvous value for maximal speed v, and the next-to-optimal rendezvous value, it follows that if and the strategy leading to and is the same, then the strategy is optimal on the entire interval . By numerical computation and using the two stated observations we obtain the following Theorem.
Theorem 3.
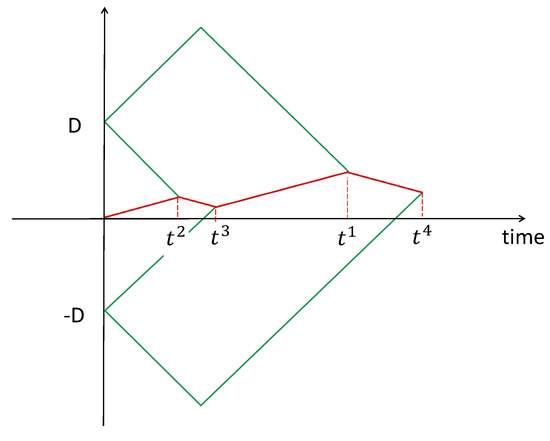
For the rendezvous value of the game is given by (13) and the optimal strategy is plotted in Figure 3; for , the rendezvous value of the game is given by (14) and the optimal strategy is plotted in Figure 4; for , the rendezvous value of the game is given by (19), the rendezvous values are plotted in Figure 7 and the optimal strategy is plotted in Figure 8.

Figure 8.
Optimal solutions with marker, i.e., (19) for ; for lower speeds the optimal solutions are the ones without marker (Theorem 1). The fast player holds the marker.
It is relevant to point out the difference between the optimal strategies when the marker is held by the slow (Figure 5) or fast player (Figure 8). After the rendezvous time in Figure 5 the slow player (who holds the marker) turns, while in Figure 8, the fast player (who holds the marker) continues on their way. The transition from the two strategies is “continuous” in the sense that when the speeds are equal at time , the two remaining agents to be found are at equal distance from player I. Hence, both strategies are optimal (turning or continuing).
7. Conclusions
In this paper, we presented variations and solutions of the classical rendezvous problem on the line. In particular, we considered that players moved at different speeds and made use of markers as communication channels. We showed, for instance, that in some conditions the slow player had better waiting still for the fast one.
We showed how the search space given by (1) can be reduced to a space of much smaller dimension making the enumeration of all elements realistic, in order to find the ones leading to the optimal solution of our problem. The reduction follows from Proposition 1. This new formulation is compatible with mixed-integer linear programming and is shown to lead to a solution efficiently using the Gurobi solver [40].
Author Contributions
Writing—original draft preparation, P.L. and N.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alpern, S.; Gal, S. Rendezvous search on the line with distinguishable players. SIAM J. Control Optim. 1995, 33, 1270–1276. [Google Scholar] [CrossRef]
- Alpern, S. The Rendezvous Search Problem. SIAM J. Control Optim. 1995, 33, 673–683. [Google Scholar] [CrossRef]
- Anderson, E.J.; Essegaier, S. Rendezvous Search on the Line with Indistinguishable Players. SIAM J. Control Optim. 1995, 33, 1637–1642. [Google Scholar] [CrossRef]
- Baston, V. Note: Two rendezvous search problems on the line. Nav. Res. Logist. 1999, 46, 335–340. [Google Scholar] [CrossRef]
- Uthaisombut, P. Symmetric Rendezvous Search on the Line Using Move Patterns with Different Lengths. Citeseer. 2006. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.59.6033 (accessed on 14 December 2021).
- Han, Q.; Du, D.; Vera, J.; Zuluaga, L.F. Improved Bounds for the Symmetric Rendezvous Value on the Line. Oper. Res. 2008, 56, 772–782. [Google Scholar] [CrossRef]
- Baston, V.; Gal, S. Rendezvous on the Line when the Players’ Initial Distance is Given by an Unknown Probability Distribution. SIAM J. Control Optim. 1998, 36, 1880–1889. [Google Scholar] [CrossRef]
- Alpern, S.; Beck, A. Rendezvous Search on the Line with Limited Resources: Maximizing the Probability of Meeting. Oper. Res. 1999, 47, 849–861. [Google Scholar] [CrossRef]
- Alpern, S.; Beck, A. Pure Strategy Asymmetric Rendezvous on the Line with an Unknown Initial Distance. Oper. Res. 2000, 48, 498–501. [Google Scholar] [CrossRef][Green Version]
- Ozsoyeller, D.; Beveridge, A.; Isler, V. Symmetric Rendezvous Search on the Line With an Unknown Initial Distance. IEEE Trans. Robot. 2013, 29, 1366–1379. [Google Scholar] [CrossRef]
- Stachowiak, G. Asynchronous deterministic rendezvous on the line. In Proceedings of the International Conference on Current Trends in Theory and Practice of Computer Science, Špindleruv Mlýn, Czech Republic, 24–30 January 2009; pp. 497–508. [Google Scholar]
- Czyzowicz, J.; Killick, R.; Kranakis, E. Linear rendezvous with asymmetric clocks. In Proceedings of the 22nd International Conference on Principles of Distributed Systems (OPODIS 2018), Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, Hong Kong, China, 17–19 December 2018. [Google Scholar]
- Chrobak, M.; Gąsieniec, L.; Gorry, T.; Martin, R. Group search on the line. In Proceedings of the International Conference on Current Trends in Theory and Practice of Informatics, Pecpod Snežkou, Czech Republic, 24–29 January 2015; pp. 164–176. [Google Scholar]
- Howard, J.V. Rendezvous Search on the Interval and the Circle. Oper. Res. 1999, 47, 550–558. [Google Scholar] [CrossRef]
- Kranakis, E.; Santoro, N.; Sawchuk, C.; Krizanc, D. Mobile agent rendezvous in a ring. In Proceedings of the 23rd International Conference on Distributed Computing Systems, Providence, RI, USA, 19–22 May 2003; pp. 592–599. [Google Scholar]
- Flocchini, P.; Kranakis, E.; Krizanc, D.; Santoro, N.; Sawchuk, C. Multiple mobile agent rendezvous in a ring. In Latin American Symposium on Theoretical Informatics; Springer: Berlin/Heidelberg, Germany, 2004; pp. 599–608. [Google Scholar]
- Kranakis, E.; Krizanc, D.; Markou, E. The mobile agent rendezvous problem in the ring. Synth. Lect. Distrib. Comput. Theory 2010, 1, 1–122. [Google Scholar] [CrossRef]
- Di Stefano, G.; Navarra, A. Optimal gathering of oblivious robots in anonymous graphs and its application on trees and rings. Distrib. Comput. 2017, 30, 75–86. [Google Scholar] [CrossRef]
- Czyzowicz, J.; Dobrev, S.; Kranakis, E.; Krizanc, D. The power of tokens: Rendezvous and symmetry detection for two mobile agents in a ring. In Proceedings of the International Conference on Current Trends in Theory and Practice of Computer Science, Nový Smokovec, Slovakia, 19–25 January 2008; pp. 234–246. [Google Scholar]
- Flocchini, P.; Kranakis, E.; Krizanc, D.; Luccio, F.L.; Santoro, N.; Sawchuk, C. Mobile agents rendezvous when tokens fail. In International Colloquium on Structural Information and Communication Complexity; Springer: Berlin/Heidelberg, Germany, 2004; pp. 161–172. [Google Scholar]
- Das, S.; Mihalák, M.; Šrámek, R.; Vicari, E.; Widmayer, P. Rendezvous of mobile agents when tokens fail anytime. In Proceedings of the International Conference on Principles of Distributed Systems, Luxor, Egypt, 15–18 December 2008; pp. 463–480. [Google Scholar]
- Baston, V.; Gal, S. Rendezvous search when marks are left at the starting points. Nav. Res. Logist. 2001, 48, 722–731. [Google Scholar] [CrossRef]
- Leone, P.; Alpern, S. Rendezvous Search With Markers That Can Be Dropped at Chosen Times. Nav. Res. Logist. 2018, 65, 6–7. [Google Scholar] [CrossRef]
- Das, S.; Luccio, F.L.; Markou, E. Mobile agents rendezvous in spite of a malicious agent. In Proceedings of the International Symposium on Algorithms and Experiments for Wireless Sensor Networks, Patras, Greece, 17–18 September 2015; pp. 211–224. [Google Scholar]
- Das, S.; Focardi, R.; Luccio, F.L.; Markou, E.; Squarcina, M. Gathering of robots in a ring with mobile faults. Theor. Comput. Sci. 2019, 764, 42–60. [Google Scholar] [CrossRef]
- Alpern, S.; Gal, S. The Theory of Search Games and Rendezvous; Springer: Berlin/Heidelberg, Germany, 2006; Volume 55. [Google Scholar]
- Alpern, S. Ten open problems in rendezvous search. In Search Theory; Springer: Berlin/Heidelberg, Germany, 2013; pp. 223–230. [Google Scholar]
- Pelc, A. Deterministic Rendezvous Algorithms. In Distributed Computing by Mobile Entities; Springer: Berlin/Heidelberg, Germany, 2019; pp. 423–454. [Google Scholar]
- Lidbetter, T. Search and rescue in the face of uncertain threats. Eur. J. Oper. Res. 2020, 285, 1153–1160. [Google Scholar] [CrossRef]
- Baston, V.; Kikuta, K. Search games on a network with travelling and search costs. Int. J. Game Theory 2015, 44, 347–365. [Google Scholar] [CrossRef]
- Baston, V.; Kikuta, K. A search problem on a bipartite network. Eur. J. Oper. Res. 2019, 277, 227–237. [Google Scholar] [CrossRef]
- Baston, V.; Kikuta, K. Search games on networks with travelling and search costs and with arbitrary searcher starting points. Networks 2013, 62, 72–79. [Google Scholar] [CrossRef]
- Hohzaki, R. Search games: Literature and survey. J. Oper. Res. Soc. Jpn. 2016, 59, 1–34. [Google Scholar] [CrossRef]
- Alpern, S.; Fokkink, R.; Gasieniec, L.; Lindelauf, R.; Subrahmanian, V. Search Theory; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Alpern, S.; Beck, A. Asymmetric rendezvous on the line is a double linear search problem. Math. Oper. Res. 1999, 24, 604–618. [Google Scholar] [CrossRef]
- Leone, P.; Buwaya, J.; Alpern, S. Search-and-Rescue Rendezvous. Eur. J. Oper. Res. 2021, 297, 579–591. [Google Scholar] [CrossRef]
- Isaacs, R. Differential Games: A Mathematical Theory with Applications to Warfare and Pursuit, Control and Optimization; Courier Corporation: Chelmsford, MA, USA, 1999. [Google Scholar]
- Mehlmann, A. Applied Differential Games; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Friedman, A. Differential Games; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- Gurobi Optimizer Reference Manual; Gurobi Optimization, LLC: Houston, TX, USA, 2021.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).