Converting of Boolean Expression to Linear Equations, Inequalities and QUBO Penalties for Cryptanalysis
Abstract
1. Introduction
2. Methods
2.1. Transformation to One Equation with Binary Ancillaries
2.2. Transformation to a System of Linear Inequalities
- Every vector is an extreme point of convex hull (i.e., is a vertex of polyhedron );
- If and then .
- (1)
- To obtain polyhedron for n-variant function , we need to calculate all values for all ;
- (2)
- The complexity of the facet enumeration algorithm grows dramatically as the value of n increases.
2.3. Comparison of Two Ways of Reducing Boolean Expressions to MILP Problem
- By equations with binary ancillaries, see Section 2.1—Boolean expressions of cryptography algorithms are reduced to equations with binary ancillaries; CPLEX-solver is used to obtain coefficients of the desired equation for a given Boolean expression;
- By inequalities without binary ancillaries, see Section 2.2—Boolean expressions are replaced with systems of linear inequalities without any extra binary variables; polyhedra-handling application LRS [13] is used to generate these inequalities in explicit form.
2.4. The Case of Boolean Functions with Many Binary Arguments
2.4.1. Linear Equations with Binary Ancillaries for Composition of Boolean Functions
2.4.2. Linear Inequalities without Binary Ancillaries for Composition of Boolean Functions
2.5. Transform Subproblems from the MILP to QUBO
3. Results
3.1. Transform Addition Modulo into the MILP
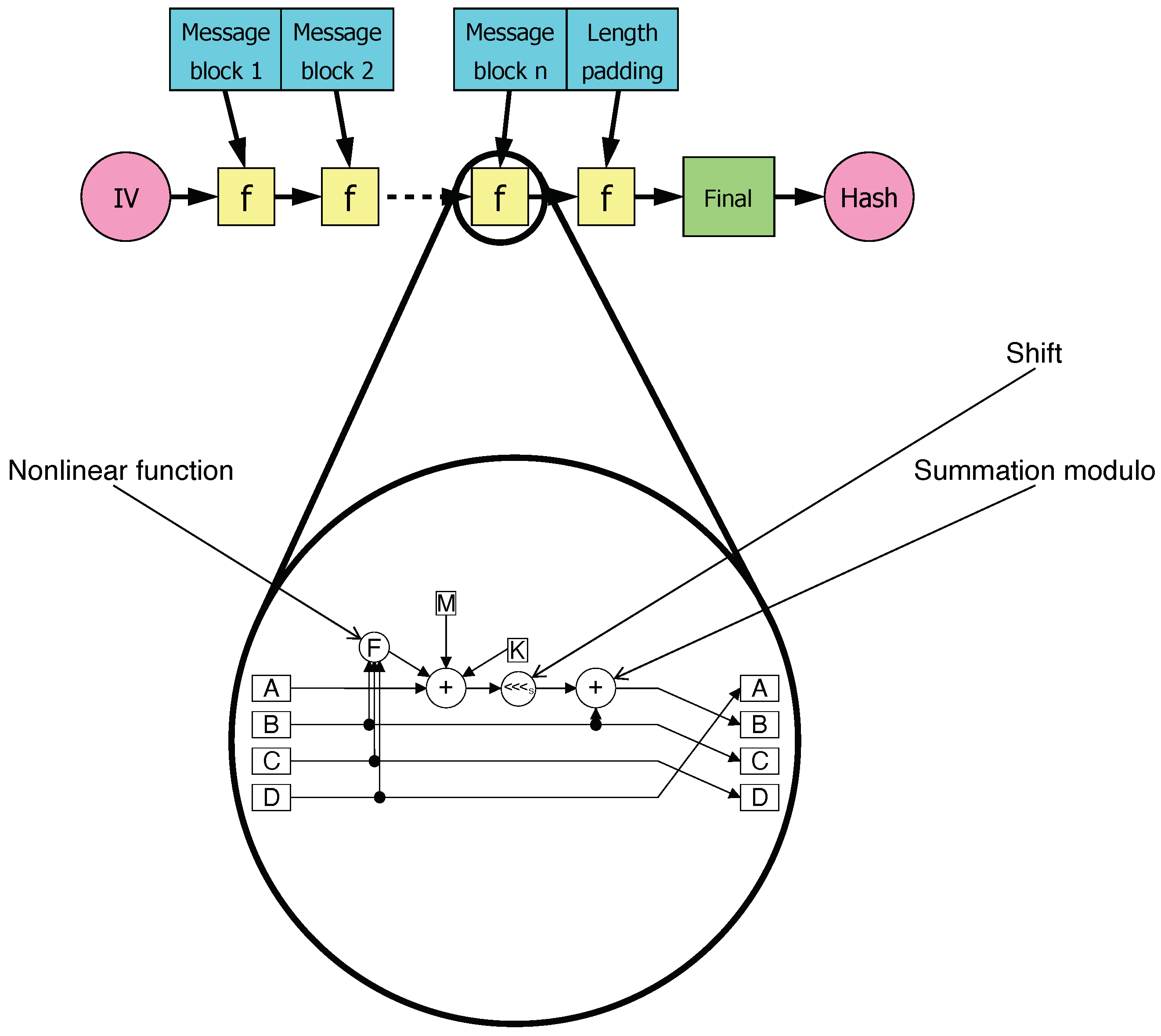
3.2. The MD5
- For any x number, there is easy to compute .
- For any y number, there is hard to find x such that .
- ;
- ;
- ;
- .
- ;
- ;
- ;
- .
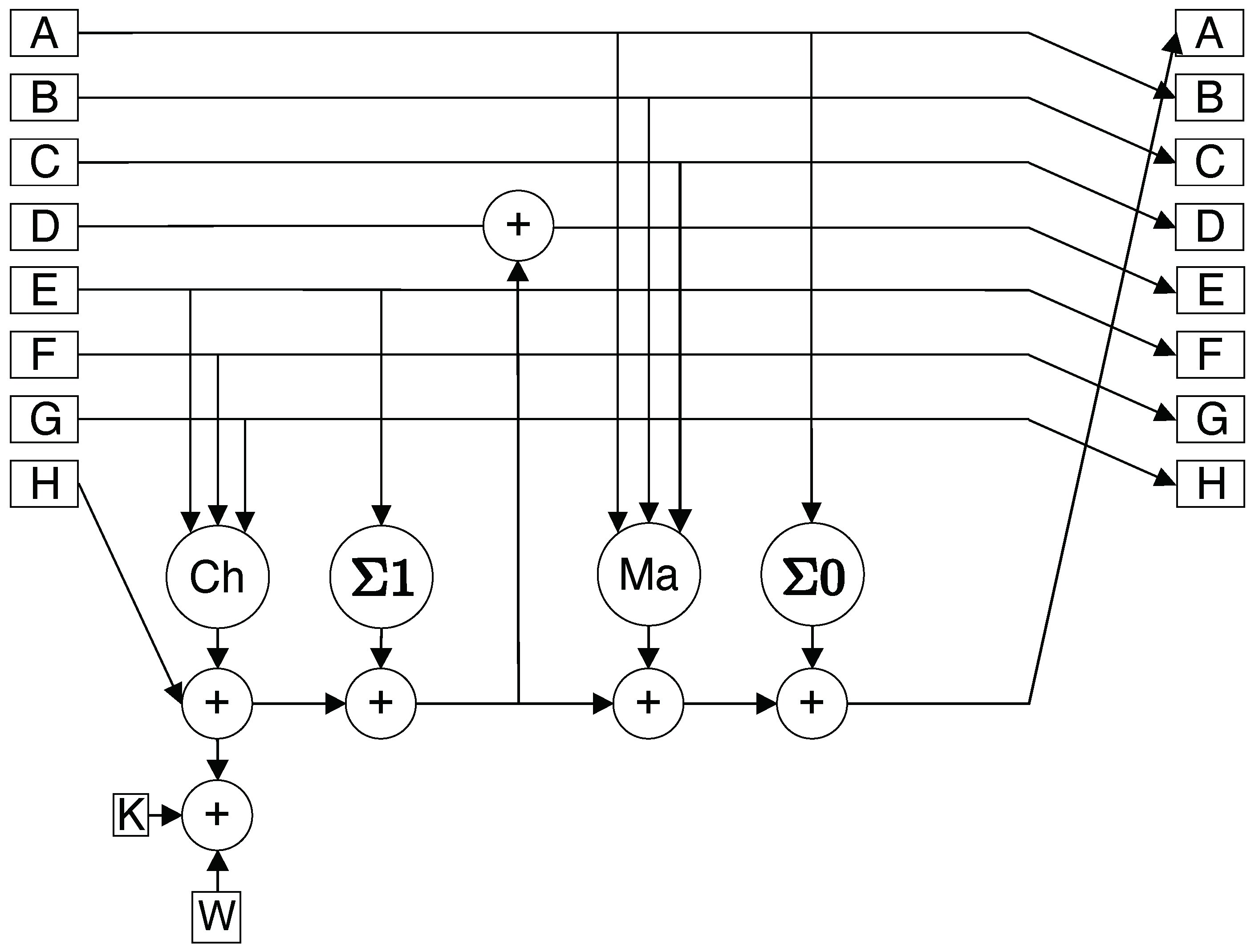
3.3. The SHA-256
- Each intermediate hash value has 256 bits, which is divided into 8 blocks with 32 bits.
- A round has four nonlinear functions (Ch, Ma, ).
- The input message has 512 bits (16 blocks with 32 bits), and it is extended to 64 blocks using right circular shift and XOR.
3.4. The AES
- KeyExpansion—round keys are derived from the cipher key using the AES key schedule. AES requires a separate 128-bit round key block for each round plus one more.
- Initial round key addition:
- (a)
- AddRoundKey—each byte of the state is combined with a byte of the round key using bitwise XOR.
- 9, 11 or 13 rounds:
- (a)
- SubBytes—a non-linear substitution step where each byte is replaced with another according to a lookup table.
- (b)
- ShiftRows—a transposition step where the last three rows of the state are shifted cyclically a certain number of steps.
- (c)
- MixColumns—a linear mixing operation which operates on the columns of the state, combining the four bytes in each column.
- (d)
- AddRoundKey
- Final round (making 10, 12 or 14 rounds in total):
- (a)
- SubBytes;
- (b)
- ShiftRows;
- (c)
- AddRoundKey.
3.4.1. Rijndael’s Finite Field
- Inverse operation in ;
- Multiplication by and 3.
3.4.2. The Full MILP for the AES
3.5. Summary about Cryptography
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Balas, E.; Mazzola, J.B. Nonlinear 0–1 programming: I. Linearization techniques. Math. Program. 1984, 30, 1–21. [Google Scholar] [CrossRef]
- Milano, M.; Trick, M. Constraint and integer programming. In Constraint and Integer Programming; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1–31. [Google Scholar]
- Hooker, J.N. Logic-based modeling. In Handbook on Modelling for Discrete Optimization; Springer: Berlin/Heidelberg, Germany, 2006; pp. 61–102. [Google Scholar]
- Bian, Z.; Chudak, F.; Israel, R.; Lackey, B.; Macready, W.G.; Roy, A. Mapping constrained optimization problems to quantum annealing with application to fault diagnosis. arXiv 2016, arXiv:1603.03111. [Google Scholar] [CrossRef]
- Bian, Z.; Chudak, F.; Israel, R.; Lackey, B.; Macready, W.G.; Roy, A. Discrete optimization using quantum annealing on sparse Ising models. Front. Phys. 2014, 2, 56. [Google Scholar] [CrossRef]
- Ramos-Calderer, S.; Bellini, E.; Latorre, J.I.; Manzano, M.; Mateu, V. Quantum search for scaled hash function preimages. Quantum Inf. Processing 2021, 20, 180. [Google Scholar] [CrossRef]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing—STOC ’96, New York, NY, USA, 24–26 May 1996. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 1970; p. 452. [Google Scholar]
- Avis, D.; Fukuda, K. A pivoting algorithm for convex hulls and vertex enumeration of arrangements and polyhedra. Discret. Comput. Geom. 1992, 8, 295–313. [Google Scholar] [CrossRef]
- Fukuda, K. Polyhedral Computation; Department of Mathematics, Institute of Theoretical Computer Science ETH Zurich: Zurich, Switzerland, 2020. [Google Scholar] [CrossRef]
- Avis, D.; Fukuda, K.; Picozzi, S. On canonical representations of convex polyhedra. In Mathematical Software; World Scientific: Singapore, 2002; pp. 350–360. [Google Scholar] [CrossRef]
- Fukuda, K. cdd, cddplus and cddlib Homepage. Swiss Federal Institute of Technology. 1997. Available online: http://www.inf.ethz.ch/personal/fukudak/cddhome/index.html (accessed on 12 July 2021).
- Avis, D. lrs Homepage. McGill University. 2000. Available online: http://cgm.cs.mcgill.ca/~avis/C/lrs.htm (accessed on 12 July 2021).
- Rosenberg, I. Reduction of bivalent maximization to the quadratic case. Cah. Cent. D’etudes Rech. Oper. 1975, 17, 71–74. [Google Scholar]
- Sasaki, Y.; Aoki, K. Finding Preimages in Full MD5 Faster Than Exhaustive Search. In Advances in Cryptology—EUROCRYPT 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 134–152. [Google Scholar] [CrossRef]
- Preimage Attack on MD4 Hash Function as a Problem of Parallel Sat-Based Cryptanalysis. Bull. South Ural State Univ. Ser. Comput. Math. Softw. Eng. 2017, 6, 16–27. [CrossRef][Green Version]
- Mironov, I.; Zhang, L. Applications of SAT Solvers to Cryptanalysis of Hash Functions. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; pp. 102–115. [Google Scholar] [CrossRef]
- Dobbertin, H. The First Two Rounds of MD4 are Not One-Way. In Fast Software Encryption; Springer: Berlin/Heidelberg, Germany, 1998; pp. 284–292. [Google Scholar] [CrossRef]
- Rivest, R.L. The MD5 Message-Digest Algorithm; RFC, Ed.; RFC 1321; IETF: Fremont, CA, USA, 1992. [Google Scholar] [CrossRef]
- Dang, Q.H. Secure Hash Standard; Technical Report, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. [Google Scholar] [CrossRef]
- Daor, J.; Daemen, J.; Rijmen, V. AES Proposal: Rijndael. 1999. Available online: https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.36.640 (accessed on 24 June 2021).
- Canright, D. A Very Compact S-Box for AES. In Cryptographic Hardware and Embedded Systems—CHES 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 441–455. [Google Scholar] [CrossRef]
- Courtois, N.T. General Principles of Algebraic Attacks and New Design Criteria for Cipher Components. In Advanced Encryption Standard—AES; Springer: Berlin/Heidelberg, Germany, 2005; pp. 67–83. [Google Scholar] [CrossRef]
- Cai, J.; Macready, W.G.; Roy, A. A practical heuristic for finding graph minors. arXiv 2014, arXiv:1406.2741. [Google Scholar]

| Formula | Systems of Linear Inequalities | Linear Equation | |
|---|---|---|---|
| AND | |||
| OR | |||
| XOR | |||
| NOR | |||
| NAND |
| Boolean Formula | Linear Equation | |
|---|---|---|
| Boolean Formula | Linear Equation |
|---|---|
| Formula | Linear Equation | |
|---|---|---|
| AND | ||
| OR | ||
| XOR | ||
| NOR | ||
| NAND |
| MD5 | SHA-256 | AES-128 | AES-192 | AES-256 |
|---|---|---|---|---|
| 17,280 | 47,808 | ≈90,000 | ≈2 · 100,000 | ≈2 · 125,000 |
| MD5 | SHA-256 | |
|---|---|---|
| Original | 224 | 415 |
| Chimera | 943.2 | - |
| Pegasus | 461.1 | 1205.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pakhomchik, A.I.; Voloshinov, V.V.; Vinokur, V.M.; Lesovik, G.B. Converting of Boolean Expression to Linear Equations, Inequalities and QUBO Penalties for Cryptanalysis. Algorithms 2022, 15, 33. https://doi.org/10.3390/a15020033
Pakhomchik AI, Voloshinov VV, Vinokur VM, Lesovik GB. Converting of Boolean Expression to Linear Equations, Inequalities and QUBO Penalties for Cryptanalysis. Algorithms. 2022; 15(2):33. https://doi.org/10.3390/a15020033
Chicago/Turabian StylePakhomchik, Aleksey I., Vladimir V. Voloshinov, Valerii M. Vinokur, and Gordey B. Lesovik. 2022. "Converting of Boolean Expression to Linear Equations, Inequalities and QUBO Penalties for Cryptanalysis" Algorithms 15, no. 2: 33. https://doi.org/10.3390/a15020033
APA StylePakhomchik, A. I., Voloshinov, V. V., Vinokur, V. M., & Lesovik, G. B. (2022). Converting of Boolean Expression to Linear Equations, Inequalities and QUBO Penalties for Cryptanalysis. Algorithms, 15(2), 33. https://doi.org/10.3390/a15020033







