Do Neural Transformers Learn Human-Defined Concepts? An Extensive Study in Source Code Processing Domain †
Abstract
1. Introduction
Contributions and Outline
- The validation of the approach on the state-of-the-art CuBERT [1] transformer, fine-tuned in the detection of software vulnerabilities.
- The definition of a fitness function for a (grammar-based) evolutionary algorithm defined as the distance from an hyperplane that, according to the presence of a given concept, separates input instances when seen as points in a space defined over the neural activations.
- A study on how the presence (or the absence) of the emerging concepts affects the decision process of the network on its original task.
2. Related Work
2.1. ML for Static Analysis
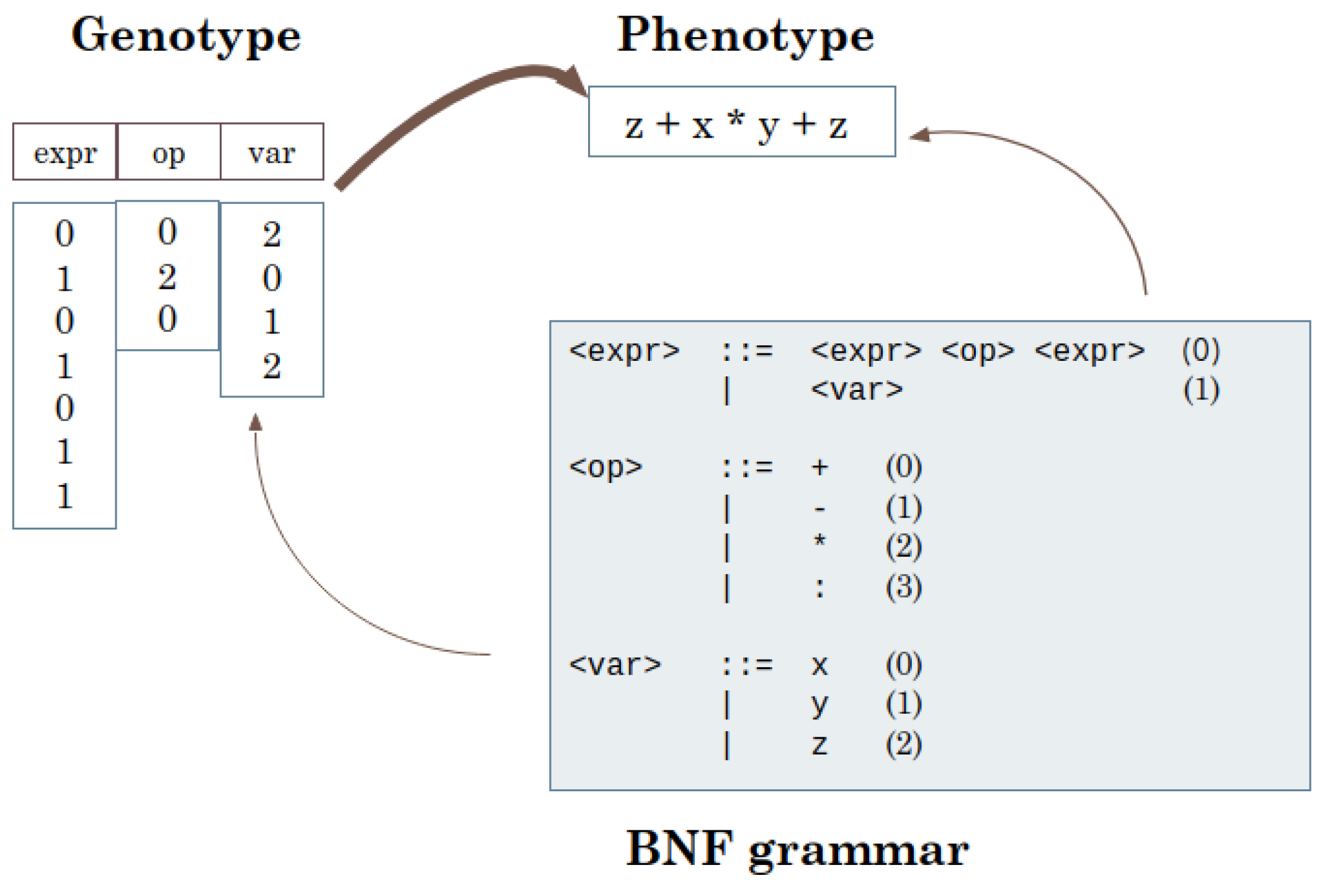
2.2. Evolutionary Program Synthesis
2.3. Concept-Based Explainability
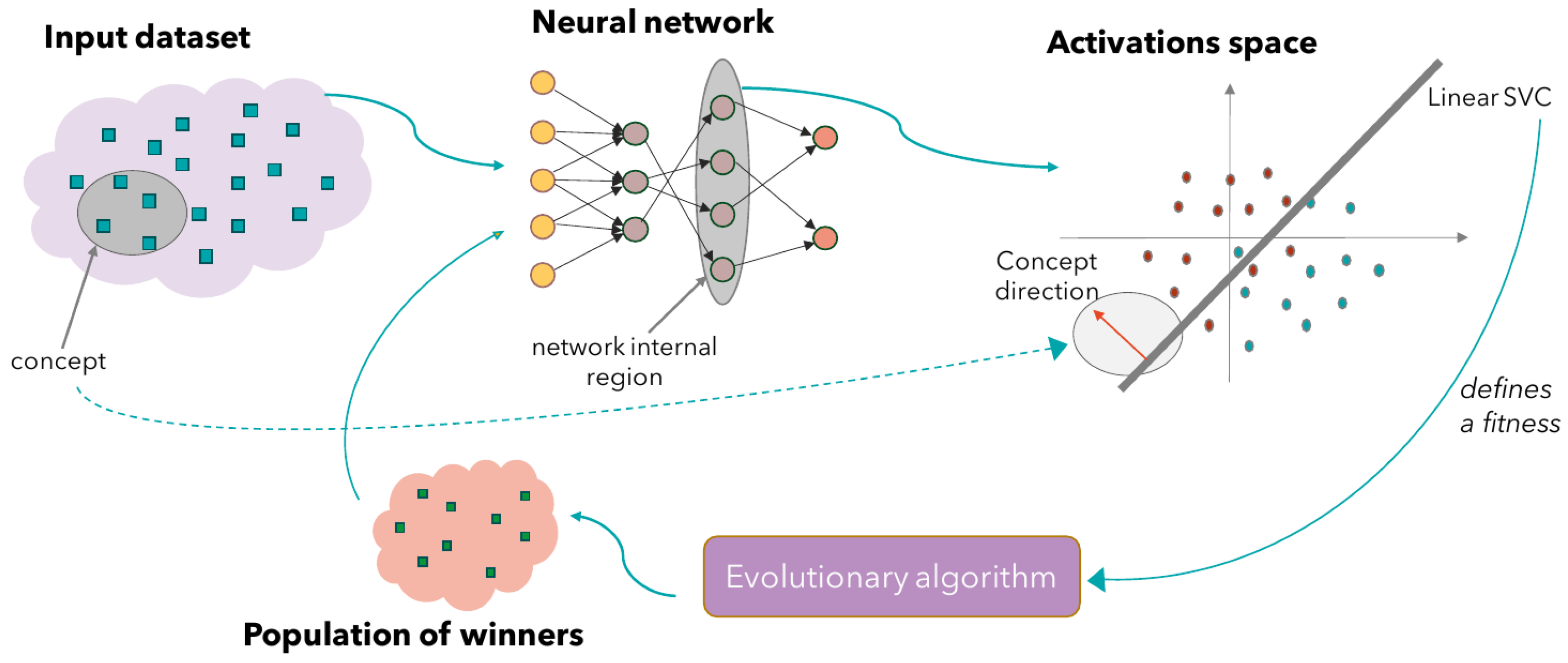
3. Proposed Approach
3.1. Input Instances and Sub-Concepts
3.2. Activations Space, Linear SVCs and Concept-Based Neural Fitness Function
3.3. Sensitivity to Sub-Concepts
- The first is similar to the original TCAV [2], which uses directional derivatives to compute the conceptual sensitivity on entire classes of inputs;
- The second is based on the evolutionary synthesis of classes of inputs and on a subsequent test of the classification performance on these evolved sets.
- By using a simplified Java grammar (Figure 3) we generate sets of individuals that maximize the fitness, and on these sets we count the number of instances that are classified as vulnerable.
- By using a grammar that forces the presence of the vulnerability that the model is trained on, we generate sets of individuals that minimize the fitness, and on these sets, we count the number of instances that are classified as vulnerable.
4. Experiments
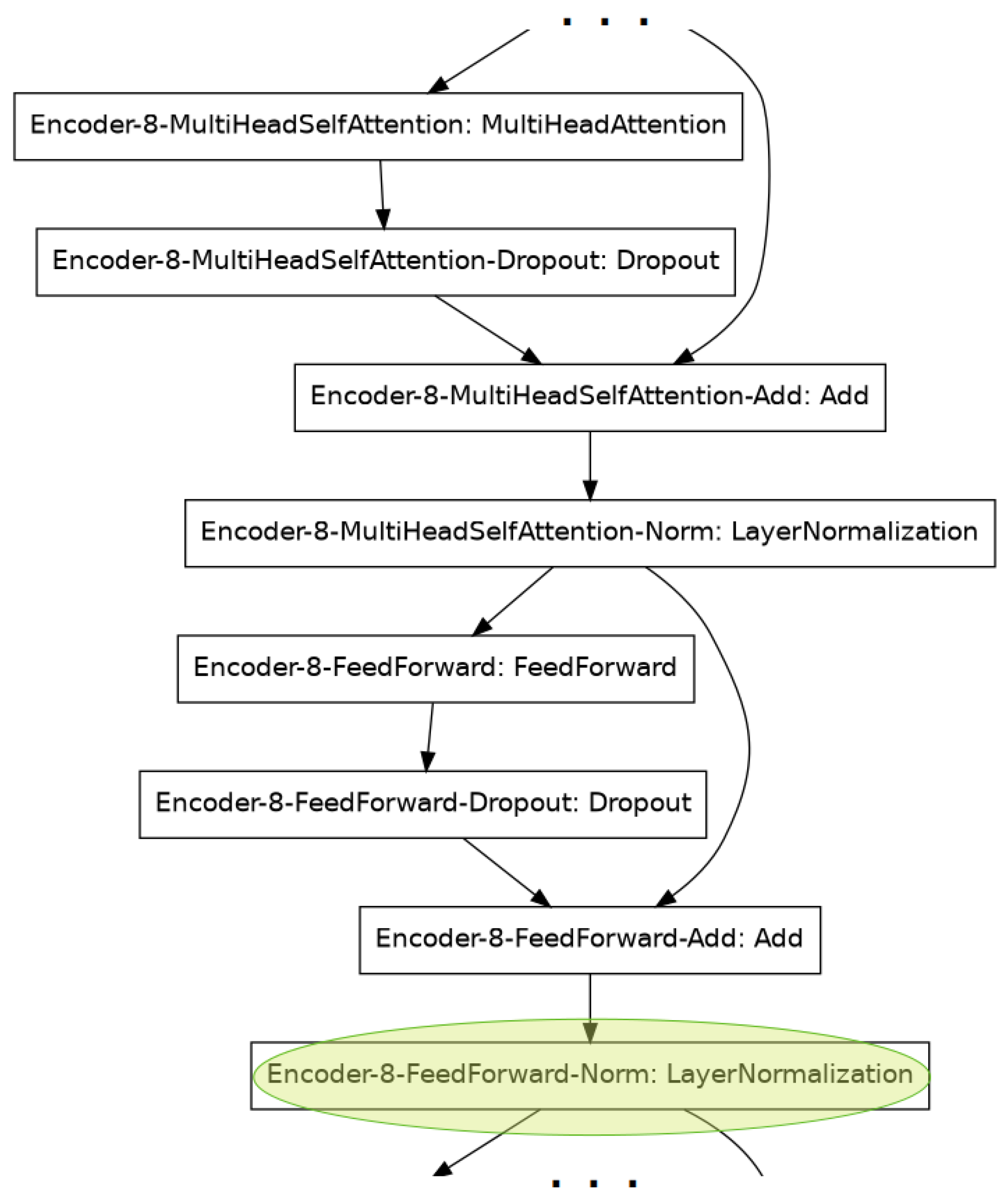
4.1. The CuBERT Transformer
4.2. Sub-Concepts Formulation
- Cast to integer
- The presence (or absence) of a cast-to-integer operation. This sub-concept can be significant when dealing with both the divide-by-zero and uncontrolled memory-allocation vulnerabilities.
- Square brackets
- The presence of an high number (i.e., >=12) of square brackets. This concept can be relevant in general since it is strictly related to the presence of an high number of accesses to array elements.
- Cyclomatic complexity
- This sub-concept [31] addresses the structural complexity of a program, and it is a classical software engineering metric. It is defined as the number of linearly independent paths in the control flow graph of a program and, dealing with Java programs, can be easily computed by counting 1 point for the beginning of the method, 1 point for each conditional construct and for each case or default block in a switch-case statement, 1 point for each iterative structure and 1 point for each Boolean condition. We consider, as a sub-concept, a cyclomatic complexity higher than 10.
- I/O relationship
- This sub-concept considers the semantic of a method in terms of the relation between what is passed as argument (i.e., the input) and the returned object (i.e., the output). We only consider a subset of all the possible I/O relations, namely, the presence or the absence of an array among the input arguments and whether the returned object is an array or a single element. In particular, in our experiments, we consider as a sub-concept the many-to-many relation, namely the methods that contain (at least) an array among their arguments, and that return an array.
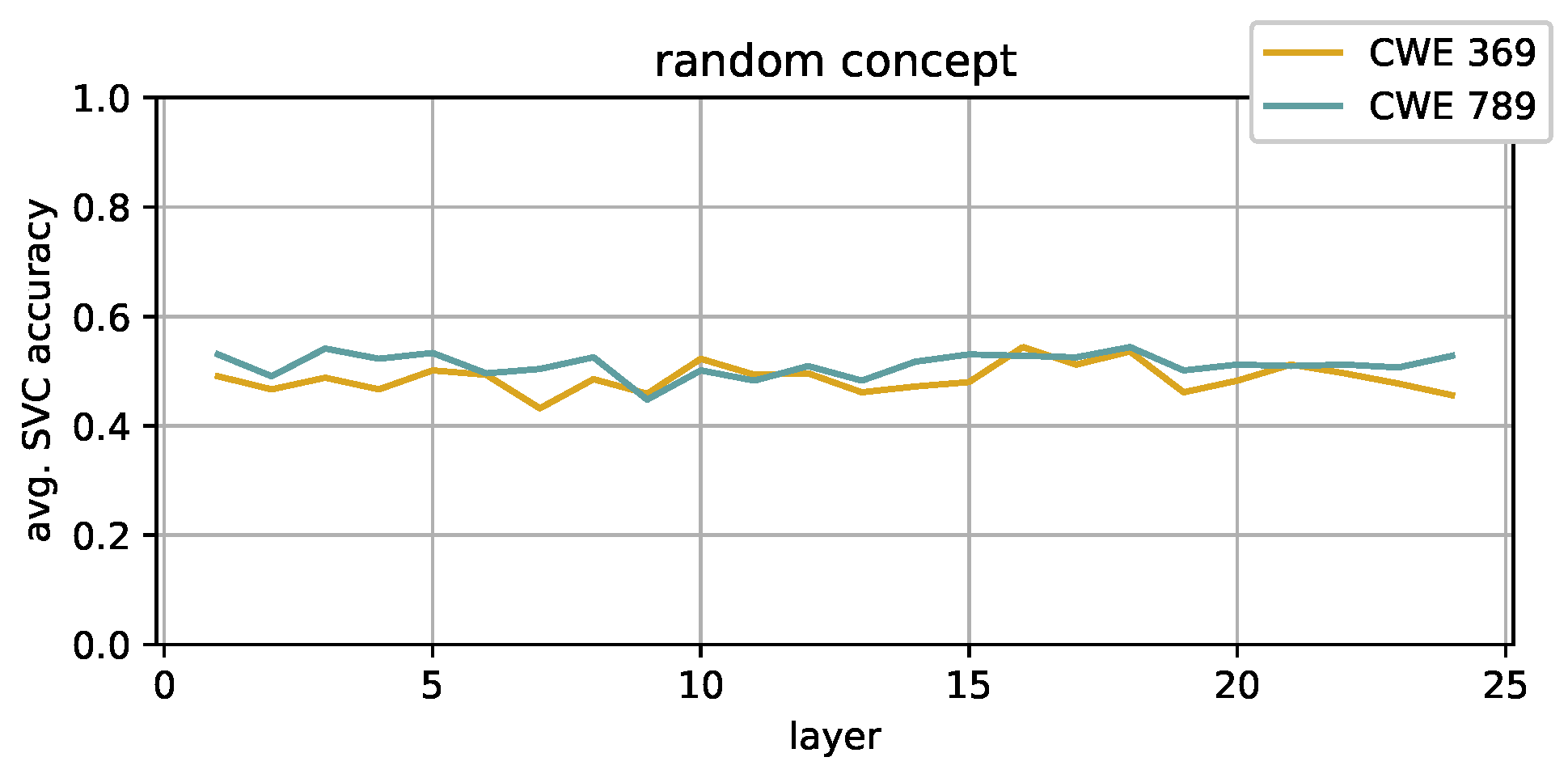
- Random
- This concept is defined by simply assigning random labels to the methods in the dataset. The obtained partition is obviously meaningless, and the experiments on this concept are used as a baseline to assess the validity of the other results.
4.3. SVCs and Activations Spaces
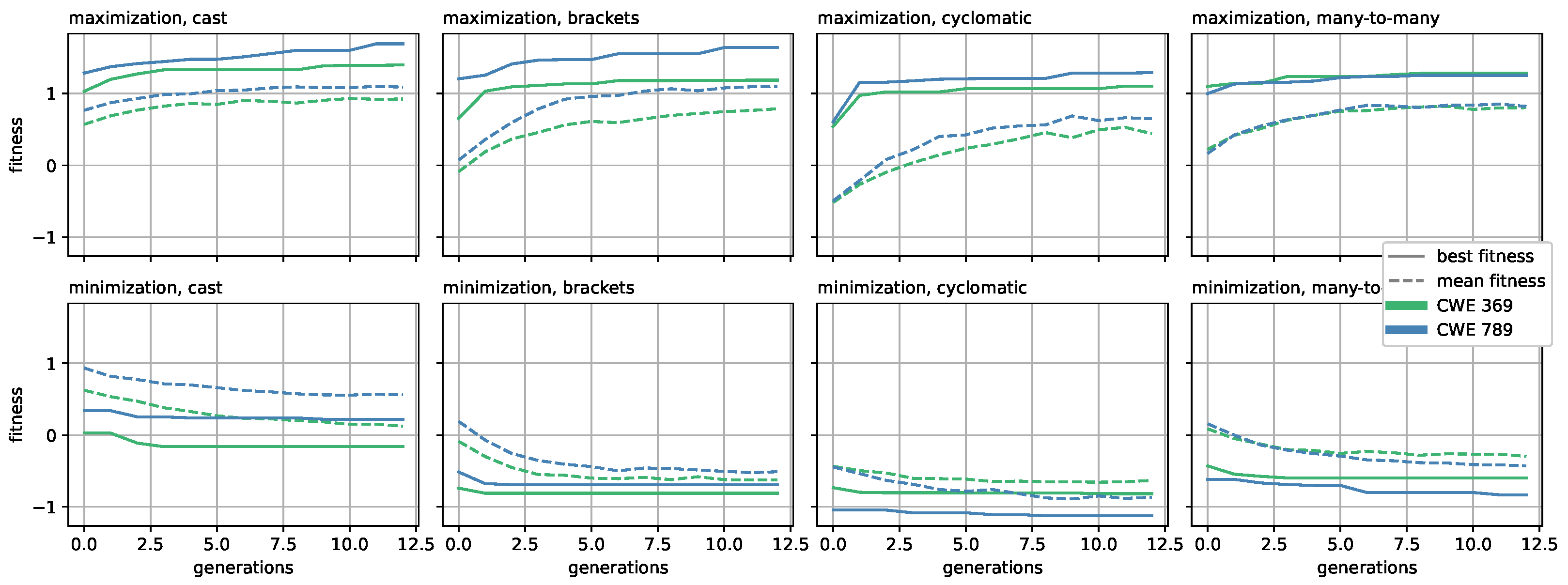
4.4. Evolutionary Search along Sub-Concepts Directions
- The considered concept, among the five we described in Section 4.2;
- The considered CWE, between CWE-369 and CWE-789;
- Whether we define a grammar which forces the corresponding vulnerability or not;
- Whether we maximize or minimize the fitness value.
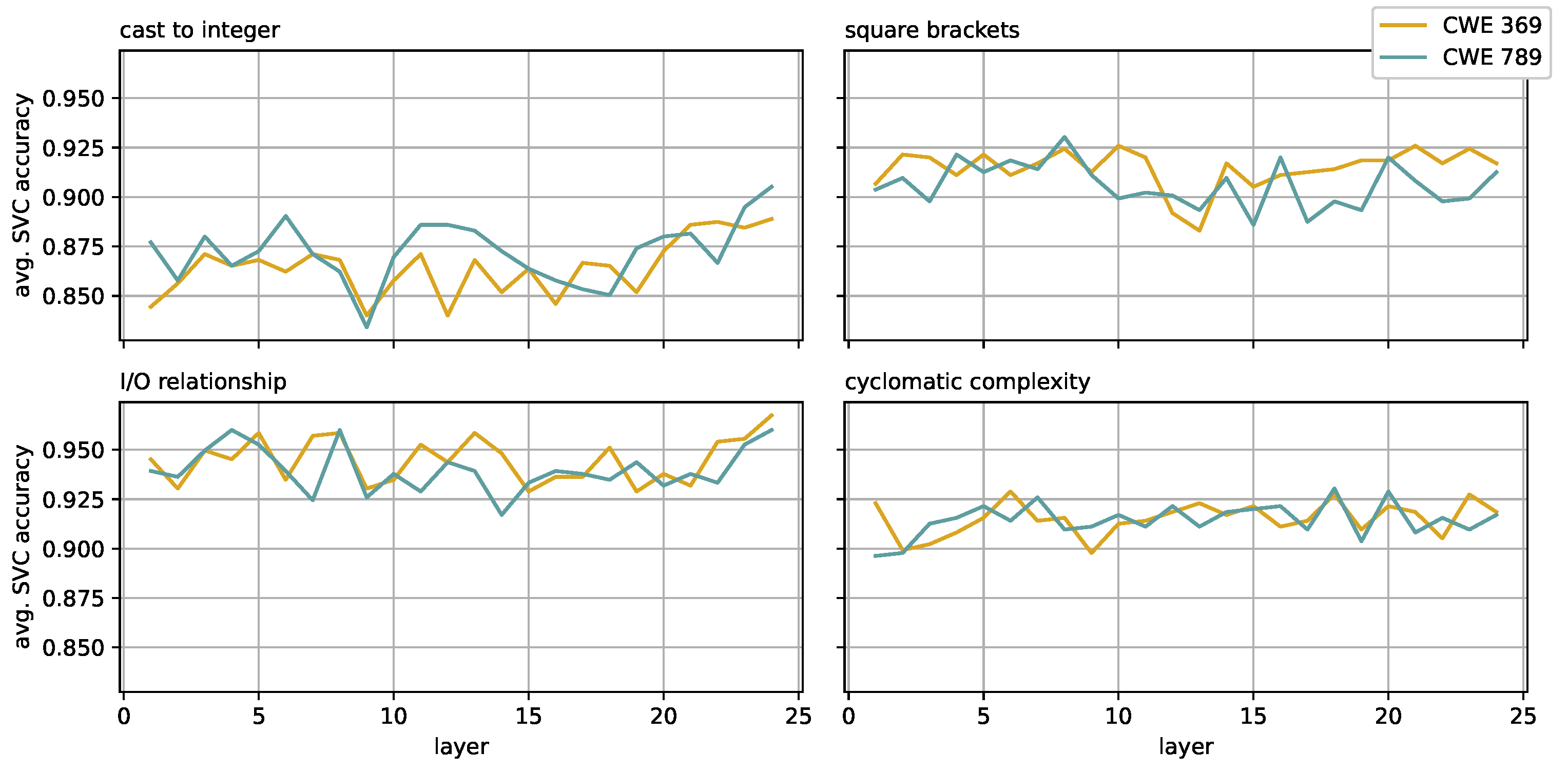
4.5. Measuring Sensitivity to Sub-Concepts
- Instances that are not vulnerable, and whose fitness value is maximized (the presence of the chosen concept is strong);
- Instances that are vulnerable, and whose fitness value is minimized (the presence of the chosen concept is weak).
5. Results
6. Discussion
7. Conclusions and Further Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| BNF | Backus–Naur Form |
| CAV | Concept Activation Vector |
| CFG | Context Free Grammar |
| CWE | Common Weakness Enumeration |
| DSGE | Dynamic Structured Grammatical Evolution |
| GE | Grammatical Evolution |
| GP | Genetic Programming |
| ML | Machine Learning |
| NLP | Natural Language Processing |
| SVC | Support Vector Classifier |
| XAI | Explainable Artificial Intelligence |
References
- Kanade, A.; Maniatis, P.; Balakrishnan, G.; Shi, K. Learning and evaluating contextual embedding of source code. In Proceedings of the 37th International Conference on Machine Learning, ICML 2020, Virtual, 13–18 July 2020. [Google Scholar]
- Kim, B.; Wattenberg, M.; Gilmer, J.; Cai, C.J.; Wexler, J.; Viégas, F.B.; Sayres, R. Interpretability Beyond Feature Attribution: Quantitative Testing with Concept Activation Vectors (TCAV). In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 2673–2682. [Google Scholar]
- Saletta, M.; Ferretti, C. Towards the Evolutionary Assessment of Neural Transformers Trained on Source Code. In Proceedings of the GECCO ’22: Genetic and Evolutionary Computation Conference, Companion Volume, Boston, MA, USA, 9–13 July 2022. [Google Scholar]
- Gosain, A.; Sharma, G. Static analysis: A survey of techniques and tools. In Intelligent Computing and Applications; Springer: Berlin/Heidelberg, Germany, 2015; pp. 581–591. [Google Scholar]
- Allamanis, M.; Barr, E.T.; Devanbu, P.T.; Sutton, C. A Survey of Machine Learning for Big Code and Naturalness. ACM Comput. Surv. 2018, 51, 1–37. [Google Scholar] [CrossRef]
- Le, T.H.M.; Chen, H.; Babar, M.A. Deep Learning for Source Code Modeling and Generation: Models, Applications, and Challenges. ACM Comput. Surv. 2020, 53, 1–38. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Ahmad, W.; Chakraborty, S.; Ray, B.; Chang, K.W. Unified Pre-training for Program Understanding and Generation. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Online, 6–11 June 2021; pp. 2655–2668. [Google Scholar]
- Devlin, J.; Chang, M.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT, Minneapolis, MN, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar]
- Koza, J.R. Hierarchical Genetic Algorithms Operating on Populations of Computer Programs. In Proceedings of the 11th International Joint Conference on Artificial Intelligence, Detroit, MI, USA, 20–25 August 1989; pp. 768–774. [Google Scholar]
- O’Neill, M.; Ryan, C. Grammatical evolution. IEEE Trans. Evol. Comput. 2001, 5, 349–358. [Google Scholar] [CrossRef]
- Sobania, D.; Rothlauf, F. Challenges of Program Synthesis with Grammatical Evolution. In Proceedings of the Genetic Programming—23rd European Conference (EuroGP), Seville, Spain, 15–17 April 2020; Volume 12101, pp. 211–227. [Google Scholar]
- Hemberg, E.; Kelly, J.; O’Reilly, U. On domain knowledge and novelty to improve program synthesis performance with grammatical evolution. In Proceedings of the Genetic and Evolutionary Computation Conference, Prague, Czech Republic, 13–17 July 2019; Auger, A., Stützle, T., Eds.; ACM: New York, NY, USA, 2019; pp. 1039–1046. [Google Scholar]
- O’Neill, M.; Nicolau, M.; Agapitos, A. Experiments in program synthesis with grammatical evolution: A focus on Integer Sorting. In Proceedings of the IEEE Congress on Evolutionary Computation, Beijing, China, 6–11 July 2014; pp. 1504–1511. [Google Scholar]
- Lourenço, N.; Assunção, F.; Pereira, F.B.; Costa, E.; Machado, P. Structured grammatical evolution: A dynamic approach. In Handbook of Grammatical Evolution; Springer: Berlin/Heidelberg, Germany, 2018; pp. 137–161. [Google Scholar]
- Lourenço, N.; Pereira, F.B.; Costa, E. Unveiling the properties of structured grammatical evolution. Genet. Program. Evol. Mach. 2016, 17, 251–289. [Google Scholar] [CrossRef]
- Doshi-Velez, F.; Kim, B. Towards a rigorous science of interpretable machine learning. arXiv 2017, arXiv:1702.08608. [Google Scholar]
- Erhan, D.; Bengio, Y.; Courville, A.; Vincent, P. Visualizing higher-layer features of a deep network. Univ. Montr. 2009, 1341, 1. [Google Scholar]
- Olah, C.; Mordvintsev, A.; Schubert, L. Feature visualization. Distill 2017, 2, e7. [Google Scholar] [CrossRef]
- Nguyen, A.M.; Dosovitskiy, A.; Yosinski, J.; Brox, T.; Clune, J. Synthesizing the preferred inputs for neurons in neural networks via deep generator networks. In Proceedings of the Advances in Neural Information Processing Systems 29: Annual Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 3387–3395. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In Proceedings of the 13th European Conference of Computer Vision ECCV, Zurich, Switzerland, 6–12 September 2014; Volume 8689, pp. 818–833. [Google Scholar]
- Shrikumar, A.; Greenside, P.; Kundaje, A. Learning Important Features Through Propagating Activation Differences. In Proceedings of the 34th International Conference on Machine Learning, ICML, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 3145–3153. [Google Scholar]
- Zügner, D.; Akbarnejad, A.; Günnemann, S. Adversarial Attacks on Neural Networks for Graph Data. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2847–2856. [Google Scholar]
- Le, Q.V.; Ranzato, M.; Monga, R.; Devin, M.; Corrado, G.; Chen, K.; Dean, J.; Ng, A.Y. Building high-level features using large scale unsupervised learning. In Proceedings of the 29th International Conference on Machine Learning, ICML, Edinburgh, UK, 26 June–1 July 2012; pp. 507–514. [Google Scholar]
- McGrath, T.; Kapishnikov, A.; Tomašev, N.; Pearce, A.; Hassabis, D.; Kim, B.; Paquet, U.; Kramnik, V. Acquisition of Chess Knowledge in AlphaZero. arXiv 2021, arXiv:2111.09259. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.; Vapnik, V. A Training Algorithm for Optimal Margin Classifiers. In Proceedings of the 5th Annual ACM Conference on Computational Learning Theory, COLT, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Schrimpf, M.; Kubilius, J.; Hong, H.; Majaj, N.J.; Rajalingham, R.; Issa, E.B.; Kar, K.; Bashivan, P.; Prescott-Roy, J.; Geiger, F.; et al. Brain-score: Which artificial neural network for object recognition is most brain-like? BioRxiv 2020, 2020, 407007. [Google Scholar]
- Khan, S.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in Vision: A Survey. ACM Comput. Surv. 2021, 54, 1–41. [Google Scholar] [CrossRef]
- Boland, F.E.; Black, P.E. The Juliet C/C++ and Java Test Suite. Comput. IEEE Comput. 2012, 45, 88–90. [Google Scholar] [CrossRef]
- Black, P.E. Juliet 1.3 Test Suite: Changes From 1.2; Technical Note; NIST National Institute for Standard and Technology: Gaithersburg, MD, USA, 2018.
- McCabe, T.J. A Complexity Measure. IEEE Trans. Softw. Eng. 1976, 2, 308–320. [Google Scholar] [CrossRef]

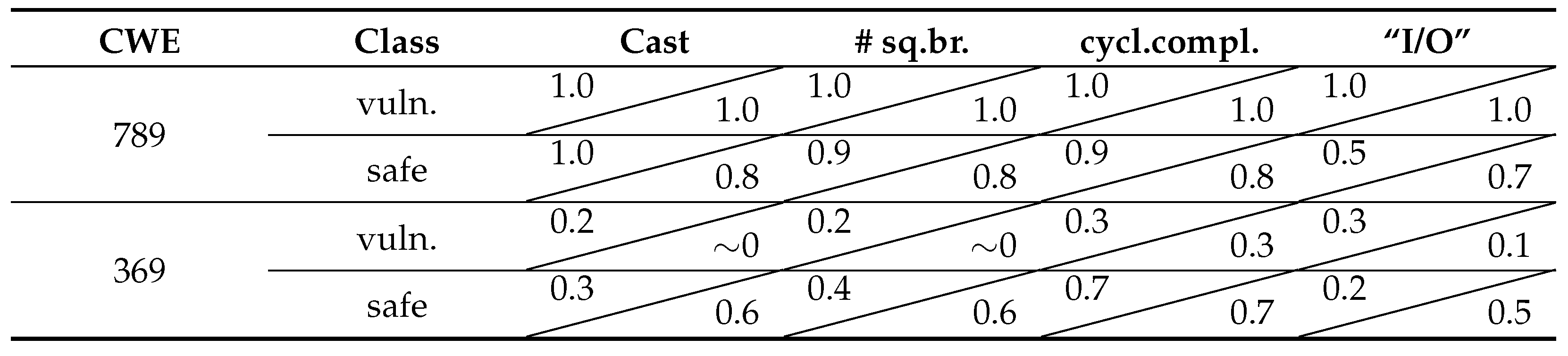
| CWE 789 | CWE 369 | |
|---|---|---|
| Cast to integer | 1.0 | 0.95 |
| Square brackets | 0.74 | 0.84 |
| Cyclomatic complexity | 0.58 | 0.82 |
| Many-to-many | 0.26 | 0.15 |
| Random | 0.49 | 0.51 |
 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferretti, C.; Saletta, M. Do Neural Transformers Learn Human-Defined Concepts? An Extensive Study in Source Code Processing Domain. Algorithms 2022, 15, 449. https://doi.org/10.3390/a15120449
Ferretti C, Saletta M. Do Neural Transformers Learn Human-Defined Concepts? An Extensive Study in Source Code Processing Domain. Algorithms. 2022; 15(12):449. https://doi.org/10.3390/a15120449
Chicago/Turabian StyleFerretti, Claudio, and Martina Saletta. 2022. "Do Neural Transformers Learn Human-Defined Concepts? An Extensive Study in Source Code Processing Domain" Algorithms 15, no. 12: 449. https://doi.org/10.3390/a15120449
APA StyleFerretti, C., & Saletta, M. (2022). Do Neural Transformers Learn Human-Defined Concepts? An Extensive Study in Source Code Processing Domain. Algorithms, 15(12), 449. https://doi.org/10.3390/a15120449







