Efficient 0/1-Multiple-Knapsack Problem Solving by Hybrid DP Transformation and Robust Unbiased Filtering
Abstract
:1. Introduction
2. Related Work
2.1. 0/1-KP Solving by Dynamic Programming Algorithm
| Algorithm 1: Basic DP with 2D array (for soltp, soltw, solx[n]) in O(nC). |
|
| Algorithm 2: Fast DP with 1D array (for soltp, soltw) in O(nC). |
|
| Algorithm 3: Full DP with 1D array (for soltp, soltw, solx[n]) in O(knC). |
|
2.2. 0/1-KP Solving by Time-Space Reduction Algorithm
| Algorithm 4: Time-space reduction for 0/1-KP in O(n + C’). |
|
2.3. 0/1-KP Solving by Quantim-Inspired Differential Evolution Algorithm
2.4. 0/1-mKP Solving by Mathematical HyMKP Algorithm
| Algorithm 5: Mathematical HyMKP model. |
| Step 1: perform the existing preprocessing: Instance reduction, Capacity lifting, and Item dominance. Step 2: call MULKNAP branch-and-bound (BnB) for τ secs. if (the solution is optimal) then return. Step 3: call Create-reflect-multigraph-MKP (Algorithm 6). Step 4: for (i = 1 to v) do execute the knapsack-based decomposition. if (an optimal solution has been obtained) then return. else add the resulting no-good-cut. end for i Step 5: if (the instance is not solved) then execute the reflect-based decomposition and return. |
| Algorithm 6: Create-reflect-multigraph-MKP in O(mnC). |
|
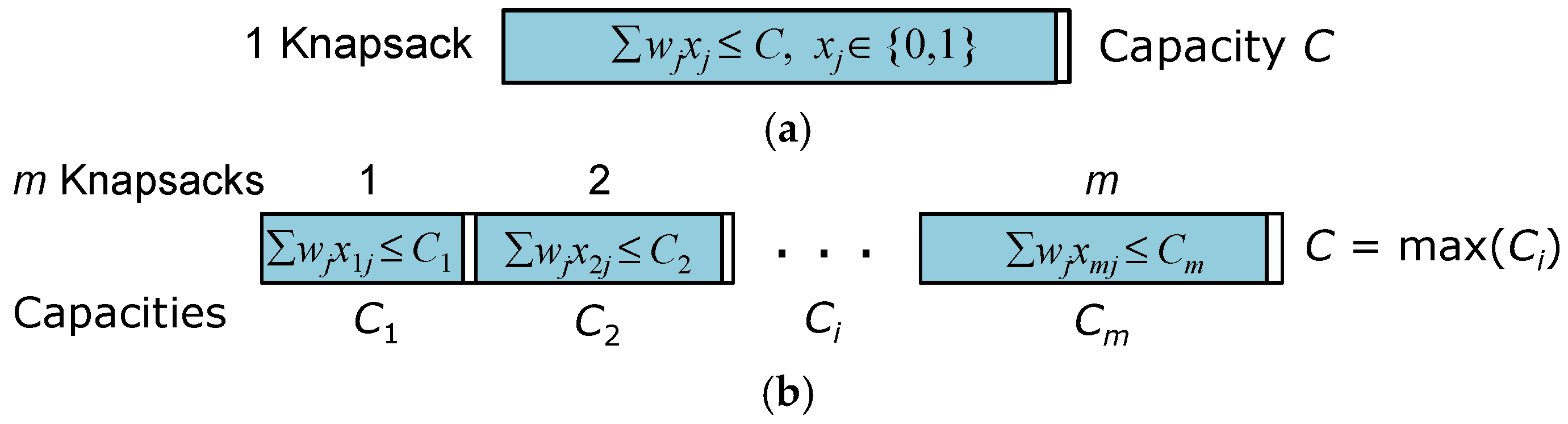
- As =
- {(d, d + wj, j, 0), 1 ≤ j ≤ n} is the set of standard item arcs.
- Ar =
- {(d, Ci-(d + wj), j, i), 1 ≤ i ≤ m, 1 ≤ j ≤ n} is the set of reflected item arcs (satisfying d + wj > Ci/2 and d ≤ Ci-wj).
- Ac =
- {(Ci/2, Ci/2, 0, i)} is the set of reflected connection arcs.
- Al =
- {(d, e, 0, 0), d < e} is the set of loss arcs.
- Exact DP transformation (DPT) algorithm (in Section 3) to find the optimal solutions of the 0/1-KP (in each knapsack).
- m!-to-m2 knapsack-order reduction (in Section 4.1.2) to define the exact-fit (best) knapsack order for the 0/1-mKP (m knapsacks).
- Robust unbiased filtering (in Section 4.2) to improve/reduce time complexity to polynomial time while retaining the high optimal performance.
3. 0/1-KP Solving by DP Transformation to List-Based Time-Space Reduction
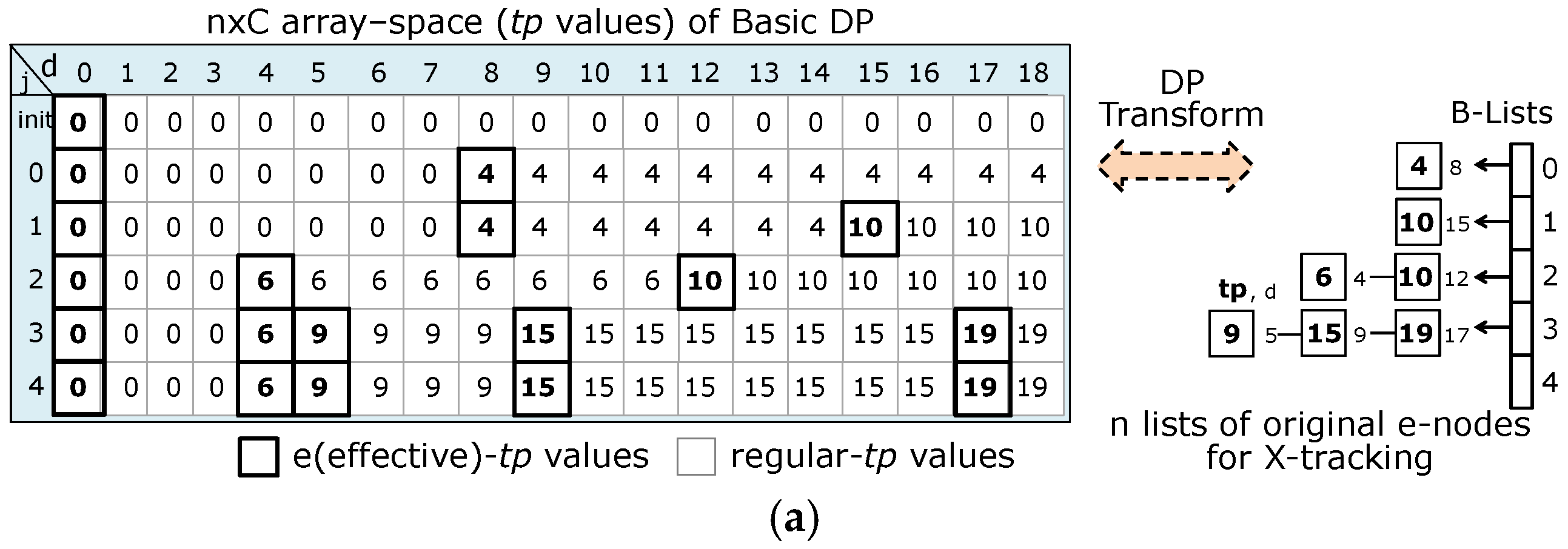
3.1. Preprocessing of the DPT-ListTSR Algorithm
| Algorithm 7: Preprocessing of the DPT-ListTSR algorithm. |
|
- ▪
- For object j = 0 (w0 = 8, p0 = 4), Step 1 copies the first e-node cn = (tp, d) = (0, 0) of F-list j − 1 to F-list j (since cn.tp < p0 and cn.d < w0). In Step 2 (from head of F-list j − 1), at e-node en = (0, 0), Step 2.1 computes d = en.d + w0 = 8, tp = en.tp + p0 = 4, and decode TP = 0 [(n1.d = 0, n1.tp = 0), (n2.d = C = 18, n2.tp = 0)]. Since d < C and tp = 4 > TP = 0, Step 2.2 adds new e-node = (4, 8) in F-list j = 0 and B-list L0.
- ▪
- For object j = 1 (w1 = 15, p1 = 10), Step 1 copies (0, 0), (4, 8) of F-list j − 1 to F-list j (while cn.tp < p1 and cn.d < w1). In Step 2, at e-node en = (0, 0) of F-list j − 1, compute d = 15, tp = 10, TP = 4 ((n1.d = 8, n1.tp = 4), (n2.d = C = 18, n2.tp = 4)). Since tp = 10 > TP = 4, add new e-node (10, 15) in F-list j = 1 and B-list L1. At en = (4, 8), d = 8 + 15 = 23 > C (no new e-node added).
- ▪
- For object j = 2 (w2 = 4, p2 = 6), Step 1 copies (0, 0) of F-list j − 1 to F-list j. In Step 2, at en = (0, 0) of F-list j − 1, d = 4, tp = 6 > TP = 0, add new e-node (6, 4) in F-list j = 2 and B-list L2. At en = (4, 8) of F-list j − 1, d = 8 + 4 = 12, tp = 4 + 6 = 10 > TP = 4, add new e-node (10, 12). At en = (10, 15), d = 15 + 4 = 19 > C (no new e-node added).
- ▪
- For object j = 3 (w3 = 5, p3 = 9), Step 1 copies (0, 0), (6, 4) of F-list j − 1 to F-list j. In Step 2, at en = (0, 0) of F-list j − 1, d = 5, tp = 9 > TP = 6 (add new e-node (9, 5)). At en = (6, 4) of F-list j − 1, d = 4 + 5 = 9, tp = 6 + 9 = 15 > TP = 6 (add new e-node (15, 9)). At en = (10, 12), d = 17, tp = 19 > TP = 10 (add new e-node (19, 17)).
- ▪
- For object j = 4 (w4 = 12, p4 = 8), Step 1 copies (0, 0), (6, 4) of F-list j − 1 to F-list j. In Step 2, at en = (0, 0) of F-list j − 1, compute d = 12, tp = 8 < TP = 15 (no new e-node added). At en = (6, 4), compute d = 4 + 12 = 16, tp = 6 + 8 = 14 < TP = 15 (no new e-node added). At en = (9, 5), add this remaining (worth) e-node to F-list j and compute d = 5 + 12 = 17, tp = 9 + 8 = 17 < TP = 19 (no new e-node added). At en = (15, 9), add this remaining e-node to F-list j and compute d = 9 + 12 = 21 > C (no new e-node added). At en = (19, 17), add this remaining e-node to F-list j and compute d = 17 + 12 = 29 > C (no new e-node added).
3.2. X-Tracking of the DPT-ListTSR Algorithm
| Algorithm 8: X-tracking (for solx) on B-lists of the DPT-ListTSR algorithm. |
|
4. 0/1-mKP Solving by Multi-DPT-ListTSR Plus Unbiased Filtering in Efficient Time
4.1. Efficient Multi-DPT-ListTSR Algorithm for Solving 0/1-mKP
4.1.1. Top Nine Knapsack Orders for Regular Datasets
| Algorithm 9: Multi-DPT-ListTSR for one proper order: O(m[n2,nC]). |
|
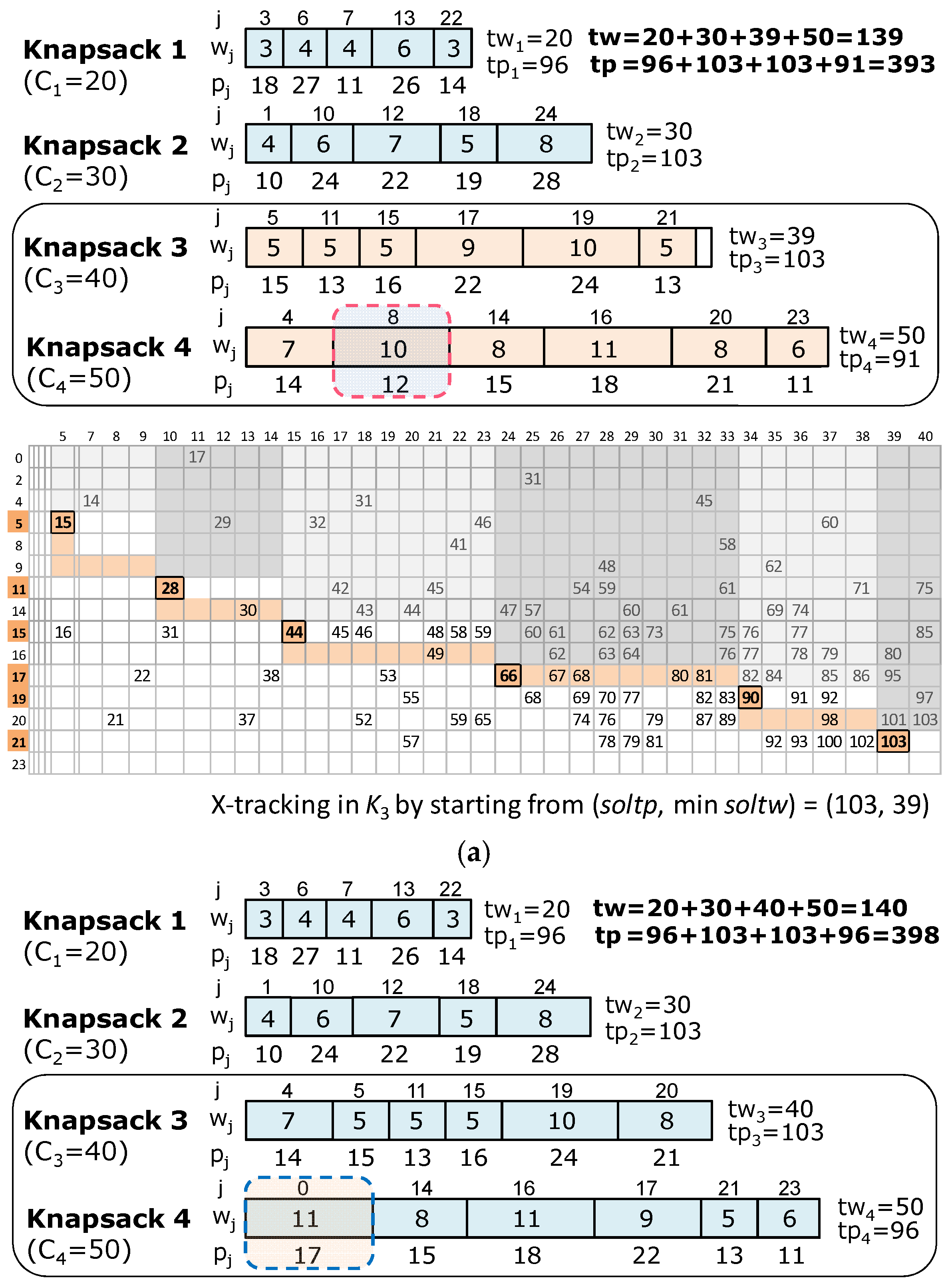
4.1.2. The Exact-Fit (Best) Knapsack Order for Regular and Irregular Datasets
- ▪
- In the first Ki selection, there are m dFiti-results (in m = 5 steps) with two min(dFits) = 0 (in K2, K3) and K2 (min C2) is selected (see conditions in Step 2 of Algorithm 10).
- ▪
- In the second Ki selection, there are 4 dFiti-results and K4 (min(dFit4) = 0) is selected.
- ▪
- In the third Ki selection, there are 3 dFiti-results and K1 (min(dFit1) = 0) is selected.
- ▪
- In the fourth Ki selection, there are 2 dFiti-results and K5 (min(dFit5) = 0) is selected.
- ▪
- In the fifth Ki selection, the last K3 (min(dFit3) = 0) in the last step is selected.
| Algorithm 10: multi-DPT-ListTSR (the exact-fit (best) knapsack order). | ||
| ||
| Policy 1: if (there are equal min(dFiti)s), select best Ki with min(Ci); if (there are equal min(Ci)s), select best Ki with max(TPi); | ||
| Policy 2: if (there are equal min(dFiti)s), select best Ki with max(TPi/TWi); if (there are equal max(TPi/TWi)s), select best Ki with min(Ci); if (there are equal min(Ci)s), select best Ki with max(TPi); | ||
| Policy 3: if (there are equal min(dFiti)s), select best Ki with max(TPi); if (there are equal max(TPi)s), select best Ki with min(Ci); | ||
| ||
4.2. Efficient Robust Unbiased Filtering for Polynomial Time Reduction
| Algorithm 11: Multi-DPT-ListTSR + robust unbiased filtering. |
|
5. Analysis of Proposed Algorithms
5.1. Correctness of the DPT-ListTSR Algorithm
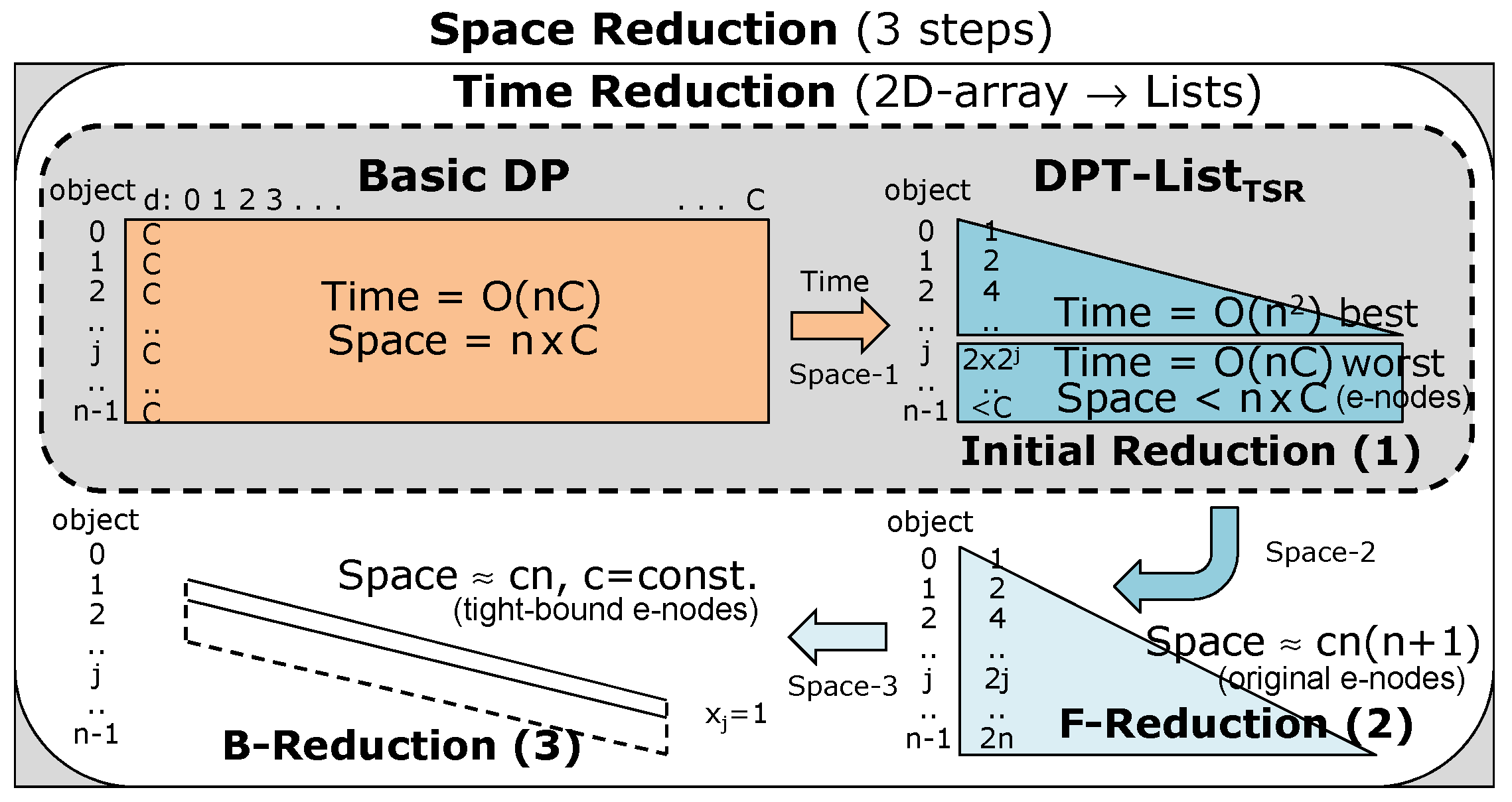
5.2. Complexity Analysis of the DPT-ListTSR Algorithm
- -
- Best case: Total steps (n objects (j = 0 to n − 1)) are approximately 1 + 2 + 4 +…+ 2(j + 1) +…+ 2n ≈ n(n + 1) = O(n2).
- -
- Worst case (rarely occurs): Total steps are approximately 1 + 2 + (≤4) + (≤8) +…+ (≤2 × 2j) +…+ (≈n × C/2) = O(nC).
5.3. High (Optimal) Precision (as m! Orders) of the Exact-Fit (Best) Knapsack Order
5.4. High (Optimal) Precision of the Robust Unbiased Filtering
6. Experimental Results
6.1. Results of the DPT-ListTSR (One Knapsack) and Robust Unbiased Filtering
6.2. Results of the Multi-DPT-ListTSR (m Knapsacks) and Robust Unbiased Filtering
| Exact | 1.1 Multi-DPT-List (exact-fit best order) | O(m2[n2,nC]) |
| Exact + Filtering | 2.1 Fast multi-DPT-List + filtering (exact-fit best order) 2.2 Fast multi-DPT-List + filtering (top 9 orders + partial LSs) 2.3 Fast multi-DPT-List + filtering (top 9 orders) | O(m2n) O(mn) O(mn) |
| Heuristic | 3.1 Quick multi-GH (P/W rank) (top 9 orders) 3.2 Improved multi-GH+ (P/W rank) (top 9 orders) 3.3 Improved multi-GH+ (P/W rank) (top 9 + full LS orders) | O(mn) O(mn) O(m2n) |
6.3. Extra Experiment and Additional Improvement on Critical Datasets
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buayen, P.; Werapun, J. Parallel time-space reduction by unbiased filtering for solving the 0/1-knapsack problem. J. Parallel Distrib. Comput. 2018, 122, 195–208. [Google Scholar] [CrossRef]
- Aisopos, F.; Tserpes, K.; Varvarigou, T. Resource management in software as a service using the knapsack problem model. Int. J. Prod. Econ. 2013, 141, 465–477. [Google Scholar] [CrossRef]
- Vanderster, D.C.; Dimopoulos, N.J.; Parra-Hernandez, R.; Sobie, R.J. Resource allocation on computational grids using a utility model and the knapsack problem. Future Gener. Comput. Syst. 2009, 25, 35–50. [Google Scholar] [CrossRef]
- Bas, E. A capital budgeting problem for preventing workplace mobbing by using analytic hierarchy process and fuzzy 0-1 bidimensional knapsack model. Expert Syst. Appl. 2011, 38, 12415–12422. [Google Scholar] [CrossRef]
- Camargo, V.C.B.; Mattiolli, L.; Toledo, F.M.B. A knapsack problem as a tool to solve the production planning problem in small foundries. Comput. Oper. Res. 2012, 39, 86–92. [Google Scholar] [CrossRef]
- Fukunaga, A.S.; Korf, R.E. Bin completion algorithms for multicontainer packing, knapsack, and covering problems. J. Artif. Intell. Res. 2007, 28, 393–429. [Google Scholar] [CrossRef]
- Rooderkerk, R.P.; van Herrde, H.J. Robust optimization of the 0-1 knapsack problem: Balancing risk and return in assortment optimization. Eur. J. Oper. Res. 2016, 250, 842–854. [Google Scholar] [CrossRef]
- Ahmad, S.J.; Reddy, V.S.K.; Damodaram, A.; Krishna, P.R. Delay optimization using Knapsack algorithm for multimedia traffic over MANETs. Expert Syst. Appl. 2015, 42, 6819–6827. [Google Scholar] [CrossRef]
- Wang, E.; Yang, Y.; Wu, J. A Knapsack-based buffer management strategy for delay-tolerant networks. J. Parallel Distrib. Comput. 2015, 86, 1–15. [Google Scholar] [CrossRef]
- Wedashwara, W.; Mabu, S.; Obayashi, M.; Kuremoto, T. Combination of genetic network programming and knapsack problem to support record clustering on distributed databases. Expert Syst. Appl. 2016, 46, 15–23. [Google Scholar] [CrossRef]
- Kellerer, H.; Pferschy, U.; Pisinger, D. Dynamic Programming. In Knapsack Problem; Springer: Berlin, Germany; New York, NY, USA, 2004; pp. 20–26. [Google Scholar]
- Monaci, M.; Pferschy, U.; Serafini, P. Exact solution of the robust knapsack problem. Comput. Oper. Res. 2013, 40, 2625–2631. [Google Scholar] [CrossRef] [PubMed]
- Rong, A.; Figueira, J.R.; Klamroth, K. Dynamic programming based algorithms for the discounted {0-1} knapsack problem. Appl. Math. Comput. 2012, 218, 6921–6933. [Google Scholar] [CrossRef]
- Rong, A.; Figueira, J.R.; Pato, M.V. A two state reduction based dynamic programming algorithm for the bi-objective 0-1 knapsack problem. Comput. Math. Appl. 2011, 62, 2913–2930. [Google Scholar] [CrossRef]
- Rong, A.; Figueira, J.R. Dynamic programming algorithms for the bi-objective integer knapsack problem. Eur. J. Oper. Res. 2014, 236, 85–99. [Google Scholar] [CrossRef]
- Cunha, A.S.; Bahiense, L.; Lucena, A.; Souza, C.C. A new lagrangian based branch and bound algorithm for the 0-1 knapsack problem. Electron. Notes Discret. Math. 2010, 36, 623–630. [Google Scholar] [CrossRef]
- Li, X.; Liu, T. On exponential time lower bound of knapsack under backtracking. Theor. Comput. Sci. 2010, 411, 1883–1888. [Google Scholar] [CrossRef]
- Calvin, J.M.; Leung, J.Y.-T. Average-case analysis of a greedy algorithm for the 0/1 knapsack problem. Oper. Res. Lett. 2003, 31, 202–210. [Google Scholar] [CrossRef]
- Truong, T.K.; Li, K.; Xu, Y. Chemical reaction optimization with greedy strategy for the 0-1 knapsack problem. Appl. Soft Comput. 2013, 13, 1774–1780. [Google Scholar] [CrossRef]
- Balas, E.; Zemel, E. An algorithm for large zero-one knapsack problems. Oper. Res. 1980, 28, 1130–1154. [Google Scholar] [CrossRef]
- Guastaroba, G.; Savelsbergh, M.; Speranza, M.G. Adaptive kernal search: A heuristic for solving mixed integer linear programs. Eur. J. Oper. Res. 2017, 263, 789–804. [Google Scholar] [CrossRef]
- Lim, T.Y.; Al-Betar, M.A.; Khader, A.T. Taming the 0/1 knapsack problem with monogamous pairs genetic algorithm. Expert Syst. Appl. 2016, 54, 241–250. [Google Scholar] [CrossRef]
- Sachdeva, C.; Goel, S. An improved approach for solving 0/1 knapsack problem in polynomial time using genetic algorithms. In Proceedings of the IEEE International Conference on Recent Advances and Innovations in Engineering, Jaipur, India, 9–11 May 2014. [Google Scholar]
- Bansal, J.C.; Deep, K. A modified binary particle swarm optimization for knapsack problems. Appl. Math. Comput. 2012, 218, 11042–11061. [Google Scholar] [CrossRef]
- Bhattacharjee, K.K.; Sarmah, S.P. Shuffled frog leaping algorithm and its application to 0/1 knapsack problem. Appl. Soft Comput. 2014, 19, 252–263. [Google Scholar] [CrossRef]
- Moosavian, N. Soccer league competition algorithm for solving knapsack problem. Swarm Evol. Comput. 2015, 20, 14–22. [Google Scholar] [CrossRef]
- Zhang, J. Comparative study of several intelligent algorithms for knapsack problem. Procedia Environ. Sci. 2011, 11, 163–168. [Google Scholar] [CrossRef]
- Zou, D.; Gao, L.; Li, S.; Wu, J. Solving 0-1 knapsack problem by novel global harmony search algorithm. Appl. Soft Comput. 2011, 11, 1556–1564. [Google Scholar] [CrossRef]
- Lv, J.; Wang, X.; Huang, M.; Cheng, H.; Li, F. Solving 0-1 knapsack problem by greedy degree and expectation efficiency. Appl. Soft Comput. 2016, 41, 94–103. [Google Scholar] [CrossRef]
- Pavithr, R.S. Gursaran, Quantum inspired social evolution (QSE) algorithm for 0-1 knapsack problem. Swarm Evol. Comput. 2016, 29, 33–46. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, T.; Pang, F.; Liu, Y. Genetic algorithm based on greedy strategy in the 0-1 knapsack problem. In Proceedings of the 2009 Third International Conference on Genetic and Evolutionary Computing, Guilin, China, 14–17 October 2009. [Google Scholar]
- Zhou, Y.; Chen, X.; Zhou, G. An improved monkey algorithm for 0-1 knapsack problem. Appl. Soft Comput. 2016, 38, 817–830. [Google Scholar] [CrossRef]
- Sanchez-Diaz, X.; Ortiz-Bayliss, J.C.; Amaya, I.; Cruz-Duarte, J.M.; Conant-Pablos, S.E.; Terashima-Marin, H. A feature-independent hyper-heuristic approach for solving the knapsack problem. Appl. Sci. 2021, 11, 10209. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Delorme, M.; Iori, M.; Martello, S. Mathematical models and decomposition methods for the multiple knapsack problem. Eur. J. Oper. Res. 2019, 274, 886–899. [Google Scholar] [CrossRef]
- Fukunaga, A.S. A branch-and-bound algorithm for hard multiple knapsack problems. Ann. Oper. Res. 2011, 184, 97–119. [Google Scholar] [CrossRef]
- Martello, S.; Monaci, M. Algorithmic approaches to the multiple knapsack assignment problem. Omega 2020, 90, 102004. [Google Scholar] [CrossRef]
- Angelelli, E.; Mansini, R.; Speranza, M.G. Kernal search: A general heuristic for the multi-dimensional knapsack problem. Comput. Oper. Res. 2010, 37, 2017–2026. [Google Scholar] [CrossRef]
- Haddar, B.; Khemakhem, M.; Hanafi, S.; Wilbaut, C. A hybrid quantum particle swarm optimization for the multidimensional knapsack problem. Eng. Appl. Artif. Intell. 2016, 55, 1–13. [Google Scholar] [CrossRef]
- Meng, T.; Pan, Q.-K. An improved fruit fly optimization algorithm for solving the multidimensional knapsack problem. Appl. Soft Comput. 2017, 50, 79–93. [Google Scholar] [CrossRef]
- Wang, L.; Yang, R.; Ni, H.; Ye, W.; Fei, M.; Pardalos, P.M. A human learning optimization algorithm and its application to multi-dimensional knapsack problems. Appl. Soft Comput. 2015, 34, 736–743. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, C.; Li, J.; Wang, X.; Yang, Z.; Lee, J.-M.; Jung, K.-H. Binary artificial algae algorithm for multidimensional knapsack problems. Appl. Soft Comput. 2016, 43, 583–595. [Google Scholar] [CrossRef]
- Gao, C.; Lu, G.; Yao, X.; Li, J. An iterative pseudo-gap enumeration approach for the multidimensional multiple-choice knapsack problem. Eur. J. Oper. Res. 2017, 260, 1–11. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W. Quantum-inspired differential evolution with gray wolf optimizer for 0-1 knapsack problem. Mathematics 2021, 9, 1233. [Google Scholar] [CrossRef]






















| m Knapsacks | All Orders (m!) | Exact-Fit/Best (m(m + 1)/2) | Top (9) Orders | Partial LS Min (9 m, 9 × 9) | Full LS (9 m) |
|---|---|---|---|---|---|
| 5 | 120 | 15 | 9 | 45 | 45 |
| 6 | 720 | 21 | 9 | 54 | 54 |
| 7 | 5040 | 28 | 9 | 63 | 63 |
| 8 | 40,320 | 36 | 9 | 72 | 72 |
| 9 | 326,880 | 45 | 9 | 81 | 81 |
| 10 | 3,268,800 | 55 | 9 | 81 | 90 |
| 20 | 20! | 210 | 9 | 81 | 180 |
| 50 | 50! | 1275 | 9 | 81 | 450 |
| 100 | 100! | 5050 | 9 | 81 | 900 |
| Total Weight (soltw) | Total Profit (soltp) | ||||||
|---|---|---|---|---|---|---|---|
| n | C | DPT-List (Opt.) | DPT + rFilter | TSR + uFilter [1] | DPT-List (Opt.) | DPT + rFilter | TSR + uFilter [1] |
| 12 | 96 | 96 | 96 | 92 | 282 | 282 | 280 |
| 14 | 112 | 111 | 111 | 109 | 365 | 365 | 362 |
| 21 | 168 | 168 | 168 | 167 | 500 | 500 | 498 |
| 26 | 208 | 208 | 208 | 203 | 637 | 637 | 636 |
| 39 | 312 | 312 | 312 | 312 | 868 | 868 | 866 |
| 45 | 360 | 360 | 360 | 360 | 1177 | 1177 | 1172 |
| 73 | 510 | 510 | 510 | 509 | 1640 | 1640 | 1639 |
| 80 | 559 | 559 | 559 | 558 | 1712 | 1712 | 1711 |
| 81 | 566 | 566 | 566 | 566 | 1888 | 1888 | 1886 |
| 143 | 1000 | 1000 | 1000 | 1000 | 3084 | 3084 | 3082 |
| 147 | 1028 | 1028 | 1028 | 1028 | 3250 | 3250 | 3239 |
| 155 | 1084 | 1084 | 1084 | 1083 | 3440 | 3440 | 3437 |
| 166 | 1161 | 1161 | 1161 | 1161 | 3617 | 3617 | 3616 |
| 182 | 1273 | 1273 | 1273 | 1273 | 3967 | 3967 | 3966 |
| 197 | 1378 | 1378 | 1378 | 1378 | 4534 | 4534 | 4533 |
| 199 | 1392 | 1392 | 1392 | 1391 | 4561 | 4561 | 4560 |
| 247 | 1481 | 1481 | 1481 | 1480 | 4822 | 4822 | 4821 |
| 276 | 1655 | 1655 | 1655 | 1655 | 5446 | 5446 | 5445 |
| 286 | 1715 | 1715 | 1715 | 1715 | 5889 | 5889 | 5888 |
| 316 | 1895 | 1895 | 1895 | 1895 | 6266 | 6266 | 6257 |
| 329 | 1973 | 1973 | 1973 | 1973 | 6484 | 6484 | 6469 |
| 360 | 2159 | 2159 | 2159 | 2159 | 6985 | 6985 | 6984 |
| 385 | 2309 | 2309 | 2309 | 2309 | 7710 | 7710 | 7709 |
| DPT-List + Robust Filtering | TSR + Unbiased Filtering [1] | |||||
|---|---|---|---|---|---|---|
| n: Datasets | not Opt. | Optimal | Precision | not Opt. | Optimal | Precision |
| 5 ≤ n ≤ 100 | 0 | 95 | 99.9% | 9 | 86 | 90.0% |
| 5 ≤ n ≤ 200 | 0 | 195 | 99.9% | 16 | 179 | 92.0% |
| 5 ≤ n ≤ 500 | 0 | 495 | 99.9% | 23 | 472 | 95.4% |
| 5 ≤ n ≤ 2000 | 0 | 1995 | 99.9% | 28 | 1967 | 98.6% |
| 5 ≤ n ≤ 5000 | 0 | 4995 | 99.9% | 109 | 4886 | 97.8% |
| 5 ≤ n ≤ 10,000 | 0 | 9995 | 99.9% | 223 | 9772 | 97.8% |
| n | n × C (Full Space) | e-Nodes (1. Initial Reduction) | Original e-Nodes (2. F-reduction) | Tight-Bound e-Nodes (3. B-Reduction) | |||
|---|---|---|---|---|---|---|---|
| 5 | 90 | 13 | 86% | 7 | 92% | 6 | 93% |
| 15 | 600 | 223 | 63% | 103 | 83% | 50 | 92% |
| 50 | 17,450 | 6559 | 62% | 2465 | 86% | 1917 | 89% |
| 100 | 69,900 | 35,852 | 49% | 15,263 | 78% | 10,849 | 84% |
| 200 | 239,800 | 150,518 | 37% | 66,883 | 72% | 35,932 | 85% |
| 500 | 1,250,000 | 915,303 | 27% | 374,729 | 70% | 173,786 | 86% |
| 1000 | 5,000,000 | 3,832,827 | 23% | 1,566,414 | 69% | 692,691 | 86% |
| 1500 | 11,250,000 | 8,669,932 | 23% | 3,364,525 | 70% | 1,581,133 | 86% |
| 2000 | 11,998,000 | 10,322,643 | 14% | 3,293,641 | 73% | 1,115,040 | 91% |
| 2500 | 18,747,500 | 16,071,768 | 14% | 5,338,435 | 72% | 1,752,052 | 91% |
| 3000 | 26,997,000 | 23,225,460 | 14% | 7,497,627 | 72% | 2,620,552 | 90% |
| m = 2 | Optimal | mDPT-L m! O(m[n2, nC]) | mDPT-L + Filter m! O(mn) | mGH m! O(mn) | mGH+ m! O(mn) |
|---|---|---|---|---|---|
| n | m! = 2 | m! = 2 | m! = 2 | m! = 2 | |
| 15 | 315 | 315 | 315 | 308 | 310 |
| 20 | 420 | 420 | 420 | 393 | 420 |
| 30 | 800 | 800 | 800 | 790 | 796 |
| 40 | 1050 | 1050 | 1050 | 1022 | 1047 |
| 50 | 1019 | 1019 | 1019 | 1006 | 1013 |
| 100 | 2359 | 2359 | 2359 | 2313 | 2357 |
| 200 | 3878 | 3878 | 3878 | 3860 | 3870 |
| 300 | 6202 | 6202 | 6202 | 6171 | 6196 |
| 400 | 7686 | 7686 | 7686 | 7654 | 7683 |
| 500 | 9074 | 9074 | 9074 | 9045 | 9072 |
| 1000 | 18,038 | 18,038 | 18,038 | 18,002 | 18,031 |
| m = 3 | Optimal | mDPT-L m! O(m[n2, nC]) | mDPT-L + Filter m! O(mn) | mGH m! O(mn) | mGH+ m! O(mn) |
|---|---|---|---|---|---|
| n | m! = 6 | m! = 6 | m! = 6 | m! = 6 | |
| 15 | 327 | 327 | 327 | 320 | 322 |
| 20 | 466 | 466 | 466 | 454 | 466 |
| 30 | 840 | 840 | 840 | 829 | 839 |
| 40 | 1103 | 1103 | 1103 | 1090 | 1099 |
| 50 | 1067 | 1067 | 1067 | 1031 | 1062 |
| 100 | 2427 | 2427 | 2427 | 2390 | 2426 |
| 200 | 3949 | 3949 | 3949 | 3908 | 3943 |
| 500 | 9150 | 9150 | 9150 | 9133 | 9148 |
| 1000 | 18,112 | 18,112 | 18,112 | 18,088 | 18,110 |
| 2000 | 25,547 | 25,547 | 25,547 | 25,524 | 25,544 |
| m = 4 | Optimal | mDPT-L m! O(m[n2, nC]) | mDPT-L + Filter m! O(mn) | mGH m! O(mn) | mGH+ m! O(mn) |
|---|---|---|---|---|---|
| n | m! = 24 | m! = 24 | m! = 24 | m! = 24 | |
| 20 | 495 | 495 | 495 | 490 | 490 |
| 30 | 884 | 884 | 884 | 884 | 884 |
| 40 | 1200 | 1200 | 1200 | 1187 | 1192 |
| 50 | 1137 | 1137 | 1136 | 1121 | 1136 |
| 60 | 1504 | 1504 | 1504 | 1472 | 1499 |
| 100 | 2548 | 2548 | 2548 | 2534 | 2546 |
| 200 | 4098 | 4098 | 4098 | 4071 | 4088 |
| 500 | 9318 | 9318 | 9318 | 9297 | 9314 |
| 1000 | 18,284 | 18,284 | 18,284 | 18,249 | 18,280 |
| 2000 | 25,760 | 25,760 | 25,760 | 25,735 | 25,752 |
| 3000 | 38,941 | 38,941 | 38,941 | 38,899 | 38,930 |
| m | Optimal | mDPT-L O(m2[n2, nC]) | mDPT-L + LS Filter O(m2n) | mDPT-L + Filter O(mn) | mGH+ O(mn) | mGH+ + LS O(m2n) |
|---|---|---|---|---|---|---|
| n = 1000 | Best | 9 m | 9 | 9 | 9 m | |
| 6 | 18,541 | 18,541 | 18,541 | 18,541 | 18,535 | 18,535 |
| 7 | 18,703 | 18,703 | 18,703 | 18,703 | 18,684 | 18,693 |
| 8 | 18,889 | 18,889 | 18,889 | 18,889 | 18,879 | 18,884 |
| 9 | 19,079 | 19,079 | 19,079 | 19,079 | 19,068 | 19,071 |
| n = 2000 | Best | 9 × 9 | 9 | 9 | 9 m | |
| 12 | 27,769 | 27,769 | 27,769 | 27,769 | 27,742 | 27,753 |
| 13 | 28,154 | 28,154 | 28,154 | 28,154 | 28,127 | 28,127 |
| 14 | 28,547 | 28,547 | 28,547 | 28,547 | 28,498 | 28,517 |
| 15 | 28,948 | 28,948 | 28,948 | 28,948 | 28,900 | 28,935 |
| n = 5000 | Best | 9 × 9 | 9 | 9 | 9 m | |
| 20 | 54,736 | 54,736 | 54,736 | 54,736 | 54,680 | 54,695 |
| 30 | 62,496 | 62,496 | 62,496 | 62,496 | 62,410 | 62,450 |
| 40 | 72,417 | 72,417 | 72,417 | 72,417 | 72,323 | 72,331 |
| 50 | 84,051 | 84,051 | 84,051 | 84,051 | 83,943 | 83,963 |
| m | Optimal | mDPT-L O(m2[n2, nC]) | mDPT-L + LS Filter O(m2n) | mDPT-L + Filter O(mn) | mGH+ O(mn) | mGH+ + LS O(m2n) |
|---|---|---|---|---|---|---|
| Ci ± 10 | Best | 9 × 9 | 9 | 9 | 9 m | |
| 40 | 53,669 | 53,669 | 53,669 | 53,669 | 53,494 | 53,520 |
| 50 | 54,803 | 54,803 | 54,803 | 54,803 | 54,538 | 54,655 |
| 60 | 58,614 | 58,614 | 58,614 | 58,614 | 58,425 | 58,450 |
| 70 | 64,018 | 64,018 | 64,018 | 64,018 | 63,689 | 63,784 |
| Ci ± 20 | Best | 9 × 9 | 9 | 9 | 9 m | |
| 40 | 85,380 | 85,380 | 85,380 | 85,380 | 85,203 | 85,286 |
| 50 | 100,859 | 100,859 | 100,859 | 100,859 | 100,683 | 100,724 |
| 60 | 118,729 | 118,729 | 118,729 | 118,729 | 118,525 | 118,616 |
| 70 | 138,195 | 138,195 | 138,195 | 138,195 | 137,963 | 138,038 |
| 80 | 158,983 | 158,983 | 158,983 | 158,983 | 158,722 | 158,857 |
| 90 | 180,054 | 180,054 | 180,054 | 180,054 | 179,873 | 179,981 |
| n ≤ 10,000 | Optimal | mDPT-L O(m2[n2, nC]) | mDPT-L + LS Filter O(m2n) | mDPT-L + Filter O(mn) | mGH+ O(mn) | mGH+ + LS O(m2n) |
|---|---|---|---|---|---|---|
| m:n | m! | m! | m! | m! | m! | |
| 3:51 | 1318 | 1318 | 1317 | 1317 | 1315 | 1315 |
| 3:73 | 1727 | 1727 | 1725 | 1725 | 1725 | 1725 |
| 4:33 | 752 | 752 | 747 | 747 | 747 | 747 |
| 4:49 | 1264 | 1264 | 1263 | 1263 | 1254 | 1254 |
| 4:50 | 1137 | 1137 | 1136 | 1136 | 1136 | 1136 |
| 4:65 | 1565 | 1565 | 1563 | 1563 | 1563 | 1563 |
| m:n | Best | 9 m | 9 | 9 | 9 m | |
| 5:89 | 2366 | 2366 | 2365 | 2365 | 2359 | 2359 |
| 7:77 | 1834 | 1834 | 1833 | 1833 | 1829 | 1830 |
| 7:138 | 3263 | 3263 | 3262 | 3262 | 3256 | 3256 |
| 7:148 | 3780 | 3780 | 3799 | 3799 | 3773 | 3777 |
| n ≤ 10,000 | mDPT-L: O(m2[n2, nC]) | mDPT-L + Filtering: O(m2n) | |||
|---|---|---|---|---|---|
| m | Best | 9 m (LS) | Best | 9 m (LS) | Top 9 |
| 5 | 0 | 0 | 0 | 1 | 2 |
| 6 | 0 | 0 | 0 | 1 | 3 |
| 7 | 0 | 1 | 0 | 3 | 6 |
| 8–14 | 0 | 0 | 0 | 2 | 1.6 (ave. per m) |
| 15–19 | 0 | 0 | 0 | 0 | 1.6 (ave. per m) |
| 20–24 | 0 | 0 | 0 | 0 | 2.6 (ave. per m) |
| 25–29 | 0 | 0 | 0 | 0 | 4.8 (ave. per m) |
| 30–34 | 0 | 0 | 0 | 0 | 5.4 (ave. per m) |
| 35–39 | 0 | 0 | 0 | 0 | 13.8 (ave. per m) |
| 40–44 | 0 | 0 | 0 | 0 | 31.4 (ave. per m) |
| 45–49 | 0 | 0 | 0 | 0 | 34.8 (ave. per m) |
| 50–54 | 0 | 0 | 0 | 0 | 69.2 (ave. per m) |
| Research Approach | Exact | Exact + Filtering | Heuristic | ||||
|---|---|---|---|---|---|---|---|
| mDP | mDPT-L | mDPT-L + Filter: O(m2n) | mGH+ | ||||
| n:m | Optimal | Best | Best | Best | 9 m | 9 | 9 m |
| 100:10-1 | 26,797 | 26,797 | 26,797 | 26,797 | 26,797 | 26,797 | 26,763 |
| 100:10-2 | 24,116 | 24,116 | 24,116 | 24,116 | 24,116 | 24,116 | 24,093 |
| 100:10-3 | 25,828 | 25,828 | 25,828 | 25,828 | 25,828 | 25,828 | 25,812 |
| 100:10-4 | 24,004 | 24,004 | 24,004 | 24,004 | 24,004 | 24,004 | 23,977 |
| 100:10-5 | 23,958 | 23,958 | 23,958 | 23,958 | 23,958 | 23,958 | 23,933 |
| 100:10-6 | 24,650 | 24,650 | 24,650 | 24,650 | 24,650 | 24,650 | 24,614 |
| 100:10-7 | 23,911 | 23,911 | 23,911 | 23,911 | 23,911 | 23,911 | 23,886 |
| 100:10-8 | 26,612 | 26,612 | 26,612 | 26,612 | 26,612 | 26,612 | 26,579 |
| 100:10-9 | 24,588 | 24,588 | 24,588 | 24,588 | 24,588 | 24,588 | 24,565 |
| 100:10-10 | 24,617 | 24,617 | 24,617 | 24,617 | 24,617 | 24,617 | 24,591 |
| Research Approach | Exact | Exact + Filtering | Heuristic | ||||
|---|---|---|---|---|---|---|---|
| Over Packing * | mDPT-L O(m2[n2, nC]) | mDPT-L + Filter O(m2n) | mGH+ O(m2n) | ||||
| n:m | Optimal | Best of this study | Best +extra | Best | Best | 9 m | 9 m |
| 200:20-1 | 80,260 * | 80,205 | 80,205 | 80,163 | 80,196 | 80,121 | 79,606 |
| 200:20-2 | 80,171 * | 80,122 | 80,122 | 80,122 | 80,121 | 80,069 | 79,488 |
| 200:20-3 | 79,101 * | 79,083 | 79,083 | 79,061 | 79,083 | 79,041 | 78,561 |
| 200:20-4 | 76,264 * | 76,208 | 76,208 | 76,174 | 76,174 | 76,149 | 75,823 |
| 200:20-5 | 79,619 | 79,619 | 79,619 | 79,581 | 79,581 | 79,515 | 78,886 |
| 200:20-6 | 76,749 * | 76,711 | 76,711 | 76,711 | 76,711 | 76,612 | 76,203 |
| 200:20-7 | 76,543 * | 76,474 | 76,474 | 76,429 | 76,474 | 76,402 | 75,959 |
| 300:30-1 | 121,806 * | 121,756 | 121,742 | 121,742 | 121,756 | 121,654 | 120,842 |
| 300:30-2 | 119,877 * | 119,828 | 119,828 | 119,795 | 119,828 | 119,743 | 118,938 |
| 300:30-3 | 119,806 * | 119,762 | 119,762 | 119,756 | 119,749 | 119,684 | 118,937 |
| 300:30-4 | 115,567 * | 115,556 | 115,529 | 115,516 | 115,556 | 115,434 | 114,767 |
| 300:30-5 | 117,204 * | 117,175 | 117,175 | 117,160 | 117,168 | 117,065 | 116,350 |
| 300:30-6 | 118,516 * | 118,493 | 118,493 | 118,493 | 118,450 | 118,386 | 117,737 |
| 300:30-7 | 115,793 * | 115,752 | 115,752 | 115,706 | 115,693 | 115,641 | 115,093 |
| 300:30-8 | 123,664 * | 123,624 | 123,624 | 123,620 | 123,620 | 123,552 | 122,570 |
| 500:50-1 | 205,672 * | 205,645 | 205,645 | 205,645 | 205,645 | 205,488 | 204,132 |
| 500:50-2 | 199,868 * | 199,781 | 199,775 | 199,775 | 199,781 | 199,681 | 198,462 |
| 500:50-3 | 202,321 * | 202,286 | 202,286 | 202,277 | 202,277 | 202,164 | 201,102 |
| 500:50-4 | 136,669 * | 136,657 | 136,657 | 136,653 | 136,652 | 136,595 | 135,409 |
| 500:50-5 | 135,806 * | 135,796 | 135,795 | 135,795 | 135,796 | 135,736 | 134,793 |
| For Regular and Irregular Datasets (n ≤ 10,000, m ≤ 100) | ||
|---|---|---|
| Exact + Filtering | Our multi-DPT-List + robust filtering (the exact-fit best order) could find most optimal solutions (≥99%) in efficient response time (<1 s per n); see confirmed results in Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12. | O(m2n) |
| Exact | Mathematical HyMKP [34] can execute in τ secs. with Algorithm 6 (reflect multi-graph MKP with decreasing n weights (wj)) like the basic DP for each of m knapsacks. That initial solution can be improved by the knapsack decomposition in v iterations to find the optimal solution (n ≤ 500) in τ secs. However, no available results for n > 500 in that study. | O(mnC) |
| Heuristic | Multi-GH+ (Latin squares of top nine orders) could find good solutions in efficient time (< 1 s) but they are not optimal (see the last column results in Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10 and Table 12). Note: LSs of top 9 orders could emulate 9 m iterations/evolutions in the GA/swarm optimization with good results (near optimal in each knapsack for small m). | O(m2n) |
| For critical and special benchmark datasets (n ≤ 500) [34] | ||
| Exact | Partial BnB (in HyMKP) [34]: The existing BnB (MULKNAP program) could find most optimal solutions (≥99.9%) in τ secs for n ≤ 500. | O((m + 1)n) |
| Exact + Filtering | Our multi-DPT-List + robust filtering (the best order): For critical datasets in 0/1-mKP applications, we can adopt the MULKNAP program [34] for n ≤ 500 in our approach to achieve 99.9% optimal solutions. For n > 500 we can apply our efficient multi-DPT-List + filtering in efficient time. | O(m2n) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buayen, P.; Werapun, J. Efficient 0/1-Multiple-Knapsack Problem Solving by Hybrid DP Transformation and Robust Unbiased Filtering. Algorithms 2022, 15, 366. https://doi.org/10.3390/a15100366
Buayen P, Werapun J. Efficient 0/1-Multiple-Knapsack Problem Solving by Hybrid DP Transformation and Robust Unbiased Filtering. Algorithms. 2022; 15(10):366. https://doi.org/10.3390/a15100366
Chicago/Turabian StyleBuayen, Patcharin, and Jeeraporn Werapun. 2022. "Efficient 0/1-Multiple-Knapsack Problem Solving by Hybrid DP Transformation and Robust Unbiased Filtering" Algorithms 15, no. 10: 366. https://doi.org/10.3390/a15100366
APA StyleBuayen, P., & Werapun, J. (2022). Efficient 0/1-Multiple-Knapsack Problem Solving by Hybrid DP Transformation and Robust Unbiased Filtering. Algorithms, 15(10), 366. https://doi.org/10.3390/a15100366





