Abstract
Complex networks usually consist of dense-connected cliques, which are defined as communities. A community structure is a reflection of the local characteristics existing in the network topology, this makes community detection become an important research field to reveal the internal structural characteristics of networks. In this article, an information-based community detection approach MINC-NRL is proposed, which can be applied to both overlapping and non-overlapping community detection. MINC-NRL introduces network representation learning (NRL) to represent the target network as vectors, then generates a community evolution process based on these vectors to reduce the search space, and finally, finds the best community partition in this process using mutual information between network and communities (MINC). Experiments on real-world and synthetic data sets verifies the effectiveness of the approach in community detection, both on non-overlapping and overlapping tasks.
1. Introduction
Complex networks are a kind of graph-structured data which abstractly represents the real-world systems and structures. Nodes and edges of a network respectively represent elements and relationships of a system to show its topological characteristics. It has been shown that there are clusters of nodes that can be regarded as an independent whole according to some precisely defined and quantifiable attributes generally exist in many networks. Typically, the density of edges between nodes in a cluster. A group of nodes can be defined as a community if it has a higher density of internal edges than the average edge density of the whole network. Detecting communities in complex networks plays a vital role in understanding the structure and functions of the entire network system and can help us analyze and predict the interactions between the elements of it. Many researchers have focused on methods that can efficiently detect community structure in complex networks.
Traditional community detection algorithms often use modularity [1] to measure the strength and weakness of a community partition of a network; then, by using some process, such as the top-down split GN algorithm [2] and LFM algorithm [3], the maximum or extreme value of community evaluation index is reached. In this way, the best community partition of a network is found. Apart from modularity, some methods define and use other community evaluation index to detect communities more accurately, e.g., the IE [4] model, which aims to reveal the characteristics of the complex networks in an information theoretic view, by defining and calculating the information entropy of communities. Another information-theoretic index for evaluating partitions is the mutual information between network and communities(or MINC for short), proposed by L.C. Reidy et al. By defining structural information and community information between node pairs, the MINC approach specializes the general mutual information formula to calculating the mutual information between network structures and partitions in unweighted and undirected networks.
In recent years, with the development of representation learning algorithm in natural language processing (NLP) and other fields, researchers have begun to work on the relationship between network representation learning and community detection, such as using community annotations to improve network representation algorithms [5,6] and using network representation algorithms to improve the accuracy of community detection [6].
After induction and summary of these studies, we found that a typical community detection method often consists of two parts: The first is the community evaluation index, which measures the strength and weakness of a community structure; the second is the community transformer, which constantly change the community structure and tries to find a partition that reach some peak values of the evaluation index, that is, the solutions of community detection.
In the ideal case, the community evaluation index is able to evaluate the goodness of the community structure precisely, and the community transformer can efficiently search to give a set of partitions which cover the optimal partition. Unfortunately, for the former, since there is no accurate definition of the merits of community structure, researchers can only design community evaluation indices by means of edge density (e.g., modularity) or information-theoretic representation of node clusters (e.g., information entropy), so as to fit the real-world cases as well as possible. For the latter, community transformers have to make a trade-off between efficiency and the accuracy. Most of the methods have no way to use the global information of the network while transforming the community structure. For instance, while propagating labels in label propagation algorithm, to which a node propagates a label depends only on its local structural environment.
Aiming at the problems above, a new approach called MINC-NRL is proposed. The main idea is by using network representation learning (NRL) algorithms such as the Deepwalk method [7], the network is represented as vectors, which reflects the global information of the network. A community evolution process is then generated based on these vectors using hierarchically clustering to reduce the search space. Finally, by the usage of mutual information between network and communities (MINC), the best state in this community evolution process is found, as the final result of community detection.
The main contributions of this paper can be summarized as follows:
- Extend the original MINC evaluation index to make it possible to evaluate overlapping communities in unweighted and undirected networks;
- A community detection approach MINC-NRL is proposed based on network representation learning and MINC;
- Experiments are conducted on real-world data sets and synthetic data sets to verify the effect of the MINC-NRL approach.
The rest of this paper is organized as follows: Section 2 gives a short review of the community detection algorithms. Section 3 discusses how to detect communities using the MINC evaluation index and expand its definition to fit overlapping community detection tasks. In Section 4, the MINC-NRL method is introduced and explained in detail. Section 5 implements the method and verifies its accuracy by experiments. Section 6 is the summary and prospect of our research.
2. Related Work
Detecting community structure on different varieties of networks proves to be a hard task [8]. Various types of approaches for community detection have been proposed including modularity optimization, label propagation, spectral clustering, dynamic analysis, clique percolation, etc. [9].
Since Girvan and Newman pioneered the community evaluation index called modularity [1], modularity optimization is widely applied and studied for its general applicability to network topology which consist only of nodes and edges. GN, FN, and Louvain are typical modularity optimization algorithms. The main motivation of these algorithms is to find a maximum value of modularity on a given network through constantly transforming the community partition. For instance, GN initializes the network as whole community and breaks it into smaller ones by deleting the edge with the greatest edge-betweenness step by step and tracking the maximum modularity value in the process; FN uses a greedy technique to merge small communities to large ones, following the direction that raises the value of modularity. Modularity provides a link-based criterion to evaluate the goodness of partitions of a network, but it is showed that the modularity values of ground-truth partition on a large number of data sets are usually not the maximum. In addition, modularity has a problem called resolution limit, which means, in some cases, modularity optimization algorithms unreasonably divide a community to smaller ones or combine communities into a large one [10]. Aiming at such problems, researchers have proposed other community evaluation indices as objective functions. By labeling the communities and nodes using two-level encoding, Rosvall et al. have proposed a metric which uses the average length of the description codes generated by random walkers to measure a partition [11]. The accuracy of this evaluation index is time-dependent. In order to obtain a more accurate evaluation, more iterations and more time are needed. R. Lambiotte et al. have proposed a stability index to find and judge which partition has a high degree of stability during the random walking through a network and use stability as the basis for community detection [12]. Stability is defined as a time-dependent function, and when the time parameter t changes, the stability index also changes, hence it is hard to determine the value of t to obtain the best result. L. C. Reidy proposed an information-theoretic index to evaluate the mutual information between network and communities (hereafter referred as MINC) [13]. The MINC approach specializes the general mutual information formula to calculating the mutual information between network structures and partitions, which offers a new thought on detecting community structure within an information-theoretic framework. In our approach, the idea of MINC as a community evaluation index is adopted and extended to figure out the best partition at different resolutions.
Community evaluation indices provide a quantitative manner to evaluate a given partition on a specific network. However, due to the huge number of ways to partition a network, it is impossible to find the maximum value of the evaluation indices by exhausting all possible partitions. Thus, most of community detection algorithms uses community transformers to search local optimal solutions of the evaluation indices by gradually changing the ownership of the nodes. These community transform techniques mainly include greedy techniques, simulated annealing, extremal optimization, spectral optimization, etc. [8]. For instance, local expansion methods such as LFM [3] and GCE [14] are typical greedy techniques for local optimization. The algorithms follow the idea that starting from core nodes as the initial communities, and then greedy include neighbor nodes that are likely to be in the same community until a local maximum of the evaluation index called fitness is reached, and then continue to search other communities one by one in the rest of the network. Such type of methods is often used for the detection of overlapping communities, but the local optimums as the final solutions usually have significant difference with the ground-truths.
Aiming at improving the accuracy of the results and reducing the convergence time while searching optimal partitions, recent research is trying to add some pre-processing steps before community transforming to collect more structural information from the network. For example, the community detection method based on positive/negative connections [15] runs a random walking process in the network and performs statistical analysis on the random-walking sequence. Then, the relationships of the nodes are evaluated as positive/negative for further detection. With a similar idea, the EdMot algorithm [16] uses a motif-based hypergraph of the target network to enhance the edge, and applies other state-of-the-art algorithms to partition the network. The DEMON [17] methods builds an EgoMinusEgo network from the original network, by combining the ego network extraction and the graph-vertex difference operation. In addition, based on an ego network, SONIC-MAN [18] use moderator nodes to integrate the local structural information in distributed online social networks. Such pre-processing steps are verified to be effective in improving the community detection performance of existing approaches.
In recent years, with the development of representation learning algorithms in areas such as natural language processing, researchers have adopted the technique on deep learning to community detection. The idea of these approaches, in general, is to compress the high-dimensional structural information of the network (e.g., an adjacency matrix) into a set of low-dimensional vectors. Such vectors are defined as a low-dimensional representation of the network, which brings two main advantages: (1) Distance and density of nodes can be easily defined based on their representations; (2) The compression of structural information greatly reduces the time and space costs on detecting communities. For example, the ComE algorithm constructs the “Community Detection–Community Representation–Node Representation” closed-loop framework [6] to optimize both the node embedding and community embedding. The model improves the accuracy of community detection on multiple real-world datasets, together with better results in node classification and graph visualization. Based on a two-level representation learning strategies, MemeRep [19] adopts a genetic framework to optimize the representation which preserves the topology structure of the network. It is shown that the algorithm is effective on community detection for that it can make full use of the modularity density to preserve communities. Different from improving the quality of representation learning, our research pays more attention on getting community partitions with high scalability and accuracy, and preserve the structural information of the network at the same time.
3. Mutual Information between Network and Communities
3.1. Original Definition
It is well known that the key part of community detection approach is to design an effective community evaluation index. A well-defined community evaluation index should satisfy the following: The better the given partition is, the higher its value is. Thus, when an optimal partition is given, the index reaches its maximum value. The mutual information between network and communities (or MINC for short) is a community evaluation index defined in a view of informatic theory. Mutual information is a measure of the mutual dependencies of two random variables, i.e., the amount of information that one random variable contains about the other. If the two variables refer to networks and communities, respectively, we can obtain a definition of the mutual information between network X and community partition C as follows:
Note that X and C are variables related to the structure of the network and community ownership of nodes, which will be specifically defined in the following section. denotes the entropy of network X, which can be defined as the number of bits on average to describe the network. denotes the conditional entropy of X and C, which quantifies the amount of information needed to describe X given that the value of the known variable C. Based on the perspective of information, the following assertions are made:
- (1)
- is determined only by the connectivity of nodes of network.
- (2)
- For a certain network, the better a given partition of it is, the less the amount of information is needed to describe the network. This results in a smaller value of and a larger value of .
Therefore, can be used as a community evaluation index to quantify the merits of a partition.
The value of and can be calculated by:
The above equations are derived from the general definition of the mutual information. As for how to calculate the probability distributions (e.g., ), further definition is needed, and here comes the core idea of the MINC approach.
First, we consider the random variables X and C. X is a variable related to the structure of the network, which can be defined at the micro level of each pair of nodes in the network:
In the same way, the variable for community partition C of the network can be defined as:
Then by considering the connectivity and community ownership of nodes, the probability distributions can be defined as:
In the above equations, t denotes the number of possible node pairs, which is constantly for a particular network with n nodes. m is the number of adjacent node pairs, which is equal to the number of edges. is the number of node pairs in same community. is the number of adjacent node pairs in the same community.
By using the above definitions, the mutual information between a particular network and one of its partitions can be calculated. Based on the assertions that a better partition of a network will have a higher value, can be used as an index to evaluate the community structure and guide the community detection progress.
3.2. Extending the Definition of MINC for Overlapping Communities
The original definition of is not compatible with overlapping communities. This is due to the fact that it divides the edges of a network into two types: intra-community edges and inter-community edge to calculate the probability distributions by counting the number of them. For instance, denotes the probability that a pair of randomly selected nodes in the same community have an edge between them in network X. The value of this probability is equal to the number of intra-community edges divided by the combinatorial number of selecting a pair of nodes in the same community.
However, in the case of overlapping communities, an edge can be ambiguous, which can hardly be defined as being inside or outside the community. As shown in Figure 1, edge a is an internal edge in community A, and edge b is an inter-community edge between communities A and B. However, edge c can be considered either as an internal edge of community A or as an edge between communities A and B because the nodes at both ends of such an edge can either belong to the same community A or to two different communities A and B. This makes it difficult to count the number of edges and calculate the probability distributions in Equations (4)–(11).
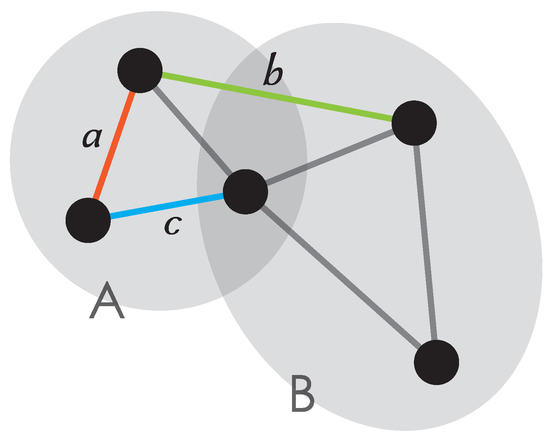
Figure 1.
Ambiguous edges between two communities.
This problem can be solved by appending definitions for the ambiguous edges in overlapping communities. A possible solution is that for such an ambiguous edge, it is counted as 0.5 intra-community edges and 0.5 inter-community edges. However, such a solution is not reasonable in some more complicated cases. Consider edges m and n in Figure 2:
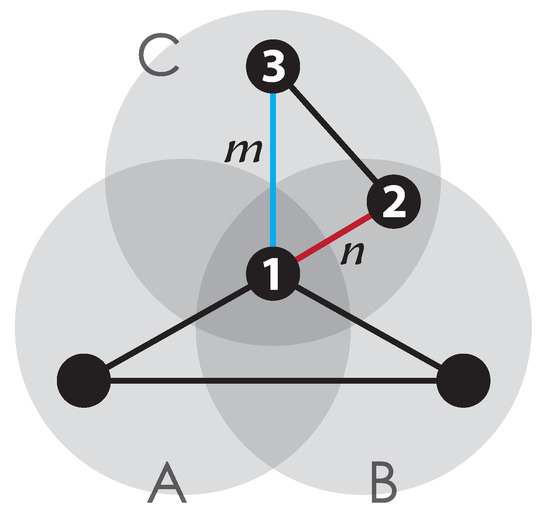
Figure 2.
Ambiguous edges among three communities.
For edge m:
- In one case, it can be regarded as an internal edge (in community C);
- In two cases, it can be regarded as an inter-community edge (between communities A and C and between communities B and C).
For edge n:
- In two cases, it can be regarded as an internal edge (in community B and in community C);
- In three cases, it can be regarded as an inter-community edge (between communities A and B, between communities B and C, and between communities A and C).
The two edges m and n are in obviously different conditions, but if using the solution above, they will both be counted as 0.5 intra-community edges and 0.5 inter-community edges. Therefore, a more rigorous method is proposed to count the number of edges within and between communities, when there is overlap between communities. The number of edges in the same community is defined as:
where and denote the ends of edge l, and M denotes the set of all the edges of the network. is defined as:
where R and S denote the community sets to which node r and s belong, respectively. and are the i-th and j-th communities in R and S, respectively. is the Kronecker delta, which equals to 1 if and 0 otherwise. and are the numbers of communities in R and S, respectively.
For the number of node pairs in same community, it can be calculated in the same way by replacing with , where L denotes the edge set formed by selecting any pair of two nodes in the network:
After appending the above definitions for counting the ambiguous edges in overlapping communities, the index is able to be applied to overlapping community partitions.
4. Community Detection Based on MINC
4.1. Community Evolution Process
Apart from as a community evaluation index, a community transformer is still needed to constantly transform the community structure, find the peak value of the evaluation index and finally carry out a solution of community detection. Here, we introduce the community evolution process, which will play a role as a community transformer in the MINC-NRL approach.
Definition 1.
Community evolution process
A community evolution process P is an ordered set consist of a series of state, defined as:
where each state is essentially a community partition of the same network.
Definition 2.
Community evolution process of bottom-up cohesion
If adjacent states and in community evolution process P satisfy the following:
such process can be named as a community evolution process of bottom-up cohesion.
As a special kind of community evolution process, the community evolution process of bottom-up cohesion is used to represent the evolution process of constant merging of communities over time, as shown in Figure 3.
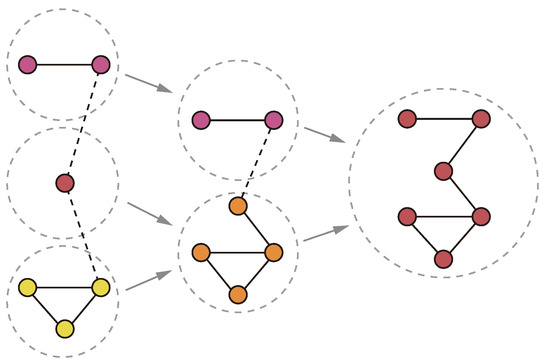
Figure 3.
Community evolution process of bottom-up cohesion.
For a given network, the main idea of the approach is to generate a community evolution process as a community transformer, which simulates a real-world community evolution. That means in any state of such a process, nodes with closer distance or more similar structural environment will have a greater probability to be in the same community, and it brings three advantages comparing with other typical community transformer:
- (1)
- Each state of the generated process is itself a high-quality partition of the network, and there would be no unreasonable case where a node tries to pull adjacent nodes into its community without discrimination.
- (2)
- The number of states of the generated process is less, which reduces the calculation time to evaluate the merits of each state.
- (3)
- For such community evolution process, a stable and unique result can be obtained by finding the maximum of community evaluation index, or by filtering out the states with larger evaluation index, result partitions with different resolution can be output as well.
To generated a community evolution process for given network, network representation learning (NRL) and hierarchical clustering are used in the approach, which will be illustrated in detail in the next subsection.
4.2. The Generation of the Community Evolution Process
4.2.1. Network Representation Learning
The generation of the community evolution process in the approach follows the idea that it simulates a real-world community evolution. To achieve this, the first step is sampling the network to vectorize the nodes, which preserves and reveals the structural information of the network. Such process is also known as network representation learning.
Multiple methods can be used to learn representations of nodes in network, e.g., neural-network method including Deepwalk [7], Node2Vec [20], BoostNE [21], Graph-Wave [22], and spectral method such as GLEE [23]. By comparing the results of these methods on our experimental datasets, Deepwalk is finally select in our approach for its balanced and stable result on undirected real-world networks. The details of the comparative experiments are illustrated in Section 5.3.
4.2.2. Non-Overlapping Hierarchical Clustering
After obtaining the vector representation of the nodes, these vectors are then clustered using hierarchical clustering to form a community evolution process. For non-overlapping community detection, an agglomerative hierarchical clustering (AHC) is used to construct a bottom-up cohesion community evolution process.
The distance between two vectors is measured using the Euclidean distance, while that between two clusters is measured using Ward’s method [24]. By clustering the vectors, the distance between each pair of vectors will be smaller when they represent a pair of nodes with closer distances or more similar environments in the network. When we alter the cluster distance threshold from small to large, the nodes will be first completely separated, and then the clusters merge in pairs based on the similarity between them, and eventually, the entire network is merged into one large cluster. Since these vector clusters are the representation of communities in the network, we have obtained a bottom-up cohesion community evolution process P in this way.
4.2.3. Overlapping Hierarchical Clustering
For overlapping community detection, the vectors are clustered using the overlapping hierarchical clustering algorithm (OHC) proposed by I. Jeantet et al. [25]. Different from classical hierarchy clustering, the OHC algorithm produces a directed acyclic graph called a quasi-dendrogram while clustering, which avoids early cluster merging and creates overlapping clusters on each level of the clustering process. Figure 4 shows a quasi-dendrogram produced by OHC.
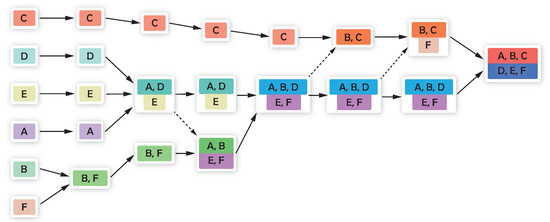
Figure 4.
Quasi-dendrogram generated by OHC.
As shown in the figure, each node of the quasi-dendrogram denotes a cluster, and each level in vertical represents a cover (either non-overlapping or overlapping) of the input vectors. A node (except the root) can have one or more parent nodes. Note that a cover here in the clustering process of the representation vectors is essentially a corresponding partition of the network.
Same as AHC for non-overlapping clustering, the OHC algorithm generated a state sequence from individual nodes to one large cluster, which can be directly convert to a community evolution process as an outcome.
4.3. Find the Peak Value of MINC through the Process
The community evolution process is a topological miniature which covers the integration and fragmentation of the communities in real-world networks. The final step of the approach, is to find the state with the largest value, as the final result of community detection.
Figure 5 shows the MINC values of the first 20 states in the community evolution process constructed on Polbooks [26] network, with the abscissa indicating the corresponded CN values of the states. As shown in the figure, with the largest MINC value, the state with 3 communities will be output as the result partition.
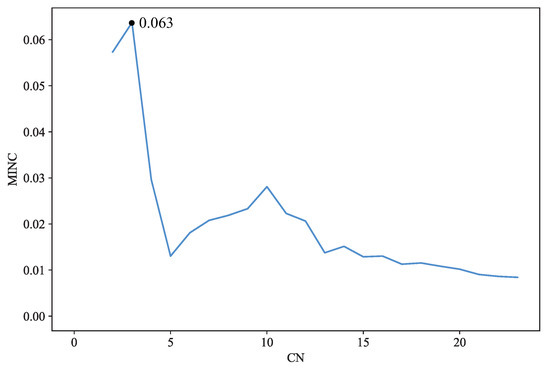
Figure 5.
MINC value of community evolution process generated from Polbooks.
As a summary, the basic process of MINC-NRL is listed below:
- (1)
- Perform random walks in the network, and obtain random-walking sequences by tracking the passing nodes;
- (2)
- Input the random-walking sequences into the Word2vec [27] model, which outputs the vector representation of each node;
- (3)
- Perform a hierarchical clustering to the vectors. For non-overlapping community detection tasks, AHC is used; for overlapping community detection tasks, OHC is used. Each level of the dendrogram generated by the clustering algorithm will be convert to each state of the community evolution process ;
- (4)
- Calculate the value of each states in P;
- (5)
- Output the state with the largest value as the result of community detection.
The pseudo-codes in Algorithm 1 gives a brief description of MINC-NRL.
| Algorithm 1: MINC-NRL |
 |
4.4. Time Complexity Analysis
The time complexity of this algorithm can be calculated in three parts:
- (1)
- Network Representation Learning Firstly, random walks are perform in the network. Starting from each node, the random walker need to go L steps in the network, and such process will iterate R times. Hence the time complexity for random-walk is , where n is the number of nodes of the network. Then the sequences will be input into the Word2vec model. The model first uses a window of size W sliding through these sequences to count the co-occurrence frequency between nodes, which need a time complexity of . Meanwhile, the representation vectors for the nodes will be updated using a stochastic gradient descent process of E epochs in time, with the acceleration of the hierarchical softmax. To sum up, the overall time complexity of the network representation learning part is .
- (2)
- Hierarchical Clustering With the acceleration by a nearest neighbor chain, the agglomerative hierarchical clustering (AHC) needs a time complexity of . For the overlapping hierarchical clustering (OHC), in each iteration, or each level of the dendrogram, each cluster should traverse all nodes to decide which one is the closest, this leads to time, where C is the number of clusters for each level. The number of levels of the dendrogram created by OHC is proportional to the number of nodes n. Thus, the total time complexity for OHC is .
- (3)
- Find the Peak Value of MINC For a partition, the main time cost for MINC calculation comes form obtaining and , which need a traverse of all edges for their belonging community. To achieve this, a map is first built to store which community each node belongs to, with a time complexity of . Hence, is needed, where m is the number of edges of the network. Since the dendrogram created by hierarchical clustering has levels, and each level will be regraded as a partition for MINC calculation, the overall time complexity for this part is .
In conclusion, the time complexity for the approach is for non-overlapping community detection and for overlapping community detection. During the actual running of the approach, random-walk length L, iteration R, window size W, and update epochs E are much smaller than the number of nodes n and the number of edges m, the main time cost comes from the clustering part and MINC calculation part. For non-overlapping community detection, the total time complexity is ; for overlapping community detection, it is . It should be noted that the number of clusters C for each level in OHC depends on the merging criterion in OHC algorithm. When the increases, clusters are more likely to merge, which decrease C. When setting , the OHC algorithm tends to have a time cost of about [25]. Hence, the time for OHC becomes the major bottleneck in computational efficiency of the approach in overlapping community detection tasks.
5. Experiments
In this section, experiments are conducted to confirm the effectiveness of MINC-NRL.
5.1. Preparation of the Experiment
To verify the accuracy of MINC-NRL, experiments are conducted on both non-overlapping and overlapping community detection tasks. For non-overlapping community detection, we include 4 non-overlapping community detection algorithms as baselines and use the number of communities (CN) and normalized mutual information (NMI) to verify the accuracy of MINC-NRL. For overlapping community detection, 3 overlapping community detection algorithms are included, and 4 accuracy evaluation indices are used, including CN, Overlapping Modularity (), Extended Modularity (EQ), and Average Conductance (AC).
The data sets used in the experiment are all undirected and unweighted networks with ground-truth partition labels. Among them, the Karate Club [28], Dolphins [29], Football [30], and Polbooks [26] are real-world networks, and LFR500, LFR2000, LFR10000_a, and LFR10000_b are synthetic networks generated with scale-free features according to parameters [31]. Table 1 and Table 2 list the main properties of data sets and the hardware and system information of the experiments, respectively, where k is the average degree and is the mixed parameter of LFR networks.

Table 1.
Main properties of data sets.

Table 2.
Hardware and system information.
5.2. Benchmarks
For non-overlapping community detection, since the data sets are partition-labeled, the number of communities (CN) and normalized mutual information (NMI) [32] are used to measure the accuracy of community detection. As a general rule, it is better that the CN of community detection result is exactly the same as labeled, or at least similar with labeled. NMI can be used to evaluate the difference between the result partition and labeled partition based on an information theory framework. The NMI value between partition A and B can be formulated as:
where N is the total number of nodes, C is a confusion matrix, whose element denotes the number of nodes belonging to Community i in Partition A and also belonging to Community j in Partition B. and denote the number of communities of Partition A and B, respectively. and denote the sum of all elements of a row or column in Matrix C. The value of NMI is between 0 and 1, and it becomes larger when the two partitions are more similar. If the two partitions are exactly the same, the NMI value reaches 1. The NMI index is used in our experiments to compare the result partitions with the labeled partitions. A higher NMI value stands for a better result.
For overlapping community detection, we use overlapping modularity () [33], extended modularity (EQ) [34], and average conductance (AC) to evaluate the structural merits of the result partitions, instead of comparing the result partition with the labeled networks. Although we did not use the partition labels directly, we still compared the result CN with the labeled CN because the number of communities still has reference value on overlapping community networks.
The extended modularity (EQ) is a community quality index which extends the definition of Newman’ s modularity to overlapping community structures. The definition of EQ is shown as follows:
where m is the total number of edges in the network, and c is one of the communities. i and j are nodes belonging to Community c; and are their respective degrees. is the element of the adjacency matrix which follows the condition that when node i and j are linked, the value of is 1, otherwise 0. and are the numbers of communities to which node i and j belong, respectively, and give EQ the ability to deal with the case that a node belongs to more than one community. A high value of EQ indicates a significant overlapping community structure for a particular network.
The overlapping modularity index is another quality function proposed by V. Nicosia et al. [33] to extend modularity to the more general case of overlapping communities, defined as:
Same as that in EQ, m is the total number of edges in the network. are the elements of the adjacency matrix. i,j are nodes of the network. is the out-degree of Node i, while is the in-degree of Node j. Instead of the number of communities to which a node belongs to, uses the belonging coefficients and to calculate the weight for each link existing between node i and j. Similar to EQ, a higher value of indicates a stronger community structure.
Another index used in our experiment to evaluate the quality of overlapping community detection result is the average conductance (AC). Conductance is a local measure for the goodness of a node cluster in the network [35]. For a cluster c, conductance is defined as:
where is the number of internal edges of Cluster c, is the number of edges that links the cluster to other parts of the network. To evaluate a partition of the network, average conductance (AC) is used, which is defined as:
where C is a community partition of a network. The equation averages the conductance of all communities of the partition.
5.3. Preliminary Experiments: Comparison on Different Network Representation Methods
As a pre-step to hierarchical clustering, the network representation method can significantly affect the community evolution process generated. As mentioned in Section 4.2, comparative experiments are conducted to evaluate the impact of the network representation methods on the final results and find which of the network representation method is the most appropriate for our framework. The first comparison is made by replacing the network representation process of MINC-NRL (Step (1) and (2) in Section 4.3) by different network representation methods, including Deepwalk [7], Node2Vec [20], Walklets [36], RandNE [37], BoostNE [21], GLEE [23], NetMF [38], GraRep [22], NMFADMM [39], and verified with non-overlapping community detection tasks on real-world datasets.
The following table shows the NMI of using different network representation methods in MINC-NRL. The bold numbers emphasize the best experimental results within each data set.
As illustrated in Table 3, random-walk-based methods perform better than the other algorithms, including Deepwalk, Node2vec, and Walklets, and Deepwalk reaches the highest NMI on most of the datasets. Figure 6 shows the representation of Football network using Deepwalk, which is reduced to 2D by a principal component analysis (PCA). The results indicate that Deepwalk is more appropriate for MINC-NRL.

Table 3.
NMI of using different network representation methods in MINC-NRL.
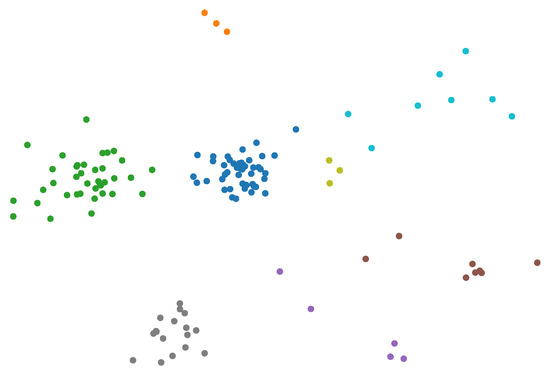
Figure 6.
Network representation of Football using Deepwalk.
5.4. Comparison Results with the Other Algorithms
5.4.1. Non-Overlapping Community Detection
The following Table 4 and Table 5 show the CN and NMI of running the MINC-NRL algorithm on the data sets, compared with non-overlapping community detection algorithms GN [2], FN [40], Louvain [41], and EdMot [16]. Note that the NMI values quantify the differences between the result partitions with the ground-truth partitions of the data sets.

Table 4.
CN of MINC-NRL compared with other algorithms.

Table 5.
NMI of MINC-NRL compared with other algorithms.
The results show that MINC-NRL performs well on both real-world networks and LFR synthetic networks. The numbers of communities of the networks are correctly figured out by MINC-NRL. It also obtains the highest average NMIs on most of the data sets compared with the other algorithms.
5.4.2. Overlapping Community Detection
The following Table 6, Table 7, Table 8 and Table 9 show the CN, , AC, and EQ values, respectively, of the results of MINC-NRL algorithm on the data sets, compared with overlapping community detection algorithms ASLPAw [42], DEMON [17], and Ego-splitting [43]. Note that smaller values are better when evaluated by AC.

Table 6.
CN of MINC-NRL compared with other algorithms.

Table 7.
of MINC-NRL compared with other algorithms.

Table 8.
EQ of MINC-NRL compared with other algorithms.

Table 9.
AC of MINC-NRL compared with other algorithms.
As illustrated in the above tables, the algorithm correctly figured out the number of communities on almost all networks. Although it does not get the best result on every data sets, but the average accuracy is the best compared with the other algorithms.
6. Conclusions
In this paper, an information-based approach for community detection MINC-NRL is proposed. The approach adopts network representation learning techniques to obtain the vectorial representation of each node of a network. Then, a community evolution process is generated with these vectors, through an agglomerative hierarchical clustering or overlapping hierarchical clustering, according to a non-overlapping/overlapping community detection task. Finally, the MINC index is used to figure out the optimum partition in the community evolution process. The experimental results show the effectiveness of MINC-NRL on both real-world and synthetic networks.
Due to the definition of MINC, a limitation of the current approach is that it can only be applied in unweighted and undirected networks. In the future, we will try to further extend the definition of MINC to address this limitation. The approach achieves a high degree of accuracy on 10,000 nodes LFR synthetic networks, but it is still difficult to be applied to larger-scale networks. This is mainly due to the time complexity bottleneck of the clustering algorithms. We will continue our research on improving the accuracy and time efficiency of the clustering part and try to extend the algorithm to detect communities on larger-scale networks.
Author Contributions
Conceptualization, Y.C. and D.L.; methodology, Y.C.; software, Y.C.; validation, Y.C. and C.W.; formal analysis, C.W.; investigation, C.W.; resources, C.W.; data curation, C.W.; writing—original draft preparation, Y.C.; writing—review and editing, Y.C.; visualization, Y.C.; supervision, D.L.; project administration, D.L.; funding acquisition, D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Science and Technology Program of Guangzhou City (Grant No. 201707010052) and Natural Science Foundation of Guangdong Province, China (Grant No. 2020A1515010696).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| MINC | Mutual Information between Network and Community |
| NRL | Network Representation Learning |
| AHC | Agglomerative Hierarchical Clustering |
| OHC | Overlapping Hierarchical Clustering |
References
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [Green Version]
- Lancichinetti, A.; Fortunato, S.; Kertész, J. Detecting the Overlapping and Hierarchical Community Structure in Complex Networks. New J. Phys. 2009, 11, 033015. [Google Scholar] [CrossRef]
- Deng, X.; Wang, B.; Wu, B.; Yang, S. Research and evaluation on modularity modeling in community detecting of complex network based on information entropy. In Proceedings of the 2009 Third IEEE International Conference on Secure Software Integration and Reliability Improvement, Shanghai, China, 8–10 July 2009; pp. 297–302. [Google Scholar]
- Tu, C.; Zeng, X.; Wang, H.; Zhang, Z.; Liu, Z.; Sun, M.; Lin, L. A unified framework for community detection and network representation learning. IEEE Trans. Knowl. Data Eng. 2018, 31, 1051–1065. [Google Scholar] [CrossRef] [Green Version]
- Cavallari, S.; Zheng, V.W.; Cai, H.; Chang, K.C.C.; Cambria, E. Learning community embedding with community detection and node embedding on graphs. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 377–386. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Fortunato, S.; Castellano, C. Community structure in graphs. arXiv 2007, arXiv:0712.2716. [Google Scholar]
- Jin, D.; Yu, Z.; Jiao, P.; Pan, S.; Yu, P.S.; Zhang, W. A survey of community detection approaches: From statistical modeling to deep learning. arXiv 2021, arXiv:2101.01669. [Google Scholar] [CrossRef]
- Chen, M.; Nguyen, T.; Szymanski, B.K. A new metric for quality of network community structure. ASE Hum. 2013, 2, 226–240. [Google Scholar]
- Rosvall, M.; Bergstrom, C.T. Maps of random walks on complex networks reveal community structure. Proc. Natl. Acad. Sci. USA 2008, 105, 1118–1123. [Google Scholar] [CrossRef] [Green Version]
- Lambiotte, R.; Delvenne, J.C.; Barahona, M. Random walks, Markov processes and the multiscale modular organization of complex networks. IEEE Trans. Netw. Sci. Eng. 2014, 1, 76–90. [Google Scholar] [CrossRef] [Green Version]
- Reidy, L.C. An Information-Theoretic Approach to Finding Community Structure in Networks. Bachelor’s Thesis, Trinity College, Dublin, Germany, 2009. [Google Scholar]
- Lee, C.; Reid, F.; McDaid, A.; Hurley, N. Detecting highly overlapping community structure by greedy clique expansion. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2010), Anchorage, AK, USA, 4–8 August 2010. [Google Scholar]
- Su, Y.; Wang, B.; Cheng, F.; Zhang, L.; Zhang, X.; Pan, L. An algorithm based on positive and negative links for community detection in signed networks. Sci. Rep. 2017, 7, 10874. [Google Scholar] [CrossRef] [Green Version]
- Li, P.Z.; Huang, L.; Wang, C.D.; Lai, J.H. Edmot: An edge enhancement approach for motif-aware community detection. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 479–487. [Google Scholar]
- Coscia, M.; Rossetti, G.; Giannotti, F.; Pedreschi, D. Demon: A local-first discovery method for overlapping communities. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Beijing, China, 12–16 August 2012; pp. 615–623. [Google Scholar]
- Guidi, B.; Michienzi, A.; Ricci, L. Sonic-man: A distributed protocol for dynamic community detection and management. In Proceedings of the IFIP International Conference on Distributed Applications and Interoperable Systems, Madrid, Spain, 18–21 June 2018; Springer: Cham, Switzerland, 2018; pp. 93–109. [Google Scholar]
- Gong, M.; Chen, C.; Xie, Y.; Wang, S. Community preserving network embedding based on memetic algorithm. IEEE Trans. Emerg. Top. Comput. Intell. 2018, 4, 108–118. [Google Scholar] [CrossRef]
- Grover, A.; Leskovec, J. Node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Li, J.; Wu, L.; Guo, R.; Liu, C.; Liu, H. Multi-level network embedding with boosted low-rank matrix approximation. In Proceedings of the 2019 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Vancouver, BC, Canada, 27–30 August 2019; pp. 49–56. [Google Scholar]
- Donnat, C.; Zitnik, M.; Hallac, D.; Leskovec, J. Learning structural node embeddings via diffusion wavelets. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1320–1329. [Google Scholar]
- Torres, L.; Chan, K.S.; Eliassi-Rad, T. GLEE: Geometric Laplacian eigenmap embedding. J. Complex Netw. 2020, 8, cnaa007. [Google Scholar] [CrossRef] [Green Version]
- Ward, J.H., Jr. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Jeantet, I.; Miklos, Z.; Gross-Amblard, D. Overlapping Hierarchical Clustering (OHC); Inteligent Data Analysis: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Krebs, V. Books about US Politics. Available online: Http://www.orgnet.com/ (accessed on 5 December 2021).
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. In Proceedings of the ICLR Workshop, Scottsdale, AZ, USA, 2–4 May 2013. [Google Scholar]
- Zachary, W.W. An Information Flow Model for Conflict and Fission in Small Groups. J. Anthropol. Res. 1977, 33, 452–473. [Google Scholar] [CrossRef] [Green Version]
- Lusseau, D.; Schneider, K.; Boisseau, O.J.; Haase, P.; Slooten, E.; Dawson, S.M. The Bottlenose Dolphin Community of Doubtful Sound Features a Large Proportion of Long-lasting Associations. Behav. Ecol. Sociobiol. 2003, 54, 396–405. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M. Community Structure in Social and Biological Networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [Green Version]
- Lancichinetti, A.; Fortunato, S.; Radicchi, F. Benchmark graphs for testing community detection algorithms. Phys. Rev. E 2008, 78, 046110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Danon, L.; Diaz-Guilera, A.; Duch, J.; Arenas, A. Comparing Community Structure Identification. J. Stat. Mech. 2005, 2005, 09008. [Google Scholar] [CrossRef]
- Nicosia, V.; Mangioni, G.; Carchiolo, V.; Malgeri, M. Extending the definition of modularity to directed graphs with overlapping communities. J. Stat. Mech. Theory Exp. 2009, 2009, P03024. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.; Cheng, X.; Cai, K.; Hu, M.B. Detect overlapping and hierarchical community structure in networks. Phys. A Stat. Mech. Its Appl. 2009, 388, 1706–1712. [Google Scholar] [CrossRef] [Green Version]
- Gleich, D. Hierarchical Directed Spectral Graph Partitioning. Stanford University Technical Report. 2005. Available online: https://www.cs.purdue.edu/homes/dgleich/publications/Gleich%202005%20-%20hierarchical%20directed%20spectral.pdf (accessed on 5 December 2021).
- Perozzi, B.; Kulkarni, V.; Chen, H.; Skiena, S. Don’t Walk, Skip! Online learning of multi-scale network embeddings. In Proceedings of the 2017 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Sydney, Australia, 31 July–3 August 2017; pp. 258–265. [Google Scholar]
- Zhang, Z.; Cui, P.; Li, H.; Wang, X.; Zhu, W. Billion-scale network embedding with iterative random projection. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018; pp. 787–796. [Google Scholar]
- Qiu, J.; Dong, Y.; Ma, H.; Li, J.; Wang, K.; Tang, J. Network embedding as matrix factorization: Unifying deepwalk, line, pte, and node2vec. In Proceedings of the 11th ACM International Conference on Web Search and Data Mining, Los Angeles, CA, USA, 5–9 February 2018; pp. 459–467. [Google Scholar]
- Sun, D.L.; Fevotte, C. Alternating direction method of multipliers for non-negative matrix factorization with the beta-divergence. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 6201–6205. [Google Scholar]
- Newman, M.E.J. Fast algorithm for detecting community structure in networks. Phys. Rev. E 2004, 69, 066133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 10, P10008. [Google Scholar] [CrossRef] [Green Version]
- Xie, J.; Szymanski, B.K.; Liu, X. Slpa: Uncovering overlapping communities in social networks via a speaker-listener interaction dynamic process. In Proceedings of the 2011 IEEE 11th International Conference on Data Mining Workshops, Vancouver, BC, Canada, 11 December 2011; pp. 344–349. [Google Scholar]
- Epasto, A.; Lattanzi, S.; Paes Leme, R. Ego-splitting framework: From non-overlapping to overlapping clusters. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, USA, 13–17 August 2017; pp. 145–154. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).