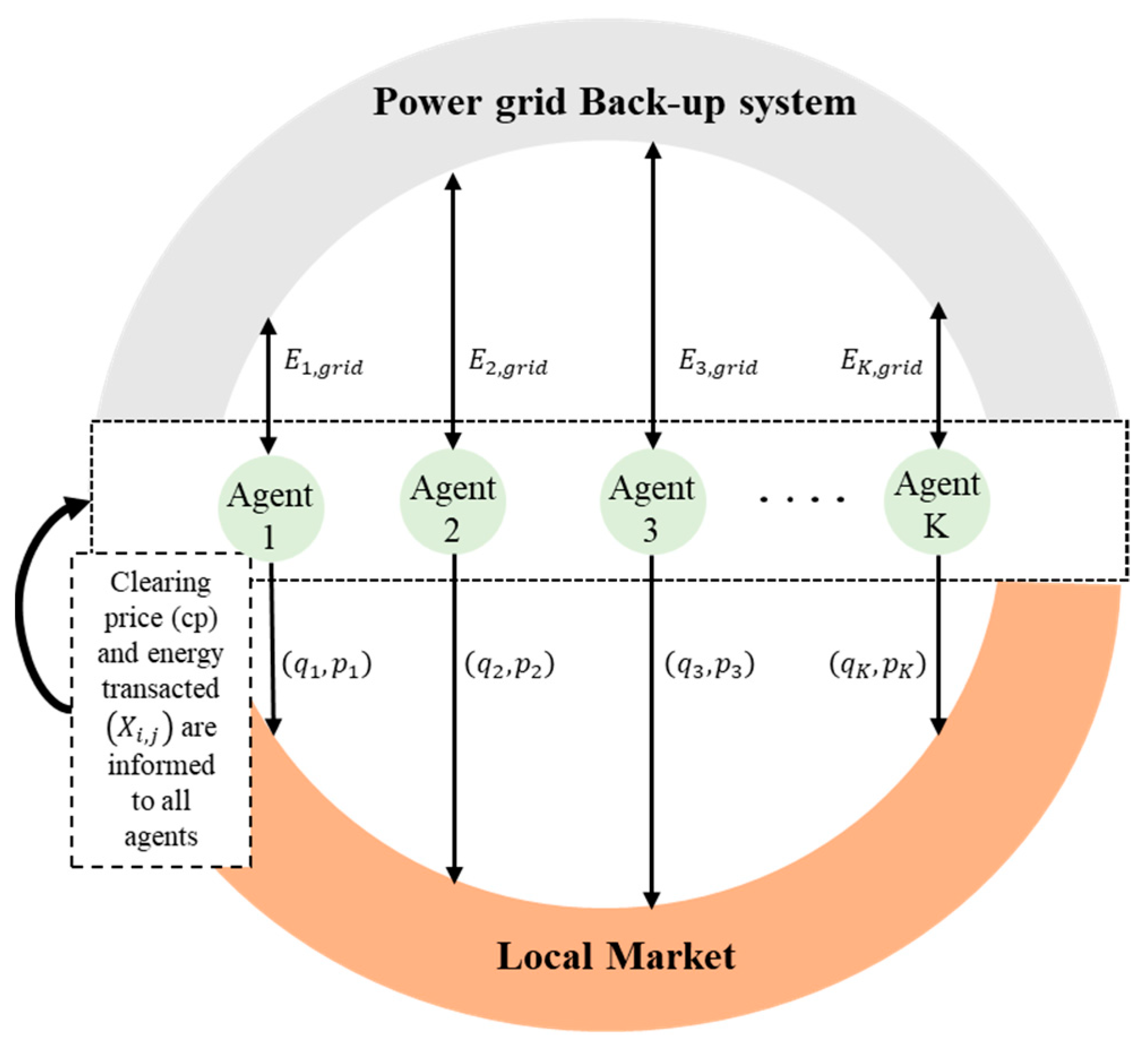
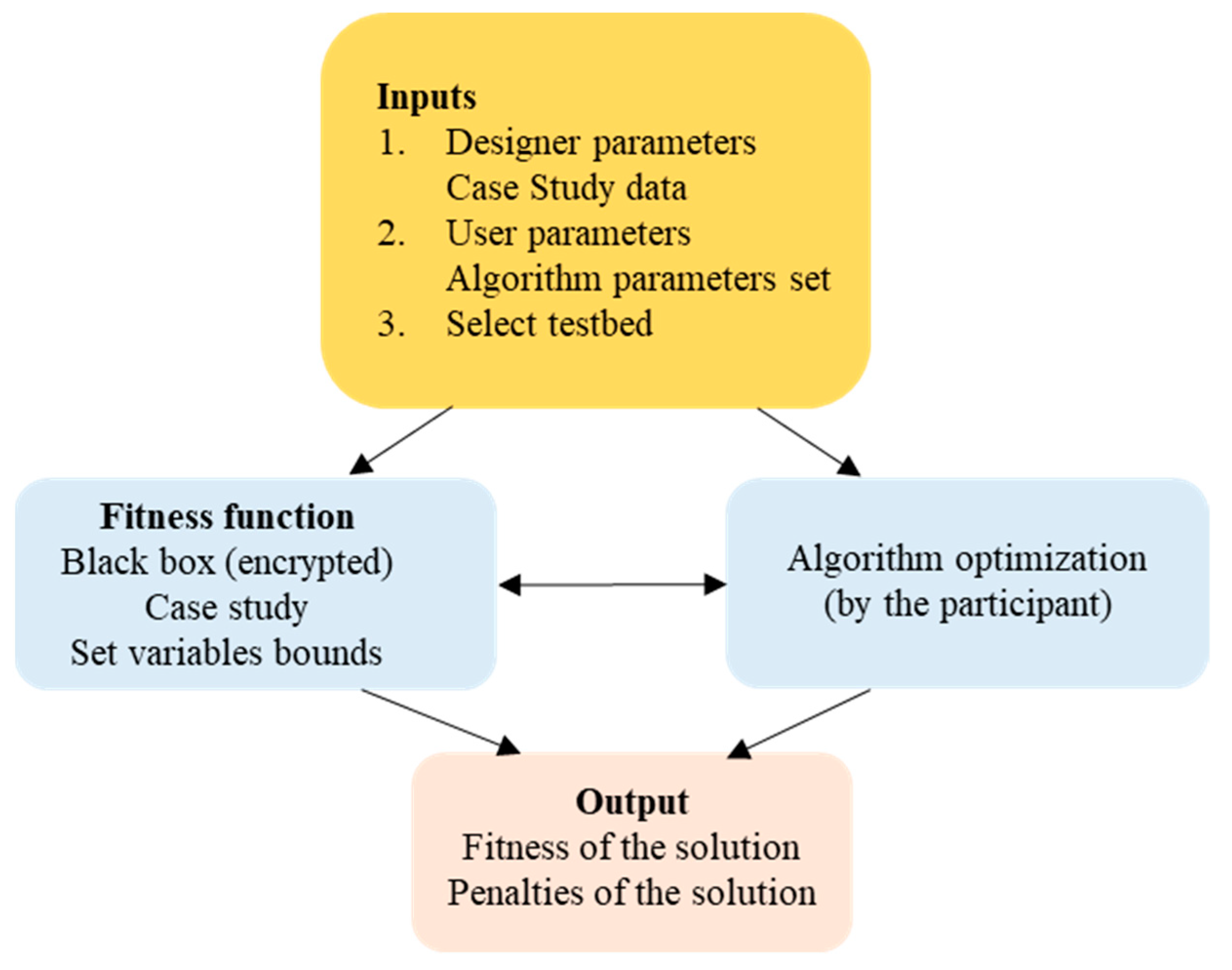
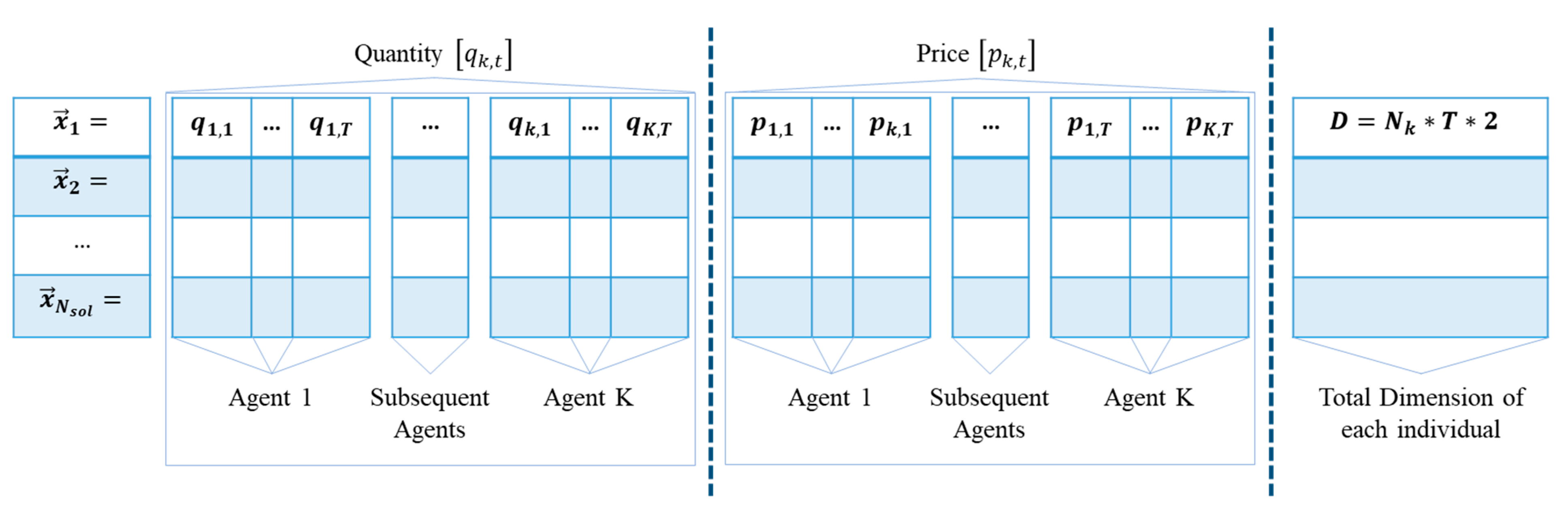
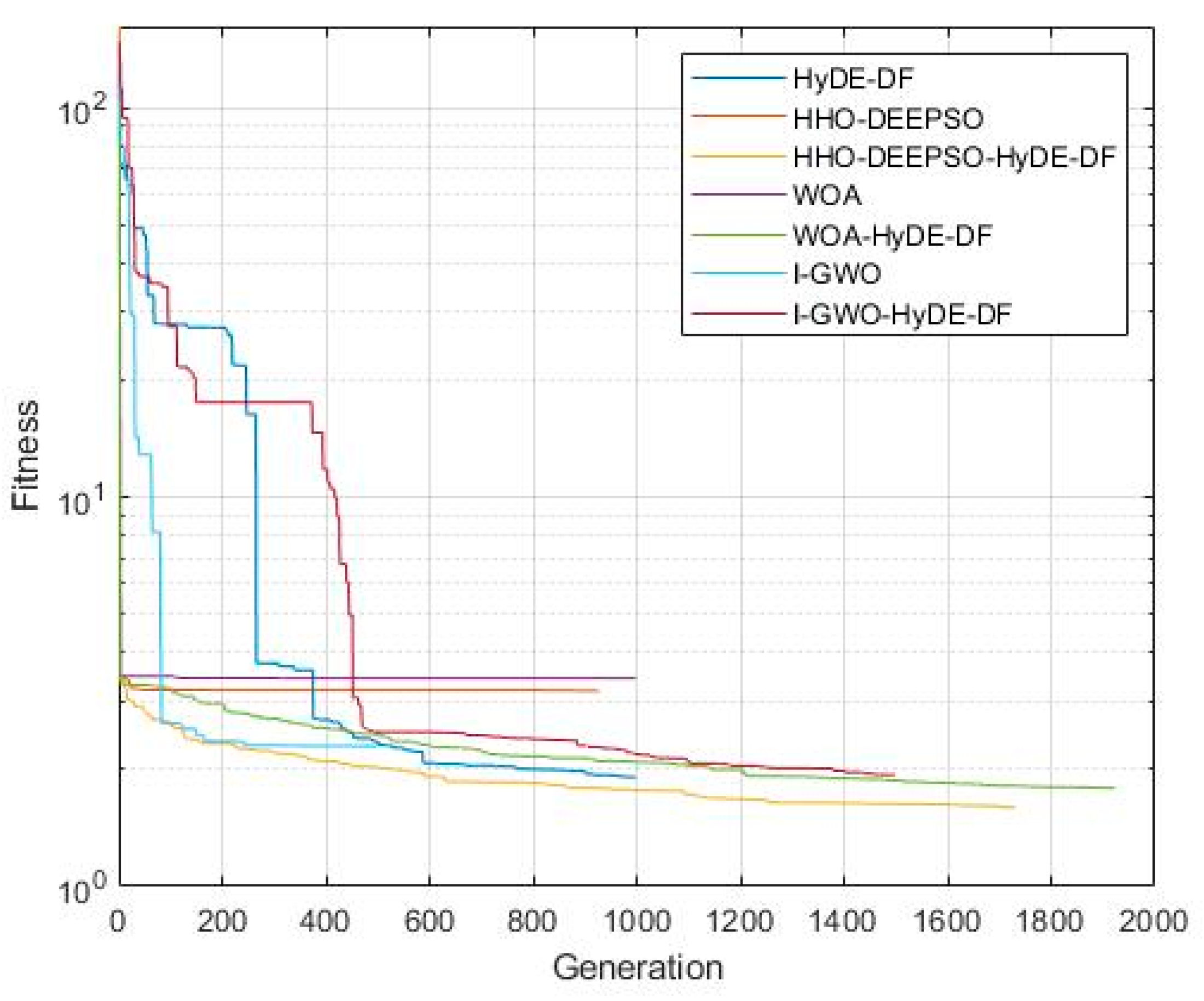
These days, there are multiples changes in the structure of transmission and distribution of electric energy that allows the integration of new technologies notions in generation, storage, electric mobility [
1,
2], and energy metering [
3]. As a result of these system changes, electricity dependence and energy transactions have increased. The Local Energy Markets (LEM) is an opportunity for small grid actors to actively take part in the bidding process. LEM allows local transactions that empower consumers, producers, and prosumers in the goal of creating energy balances [
4].
LEM are defined locally in terms of residential customers close enough in the same geographical and social area. However, the larger the number of actors, the harder the synchronization, control, and optimal market operation. To replicate and achieve optimal local energy market responses, it is necessary to guarantee coordination among the different market participants and appropriate tools for proper decision making [
4,
5].
The CEC (Congress on Evolutionary Computation) and GECCO (Genetic and Evolutionary Computation Conference) 2021 competition on “Evolutionary Computation in the Energy Domain: Smart Grid Applications” called for participants to develop metaheuristic optimization solutions for LEMs operation under complex conditions such as those that include trading energy in an LM (Local Market) [
6]. Considering several explicit mathematical formulations, these problems cannot be solved efficiently due to the complex nature of LEM models. Heuristic and metaheuristic algorithms have been shown to be a reliable option in problems that include energy transactions [
7]. An example of this is the different set of evolutionary algorithms explored for the solution of a bi-level energy market problem of nine participants in [
6,
7]. Track 1 of a 2021 competition includes a complex bi-level market problem with nine different participants. The upper-level agents try to maximize their profits, depending on the solution of the lower level problem. This interdependency between decisions makes the problem not an easy task [
6,
8]. Therefore, the complexity of this problem with the high number of variables is adequate for the application of different heuristics-based algorithms and special computational structures [
6].
More complex computational architectures had been required for the development of electrical networks, control strategies, and optimal decisions. In order, to obtain optimal and feasible solutions in recent times for the planning and operation of complex systems with a high number of devices, one of the proposed architectures is the use of Parallel Computing (PC). PC allows the execution of tasks in parallel, thus avoiding the long processing times required in the execution of activities sequentially [
9]. In this work, a parallel architecture is used to reach a global optimum in a bi-level local market with different agents using brute force [
10,
11]. In this way, not only a complex optimization problem is solved, but it is also possible to measure the performance of different metaheuristic algorithms.
The remainder of this document includes the following:
Section 1.1—a summary of the state-of-the-art for different approaches in terms of metaheuristic algorithm for SMGs operation planning and PC power system applications. The next section is a presentation of a test case.
Section 3 is a presentation of the HyDE-DF (hybrid-adaptive differential evolution with a decay function), HHO (Harris Hawks Optimization), WOA (whale optimization algorithm), and DEEPSO (Differential Evolutionary Particle Swarm Optimization) algorithms.
Section 4 presents the algorithm for PC; then, it presents the evaluation of a metaheuristic algorithm using PC global optimal. Finally, the last section shows the conclusion of the work.
State of Art
In recent years, the concerns of fossil fuel reduction and climate change, combined with the gradual decrease in costs of unconventional sources, are pushing the incorporation of renewable energy or other types of sources on isolated networks (PV, EV, Genset, BESS) or small grids that allow local energy transactions, as seen in LEM. Nevertheless, the changeable and undefined nature of renewable energy has created significant challenges for power networks because the power produced by renewable energy is not completely dispatchable and therefore cannot be controlled. For this reason, new approaches have developed to integrate large amounts of renewable energy in smart grids and local markets, leading them to operate in a more effective, efficient, economical, and sustainable direction [
4,
12].
A local grid could include loads and distributed energy resources, storage, and controllable loads, and it should be managed in a controlled manner whether or not it is interconnected to the main power grid [
12]. A local small grid could deliver auxiliary services to TSO or DSO could operate energy arbitrage (store energy when the price is low to sell it or use it when the price is high) and actively participate in energy markets, in addition to participating in the distribution systems with the sell or bid of additional or required energy. However, to ensure that these activities are achievable, a small grid has to optimize the utilization of its resources, pursuing economic profit. Due to the nature of renewable energy sources, load forecasting elements, and the energy market, the time horizon for the optimization and dispatch is the day-ahead. On the other hand, LEMs whose energy prices can vary hourly may require optimization with an equivalent time horizon. Thus, day-ahead and intra-day optimal load balances are the most important requirements in an LEM.
The operation of LEMs is one of the main problems in recent years due to the increased number of agents in the grid. The growing interest in these systems has been the result of [
13,
14], the integration of renewable sources, DGs price reduction, community self-resilience strategies, market flexibility, and dynamic loads, among other factors. LEM requires two main elements: a market controller that creates conditions and policies to carry out the local balance and maximize their economic gains [
8], and an energy controller that distributes and schedules the available energy request and resources [
8]. A good number of publications had been conducted in the area of autonomous generation and load control, including intermittent sources and demand response [
15,
16,
17,
18,
19,
20,
21,
22,
23]; however, few have investigated the operation of autonomous market controllers [
8]. Some efforts have focused on the theoretical assessment of optimal strategies. The solutions include the performance evaluation of real customer behavior, making the problem complex [
24].
Since these types of problems are normally non-convex with a wide search space, they can become NP-hard problems [
25]. This characteristic results in high computation time that limits the possibility of mathematical simplifications that allow finding points closer to the global optimal solution. Different alternatives have emerged to solve these problems. (a) Metaheuristic solutions search for problem optimization in efficient time; nevertheless, the formulation does not guarantee global optimal solutions. (b) Exhaustive searches guarantee feasible and global optimal solutions with the evaluation of various combinations of different decision variables. The last process can be cumbersome, making the problem unfeasible for applications that require responses in time frames of a day or hours.
Metaheuristic algorithms are presented as possible strategies for optimal bidding in an LEM. Different computational strategies for optimal agents bidding are assessed in [
6]. In that research, the authors evaluate different LEM strategies based on the community storage and agent’s revenues, cost, and local electricity consumption. The evaluation results suggest different opportunities to increase the energy transactions in the system. On the other hand, parallel structures are useful when problems depicts high complexity, which leaves the exhaustive enumeration as the only way to find the global optimum [
11]. However, this search was previously dependent on human calculations, which led it to becoming error-prone, exhausting, and without coherent results that allowed concise conclusions. Nowadays, with the development of computers and more suitable structures for the parallelization of activities, brute force algorithms have become feasible possibilities to support the exhaustive search and the solutions of these problems. This computational development was initially shown with the use of Message Passing Interfaces—MPI architectures. Currently, cloud or fog architectures, along with FPGA and GPU architectures, are used in the parallel processing of operations. In the case of power systems, some parallelization applications have been shown in solving different problems. Some researchers have used parallel architectures mainly for the solution of power flow [
26], transient stability [
27,
28,
29], EMT analysis [
30,
31], and the integration of renewable energy sources [
32] problems. Reduced applications in power systems have been cited in the exhaustive search for solutions through brute force algorithms.