A Greedy Heuristic for Maximizing the Lifetime of Wireless Sensor Networks Based on Disjoint Weighted Dominating Sets
Abstract
1. Introduction
- Sleep–wake cycling (also called duty cycling): Sensors switch between active and sleep mode.
- Power control by adjusting the transmission range of wireless nodes.
- Energy efficient routing, and data gathering.
- Reducing the amount of transmitted data and avoiding useless activity.
- We introduce an integer linear programming (ILP) model for the MWDDS problem.
- We propose an efficient greedy heuristic for the MWDDS problem.
- We conduct comprehensive experiments on a set of 640 problem instances in order to investigate the performance and the advantages of our greedy heuristic in comparison to the application of CPLEX and to recent state-of-the-art methods.
2. The Maximum Weighted Disjoint Dominating Sets Problem
Illustrative Example
3. An ILP Model for the MWDDS Problem
4. Proposed Greedy Heuristic
| Algorithm 1 GH-MWDDS: A Greedy heuristic for the MWDDS problem |
|
- Black nodes: Nodes that are part of .
- Gray nodes: Nodes in , that is, nodes that are not contained in but that are adjacent to at least one black node.
- White nodes: Nodes in , that is, nodes that are neither gray nor black.
Time Complexity of GH-MWDDS
5. Experimental Evaluation
5.1. Problem Instances
5.2. Results and Discussion
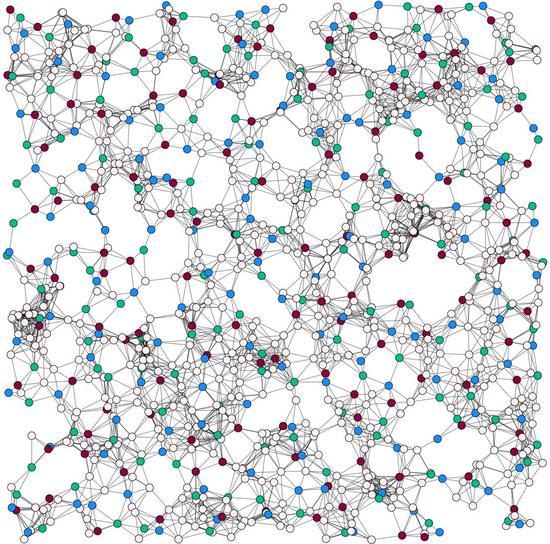
- First of all, the ILP model (solved by CPLEX) is only useful in the context of the smallest problem instances. In fact, CPLEX obtains the best results for all networks with 50 nodes. As an additional information we can say that CPLEX was able to solve 8 out of 20 problem instances with 50 nodes and an average degree of 15 to optimality. Figure 2 exemplary shows the optimal solution obtained by CPLEX for network number 14 of those networks with 50 nodes and an average node degree of 15. Note that the nodes are divided into six dominating sets (as indicated by the colors of the nodes). The nodes which are colored in green are not assigned to any dominating set.
- CPLEX already starts to fail for the instances with 100 nodes, for which the results are already inferior to those of GH-MWDDS. In fact, for most of the problem instances (starting from 150 nodes and an average degree of 60) CPLEX is unable to find anything but the trivial solution that contains no dominating set.
- Concerning GH-MWDDS, we can observe that it dominates the three competitors from the literature for all problem instances in terms of solution quality as well as computational time. It is significantly better than the best of the other three approaches, while requiring a computation time that is approximately five orders of magnitude smaller than the time needed by the other methods. The improvement ratio of our algorithm with respect to VD (the best approach from the literature) is about 5.37.
- As expected, most solutions suffer from the existence of redundant nodes. As a result, GH-MWDDS is able to produce solutions whose size (in terms of the number of disjoint dominating sets) is increased with respect to the solutions produced by GH-MWDDS. This is achieved without compromising the quality of the generated solutions. On the contrary, the quality of the obtained solutions is slightly improved, at the cost of a negligible amount of computation time.
- In addition, from Table 2 we can observe that GH-MDDS and GH-MWDDS achieve an overall average solution quality (see that last row of Table 2) of 3.667 and 9.515, respectively, and an average solution size (in terms of the number of disjoint dominating sets) of 24.089 and 21.541, respectively. It is worthwhile to note that GH-MDDS always produces solutions with the maximum possible size (equal to ). However, the quality of these solutions (as measured by the objective function of the MWDDS problem) is, of course, lower than the quality of the solutions produced by GH-MWDDS. This is because GH-MDDS is primarily focused on finding solutions of large size, without taking into consideration the problem-specific knowledge of the lifetime values of the nodes. Therefore, a solution to the MWDDS problem with the maximum size does not necessarily correspond to the best MWDDS-solution. For example, in the case where n = 250 and d = 140, for which GA-MDDS finds a solution with an average value 9.584 and an average size 53.6, GH-MWDDS finds solutions with an average value 22.514 and average size 47.7.
- From above observations we can say that the poor performance of the three local search algorithms proposed by Pino et al. [23] is mainly due to greedy heuristic used for producing the initial solutions for their local search approaches. Since this greedy heuristic was developed for the MDDS problem, and the local search approaches try to improve these solutions by making swaps among nodes of different disjoint dominating sets, they are limited to the size of the solutions found by the initial greedy heuristic, which cannot be changed later. As can be seen by our results, this way of proceeding limits too much the possibility of the local search algorithms to find improvements.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Yetgin, H.; Cheung, K.T.K.; El-Hajjar, M.; Hanzo, L.H. A survey of network lifetime maximization techniques in wireless sensor networks. IEEE Commun. Surv. Tutor. 2017, 19, 828–854. [Google Scholar] [CrossRef]
- Rodrigues, L.M.; Montez, C.; Budke, G.; Vasques, F.; Portugal, P. Estimating the lifetime of wireless sensor network nodes through the use of embedded analytical battery models. J. Sens. Actuator Netw. 2017, 6, 8. [Google Scholar] [CrossRef]
- Lewandowski, M.; Płaczek, B.; Bernas, M. Classifier-Based Data Transmission Reduction in Wearable Sensor Network for Human Activity Monitoring. Sensors 2021, 21, 85. [Google Scholar] [CrossRef] [PubMed]
- Sharma, H.; Haque, A.; Jaffery, Z.A. Maximization of wireless sensor network lifetime using solar energy harvesting for smart agriculture monitoring. Ad Hoc Netw. 2019, 94, 101966. [Google Scholar] [CrossRef]
- Lewandowski, M.; Bernas, M.; Loska, P.; Szymała, P.; Płaczek, B. Extending Lifetime of Wireless Sensor Network in Application to Road Traffic Monitoring. In International Conference on Computer Networks; Springer: Berlin/Heidelberg, Germany, 2019; pp. 112–126. [Google Scholar]
- Mansourkiaie, F.; Ismail, L.S.; Elfouly, T.M.; Ahmed, M.H. Maximizing lifetime in wireless sensor network for structural health monitoring with and without energy harvesting. IEEE Access 2017, 5, 2383–2395. [Google Scholar] [CrossRef]
- Cardei, M.; Thai, M.T.; Li, Y.; Wu, W. Energy-efficient target coverage in wireless sensor networks. In Proceedings of the IEEE 24th Annual Joint Conference of the IEEE Computer and Communications Societies, Miami, FL, USA, 13–17 March 2005; Volume 3, pp. 1976–1984. [Google Scholar]
- Slijepcevic, S.; Potkonjak, M. Power efficient organization of wireless sensor networks. In Proceedings of the ICC 2001—IEEE International Conference on Communications, Helsinki, Finland, 11–14 June 2001; Volume 2, pp. 472–476. [Google Scholar]
- Wang, H.; Li, Y.; Chang, T.; Chang, S. An effective scheduling algorithm for coverage control in underwater acoustic sensor network. Sensors 2018, 18, 2512. [Google Scholar] [CrossRef] [PubMed]
- Liao, C.C.; Ting, C.K. A novel integer-coded memetic algorithm for the set k-cover problem in wireless sensor networks. IEEE Trans. Cybern. 2017, 48, 2245–2258. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Li, S.; Yue, W. Memetic algorithm-based multi-objective coverage optimization for wireless sensor networks. Sensors 2014, 14, 20500–20518. [Google Scholar] [CrossRef] [PubMed]
- Balaji, S.; Anitha, M.; Rekha, D.; Arivudainambi, D. Energy efficient target coverage for a wireless sensor network. Measurement 2020, 165, 108167. [Google Scholar] [CrossRef]
- D’Ambrosio, C.; Iossa, A.; Laureana, F.; Palmieri, F. A genetic approach for the maximum network lifetime problem with additional operating time slot constraints. Soft Comput. 2020, 1–7. [Google Scholar] [CrossRef]
- Li, J.; Potru, R.; Shahrokhi, F. A Performance Study of Some Approximation Algorithms for Computing a Small Dominating Set in a Graph. Algorithms 2020, 13, 339. [Google Scholar] [CrossRef]
- Li, R.; Hu, S.; Liu, H.; Li, R.; Ouyang, D.; Yin, M. Multi-Start Local Search Algorithm for the Minimum Connected Dominating Set Problems. Mathematics 2019, 7, 1173. [Google Scholar] [CrossRef]
- Bouamama, S.; Blum, C. An Improved Greedy Heuristic for the Minimum Positive Influence Dominating Set Problem in Social Networks. Algorithms 2021, 14, 79. [Google Scholar] [CrossRef]
- Garey, M.; Johnson, D. Computers and Intractability. A Guide to the Theory of NP-Completeness; W. H. Freeman: New York, NY, USA, 1979. [Google Scholar]
- Cardei, M.; MacCallum, D.; Cheng, M.X.; Min, M.; Jia, X.; Li, D.; Du, D.Z. Wireless sensor networks with energy efficient organization. J. Interconnect. Netw. 2002, 3, 213–229. [Google Scholar] [CrossRef]
- Feige, U.; Halldórsson, M.M.; Kortsarz, G.; Srinivasan, A. Approximating the domatic number. SIAM J. Comput. 2002, 32, 172–195. [Google Scholar] [CrossRef]
- Moscibroda, T.; Wattenhofer, R. Maximizing the lifetime of dominating sets. In Proceedings of the 19th IEEE International Parallel and Distributed Processing Symposium, Denver, CO, USA, 4–8 April 2005. [Google Scholar]
- Nguyen, T.N.; Huynh, D.T. Extending sensor networks lifetime through energy efficient organization. In Proceedings of the International Conference on Wireless Algorithms, Systems and Applications (WASA 2007), Chicago, IL, USA, 1–3 August 2007; pp. 205–212. [Google Scholar]
- Islam, K.; Akl, S.G.; Meijer, H. Maximizing the lifetime of wireless sensor networks through domatic partition. In Proceedings of the 2009 IEEE 34th Conference on Local Computer Networks, Zurich, Switzerland, 20–23 October 2009; pp. 436–442. [Google Scholar]
- Pino, T.; Choudhury, S.; Al-Turjman, F. Dominating set algorithms for wireless sensor networks survivability. IEEE Access 2018, 6, 17527–17532. [Google Scholar] [CrossRef]
- Haynes, T.W.; Hedetniemi, S.T.; Henning, M.A. Topics in Domination in Graphs; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Bouamama, S.; Blum, C. A hybrid algorithmic model for the minimum weight dominating set problem. Simul. Model. Pract. Theory 2016, 64, 57–68. [Google Scholar] [CrossRef]
- Pang, C.; Zhang, R.; Zhang, Q.; Wang, J. Dominating sets in directed graphs. Inf. Sci. 2010, 180, 3647–3652. [Google Scholar] [CrossRef]
- Blum, C.; Davidson, P.P.; López-Ibáñez, M.; Lozano, J.A. Construct, Merge, Solve & Adapt: A new general algorithm for combinatorial optimization. Comput. Oper. Res. 2016, 68, 75–88. [Google Scholar]


| n | d | CPLEX | LS | FD | VD | |DP| | GH-MWDDS | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | Gap(%) | Value | Time(s) | Value | Time(s) | Value | Time(s) | Value | Time(s) | |DP| | |||
| 50 | 15 | 2.779 | 32.839 | 0.395 | 0.003 | 0.477 | 0.019 | 0.555 | 1.984 | 2.55 | 2.155 | 0.000 | 5.75 |
| 20 | 3.922 | 121.088 | 0.649 | 0.004 | 0.825 | 0.055 | 1.014 | 7.651 | 3.55 | 3.353 | 0.001 | 8.05 | |
| 25 | 5.098 | 158.038 | 1.011 | 0.006 | 1.245 | 0.055 | 1.490 | 4.885 | 4.05 | 4.595 | 0.001 | 10.05 | |
| 30 | 6.432 | 200.567 | 1.664 | 0.007 | 2.460 | 0.124 | 2.780 | 13.117 | 6.30 | 5.926 | 0.001 | 12.90 | |
| 35 | 7.929 | 197.434 | 2.200 | 0.012 | 2.914 | 0.204 | 3.166 | 25.048 | 6.85 | 7.376 | 0.000 | 15.30 | |
| 100 | 20 | 2.467 | 405.669 | 0.283 | 0.023 | 0.333 | 0.188 | 0.423 | 30.458 | 2.45 | 2.784 | 0.001 | 7.00 |
| 30 | 3.202 | >1000.0 | 0.431 | 0.017 | 0.535 | 0.165 | 0.576 | 31.796 | 2.95 | 4.501 | 0.003 | 10.90 | |
| 40 | 3.338 | >1000.0 | 0.859 | 0.021 | 1.259 | 0.394 | 1.341 | 183.921 | 4.75 | 6.679 | 0.002 | 14.80 | |
| 50 | 3.857 | >1000.0 | 1.361 | 0.038 | 2.018 | 0.796 | 2.407 | 225.704 | 6.00 | 8.500 | 0.001 | 18.65 | |
| 60 | 5.804 | 823.022 | 2.019 | 0.027 | 2.884 | 0.830 | 3.226 | 362.775 | 7.15 | 11.131 | 0.001 | 23.40 | |
| 150 | 30 | 0.055 | >1000.0 | 0.287 | 0.053 | 0.326 | 0.316 | 0.326 | 106.602 | 2.85 | 4.098 | 0.002 | 10.65 |
| 40 | 0.028 | >1000.0 | 0.557 | 0.050 | 0.670 | 0.595 | 0.745 | 156.994 | 3.80 | 5.816 | 0.003 | 14.05 | |
| 50 | 0.011 | >1000.0 | 0.615 | 0.077 | 0.927 | 1.139 | 1.009 | 182.630 | 3.95 | 7.479 | 0.003 | 17.50 | |
| 60 | 0 | >1000.0 | 0.848 | 0.046 | 1.506 | 2.576 | 1.521 | 646.268 | 4.90 | 9.281 | 0.002 | 21.00 | |
| 70 | 0 | >1000.0 | 1.373 | 0.066 | 2.293 | 4.219 | 2.464 | 1028.650 | 6.65 | 11.388 | 0.004 | 24.45 | |
| 80 | 0 | >1000.0 | 1.689 | 0.065 | 2.729 | 2.599 | 3.036 | 549.900 | 7.20 | 13.508 | 0.005 | 28.90 | |
| 90 | 0 | >1000.0 | 2.209 | 0.055 | 3.817 | 3.793 | 4.193 | 906.030 | 9.05 | 15.485 | 0.006 | 32.95 | |
| 200 | 40 | 0 | >1000.0 | 0.256 | 0.049 | 0.317 | 0.648 | 0.370 | 81.750 | 2.65 | 5.424 | 0.004 | 13.65 |
| 50 | 0 | >1000.0 | 0.374 | 0.099 | 0.475 | 1.252 | 0.483 | 186.900 | 3.45 | 6.784 | 0.005 | 16.60 | |
| 60 | 0 | >1000.0 | 0.678 | 0.112 | 0.897 | 2.083 | 0.917 | 313.850 | 3.75 | 8.656 | 0.005 | 20.35 | |
| 70 | 0 | >1000.0 | 1.004 | 0.170 | 1.652 | 6.463 | 1.680 | 3112.950 | 5.95 | 10.351 | 0.006 | 23.65 | |
| 80 | 0 | >1000.0 | 0.840 | 0.076 | 1.624 | 5.874 | 1.795 | 1629.400 | 5.35 | 12.447 | 0.008 | 27.15 | |
| 90 | 0 | >1000.0 | 1.153 | 0.109 | 1.924 | 5.260 | 2.045 | 1364.400 | 5.65 | 13.978 | 0.012 | 30.55 | |
| 100 | 0 | >1000.0 | 1.503 | 0.091 | 2.836 | 9.396 | 3.098 | 3024.830 | 7.65 | 15.868 | 0.009 | 34.30 | |
| 250 | 50 | 0 | >1000.0 | 0.266 | 0.136 | 0.314 | 0.867 | 0.329 | 557.676 | 2.95 | 6.681 | 0.016 | 16.85 |
| 60 | 0 | >1000.0 | 0.526 | 0.221 | 0.892 | 7.638 | 0.945 | 1400.788 | 4.55 | 8.244 | 0.012 | 19.70 | |
| 70 | 0 | >1000.0 | 0.689 | 0.264 | 1.050 | 6.906 | 1.326 | 2380.366 | 5.10 | 9.636 | 0.013 | 22.95 | |
| 80 | 0 | >1000.0 | 0.652 | 0.241 | 1.163 | 9.801 | 1.445 | 647.763 | 5.40 | 11.520 | 0.013 | 26.15 | |
| 90 | 0 | >1000.0 | 0.841 | 0.324 | 1.448 | 18.394 | 1.591 | 1242.663 | 5.80 | 12.938 | 0.013 | 29.55 | |
| 100 | 0 | >1000.0 | 1.117 | 0.228 | 1.981 | 20.789 | 2.443 | 2210.880 | 6.45 | 14.733 | 0.016 | 32.70 | |
| 120 | 0 | >1000.0 | 1.259 | 0.146 | 2.577 | 10.442 | 2.781 | 2249.350 | 7.20 | 18.348 | 0.016 | 39.70 | |
| 140 | 0 | >1000.0 | 2.135 | 0.121 | 4.275 | 16.885 | 4.713 | 6624.596 | 10.50 | 22.478 | 0.020 | 47.25 | |
| Avg | 1.404 | 0.992 | 0.092 | 1.583 | 4.399 | 1.757 | 984.143 | 5.231 | 9.442 | 0.006 | 21.169 | ||
| n | d | GH-MDDS | GH-MWDDS | GH-MWDDS | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Value | Time(s) | |DP| | Value | Time(s) | |DP| | Value | Time(s) | |DP| | ||
| 50 | 15 | 1.111 | 0.001 | 6.75 | 2.155 | 0.000 | 5.75 | 2.191 | 0.002 | 6.150 |
| 20 | 1.548 | 0.001 | 9.05 | 3.353 | 0.001 | 8.05 | 3.450 | 0.000 | 8.350 | |
| 25 | 2.630 | 0.001 | 11.85 | 4.595 | 0.001 | 10.05 | 4.672 | 0.000 | 10.550 | |
| 30 | 3.510 | 0.001 | 14.60 | 5.926 | 0.001 | 12.90 | 6.042 | 0.000 | 13.350 | |
| 35 | 4.772 | 0.001 | 17.25 | 7.376 | 0.000 | 15.30 | 7.546 | 0.000 | 15.900 | |
| 100 | 20 | 0.841 | 0.001 | 8.50 | 2.784 | 0.001 | 7.00 | 2.842 | 0.001 | 7.400 |
| 30 | 1.714 | 0.004 | 12.70 | 4.501 | 0.003 | 10.90 | 4.580 | 0.001 | 11.150 | |
| 40 | 2.900 | 0.002 | 17.15 | 6.679 | 0.002 | 14.80 | 6.794 | 0.002 | 15.200 | |
| 50 | 3.908 | 0.002 | 21.40 | 8.500 | 0.001 | 18.65 | 8.525 | 0.002 | 19.100 | |
| 60 | 6.111 | 0.004 | 26.30 | 11.131 | 0.001 | 23.40 | 11.174 | 0.002 | 23.600 | |
| 150 | 30 | 1.036 | 0.003 | 12.00 | 4.098 | 0.002 | 10.65 | 4.141 | 0.002 | 10.900 |
| 40 | 1.769 | 0.002 | 16.20 | 5.816 | 0.003 | 14.05 | 5.872 | 0.002 | 14.350 | |
| 50 | 2.553 | 0.003 | 20.00 | 7.479 | 0.003 | 17.50 | 7.570 | 0.002 | 17.850 | |
| 60 | 3.647 | 0.004 | 24.10 | 9.281 | 0.002 | 21.00 | 9.371 | 0.005 | 21.450 | |
| 70 | 4.789 | 0.002 | 28.10 | 11.388 | 0.004 | 24.45 | 11.446 | 0.005 | 25.050 | |
| 80 | 6.468 | 0.005 | 33.00 | 13.508 | 0.005 | 28.90 | 13.611 | 0.003 | 29.150 | |
| 90 | 7.143 | 0.006 | 36.55 | 15.485 | 0.006 | 32.95 | 15.589 | 0.005 | 33.550 | |
| 200 | 40 | 1.350 | 0.006 | 15.50 | 5.424 | 0.004 | 13.65 | 5.486 | 0.005 | 13.950 |
| 50 | 1.719 | 0.006 | 18.95 | 6.784 | 0.005 | 16.60 | 6.848 | 0.006 | 17.050 | |
| 60 | 2.551 | 0.007 | 23.35 | 8.656 | 0.005 | 20.35 | 8.710 | 0.008 | 20.550 | |
| 70 | 3.566 | 0.008 | 26.80 | 10.351 | 0.006 | 23.65 | 10.395 | 0.008 | 24.100 | |
| 80 | 4.466 | 0.015 | 30.70 | 12.447 | 0.008 | 27.15 | 12.529 | 0.003 | 27.400 | |
| 90 | 5.368 | 0.009 | 34.80 | 13.978 | 0.012 | 30.55 | 14.046 | 0.009 | 31.000 | |
| 100 | 6.425 | 0.011 | 38.50 | 15.868 | 0.009 | 34.30 | 15.993 | 0.009 | 34.650 | |
| 250 | 50 | 1.643 | 0.013 | 19.05 | 6.681 | 0.016 | 16.85 | 6.783 | 0.008 | 16.950 |
| 60 | 2.062 | 0.010 | 22.70 | 8.244 | 0.012 | 19.70 | 8.285 | 0.010 | 19.950 | |
| 70 | 2.613 | 0.012 | 26.15 | 9.636 | 0.013 | 22.95 | 9.699 | 0.013 | 23.150 | |
| 80 | 3.348 | 0.013 | 29.55 | 11.520 | 0.013 | 26.15 | 11.571 | 0.013 | 26.500 | |
| 90 | 4.030 | 0.016 | 33.50 | 12.938 | 0.013 | 29.55 | 12.978 | 0.016 | 29.900 | |
| 100 | 5.024 | 0.016 | 37.15 | 14.733 | 0.016 | 32.70 | 14.800 | 0.016 | 33.150 | |
| 120 | 7.134 | 0.017 | 45.05 | 18.348 | 0.016 | 39.70 | 18.418 | 0.018 | 40.250 | |
| 140 | 9.584 | 0.020 | 53.60 | 22.478 | 0.020 | 47.25 | 22.514 | 0.020 | 47.700 | |
| Avg | 3.667 | 0.007 | 24.089 | 9.442 | 0.006 | 21.169 | 9.515 | 0.006 | 21.541 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balbal, S.; Bouamama, S.; Blum, C. A Greedy Heuristic for Maximizing the Lifetime of Wireless Sensor Networks Based on Disjoint Weighted Dominating Sets. Algorithms 2021, 14, 170. https://doi.org/10.3390/a14060170
Balbal S, Bouamama S, Blum C. A Greedy Heuristic for Maximizing the Lifetime of Wireless Sensor Networks Based on Disjoint Weighted Dominating Sets. Algorithms. 2021; 14(6):170. https://doi.org/10.3390/a14060170
Chicago/Turabian StyleBalbal, Samir, Salim Bouamama, and Christian Blum. 2021. "A Greedy Heuristic for Maximizing the Lifetime of Wireless Sensor Networks Based on Disjoint Weighted Dominating Sets" Algorithms 14, no. 6: 170. https://doi.org/10.3390/a14060170
APA StyleBalbal, S., Bouamama, S., & Blum, C. (2021). A Greedy Heuristic for Maximizing the Lifetime of Wireless Sensor Networks Based on Disjoint Weighted Dominating Sets. Algorithms, 14(6), 170. https://doi.org/10.3390/a14060170