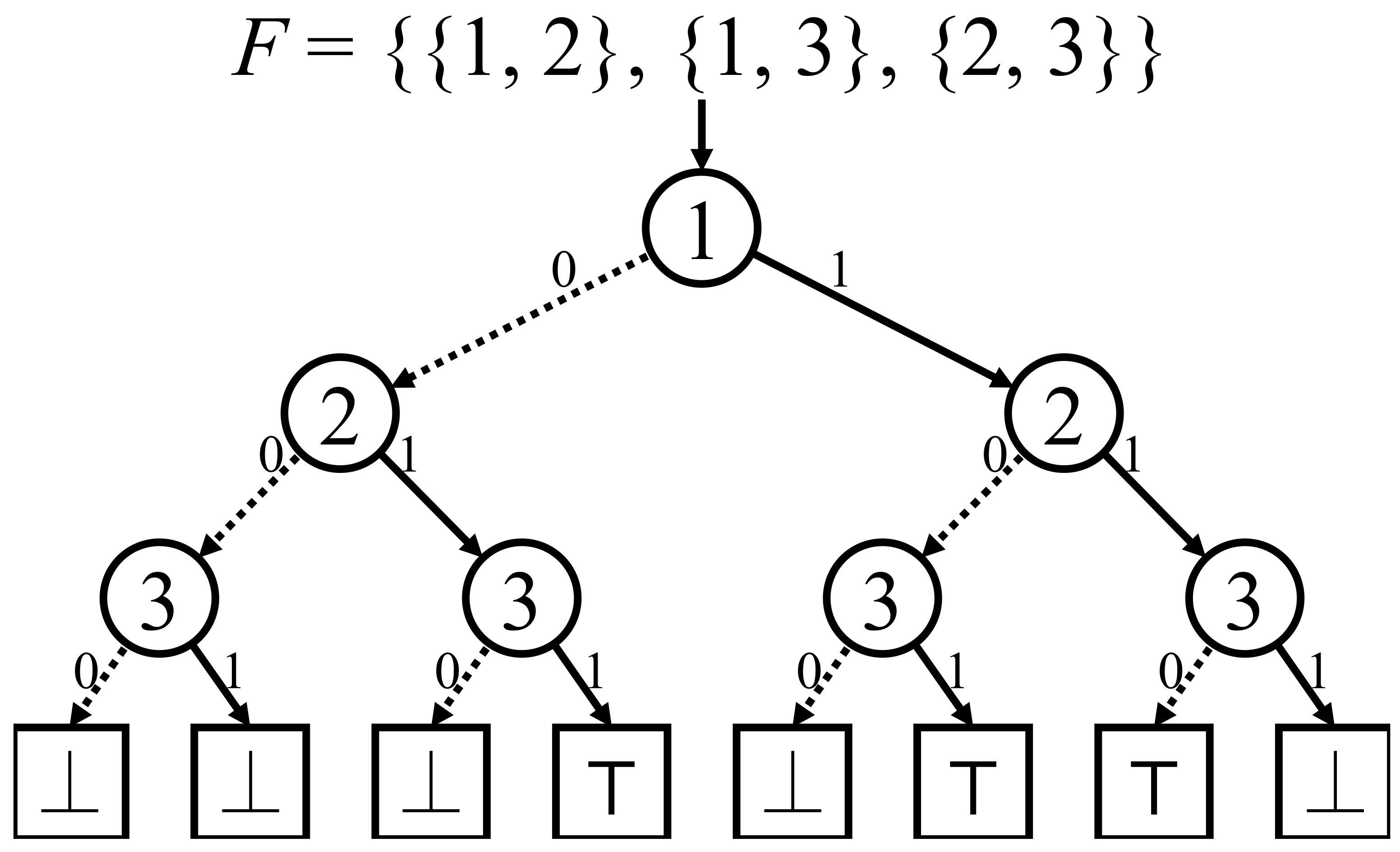
Figure 1.
The binary tree that represents a family of sets .
Figure 1.
The binary tree that represents a family of sets .
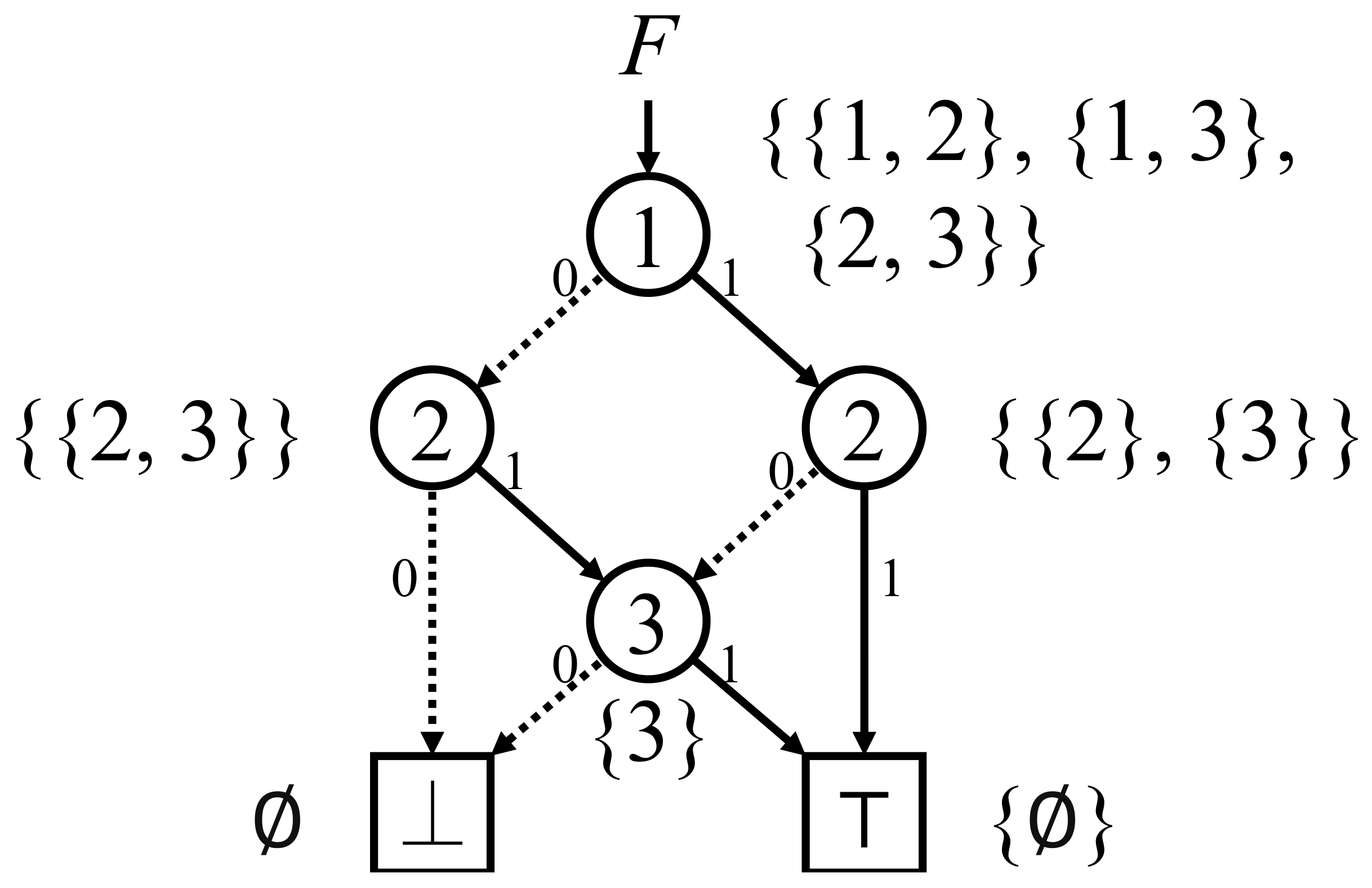
Figure 2.
The ZDD obtained from the binary tree in
Figure 1 by merging equivalent nodes and deleting redundant nodes. Terminal nodes and branching nodes are depicted by squares and circles, respectively, and 0-edges and 1-edges are depicted by dashed and solid lines, respectively. The family of sets represented by each node is indicated beside it.
Figure 2.
The ZDD obtained from the binary tree in
Figure 1 by merging equivalent nodes and deleting redundant nodes. Terminal nodes and branching nodes are depicted by squares and circles, respectively, and 0-edges and 1-edges are depicted by dashed and solid lines, respectively. The family of sets represented by each node is indicated beside it.
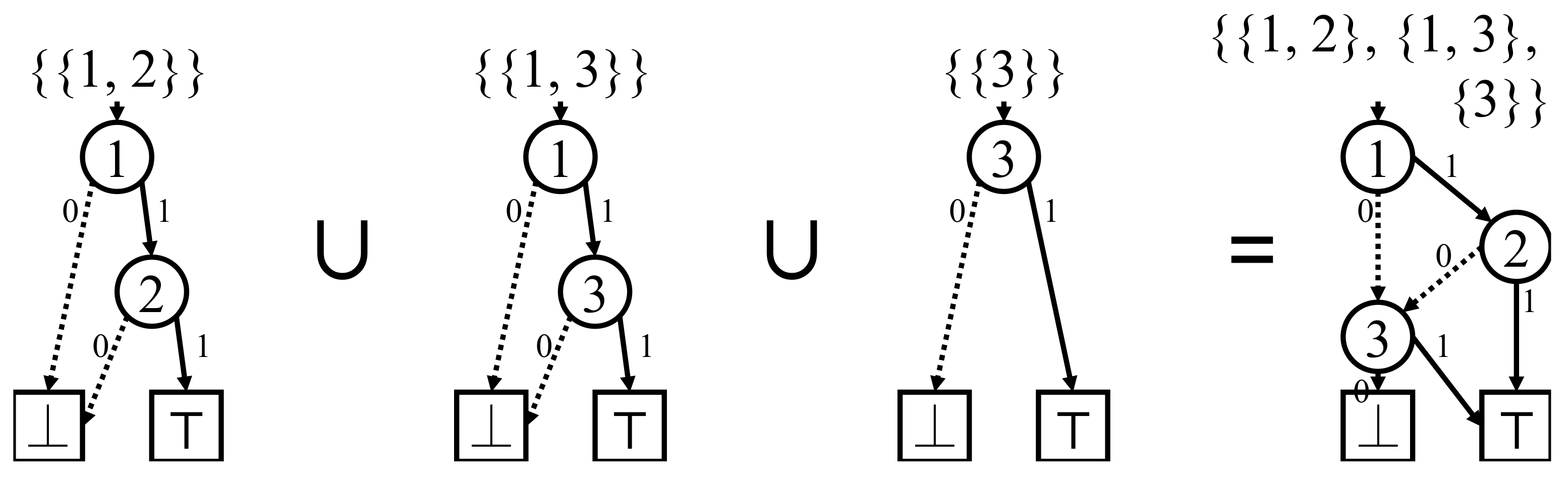
Figure 3.
Example of how ZDDs are utilized to obtain a new ZDD from given ZDDs via a set operation.
Figure 3.
Example of how ZDDs are utilized to obtain a new ZDD from given ZDDs via a set operation.
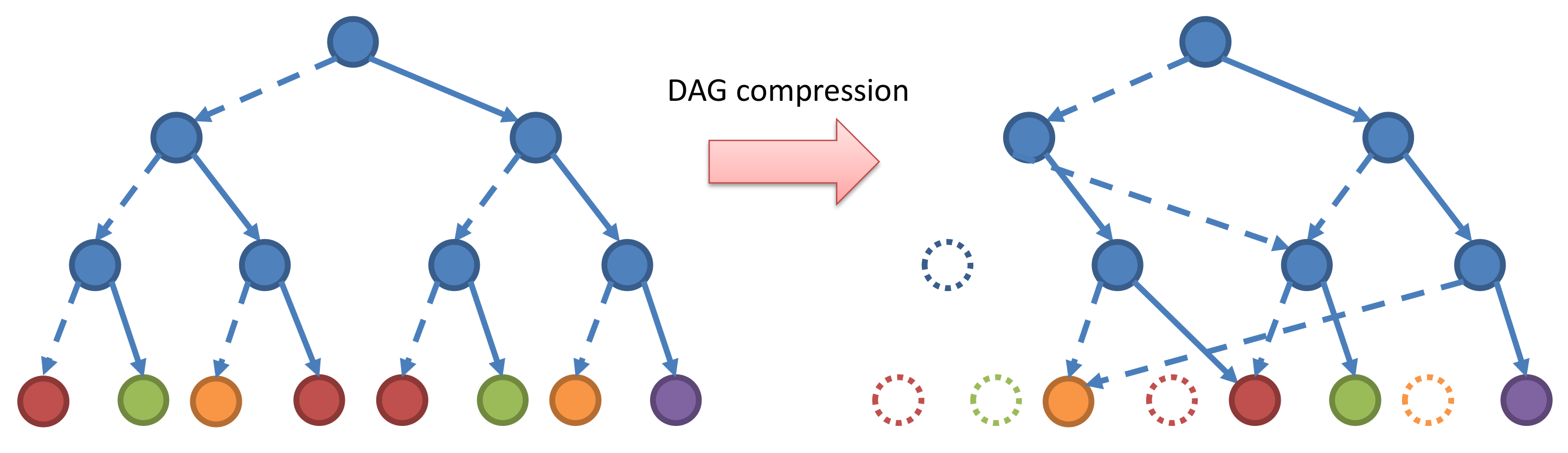
Figure 4.
An example of DAG compression. Dashed lines are 0-edges, and solid lines are 1-edges. Leaves of the same colour represent the identical subtrees.
Figure 4.
An example of DAG compression. Dashed lines are 0-edges, and solid lines are 1-edges. Leaves of the same colour represent the identical subtrees.
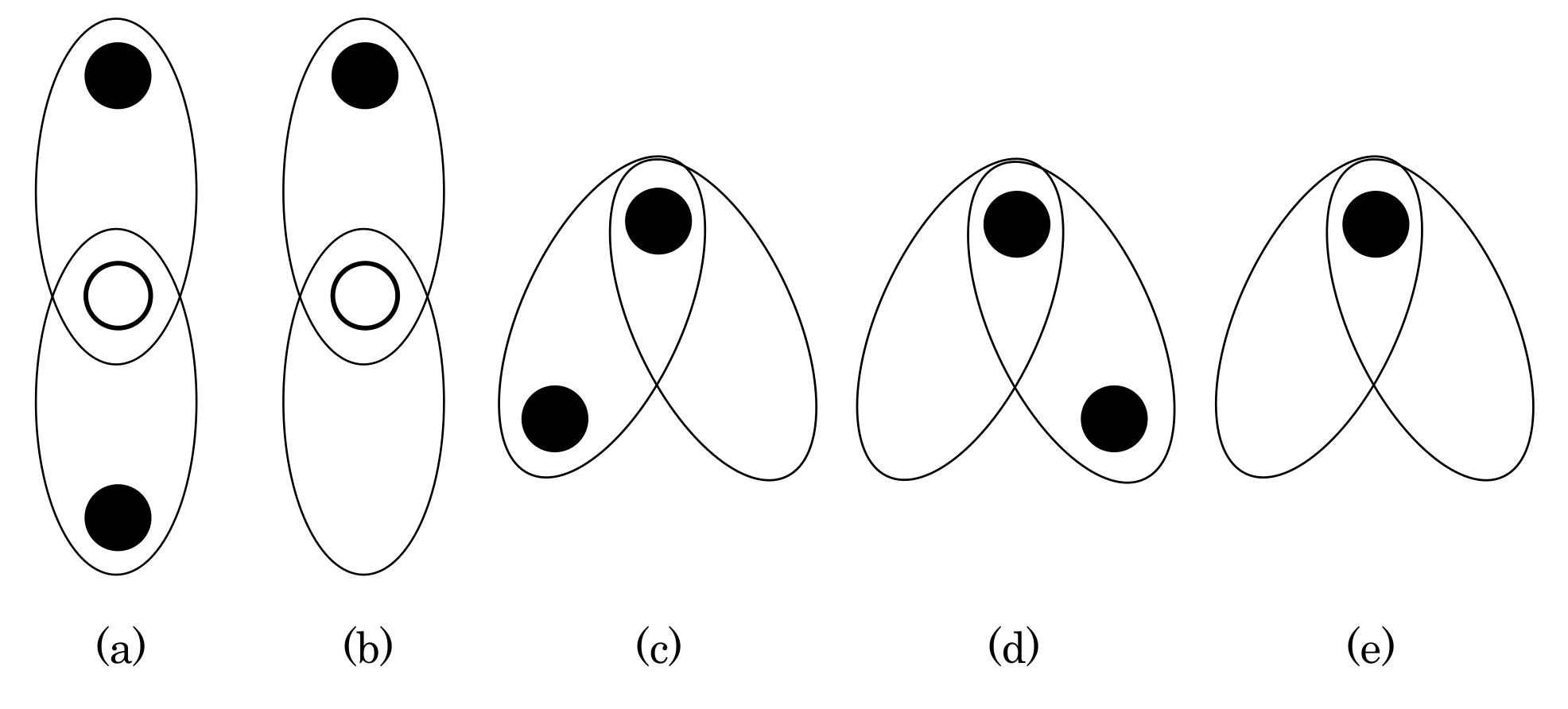
Figure 5.
Merging clusters. These five merges are divided into two. (a,b) Vertical merge: two clusters can be merged vertically if the top boundary node of one cluster coincides with the bottom boundary node of the other cluster, and there are no edges from the common boundary node to nodes outside the two clusters. (c–e) Horizontal merge: two clusters can be merged horizontally if the top boundary nodes of the two clusters are the same and at least one cluster does not have the bottom boundary node.
Figure 5.
Merging clusters. These five merges are divided into two. (a,b) Vertical merge: two clusters can be merged vertically if the top boundary node of one cluster coincides with the bottom boundary node of the other cluster, and there are no edges from the common boundary node to nodes outside the two clusters. (c–e) Horizontal merge: two clusters can be merged horizontally if the top boundary nodes of the two clusters are the same and at least one cluster does not have the bottom boundary node.
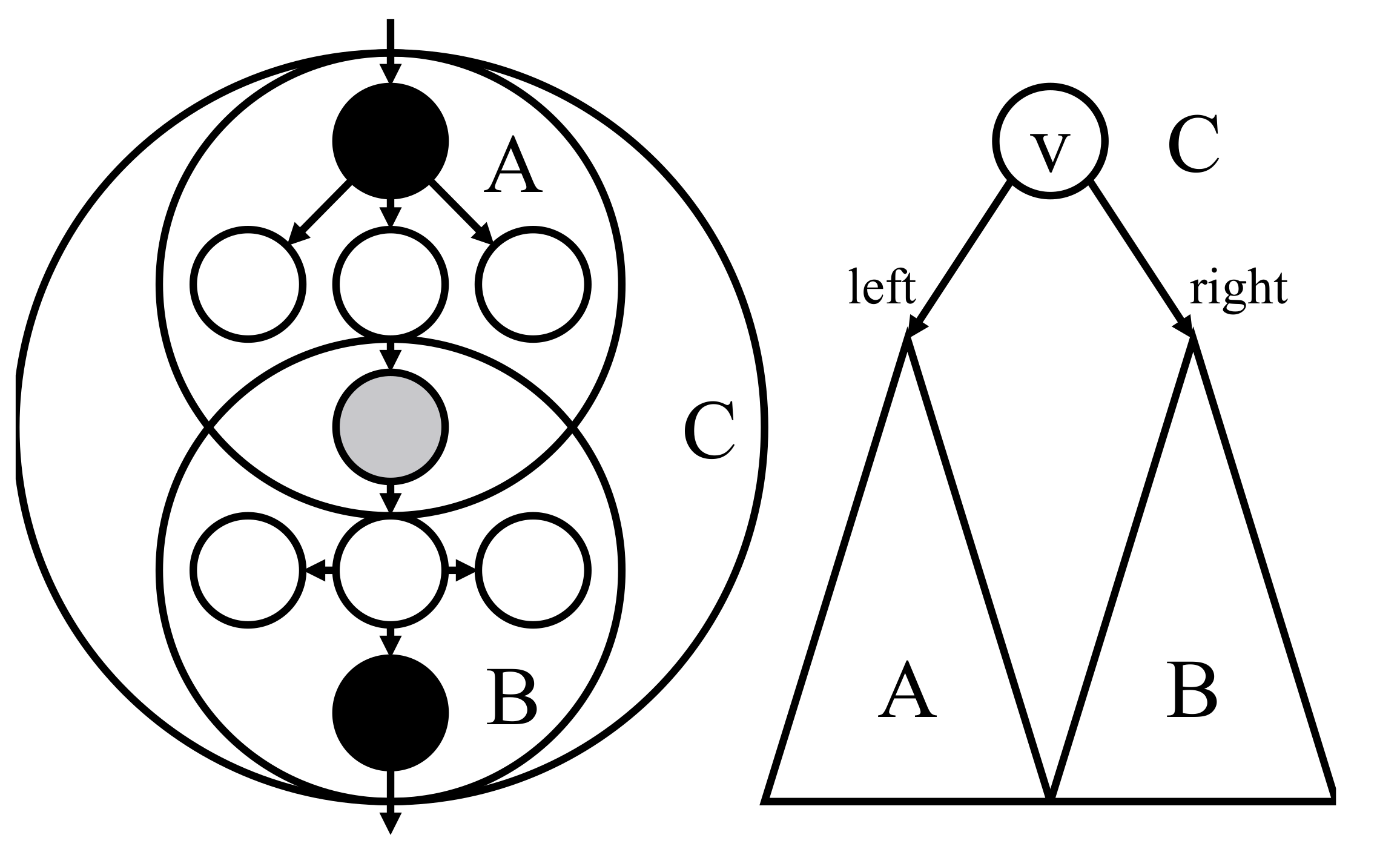
Figure 6.
An example of vertical merge of type (a). The left side is the clusters in the given tree and the right side is the corresponding top tree. A black node above is a boundary node of the clusters A and C. A black node below is a boundary node of the clusters B and C. A light gray node is a boundary node of the clusters A and B, but not of C.
Figure 6.
An example of vertical merge of type (a). The left side is the clusters in the given tree and the right side is the corresponding top tree. A black node above is a boundary node of the clusters A and C. A black node below is a boundary node of the clusters B and C. A light gray node is a boundary node of the clusters A and B, but not of C.
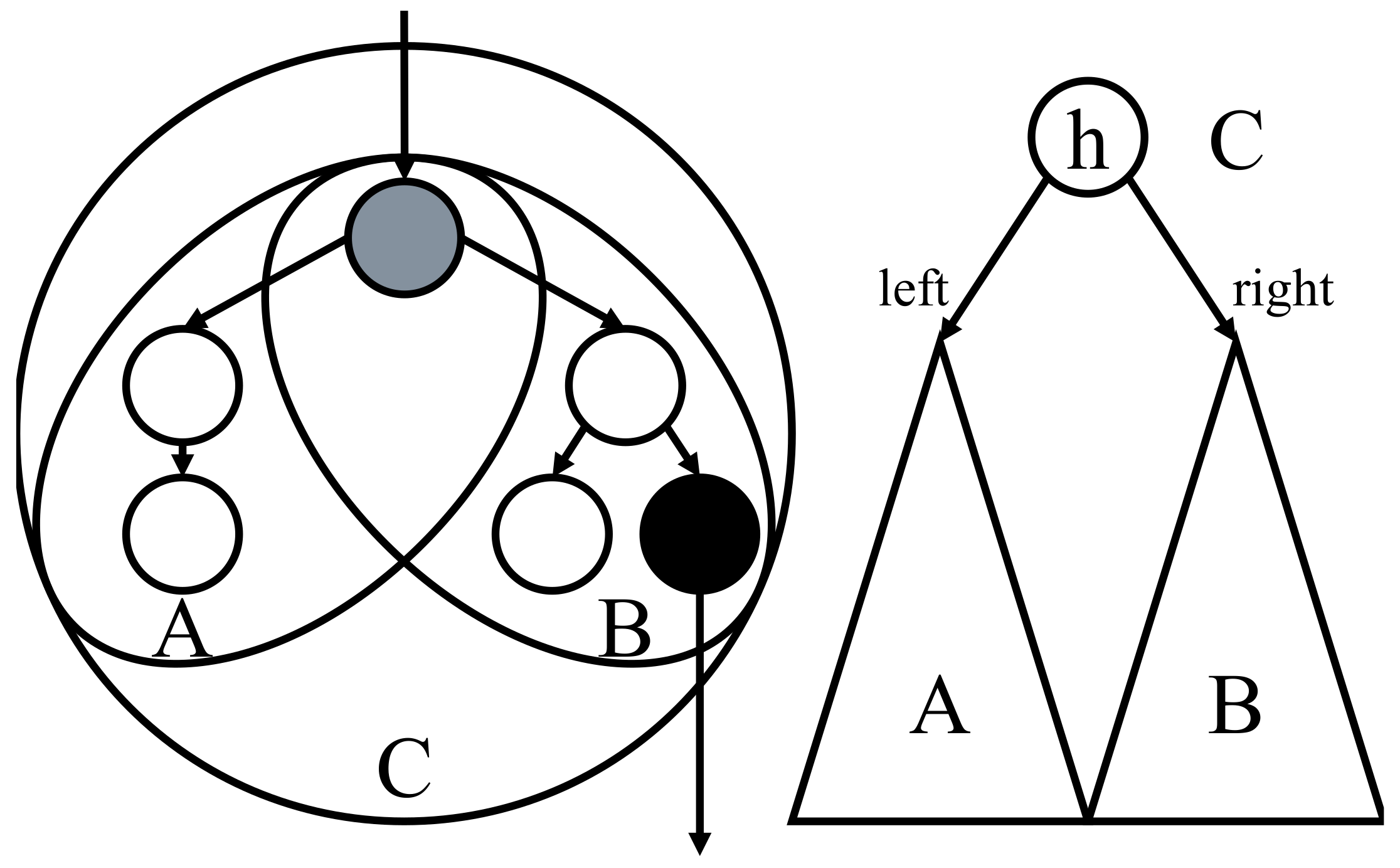
Figure 7.
An example of horizontal merge of type (d). The left side is the clusters in the given tree and the right side is the corresponding top tree. A black node is a boundary node of the clusters B and C. A dark gray node is a boundary node of clusters A, B and C.
Figure 7.
An example of horizontal merge of type (d). The left side is the clusters in the given tree and the right side is the corresponding top tree. A black node is a boundary node of the clusters B and C. A dark gray node is a boundary node of clusters A, B and C.
Figure 8.
An example of top tree. Alongside each vertex of the top tree, the corresponding cluster is drawn. Red nodes show boundary nodes.
Figure 8.
An example of top tree. Alongside each vertex of the top tree, the corresponding cluster is drawn. Red nodes show boundary nodes.
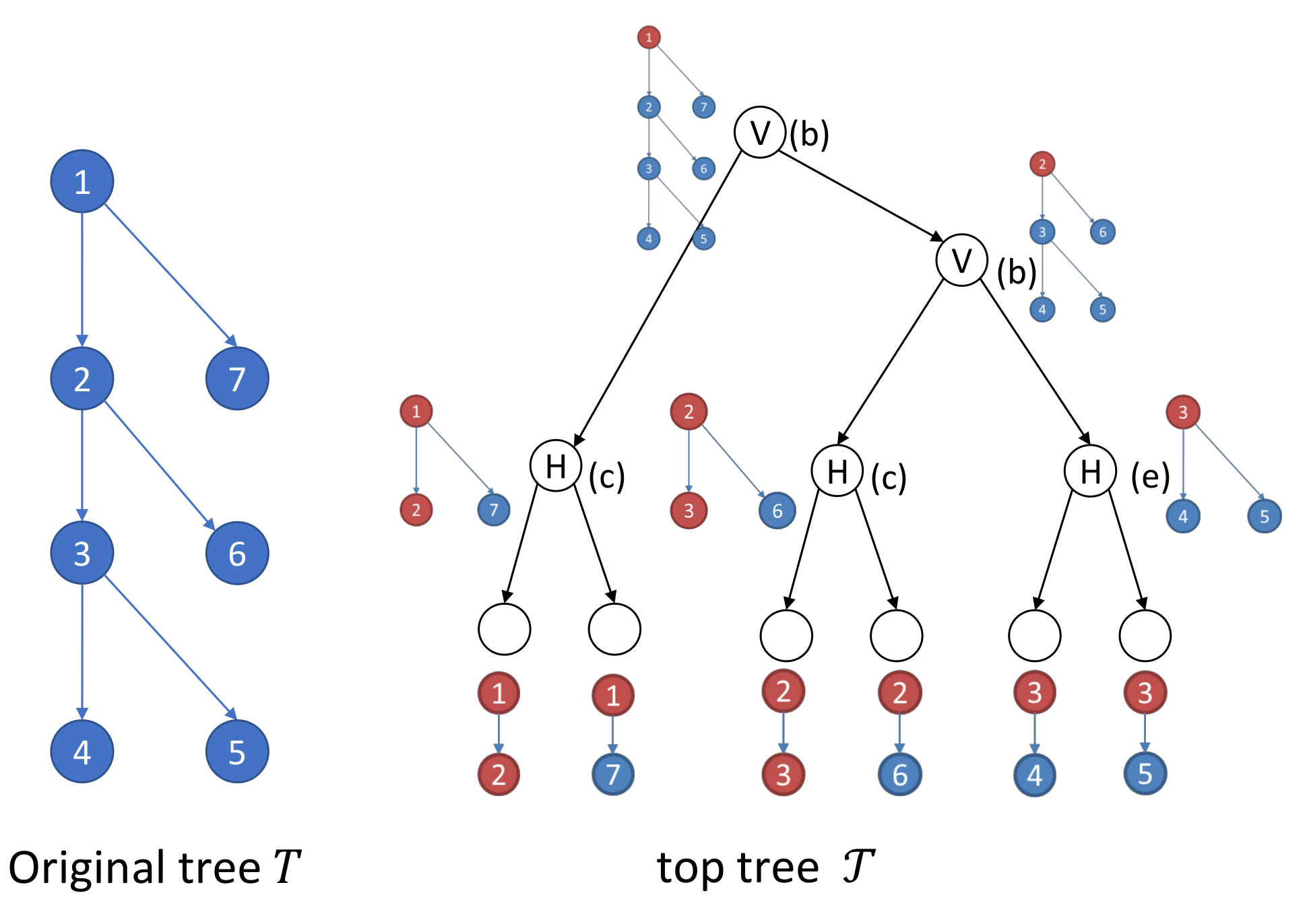
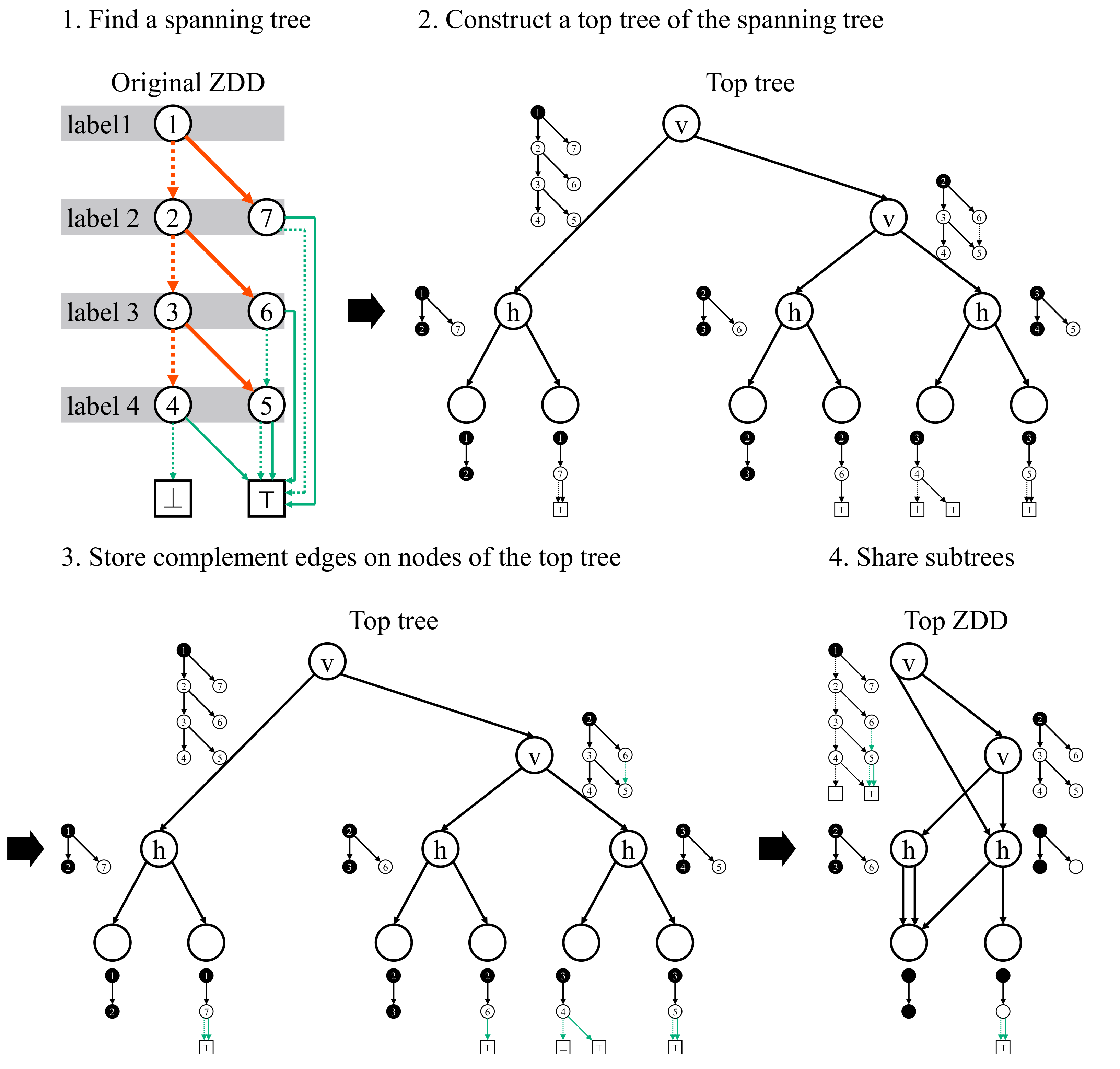
Figure 9.
Running example of the Top ZDD construction algorithm. In each branching node of the original ZDD, its preorder id is denoted instead of its label. Red edges are spanning tree edges and green edges are complement edges. For each vertex of the top tree, the corresponding cluster and the complement edges stored are shown. Boundary nodes of each cluster are denoted as black nodes.
Figure 9.
Running example of the Top ZDD construction algorithm. In each branching node of the original ZDD, its preorder id is denoted instead of its label. Red edges are spanning tree edges and green edges are complement edges. For each vertex of the top tree, the corresponding cluster and the complement edges stored are shown. Boundary nodes of each cluster are denoted as black nodes.
Figure 10.
A top ZDD with vertices, where . We omitted the middle of the graph by dots, but the height differs exponentially. In this ZDD, the spanning tree is a path consisting only of 0-edges, represented in red. The complement edges are indicated in green. In the top ZDD, the cluster corresponding to each node is shown in a smaller size next to it.
Figure 10.
A top ZDD with vertices, where . We omitted the middle of the graph by dots, but the height differs exponentially. In this ZDD, the spanning tree is a path consisting only of 0-edges, represented in red. The complement edges are indicated in green. In the top ZDD, the cluster corresponding to each node is shown in a smaller size next to it.
Table 1.
Components of the top ZDD.
Table 1.
Components of the top ZDD.
| BP sequence representing the structure of |
|---|
| bit vector showing i-th leaf is a dummy vertex or not |
| array storing cumulative sum of cluster sizes of the first to the i-th dummy leaves |
| array storing differences of labels of ending points of i-th non-dummy leaf |
| array showing the edge corresponding to the i-th non-dummy leaf is 0-edge or not |
| bit vector showing i-th internal vertex is a vertical merge or not |
| array storing differences of preorder ids between the top and the bottom boundary nodes of the vertex corresponding to i-th vertical merge |
| array storing differences of labels between the top and the bottom boundary nodes of the vertex corresponding to i-th vertical merge |
| bit vector storing in unary codes the number of complement edges from each vertex |
| array storing preorder ids of ending points of the i-th complement edge stored in root |
| array showing the i-th complement edge stored in the root is a 0-edge or not |
| bit vector storing in unary codes the number of complement edges from each vertex stored in the root |
| array storing local preorder ids of starting points of i-th complement edge stored in non-root |
| array storing local preorder ids of ending points of i-th complement edge stored in non-root |
| array showing the i-th complement edge stored in non-root is 0-edge or not |
Table 2.
The power set of .
Table 2.
The power set of .
| | Top ZDD | DenseZDD | Theoretical Size of ZDD
|
|---|
| 2297
| 4185 | 3750 |
| A = 50,000 | 2507 | 178,764 | 300,000 |
Table 3.
For the set with A elements, the family of all the set S satisfying .
Table 3.
For the set with A elements, the family of all the set S satisfying .
| | Top ZDD | DenseZDD | Theoretical Size of ZDD
|
|---|
| 2471 | 227,798 | 321,594 |
| 2551 | 321,594 | 1,440,375 |
Table 4.
For the set with A elements, the family of all the sets with cardinality at most B.
Table 4.
For the set with A elements, the family of all the sets with cardinality at most B.
| | Top ZDD | DenseZDD | Theoretical Size of ZDD
|
|---|
| 3863 | 9544 | 9882 |
| 13,654 | 146,550 | 206,025 |
| 43,191 | 966,519 | 1,440,375 |
Table 5.
Knapsack set families with random weights. A is the number of elements, W is the maximum weight of an element, C is the capacity of the knapsack.
Table 5.
Knapsack set families with random weights. A is the number of elements, W is the maximum weight of an element, C is the capacity of the knapsack.
| | Top ZDD | DenseZDD | Theoretical
Size of ZDD | t | p |
|---|
| 1,630,136 | 1,736,228 | 2,453,695 | 49 | 0 |
| 976,577 | 1,409,626 | 2,026,484 | 175 | 0 |
| 2,078,731 | 2,919,211 | 4,475,977 | 1124 | 0 |
| 1,138,778 | 1,731,654 | 2,869,185 | 1024 | 0 |
| 1,404,838 | 2,627,430 | 4,003,302 | 951 | 0 |
Table 6.
The family of edge sets which are matching of a given graph.
Table 6.
The family of edge sets which are matching of a given graph.
| | Top ZDD | DenseZDD | Theoretical Size of ZDD
|
|---|
| grid | 12,246 | 16,150 | 18,014 |
| complete graph | 23,078 | 16,304 | 25,340 |
| “Interoute” | 30,844 | 39,831 | 50,144 |
Table 7.
Set families of frequent item sets.
Table 7.
Set families of frequent item sets.
| | Top ZDD | DenseZDD | Theoretical Size of ZDD
|
|---|
| “mushroom” | 104,774 | 91,757 | 123,576 |
| “retail” | 59,894 | 65,219 | 62,766 |
| “T40I10D100K” | 177,517 | 188,400 | 248,656 |
Table 8.
Families of paths in grid graph.
Table 8.
Families of paths in grid graph.
| | Top ZDD | DenseZDD | Theoretical Size of ZDD
|
|---|
| 17,194 | 28,593 | 37,441 |
| 49,770 | 107,529 | 143,037 |
| 157,103 | 401,251 | 569,908 |
| 503,265 | 1,465,984 | 2,141,955 |
Table 9.
Families of solutions of the n-queen problem.
Table 9.
Families of solutions of the n-queen problem.
| | Top ZDD | DenseZDD | Theoretical Size of ZDD
|
|---|
| 40,792 | 35,101 | 45,950 |
| 183,443 | 167,259 | 229,165 |
| 866,749 | 799,524 | 1,126,295 |
Table 10.
The power set of .
Table 10.
The power set of .
| | Construction Time (s) | Traversal Time (s) |
|---|
| | Top ZDD | DenseZDD | Top ZDD | DenseZDD |
|---|
| 0.006 | 0.004 | 13.546 | 0.458 |
| A = 50,000 | 0.217 | 0.116 | 11.768 | 0.198 |
Table 11.
For the set with A elements, the family of all the set S satisfying .
Table 11.
For the set with A elements, the family of all the set S satisfying .
| | Construction Time (s) | Traversal Time (s) |
|---|
| | Top ZDD | DenseZDD | Top ZDD | DenseZDD |
|---|
| 0.264 | 0.078 | 9.082 | 0.244 |
| 0.776 | 0.412 | 10.419 | 0.229 |
Table 12.
For the set with A elements, the family of all the sets with cardinality at most B.
Table 12.
For the set with A elements, the family of all the sets with cardinality at most B.
| | Construction Time (s) | Traversal Time (s) |
|---|
| | Top ZDD | DenseZDD | Top ZDD | DenseZDD |
|---|
| 0.011 | 0.006 | 10.892 | 0.320 |
| 0.269 | 0.123 | 16.019 | 0.534 |
| 2.013 | 0.878 | 20.101 | 0.412 |
Table 13.
Knapsack set families with random weights. A is the number of elements, W is the maximum weight of an element, C is the capacity of the knapsack. In this experiment, the t-values ranged from 630 to 915 for all settings, and the p-values were 0.
Table 13.
Knapsack set families with random weights. A is the number of elements, W is the maximum weight of an element, C is the capacity of the knapsack. In this experiment, the t-values ranged from 630 to 915 for all settings, and the p-values were 0.
| | Construction Time (s) | Traversal Time (s) |
|---|
| | Top ZDD | DenseZDD | Top ZDD | DenseZDD |
|---|
| = 10,000 | 2.974 | 1.210 | 16.716 | 0.259 |
| 2.033 | 1.019 | 23.215 | 0.290 |
| 7.010 | 1.481 | 21.698 | 0.534 |
| 2.084 | 0.954 | 7.365 | 0.519 |
| 2.597 | 1.712 | 14.127 | 0.244 |
Table 14.
The family of edge sets which are matching of a given graph.
Table 14.
The family of edge sets which are matching of a given graph.
| | Construction Time (s) | Traversal Time (s) |
|---|
| | Top ZDD | DenseZDD | Top ZDD | DenseZDD |
|---|
| grid | 0.030 | 0.020 | 11.678 | 1.053 |
| complete graph | 0.019 | 0.009 | 14.864 | 0.290 |
| “Interoute” | 0.028 | 0.016 | 15.588 | 0.397 |
Table 15.
Set families of frequent item sets.
Table 15.
Set families of frequent item sets.
| | Construction Time (s) | Traversal Time (s) |
|---|
| | Top ZDD | DenseZDD | Top ZDD | DenseZDD |
|---|
| “mushroom” | 0.093 | 0.037 | 14.100 | 0.198 |
| “retail” | 0.099 | 0.134 | 12.857 | 0.702 |
| “T40I10D100K” | 0.198 | 0.117 | 13.788 | 0.183 |
Table 16.
Families of paths in grid graph.
Table 16.
Families of paths in grid graph.
| | Construction Time (s) | Traversal Time (s) |
|---|
| | Top ZDD | DenseZDD | Top ZDD | DenseZDD |
|---|
| 0.022 | 0.011 | 15.491 | 0.793 |
| 0.082 | 0.036 | 12.039 | 1.022 |
| 0.536 | 0.153 | 12.229 | 1.144 |
| 1.821 | 0.944 | 14.233 | 1.404 |
Table 17.
Families of solutions of the n-queen problem.
Table 17.
Families of solutions of the n-queen problem.
| | Construction Time (s) | Traversal Time (s) |
|---|
| | Top ZDD | DenseZDD | Top ZDD | DenseZDD |
|---|
| 0.038 | 0.015 | 17.184 | 0.778 |
| 0.335 | 0.065 | 21.581 | 0.900 |
| 1.722 | 0.419 | 20.173 | 1.099 |