Abstract
All-optical networks transmit messages along lightpaths in which the signal is transmitted using the same wavelength in all the relevant links. We consider the problem of switching cost minimization in these networks. Specifically, the input to the problem under consideration is an optical network modeled by a graph G, a set of lightpaths modeled by paths on G, and an integer g termed the grooming factor. One has to assign a wavelength (modeled by a color) to every lightpath, so that every edge of the graph is used by at most g paths of the same color. A lightpath operating at some wavelength uses one Add/Drop multiplexer (ADM) at both endpoints and one Optical Add/Drop multiplexer (OADM) at every intermediate node, all operating at a wavelength of . Two lightpaths, both operating at the same wavelength , share the ADMs and OADMs in their common nodes. Therefore, the total switching cost due to the usage of ADMs and OADMs depends on the wavelength assignment. We consider networks of ring and path topology and a cost function that is a convex combination of the number of ADMs and the number of OADMs deployed in the network. We showed that the problem of minimizing this cost function is NP-complete for every convex combination, even in a path topology network with . On the positive side, we present a polynomial-time approximation algorithm for the problem.
1. Introduction
1.1. Background
All-optical networks are used in scientific visualization, real-time medical imaging, video conferencing, high-speed supercomputing, distributed computing, in data centers and between them [1,2]. This is due to the data rates offered by these networks which are several orders of magnitudes higher than those offered by other networks [2,3,4].
Wavelength division multiplexing: To achieve these high data rates, all-optical networks maintain the signal in optical form. In other words, they avoid the optical–electronic–optical conversion overhead at the intermediate nodes which would otherwise have an adverse effect on the transmission rate. One of the main underlying technologies is wavelength-division multiplexing, which allows for the simultaneous transmission of signals over the same link, as long as they are transmitted on different wavelengths.
Switching cost: The focus of early research on all-optical networks was to obtain efficient topologies and wavelength allocation schemes/algorithms to minimize the total number of used wavelengths. The work in [5] is an excellent survey of the main results in this direction. More recent research on these networks considers switching cost minimization as a major design goal. These works consider the capital expenses (CAPEX) and/or operational expenses (OPEX) (expenses that are independent of usage and depend on usage, respectively) incurred in all-optical networks by the basic electronic switching units, the most prominent of them being Add-Drop multiplexers (ADMs) and optical Add-Drop multiplexers (OADMs). Every lightpath is terminated by two ADMs. If two lightpaths with a common endpoint are assigned the same wavelength, they can share the ADM operating at this wavelength at the common endpoint. Similarly, two lightpaths sharing a common intermediate node that are assigned the same wavelength can share the OADM operating at that wavelength at the common node.
Grooming: Typically, the transmission rates supported by a lightpath in an all-optical network is higher than the low-capacity demands. Consequently, a network operator puts together several low-capacity demands into one lightpath. This action of putting together is termed grooming, and the number g of communication requests that can be put together in a lightpath is termed the grooming factor. The grooming problem is the problem of assigning colors (wavelengths) to a given set of paths (communication requests) so that at every edge there are at most g of them assigned the same color. If a set of (at most g) lightpaths of the same wavelength have the same terminal node and terminal edge, they can share the ADM operating at that wavelength at that node (thus saving ADMs). In addition, in a way similar to the non-grooming case (), a second set of paths with the same terminal node but a different terminal edge can share the same ADM. As for OADMs, at most g lightpaths that are assigned the same wavelength share an OADM in a common intermediate node (thus saving OADMs). The goal is to minimize the convex combination of the number of ADMs and OADMs, for a fixed value . Clearly, our setting generalizes the well-studied ADM minimization problem (corresponding to the case of ), as well as the OADM minimization one (corresponding to the case of ).
1.2. Related Work
The ADM minimization problem is defined in [6] for ring topology and . It is proven to be NP-complete in [7], and an -approximation algorithm was presented in the study [8]. This result is improved in [9,10] to and , respectively. The current best result is a -approximation [11] which states that for every there exists a -approximation algorithm whose running time is a polynomial the degree of which depends on .
The studies [7,12] consider the ADM minimization problem for general topology, and present the approximation algorithms with an approximation ratio of and , respectively. The study [13] considers non-cooperative games in which users are selfish agents sharing the cost of the ADMs they use. This study presents games that converge in a polynomial number of steps to solutions with an approximation ratio between and where k is the maximum size of a coalition formed by the agents.
The traffic grooming problem is introduced in [14] and studied in the context of ring topologies. The study in [15] shows that the ADM minimization problem is NP-complete for this topology when g is part of the input instance. In [16], it is shown that the same hardness result also holds for path and star networks, thus generalizing the result in [15]. In [17], the authors prove the NP-completeness of the problem in the strong sense, which implies the NP-completeness for bounded degree trees and directed trees.
For ring topology, a -approximation algorithm for the ADM minimization problem is presented in [18]. The running time of this algorithm, being exponential in g, yields a polynomial-time algorithm when g is fixed, i.e., not part of the input. In [19], this algorithm is extended to directed trees, and undirected trees with the bounded degree. The problem has also been studied in [20], where it is shown to be APX-complete for fixed values of g. Namely, for each of these values of g, there exists a constant such that there is no -approximation algorithm for the problem unless P = NP. The same study also presents an -approximation algorithm, where n is the number of nodes of the network. The paper [15] studies the special case of all-to-all traffic, in which there is a demand between every pair of nodes.
The minimization of hardware components in optical networks using grooming has been studied in [21] for ring networks and in [22] for star networks, in a different scenario.
1.3. Our Contribution
In this paper, we show that for every fixed , the problem of minimizing the convex combination of the total number of ADMs and OADMs is NP-complete. This hardness result holds even for chains and . Note that for , i.e., when there is no grooming, and the network is a chain, the problem can be easily solved in polynomial time. We then present an (polynomial-time) approximation algorithm for ring and chain topologies, with an approximation ratio of . Our algorithm is the first one achieving such an approximation ratio in the time polynomial in g, even for the special case of minimizing the number of ADMs. Our model allows for multisets of requests (i.e., multiple requests using the same path between the same couple of nodes).
Finally, it is worth remarking that the optimization of the network cost due to expensive hardware components (e.g., ADMs) has been widely investigated in the context of optical networks, also in papers published after the preliminary version of this one (see for instance [11,23,24,25]). Furthermore, special cases of this problem have been investigated in the context of busy time scheduling [26,27,28,29,30].
In Section 2, we formally describe the problem and introduce definitions that will be used through the paper. In Section 3, the proof of the aforementioned NP-completeness result is presented. We present and analyze the algorithms in Section 4. Section 5 is devoted to concluding comments and the discussion of some further research directions.
2. Problem Definition
Let be an undirected graph with nodes, modeling the optical network.
A coloring (or wavelength assignment) w of a set P of simple paths in a graph is a function . A coloring w of P is g-proper if for every edge and every color , the number of paths such that and e is an edge of p is at most g.
A path p of length between two nodes u and v uses an ADM operating at wavelength at each of its endpoints, namely at u and v. Moreover, such a path uses an OADM operating at wavelength at each of its intermediate nodes. Overall, such a path uses two ADMs and OADMs.
Given a g-proper coloring w of a set of paths P, an ADM operating at a wavelength at some node v may serve all the paths terminating at v and colored , provided that they enter v via at most two edges. Therefore, an may serve at most paths.
Similarly, an OADM operating at a wavelength at some node v with two incident edges serves all the paths having v as an internal node and colored . In general, i.e., when the degree of such a node v is at least three, such an OADM may serve a set of paths having v as an internal node and colored , provided that they enter and leave v via the same pair of edges. Therefore, an may serve at most g paths.
Summarizing, in a path or ring topology, the number of ADMs operating at wavelength at node v is one if there is a path colored terminating at v, and zero otherwise. The number of OADMs operating at wavelength at node v is one if there is a path colored having v as an internal node, and zero otherwise. See Figure 1 for an example.
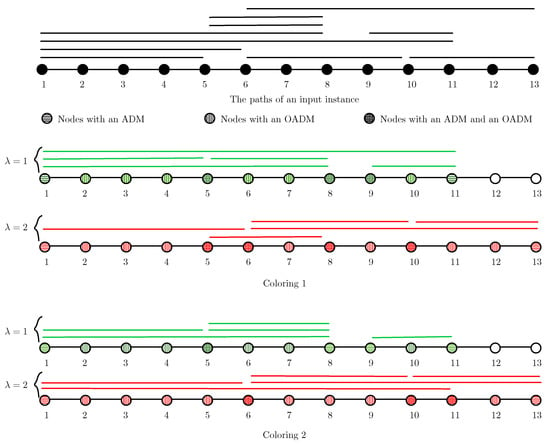
Figure 1.
An input example on a chain network with 13 nodes and at the top. Below are two possible colorings of the input paths. Both colorings use two colors. In the first coloring, the paths colored with use 5 ADMs (at nodes 1, 5, 8, 9 and 11) and 9 OADMs (at nodes 2, 3, 4, 5, 6, 7, 8, 9 and 10). The paths colored use 6 ADMs and 11 OADMs. This coloring uses 11 ADMs and 20 OADMs in total. On the other hand, the second coloring uses 10 ADMs and 18 OADMs in total.
In a general network, if the number of edges incident to v that are used by paths ending at v and colored is d, then the number of ADMs operating at wavelength at node v is . Similarly, the number of OADMs operating at wavelength at node v is equal to the number of edge pairs incident to v that are used by paths crossing v and colored . (resp. ) is the number of (resp. ) needed by a g-proper coloring w, i.e., the sum of (resp. ) over all nodes v and all colors .
We are now ready to formally define the problem under consideration.
| CombinedTrafficGrooming |
| Input: where G is a graph, P is a multiset of paths on G, g is a positive |
| integer and . |
| Output: A g-proper coloring of P. |
| Objective: Minimize . |
3. NP-Completeness
We note that Theorem 1 of [25] implies that the problem is APX-hard for . Furthermore, in this section, we prove that the decision version of CombinedTrafficGrooming is NP-complete even on a chain network with and for every . Moreover, for , i.e., for the case of ADM minimization, the problem is already known to be NP-complete (see [31]). In the following theorem, we consider the case of .
Theorem 1.
Given an instance ofCombinedTrafficGroomingfor chain topology and a real number x, the problem of deciding whether there exists a solution with a cost of at most x isNP-complete for every .
Proof.
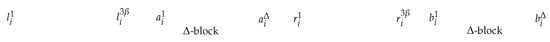
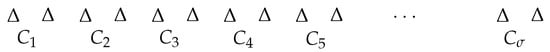
Since it can be trivially verified that the decision problem belongs to the complexity class NP, in order to prove the NP-completeness it is sufficient to provide a polynomial reduction from the TriPart problem, known to be NP-complete (see [32]).
| TriPart |
| Input: An undirected graph with and |
| Output: “YES” if there exists a partition of into triangles, “NO” otherwise. |
The TriPart problem is the problem of deciding whether for a given simple graph G, there exists a partition of its edge set into triangles. Let and be the vertex and edge sets of . Note that we can assume that the number of edges of is a multiple of 3, because otherwise a partition does not exist and the answer is trivially “NO”.
From the above instance of TriPart, we build the following instance of CombinedTrafficGrooming. For each , we add nodes to chain G, with . More precisely, we consider a subchain of nodes (see Figure 2); it is worth emphasizing that is chosen to be sufficiently big to force optimal solutions to prefer triangular sets over others, as it will be proven in the sequel. The chain G of our instance is obtained by concatenating all the subchains , (see Figure 3). Finally, we have to define the path set P. Let denote the path between u and v in G. For each with , we add the path to P.
Figure 2.
The subchain associated to node in Theorem 1.
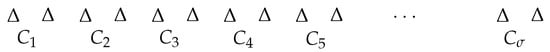
Figure 3.
The chain G with three paths corresponding to the edges of the triangle in the graph being the instance of TriPart in Theorem 1.
Since each node of G is an endpoint of at most one request in P, it holds that each solution uses exactly ADMs. Therefore, in the following, we focus only on the minimization of OADMs. In fact, let (the value of K will be chosen later). It can be noticed that there exists a solution of cost at most x if and only if there is a solution which uses a number of OADMs at most K.
Define a t-solution (where t is an integer value) as a solution using OADMs located at blocks of nodes, (i.e., the a and b nodes), in the following called -blocks. Recall that : notice that (i) it is polynomial in the size of the instance and (ii) it is sufficiently high so that the cost of a solution is mainly determined by the number of OADMs located at -blocks, that is, every t-solution uses a total number of OADMs lower than the one used by any -solution. We can conclude that a t-solution uses a total number of OADMs between and .
For each , , the number of crossed -blocks (i.e., those blocks that are completely contained in ) is . Let and .
We complete the proof by showing that a solution using at most K OADMs exists for I if and only if it is possible to partition the edge set of into triangles.
We first show that, if it is possible to partition the edge set of into triangles, then a solution using at most K OADMs exists for I. For every triangle in composed of edges , , , we consider the set of paths . Assign these paths the same color and without loss of generality, assume that is the longest path among the three. Since , it can be easily checked that such a set is 1-colorable. Moreover, the number of OADMs used at -blocks is . By summing over the sets induced by all the triangles, we obtain that the total number of OADMs used at -blocks is ; thus, we have a B-solution that can use at most K OADMs.
Conversely, we now show that, if there exists a solution for I using at most K OADMs, then it is possible to partition the edge set of into triangles. Define a component as a set of paths colored with the same color. We now show that S is a B-solution and that in a B-solution, every component is of the form with . Let us assume without loss of generality that S is using the maximum possible number of colors, that is, no set of paths colored with the same color exists, such that it can be split in two sets using two different colors without increasing the number of used OADMs. Since , each component is composed of at most two levels of requests, i.e., two sets of paths where in each set the paths are pairwise disjoint, and every OADM can be used by at most two requests. For each component C using s -blocks of OADMs, we want to distribute s among the requests belonging to C such that each request is charged with , with being the surplus of component C. First of all, notice that a component C of the desired form with , uses -blocks, and thus . The proof now proceeds by cases, considering all the possible components C not being of the desired form, and for any of them, we show that .
- Let us assume that three requests belong to a component, on the first level and and on the second one. If the ones on the second level do not correspond to consecutive edges in G, or corresponds to an edge of G that is not consecutive to both edges corresponding to the requests on the second level, C uses at least -blocks. Therefore, .
- If a component uses only one level of requests (for our assumption about the maximality of colors, in this case it can contain only a request ), it is using -blocks. Therefore, .
- If two different requests and belong to a component C, one for each level, C uses at least -blocks. Thus, .
- If requests belong to a component, at least -blocks are needed. Therefore, we obtain that .
Given that S uses at most K OADMs, by recalling the definitions of B and K, S is a t-solution with . Moreover, if there exists a component C such that , it is trivial to verify that S would be an t-solution with : we obtain a contradiction. Therefore, we have that every component is such that and thus is of the form with . □
4. Approximation Algorithms
In this section, we present and analyze the approximation algorithms for chain and ring topologies. An algorithm ALG is a -approximation algorithm for a minimization problem if, for every instance I of , its running time is polynomial in the size of I and . Here, denotes the value of the solution returned by ALG on input I and denotes the optimum of instance I. The approximation ratio of ALG is the smallest such that ALG is a -approximation algorithm.
We first present a meta algorithm that, given an r-approximation algorithm for edge instances in which all the requests share a common edge of the chain or the ring, builds an -approximation algorithm for general instances. In what remains of the section, we present two edge algorithms: the first is a two-approximation algorithm for the minimization problem, and the second one works for any linear combination of and , guaranteeing an approximation ratio of .
4.1. The Merge Meta Algorithm
Consider the following meta algorithm Merge whose pseudo-code is given in Algorithm 1. It receives an r-approximation algorithm for edge instances of CombinedTrafficGrooming and acts on an arbitrary instance of CombinedTrafficGrooming. At the first step, the set of all requests sharing the median edge of the chain are given as input to to obtain a coloring of these requests. The algorithm then splits the chain G into two sub-chains and by removing the median edge and recursively proceeds on these sub-chains. The colorings returned from the recursive invocations are modified so that they do not use the colors of .
| Algorithm 1Merge. |
| Require: is an r-approximation algorithm for edge instances of CombinedTrafficGrooming. |
| Require: an instance of CombinedTrafficGrooming. |
| Require:G is a chain with vertices . |
| Ensure: Return an -approximate solution of |
|
In ring networks, we add an initial invocation of on all the requests sharing some arbitrary edge of the ring and then proceed on the remaining chain instance.
The following theorem shows the correctness and the approximation ratio guaranteed by Merge.
Theorem 2.
If is an r-approximation algorithm for edge instances, thenMergeand its modification for ring topologies guarantee approximation ratios and , respectively.
Proof.
We prove by induction on the depth of the recursion. Correctness and running time: If there are no recursive invocations, the correctness of Merge directly follows from the one of . Otherwise, by the inductive hypothesis and by the correctness of , the colorings and are valid. The paths in and do not overlap and they are colored with colors different than those of . Therefore, the returned coloring is valid. We observe that algorithm is invoked at most n times, and thus Merge is a polynomial-time algorithm.
Approximation ratio: Since the depth of the recursion is at most , it is sufficient to prove by induction on the depth d of the recursion that is a -approximation algorithm. If , then the execution consists of one invocation of and the result follows. Otherwise, consider an execution where the depth of the recursion is . Let be the cost of an optimal solution, and let and be the cost of optimal solutions of and , respectively. Clearly, . Furthermore, since the sets and do not overlap, thus no ADM sharing or OADM sharing is possible between the instances. As for the solution of the algorithm, let m be the cost of the solution returned by Merge, and let and be the costs of and , respectively. Since is an r-approximation, we have:
By the inductive hypothesis, we have for . Summing up the inequalities, we conclude:
For ring topologies, we add an additional term of due to the initial invocation of . □
4.2. Groom-OADM: An Algorithm for the Minimization of OADMs in Edge Instances
Algorithm Groom-OADM, whose pseudo-code is given in Algorithm 2, processes the requests in the non-increasing order of their lengths and partitions the ordered requests into sets of g requests with the possible exception of the last set that may contain less than g requests. Each such set is colored with a unique color.
Lemma 1.
Groom-OADMis a two-approximation edge-algorithm for the minimization of OADMs.
Proof.
Correctness and running time: The algorithm produces a valid output since every color is assigned to at most g requests. The running time of the algorithm is dominated by the the running time of the sorting phase and is thus polynomial in the size of the instance which, in our case, is dominated by the number of requests in the instance.
Approximation ratio: Let be the number of colors used by the algorithm. Since all the requests share an edge of the chain, any one-colorable set contains at most g of them. Therefore, any solution, in particular an optimal one, uses at least k colors. Denote by the longest path of the set of the paths colored by Groom-OADM. Consider an optimal coloring, and rename its colors in the following way. The color assigned to the longest path is 0. The color assigned to the longest path that is not assigned the color 0 is 1, the color assigned to the longest path that is not assigned the colors 0 or 1 is 2, and so on. It it easy to show by induction on that for every , there is at least one path whose length is at least the length of . Therefore, an optimal solution uses at least OADMs operating at color . On the other hand, Groom-OADM uses at most OADMs since all the paths have an edge in common. Summing up, with all colors , we conclude the proof. □
In the following, we exploit the result of Lemma 1 in order to obtain an approximation algorithm for the CombinedTrafficGrooming problem. By combining Lemma 1 with Theorem 2, we are also able to derive the following theorem providing an approximation algorithm for the case ; moreover, it is worth noticing that a better approximation ratio of 4 is given in [28] for this particular case.
| Algorithm 2Groom-OADM. |
| Require: is an edge instance of CombinedTrafficGrooming. |
| Ensure: Return an two-approximate solution of : |
|
Theorem 3.
Merge(Groom-OADM)is a (and, respectively, ) approximation algorithm forCombinedTrafficGroomingin a chain (and, respectively, ring) topology with , (i.e., for the problem of minimizing the number of OADMs).
4.3. Groom: An Algorithm for Edge Instance of CombinedTrafficGrooming
Algorithm Groom is obtained from Groom-OADM with a slight modification. In the sort phase in which the paths are sorted by their lengths, Groom keeps sets of identical paths together.
Lemma 2.
Groomis a -approximation edge-algorithm forCombinedTrafficGrooming.
Proof.
Clearly, every execution of Groom is an execution of Groom-OADM. Therefore, by Lemma 1, Groom is a two-approximation edge-algorithm for the OADM minimization problem. In the following, we show that Groom is a -approximation algorithm for the ADM minimization problem. As the combined cost is a convex combination of ADM and OADM costs, this implies the Lemma.
Let be the number of colors used by some optimal solution. For , let be the set of paths colored by this solution. Notice that (where ⊎ is the union operation on multisets). Let be such that from every set of identical paths of , exactly one is in . Let also: .
Recall that we consider edge instances, in which all the paths share a common edge e. Every path has one endpoint at each side of e. Then, any subset of paths can be considered as the edge set of a bipartite graph . Specifically, U (resp. V) is the set of nodes on the left (resp. right) of e (including one endpoint of e). Every path of P with endpoints and corresponds to an edge . As does not contain identical paths, it induces a simple bipartite graph. A simple bipartite graph satisfies . For fixed this is maximized when . Therefore, the number of ADMs colored used by this solution satisfies . Then, .
By summing up over all colors, we obtain
Let W be the number of colors used by the solution returned by Groom. For , let be the set of paths colored by this solution. Notice that, also in this case, it clearly holds that . Let be such that from each (maximal) set of identical paths, exactly one path is in . Let also .
Consider a maximal nonempty set X of identical paths. Any solution must use at least different colors for these paths. In particular, this holds for our optimal solution. In other words, . Groom divides X into subsets of size g, except possibly the first and last sets. Therefore, . Summing up for all such sets X, we obtain . On the other hand, a solution returned by Groom, uses at most 2 ADMs per each path in . The remaining paths use these ADMs at no additional cost. Therefore, the number of ADMs used by Groom satisfy . □
The following theorem is a direct consequence of the previous Lemma and Theorem 2.
Theorem 4.
Merge(Groom)is a (and, respectively ) approximation algorithm forCombinedTrafficGroomingin chain (and, respectively, ring) topology.
5. Summary
In this paper, we investigated the problem of minimizing hardware cost in optical networks in the scenario in which at most g (g is the grooming factor) lightpaths can share the same color on any network edge. It is worth noticing that, while most previous work takes into account only the cost due to electronic components (i.e., ADMs), we focused on the combined cost due to ADMs and optical components (OADMs). In particular, we considered the cost function of , where , and we have studied the fundamental topologies of ring and chain networks.
We showed that finding an optimal coloring, i.e., a coloring minimizing the considered cost function, is NP-complete even on chains and when the grooming factor is , for any value of . We then presented a general technique that, given an r-approximation algorithm working on particular instances of our problem (i.e., instances in which all requests share a same edge of the network), builds a new algorithm for general instances having an approximation ratio . We exploited this technique in order to obtain an -approximation algorithms for our problem.
It is worth noticing that our approximation ratio of is better than the trivial one (which has a factor) in case . Moreover, our algorithm has the following interesting property: the returned solution simultaneously achieves the claimed approximation ratio with respect to every fixed value of .
There are several interesting left open problems:
- Strengthening the -completeness result, either towards the direction of proving an -hardness result or towards an impossibility of a sub-exponential algorithm under the exponential time hypothesis (, introduced in [33]). In this respect, it is worth noting that the current reduction cannot be exploited in order to obtain these extensions. In particular, with respect to the former direction, the considered TriPart problem is a decision problem and it is worth investigating whether a related optimization problem could be exploited in order to prove the -hardness. On the other hand, with respect to the latter direction, even if TriPart were to be proven to admit no sub-exponential algorithm under the ETH, our reduction builds an instance of CombineTrafficGrooming of quadratic size with respect to the one of TriPart and therefore would not be able to provide a similar result for CombineTrafficGrooming.
- Improving the achieved approximation ratio for the considered topologies of ring and chain networks.
- Extending the algorithm and the analysis to other network topologies.
- Considering the online version of the problem in which lightpath requests are not given in advance but arrive over time.
Author Contributions
Formal analysis, M.F., G.M., L.M., M.S. and S.Z.; Writing—original draft, G.M., L.M. and M.S.; Writing—review & editing, M.F., G.M., L.M., M.S. and S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Du, D.H.C.; Vetter, R.J. Distributed computing with high-speed optical networks. Computer 1993, 26, 8–18. [Google Scholar]
- Green, P.E. Fiber-Optic Communication Networks; Prentice Hall: Hoboken, NJ, USA, 1992. [Google Scholar]
- Brackett, C.A. Dense Wavelength Division Multiplexing Networks: Principles and applications. IEEE J. Sel. Areas Commun. 1990, 8, 948–964. [Google Scholar] [CrossRef]
- Klasing, R. Methods and problems of wavelength-routing in all-optical networks. In Proceedings of the MFCS’98 Workshop on Communication, Brno, Czech Republic, 24–25 August 1998; pp. 1–9. [Google Scholar]
- Beauquier, B.; Bermond, J.C.; Gargano, L.; Hell, P.; Perennes, S.; Vaccaro, U. Graph problems arising from Wavelength–Routing in All–Optical Networks. In Proceedings of the 2nd Workshop on Optics and Computer Science, WOCS’97, Geneva, Switzerland, 1 April 1997. [Google Scholar]
- Gerstel, O.; Lin, P.; Sasaki, G. Wavelength Assignment in a WDM Ring to Minimize Cost of Embedded SONET Rings. In Proceedings of the INFOCOM’98, Seventeenth Annual Joint Conference of the IEEE Computer and Communications Societies, San Francisco, CA, USA, 29 March–2 April 1998. [Google Scholar]
- Eilam, T.; Moran, S.; Zaks, S. Lightpath Arrangement in Survivable Rings to Minimize the Switching Cost. IEEE J. Sel. Area Commun. 2002, 20, 172–182. [Google Scholar] [CrossRef]
- Călinescu, G.; Wan, P.J. Traffic Partition in WDM/SONET rings to minimize SONET ADMs. J. Comb. Optim. 2002, 6, 425–453. [Google Scholar] [CrossRef]
- Shalom, M.; Zaks, S. A 10/7 + epsilon approximation for minimizing the number of ADMs in SONET rings. IEEE/ACM Trans. Netw. 2007, 15, 1593–1602. [Google Scholar] [CrossRef]
- Epstein, L.; Levin, A. Better bounds for minimizing SONET ADMs. J. Comput. Syst. Sci. 2009, 75, 122–136. [Google Scholar] [CrossRef]
- Epstein, L.; Levin, A.; Menahem, B. Minimization of SONET ADMs in ring networks revisited. Computing 2010, 87, 3–19. [Google Scholar] [CrossRef]
- Călinescu, G.; Frieder, O.; Wan, P.J. Minimizing Electronic Line Terminals for Automatic Ring Protection in General WDM Optical Networks. IEEE J. Sel. Area Commun. 2002, 20, 183–189. [Google Scholar] [CrossRef]
- Flammini, M.; Monaco, G.; Moscardelli, L.; Shalom, M.; Zaks, S. Selfishness, collusion and power of local search for the ADMs minimization problem. Comput. Netw. 2008, 52, 1721–1731. [Google Scholar] [CrossRef]
- Gerstel, O.; Ramaswami, R.; Sasaki, G. Cost effective traffic grooming in WDM rings. In Proceedings of the INFOCOM’98, Seventeenth Annual Joint Conference of the IEEE Computer and Communications Societies, San Francisco, CA, USA, 29 March–2 April 1998. [Google Scholar]
- Chiu, A.L.; Modiano, E.H. Traffic Grooming Algorithms for Reducing Electronic Multiplexing Costs in WDM Ring Networks. J. Light. Technol. 2000, 18, 2–12. [Google Scholar] [CrossRef]
- Huang, S.; Dutta, R.; Rouskas, G.N. Traffic grooming in path, star, and tree networks: Complexity, bounds, and algorithms. IEEE J. Sel. Areas Commun. 2006, 24, 66–82. [Google Scholar] [CrossRef]
- Shalom, M.; Unger, W.; Zaks, S. On the Complexity of the Traffic Grooming Problem in Optical Networks. In Proceedings of the Fun with Algorithms, 4th International Conference, Castiglioncello, Italy, 3–5 June 2007; pp. 262–271. [Google Scholar]
- Flammini, M.; Moscardelli, L.; Shalom, M.; Zaks, S. Approximating the Traffic Grooming Problem. J. Discret. Algorithms 2008, 6, 472–479. [Google Scholar] [CrossRef]
- Flammini, M.; Monaco, G.; Moscardelli, L.; Shalom, M.; Zaks, S. Approximating the traffic grooming problem in tree and star networks. J. Parallel Distrib. Comput. 2008, 68, 939–948. [Google Scholar] [CrossRef]
- Amini, O.; Pérennes, S.; Sau, I. Hardness and approximation of traffic grooming. Theor. Comput. Sci. 2009, 410, 3751–3760. [Google Scholar] [CrossRef]
- Chen, B.; Rouskas, G.N.; Dutta, R. Traffic Grooming in WDM Ring Networks with the Min-Max Objective. In Networking 2004, Proceedings of the International Conference on Research in Networking, Athens, Greece, 9–14 May 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 174–185. [Google Scholar]
- Chen, B.; Rouskas, G.N.; Dutta, R. Traffic Grooming in Star Networks. In Proceedings of the BROADNETS, San Jose, CA, USA, 25–29 October 2004. [Google Scholar]
- Flammini, M.; Marchetti-Spaccamela, A.; Monaco, G.; Moscardelli, L.; Zaks, S. On the complexity of the regenerator placement problem in optical networks. IEEE/ACM Trans. Netw. 2011, 19, 498–511. [Google Scholar] [CrossRef]
- Flammini, M.; Monaco, G.; Moscardelli, L.; Shalom, M.; Zaks, S. Optimizing regenerator cost in traffic grooming. Theor. Comput. Sci. 2011, 412, 7109–7121. [Google Scholar] [CrossRef]
- Flammini, M.; Monaco, G.; Moscardelli, L.; Shalom, M.; Zaks, S. On the Complexity of the Regenerator Cost Problem in General Networks with Traffic Grooming. Algorithmica 2014, 68, 671–691. [Google Scholar] [CrossRef]
- Koehler, F.; Khuller, S. Busy Time Scheduling on a Bounded Number of Machines (Extended Abstract). In Algorithms and Data Structures; Ellen, F., Kolokolova, A., Sack, J.R., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 521–532. [Google Scholar]
- Chang, J.; Khuller, S.; Mukherjee, K. LP rounding and combinatorial algorithms for minimizing active and busy time. J. Sched. 2017, 20, 657–680. [Google Scholar] [CrossRef]
- Flammini, M.; Monaco, G.; Moscardelli, L.; Shachnai, H.; Shalom, M.; Tamir, T.; Zaks, S. Minimizing total busy time in parallel scheduling with application to optical networks. Theor. Comput. Sci. 2010, 411, 3553–3562. [Google Scholar] [CrossRef]
- Mertzios, G.B.; Shalom, M.; Voloshin, A.; Wong, P.W.; Zaks, S. Optimizing busy time on parallel machines. Theor. Comput. Sci. 2015, 562, 524–541. [Google Scholar] [CrossRef]
- Khandekar, R.; Schieber, B.; Shachnai, H.; Tamir, T. Real-time scheduling to minimize machine busy times. J. Sched. 2015, 18, 561–573. [Google Scholar] [CrossRef]
- Winkler, P.; Zhang, L. Wavelength assignment and generalized interval graph coloring. In Proceedings of the SODA, Baltimore, MD, USA, 12–14 January 2003; pp. 830–831. [Google Scholar]
- Dor, D.; Tarsi, M. Graph Decomposition Is NP-Complete: A Complete Proof Of Holyer’s Conjecture. SIAM J. Comput. 1997, 26, 1166–1187. [Google Scholar] [CrossRef]
- Impagliazzo, R.; Paturi, R. On the Complexity of k-SAT. J. Comput. Syst. Sci. 2001, 62, 367–375. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).