Median Filter Aided CNN Based Image Denoising: An Ensemble Approach
Abstract
1. Introduction
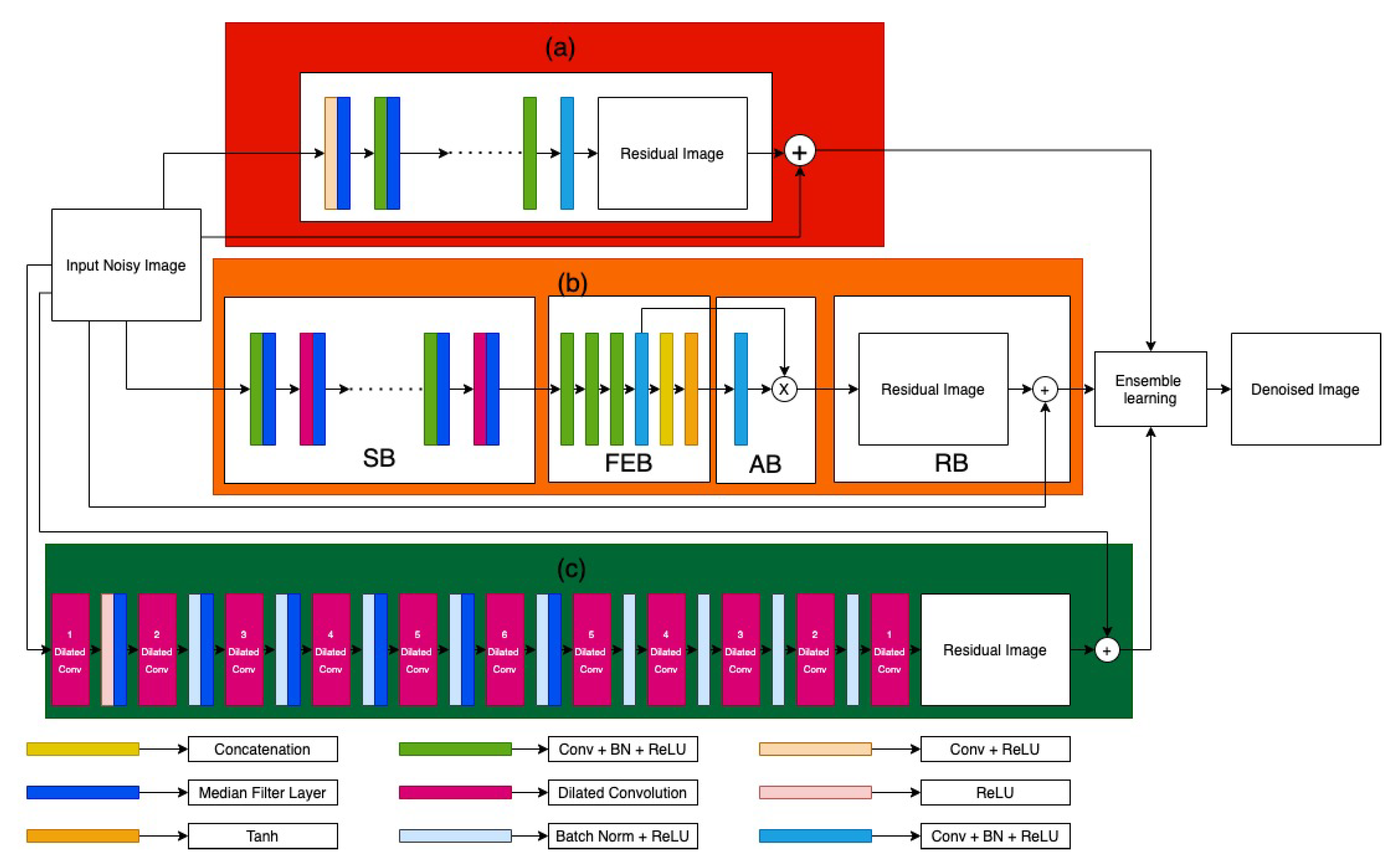
- Median filter layers are added to ADNet [4] up to the Sparse Block or SB along with a dilation rate of 8.
- Dilated convolutional layers are used in IRCNN [5] up to a dilation rate of 6, along with median filter layers for it.
- Median Filter layers are added up to half of the convolutional layers in DnCNN [6].
- An ensemble of the said models is formed and proposed by using weighted average of the output of each model in order to generate the final denoised image. We take th part of ADNet output,th part of IRCNN model and th part of DnCNN model.
2. Related Work
3. Proposed Work
3.1. Attention-Guided CNN (ADNet)
3.2. Feed Forward Denoising CNN (DnCNN)
3.3. Deep CNN Denoiser Prior (IRCNN)
3.4. Ensemble of Image Denoising Models
4. Experimental Results
4.1. Dataset
4.2. Hyperparameters
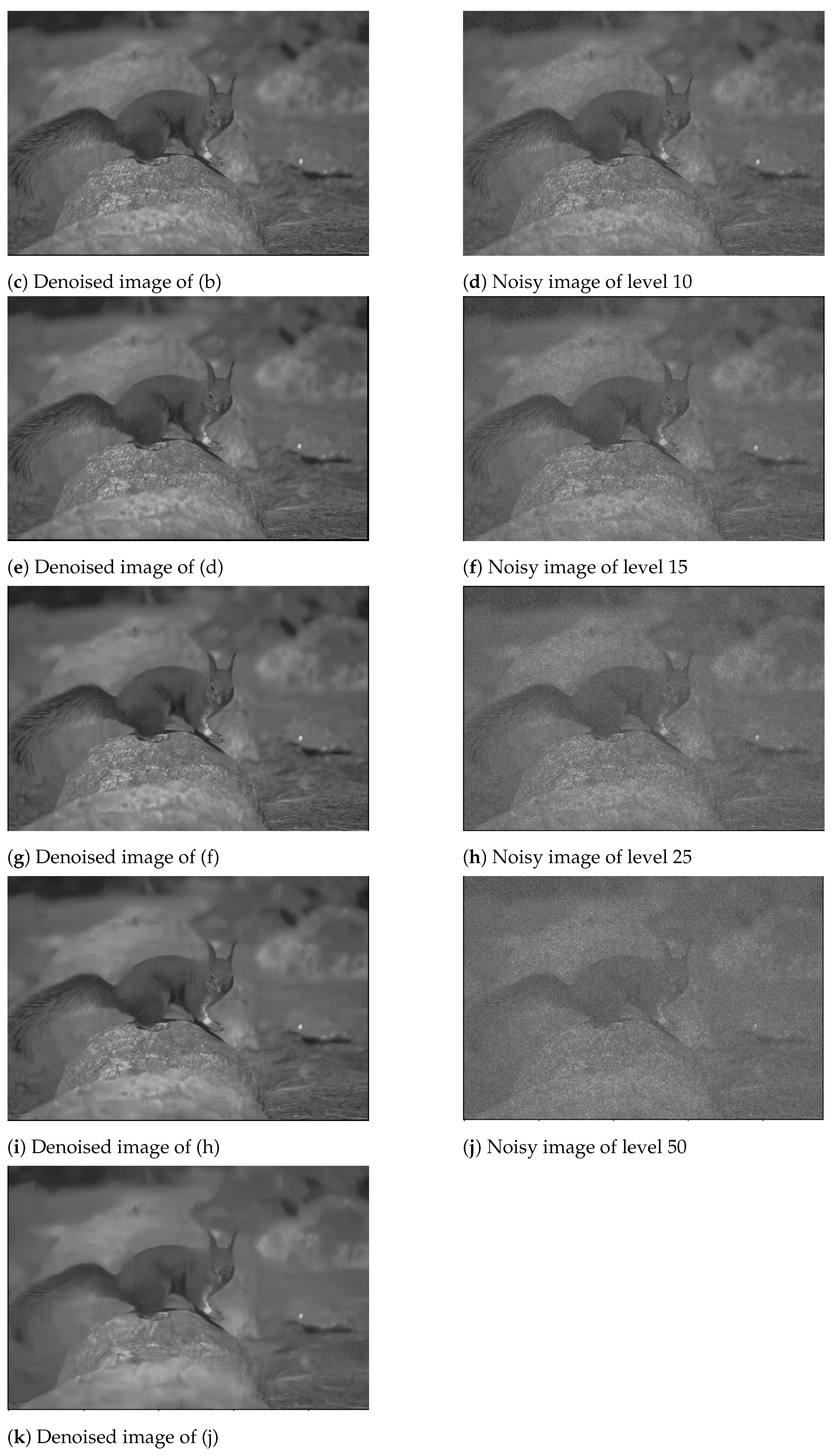
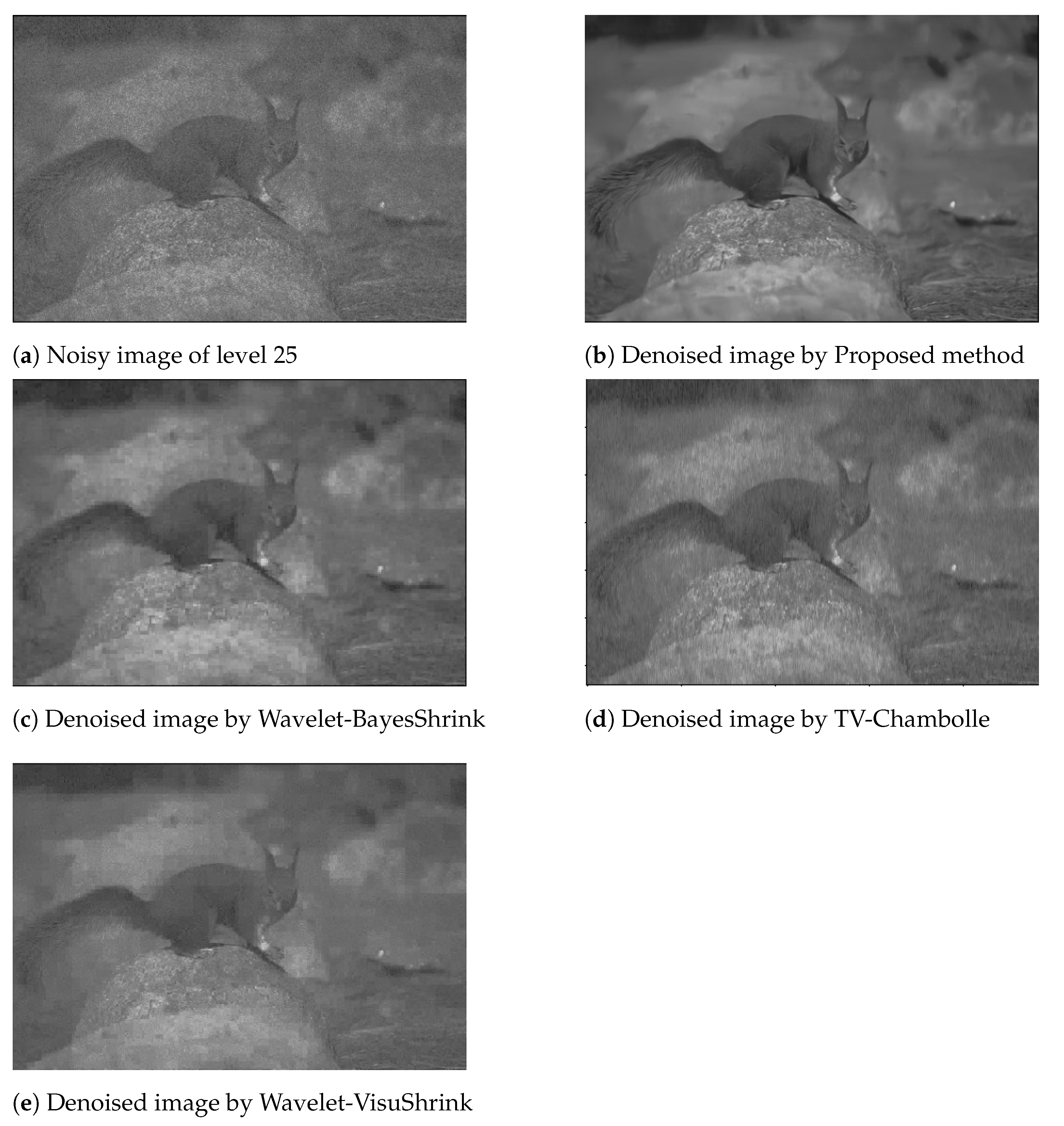
4.3. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kortli, Y.; Jridi, M.; Al Falou, A.; Atri, M. Face recognition systems: A Survey. Sensors 2020, 20, 342. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Malakar, S.; Ghosh, S.; Bhowmik, S.; Sarkar, R. Understanding contents of filled-in Bangla form images. Multimed. Tools Appl. 2020, 80, 3529–3570. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Tian, C.; Xu, Y.; Li, Z.; Zuo, W.; Fei, L.; Liu, H. Attention-guided CNN for image denoising. Neural Netw. 2020, 124, 117–129. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zuo, W.; Gu, S.; Zhang, L. Learning deep CNN denoiser prior for image restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3929–3938. [Google Scholar]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef]
- Pitas, I.; Venetsanopoulos, A. Nonlinear mean filters in image processing. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 573–584. [Google Scholar] [CrossRef]
- Hong, S.W.; Bao, P. An edge-preserving subband coding model based on non-adaptive and adaptive regularization. Image Vis. Comput. 2000, 18, 573–582. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, J.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Chang, S.G.; Yu, B.; Vetterli, M. Adaptive wavelet thresholding for image denoising and compression. IEEE Trans. Image Process. 2000, 9, 1532–1546. [Google Scholar] [CrossRef]
- Chambolle, A. An algorithm for total variation minimization and applications. J. Math. Imaging Vis. 2004, 20, 89–97. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef]
- Schmidt, U.; Roth, S. Shrinkage fields for effective image restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2774–2781. [Google Scholar]
- Chiang, Y.W.; Sullivan, B. Multi-frame image restoration using a neural network. In Proceedings of the IEEE 32nd Midwest Symposium on Circuits and Systems, Champaign, IL, USA, 14–16 August 1989; pp. 744–747. [Google Scholar]
- Zhou, Y.; Chellappa, R.; Jenkins, B. A novel approach to image restoration based on a neural network. In Proceedings of the International Conference on Neural Networks, San Diego, CA, USA, 21–24 June 1987. [Google Scholar]
- Mao, X.J.; Shen, C.; Yang, Y.B. Image restoration using convolutional auto-encoders with symmetric skip connections. arXiv 2016, arXiv:1606.08921. [Google Scholar]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image restoration. IEEE Trans. Pattern Anal. Mach. Intell. 2020. [Google Scholar] [CrossRef]
- Le Cun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; Volume 1, p. 9. [Google Scholar]
- Lefkimmiatis, S. Non-local color image denoising with convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3587–3596. [Google Scholar]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a fast and flexible solution for CNN-based image denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Chen, J.; Chao, H.; Yang, M. Image blind denoising with generative adversarial network based noise modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3155–3164. [Google Scholar]
- Guo, S.; Yan, Z.; Zhang, K.; Zuo, W.; Zhang, L. Toward convolutional blind denoising of real photographs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1712–1722. [Google Scholar]
- Liang, L.; Deng, S.; Gueguen, L.; Wei, M.; Wu, X.; Qin, J. Convolutional Neural Network with Median Layers for Denoising Salt-and-Pepper Contaminations. arXiv 2019, arXiv:1908.06452. [Google Scholar]
- Kirti, T.; Jitendra, K.; Ashok, S. Poisson noise reduction from X-ray images by region classification and response median filtering. Sādhanā 2017, 42, 855–863. [Google Scholar] [CrossRef]
- Islam, M.T.; Rahman, S.M.; Ahmad, M.O.; Swamy, M. Mixed Gaussian-impulse noise reduction from images using convolutional neural network. Signal Process. Image Commun. 2018, 68, 26–41. [Google Scholar] [CrossRef]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision. ICCV 2001, Vancouver, BC, Canada, 7–14 July 2001; Volume 2, pp. 416–423. [Google Scholar]
- Vvan der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. Scikitimage contributors. 2014. scikit-image: Image processing in python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef] [PubMed]


| Models | Noise Level 15 | Noise Level 25 | Noise Level 50 |
|---|---|---|---|
| TV-Chambolle [11] | 24.37 | 22.34 | 18.33 |
| Wavelet-VisuShrink [9] | 21.38 | 19.78 | 16.99 |
| Wavelet-BayesShrink [10] | 25.05 | 22.40 | 18.19 |
| ADNet model | 31.55 | 28.87 | 25.90 |
| IRCNN-model | 31.56 | 28.94 | 25.93 |
| DnCNN-model | 31.64 | 28.85 | 26.08 |
| ADNet(dilation rate = 8) + median layer | 31.63 | 29.12 | 25.98 |
| IRCNN-model (dilation upto 6) + median layer | 31.60 | 29.08 | 26.08 |
| DnCNN+ median layer | 31.66 | 29.08 | 26.10 |
| Ensemble-model | 31.73 | 29.20 | 26.20 |
| Denoising Models | 01. | 02. | 03. | 04. | 05. | 06. | 07. | 08. | 09. | 10. | 11. | 12. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Noise level of 15 | ||||||||||||
| TV-Chambolle [11] | 23.54 | 24.69 | 23.58 | 22.56 | 22.62 | 22.79 | 22.47 | 25.58 | 23.00 | 24.36 | 24.62 | 24.01 |
| Wavelet-VisuShrink [9] | 19.77 | 22.32 | 19.11 | 18.81 | 18.05 | 19.28 | 18.81 | 21.94 | 19.82 | 20.95 | 21.20 | 20.93. |
| Wavelet-BayesShrink [10] | 23.40 | 26.07 | 23.76 | 23.10 | 22.82 | 23.20 | 23.15 | 26.21 | 23.19 | 24.75 | 25.16 | 24.56. |
| ADNet | 32.36 | 34.46 | 33.08 | 31.80 | 32.64 | 31.58 | 31.73 | 34.12 | 31.56 | 32.16 | 32.20 | 32.12 |
| IRCNN-model | 32.40 | 34.44 | 33.07 | 31.73 | 32.65 | 31.55 | 31.75 | 34.14 | 31.82 | 32.20 | 32.21 | 32.12 |
| DnCNN-model | 32.56 | 34.66 | 33.24 | 32.00 | 32.85 | 31.66 | 31.80 | 34.28 | 32.07 | 32.28 | 32.30 | 32.25 |
| ADNet + median layer | 32.45 | 34.60 | 33.11 | 31.87 | 32.70 | 31.62 | 31.70 | 34.22 | 31.73 | 32.23 | 32.25 | 32.22 |
| IRCNN-model + median layer | 32.41 | 34.52 | 33.03 | 31.70 | 32.60 | 31.55 | 31.70 | 34.18 | 31.80 | 32.21 | 32.20 | 32.17 |
| DnCNN + median layer | 32.56 | 34.75 | 33.24 | 31.93 | 32.66 | 31.67 | 31.75 | 34.31 | 32.11 | 32.26 | 32.31 | 32.27 |
| Ensemble method | 32.60 | 34.78 | 33.27 | 32.00 | 32.81 | 31.71 | 31.84 | 34.35 | 32.13 | 32.32 | 32.34 | 32.30 |
| Noise level of 25 | ||||||||||||
| TV-Chambolle [11] | 19.89 | 20.72 | 20.20 | 19.75 | 19.77 | 19.96 | 19.32 | 21.10 | 20.14 | 20.54 | 20.85 | 20.48. |
| Wavelet-VisuShrink [9] | 18.11 | 20.66 | 17.60 | 17.49 | 16.34 | 18.04 | 16.95 | 20.14 | 18.43 | 19.59 | 19.74 | 19.67. |
| Wavelet-BayesShrink [10] | 20.91 | 23.78 | 21.07 | 20.94 | 20.52 | 20.90 | 20.30 | 24.12 | 21.44 | 22.75 | 23.25 | 22.62. |
| ADNet | 29.87 | 32.36 | 30.50 | 29.03 | 29.84 | 28.90 | 29.14 | 31.80 | 29.07 | 29.81 | 29.71 | 29.68 |
| IRCNN-model | 29.77 | 32.33 | 30.46 | 28.93 | 29.75 | 28.83 | 29.20 | 31.85 | 29.00 | 29.84 | 29.78 | 29.63 |
| DnCNN-model | 30.05 | 32.70 | 30.77 | 29.15 | 30.03 | 29.02 | 29.28 | 32.07 | 29.21 | 29.98 | 29.90 | 29.84 |
| ADNet + median layer | 30.04 | 32.60 | 30.64 | 29.26 | 29.98 | 28.98 | 29.30 | 32.04 | 29.14 | 30.00 | 29.90 | 29.82 |
| IRCNN-model + median layer | 29.98 | 32.57 | 30.65 | 29.13 | 29.90 | 28.90 | 29.22 | 32.05 | 28.70 | 29.92 | 29.86 | 29.81 |
| DnCNN + median layer | 30.03 | 32.73 | 30.76 | 29.16 | 29.47 | 29.04 | 28.81 | 32.09 | 29.35 | 30.02 | 29.93 | 29.88 |
| Ensemble method | 30.15 | 32.80 | 30.80 | 29.31 | 29.94 | 29.09 | 29.23 | 32.17 | 29.45 | 30.10 | 29.98 | 30.00 |
| Noise level of 50 | ||||||||||||
| TV-Chambolle [11] | 14.59 | 15.21 | 14.98 | 14.73 | 14.83 | 14.67 | 14.38 | 15.27 | 14.93 | 15.13 | 15.14 | 15.10. |
| Wavelet-VisuShrink [9] | 16.04 | 18.40 | 15.79 | 15.63 | 14.73 | 15.73 | 14.67 | 17.65 | 16.18 | 17.68 | 17.42 | 17.85. |
| Wavelet-BayesShrink [10] | 17.40 | 20.02 | 18.02 | 17.30 | 17.07 | 17.05 | 16.56 | 20.12 | 18.38 | 19.50 | 19.61 | 19.71. |
| ADNet | 26.87 | 29.37 | 27.03 | 25.38 | 26.27 | 25.63 | 25.97 | 28.74 | 25.43 | 26.89 | 26.87 | 26.51 |
| IRCNN-model | 26.90 | 29.51 | 27.17 | 25.40 | 26.43 | 25.68 | 26.08 | 29.00 | 25.58 | 26.98 | 27.01 | 26.56 |
| DnCNN-model | 27.10 | 29.56 | 27.23 | 25.47 | 26.47 | 25.72 | 26.24 | 28.97 | 25.53 | 27.03 | 27.02 | 26.67 |
| ADNet + median layer | 26.85 | 29.45 | 27.04 | 25.41 | 26.38 | 25.56 | 26.00 | 28.86 | 25.57 | 26.90 | 25.90 | 26.64 |
| IRCNN-model + median layer | 26.93 | 29.55 | 27.22 | 25.47 | 26.37 | 25.76 | 26.00 | 29.07 | 25.78 | 27.08 | 27.05 | 26.74 |
| DnCNN + median layer | 27.11 | 29.65 | 27.20 | 25.47 | 26.47 | 25.72 | 26.16 | 28.97 | 25.54 | 27.05 | 27.02 | 26.70 |
| Ensemble method | 27.17 | 29.80 | 27.30 | 25.56 | 26.60 | 25.78 | 26.26 | 29.11 | 25.73 | 27.12 | 27.09 | 26.81 |
| End of Table | ||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dey, S.; Bhattacharya, R.; Schwenker, F.; Sarkar, R. Median Filter Aided CNN Based Image Denoising: An Ensemble Approach. Algorithms 2021, 14, 109. https://doi.org/10.3390/a14040109
Dey S, Bhattacharya R, Schwenker F, Sarkar R. Median Filter Aided CNN Based Image Denoising: An Ensemble Approach. Algorithms. 2021; 14(4):109. https://doi.org/10.3390/a14040109
Chicago/Turabian StyleDey, Subhrajit, Rajdeep Bhattacharya, Friedhelm Schwenker, and Ram Sarkar. 2021. "Median Filter Aided CNN Based Image Denoising: An Ensemble Approach" Algorithms 14, no. 4: 109. https://doi.org/10.3390/a14040109
APA StyleDey, S., Bhattacharya, R., Schwenker, F., & Sarkar, R. (2021). Median Filter Aided CNN Based Image Denoising: An Ensemble Approach. Algorithms, 14(4), 109. https://doi.org/10.3390/a14040109







