Integrated Simulation-Based Optimization of Operational Decisions at Container Terminals
Abstract
1. Introduction
1.1. Literature Review on Integrated Decision Problems
1.2. Optimizing Objective Functions without Mathematical Optimization
1.3. Relationship between Hyper-Parameter Optimization and Simulation-Based Optimization
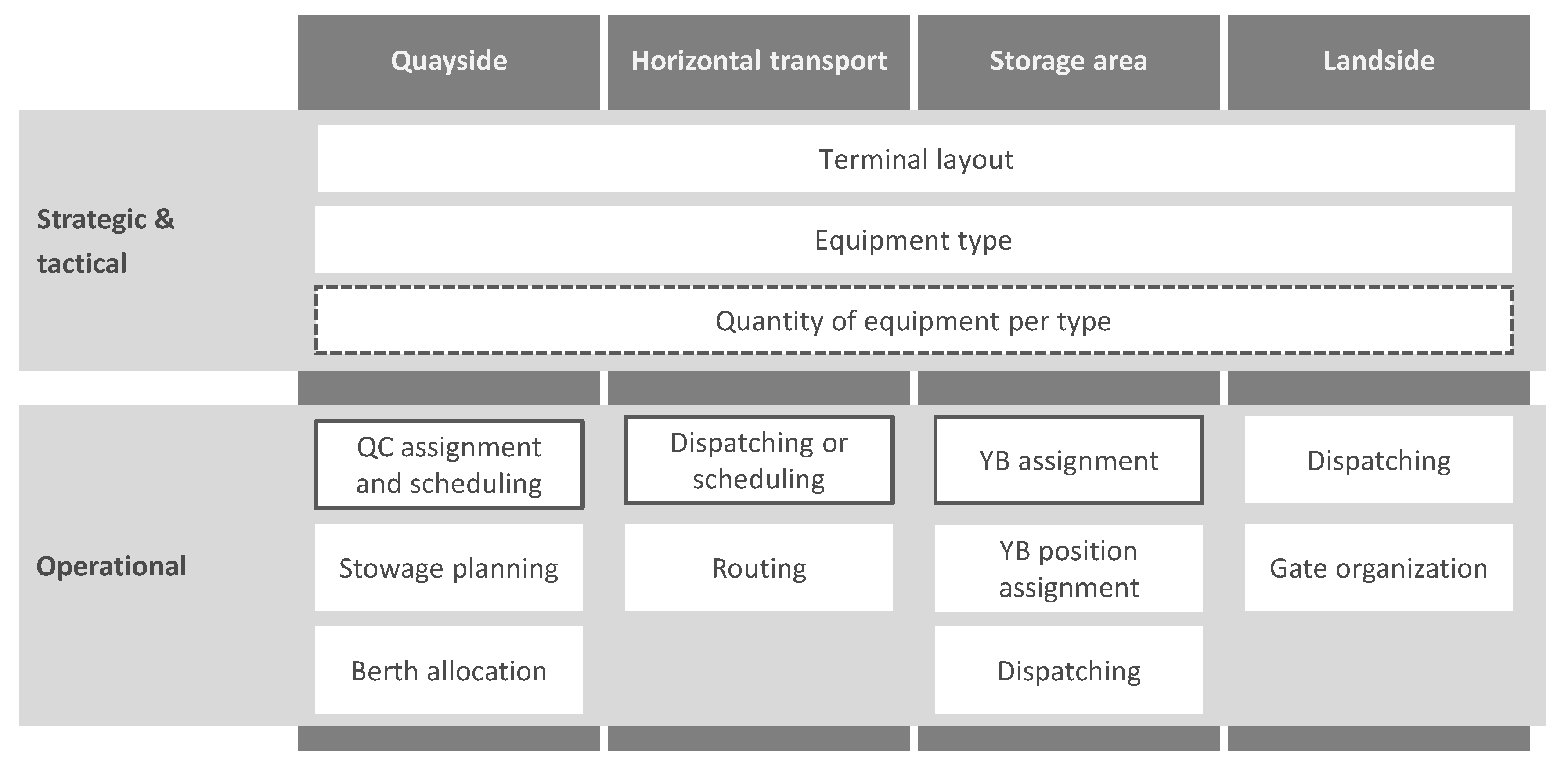
2. Materials and Methods
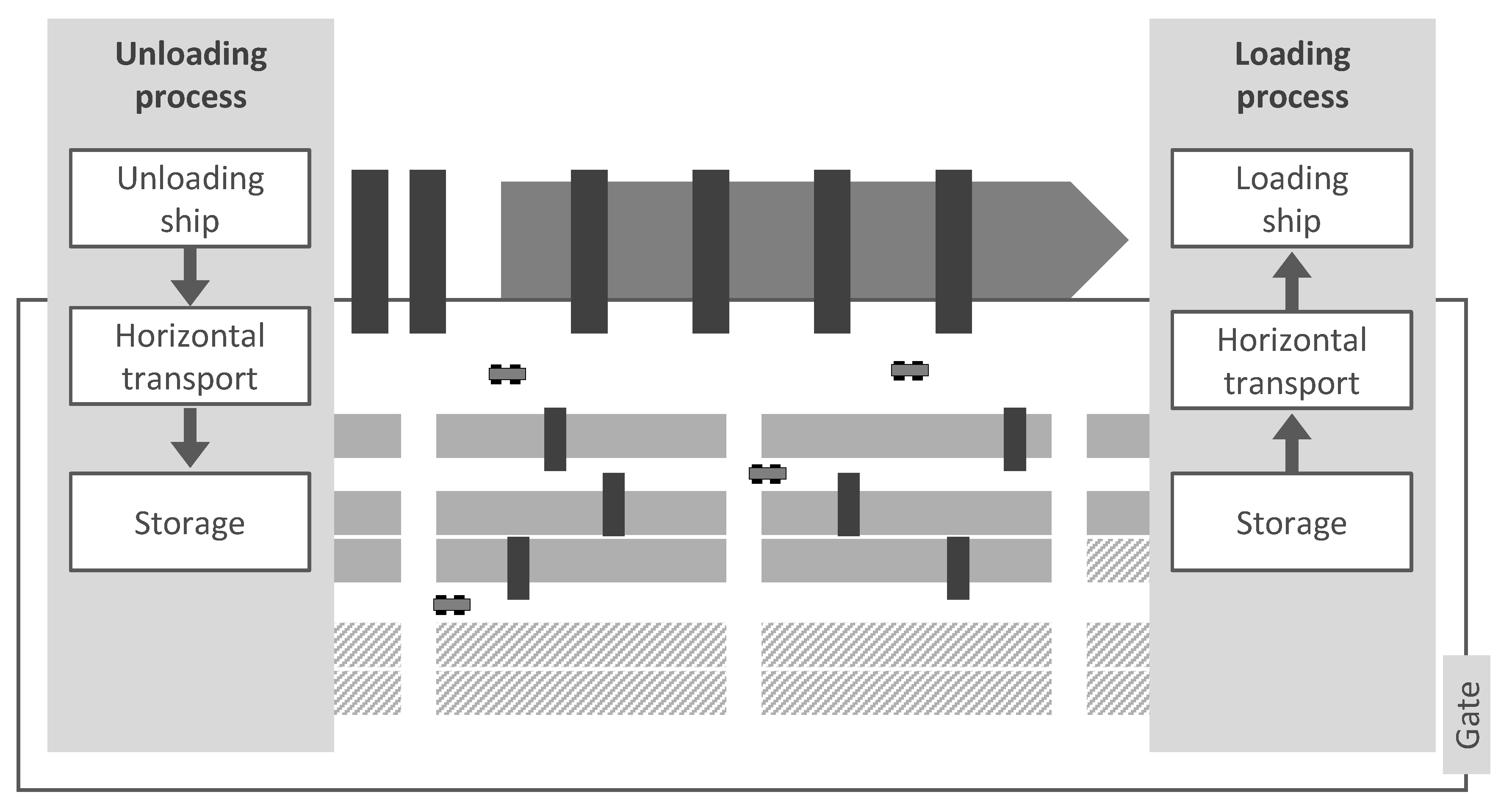
2.1. Simulation Model
2.2. Employed Meta-Heuristics
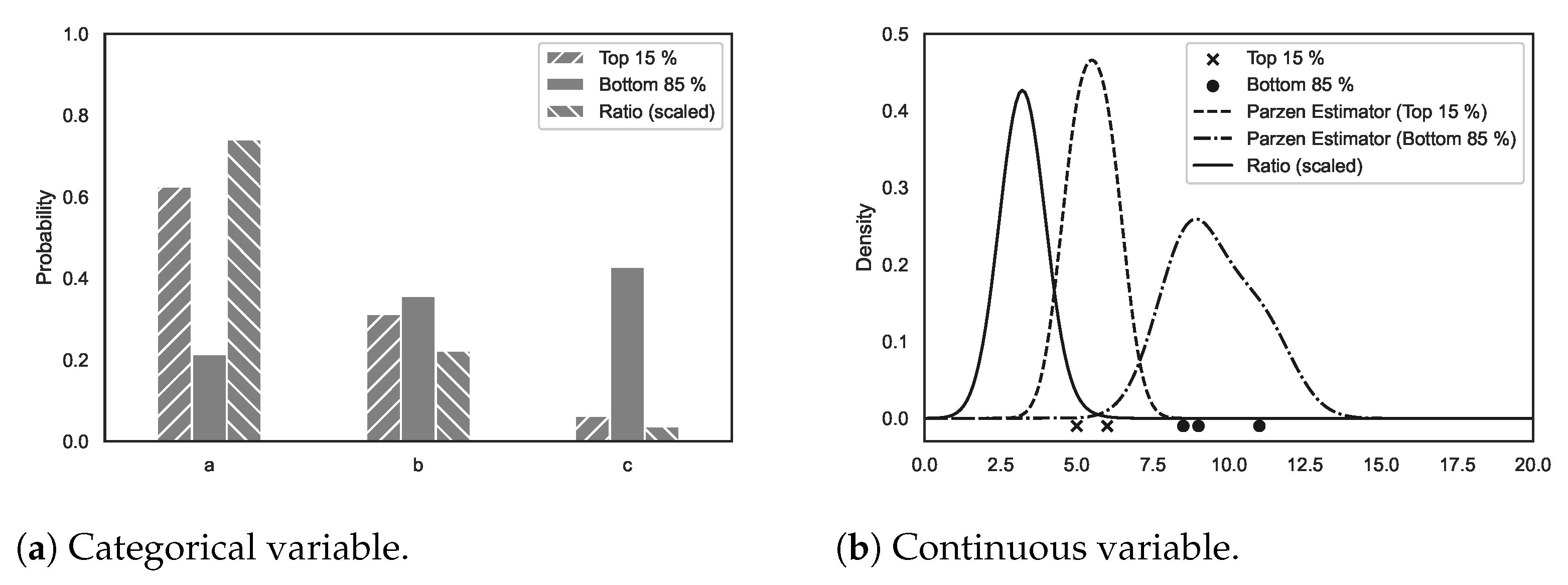
2.2.1. Tree-Structured Parzen Estimator
2.2.2. Simulated Annealing
2.2.3. Bayesian Optimization
2.2.4. Random Search
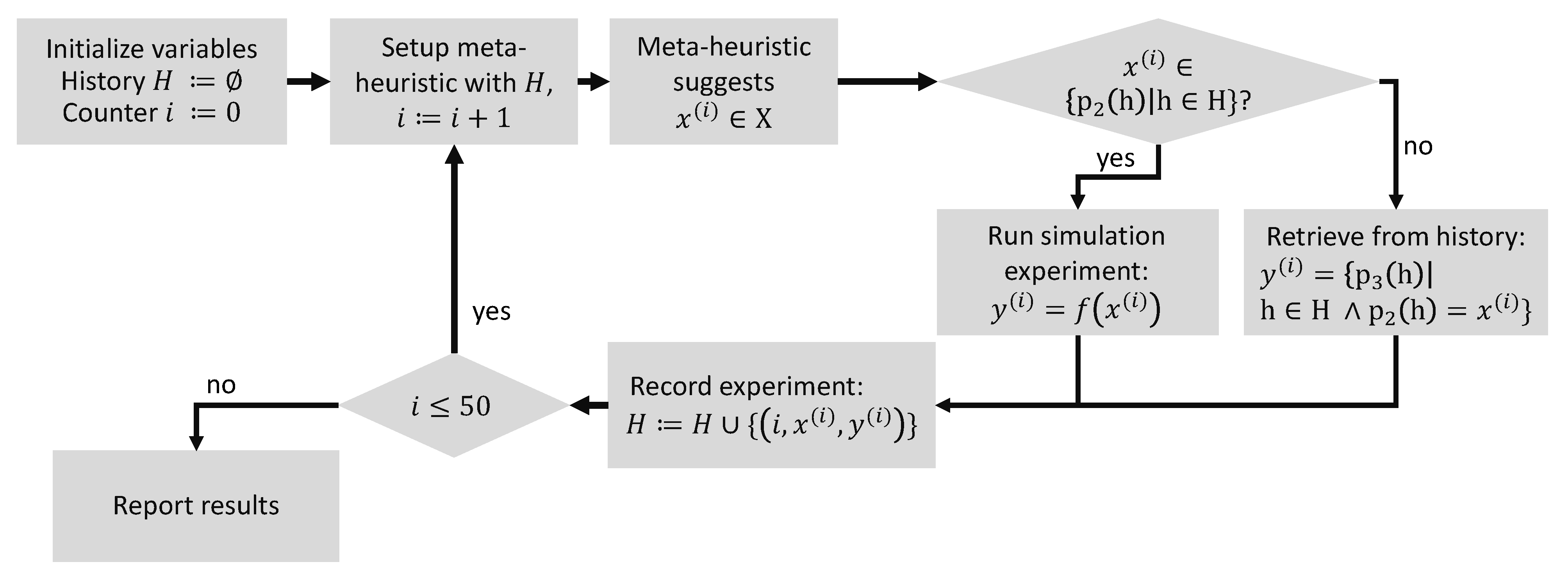
2.3. Optimization Procedure
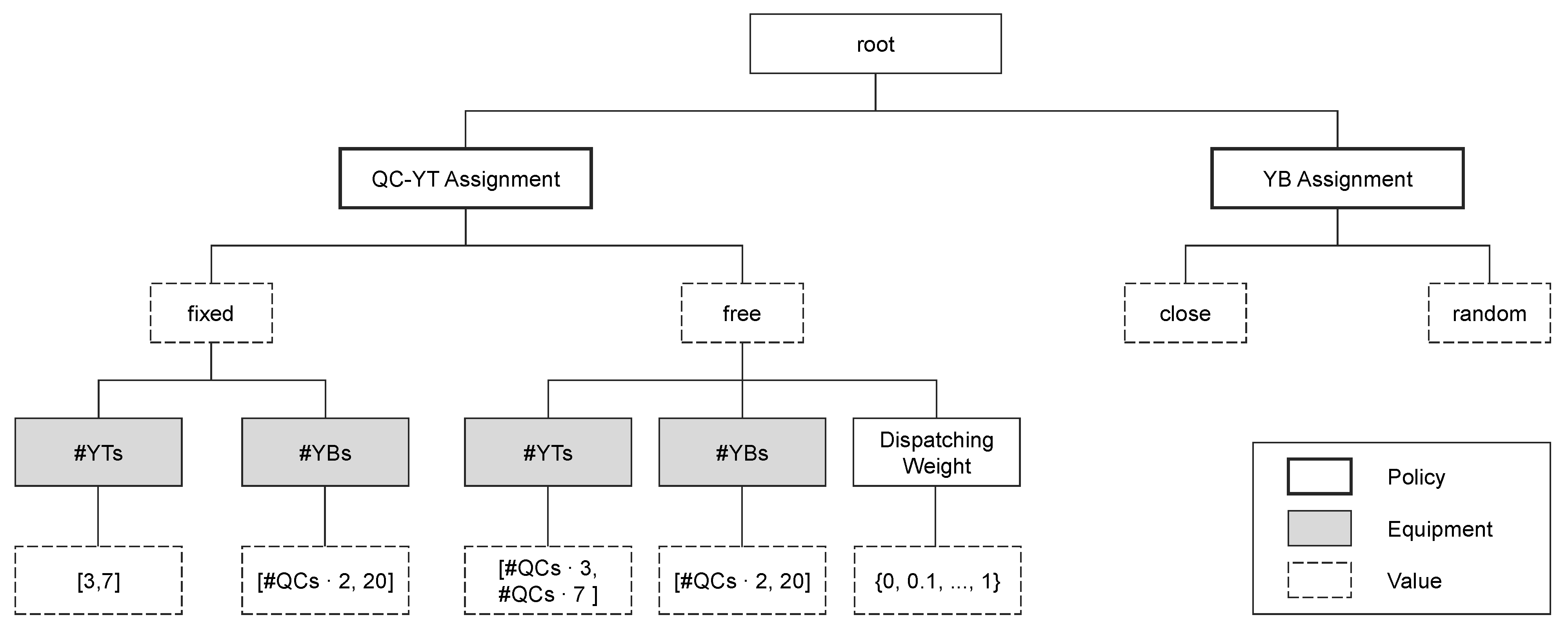
2.3.1. Parameter Configuration Space
2.3.2. Objective Function
2.3.3. Structure of Optimization Study
3. Results and Discussion
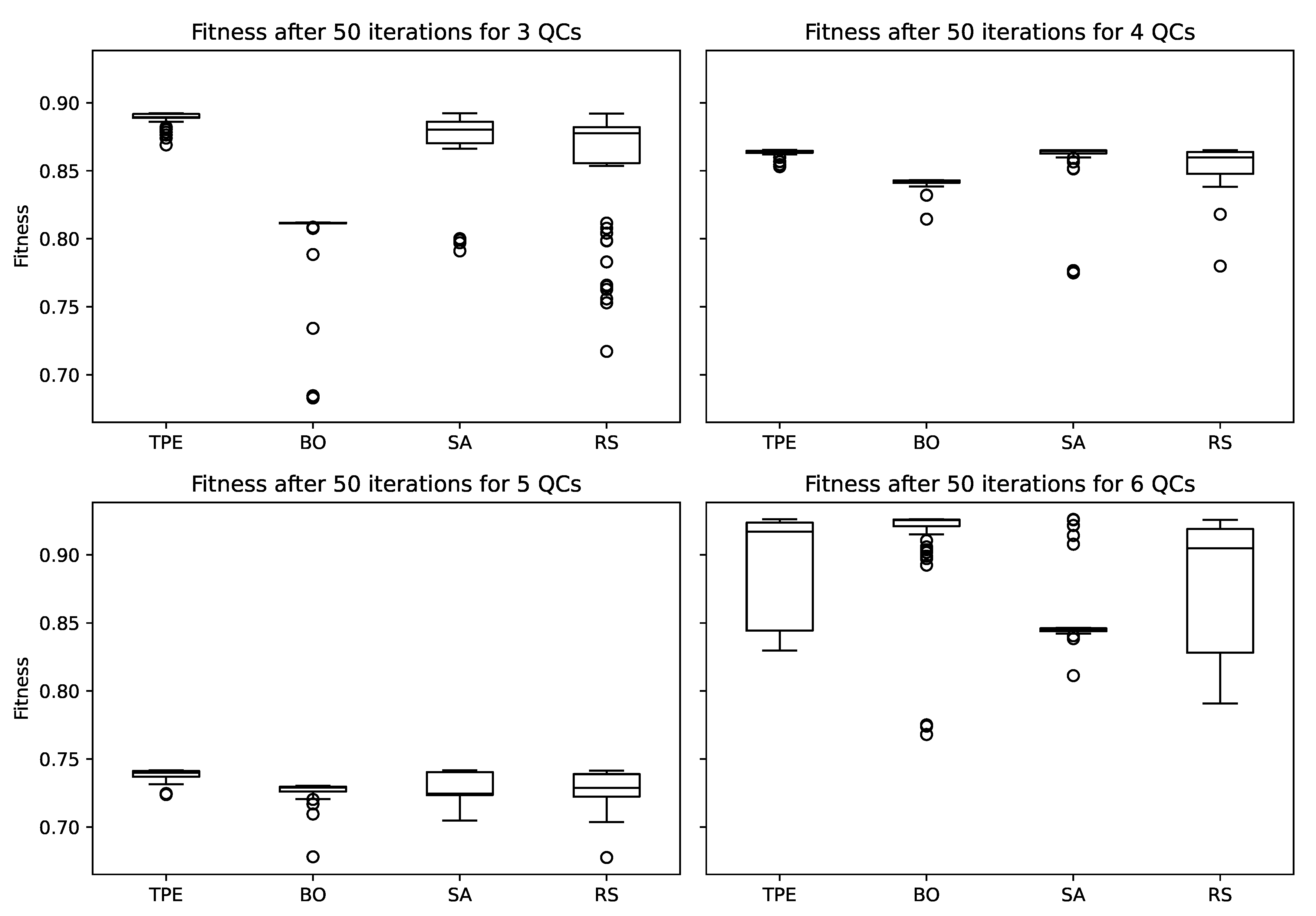
3.1. Preparatory Study
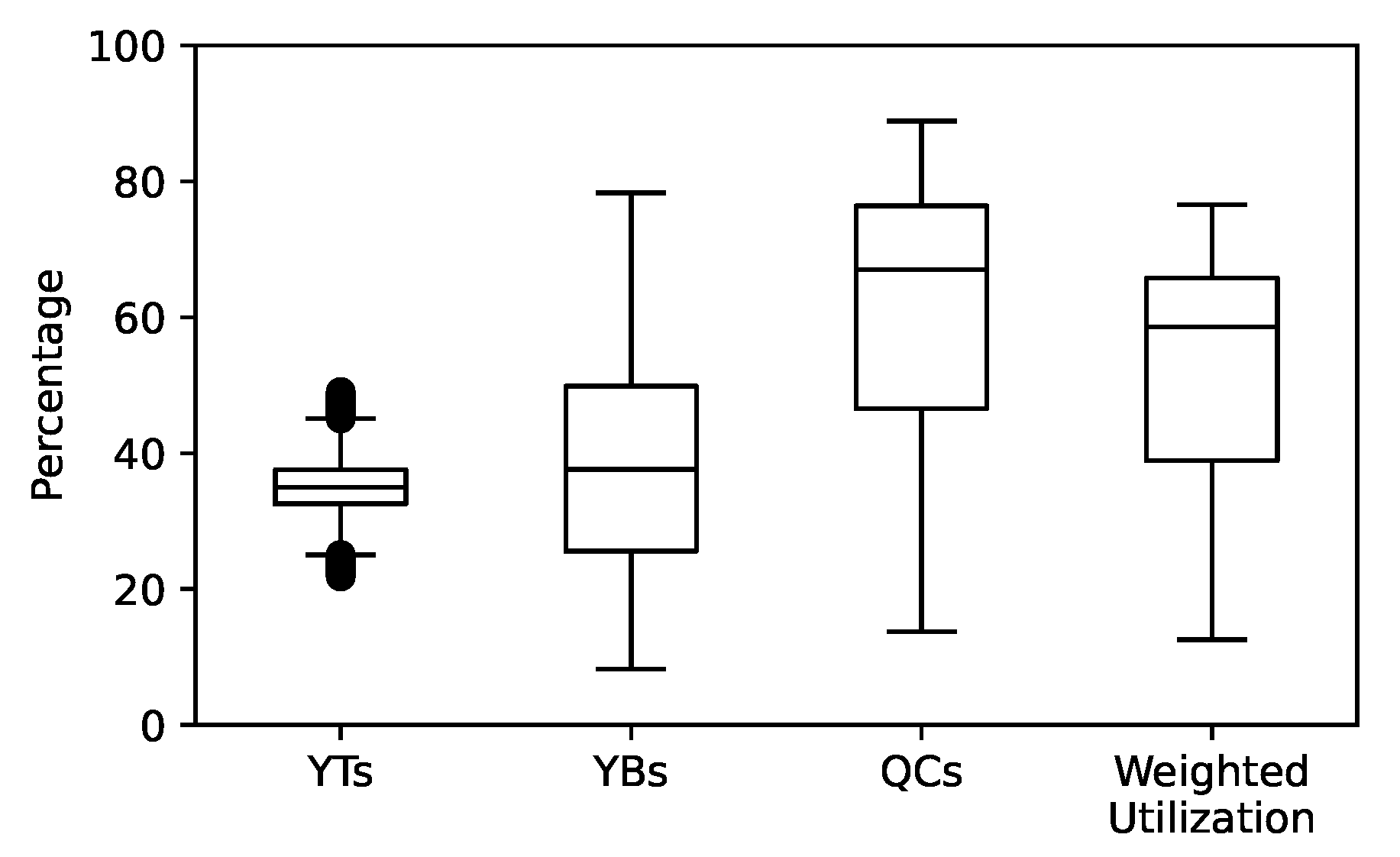
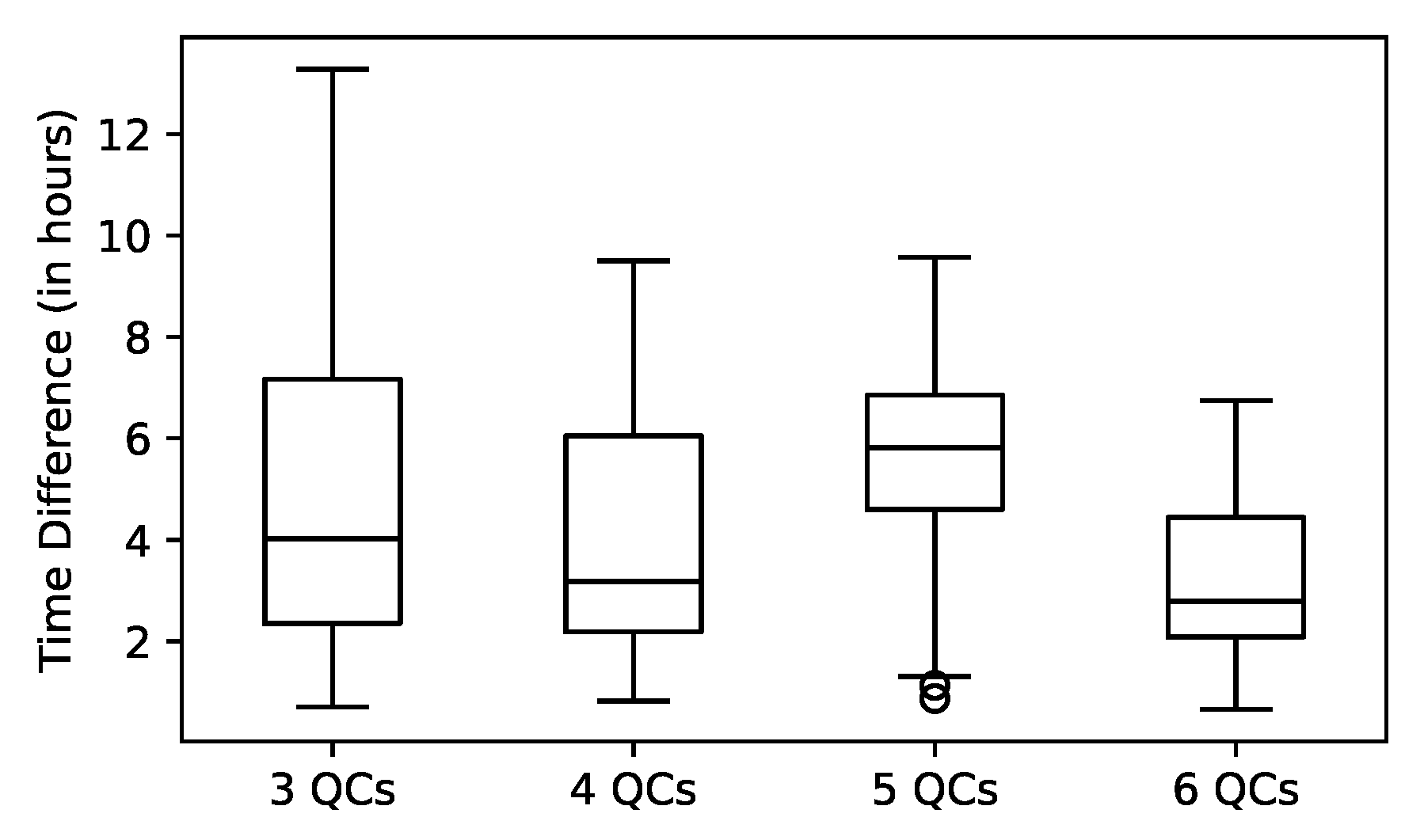
3.2. Observations from All Experiments
3.3. Approximated Optima
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BO | Bayesian Optimization |
| NFLT | No Free Lunch Theorem |
| QC | Quay Crane |
| RS | Random Search |
| RTG | Rubber-tired Gantry Crane |
| SA | Simulated Annealing |
| TPE | Tree-structured Parzen Estimator |
| TEU | Twenty-foot Equivalent Unit |
| YB | Yard Block |
| YT | Yard Truck |
References
- UNCTAD. Review of Maritime Transport; United Nations: New York, NY, USA, 2020. [Google Scholar]
- Karam, A.; Eltawil, A.; Harraz, N. Simultaneous assignment of quay cranes and internal trucks in container terminals. Int. J. Ind. Syst. Eng. 2016, 24, 107–125. [Google Scholar] [CrossRef]
- Gharehgozli, A.; Zaerpour, N.; de Koster, R. Container terminal layout design: Transition and future. Marit. Econ. Logist. 2020, 22, 610–639. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A follow-up survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2015, 244, 675–689. [Google Scholar] [CrossRef]
- Kizilay, D.; Eliiyi, D.T. A comprehensive review of quay crane scheduling, yard operations and integrations thereof in container terminals. Flex. Serv. Manuf. J. 2020, 1, 1–42. [Google Scholar] [CrossRef]
- Chen, L.; Langevin, A.; Lu, Z. Integrated scheduling of crane handling and truck transportation in a maritime container terminal. Eur. J. Oper. Res. 2013, 225, 142–152. [Google Scholar] [CrossRef]
- Lange, A.K.; Schwientek, A.K.; Jahn, C. Reducing truck congestion at ports—Classification and trends. Digitalization in Maritime and Sustainable Logistics. In Proceedings of the Hamburg International Conference of Logistics (HICL); Jahn, C., Kersten, W., Ringle, C.M., Eds.; Epubli: Berlin, Germany, 2017; pp. 37–58. [Google Scholar]
- Cordeau, J.F.; Legato, P.; Mazza, R.M.; Trunfio, R. Simulation-based optimization for housekeeping in a container transshipment terminal. Comput. Oper. Res. 2015, 53, 81–95. [Google Scholar] [CrossRef]
- Dragovic, B.; Tzannatos, E.; Park, N.K. Simulation modelling in ports and container terminals: Literature overview and analysis by research field, application area and tool. Flex. Serv. Manuf. J. 2017, 29, 4–34. [Google Scholar] [CrossRef]
- Angeloudis, P.; Bell, M.G. A review of container terminal simulation models. Marit. Policy Manag. 2011, 38, 523–540. [Google Scholar] [CrossRef]
- Schwientek, A.K.; Lange, A.K.; Jahn, C. Effects of terminal size, yard block assignment, and dispatching methods on container terminal performance. In Winter Simulation Conference 2020; Bae, K.H., Feng, B., Kim, S., Zheng, Z., Roeder, T., Thiesing, R., Eds.; IEEE Press: New York, NY, USA, 2020. [Google Scholar]
- Zhen, L.; Yu, S.; Wang, S.; Sun, Z. Scheduling quay cranes and yard trucks for unloading operations in container ports. Ann. Oper. Res. 2016, 122, 21. [Google Scholar] [CrossRef]
- He, J.; Huang, Y.; Yan, W.; Wang, S. Integrated internal truck, yard crane and quay crane scheduling in a container terminal considering energy consumption. Expert Syst. Appl. 2015, 42, 2464–2487. [Google Scholar] [CrossRef]
- Cao, P.; Jiang, G.; Huang, S.; Ma, L. Integrated simulation and optimisation of scheduling yard crane and yard truck in loading operation. Int. J. Shipp. Transp. Logist. 2020, 12, 230–250. [Google Scholar] [CrossRef]
- Castilla-Rodríguez, I.; Expósito-Izquierdo, C.; Melián-Batista, B.; Aguilar, R.M.; Moreno-Vega, J.M. Simulation-optimization for the management of the transshipment operations at maritime container terminals. Expert Syst. Appl. 2020, 139, 112852. [Google Scholar] [CrossRef]
- Kizilay, D.; Eliiyi, D.T.; van Hentenryck, P. Constraint and mathematical programming models for integrated port container terminal operations. Integration of Constraint Programming, Artificial Intelligence, and Operations Research. Lect. Notes Comput. Sci. 2018, 10848, 344–360. [Google Scholar] [CrossRef]
- Karam, A.; Eltawil, A.; Hegner Reinau, K. Energy-Efficient and Integrated Allocation of Berths, Quay Cranes, and Internal Trucks in Container Terminals. Sustainability 2020, 12, 3202. [Google Scholar] [CrossRef]
- Karam, A.; Eltawil, A. Functional integration approach for the berth allocation, quay crane assignment and specific quay crane assignment problems. Comput. Ind. Eng. 2016, 102, 458–466. [Google Scholar] [CrossRef]
- Sislioglu, M.; Celik, M.; Ozkaynak, S. A simulation model proposal to improve the productivity of container terminal operations through investment alternatives. Marit. Policy Manag. 2019, 46, 156–177. [Google Scholar] [CrossRef]
- Muravev, D.; Rakhmangulov, A.; Hu, H.; Zhou, H. The introduction to system dynamics approach to operational efficiency and sustainability of dry port’s main parameters. Sustainability 2019, 11, 2413. [Google Scholar] [CrossRef]
- Muravev, D.; Hu, H.; Rakhmangulov, A.; Mishkurov, P. Multi-agent optimization of the intermodal terminal main parameters by using AnyLogic simulation platform: Case study on the Ningbo-Zhoushan Port. Int. J. Inf. Manag. 2020, 1, 102133. [Google Scholar] [CrossRef]
- Kastner, M.; Pache, H.; Jahn, C. Simulation-based optimization at container terminals: A literature review. In Digital Transformation in Maritime and City Logistics, Proceedings of the Hamburg International Conference of Logistics (HICL); Jahn, C., Kersten, W., Ringle, C.M., Eds.; Epubli GmbH: Berlin, Germany, 2019; pp. 111–135. [Google Scholar] [CrossRef]
- Zhou, C.; Li, H.; Liu, W.; Stephen, A.; Lee, L.H.; Peng Chew, E. Challenges and opportunities in integration of simulation and optimization in maritime logistics. In Proceedings of the 2018 Winter Simulation Conference, Gothenburg, Sweden, 9–12 December 2018; pp. 2897–2908. [Google Scholar] [CrossRef]
- Kastner, M.; Nellen, N.; Jahn, C. Model-based optimisation with tree-structured parzen estimation for container terminals. In ASIM 2019 Simulation in Produktion und Logistik 2019; Putz, M., Schlegel, A., Eds.; Wissenschaftliche Scripten: Auerbach, Germany, 2019; pp. 489–498. [Google Scholar]
- Singgih, I.K.; Jin, X.; Hong, S.; Kim, K.H. Architectural design of terminal operating system for a container terminal based on a new concept. Ind. Eng. Manag. Syst. 2016, 15, 278–288. [Google Scholar] [CrossRef][Green Version]
- Schwientek, A. Abilities of the Used Terminal Operating Systems: Personal Conversation, 2012–2013.
- Barton, R.R. Simulation experiment design. In Proceedings of the 2010 Winter Simulation Conference, Piscataway, NJ, USA, 5–8 December 2010; pp. 75–86. [Google Scholar] [CrossRef]
- Li, H.; Zhou, C.; Lee, B.K.; Lee, L.H.; Chew, E.P.; Goh, R.S.M. Capacity planning for mega container terminals with multi-objective and multi-fidelity simulation optimization. IISE Trans. 2017, 49, 849–862. [Google Scholar] [CrossRef]
- Al-Salem, M.; Almomani, M.; Alrefaei, M.; Diabat, A. On the optimal computing budget allocation problem for large scale simulation optimization. Simul. Model. Pract. Theory 2017, 71, 149–159. [Google Scholar] [CrossRef]
- Ho, Y.C.; Zhao, Q.C.; Jia, Q.S. (Eds.) Ordinal Optimization: Soft Optimization for Hard Problems; Springer: New York, NY, USA, 2007. [Google Scholar]
- Xu, J.; Huang, E.; Chen, C.H.; Lee, L.H. Simulation optimization: A review and exploration in the new era of cloud computing and big data. Asia-Pac. J. Oper. Res. 2015, 32, 1–34. [Google Scholar] [CrossRef]
- Fu, M.C.; Glover, F.W.; April, J. Simulation optimization: A review, new developments, and applications. In Proceedings of the 2005 Winter Simulation Conference, Orlando, FL, USA, 4–7 December 2005; pp. 351–380. [Google Scholar]
- Figueira, G.; Almada-Lobo, B. Hybrid simulation–optimization methods: A taxonomy and discussion. Simul. Model. Pract. Theory 2014, 46, 118–134. [Google Scholar] [CrossRef]
- Hanschke, T.; Krug, W.; Nickel, S.; Zisgen, H. VDI 3633 Blatt 12 - Simulation und Optimierung. In VDI-Handbuch Fabrikplanung und -Betrieb-Band 2: Modellierung und SIMULATION; Beuth: Berlin, Germany, 2016. [Google Scholar]
- Juan, A.A.; Faulin, J.; Grasman, S.E.; Rabe, M.; Figueira, G. A review of simheuristics: Extending metaheuristics to deal with stochastic combinatorial optimization problems. Oper. Res. Perspect. 2015, 2, 62–72. [Google Scholar] [CrossRef]
- Chopard, B.; Tomassini, M. An Introduction to Metaheuristics for Optimization, 1st ed.; Natural Computing Series; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Kotachi, M.; Rabadi, G.; Seck, M.; Msakni, M.K.; Al-Salem, M.; Diabat, A. Sequence-based simulation optimization: An application to container terminals. In Proceedings of the 2018 IEEE Technology & Engineering Management Conference, Piscataway, NJ, USA, 27 June–1 July 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, 2nd ed.; O’Reilly UK Ltd.: Newton, MA, USA, 2019. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential model-based optimization for general algorithm configuration. In Learning and Intelligent Optimization; Coello, C.A.C., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 507–523. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Proceedings of the 25th Annual Conference on Neural Information Processing Systems, Granada, Spain, 12–14 December 2011; Volume 24, pp. 2546–2554. [Google Scholar]
- Eggensperger, K.; Feurer, M.; Hutter, F.; Bergstra, J.; Snoek, J.; Hoos, H.; Leyton-Brown, K. Towards an empirical foundation for assessing Bayesian optimization of hyperparameters. In Proceedings of the NIPS Workshop on Bayesian Optimization in Theory and Practice, Lake Tahoe, NV, USA, 10 December 2013; pp. 1–5. [Google Scholar]
- Madrigal, F.; Maurice, C.; Lerasle, F. Hyper-parameter optimization tools comparison for multiple object tracking applications. Mach. Vis. Appl. 2019, 30, 269–289. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Gijsbers, P.; LeDell, E.; Poirier, S.; Thomas, J.; Bischl, B.; Vanschoren, J. An open source AutoML benchmark. In Proceedings of the 6th ICML Workshop on Automated Machine Learning, Long Beach, CA, USA, 14–15 June 2019. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- McDermott, J. When and why metaheuristics researchers can ignore “No Free Lunch” theorems. Metaheuristics 2019, 1, 67. [Google Scholar] [CrossRef]
- Bergstra, J.; Yamins, D.; Cox, D.D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 115–123. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Bergstra, J. Simulated Annealing. Available online: https://github.com/hyperopt/hyperopt/blob/master/hyperopt/anneal.py (accessed on 29 December 2020).
- Močkus, J. On Bayesian methods for seeking the extremum. In Optimization Techniques IFIP Technical Conference; Springer: Berlin/Heidelberg, Germany, 1975; pp. 400–404. [Google Scholar]
- The GPyOpt Authors. GPyOpt: A Bayesian Optimization Framework in Python. Available online: http://github.com/SheffieldML/GPyOpt (accessed on 29 December 2020).
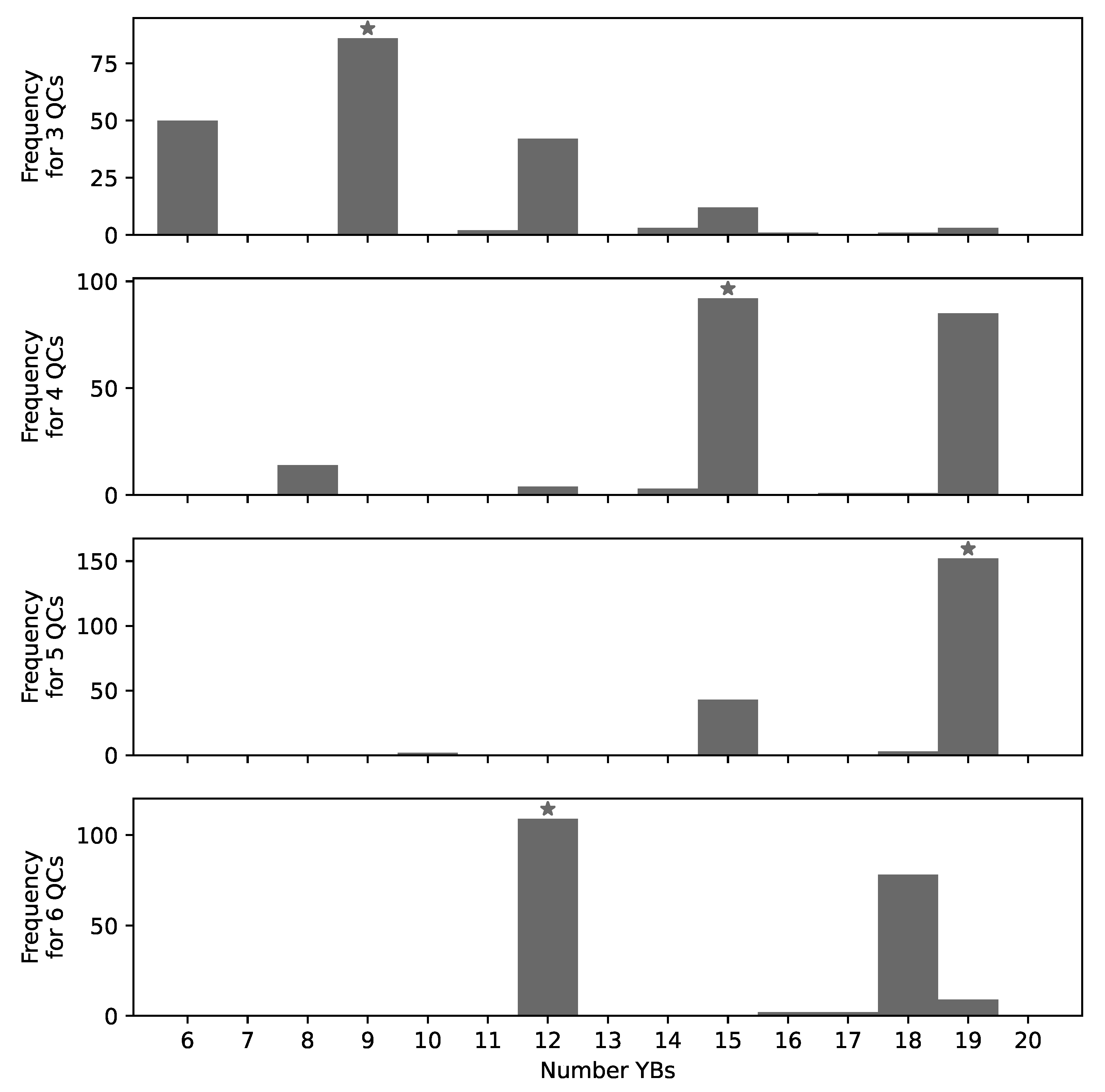
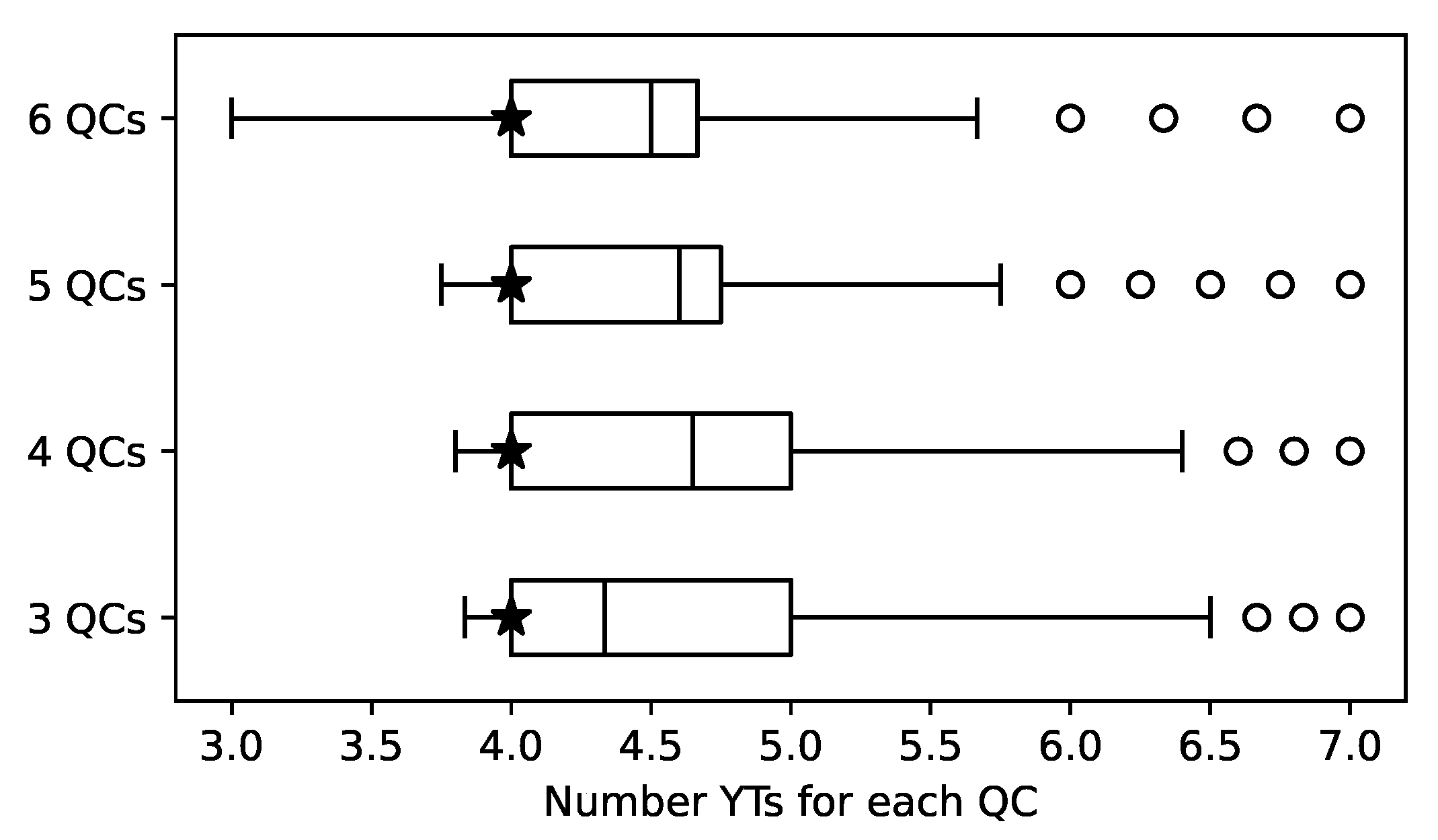
| Number of QCs | Makespan (in Hours, Rounded) | ||
|---|---|---|---|
| Median | Minimum | Maximum | |
| 3 | 61 | 51 | 158 |
| 4 | 49 | 39 | 161 |
| 5 | 47 | 38 | 160 |
| 6 | 35 | 29 | 161 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kastner, M.; Nellen, N.; Schwientek, A.; Jahn, C. Integrated Simulation-Based Optimization of Operational Decisions at Container Terminals. Algorithms 2021, 14, 42. https://doi.org/10.3390/a14020042
Kastner M, Nellen N, Schwientek A, Jahn C. Integrated Simulation-Based Optimization of Operational Decisions at Container Terminals. Algorithms. 2021; 14(2):42. https://doi.org/10.3390/a14020042
Chicago/Turabian StyleKastner, Marvin, Nicole Nellen, Anne Schwientek, and Carlos Jahn. 2021. "Integrated Simulation-Based Optimization of Operational Decisions at Container Terminals" Algorithms 14, no. 2: 42. https://doi.org/10.3390/a14020042
APA StyleKastner, M., Nellen, N., Schwientek, A., & Jahn, C. (2021). Integrated Simulation-Based Optimization of Operational Decisions at Container Terminals. Algorithms, 14(2), 42. https://doi.org/10.3390/a14020042







