A Multi-Objective Optimization Method for Hospital Admission Problem—A Case Study on Covid-19 Patients
Abstract
1. Introduction
- Develop an effective multi-objective admission system for Covid-19 patients that admits patients to the most suitable hospitals in real time and considers the comorbidities of the patients.
- The method considers two main criteria in the admission process: (1) the patient status regarding the hospital preparations and (2) the admission time (reach time and admission time). This method can minimize the in-bed time of patients as it directs each patient to the most suitable hospital.
- Provide a mathematical representation of the problem and the main constraints that affect it.
- Implement the method using the PO to vary among the conflicting objectives as admitting a patient to a non-suitable hospital in less time can result in transferring the patient to a different one.
- Test the method over a dataset that combines a real-life part that has been provided by King Faisal specialist hospital in Saudi Arabia and a synthetic part. The real-life part had the clinical symptoms of the patients and their medical conditions when they arrived at the hospital. Meanwhile, the arrival rate, admission time, time to reach, and medical devices in different hospitals have been generated randomly to mimic the real-life situation.
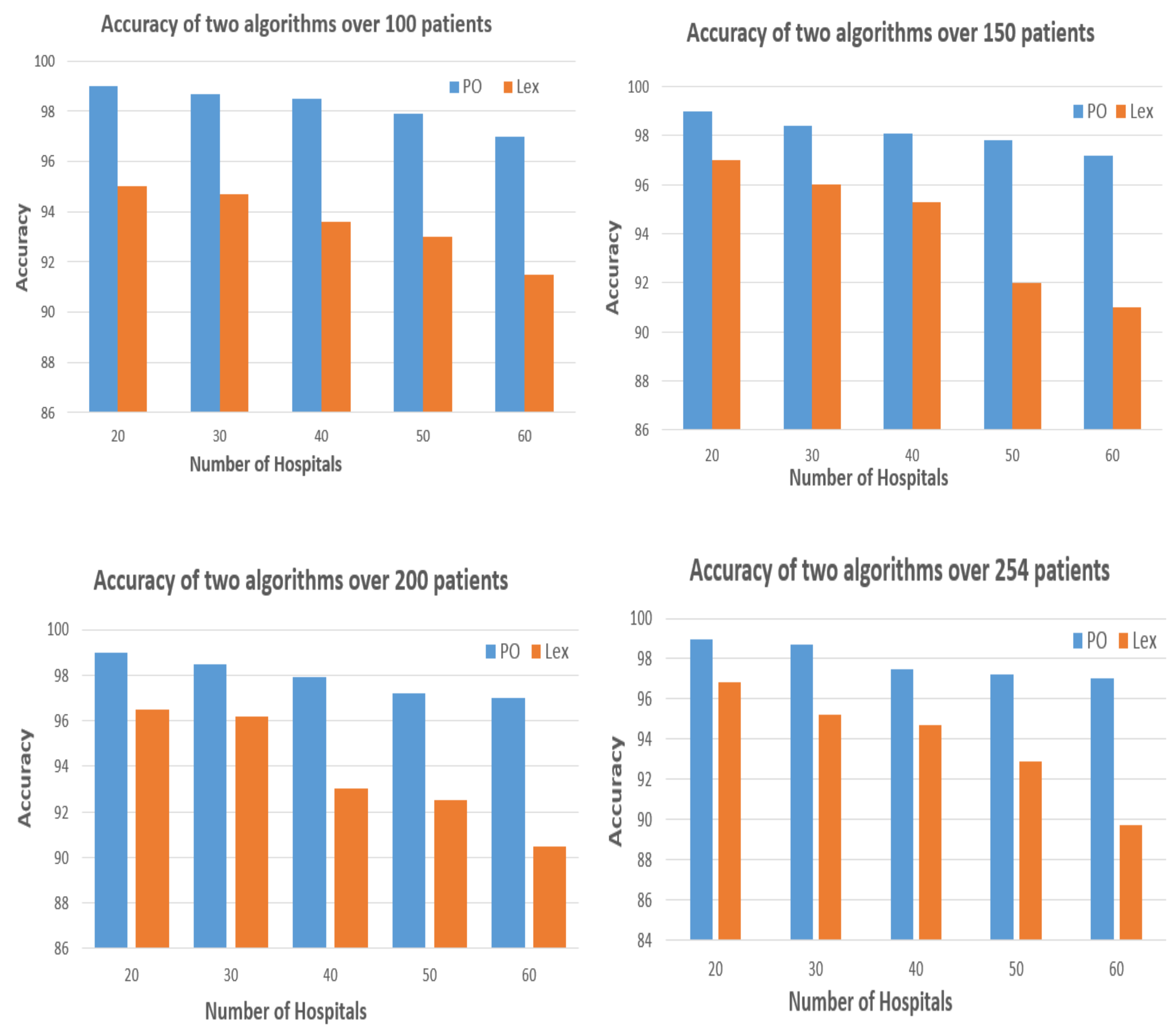
- Results show the efficiency of PO in obtaining the correct hospital for patients over the Lexicographic method [7]. Also, the method showed its effectiveness in obtaining the correct hospital in real time despite the increase in the number of hospitals.
2. Related Work
3. Background
3.1. Multi-Objective Problems (MOPs)
3.2. Pareto Optimization
3.3. Problem Definition
3.4. Problem’s Constraints
4. Methodology
4.1. The Objective Function
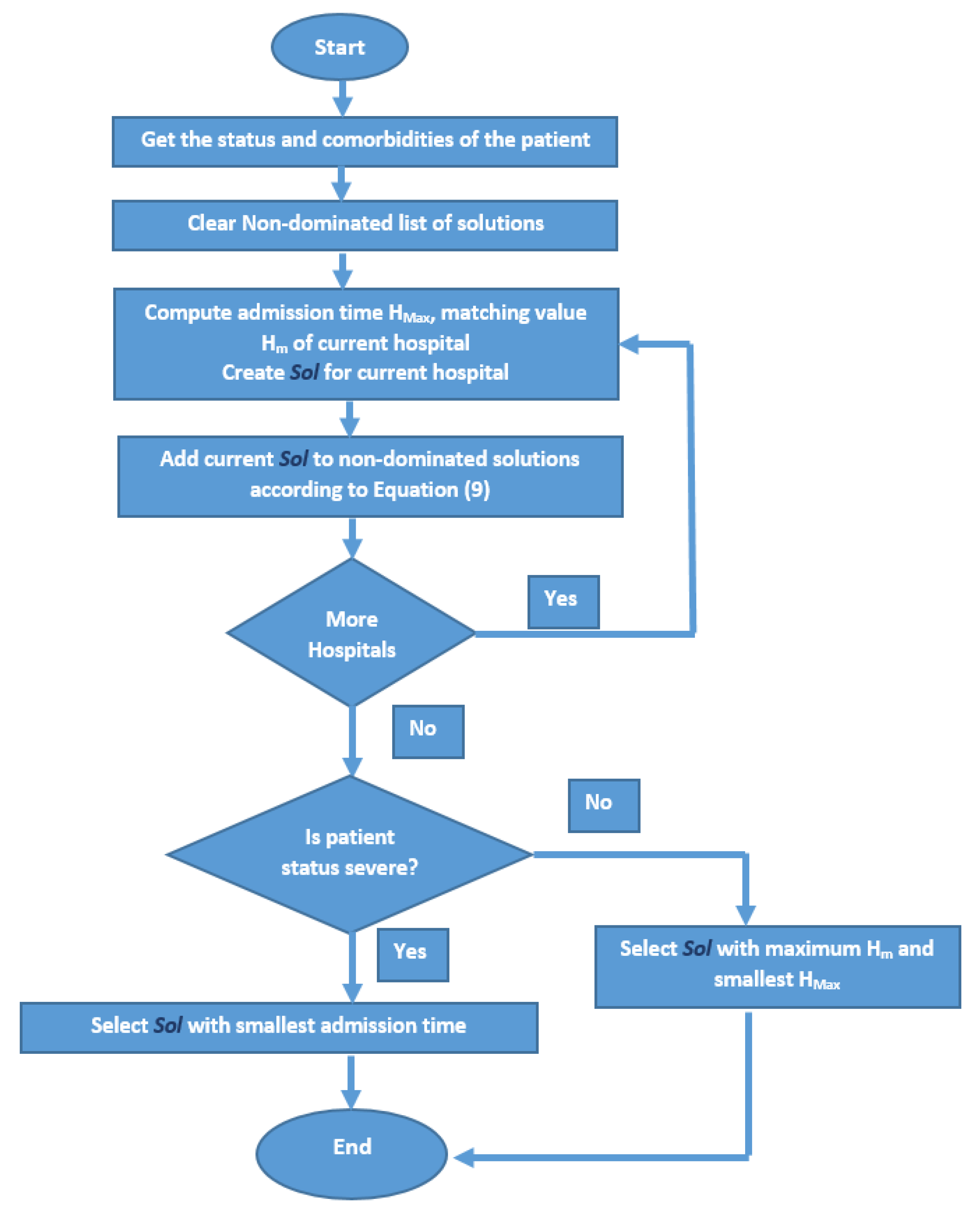
4.2. The Proposed Algorithm
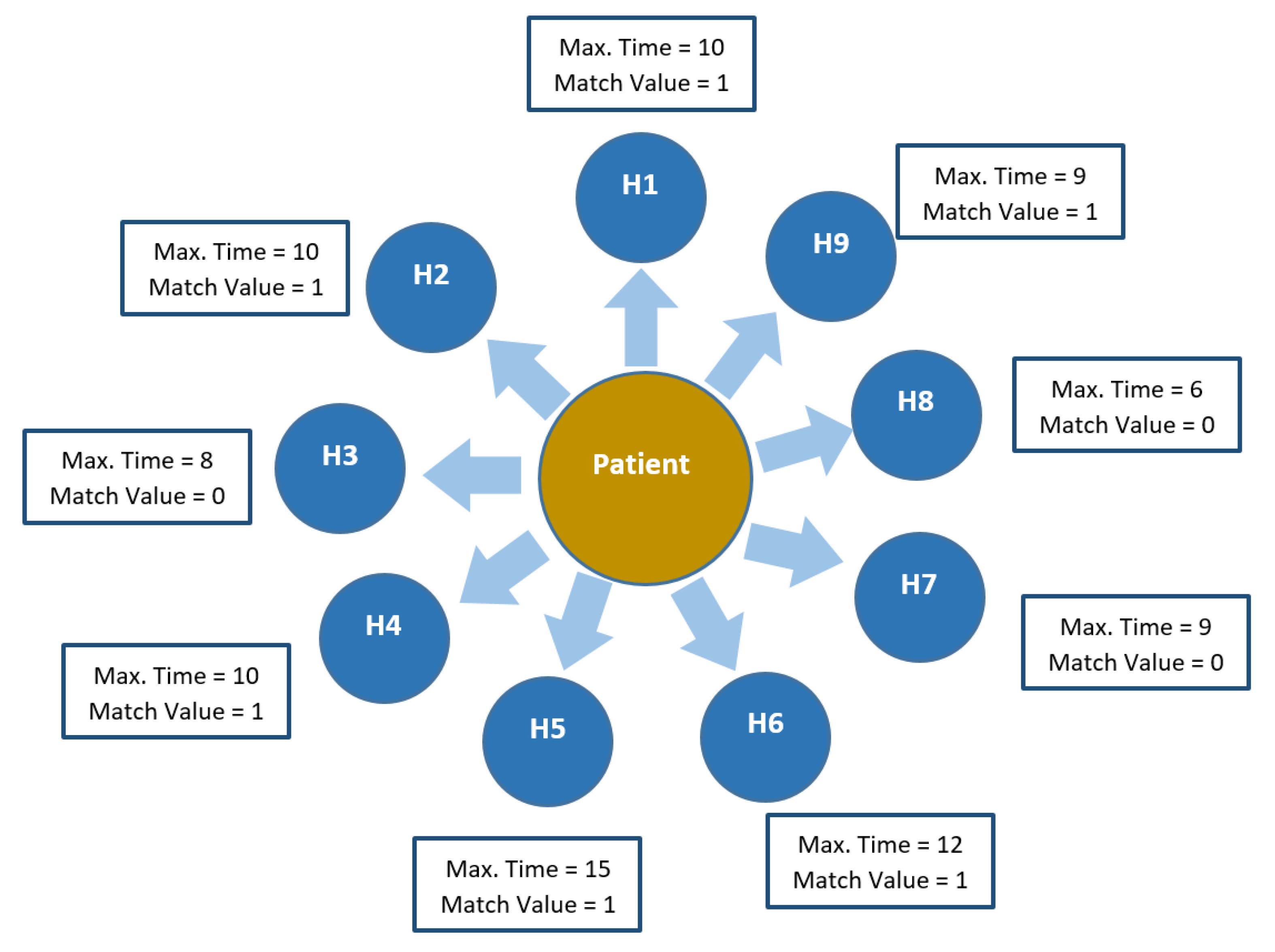
4.3. A Tracing Example of the Algorithm
| Algorithm 1 Pseudocode of Pareto optimization algorithm applied for the hospital admission problem |
|
4.4. A Complexity Analysis of the Method
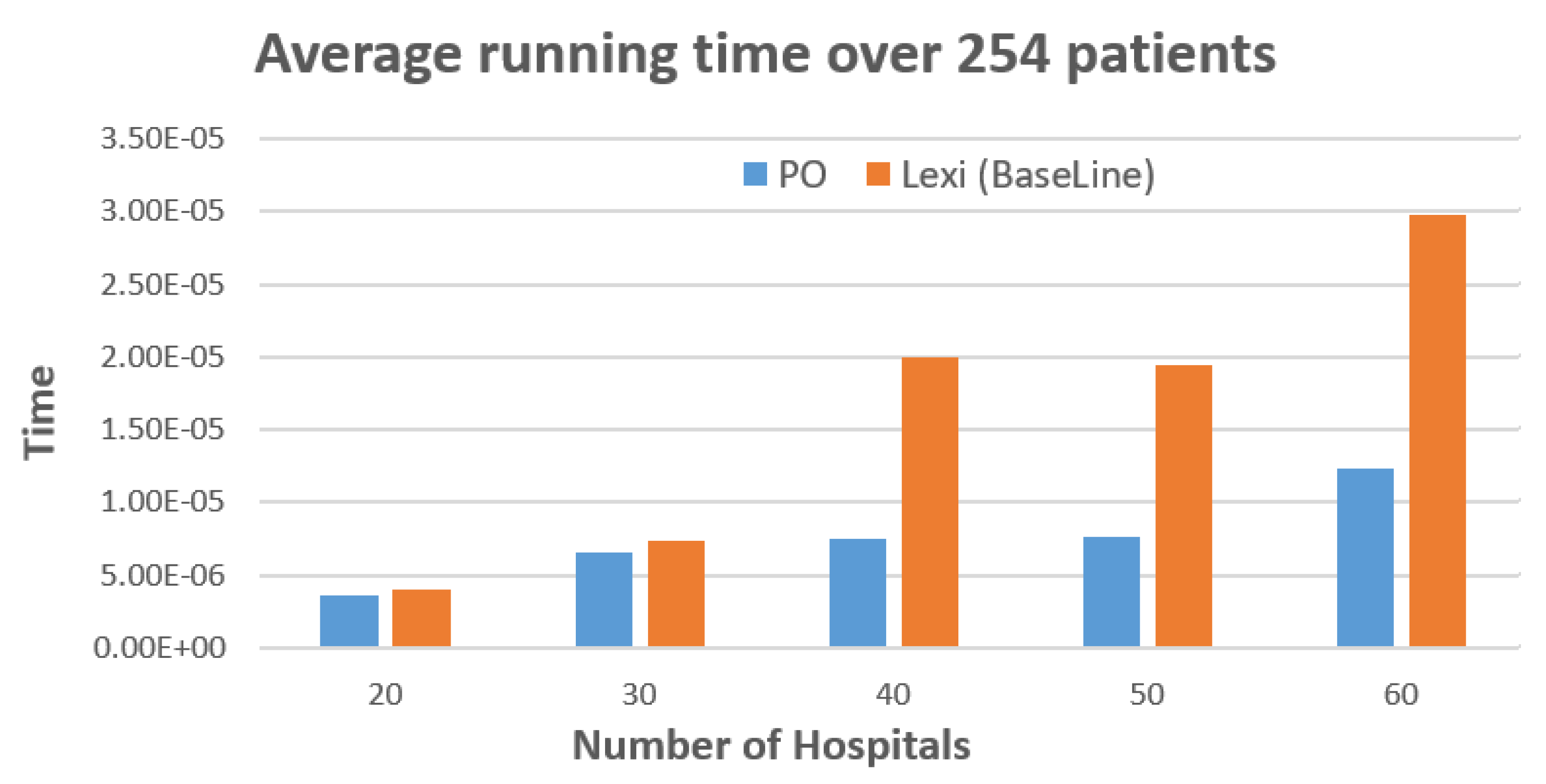
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bi, Q.; Wu, Y.; Mei, S.; Ye, C.; Zou, X.; Zhang, Z.; Liu, X.; Wei, L.; Truelove, S.A.; Zhang, T.; et al. Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: A retrospective cohort study. Lancet Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Wu, Y.C.; Chen, C.S.; Chan, Y.J. The outbreak of COVID-19: An overview. J. Chin. Med. Assoc. 2020, 83, 217–220. [Google Scholar] [CrossRef]
- Amin-Chowdhury, Z.; Aiano, F.; Mensah, A.; Sheppard, C.; Litt, D.; Fry, N.K.; Andrews, N.; Ramsay, M.E.; Ladhani, S.N. Impact of the COVID-19 Pandemic on Invasive Pneumococcal Disease and Risk of Pneumococcal Coinfection with SARS-CoV-2: Prospective national cohort study, England. Clin. Infect. Dis. 2020, 27, 1278–1286. [Google Scholar] [CrossRef]
- Fujioka, S.; Fukae, J.; Ogura, H.; Mishima, T.; Yanamoto, S.; Higuchi, M.A.; Umemoto, G.; Tsuboi, Y. Hospital-based study on emergency admission of patients with Parkinson’s disease. eNeurologicalSci 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Narzisi, G. Multi-Objective Optimization: A Quick Introduction; Courant Institute of Mathematical Sciences: New York, NY, USA, 2008. [Google Scholar]
- Freitas, A.A. A Critical Review of Multi-Objective Optimization in Data Mining: A Position Paper. ACM SIGKDD Explor. 2004, 6, 77–86. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Maulik, U.; Bandyopadhyay, S. A Survey of Multiobjective Evolutionary Clustering. ACM Comput. Surv. (CSUR) 2015, 47, 61. [Google Scholar] [CrossRef]
- Parraga-Alava, J.; Dorn, M.; Inostroza-Ponta, M. A multi-objective gene clustering algorithm guided by apriori biological knowledge with intensification and diversification strategies. BioData Min. 2018, 18, 269–283. [Google Scholar] [CrossRef] [PubMed]
- Ghany, K.K.A.; AbdelAziz, A.M.; Soliman, T.H.A.; Sewisy, A.A.E.M. A hybrid modified step Whale Optimization Algorithm with Tabu Search for data clustering. J. King Saud Univ. Comput. Inf. Sci. 2020. [Google Scholar] [CrossRef]
- Kozan, R.B.E. A multi-criteria approach for hospital capacity analysis. Eur. J. Oper. Res. 2016, 255, 505–521. [Google Scholar] [CrossRef]
- Liao, S.; Tu, H.; Hu, C.; Pan, W.; Xiong, J.; Yu, D.; Jing, L.; Pan, W. Fuzzy multi-objective medical service organization selection model considering limited resources and stochastic demand in emergency management. PLoS ONE 2019, 14, e0212308. [Google Scholar] [CrossRef]
- Apornak, A.; Raissi, S.; Keramati, A.; Khalili-Damghani, K. Optimizing human resource cost of an emergency hospital using multi-objective Bat algorithm. Int. J. Healthc. Manag. 2020. [Google Scholar] [CrossRef]
- Guedes, R.; Furtado, V.; Pequeno, T.; Rodrigues, J.J. Pareto set as a model for dispatching resources in emergency Centres. Peer-to-Peer Netw. Appl. 2019, 12, 865–880. [Google Scholar] [CrossRef]
- Abedini, A.; Li, W.; Ye, H. An Optimization Model for Operating Room Scheduling to Reduce Blocking Across the Perioperative Process. Procedia Manuf. 2017, 10, 60–70. [Google Scholar] [CrossRef]
- Benamrane, A.; Benelallam, I.; Bouyakhf, E.H. Constraint programming based techniques for medical resources optimization: Medical internships planning. J. Ambient. Intell. Humaniz. Comput. 2019. [Google Scholar] [CrossRef]
- Zhang, J.C.L. Case Mix Index weighted multi-objective optimization of inpatient bed allocation in general hospital. J. Comb. Optim. 2017, 37. [Google Scholar] [CrossRef]
- Kortbeek, N.; Braaksma, A.; Smeenk, F.H.; Bakker, P.J.; Boucherie, R.J. Integral resource capacity planning for inpatient care services based on bed census predictions by hour. J. Oper. Res. Soc. 2015, 66, 1061–1076. [Google Scholar] [CrossRef]
- Nuñez-Perez, N.; Ortíz-Barrios, M.; McClean, S.; Salas-Navarro, K.; Jimenez-Delgado, G.; Castillo-Zea, A. Discrete-Event Simulation to Reduce Waiting Time in Accident and Emergency Departments: A Case Study in a District General Clinic. In Proceedings of the International Conference on Ubiquitous Computing and Ambient Intelligence, Philadelphia, PA, USA, 7–10 November 2017. [Google Scholar] [CrossRef]
- Gorunescu, S.B.F. Improving hospital bed occupancy and resource utilization through queuing modeling and evolutionary computation. J. Biomed. Inform. 2015, 53, 261–269. [Google Scholar] [CrossRef]
- Anselmi, L.; Meacock, R.; Kristensen, S.R.; Doran, T.; Sutton, M. Arrival by ambulance explains variation in mortality by time of admission: Retrospective study of admissions to hospital following emergency department attendance in England. BMJ Open 2017. [Google Scholar] [CrossRef]
- Conway, S.P.; Littlewood, J.M. Admission to hospital with asthma. Eur. PMC 1985. [Google Scholar] [CrossRef]
- Pope, I.; Burn, H.; Ismail, S.A.; Harris, T.; McCoy, D. A qualitative study exploring the factors influencing admission to hospital from the emergency department. BMJ Open 2017. [Google Scholar] [CrossRef]
- Kamila, N.K.; Jena, L.; Bhuyan, H.K. Pareto-based multi-objective optimization for classification in data mining. Clust. Comput. 2016, 19, 1723–1745. [Google Scholar] [CrossRef]
- De Nardo, P.; Gentilotti, E.; Mazzaferri, F.; Cremonini, E.; Hansen, P.; Goossens, H.; Tacconelli, E. Multi-Criteria Decision Analysis to prioritise hospital admission of patients affected by COVID-19 in settings with hospital-bed shortage. Int. J. Infect. Dis. 2020, 494–500. [Google Scholar] [CrossRef] [PubMed]
- Batista, A.; Vera, J.; Pozo, D. Multi-objective admission planning problem: A two-stage stochastic approach. Health Care Manag. Sci. 2020, 23, 51–65. [Google Scholar] [CrossRef] [PubMed]
- Lott, A.; Haglin, J.; Belayneh, R.; Konda, S.R.; Egol, K.A. Admitting Service Affects Cost and Length of Stay of Hip Fracture Patients. Geriatr. Orthop. Surg. Rehabil. 2018, 9. [Google Scholar] [CrossRef]
- Shuja, J.; Alanazi, E.; Alasmary, W.; Alashaikh, A. Covid-19 open source data sets: A comprehensive survey. Appl. Intell. 2020. [Google Scholar] [CrossRef]
- Dunnett, S.; Leigh, J.; Jackson, L. Optimising police dispatch for incident response in real time. J. Oper. Res. Soc. 2018, 1476–9360. [Google Scholar] [CrossRef]
| Parameter | Description |
|---|---|
| the time needed for a patient to be admitted in a hospital | |
| the time needed for a patient to reach a hospital location | |
| the medical devices possessed by a hospital | |
| the comorbidities of a patient | |
| t | the time at which the event happens |
| the demand of patient p in time t | |
| the maximum number of beds in a hospital h | |
| maximum number of beds in hospitals | |
| the response time of the system to identify a hospital h for patient p |
| Diabetes Mellitus | Heart Failure | Chronic Pulmonary Disease | Chronic Liver Disease | Chronic Kidney Disease | Temp | Saturation |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 37.8 | 96 |
| Num. | Kidney Machine | Ventilator | Intensive Care Unit | Time to Reach | Time to Admit | Available Beds |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 3 | 10 | 39 |
| 2 | 1 | 1 | 1 | 2 | 10 | 10 |
| 3 | 1 | 0 | 1 | 3 | 8 | 34 |
| 4 | 0 | 1 | 1 | 5 | 10 | 31 |
| 5 | 1 | 1 | 0 | 5 | 15 | 9 |
| 6 | 1 | 1 | 0 | 6 | 12 | 55 |
| 7 | 0 | 0 | 1 | 4 | 9 | 3 |
| 8 | 1 | 0 | 1 | 1 | 6 | 43 |
| 9 | 0 | 1 | 0 | 1 | 9 | 16 |
| Iter. Num | Reach Time | Admission Time | Maximum Time | Match Value | Best Solutions |
|---|---|---|---|---|---|
| 1 | 3 | 10 | 10 | 1 | (1) |
| 2 | 2 | 10 | 10 | 1 | (1,2) |
| 3 | 3 | 8 | 8 | 0 | (1,2,3) |
| 4 | 5 | 10 | 10 | 1 | (1,2,3,4) |
| 5 | 5 | 15 | 15 | 1 | (1,2,3,4) |
| 6 | 6 | 12 | 12 | 1 | (1,2,3,4) |
| 7 | 4 | 9 | 9 | 0 | (1,2,3,4) |
| 8 | 1 | 6 | 6 | 0 | (1,2,4,8) |
| 9 | 1 | 9 | 9 | 1 | (8,9) |
| Minimum Time | Average Time | Maximum Time | |
|---|---|---|---|
| Preto Optimization | |||
| 20 Hospitals | 0 | ||
| 30 Hospitals | 0 | ||
| 40 Hospitals | 0 | ||
| 50 Hospitals | 0 | ||
| 60 Hospitals | 0 | ||
| lexicographic Method | |||
| 20 Hospitals | 0 | ||
| 30 Hospitals | 0 | ||
| 40 Hospitals | 0 | ||
| 50 Hospitals | 0 | ||
| 60 Hospitals | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
AbdelAziz, A.M.; Alarabi, L.; Basalamah, S.; Hendawi, A. A Multi-Objective Optimization Method for Hospital Admission Problem—A Case Study on Covid-19 Patients. Algorithms 2021, 14, 38. https://doi.org/10.3390/a14020038
AbdelAziz AM, Alarabi L, Basalamah S, Hendawi A. A Multi-Objective Optimization Method for Hospital Admission Problem—A Case Study on Covid-19 Patients. Algorithms. 2021; 14(2):38. https://doi.org/10.3390/a14020038
Chicago/Turabian StyleAbdelAziz, Amr Mohamed, Louai Alarabi, Saleh Basalamah, and Abdeltawab Hendawi. 2021. "A Multi-Objective Optimization Method for Hospital Admission Problem—A Case Study on Covid-19 Patients" Algorithms 14, no. 2: 38. https://doi.org/10.3390/a14020038
APA StyleAbdelAziz, A. M., Alarabi, L., Basalamah, S., & Hendawi, A. (2021). A Multi-Objective Optimization Method for Hospital Admission Problem—A Case Study on Covid-19 Patients. Algorithms, 14(2), 38. https://doi.org/10.3390/a14020038







