Agent State Flipping Based Hybridization of Heuristic Optimization Algorithms: A Case of Bat Algorithm and Krill Herd Hybrid Algorithm
Abstract
:1. Introduction
2. Related Works
3. Hybridization Method
3.1. General Description
| Algorithm 1 Proposed hybridization algorithm. |
|
3.2. Krill Herd (KH)
| Algorithm 2 Pseudo-code for the KH Algorithm. |
|
3.3. Bat Algorithm (BA)
- All bats employ echolocation to sense distance, and a bat’s location is regarded as a solution to a problem.
- Bats look for prey by flying randomly at location with variable frequency (from the smallest frequency to the largest value ) with varying wavelengths and loudness A. They can automatically alter the wavelengths (or frequencies) of their emitted pulses as well as the rate of pulse emission r based on the target’s distance.
- The value of loudness ranges from a large positive number to the smallest value .
| Algorithm 3 Bat algorithm. |
|
3.4. Summary
4. Benchmarks
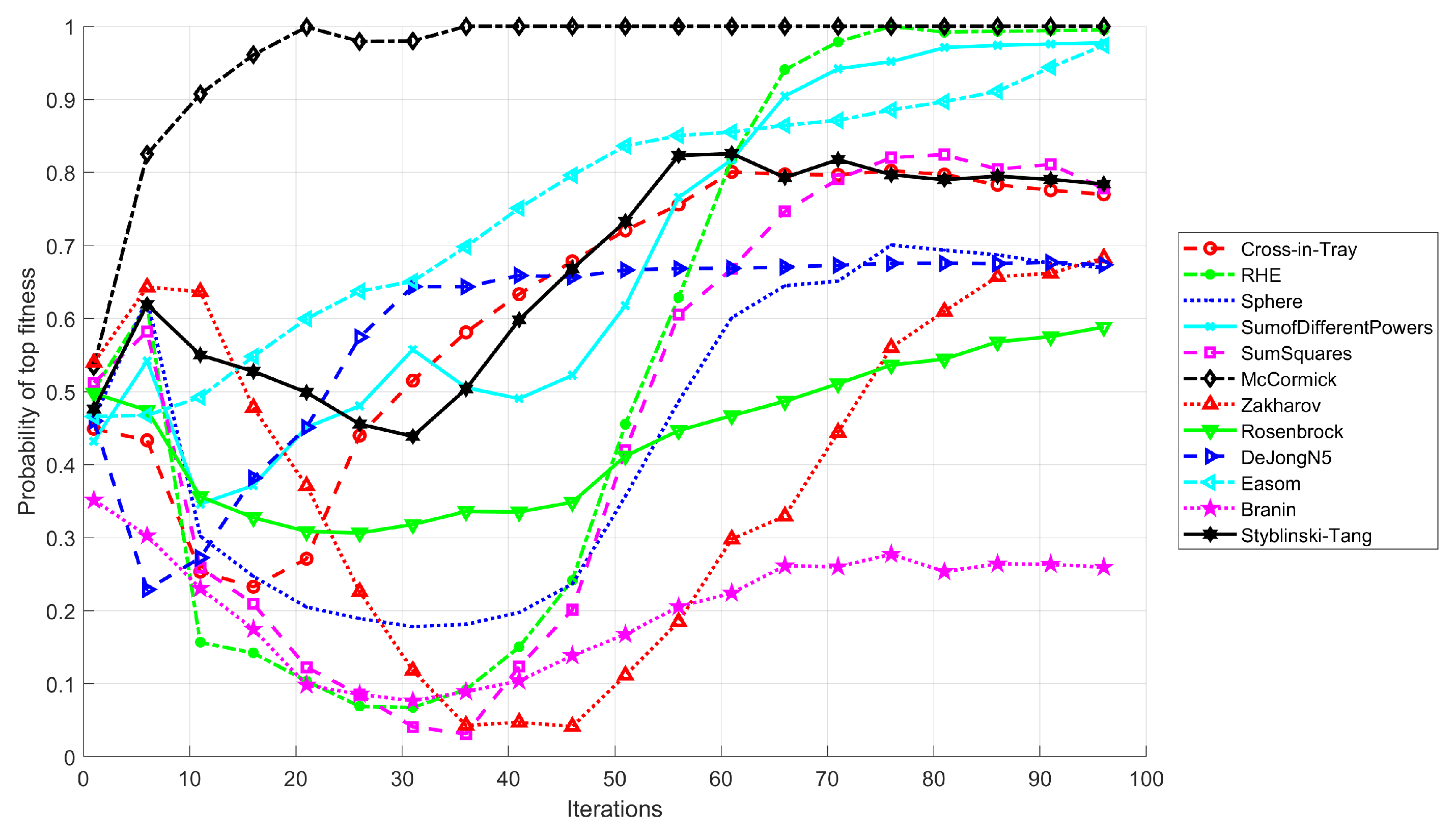
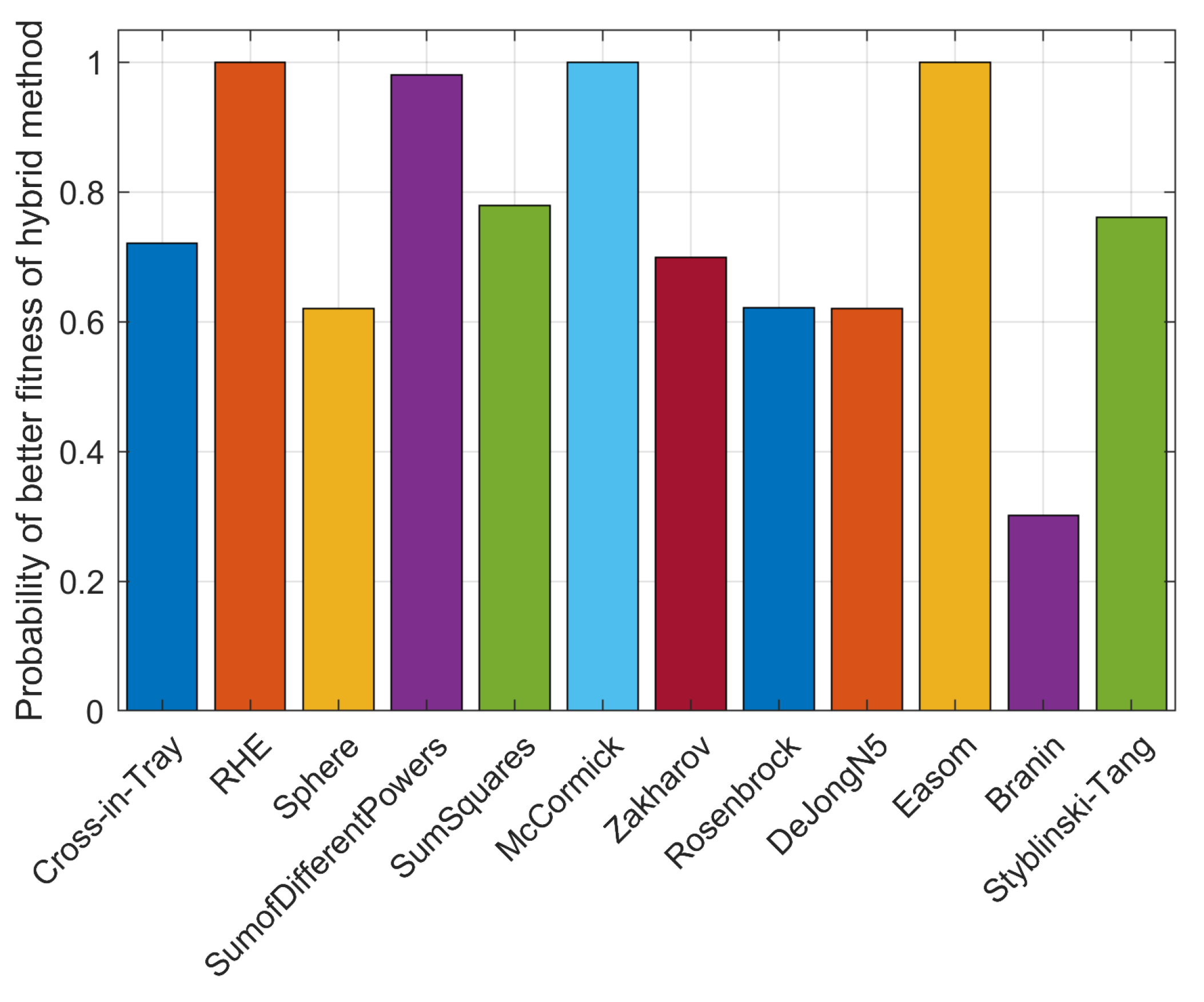
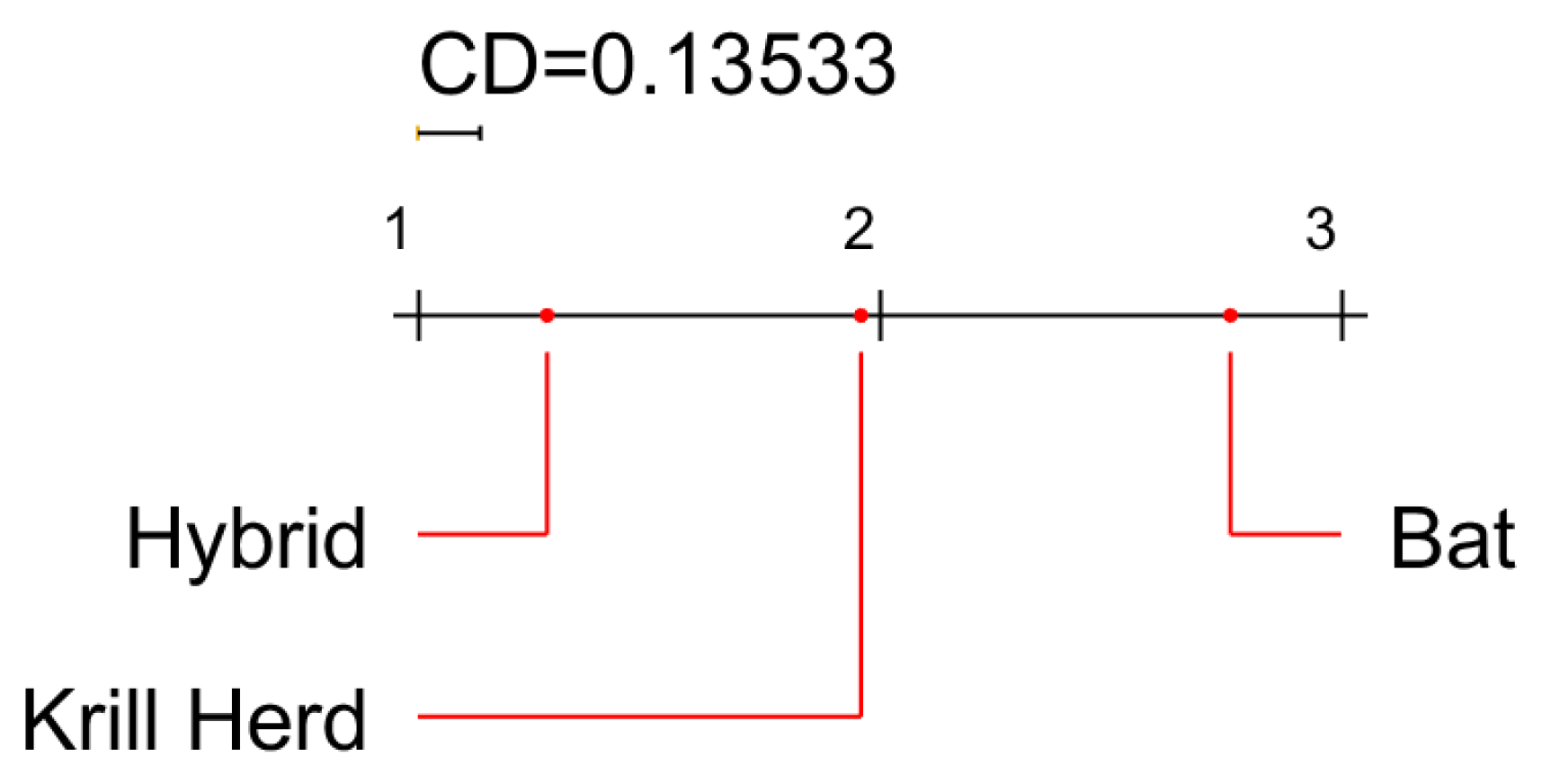
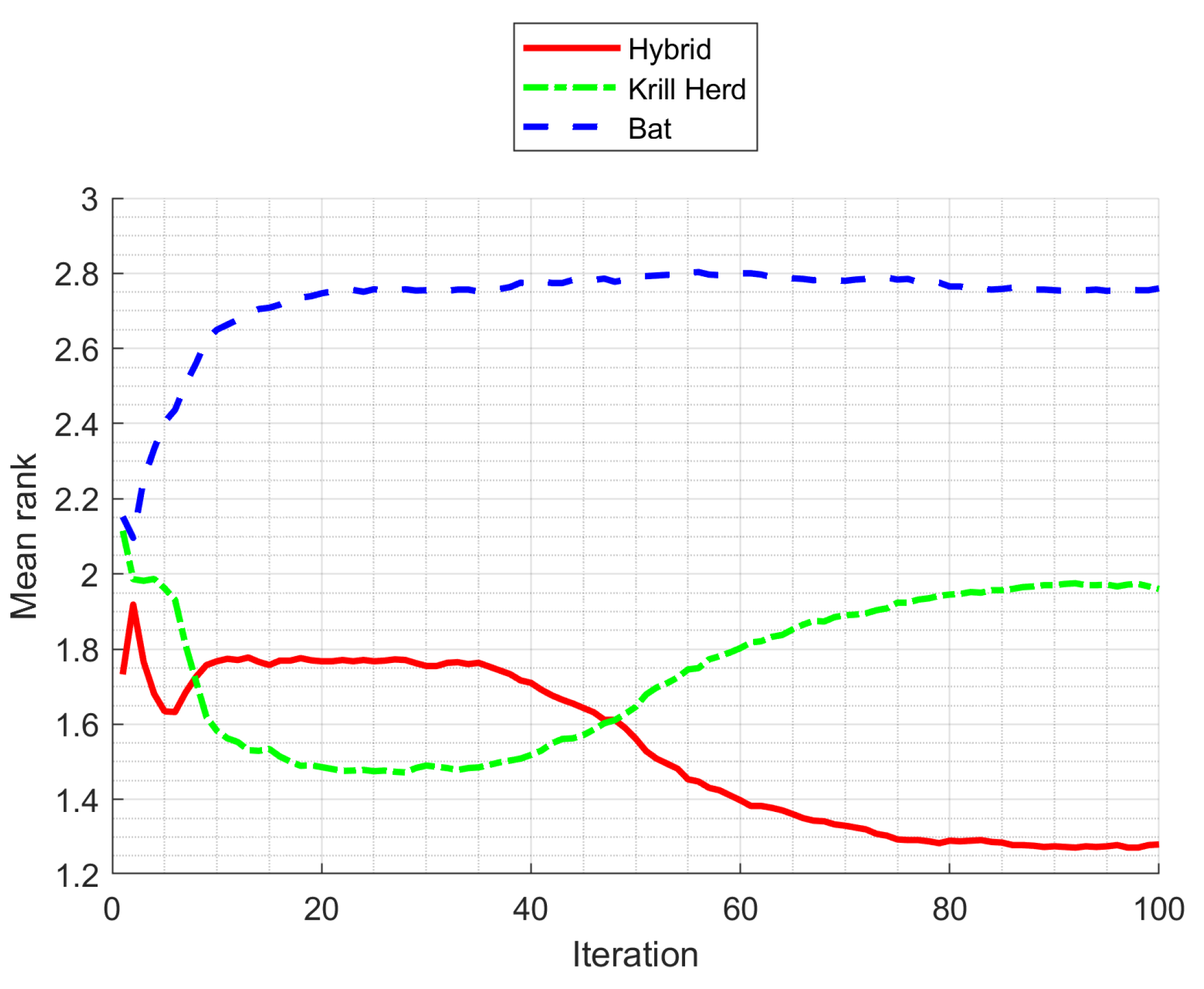
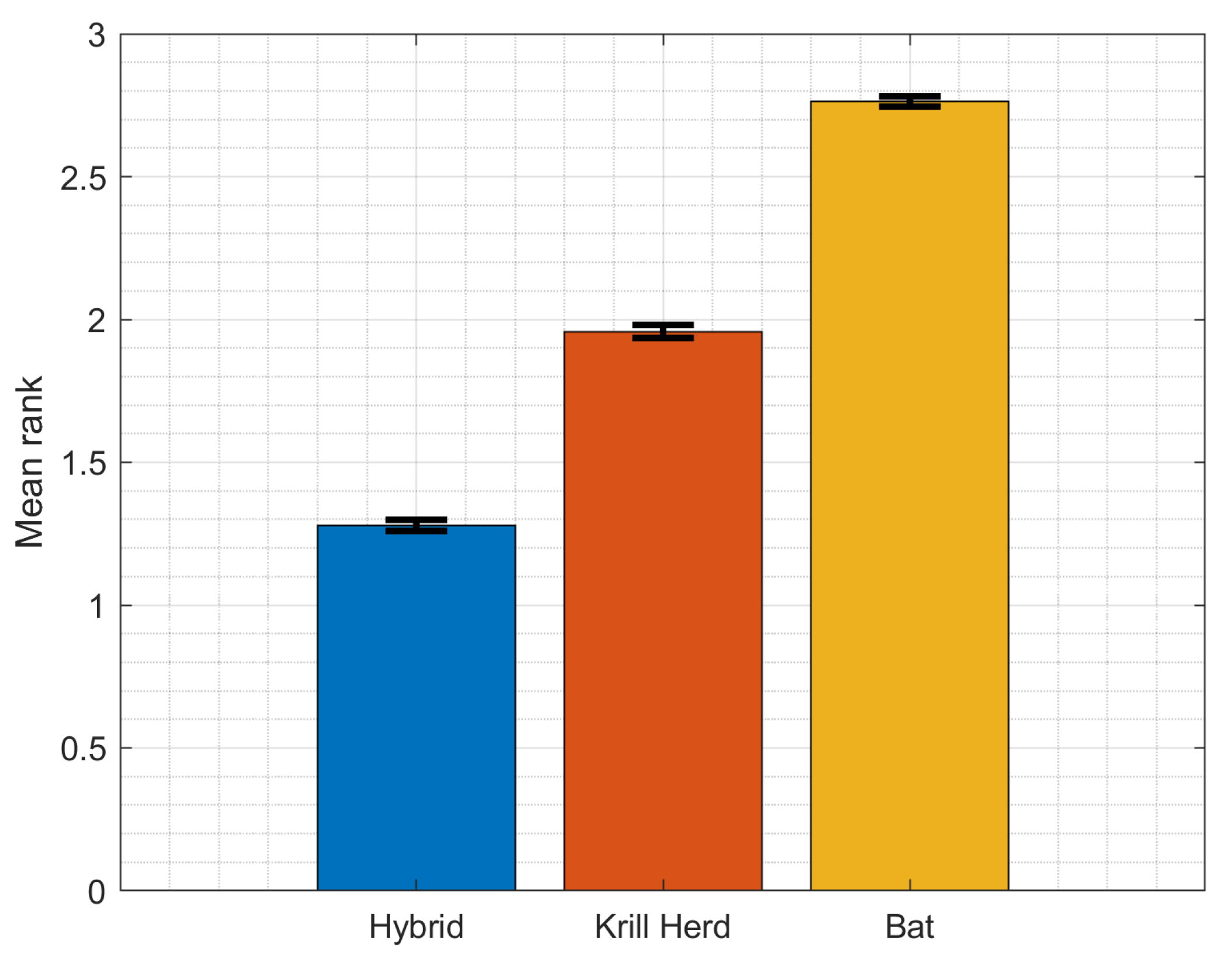
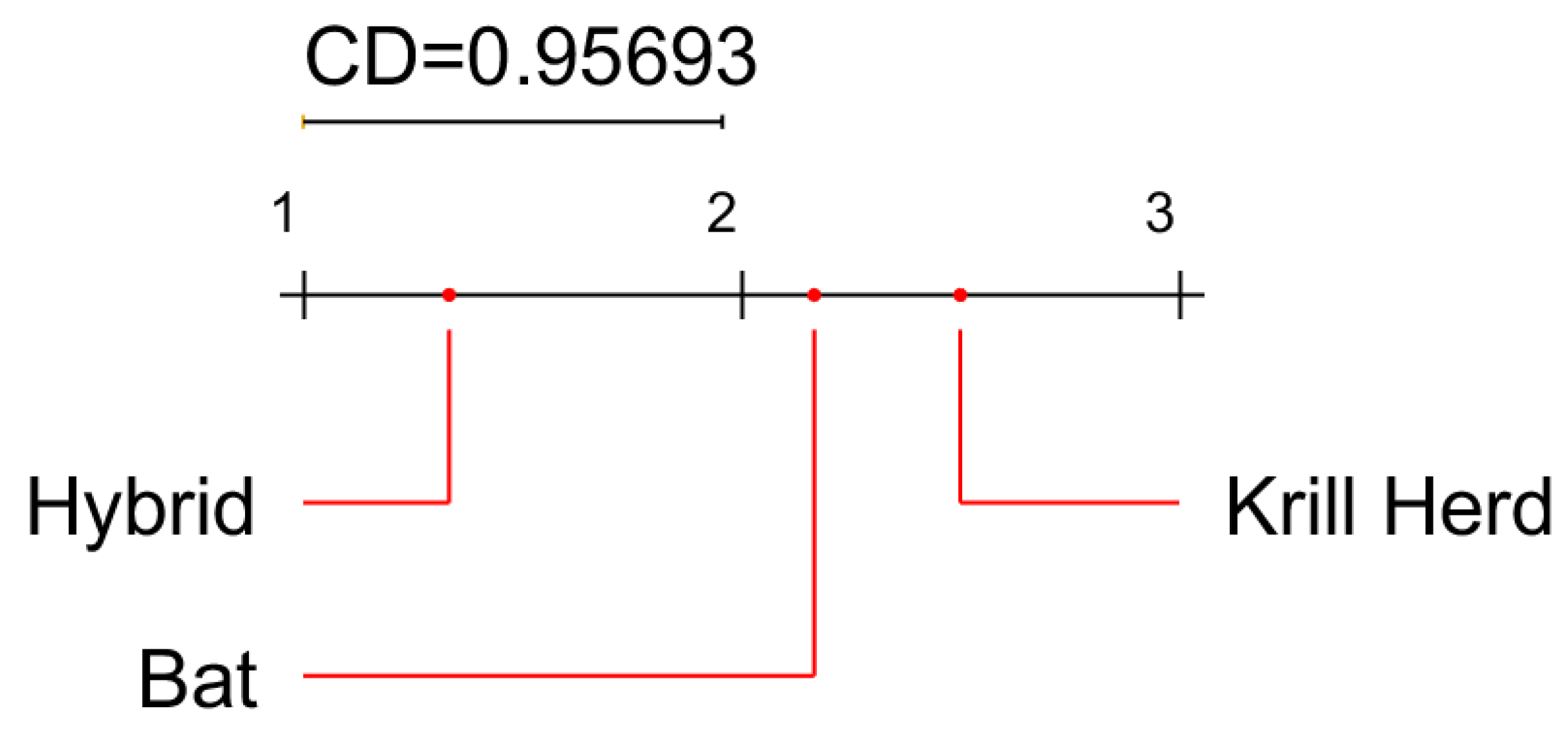
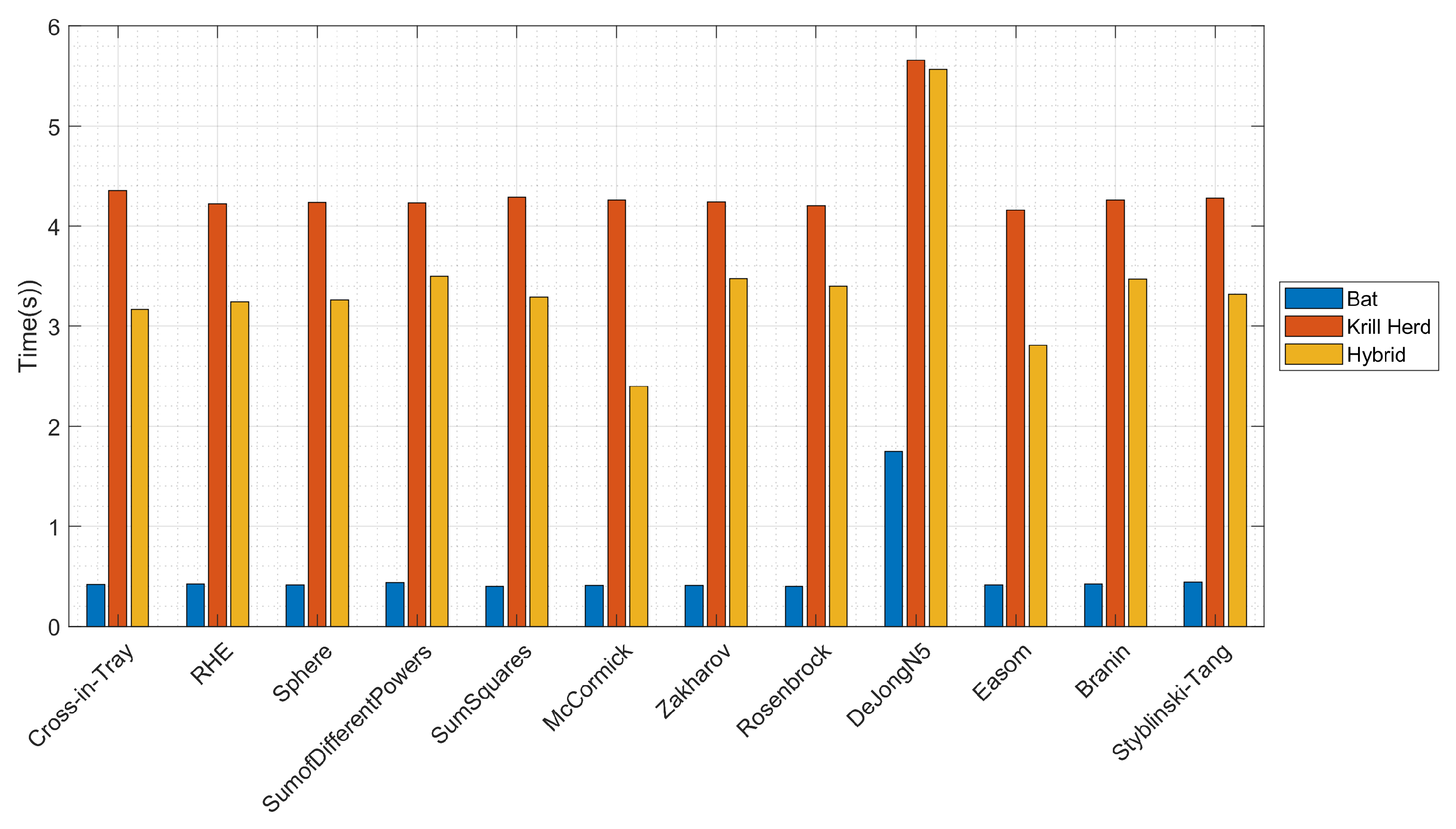
5. Results
5.1. Results with Benchmark Functions
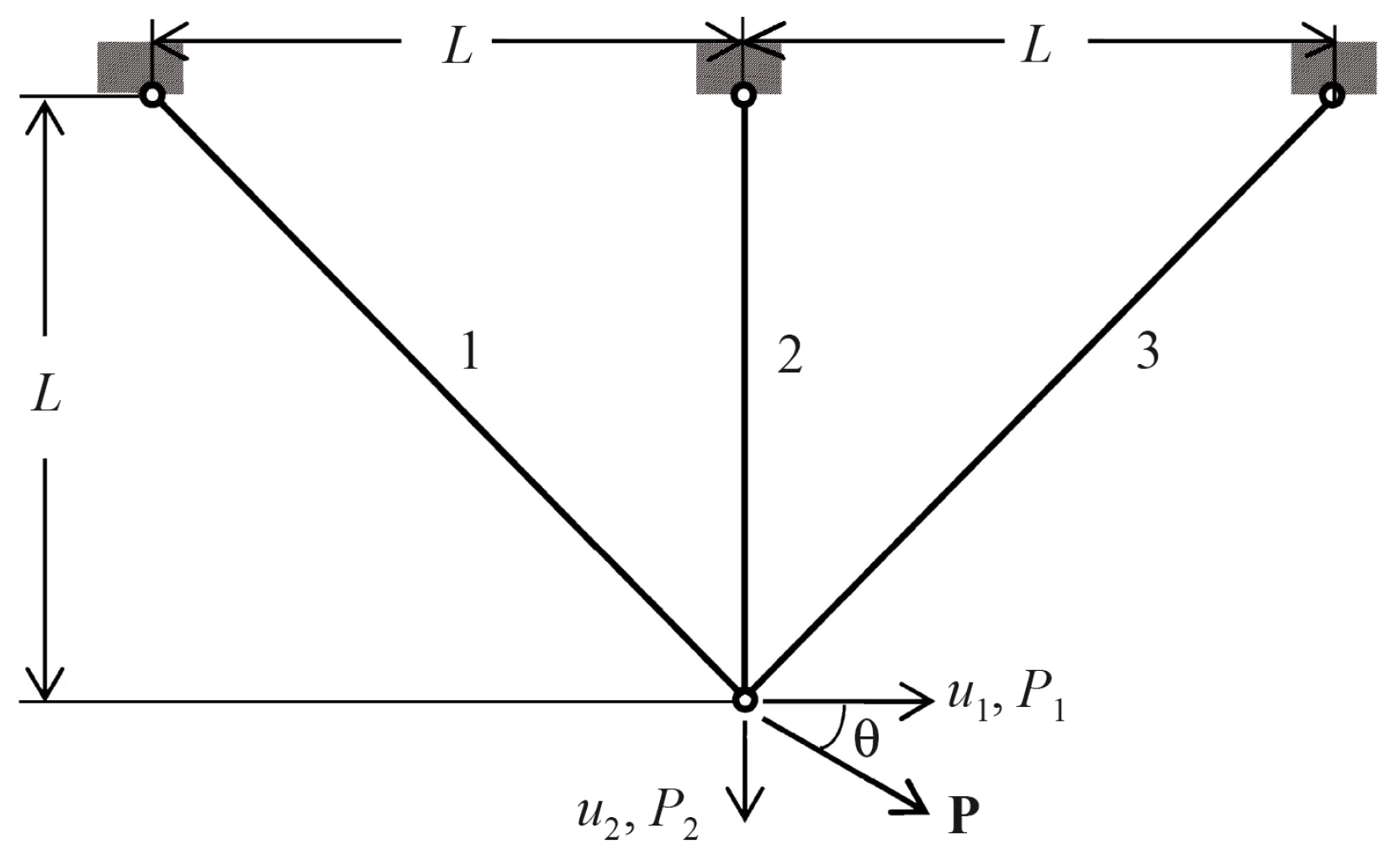
5.2. Three-Bar Truss Design Problem
6. Discussion and Conclusions
- Assess the proposed scheme’s efficiency, stability, and significance using other known unconstrained benchmark functions and several real-life problems.
- Hybridize the GA, PSO, GSA, or ACO algorithms and compare the hybrid method to these algorithms as baselines.
- Compare the proposed algorithm’s resilience and efficiency to several state-of-the-art optimization algorithms.
- Apply the proposed hybrid approach to real-life applications, such as image segmentation, clustering, and feature selection, based on its promising results in finding the best solution for the challenges that we investigated. This discovery is also being looked at as a potential new research avenue for using meta-heuristic algorithms to handle issues such as image processing and segmentation, feature selection, and industrial process parameter estimation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hanif, M.K.; Talib, R.; Awais, M.; Saeed, M.Y.; Sarwar, U. Comparison of bioinspired computation and optimization techniques. Curr. Sci. 2018, 115, 450–453. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar] [CrossRef]
- Fister, I., Jr.; Yang, X.; Brest, J. A comprehensive review of firefly algorithms. Swarm Evol. Comput. 2013, 13, 34–46. [Google Scholar] [CrossRef] [Green Version]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Polap, D.; Woźniak, M. Polar bear optimization algorithm: Meta-heuristic with fast population movement and dynamic birth and death mechanism. Symmetry 2017, 9, 203. [Google Scholar] [CrossRef] [Green Version]
- Połap, D.; Woźniak, M. Red fox optimization algorithm. Expert Syst. Appl. 2021, 166, 114107. [Google Scholar] [CrossRef]
- Parpinelli, R.S.; Lopes, H.S. An eco-inspired evolutionary algorithm applied to numerical optimization. In Proceedings of the 2011 Third World Congress on Nature and Biologically Inspired Computing, Salamanca, Spain, 19–21 October 2011. [Google Scholar] [CrossRef]
- Połap, D.; Woźniak, M.; Napoli, C.; Tramontana, E.; Damaševičius, R. Is the Colony of Ants Able to Recognize Graphic Objects? In Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2015; pp. 376–387. [Google Scholar] [CrossRef]
- Khurma, R.A.; Alsawalqah, H.; Aljarah, I.; Elaziz, M.A.; Damaševičius, R. An enhanced evolutionary software defect prediction method using island moth flame optimization. Mathematics 2021, 9, 1722. [Google Scholar] [CrossRef]
- Woźniak, M.; Książek, K.; Marciniec, J.; Połap, D. Heat production optimization using bio-inspired algorithms. Eng. Appl. Artif. Intell. 2018, 76, 185–201. [Google Scholar] [CrossRef]
- Khan, M.A.; Sharif, M.; Akram, T.; Damaševičius, R.; Maskeliūnas, R. Skin lesion segmentation and multiclass classification using deep learning features and improved moth flame optimization. Diagnostics 2021, 11, 811. [Google Scholar] [CrossRef] [PubMed]
- Kadry, S.; Rajinikanth, V.; Damasevicius, R.; Taniar, D. Retinal Vessel Segmentation with Slime-Mould-Optimization based Multi-Scale-Matched-Filter. In Proceedings of the 2021 IEEE 7th International Conference on Bio Signals, Images and Instrumentation, Chennai, India, 25–27 March 2021. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Ting, T.O.; Yang, X.S.; Cheng, S.; Huang, K. Hybrid Metaheuristic Algorithms: Past, Present, and Future. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2014; pp. 71–83. [Google Scholar] [CrossRef]
- Özcan, E.; Bilgin, B.; Korkmaz, E.E. A comprehensive analysis of hyper-heuristics. Intell. Data Anal. 2008, 12, 3–23. [Google Scholar] [CrossRef]
- Burke, E.; Kendall, G.; Newall, J.; Hart, E.; Ross, P.; Schulenburg, S. Hyper-Heuristics: An Emerging Direction in Modern Search Technology. In Handbook of Metaheuristics; Kluwer Academic Publishers: Boston, MA, USA, 2003; pp. 457–474. [Google Scholar] [CrossRef]
- Chakhlevitch, K.; Cowling, P. Hyperheuristics: Recent Developments. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2008; Volume 136, pp. 3–29. [Google Scholar]
- Özcan, E.; Kheiri, A. A hyper-heuristic based on random gradient, greedy and dominance. In Proceedings of the Computer and Information Sciences II—26th International Symposium on Computer and Information Sciences, London, UK, 26–28 September 2011; pp. 557–563. [Google Scholar]
- Cowling, P.; Kendall, G.; Han, L. An investigation of a hyperheuristic genetic algorithm applied to a trainer scheduling problem. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1185–1190. [Google Scholar]
- Asta, S.; Özcan, E. A tensor-based selection hyper-heuristic for cross-domain heuristic search. Inf. Sci. 2015, 299, 412–432. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Zhang, L.; Gu, X. A hybrid co-evolutionary cultural algorithm based on particle swarm optimization for solving global optimization problems. Neurocomputing 2012, 98, 76–89. [Google Scholar] [CrossRef]
- Pan, Q. An effective co-evolutionary artificial bee colony algorithm for steelmaking-continuous casting scheduling. Eur. J. Oper. Res. 2016, 250, 702–714. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Cosar, A. A novel multistart hyper-heuristic algorithm on the grid for the quadratic assignment problem. Eng. Appl. Artif. Intell. 2016, 52, 10–25. [Google Scholar] [CrossRef]
- Damaševičius, R.; Woźniak, M. State flipping based hyper-heuristic for hybridization of nature inspired algorithms. In Proceedings of the 16th International Conference, ICAISC 2017, Zakopane, Poland, 11–15 June 2017; Lecture Notes in Computer Science. 2017; Volume 10245 LNAI, pp. 337–346. [Google Scholar]
- Gandomi, A.H.; Yang, X.S.; Talatahari, S.; Alavi, A.H. Metaheuristic Algorithms in Modeling and Optimization. Metaheuristic Appl. Struct. Infrastructures 2013, 1–24. [Google Scholar] [CrossRef]
- Molina, D.; Poyatos, J.; Ser, J.D.; García, S.; Hussain, A.; Herrera, F. Comprehensive Taxonomies of Nature- and Bio-inspired Optimization: Inspiration Versus Algorithmic Behavior, Critical Analysis Recommendations. Cogn. Comput. 2020, 12, 897–939. [Google Scholar] [CrossRef]
- Raidl, G.R. A Unified View on Hybrid Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–12. [Google Scholar] [CrossRef]
- Wang, X. Hybrid Nature-Inspired Computation Methods for Optimization. Ph.D. Thesis, Helsinki University of Technology, Espoo, Finland, 2009. [Google Scholar]
- Stegherr, H.; Heider, M.; Hähner, J. Classifying Metaheuristics: Towards a unified multi-level classification system. Nat. Comput. 2020, 1–17. [Google Scholar] [CrossRef]
- Abd-Alsabour, N. Hybrid Metaheuristics for Classification Problems. In Pattern Recognition—Analysis and Applications; InTech: Rijeka, Croatia, 2016. [Google Scholar] [CrossRef] [Green Version]
- Eiben, A.E.; Michalewicz, Z.; Schoenauer, M.; Smith, J.E. Parameter Control in Evolutionary Algorithms; Springer: Berlin/Heidelberg, Germany, 2007; pp. 19–46. [Google Scholar] [CrossRef] [Green Version]
- Dioşan, L.; Oltean, M. Evolutionary design of Evolutionary Algorithms. Genet. Program. Evolvable Mach. 2009, 10, 263–306. [Google Scholar] [CrossRef]
- Harding, S.; Miller, J.F.; Banzhaf, W. Developments in Cartesian Genetic Programming: Self-modifying CGP. Genet. Program. Evolvable Mach. 2010, 11, 397–439. [Google Scholar] [CrossRef] [Green Version]
- Grobler, J.; Engelbrecht, A.P.; Kendall, G.; Yadavalli, V.S.S. Heuristic space diversity control for improved meta-hyper-heuristic performance. Inf. Sci. 2015, 300, 49–62. [Google Scholar] [CrossRef]
- Alrassas, A.M.; Al-Qaness, M.A.A.; Ewees, A.A.; Ren, S.; Elaziz, M.A.; Damaševičius, R.; Krilavičius, T. Optimized anfis model using aquila optimizer for oil production forecasting. Processes 2021, 9, 1194. [Google Scholar] [CrossRef]
- Helmi, A.M.; Al-Qaness, M.A.A.; Dahou, A.; Damaševičius, R.; Krilavičius, T.; Elaziz, M.A. A novel hybrid gradient-based optimizer and grey wolf optimizer feature selection method for human activity recognition using smartphone sensors. Entropy 2021, 23, 1065. [Google Scholar] [CrossRef] [PubMed]
- Jouhari, H.; Lei, D.; Al-qaness, M.A.A.; Abd Elaziz, M.; Damaševičius, R.; Korytkowski, M.; Ewees, A.A. Modified Harris Hawks optimizer for solving machine scheduling problems. Symmetry 2020, 12, 1460. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Al-Betar, M.A.; Alyasseri, Z.A.A.; Abasi, A.K.; Khader, A.T.; Damaševičius, R.; Mohammed, M.A.; Abdulkareem, K.H. Smart home battery for the multi-objective power scheduling problem in a smart home using grey wolf optimizer. Electronics 2021, 10, 447. [Google Scholar] [CrossRef]
- Neggaz, N.; Ewees, A.A.; Elaziz, M.A.; Mafarja, M. Boosting salp swarm algorithm by sine cosine algorithm and disrupt operator for feature selection. Expert Syst. Appl. 2020, 145, 113103. [Google Scholar] [CrossRef]
- Ksiazek, K.; Połap, D.; Woźniak, M.; Damaševičius, R. Radiation heat transfer optimization by the use of modified ant lion optimizer. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence, Honolulu, HI, USA, 27 November–1 December 2018; pp. 1–7. [Google Scholar]
- Cruz-Duarte, J.M.; Amaya, I.; Ortiz-Bayliss, J.C.; Conant-Pablos, S.E.; Terashima-Marín, H.; Shi, Y. Hyper-Heuristics to customise metaheuristics for continuous optimisation. Swarm Evol. Comput. 2021, 66, 100935. [Google Scholar] [CrossRef]
- Turky, A.; Sabar, N.R.; Dunstall, S.; Song, A. Hyper-heuristic local search for combinatorial optimisation problems. Knowl.-Based Syst. 2020, 205, 106264. [Google Scholar] [CrossRef]
- Wang, S.; Jia, H.; Abualigah, L.; Liu, Q.; Zheng, R. An improved hybrid aquila optimizer and harris hawks algorithm for solving industrial engineering optimization problems. Processes 2021, 9, 1551. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Ewees, A.A.; Neggaz, N.; Ibrahim, R.A.; Al-qaness, M.A.A.; Lu, S. Cooperative meta-heuristic algorithms for global optimization problems. Expert Syst. Appl. 2021, 176, 114788. [Google Scholar] [CrossRef]
- Dabba, A.; Tari, A.; Meftali, S. Hybridization of Moth flame optimization algorithm and quantum computing for gene selection in microarray data. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 2731–2750. [Google Scholar] [CrossRef]
- Huo, L.; Zhu, J.; Li, Z.; Ma, M. A hybrid differential symbiotic organisms search algorithm for UAV path planning. Sensors 2021, 21, 3037. [Google Scholar] [CrossRef] [PubMed]
- Shehadeh, H.A. A hybrid sperm swarm optimization and gravitational search algorithm (HSSOGSA) for global optimization. Neural Comput. Appl. 2021, 33, 11739–11752. [Google Scholar] [CrossRef]
- Kundu, T.; Garg, H. A hybrid ITLHHO algorithm for numerical and engineering optimization problems. Int. J. Intell. Syst. 2021. [Google Scholar] [CrossRef]
- Chiu, P.C.; Selamat, A.; Krejcar, O.; Kuok, K.K. Hybrid Sine Cosine and Fitness Dependent Optimizer for Global Optimization. IEEE Access 2021, 9, 128601–128622. [Google Scholar] [CrossRef]
- Alkhateeb, F.; Abed-alguni, B.H.; Al-rousan, M.H. Discrete hybrid cuckoo search and simulated annealing algorithm for solving the job shop scheduling problem. J. Supercomput. 2021, 1–28. [Google Scholar] [CrossRef]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm; Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H.; Gong, D. A comprehensive review of krill herd algorithm: Variants, hybrids and applications. Artif. Intell. Rev. 2017, 51, 119–148. [Google Scholar] [CrossRef]
- Kumar, A.; Misra, R.K.; Singh, D.; Mishra, S.; Das, S. The spherical search algorithm for bound-constrained global optimization problems. Appl. Soft Comput. J. 2019, 85, 105734. [Google Scholar] [CrossRef]
- Liang, Y.; Cuevas Juarez, J.R. A self-adaptive virus optimization algorithm for continuous optimization problems. Soft Comput. 2020, 24, 13147–13166. [Google Scholar] [CrossRef]
- Li, X.; Tang, K.; Omidvar, M.N.; Yang, Z.; Qin, K. Benchmark Functions for the CEC’2013 Special Session and Competition on Large-Scale Global Optimization. Gene 2013, 7, 8. [Google Scholar]
- Jamil, M.; Yang, X.S. A literature survey of benchmark functions for global optimisation problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150. [Google Scholar] [CrossRef] [Green Version]
- Al-Roomi, A.R. Unconstrained Single-Objective Benchmark Functions Repository. 2015. Available online: https://www.al-roomi.org/benchmarks/unconstrained (accessed on 9 December 2021).
- Surjanovic, S.; Bingham, D. Virtual Library of Simulation Experiments: Test Functions and Datasets. Available online: http://www.sfu.ca/~ssurjano (accessed on 13 November 2021).
- Chen, H.; Heidari, A.A.; Zhao, X.; Zhang, L.; Chen, H. Advanced orthogonal learning-driven multi-swarm sine cosine optimization: Framework and case studies. Expert Syst. Appl. 2020, 144, 113113. [Google Scholar] [CrossRef]
- Chen, H.; Heidari, A.A.; Chen, H.; Wang, M.; Pan, Z.; Gandomi, A.H. Multi-population differential evolution-assisted Harris hawks optimization: Framework and case studies. Future Gener. Comput. Syst. 2020, 111, 175–198. [Google Scholar] [CrossRef]
- Tawhid, M.A.; Ibrahim, A.M. A hybridization of grey wolf optimizer and differential evolution for solving nonlinear systems. Evol. Syst. 2020, 11, 65–87. [Google Scholar] [CrossRef]
- Chakraborty, S.; Sharma, S.; Saha, A.K.; Chakraborty, S. SHADE–WOA: A metaheuristic algorithm for global optimization. Appl. Soft Comput. 2021, 113, 107866. [Google Scholar] [CrossRef]
- Jan, M.A.; Mahmood, Y.; Khan, H.U.; Mashwani, W.K.; Uddin, M.I.; Mahmoud, M.; Khanum, R.A.; Ikramullah; Mast, N. Feasibility-Guided Constraint-Handling Techniques for Engineering Optimization Problems. Comput. Mater. Contin. 2021, 67, 2845–2862. [Google Scholar]
- Sattar, D.; Salim, R. A smart metaheuristic algorithm for solving engineering problems. Eng. Comput. 2021, 37, 2389–2417. [Google Scholar] [CrossRef]
- Yildiz, B.S.; Pholdee, N.; Bureerat, S.; Yildiz, A.R.; Sait, S.M. Enhanced grasshopper optimization algorithm using elite opposition-based learning for solving real-world engineering problems. Eng. Comput. 2021, 1–13. [Google Scholar] [CrossRef]
- Massoudi, M.S.; Sarjamei, S.; Esfandi Sarafraz, M. Smell Bees Optimization algorithm for continuous engineering problem. Asian J. Civ. Eng. 2020, 21, 925–946. [Google Scholar] [CrossRef]
- Peraza-Vázquez, H.; Peña-Delgado, A.F.; Echavarría-Castillo, G.; Morales-Cepeda, A.B.; Velasco-Álvarez, J.; Ruiz-Perez, F. A Bio-Inspired Method for Engineering Design Optimization Inspired by Dingoes Hunting Strategies. Math. Probl. Eng. 2021, 2021, 9107547. [Google Scholar] [CrossRef]

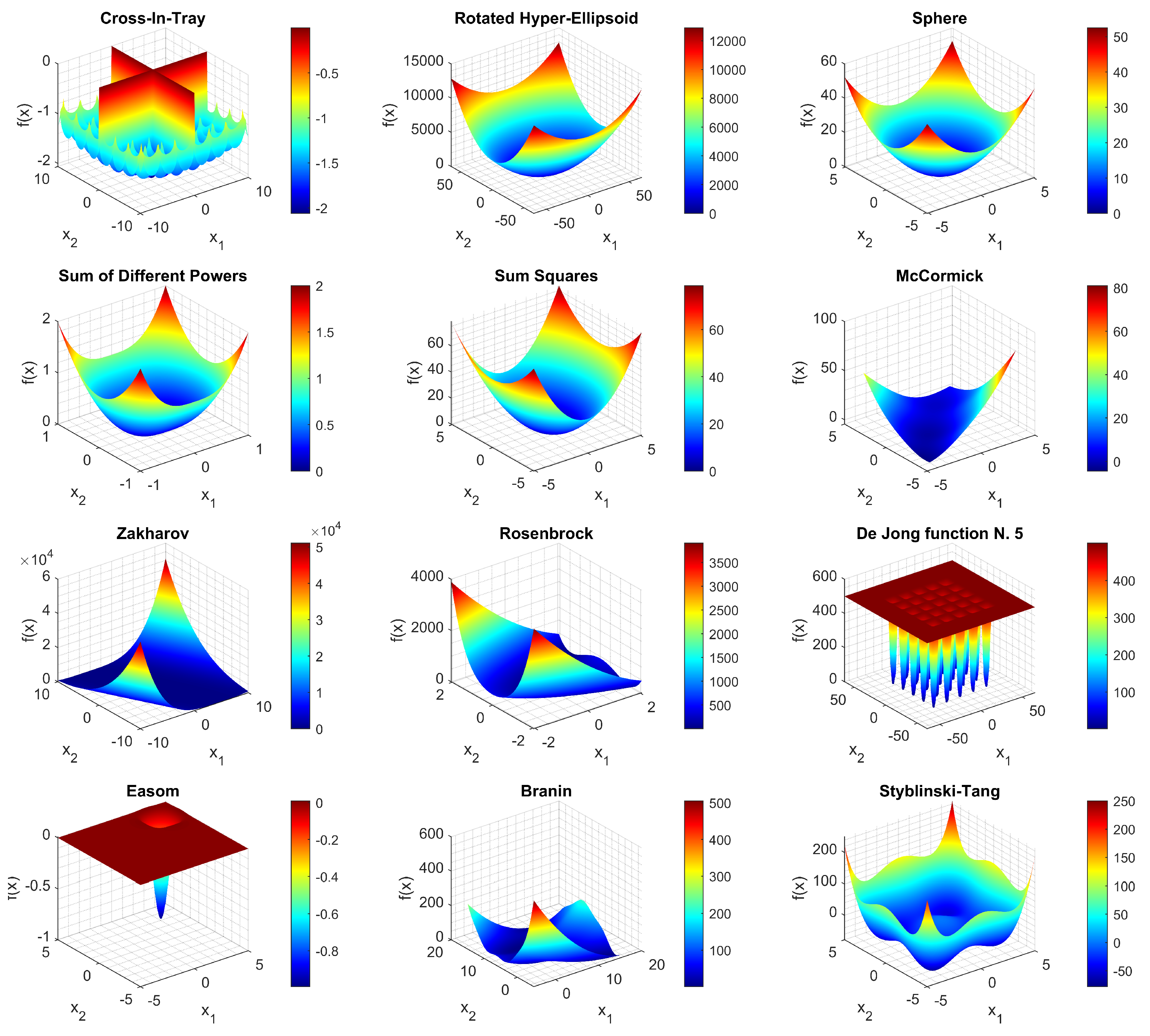
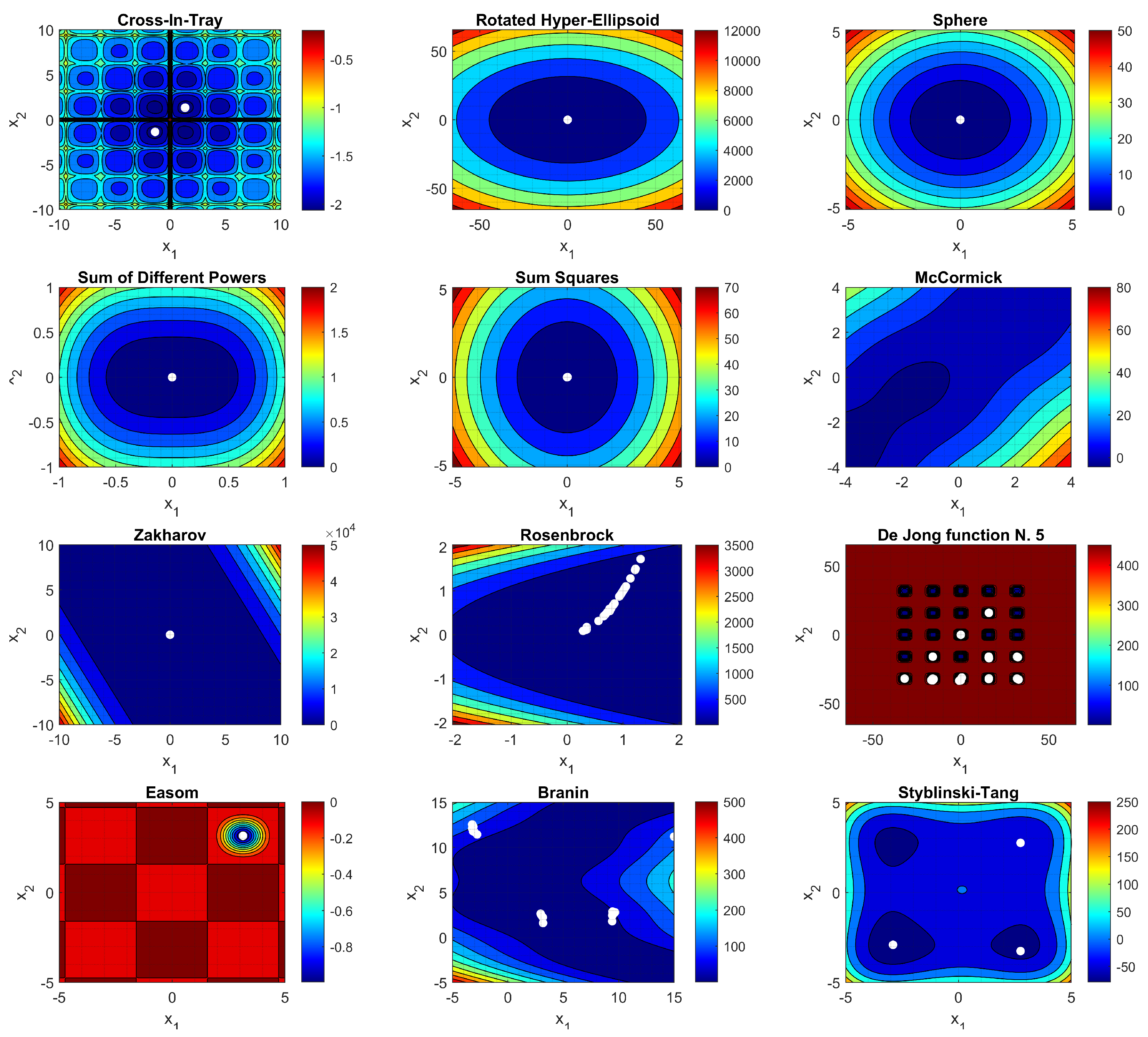
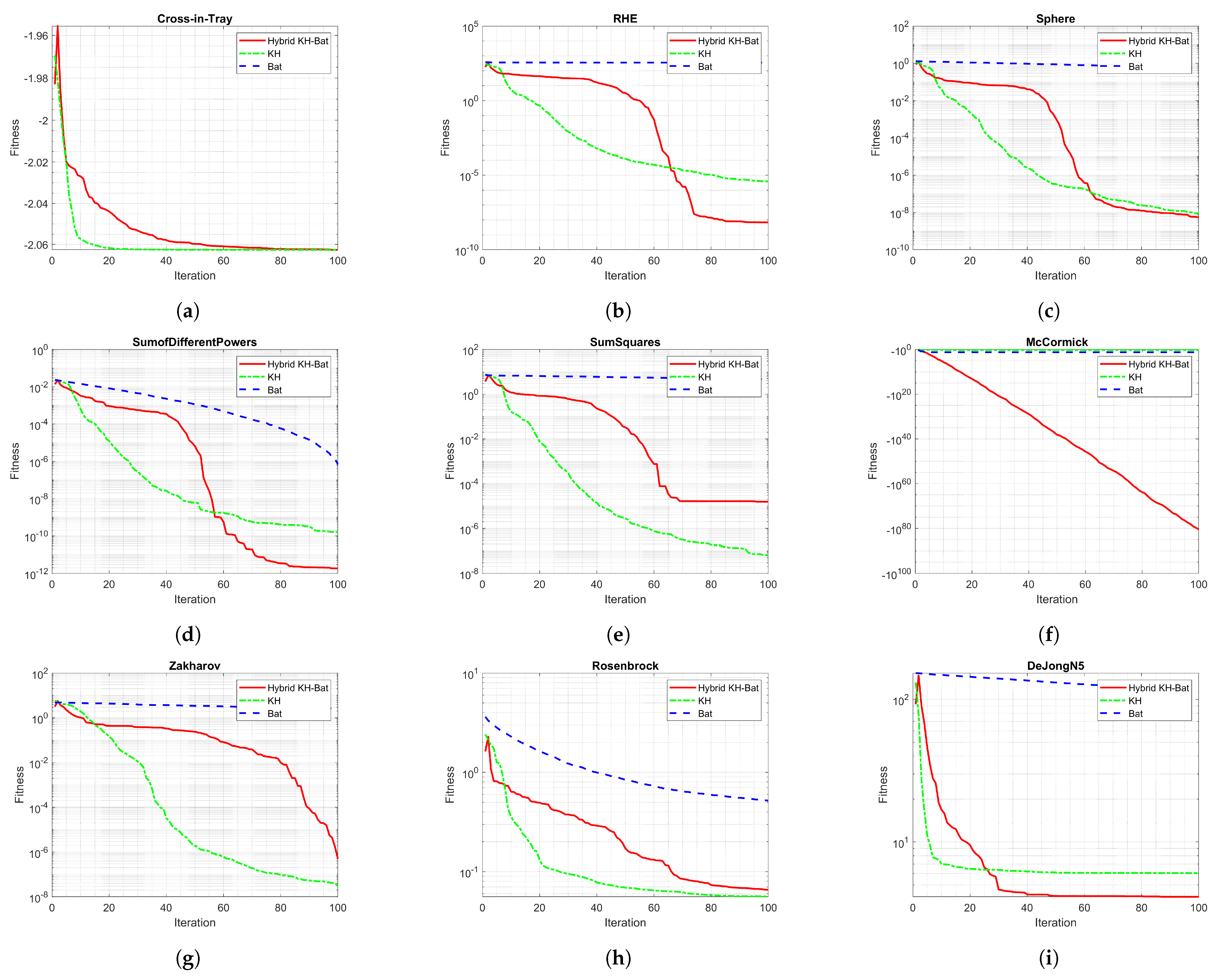
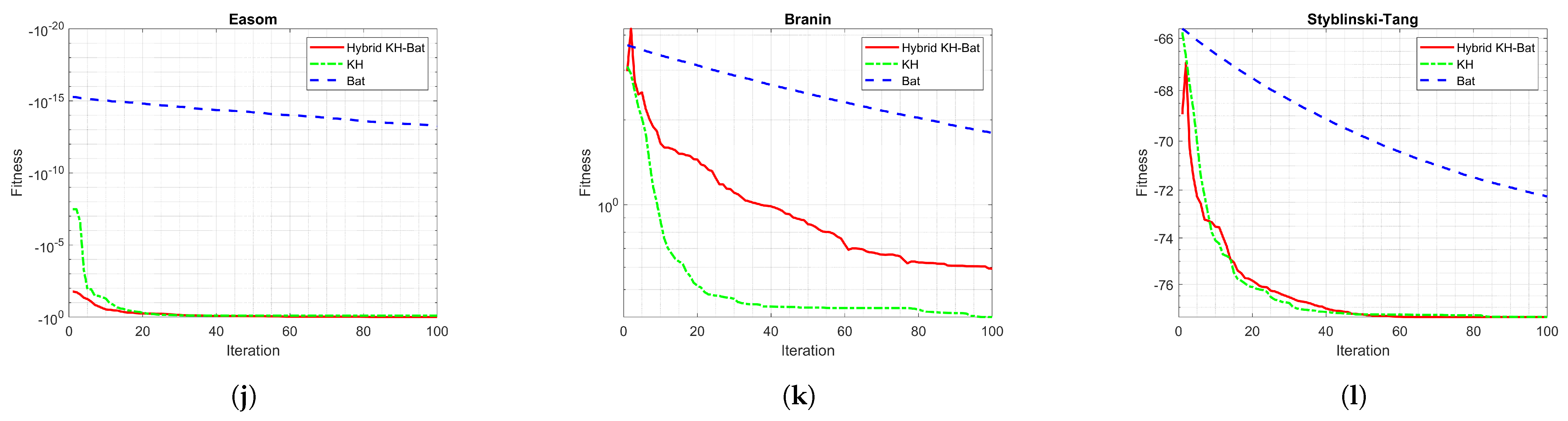
| Function | Ref. | Continuous | Differentiable | Separable | Scalable | Unimodal |
|---|---|---|---|---|---|---|
| Cross-In-Tray | [58] | Yes | No | No | No | No |
| Rotated Hyper-Ellipsoid | [59] | Yes | Yes | Yes | Yes | Yes |
| Sphere | [58] | Yes | Yes | Yes | Yes | No |
| Sum of Different Powers | [60] | Yes | Yes | Yes | Yes | Yes |
| Sum of Squares | [58] | Yes | Yes | Yes | Yes | Yes |
| McCormick | [58] | Yes | Yes | No | No | No |
| Zakharov | [58] | Yes | Yes | No | Yes | No |
| Rosenbrock | [58] | Yes | Yes | No | Yes | Yes |
| De Jong No. 5 | [60] | Yes | Yes | Yes | Yes | No |
| Easom | [58] | Yes | Yes | Yes | No | No |
| Branin | [60] | Yes | Yes | No | No | No |
| Styblinski–Tang | [58] | Yes | Yes | No | No | No |
| Algorithm | Optimum Weight | ||
|---|---|---|---|
| DOA | 0.788675095 | 0.40824840 | 263.8958434 |
| MBA | 0.78856500 | 0.40855970 | 263.8958522 |
| SSA | 0.78866541 | 0.40827578 | 263.8958434 |
| PSO-DE | 0.78867510 | 0.40824820 | 263.8958433 |
| DEDS | 0.78867513 | 0.40824828 | 263.8958434 |
| Proposed | 0.78853476 | 0.40866456 | 263.8958434 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Damaševičius, R.; Maskeliūnas, R. Agent State Flipping Based Hybridization of Heuristic Optimization Algorithms: A Case of Bat Algorithm and Krill Herd Hybrid Algorithm. Algorithms 2021, 14, 358. https://doi.org/10.3390/a14120358
Damaševičius R, Maskeliūnas R. Agent State Flipping Based Hybridization of Heuristic Optimization Algorithms: A Case of Bat Algorithm and Krill Herd Hybrid Algorithm. Algorithms. 2021; 14(12):358. https://doi.org/10.3390/a14120358
Chicago/Turabian StyleDamaševičius, Robertas, and Rytis Maskeliūnas. 2021. "Agent State Flipping Based Hybridization of Heuristic Optimization Algorithms: A Case of Bat Algorithm and Krill Herd Hybrid Algorithm" Algorithms 14, no. 12: 358. https://doi.org/10.3390/a14120358
APA StyleDamaševičius, R., & Maskeliūnas, R. (2021). Agent State Flipping Based Hybridization of Heuristic Optimization Algorithms: A Case of Bat Algorithm and Krill Herd Hybrid Algorithm. Algorithms, 14(12), 358. https://doi.org/10.3390/a14120358






