Abstract
The field of explainable artificial intelligence (XAI) aims to build explainable and interpretable machine learning (or deep learning) methods without sacrificing prediction performance. Convolutional neural networks (CNNs) have been successful in making predictions, especially in image classification. These popular and well-documented successes use extremely deep CNNs such as VGG16, DenseNet121, and Xception. However, these well-known deep learning models use tens of millions of parameters based on a large number of pretrained filters that have been repurposed from previous data sets. Among these identified filters, a large portion contain no information yet remain as input features. Thus far, there is no effective method to omit these noisy features from a data set, and their existence negatively impacts prediction performance. In this paper, a novel interaction-based convolutional neural network (ICNN) is introduced that does not make assumptions about the relevance of local information. Instead, a model-free influence score (I-score) is proposed to directly extract the influential information from images to form important variable modules. This innovative technique replaces all pretrained filters found by trial-and-error with explainable, influential, and predictive variable sets (modules) determined by the I-score. In other words, future researchers need not rely on pretrained filters; the suggested algorithm identifies only the variables or pixels with high I-score values that are extremely predictive and important. The proposed method and algorithm were tested on real-world data set and a state-of-the-art prediction performance of 99.8% was achieved without sacrificing the explanatory power of the model. This proposed design can efficiently screen patients infected by COVID-19 before human diagnosis and can be a benchmark for addressing future XAI problems in large-scale data sets.
1. Introduction
1.1. AI Systems for COVID-19 Chest X-rays
In the sixteen months since the WHO Emergency Committee declared a global health emergency on 30 January 2020 based on the outbreak of novel coronavirus SARS-Cov-2 (previously 2019-nCov, also known as COVID-19), the disease has spread to nearly every country in the world [1,2,3]. Globally, as of 25 April 2021, there have been 146,054,107 confirmed cases of COVID-19, including 3,092,410 deaths, reported to the World Health Organization (Source: https://covid19.who.int/ (accessed on 2 November 2021)). The initial clinical sign of the disease that allowed case detection was pneumonia [1]. Pneumonia mostly occurs in the second or third week of a symptomatic infection, with an average incubation period of five days [1,4]. Prominent signs of viral pneumonia include decreased oxygen saturation and blood gas deviations, as well as changes visible in the lungs through chest X-rays and other imaging techniques [1].
Since the start of the pandemic, the top priority for controlling the spread of COVID-19 has been monitoring suspected cases for appropriate quarantine measures and treatment. Pathogenic laboratory tests are the standard procedure (RT-PCR, collected with the invasive nasal swab most readers will be familiar with), but the accuracy of this test suffers from significantly occurring false negatives [1]. According to a study conducted early in the pandemic consisting of 1014 patients in Wuhan, China [5], the authors concluded that chest CT has a high sensitivity for diagnosis of COVID-19. Moreover, chest CT may be considered a primary tool for the current COVID-19 detection in epidemic areas [5]. This innovation, if used earlier, could have revolutionized the initial screening procedure of COVID-19 and might have prevented many unnecessary deaths. Looking forward, we theorize that other related diseases could use similar detection methods to prevent future epidemics and pandemics. Creating these methods now will ensure the development of testing procedures with the speed, accuracy, and explainability that will be required to deploy such artificial untelligence (AI) systems into future testing environments.
AI-centered medical-imaging-based deep learning systems have already been developed for image feature extraction, including shape and spatial relation features. Specifically, the convolutional neural network (CNN) has shown promising results in feature extraction and learning [3]. However, traditional CNNs heavily rely on pretrained filters (also known as kernels) that are designed to extract certain features from images, and are trained with past data sets that may or may not be relevant to the data at hand [6,7,8]. This traditional design has little ability to extract only the useful information, and creates noisy features that must be sifted. CNN models have many convolutional layers, and each convolutional layer uses many pretrained filters with no feature selection methods. Hence, any and all information created using pretrained filters, noisy or not, is included in those convolutional layers for later analysis. This architecture does nothing to further refine the features, which can therefore negatively affect the prediction performance. Moreover, there is no known CNN architecture that uses model-free (well-selected) feature selection methods designed to screen for the actually influential features used in the construction of each convolutional layer. In addition, common practices tend to increase the number of layers of CNN architectures to frustratingly large numbers [8,9,10,11]. Therefore, these deep CNNs consist of tens and sometimes hundreds of millions of parameters, so it is almost impossible to explain these models.
Although the advantage of the I-score is shown using a CNN in image classification tasks in this paper, the application of the I-score can be adapted to any large-scale data set in any supervised learning research task. The proposed methodology can be applied in a variety of different fields such as human computer interaction using brain waves [12,13], brain–computer interfaces [14], PEBL-based attention tests [14], and potentially advanced eye-tracking based evaluation that assist human–computer interaction [15].
To better assist the medical community by providing and deploying explainable artificial intelligence (XAI) systems for analyzing chest scans to save critical time that is necessary for disease control, we call for immediate attention to developing a self-interpretable and explainable convolutional beural network architecture capable of early disease detection.
1.2. What Is XAI?
In 2016, DARPA initiated the explainable artificial intelligence (XAI) challenge. The goal is to build suites of machine learning algorithms that are interpretable without sacrificing prediction performance (Figure 1). The trade-off between learning performance and the effectiveness of explanation is illustrated in Figure 1. The work in this paper delivers a novel interaction-based methodology that produces the power of interpretability and explainability while maintaining state-of-the-art learning performance.
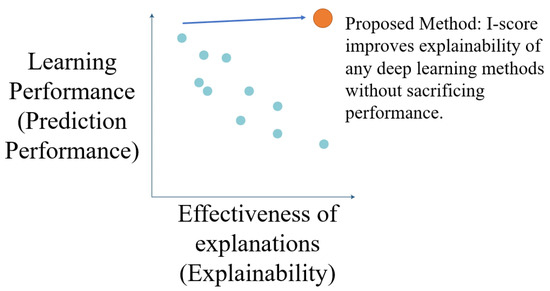
Figure 1.
DARPA document (DARPA-BAA-16-53) proposed this figure to illustrate a basic Explainable AI problem [19,20]. It presents the relationship between learning performance (usually measured by prediction performance) and effectiveness of explanations (also known as explainability). The proposed method in our work aims to take any deep learning method and provide explainability without sacrificing prediction performance. In the diagram, the proposed method is the orange dot on the upper right corner of the relationship plot.
A popular description of interpretability states the essential element for XAI is the ability to explain or to present in understandable terms to a human [16]. Another popular version defines interpretability as the degree to which a human can understand the cause of a decision [17]. Though intuitive, these definitions lack mathematical formality and rigorousness as certain perspectives [18].
In this paper, we regard the core issue of an XAI problem to be how features or variables are used to produce the prediction performance. In other words, the effectiveness of explanations in the DARPA document (Figure 1) is innately a variable set assessment and selection problem. This means the explainability and interpretability of a machine learning algorithm directly refer to what measures statisticians use to assess how the features or variables affect the final prediction results. In order to establish accountability, responsibility, and transparency in an AI system, one must first address an explainable and interpretable measure to assess feature importance. We define the following three dimensions, , , and , for a measure to be interpretable and explainable. In other words, these three dimensions serve as the key premises of the definition of an explainable and interpretable measure. This means that a measure that assesses the importance of a variable set needs to satisfy all three dimensions in order to be considered interpretable and explainable. We regard AI systems that explain features using an explainable measure such as explainable AI frameworks. This can be regarded as a heuristic framework for the existing concepts of interpretability and explainability.
: A quantifiable measure for interpretability and explainability does not need to rely on the knowledge of correct specification of the underlying model. In other words, any interpretable explanation of features used in making predictions should be directly associated with the response variable. If a model is used in explaining the feature importance and mistakes are carried over from model fitting to providing explanations, it is exceptionally challenging to differentiate the mistakes occurring in feature selection from mistakes created in the fitted model. Suppose a data set has input variables X and response variable Y, let us assume we use a fitted model , an ultra-deep neural network, to compute estimated label . Then, the conventional approach is to compute the loss between and ground truth Y, i.e., . In this case, the explanations of how input variables X affect the response variable Y have contributions from both the input variables X and the fitted model . In the cases of using ultra-deep neural networks as the fitted model, there are hundreds of millions of parameters, which makes expressing exceedingly challenging or an almost impossible task. This implies that the explanation is clouded by this fitted model and we cannot explicitly establish how the explanatory variables X affect the outcome variable (or response variable) Y. The requirement for this dimension is to directly create an understanding between X and outcome variable Y without searching for the fitted model . The notion of model-free is essential because it specifies a procedure such that any error calculated is solely dependent on the explanatory variables X and its labels Y (and thus independent of the model ). Therefore, a measure that is model-free and nonparametric is extremely crucial, and it is necessary to be defined as the first dimension .
: Any desirable measure for interpretability and explainability should clearly state how a combination of explanatory variables influence the response variable. Moreover, it is optimal if any audience can directly compute a score for a set of variables in order to perform reasonable comparisons. This means that any additional influential variables should raise this measure, whereas any existence of redundant or noisy variables should decrease the value of this measure. Hence, this second dimension, , states that a necessary condition for any measure to be interpretable and explainable is to allow its users to conduct comparisons and, potentially, select features.
: A measure appropriate for interpretability and explainability needs to clearly state the impact of the influential explanatory variables on the predictivity of the response variable. In other words, this measure should directly represent the predictivity (see Equation (2) of [21]) of the explanatory variables. This allows us to associate the importance of a set of variables with the learning performance (measured by prediction rate) of a set of variables. With the above three dimensions defined, research agendas toward searching for a criterion to locate highly predictive variables using an interpretable measure are imminent.
We regard a measure to be explainable and interpretable only when all three dimensions described above are satisfied. We illustrate in the next subsection why common practices involving deep CNNs are not satisfactory as an explainable methodology. To shed light on this problem, we recommend a fundamentally different approach, using the influence score (I-score), as an explainable and interpretable measure to extract features from image data, and construct important modules as input variables for neural network classifier. The proposed approach fulfills the requirement of all three dimensions (, , and ), and hence can be regarded as an explainable and interpretable CNN framework.
1.3. Problems in Image Classification and Deep CNNs
In the field of image classification, CNNs are well-known for their accurate prediction performance in image classification. This developing field of CNN architecture originated from LeNet-style [22], which consists of stacks of convolutional operation for feature extraction. In 2012, the procedure was improved by Krizhevsky et al. [8] using AlexNet. The refined architecture involves using convolutional operations many times in between max-pooling operations. Afterward, researchers constructed many deep CNNs. Amongst the family of these models, ultra-deep CNNs, including VGG16 [11], VGG19 [11], DenseNet121 [10], DenseNet169 [10], DenseNet201 [10], ResNet [9], and Xception [23], have produced good performance.
Though CNNs are successful in their application areas, no theoretical proof explains why they perform so well [6]. In addition, Khan et al. stated that a major challenge for the family of ultra-deep CNNs is the large size of the filters [7]. Another challenge is the underlying assumption of using learned feature maps due to the large filter size [7,8]. The issues to these problems described, above all, are related to the attempt to guess the feature map among many convolutional layers by using trial and error. Specifically, the procedure of building convolutional layers in the literature relies heavily on many different filters with each one designed to capture certain information that was previously discovered in other data sets that may or may not be related to the current practice. In other words, there is no comparison or any feature selection procedure adapted among the filters used or identified in constructing these ultra-deep CNNs. Because no feature selection is conducted amongst the filters, all useful and noisy filters remain in the operation to construct convolutional features, which are later used in many deep hidden layers of the neural network classifier to perform predictions. Thus, we cannot easily trace back to the original variables and observe which variables have a large impact on the response variable. We regard this as the major drawback and disadvantage of using too many pretrained filters that are uninformative and noisy.
This doctrine is problematic because it is challenging for human decision makers to directly investigate the data and interpret the information that is locally preserved in the image data. In other words, we still face difficulties to explain feature importance using models when the statistician has no knowledge of the ground truth of the real situation. Any mistake in searching for this model would be carried over when explaining the features. Because the procedure seeks the correct specification of the underlying model when it tries to explain the features, the explainability of the feature importance fails to check the first dimension. In other words, this does not satisfy the condition in , which fails to serve as the rightful candidate to address XAI problems.
In ResNet [9], questions arise in its many layers of convolutional architecture, with an astounding number of over 25 million parameters that may or may not contribute any information to making predictions. In the same architecture, the procedure recommends relearning of feature maps when making interpretable predictions [7]. The same issues also appear in DenseNet [10]. The DenseNet family has many versions in their design. The simpler one has approximately one million parameters for DenseNet121 and some upgraded versions of DenseNet have 40 million parameters [10]. Another related drawback is its heavy computational cost in training and tuning these ultra-deep CNNs [7]. A short summary of the number of parameters for some well-known architectures is provided in Table 1. Due to the large number of parameters, it is difficult to explain how every parameter contributes to the prediction performance and to delivering the explainability that satisfies the three dimensions defined above. Some may also consider background information when the algorithm is making predictions. This problem arises because many convolutional layers are built in the network architecture and there is no procedure of screening for noisy variables that hinder the explainability power. In other words, it cannot be explained how a certain feature or a combination of features can assist us in classifying the target variable. Hence, this does not satisfy the second dimension , and it is complicated for users to understand the exact information that needs to be used for making predictions. Since it is difficult to search for an understanding to discriminate important variables from noisy ones, the second dimension is not met and, hence, it is suboptimal to use these ultra-deep CNNs when building interpretable models.

Table 1.
Summary of some well-known CNNs and their number of parameters.
Thus far, we do not have an ideal deep CNN architecture that can satisfy all three dimensions (, , and ) of the definition of interpretability. Due to the above reasoning, the conventional methodologies cannot serve as good candidates to address XAI problems.
1.4. An Interaction-Based Convolutional Neural Network (ICNN) to Address XAI Problems
Chernoff, Lo, and Zheng [24] presented a general intensive approach, based on a method pioneered by Lo and Zheng [25] for detecting which, out of many potential explanatory variables, have an influence (impact) on a dependent variable Y. This paper presents an interaction-based feature selection methodology incorporating the notion of an influence score (I-score) as a major technique to detect the higher-order interactions in complex and large-scale data sets. In our work, we investigated the potential usage of the I-score and a novel deep learning framework. The executive diagram is shown in Figure 2, which outlines the road map of the proposed methodology and the architecture of a novel interaction-based convolutional neural network (ICNN). This novel architecture takes full advantage of the I-score and the backward dropping algorithm. In other words, it produces convolutional layers that are self-interpretable, which provides explainability power to the features of image data at any convolutional layer if this design is implemented. In the following section, we discuss the contribution of our work and why the proposed method satisfies the three dimensions defined in Section 1. With all three dimensions satisfied (, , and ), the proposed design of an ICNN is the ideal candidate to address XAI problems.
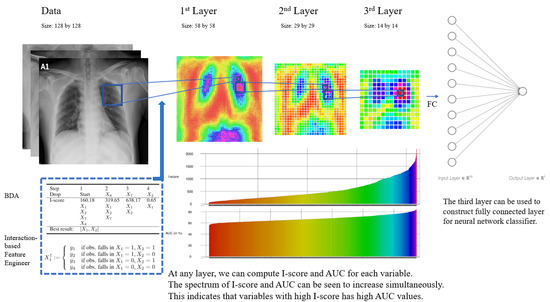
Figure 2.
This executive diagram summarizes the key components of the methods proposed in this paper. We start with the COVID-19 image data. With a small rolling window defined, we execute the backward dropping algorithm to select the important features within this window. For example, the rolling window may cover 4 variables, , and the BDA could select as a variable module. Then, we can construct a new variable using the interaction-based feature engineer technique (see the construction of in Equation (6) to appreciate this new design). In other words, using the selected variables and , we construct . The procedure of the BDA is illustrated in the bottom left corner of the figure (we use a 2 × 2 window for simplicity). We set the starting point to be 12 (i.e., start from the pixel in the 12th row and the 12th column). From the data (size of 128 × 128) to the 1st layer (58 × 58), this gives us a new dimension that is computed by (see Equation (18)). We can repeat the process in the 2nd layer and the 3rd layer. After the 3rd layer, we shrink the dimension to 14 × 14 (which gives us 196 new variable modules, i.e., the new ). We fully connect these 196 variable modules with the 10 neurons in the hidden layer (in practice, the number of hidden layers and the number neurons are tuning parameters). This novel design is fundamentally different than the conventional practice of using pretrained filters because it proposes to use an explainable measure, the I-score, to extract and build information directly from images in the training data. For each local variable (in the data, this refers to pixels; in the layers, it is referred to as variables), we compute the I-score values and the AUC (see Section 4.4 for a detailed discussion of AUC values) for that variable (using this variable as a predictor alone). We observe that the I-score value fully represents the predictivity of each local variable, which can be confirmed by the variable’s AUC value. The color spectrum of both the I-score and AUC are presented in the bottom part of the diagram. We observe I-score values exhibiting behavior parallel to AUC values. This means the variables with high I-score values have high AUC values, which indicates strong predictive power for the information in that location. This design heavily relies on the I-score and has an architecture that is interpretable at each location of the image at each convolutional layer. More importantly, the proposed design satisfies all three dimensions (, , and in the Introduction) of the definition of interpretability and explainability.
2. Contributions of the Paper
The contributions of the proposed work are as follows. We remark here that the three contributions listed above meet the three dimensions outlined in the previous section (, , and ).
First, we introduce a model-free and interaction-based learning methodology, the influence score (I-score). We illustrate how to use the I-score to select and measure features that are directly linked to the predictivity of the response variable [21,26]. Moreover, this quantifiable measure does not rely on any specification of the underlying model. Hence, this meets the first and the third requirements, i.e., and of interpretability and explainability. We apply this measure along with a greedy search algorithm called the backward dropping algorithm (see Section 3.2 for a detailed discussion to appreciate this method) locally to image data. In other words, instead of using a set of predefined filters (or kernel) that are applicable to various kinds of deep CNNs on image data by trial and error, we propose using the I-score and the backward dropping algorithm on a local window to extract important and influential features from image data.
Second, we show that the selection of explanatory variables relying heavily on the proposed I-score method can produce robust prediction performance. The removal of these influential features produces subpar performance along with a reduced I-score. The phenomenon of reduced I-score allows us to compare the explanatory power of any combination of variables. This desired property of the I-score allows us to directly compare any variables or any combination of variables. Furthermore, this makes the I-score the ideal candidate for feature selection and for removing noisy variables in the data. This satisfies the requirement of the second dimension .
Third, we propose and implement a novel method of combining features from any combination of variables in order to construct interpretable and explainable convolutional layers to represent the information in image data. This methodology heavily relies on the usage of the I-score, which satisfies all three dimensions , , and .
The key novelty of our proposed approach (see the executive design in Figure 2) rests on the collection of features identified by the I-score. Based on the contributions described above, the proposed method is model-free and hence meets the first requirement . It describes a quantifiable measure of how much a combination of explanatory variables impacts the outcome variable, which allows statisticians to perform comparisons and screen for influential features. This phenomenon meets the second requirement . In addition, the statistics, the I-score, provides a measurement for explanatory variables that is directly associated with the predictivity of the explanatory variables on the outcome, variable which satisfies the third condition . With all three conditions (, , and ) satisfied, the design of the proposed architecture produces an interaction-based convolutional neural network (ICNN) that is innately interpretable and explainable. It extracts influential information from the image data and generates explanatory features that directly associate with the predictivity of the data. Because all three conditions are met, the proposed design of CNN is interpretable and it serves as a touchstone in the field of XAI.
2.1. Why the Proposed Methodology Satisfies XAI Dimensions
The illustration of the proposed ICNN is presented in Figure 2. This executive diagram describes the step-by-step procedure of how the proposed network architecture was designed and why it satisfies the three dimensions (, , and ) in the definition of interpretability and, hence, can be the benchmark in addressing XAI problems.
Proposed Architecture. The executive diagram of the proposed architecture is presented in Figure 2. First, the architecture starts with image data that consists of X-ray pictures sized 128 × 128 (see detailed discussion of COVID-19 data set in Section 4). The architecture proposes using a 2 ×2 rolling window (we use a 2 × 2 window for simplicity; larger sizes can be applicable as well in practice depending on the data). Since the window size is 2 × 2, this means there are four variables every time the window rests on a certain location of the image. Within this subset of variables, we execute the proposed backward dropping algorithm (BDA). This procedure finely selects a subset of variables that is highly predictive by omitting the noisy variables in this small neighborhood on the image. Next, the selected variables (which can be any subset of the original four) undergo a proposed procedure called interaction-based feature engineer (see (6) for a definition). The BDA procedure is illustrated in the bottom left corner of Figure 2 (we use a 2 × 2 window for demonstration purpose). In addition, we set the starting point to be 12 which means we start from the pixel in the 12th row and the 12th column. From data (size of 128 × 128) to the 1st layer (58 × 58), this procedure produces a new feature matrix with size on both edges, which means the new feature matrix has 58 × 58 variables (the formula is presented in Equation (18)). This feature matrix constitutes the first interaction-based convolutional layer. We can then use the same methodology to construct the second and third interaction-based convolutional layers. The third interaction-based convolutional layer can be used as the input layer for a neural network classifier. For each layer, we can compute the proposed I-score and the AUC value (see Section 4.4 for a detailed discussion of AUC values) for each variable (assuming using this variable as a predictor when computing the AUC value). The paths of the I-score and AUC values have parallel behavior, which is shown in the color palette of the spectrum in Figure 2.
Why the Proposed I-score Satisfies XAI Dimensions. The design of the proposed architecture in Figure 2 mainly focuses on using the I-score and the BDA to extract and engineer features from the original images. The proposed I-score is nonparametric (see Section 3.1 for a definition of this measure). This means the impact of the explanatory variables on the response variable measured by the I-score does not rely on the knowledge of the correct specification of the underlying model. In other words, the computation of the I-score does not rely on any model fitting procedure. This characteristic satisfies the first dimension, , defined in Section 1 about interpretable measures.
Next, the proposed architecture is transparent at disclosing to its human users what locations of the image are important in making decisions about prediction and what locations are noisy. In every interaction-based convolutional layer, we can compute the proposed I-score for any single variable. We can also compute the I-score and finely select predictive variables from any combination of variables. The larger the I-score, the more important the variables in making predictions. With the simple visualization presented in Figure 2, we are able to use a spectrum of different colors to illustrate this phenomenon. We can code high I-score values as one side of the color spectrum and the low I-score values as the opposite side. The areas that are informative have high I-score values and have very different colors than the areas that are noisy. This characteristics of the I-score allows the statistician to perform comparisons and variable selection assessment. Therefore, it satisfies the second dimension, , defined in Section 1.
Third, the proposed architecture has a direct association with the predictivity (see Equation (2) in [21]) of a variable set. This means that the important features screened by the I-score describe to the statistician how much impact this variable set has on the response variable. In addition, it is beneficial to be able to compute the I-score for any variable in any interaction-based convolution layer, which implies that the association with the predictivity is well-stated in each step of the architecture. This can be visualized using the AUC values (see Section 4.4 for a detailed discussion of AUC values) that are coded onto the same spectrum location of the I-score values. Moreover, the paths of the I-score and AUC values show parallel behavior. This implies that the values of the I-score and AUC increase and decrease together, which means each variable with a high I-score measure would have a high AUC value and vice versa. This interesting yet powerful phenomenon allows this architecture to satisfy the third criteron, , stated in the definition of an interpretable measure, which is novel in the literature.
As a summary, we identified that the proposed ICNN relies on the I-score, which is a measure that satisfies the three criteria of an explainable and interpretable measure. We regard the proposed ICNN as an explainable and interpretable deep learning algorithm. Thus far, we have not been able to identify other methods and procedures that satisfy all three dimensions defined in Section 1.
2.2. Organization of the Paper
Section 2 starts with introduction of two adopted techniques: the influence score (I-score) and the backward dropping algorithm. In addition, we introduce an interaction-based convolutional neural network that is different than any previously designed CNN architecture. The key advantages of this proposed approach add autonomy and flexibility when seeking for the variable set, which are powerfully influential on outcome variable. Another advantage is that the selection of these variables is automatically dependent on the combined essential tools that were developed in previous papers [24,25,27], which revolve the usage of the I-score and the backward dropping algorithm. With simulation, we present examples of how the proposed methodology operates. In the last section, Experimental Results, we introduce our laboratory procedure including model training, parameters’ and hyper-parameters’ tuning, evaluation metrics, performance, and visualizations.
3. Proposed Method
The proposed methodology involves three stages. First, we investigate variables to identify those with high potential to form influential modules. Secondly, we generate highly influential variable modules from variables selected in the first stage, where variables of the same module interact with each other to produce a strong effect on Y. Lastly, we combine the variable modules to perform the prediction process.
From prior simulation experience, we demonstrated that the two basic tools, the I-score and backward dropping algorithm, can extract influential variables from data sets with regard to modules and interaction effect. However, questions remain on how to determine the input to the backward dropping algorithm and how to use the output from the algorithm results to construct prediction estimates. Unless we can appropriately use the input to and output from the backward dropping algorithm, the strength of the algorithm cannot be fully used. In this sense, the innovation of the proposed method manifests in three ways. First, if we directly apply the backward dropping algorithm on high-dimensional data sets, we may miss some useful information. We propose a two-stage feature selection procedure: interaction-based variable screening (this is called the interaction-based convolutional layer, see Section 3.3) and variable module generation via the backward dropping algorithm (which is called the interaction-based feature engineer, see Section 3.4). Since the impurity of features is largely enhanced by the interaction-based variable selection algorithm in the first stage, we were able to construct variable modules that have higher-order interactions with large amounts of information in the second stage. These variable modules provide support as building blocks for us to form classification rules. These schools of thoughts produce results significantly better than directly applying the backward dropping algorithm.
The statistics, the influence score (I-score), works better with discrete variables. If some explanatory variables are continuous, we first convert them into discrete ones for feature selection purpose. After we have selected the important variables, we use the original values to estimate their effects. We rely on the influence score when we convert continuous variables into discrete variables. For example, if a random variable is drawn from normal distribution, then one optimal cutoff is to use the one that has the largest marginal I-score. There is a trade-off induced from this process: the information loss due to discretizing variables from continuous to discrete forms versus the information gain from robust detection of interactions by discretization. Wang et al. [27] demonstrated that the gain from robust detection of interactions is much more than enough to offset possible information loss due to discretization. Wang et al. [27] used the two-mean clustering algorithm to convert the gene expression level into a variable with two categories: high and low. As an additional piece of evidence supporting the proposed preprocessing step, the authors tried more than two categories, i.e., three categories of high, medium, and low. The empirical results showed that the more the categories used, the worse the classification error rates.
3.1. Influence Score (I-Score)
Assume that we have a binary response variable Y (taking values of 0 and 1) and all explanatory variables are discrete. Consider the partition generated by a subset of k explanatory variables . Assume all variables in this subset are binary. Then, we have partition elements; see the first paragraph of Section 3 in Chernoff et al. [24]. Let be the number of observations with in partition element j. Let be the expected number of in element j. Under the null hypothesis, the subset of explanatory variables has no association with Y, where is the total number of observations in element j and is the proportion of observations in the sample. In Lo and Zheng [25], the influence score is defined as
The I statistic is the summation of the squared deviations of the frequency of Y from what is expected under the null hypothesis. There are two properties associated with the I statistic. First, the measure I is nonparametric, which does not require the specification of a model for the joint effect of on Y. This measure I is created to describe the discrepancy between the conditional means of Y on , disregarding the form of the conditional distribution. Secondly, under the null hypothesis that the subset has no influence on Y, the expectation of I remains nonincreasing when dropping variables from the subset. The second property makes I fundamentally different from Pearson’s statistic, the expectation of which is dependent on the degrees of freedom and, hence, on the number of variables selected to define the partition. We can rewrite the I statistic in its general form when Y is not necessarily discrete:
where is the average of Y observations over the jth partition element (local average), and is the global average. Under the same null hypothesis, Chernoff et al. [24] showed that the normalized I, (where is the variance of Y), is asymptotically distributed as a weighted sum of independent random variables of one degree of freedom each such that the total weight is less than one. It is precisely this property that serves as the theoretical foundation for the following algorithm.
3.2. Backward Dropping Algorithm (BDA)
The BDA is a greedy algorithm that searches for the optimal subsets of variables that maximizes the I-score through step-wise elimination of variables from an initial subset sampled using in some method from the variable space. The steps of the algorithm are as follows:
- Training Set: Consider a training set of n observations, where is a p-dimensional vector of explanatory variables. The size p can be very large. All explanatory variables are discrete.
- Sampling from Variable Space: Select an initial subset of k explanatory variables ,
- Compute Standardized I-score: Calculate . For the rest of the paper, we refer o this formula as the influence measure or influence score (I-score).
- Drop Variables: Tentatively drop each variable in and recalculate the I-score with one variable less. Then drop the one that produces the highest I-score. Call this new subset , which has one variable less than .
- Return Set: Continue to the next round of dropping variables in until only one variable is left. Keep the subset that yields the highest I-score in the entire process. Refer to this subset as the return set, . This will be the most important and influential variable module from this initial training set.
3.3. Interaction-Based Convolutional Layer
This section proposes an interaction-based convolutional neural network. This action is presented in Figure 3. In this diagram, we start with an image that is sized 64 × 64 and suppose we use a window that has a size of 4 × 4. Thus, this small window has 16 pixels locally. This set of 16 pixels can be converted into binary variables, which hence provides a well-defined partition. For example, we can discretize these pixels into black and white. In other words, each pixel takes value 1 or 0 (two levels) and the set of 16 pixels would create a partition that is sized . This is the set up for us to run the BDA. Based on the definition of the BDA, in each round, we take turns dropping one variable iteratively. Every time we drop a variable, we compute the I-score. We drop the variable at each step such that the I-score is the highest if that variable is dropped. Using this procedure, we are able to select a subset of variables out of the original 16 pixels.
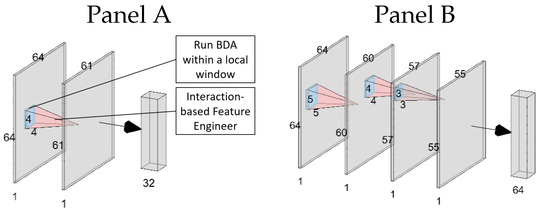
Figure 3.
This is the architecture of the interaction-based convolutional neural network (ICNN). In Panel A, the input matrix is 64 × 64. Suppose the small rolling window is 4 × 4. By rolling this small window from the top left corner to the bottom right corner of the input matrix, we create a 61 × 61 output matrix. These 61 × 61 variables are then used to build a neural network classifier with a hidden layer that has 32 units. The number of hidden layers and number of units per layer are tuning parameters. Panel B depicts an architecture that is much deeper, with each layer adopting the design in Panel A.
A deeper but similar architecture can be constructed using the following diagram. In Figure 3, we propose a deep interaction-based convolutional neural network. Instead of building a single ICNN, multiple such layers can be constructed using the same procedure. Suppose we start with an image that is sized 64 × 64. Further suppose we use a window that is sized 5 × 5. This provides 25 pixels to work with locally and to run the BDA. We start rolling this small window from the first row and the first column. Next, we shift this small window to the right and then to the bottom until we hit the 60th row and the 60th column (this can be understood as rolling a small window from the top left corner to the bottom right corner of the image). After constructing the first interaction-based convolutional layer, we shrink the size from to . In the next step, we operate with the same procedure by using a window of size 4 × 4, which allows us to further shrink the dimension to . After constructing the interaction-based convolutional layers, the number of hidden layers and the number of units per hidden layer are both tuning parameters.
3.4. Interaction-Based Feature Engineer
This subsection defines a procedure to mechanically engineer an interaction-based feature.
For a image (that is, an image that has 9 pixels), we write these pixels as . Consider a small window of passing from the first row and the first column of this image. This means we start with within this small 2 × 2 window in this example. We use the BDA to narrow down to because we observed that this subset of variables delivers the highest I-score. Since both and are discretized into two partitions, we have partition well-defined (see Equation (3)). In other words, assume and both only take values of 0 and 1. Then, the partition is defined as:
In this case, each partition , while ; we can compute the local mean of response variable Y from observations in the training set. Hence, a new interaction-based feature can be constructed:
In the general situation, let us consider an input matrix with size by . Suppose the window size is and the stride level is l (notice in the above example that and ). Using Equation (5), which is defined below,
we can compute an output matrix with size × (which coincides with the matrix). In this case, we define running index b to take values . In the example in the previous paragraph, b can take value because , thus . For each round b of the backward dropping algorithm (b takes a value from in this example), we can construct a new variable module that takes Formula (6), defined below,
whereas is defined as using observations in training set, and j indicates the jth partition of that is formed by the variables selected from the b round of the BDA. Hence, the relationship of the input matrix and output matrix can be visualized using the following diagram.
where the input matrix is 3 × 3 and the output matrix is 2 × 2. In the output matrix, is defined using Equation (6) with observations in the training set.
3.5. Simulation with Artificial Examples
In this section, we illustrate the proposed methodologies on the following artificial examples.
3.5.1. Artificial Example I: Variable Investigation
In the first artificial example, we demonstrate the procedure followed to construct the interaction-based convolutional layer and the engineer interaction-based features.
Let us consider the following experiment. We create an artificial data set with 500 data points in he training set and 10,000 data points in the testing set. These observations are randomly drawn from independently. In other words, we independently generate , where . We define the underlying model to be the following (here known as Model (7)),
Model (7) is a two-module example. The first module is a two-way interaction in modulo 2. The second module is a three-way interaction in modulo 2. The response variable Y is defined as 50% first module and 50% second module. In this setup, the individual explanatory variable does not have any predictive power on the response variable Y.
Scenario I. Assume the statistician knows the model in this simulation. This means they are fully aware of as an important variable set and as the other. In other words, they can use the first module as a predictor to make predictions on response variable Y. They are able to compute the theoretical prediction rate of the first variable set as 75%. This is because the response variable is defined as the first variable module exactly 50% of the times, so is able to guess Y correctly at least 50% of the time. The other 50% of the time, the response variable is defined as the second variable module . Since there is no marginal signal, the performance is exactly like random guessing, so the rest of the occurrences are only correct 50% of the time. In other words, assuming training sample size has n data points, we can write the following:
This result can be extended to the other variable module as well. If this statistician uses the second variable module , then a similar calculation can be carried out in the following.
The theoretical prediction rate for Model (7) is the maximum percentage accuracy delivered by and . In this case, we have .
Scenario II. In practice, it is often the case that we do not exactly observe the underlying model in a given data set. The recommendation is to use the I-score to select the important local information and then create an interaction-based feature based on the selected variable. The diagram for this action is depicted in Figure 4.
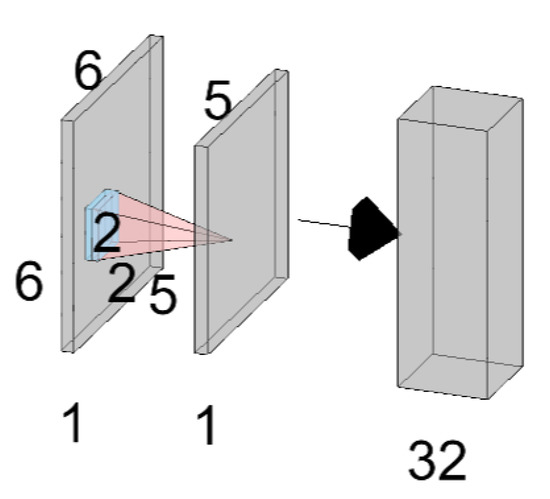
Figure 4.
The network architecture with simulated data. The artificial data has variables, which can be arranged in a grid structure with shape of 6 × 6. We use a window size that is 2 × 2. By passing this window from the top left corner of the original 6 × 6 matrix, we create a new 5 × 5 matrix. The number 32 is the number of units in the hidden layer. In this example, there is one hidden layer, which is sufficient for the dimension of the data in the example.
The classical procedure of a convolutional neural network starts with many predefined filters (or kernels) from a previous data set. The size of this filter can be , , or any other higher dimension. The procedure starts with the first row and the first column. Then, the process passes the filter over and across rows and columns in the image. The proposed methodology shares similar characteristics. However, instead of using a pretrained filter, we apply the BDA in this local area.
Constructing the Proposed Convolutional Layer. In the proposed artificial example, we have a data set with 36 variables. This means each observation can be reshaped into a grid structure. In other words, each observation can be considered as an image. The first row and the first column is variable . The first row and the last column is variable , so we can arrange these variables into the following structure:
and the 4 red-colored variables are the first used in the BDA. If the window size is , we would use and execute the BDA on the variables within this window.
Notice that in the diagram (Figure 4), the blue region indicates a local area where we run the backward dropping algorithm. The pink region indicates the engineering workflow of building interaction-based features using Equation (4). For each window, we run the BDA. The procedure adopts the steps introduced in Section 2.2. The steps are listed in Table 2. First, we start with all 4 variables, which are . For each step, we take turns dropping one variable and compute the I-score for the remaining variables. It can be seen that should be dropped because the I-score raises from 160.18 in step 1 to 319.65 to step 2. We conduct the same procedure in step 2 and realize that needs to be dropped. Then, the I-score increases to 638.17. We can keep dropping variables, but the statistician realizes that the I-score is the highest when there are only two variables left: . Hence, we place an up-arrow at the step to indicate the optimal variable selection (see the up-arrow in Table 2). In this experiment, the most optimal selection is the variable module with an I-score of 638.17.

Table 2.
The steps of the backward dropping algorithm in a window.
For each local area with a window size of , we discussed in the above how to finely select the important variable. Similar to the standard procedure of convolutional neural networks using a filter on a local area of an image, the proposed method also investigates local information. However, instead of relying on many filters that are predefined, the proposed approach uses the I-score, a model free influence measure that directly associates with predictivity. After the variable module is selected within a local window, we adopt Formula (4) to create interaction-based features. For example, in the local window above, we narrow down to variable module . This means we can create the first interaction-based feature as the following:
where , which corresponds to the partitions generated by . This provides the first predictor to allow us to build classifier and to make predictions.
The experimental results from the first artificial example are listed in Table 3, Table 4 and Table 5. Suppose a statistician knows the model. The theoretical prediction rate is 75% (which is derived using Formulas (8) and (9)). In reality, we suppose that a statistician has no knowledge of the data set. In this case, they can directly proceed using a neural network or even CNN to make predictions. However, without the correct model specification, the performance for these models is subpar. We can see that the neural network and CNN both performed 50% on he test set. This performance is rather like random guessing. Alternatively, this statistician can perform the experiment using the proposed methods. First, we can generate an interaction-based convolutional layer. Instead of using many pretrained filters for feature mapping, the proposed method adopts the I-score and the backward dropping algorithm to construct , , and so on. The proposed methodology also has an exact I-score that is associated to each variable module, which allows us to rank feature importance. With the I-score, the first variable module is much more influential than the other variable modules.

Table 3.
Interaction-based convolutional layer. Foran artificial data set with variables and a window size of , we pass the window from the top left corner down to the bottom right corner. For each particular location, we have 4 variables to run the BDA. Before each observation had 36 features that could be sized . Afterward, each observation has 25 new features that have the shape of . In other words, we create , where . The asterisk indicates extremely influential variable module(s). For each variable module, we also present the AUC value (see Section 4.4 for a detailed discussion of AUC values) assuming a classifier is built using this variable module alone.

Table 4.
Interaction-based convolutional layer. For an artificial data set with variables and a window size of , we create 16 new features that can be shaped into . The procedure of generating these 16 new features follows the same procedure as in Table 3. The only difference is the window size, i.e., here, we use . In other words, we are able to create while . The asterisk indicates extremely influential variable module(s). For each variable module, we also present the AUC value (see Section 4.4 for a detailed discussion of AUC values) assuming a classifier built using this variable module alone.

Table 5.
The performance of a simulation. In this simulation, we defined the underlying model to be (7). The theoretical prediction rate is 75%. A conventional model such as Net-3 and LeNet-5 does not perform well in this example [28,29]. The proposed method that uses the I-score has prediction performance that is close to the theoretical prediction rate (see Section 4.4 for a detailed discussion of AUC values). NN, neural network. This is discussed in Section 4.2 and please review the architecture in Figure 5 for a detailed description.
We proceed using a window size of . In a data set with variables, this produces variable modules. Using these 25 variable modules, we are able to build a classifier and achieve a performance of 76% AUC (see Section 4.4 for a detailed discussion of AUC values) on the test set, much higher than the previous 50%. We can also use a window size of . This produces variable modules. These 16 modules allow us to build another classifier using a neural network and delivers a 76% AUC on the test set as well.
The detailed variable modules and their corresponding I-scores are exhibited in Table 3. In this table, we present four columns: New Modules, Variables, Associated I-score, and Corresponding AUC. The new module is constructed using (6). The variables were obtained from the BDA. The I-score of a variable set is computed using Equation (2). For computation of the AUC, please see Section 4.4 In the artificial data set that has variables, a window size of allows us to generate variable modules. Each module is created using the selected variables from a local window after using the BDA, and the module is generated using Formula (4). We observe that the variable module that is formed based on is the most influential candidate because it directly links to predictivity. This can be confirmed using the AUC value if this module is used to build a classifier by itself.
A different window size can be selected. In this artificial example, we attempt . For data with variables, a window size of allows us to create variable modules. The results of this experiment are listed in Table 4. In Table 4, we observe a slightly different set of variable modules selected. We notice that the most influential variable module that is based on remains the same. In other words, if a local section of the data has real predictive power, the proposed method will almost always identify the information.
This can be verified using the AUC value associated with the variable module. Since we pass a window, we are able to sometimes screen for higher-order interactions. As discussed above, we have the I-score presented in Table 4, so that feature ranking is possible if desired. From this table, we observe that another module , that was constructed using , is also important. Though it has a lower I-score than the first module , it has a higher I-score than any other candidates in the data set.
Prediction. After the variable modules (the variables named ’s) are constructed, we can proceed with building the neural network classifier. In Table 3, there are 25 variable modules, i.e., . We use these variable modules as the input layer of a neural network architecture. In other words, the input layer has 25 neurons (these neurons are the exact 25 variable modules named ’s). For the variable modules in Table 4, the input layer consists of 16 neurons, which are . Since we are dealing with a rather small input layer (only 25), no hidden layer is recommended. The output layer can simply be one neuron, and the final outcome can be computed using a sigmoid function as follows:
assuming we use the 25 variable modules (the ) in Table 3. Alternatively, suppose we use the 16 variables modules, , in Table 4. We can compute using the following:
assuming the same activation function to be sigmoid (the same as (10)). This architecture is called forward propagation ( standard architecture widely used in neural network). This is discussed in Section 4.2 and review the architecture in Figure 5 for a detailed description. We assume there is no bias term. Then, the objective is to minimize the loss between Y and . Hence, we write . We can simply choose the loss function to be square-error, which means . In order to minimize this loss function, an optimizer algorithm is required and we can choose the standard gradient descent algorithm.
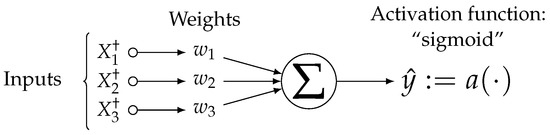
Figure 5.
The above architecture presents a feed forward neural network with three input variables. The input variables are , which are variable modules created using Equation (6).
The results for the first artificial example are presented in Table 5. We discussed in Scenario I that the theoretical prediction rate is 75% if a statistician knows the model. In practice, we assume that the statistician has no knowledge of the model. In this case, the standard approach is to directly work with all variables. This means we can build a classifier by, e.g., using a neural network. In this example, we observe the data set has variables. This means we can also adopt a convolutional neural network by reshaping the input dimension for an observation from into . Both the neural network and CNN perform poorly, i.e., an AUC of approximately 50%. This is because the underlying model is in binary form and there is no marginal signal. In addition, the in-sample training set has only 500 observations, which further increases the difficulty for complex architectures such as deep learning models. However, this issue can be resolved if we have the correct model specification. Based on the proposed methodology, we are able to create the variable modules presented in Table 3 and Table 4. Their performance on the test set is presented in Table 5. A window size of produces 25 variable modules and achieves an AUC of 75%. A window size of produces 16 variable modules and achieves an AUC of 76%. These results approximate to a 75% theoretical prediction rate.
3.5.2. Artificial Example II: Four Modules with Discrete Variables
For a more complex example, we designed an experiment that is similar to the one before but with more high-order interactions. We create a data set with 49 variables, . Each takes binary form, 0 or 1. We define dependent variable Y as the following form, namely Model (12),
which is a more complicated problem than Model (7). The complexity is higher since there are four modules instead of two modules in Model (12).
Scenario I. Suppose we know the model formulation. We see that the first module occurs with a probability of 0.5. In this case, by correctly identifying the first module, we achieve a 50% accuracy rate. Additionally, this module is able to determine half of the rest of the occurrences in the data. Hence, the theoretical Bayes’ rate for model is 75%, which is computed below. Consider the first correct module identified as . In this case, the theoretical prediction rate can be calculated, assuming n samples in the training data,
The second correct module, though informative, occurs less frequently than the first module. Consider this second variable module , then we can compute the theoretical prediction rate as the following:
which means the correct identification of the second variable module should be 62.5%. In this case, this second variable module together occurs 25%, so these appearances should correctly make the prediction. For the remaining observations that occur of the times, the second variable module only makes correct guesses half of the time. Hence, this computation takes the form of Equation (14), which results in 62.5%. Though not as high as , it is better than random guessing. Similarly, we can compute the theoretical prediction rate for the remaining modules as , which is only slightly higher than random guessing. All together, we should expect . In other words, the derivation for the theoretical prediction of each variable module in the underlying Model (12) helps us to understand that with correct model specification, we should expect simulation results to be approximately 75% on average.
Scenario II. In practice, we assume we do not have the knowledge of the underlying model. To illustrate the performance of the I-score as a feature selection methodology, we conducted the following simulation: We created data with 49 variables drawn from random variables independently. We allowed the number of in-sample training size to be . For each value of the training sample size, we conducted experiments using machine learning algorithms such as bagging (We used the statistical package called ipred: Improved Predictors. Source: https://cran.r-project.org/web/packages/ipred/index.html (2 November 2021)), logistic, random forest (RF) (We used the statistical package called randomForest. Source: https://www.rdocumentation.org/packages/randomForest/versions/4.6-14/topics/randomForest (2 November 2021)), iterative random forest (iRF) (We use the statistical package irf. Source: https://www.rdocumentation.org/packages/vars/versions/1.5-3/topics/irf (2 November 2021)), and neural network (NN) (We used the Keras package and produced a neural network with no hidden layer and one output neuron. Source: https://github.com/yiqiao-yin/YinsLibrary__/blob/9822f36ca097b1e19f7b669e4f42ca39ea9aa608/r/KerasNN.R#L50-L57 (2 November 2021)). We used default values from the packages for the first four algorithms. For the NN, we used the variables modules (i.e., ) as the input layer and the architecture takes the form shown in Figure 5, which states the classification rules using a forward propagation structure (as shown in Section 4.2, Figure 5, there is a linear transformation using weights and a nonlinear transformation using an activation function ). The performance was measured using out-of-sample test set with 1000 data points. The metric for performance is area under the curve (AUC) from the receiver operating characteristic (ROC) curve (see Section 4.4 for a detailed discussion of AUC values). An AUC value of 50% indicates that the area under the curve mapped from a list of precision and recall rates has no prediction power of the ground truth. An AUC value of 100% indicates that the predictor can perfectly guess the ground truth. For each machine learning algorithm with each value in the training size, we conducted experiments using all variables as the benchmark. We also ran the same experiments using variable modules selected by the I-score.
From the results in Table 6, we can observe that with an insufficient sample size in the training set, the performance is poor overall. However, the I-score is able to identify important signals to increase performance into the 60% range. This is a good signal that the I-score is less affected by a small sample size. As we increased the sample size in the training set to 100 or even 1000 data points, we observed that performance improved. However, to achieve the theoretical prediction rate, we still needed the I-score as the feature selection methodology. This is important because with 100 data points, the performance of common machine learning algorithms was still around 50%, but with the proposed module selected, we were able to achieve approximately 75% performance. The NN uses the data much more than the other algorithms, which can be observed with 100 data points because it is the only algorithm that did not reach theoretical prediction rate. We can further increase the data points in the training set, i.e., to 1000 data points for the in-sample training. This is somewhat helpful because even without the I-score, we observed that bagging and iRF are both able to identify some signals. However, they still do not produce performance near to the theoretical rate. With the help of the I-score, we were able to increase the performance of all machine learning algorithms to approximately 75% with a sufficient sample size.

Table 6.
Simulation results for Model (12). The theoretical prediction rate was calculated using Equation (13) as 75%. In other words, we expected prediction performance on th out-of-sample test set to be approximately 75% on average. For each experiment below, the out-of-sample test set had 1000 sample data points and the performance was calculated using the area under the curve (AUC) from the receiver operating characteristic (ROC). For each experiment, we changed the in-sample training size to be 50, 100, or 1000, and we fixed all data to have 49 variables. For each pair of in-sample training size and number of variables, we ran experiments using all original variables, i.e., “All Var.”, with a variety of different classifiers. Alternatively, we used the proposed method to construct new variable modules, which were used as new features on the same classifier. The table shows that the proposed method provides improved prediction performance regardless of sample size or classifier used.
With the above understanding, we show that the I-score can help us to achieve near-perfect performance even with a very small sample size relative to the number of features. In the following, we further explore its capabilities with a fixed a sample size but with varying numbers of variables. In the experiments, we fixed the in-sample training size to 1000 and we changed the number of variables in the data to 100 and then 200. The underlying model remained the same and took the form of Equation (12). In other words, we increasingly inserted noisy variables. If we have 100 variables in the data, there are only 9 important variables, while the other 92 variables are noisy and noninformative. The challenge here was to test the performance of using all variables in the data versus the informative modules to make predictions.
This idea is illustrated using the following experiments (Table 7). We created data fixing the in-sample training size to 1000 data points. Then, we set the number of variables in the data to 100 or 200. For each number of variables, we ran experiments using common machine learning algorithms such as bagging, logistic, random forest (RF), iterative random forest (iRF), and neural network (NN). For each experiment, we usedvall variables as covariates. Then we used variables selected by the I-score instead of all variables to make predictions using the exact same procedure and machine learning algorithms. We tested the performance on the out-of-sample test set. We use the AUC from the ROC as the metric (see Section 4.4 for a detailed discussion of AUC values).

Table 7.
The simulation results for Model (12). The theoretical prediction rate was calculated using Equations (13) as 75%. In other words, we expected the prediction performance on the out-of-sample test set to be approximately 75% on average. For each experiment below, the out-of-sample test set had 1000 sample data points and the performance was calculated using the AUC from the ROC (see Section 4.4 for detailed discussion of AUC values). Continuing from Table 6, we fixed the in-sample training size to 1000 data points and we allowed the of variables in the toy data to be 100 or 200. From 49 variables, this is a more challenging situation because it lowers the chance of finding the correct variable modules.
From the results in Table 7, we can observe that the overall performance is slightly lower when we increased the number of variables from to while fixing the in-sample training set size to 1000 data points. This is not entirely surprising because we used the same underlying Model (12) when increasing the number of noisy variables. In other words, we injected noninformative features in the data set on purpose to increase the difficulty of learning and searching for the correct variable set. For the experiments with variables, we had noisy variables. Assume a statistician has no knowledge of the model. The basic procedure involves using all the features in the neural network architecture. To facilitate comparison, we also used some common machine learning algorithms outside the neural network family: bagging, logistic model, RF, and iRF. The overall performance was around 51–54% AUC on the out-of-sample test set for all algorithms. Alternatively, we recommend using the I-score to construct the interaction-based convolutional layer (explained in Section 3.3). We used a window size of , , and , which produced different numbers of variable modules. We can observe from Table 7 that the amount of noisy variables is quite challenging for common machine learning algorithms. For 100 variables, there are over 90 noisy variables. Without the I-score, we are only able to feed all variables without any selection into the algorithms, which results in poor performance. With the top variable module selected by the I-score, we are able to approximately achieve the theoretical prediction rate at around 75%. When we further injected more noisy variables, performance worsened for the common machine learning algorithms using all of the features including noisy variables, which reduced the prediction power when the algorithm was building its classifier. However, such limitation can be overcome by the usage of the I-score. Even with 200 variables, which means over 190 noisy variables, we are able to achieve a near-perfect prediction rate.
4. Application
This section presents the results of the experiments.
4.1. Background
The COVID-19 pandemic has been the top concern and roadblock since 2019 in more than 150 countries around the world. This disease has had extreme impacts on the health and lives of many on a global scale. In the fight to overcome COVID-19, it is essential to quickly detect the infected patients. Investigation through radiography images is the basic procedure used for diagnosing abnormalities in infected patients. Several deep learning algorithms have been proposed for the detection of COVID-19 on CT scans. Bai et al. provided the model output to radiologists, and demonstrated that AI assistance significantly improves radiologist diagnostic accuracy from 85% to 90% in distinguishing COVID classes from non-COVID classes [30]. Minaee et al. [31] demonstrated the possibility of using deep CNNs including ResNet18, ResNet50, and DenseNet-121 to classify COVID-19 disease using X-ray images. They achieved a sensitivity of 98% and a specificity of 90% on 5000 chest X-ray images.
In this study, the data were sourced from [31]. We downloaded 576 COVID images directly from their work. We also collected 2000 chest X-ray images of healthy individuals from their database and used these images as non-COVID cases. The database created by Minaee et al. [31] also includes other diseases such as pneumonia. The goal in our work was to understand the difference between COVID and healthy chest X-ray images. Therefore, we did not consider other diseases. We present the summary of these data in Table 8. We first randomly selected 60 images each from the COVID and non-COVID class and used these images as the out-of-sample test set. We did not use the images in the test set until the end after training and validation were complete. For the remaining images, we used data augmentation technique by adding noise drawn from normal distribution. This produced a total of 5000 COVID cases and 5000 non-COVID cases. These 10,000 images composed the training and validating sets (tr. and val. in Table 8, repsectively). These 10,000 images have two classes: COVID and non-COVID.

Table 8.
The dimensions of the data. We downloadeed the COVID data from Minaee et al. [31]. This totalled 576 COVID images and 2000 non-COVID images. First, we split the test set from the total images. The test consisted of 60 COVID cases and 60 non-COVID cases. Then, we were left with 516 images for the COVID class and 1940 images for the non-COVID class. This was our in-sample set, which we used for training and validating (Tr. and Val., respectively). For the in-sample set, we upsampled the images by adding noise drawn from normal distribution. This produced 5000 COVID images and 5000 non-COVID images for training and testing. The out-of-sample test set had 120 observations, which wre only used in the end to verify the learning performance.
Figure 6 shows that for healthy individuals, the chest areas are clear in the X-ray images. However, the images for COVID cases are not as clear. This is an indication that there are inflammatory cells or other related body fluids in the chest. Instead of air, which shows up on the X-rays as clear areas, these areas in COVID cases tend to be cloudy and unclear.
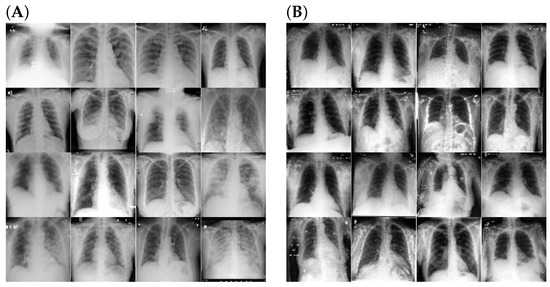
Figure 6.
A total of 16 images randomly sampled from each of the (A) COVID class and (B) non-COVID class. The images for the COVID class appear cloudier and more unclear than the images for the non-COVID class. This is because in the X-ray images for the COVID class contain substances that are not air. These substances may be liquid, germs, or inflammatory fluid, which causes the images to have cloudy, unclear, and shady areas.
4.2. Model Training
For the neural network classifier adopted in this paper, we used a standard neural network architecture with some basic designs (see the diagram after Equation (15)). This procedure has input variables (known as the input layer), an optional hidden layer, and an output layer. The input layer contains sets of variables ready to be fed into the machine to build the classifier. The hidden layer consists of any number of units and it is an optional to deepen the network architecture. The output layer is constructed in order for comparing the output variables. This comparison can be quantified by a loss function. The path from the input layer to output layer completes the procedure of forward propagation. Based on the loss function, we are able to compute the gradient that allows us to conduct optimize the weights of the architecture backward by using gradient descent (or some upgraded version of gradient descent). This completes backward propagation. The training of a neural network model is based on many iterations of forward and backward propagation.
Forward Propagation. To illustrate the procedure of model training, let us consider a set of input variables . In the proposed work, this refers to the variable modules, also notated as , that we created using the interaction-based feature engineer (see Equation (6)). For this discussion, we define a set of weights to construct a linear transformation. The symbol in the following diagram represents this linear transformation that takes the form . For simplicity of notation, we write . Then, we denote as an activation function. We chose sigmoid to be this activation function . This means we have output to be defined as . In other words, we can write the following:
The general form (assuming there are p variable modules) is expressed as:
Architecture. This architecture of a neural network is presented below. For simplicity when drawing this picture, we assume there are 3 input variable modules: . In practice, the number of variable modules (the total number of ) depends on image data dimensions, window size, stride level, and starting point (please see Section 4.3 and Equation (18) for the exact calculation).
For the loss function, we used the binary cross-entropy loss function. This loss function is designed to minimize the distance between a target probability distribution P and an estimated target distribution Q when the task is a two-class classification problem. The cross-entropy loss function is defined as:
where is the ground truth of the response variable for the ith observation and is the predicted value of response variable for the ithe observation. The linear transformation, nonlinear transformation, and the computation of the loss function complete the forward propagation.
Backward Propagation. To search for the optimal weights, we used an optimizer algorithm called root mean square propagation (RMSprop), a named suggested by Geoffrey Hinton. With the loss function computed above, we derive the gradient of the loss function as . At each iteration t, we compute , where is a tuning parameter. Note that the square term on is element-wise multiplication. Then, we can update the weights using , where is learning rate. The value of learning rate is a tuning parameter, which is usually a very small number. This process starts with the loss function and returns to the beginning to update the weights . Hence, it earned the name backward propagation.
4.3. Model Parameters
This section investigates the tuning of the parameters of the proposed method. In the design of the interaction-based convolutional neural network (ICNN), the window size and the level of stride are hyper-parameters.
Window Size. Window size is the size of the local area that we focus on run the backward dropping algorithm. For example, in the first artificial example in Section 3.3, the data size is . A window means that we start with a local area that investigates the first row and the first two columns and the second row and the first two columns. For each row i and each column j in this grid structure, a window size of means a local area of the following matrix:
For a matrix, the BDA iteratively drops a variable amongst these four variables to compute the I-score. The result is a subset of this four variables.
We can also change the size of this window to , which means we investigate the following matrix:
This means that the BDA will start with nine variables. After omitting the noisy variables within this set, the resulting predictive set is a subset of these nine variables.
Stride Level. The level of stride is the number of rows or columns that is skipped. This tuning parameter allows the algorithm to move faster but its disadvantage is that some variables are skipped. For example, we investigate a stride level of one starting from row i and column j. Assume we use a window and let us start from . We can visualize this action using the following diagram:
If we are at the end of the column for a row, we move down by moving to the first column of the next row. For example, in a grid structure, assume we are in the last position in a certain row i. The action of a stride level of one can be taken using the following:
Again assume we are at row i and column j. Suppose we set the stride level to two and we want to move down. This means we proceed by an increment of two on the number of rows; the action is as follows:
If this window is located in the final position of a row, then we move down by skipping one row and we start with the first column. If we have a grid structure, this action is as follows:
Starting Point. Another tuning parameter that we recommend to adjust is the starting point. The starting point represents the location of the first pixel in the proposed operation. The most common point is starting the rolling window from the pixel located in the first row and the first column. This is illustrated in the following matrix:
where the starting point is colored in red.
Alternatively, we can initiate the starting point at a higher level such as two or three. This allows algorithms to run more efficiently in large-scale data sets. For a simple example, in a matrix (see Section 3.3 for the first artificial example), the first row of variables is and the second row of variables is . At a starting point of two, we start with to pass over with the rolling window, because this variable sits at the position in the second row and the second column. This is illustrated in the following matrix;
where the starting point is colored in red.
This tuning parameter is particularly useful when the edge of the images is noisy and noninformative. For example, in Section 4.1, we notice from training images of the COVID-19 chest X-ray data set that the margins of the X-ray images are dark and do not contain the human body for a few pixels in length. This is an example of when this tuning parameter can be helpful as it speeds up the training process.
Computation of Dimensions. The above discussion introduced the tuning parameters: window size, stride level, and starting point. These parameters update our input matrix and generate a new matrix with different sizes. Let us denote window size as w, stride level as l, and starting point as p. Given a by input matrix, the output matrix has new dimensions computed as:
For simplicity in this investigation, we assume the input matrices are a square. In other words, in the application in this paper, we process the input images to have the same width and height, i.e., 128 by 128 pixels. In future work, this can be extended to different shapes.
4.4. Evaluation Metrics
This paper focuses on using the AUC as the main evaluation metric. The AUC value is obtained from the ROC curve, which is a path constructed using different pairs of specificity and sensitivity.
Sensitivity and Specificity. The notion of sensitivity is interchangeable with recall or true positive rate. In a simple two-class classification problem, the goal is to investigate covariate matrix X in order to produce an estimated value of Y. From the output of a NN model, the predicted values are always between zero and one, which acts as a probabilistic statement to describe the chance an observation is class one or zero. Given a threshold between zero and one, we can compute sensitivity as:
Specificity is also used to create a ROC curve. Given a certain threshold between zero and one, we can compute specificity as:
Given different thresholds, a list of pairs of sensitivity and specificity can be created. The AUC is the area under the path plotted using pairs of sensitivity and specificity that is generated using different thresholds. An example of using Specificity and Sensitivity to draw Receiver Operating Curve (ROC) is presented in Figure 7.
Figure 7.
Two paths of ROC curves: ROC1 and ROC2. For each ROC curve, we can compute the AUC value. From ROC1, we can compute AUC1. From ROC2, we can compute AUC2. The mistake discussed in this section is reflected by a reduction in AUC values from path 1 to path 2.
Area under the curve (AUC). The AUC value is a single number derived from a predicted probability by a classification rule and the true label [32]. Given a vector of the true label Y and a vector of the predicted probability , we can use statistical package pROC (The package is called Display and Analyze ROC Curves. Source: https://github.com/xrobin/pROC (2 November 2021)) to assist this computation. The package uses automatically generated thresholds to convert into binary format. For example, we can use a threshold of to convert a vector of the predicted probabilities into binary form by writing . Let us assume the true label to be . Thus, we can compute specificity as one and sensitivity as one1. We can then change threshold to a different value to compute another pair of specificity and sensitivity. By tracking all pairs of specificity and sensitivity, we can generate a curve called the ROC curve [32]. The value of the AUC is exactly the area under the ROC. Assume the predicted probability contains some mistakes. In other words, let us assume the predicted probability vector is . It is not possible for two observations to have the same prediction probability when they come from different classes. Therefore, there must be a mistake in one of them. This information is reflected using the same procedure (Table Figure 7).
4.5. Performance: Proposed Models and AUC Values
This subsection presents the experimental results. A brief summary of a comparison of the conventional methods in the literature with the proposed method is presented in Table 9. A detailed report of the proposed methodology is presented in Table 10. We also plot the AUC values for the proposed models in Figure 8.

Table 9.
The experimental results on the COVID-19 data set from the literature. A number of different ultra-deep CNNs were used to classify COVID patients from non-COVID people. The performance is summarized below. * Minaee et al.disclosed that SqueezeNet has approximately 50 times fewer parameters than AlexNet. The proposed architecture achieves AUC values ranging from 98% to 99.8%. For details, please refer to Figure 8 and Table 10. The average number of parameters of the ultra-deep CNNs can exceed 25 million parameters with a top AUC value of 99.2%. The proposed method has an average number of parameters of less than 100,000 with a top AUC valu of 99.8%. This is a 99% reduction in th number of parameters without sacrificing prediction performance.

Table 10.
A summary of the statistics of the design of the proposed network: interaction-based convolutional neural network (ICNN), for Models 1–6. Each model can take one or two interaction-based convolutional layers (i.e., 1st Conv. or 2nd Conv. Layer). The model can be designed to directly proceed from the interaction-based convolutional layer to the output layer. For example, Models 1 and 3 proceed directly from the convolutional layer to the output layer, i.e., no hidden layer.
Figure 8.
The AUC path for all six models in the proposed work. These models are listed in Table 10 with detailed information including the parameters from each layer and the out-of-sample prediction performance.
Table 9 shows results of previous work on this data set. Minaee et al. [31] used a 50-layer CNN, ResNet50, and achieved an AUC value of 99%. They also proposed SqueezeNet, which delivered an even higher performance at 99.2% [31]. This near-perfect performance is largely due to the design of the convolutional layers and fine tuning. Their work shows that modern-day AI technology such as deep CNNs can perform the initial screening of patients infected by COVID-19 with a single scan of an image, which could reduce the workload of radiologists in practice. However, the number of parameters still far exceeds what humans can interpret. Moreover, it is unclear how these conventional methodologies can satisfy the three critria (, , and ) of the definition of interpretable measures introduced in Section 1 in this paper.
We read the experimental results of the proposed model in the following order. As stated in Section 3.3, the proposed architecture can be designed as deep or wide as desired by the user. All models start with 128 by 128 input images. In other words, the input data has pixels. For simplicity of notation, let us denote as the set of parameters with the starting point of six, window size of , and a stride level of two. Let us further denote as the collection of parameters of starting point of on, window size of , and a stride level of two.
Model 1. This model starts with input images that are sized 128 × 128. Using the parameter in set , we create the first interaction-based convolutional layer (i.e., 1st Conv. Layer in Table 10). This new matrix has dimension . These 3721 variables are directly used to create the output layer with two units (assuming using SoftMax as the loss function). Therefore, the total number of parameters for the network architecture parameters. The test set performance, measured by the AUC, is 98.5% for Model 1.
Model 2. This model builds upon the architecture of Model 1. The only difference is that there is one hidden layer with 64 units (or neurons). We fully connect each variable in the 1st Conv. Layer with each neuron in the hidden layer; afterward, we fully connect the hidden layer with the output layer. This means that from the 1st Conv. Layer to the hidden layer, there are parameters. From the hidden layer of 64 neurons to output layer with two units, there are parameters. This means that, in total, there are parameters. The performance of this architecture is 99.7%. The design of this one hidden layer with 64 units reduced the error rate from 1.5% in Model 1 to 0.3% in Model 2, which is an 80% error reduction.
Model 3. This model has two interaction-based convolutional layers. The 1st Conv. Layer uses the set of parameters in and the 2nd Conv. Layer uses the set of parameters in . From the 1st Conv. Layer in Model 1, we are left with variables. Using the parameters in , we have new matrix with size variables. These 900 variables can be the input layer and we can directly pass these 900 variables into the output layer for making predictions. In other words, the output layer has parameters. The test set AUC value is 97.0%.
Model 4. This model is the deepest amongst all six models. Model 4 has two interaction-based convolutional Llyers and one hidden layer. From the 2nd Conv. Layer in Model 3, we are left with 900 variables. The architecture has one hidden layer with 64 units. The 900 variables are fully connected with the hidden layer, which creates variables. From the hidden layer with 64 units to the output layer with 2 units, there are parameters. In total, there are parameters. The prediction performance is 99.6% on the test set.
Model 5. Both Models 5 and 6 have wider convolutional layers instead of aiming for depth. Model 5 has a concatenated of features from both convolutional layers. This means the architecture takes the 7442 variables from the 1st Conv. Layer and 900 variables from the 2nd Conv. Layer from the previous models together as one large convolutional layer. In other words, Model 5 has a 1st Conv. Layer with variables. These 4621 variables can be directly used to be fed into the output layer with two units. In total, this architecture creates parameters with a test set performance of 98.3%.
Model 6. The last model, Model 6, is just as wide as the previous Model 5. Model 6 also has a first convolutional layer that is a concatenation of features. It has variables. In addition to Model 5, it has one hidden layer with 64 units. We fully connect the convolutional layer of 4621 variables with the hidden layer of 64 variables. This results in parameters. The hidden layer with 64 units are then fully connected with the output layer, which produces parameters. In total, the model has parameters. This model has the highest AUC value on test set, i.e., 99.8%.
The proposed method was also tested on a larger data set [30,31]. Previous researchers have used portions of this data set [30,31] and sought to create high-performance CNNs. However, most of these models use millions of parameters and there is no explanation regarding why and what filters (kernels) are used in their CNNs. As a comparison, the proposed method was tested on this multiclass data set as well. The number of sample sizes for training, validating, and test set are summarized in Table 11. While the previous application investigated a data set with binary classes (COVID-19 versus non-COVID-19), this dataset investigates four different classes. These classes are the different variants in lung cancer diseases, which are COVID-19, pneumonia, and tuberculosis. Hence, this data set is a four-class classification task. The response variable for this data set is defined as:

Table 11.
Multiclass prediction data summary of the number of training set, validating set, and testing set samples in the multiclass X-ray image classification.
Since the target variable Y takes four values, the computation of the I-score needs to computed class-wise. In other words, Y is set to one or zero for each class in order to compute the I-score and to generate the proposed convolutional features. A one-hot encode can allow computation in parallel and can reduce computation cost for end users. The data set has a total 994 images with four classes (three types of lung cancer variants and the healthy class). It is a challenging data set in that there is no number of observations required for standard deep learning algorithms. This is another reason why previous scholars have used many convolutional layers in order to extract high-dimensional features in the data [30,31]. Whereas the previous model delivered relatively good performance, the explainability is somewhat lost throughout the architecture due to many hidden layers. The proposed method was tested on this data set as well and it delivered similar state-of-the-art performance while reducing the number of parameters by almost 99%. With the proposed convolutional features based on the I-score, backward dropping algorithm, and the interaction-based features, the extremely predictive information can be extracted in as little as one layer. In addition, a single hidden layer is recommended to boost performance to the level of its peers; this design has approximately 12,000–13,000 parameters, which is much less than the millions of parameters needed for deep CNNs. The results of this multiclass experiment is summarized in Table 12.

Table 12.
Multiclass lung cancer variants diagnosis: the experiment results for multiclass lung cancer variants classification. In total, there are 4 classes (0: healthy, 1: COVID-19, 2: pneumonia, and 3: tuberculosis). The table summarizes the benchmark performance as well as the prediction performance of the proposed method. All results are measured in area under the curve (AUC). Multiclass AUC values are the average of the AUC values from the 4 different classes, which were calculated using a statistical software package named pROC, which requires the same computation of sensitivity and specificity (these definitions are discussed in Equations (19) and (20)). The average prediction performance for 4-class diagnosis is 89% with 26 million parameters in a variety of different neural networks designs. The average prediction performance for 4-class diagnosis is 97.5% with only 13,000 parameters in the proposed network architecture.
4.6. Visualization: Images and Convolutional Layer
This section presents a visualization of the proposed architecture. These visualizations are presented in Figure 9. Unlike Figure 2, which is an executive summary with each position representing many samples, the visualizations in Figure 9 are sample-wise plots. In other words, the 10 original images that are sized 128 by 128 in panels A and B are the same samples in the second row (1st Conv. Layer) and the third row (2nd Conv. Layer).
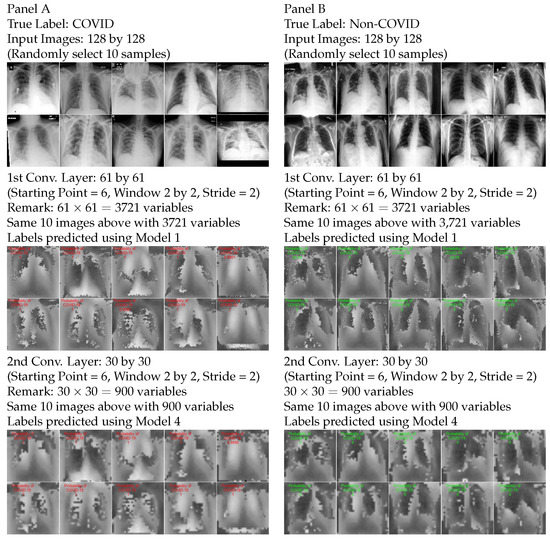
Figure 9.
A summary of randomly sampled images from the COVID and non-COVID classes (10 each). Panel A represents COVID patients and panel B represents non-COVID individuals. The first row plots the original 128 by 128 images. The 1st Conv. Layer generates new variables. We plot the same 10 images from both classes using these 3721 variables in the second row. We also provide the predicted COVID probabilities on top left corner of each image. The 2nd Conv. Layer generates variables. We plot the same 10 images from both classes using these 900 variables in the third row. We also provide the predicted COVID probabilities in the top left corner of each image assuming only these 900 variables are used as predictors. The plot of the original images for patients infected by COVID-19 has grey and cloudy textures in the chest area, which are due to inflammatory fluid produced when patients exhibit pneumonia-like symptoms. This shaded area (as seen in panel A) prevents us from clearly observing the lungs. This is different in panel B, where the lung areas are dark and almost black, which means the lung is filled with air (i.e., normal cases). The black/white contrast in the two panels is directly related to the amount of much inflammatory fluid in human lungs, which translates to greyscale on pictures. The same contrast can be seen using the new variables (these are based on Equation (6)) in the 1st Conv. Layer (sized 61 by 61). For COVID-19 patients, the lung area is cloudy and unclear, whereas for the healthy cases, it is clearly visible.
Original Images in the 1st Conv. Layer. The input images are sized 128 by 128. With the 1st Conv. Layer constructed, we have new variables. We return to the same samples as shown in the first row in Figure 9 and use these 3721 variables only. When we plot these samples with these new variables, we resize them back in a 61 by 61 matrix form. Panel A represents the COVID class and panel B represents the non-COVID class. In addition, we use Model 1 in Table 10 to produce the texts that state the predicted probability of the COVID class. The red indicates the ground truth as COVID class (panel A) and the green indicates ground truth as non-COVID class (panel B).
1st Conv. Layer. to 2nd Conv. Layer. From the resulting matrix of the 1st Conv. Layer, we are left with 3721 variables. We apply the proposed design in Table 10 and we create a new convolutional layer, i.e., the 2nd Conv. Layer. This new layer has variables. We take the same 10 sampled images from before and use these 900 variables to present these images. In this presentation, we resize these 900 variables into 30 by 30. In other words, we obtain a smaller matrix that is a smaller version with similar patterns as before. We use Model 4 to generate the predicted probabilities. These probabilities are printed on the top left corner of each image and they are color-coded similar as before (red probabilities indicate the ground truth of COVID class and green probabilities indicate the ground truth of non-COVID class).
Visualization Interpretation. The plot in Figure 9 of the original images for patients infected by COVID-19 has grey and cloudy textures in the chest area. Because an X-ray is at its brightest when most of the light beams emitted bounce back from the object, bones show as white and the margin is completely black. For muscle and organs inside the human body, X-rays that are emitted can only be partially collected; this causes the greyscale on the X-ray images in the chest area. For COVID-19 patients, there are grey and shaded areas in the chest X-rays. This is due to the inflammatory fluid produced when patients exhibit pneumonia-like symptoms. The fluid inside the chest area is a consequence of the human immune system fighting outside diseases. This shaded area (as seen in panel A in Figure 9) prevents us from observing clear areas in lungs. This is different in panel B, where the lung areas are dark and almost black, because a healthy lung is filled with air (i.e., the black present in normal cases’ X-ray images). The black and white contrast in the two panels is directly related to how much inflammatory fluid is present in human lungs. This contrast translates to greyscale on pictures and is directly related to COVID and non-COVID cases (i.e., response variable Y). The same contrast can be seen using the new variables (these are based on Equation (6)) in the 1st Conv. Layer (sized 61 by 61). For COVID-19 patients, the lung area is cloudy and unclear, whereas for the healthy cases, it is clearly visible. This is not a surprising coincidence because the proposed new variable modules, , are engineered using Equation (6), which relies on the response variable in the training set. The 61 by 61 images from the proposed algorithm are a direct translation of not only the original pixels but also the response variable. In other words, this visualization presents how the I-score considers image data.
5. Conclusions
Explainable AI System for Early COVID-19 Screening. As the most important contribution of this paper, an explainable artificial intelligence (XAI) system is proposed to assist radiologists in the initial screening of COVID-19 and other related diseases using chest X-ray images for treatment and disease control. This innovation can revolutionize the application of AI systems in hospitals and healthcare systems. We anticipate that other related diseases with viral pneumonia signs can use the same detection methods proposed in our paper, which ensure the development of testing procedures with accountability, responsibility, and transparency for human users and patients. A Heuristic and Theoretical Framework of XAI. This paper introduced a heuristic and theoretical framework for addressing the XAI problems in large-scale and high-dimensional data sets. We provided three criteria as necessary conditions and premises for a measure to be regarded as explainable and interpretable. The first dimension, , states that an interpretable measure does not need to rely on the knowledge of the true model, because any mistakes made in model fitting would be carried over in explaining the features. The second dimension, , states that an interpretable measure should be able to indicate the impact of a combination of variables on the response variable. This means that any inclusion of influential variables would increase this measure, whereas any injection of noisy and useless variables would decrease this measure. This desirable property allows human users to directly compare the impact of the features when any classifier is trained to make prediction decisions. Though we provided detailed work with an arbitrary image data set, the proposed method can be generalized and adapted to any big data problem. Moreover, it opens up future possibilities for feature selection and dimension reduction in any large-scale and high-dimensional data set. Last, the third dimension, , associates an interpretable measure with the predictivity of a set of features. This property benefits human users because it allows us to establish connections and foresee the potential prediction performance (such as AUC values) that a set of features can deliver before any model fitting procedure.
An ICNN. To address the XAI problems heuristically described above, this paper introduced a novel design of an explainable and self-interpretable interaction-based convolutional neural network (ICNN). We provided a flexible approach to contribute to the major issues regarding explainability, interpretability, transparency, and trustworthiness in black-box algorithms. We introduced and implemented a nonparametric and interaction-based feature selection methodology and used this as a replacement for predefined filters that are widely used in ultra-deep CNNs. Under this paradigm, we presented an ICNN that extracts important features. The proposed architecture uses these extracted features to construct influential and predictive variable modules that are directly associated with the predictivity of the response variable. The proposed design and its many characteristics provide an extremely flexible pipeline that can learn, extract useful information, and identify the hidden potential from any large-scale or high-dimensional data set. The proposed methods were presented with both artificial examples and real data applications to COVID-19 chest X-ray image data. We conclude from both simulation and empirical application results that the I-score has unparalleled potential to explain informative and influential local information in large-scale data sets. High I-score values suggest that local information possesses the capability to have higher lower bounds of the predictivity, which thus leads not only to highly accurate prediction performance but also strong explanatory power. By arranging features according to the I-score from high to low, we are able to cater the dimensions of our model to any neural network architecture. Furthermore, we also show potential applications of the interaction-based neural network architecture, which can help us advance the field of explainable artificial intelligence. We think that the proposed design can be adapted to any type of CNN. Thus, any CNN architecture that adopts the proposed technology can be regarded as in interaction-based convolutional neural network (ICNN or interaction-based network). We encourage both the statistics and computer science communities to further explore this area to increase the transparency, trustworthiness, and accountability of deep learning algorithms and to build a world with truly responsible A.I.
Author Contributions
Conceptualization, S.-H.L. and Y.Y.; methodology, S.-H.L.; software, S.-H.L.; validation, S.-H.L. and Y.Y.; formal analysis, S.-H.L. and Y.Y.; investigation, S.-H.L. and Y.Y.; resources, S.-H.L. and Y.Y.; data curation, Y.Y.; writing—original draft preparation, S.-H.L. and Y.Y.; writing—review and editing, S.-H.L. and Y.Y.; visualization, S.-H.L. and Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Science Foundation Award IIS-1741191.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data and related software are available upon requests.
Acknowledgments
We dedicate this to H. Chernoff, a well-known statistician and a mathematician worldwide, in honor of his 98th birthday and his contributions to the influence score (I-score) and the backward dropping algorithm (BDA). We are particularly fortunate to have received many useful comments from him. Moreover, we are very grateful for his guidance on how the I-score plays a fundamental role that measures the potential ability to use a small group of explanatory variables for classification, which leads to a much broader impact in the fields of pattern recognition, computer vision, and representation learning.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Velavan, T.P.; Meyer, C.G. The COVID-19 epidemic. Trop. Med. Int. Health 2020, 25, 278. [Google Scholar] [CrossRef]
- Li, F.; Wang, Y.; Li, X.Y.; Nusairat, A.; Wu, Y. Gateway placement for throughput optimization in wireless mesh networks. Mob. Netw. Appl. 2008, 13, 198–211. [Google Scholar] [CrossRef]
- Wang, S.; Kang, B.; Ma, J.; Zeng, X.; Xiao, M.; Guo, J.; Cai, M.; Yang, J.; Li, Y.; Meng, X.; et al. A deep learning algorithm using CT images to screen for Corona Virus Disease (COVID-19). Eur. Radiol. 2021, 31, 6096–6104. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.; Lau, E.H.; Wong, J.Y.; et al. Early transmission dynamics in Wuhan, China, of novel coronavirus—Infected pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef] [PubMed]
- Ai, T.; Yang, Z.; Hou, H.; Zhan, C.; Chen, C.; Lv, W.; Tao, Q.; Sun, Z.; Xia, L. Correlation of Chest CT and RT-PCR Testing in Coronavirus Disease 2019 (COVID-19) in China: A Report of 1014 Cases. Radiology 2020, 296, E32–E40. [Google Scholar] [CrossRef]
- Aloysius, N.; Geetha, M. A review on deep convolutional neural networks. In Proceedings of the 2017 International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 6–8 April 2017; pp. 0588–0592. [Google Scholar]
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A survey of the recent architectures of deep convolutional neural networks. Artif. Intell. Rev. 2020, 53, 5455–5516. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Katona, J.; Ujbanyi, T.; Sziladi, G.; Kovari, A. Examine the effect of different web-based media on human brain waves. In Proceedings of the 2017 8th IEEE International Conference on Cognitive Infocommunications (CogInfoCom), Debrecen, Hungary, 11–14 September 2017; pp. 000251–000256. [Google Scholar]
- Katona, J.; Kovari, A. Speed control of Festo Robotino mobile robot using NeuroSky MindWave EEG headset based brain-computer interface. In Proceedings of the 2016 7th IEEE International Conference on Cognitive Infocommunications (CogInfoCom), Wroclaw, Poland, 16–18 October 2016; pp. 000251–000256. [Google Scholar]
- Katona, J.; Ujbanyi, T.; Sziladi, G.; Kovari, A. Electroencephalogram-Based Brain-Computer Interface for Internet of Robotic Things. Available online: https://link.springer.com/chapter/10.1007/978-3-319-95996-2_12#citeas (accessed on 2 November 2021).
- Katona, J. Analyse the Readability of LINQ Code using an Eye-Tracking-based Evaluation. Acta Polytech. Hung. 2021, 18, 193–215. [Google Scholar] [CrossRef]
- Doshi-Velez, F.; Kim, B. Towards a rigorous science of interpretable machine learning. arXiv 2017, arXiv:1702.08608. [Google Scholar]
- Miller, T. Explanation in artificial intelligence: Insights from the social sciences. Artif. Intell. 2019, 267, 1–38. [Google Scholar] [CrossRef]
- Adadi, A.; Berrada, M. Peeking inside the black-box: A survey on explainable artificial intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- DARPA. Broad Agency Announcement, Explainable Artificial Intelligence (XAI). Available online: https://www.darpa.mil/attachments/DARPA-BAA-16-53.pdf (accessed on 2 November 2021).
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef]
- Lo, A.; Chernoff, H.; Zheng, T.; Lo, S.H. Framework for making better predictions by directly estimating variables’ predictivity. Proc. Natl. Acad. Sci. USA 2016, 113, 14277–14282. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Handwritten digit recognition with a back-propagation network. Adv. Neural Inf. Process. Syst. 1990, 2, 396–404. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. arXiv 2016, arXiv:1610.02357. [Google Scholar]
- Chernoff, H.; Lo, S.H.; Zheng, T. Discovering influential variables: A method of partitions. Ann. Appl. Stat. 2009, 3, 1335–1369. [Google Scholar] [CrossRef][Green Version]
- Lo, S.; Zheng, T. Backward haplotype transmission association algorithm—A fast multiple-marker screening method. Hum. Hered. 2002, 53, 197–215. [Google Scholar] [CrossRef]
- Lo, A.; Chernoff, H.; Zheng, T.; Lo, S.H. Why significant variables aren’t automatically good predictors. Proc. Natl. Acad. Sci. USA 2015, 112, 13892–13897. [Google Scholar] [CrossRef]
- Wang, H.; Lo, S.H.; Zheng, T.; Hu, I. Interaction-based feature selection and classification for high-dimensional biological data. Bioinformatics 2012, 28, 2834–2842. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Yann, L.; Corinna, C.; Christopher, J. The Mnist Database of Handwritten Digits. 1998. Available online: http://yhann.lecun.com/exdb/mnist (accessed on 2 November 2021).
- Bai, H.X.; Wang, R.; Xiong, Z.; Hsieh, B.; Chang, K.; Halsey, K.; Tran, T.M.L.; Choi, J.W.; Wang, D.C.; Shi, L.B.; et al. Artificial intelligence augmentation of radiologist performance in distinguishing COVID-19 from pneumonia of other origin at chest CT. Radiology 2020, 296, E156–E165. [Google Scholar] [CrossRef] [PubMed]
- Minaee, S.; Kafieh, R.; Sonka, M.; Soufi, G. Deep-COVID: Predicting COVID-19 from Chest X-ray Images Using Deep Transfer Learning. Med. Image Anal. 2020, 65, 101794. [Google Scholar] [CrossRef] [PubMed]
- Hand, D.J. Measuring classifier performance: A coherent alternative to the area under the ROC curve. Mach. Learn. 2009, 77, 103–123. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).