Feature Selection for High-Dimensional Datasets through a Novel Artificial Bee Colony Framework
Abstract
:1. Introduction
- (1)
- In order to trade off the exploitation and exploration abilities of ABC, we use operators with strong exploitation abilities to enhance the exploitation ability in the phase of onlooker bee;
- (2)
- This paper analyzes the functional behavior of the scout bee phase and finds that this phase may be redundant while dealing with high-dimensional FS problems, and so eliminating this phase can reduce the computational time of the algorithm;
- (3)
- The proposed framework is designed as a general framework that can be used to adapt many ABC variants for the FS problems.
2. Related Works
3. Introduction and Analysis of ABC Algorithm
- (1)
- Employed bee phase: According to Equation (2), a new food source is produced around the current food source, as follows:where is a random number within [−1,1]. and represent the dth dimension feature of and , respectively. is compared with , and if the fitness of is superior to , is replaced by for entry into the next step, and its counter is reset to 0. Otherwise, is retained for entry into the next step, and its counter increases by 1.
- (2)
- Onlooker bee phase: Every onlooker bee selects a food source depending on the probability value via the roulette-wheel scheme. is associated with the food resource information given by the employed bee. The value of is generated by Equation (3).where is the fitness value of solution . Each selected food source is updated using Equation (2).
- (3)
- Scout bee phase: If the counter of a food source is greater than or equal to the preset number of trials, then this food source is discarded. The value of the preset number of trials is usually called the limit for abandonment. If a food source is abandoned, then the scout bee translated from the employed bee will regenerate a food source via Equation (1) to replace the food source that is abandoned.
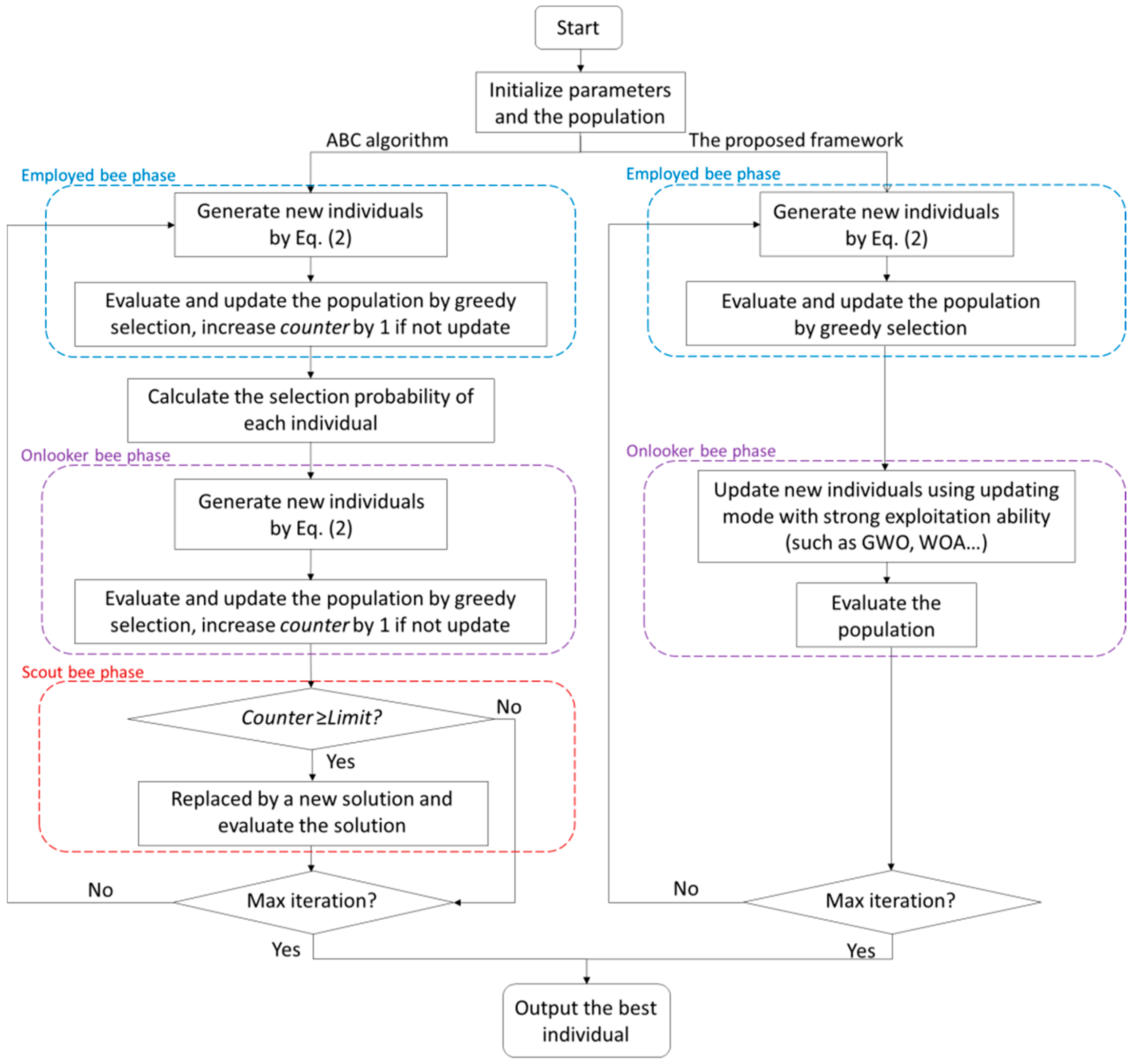
4. Proposed Algorithm for Feature Selection
4.1. The Proposed Framework
- (1)
- The employed bee phase of the ABC algorithm is retained so that it can explore the search space widely and avoid reaching the local optimum;
- (2)
- The updating mode of the ABC algorithm’s onlooker bee phase is changed to the new updating strategy, as inspired by other algorithms with more powerful exploitation capacities. The searching scheme of these algorithms with powerful exploitation abilities is introduced as an operator. According to our observation, higher diversity in the bee swarm can help the algorithm to find more potential search space, but after a certain period, the solutions should converge and approach optimal solutions with reductions in colony diversity. We believe that applying operators with strong exploitation abilities to the optimization process can reduce the diversity of the algorithm in the late stage, and bring about a higher convergence speed. Therefore, the introduction of operators with powerful exploitation abilities can help our novel ABC framework find better solutions;
- (3)
- The scout bee phase is removed, because the exploration ability of the scout bee phase will increase the diversity of the algorithm during the later period. Moreover, the scout bee phase will waste the execution time, and consume computational resources and memory during the calculation process.
4.2. Abandonment of Scout Bee Phase to Reduce the Exploration Capacity
4.3. Enhancement of Exploitation—Illustrative Example with GWO and WOA
| Algorithm 1: Pseudocode of BABCGWO/BABCWOA |
| Input: Population size SN, Maximum number of iterations NMAX.
Output: The optimal individual xbest, the best fitness value f(xbest). Initialize the population by using Equation (1). Evaluate the fitness value of each individual. For it = 1 to NMAX do For i = 1 to SN do Select a different food source xk at random. Produce a new food source according to Equation (2) and map it to discrete values by Equation (4). Evaluate the fitness value of each food source. Update xi according to greedy selection. End For i = 1 to SN do Update the position using operators of GWO algorithm or WOA algorithm and map it to discrete values by Equation (4). Evaluate the fitness value of each individual. End End Output xbest and f(xbest). |
4.4. Computational Complexity Analysis
- (1)
- In the initialization stage of the algorithm, the time complexity is ;
- (2)
- The time complexity of each iteration in the updating phase of the employed bee, the onlooker bee and the scout bee is ;
- (3)
- The time complexity in the process of calculating individual fitness is .
- (1)
- During initialization, the time complexity is ;
- (2)
- is required for each iteration in the evolution of the employed bee phase and grey wolf phase;
- (3)
- The time complexity of calculating the fitness is .
- (1)
- The time complexity of the initialization step is ;
- (2)
- The time complexity of each iteration in the updating process of employed bees and whales is ;
- (3)
- is consumed by evaluating the fitness of each individual.
5. Experimental Studies
5.1. Experimental Design
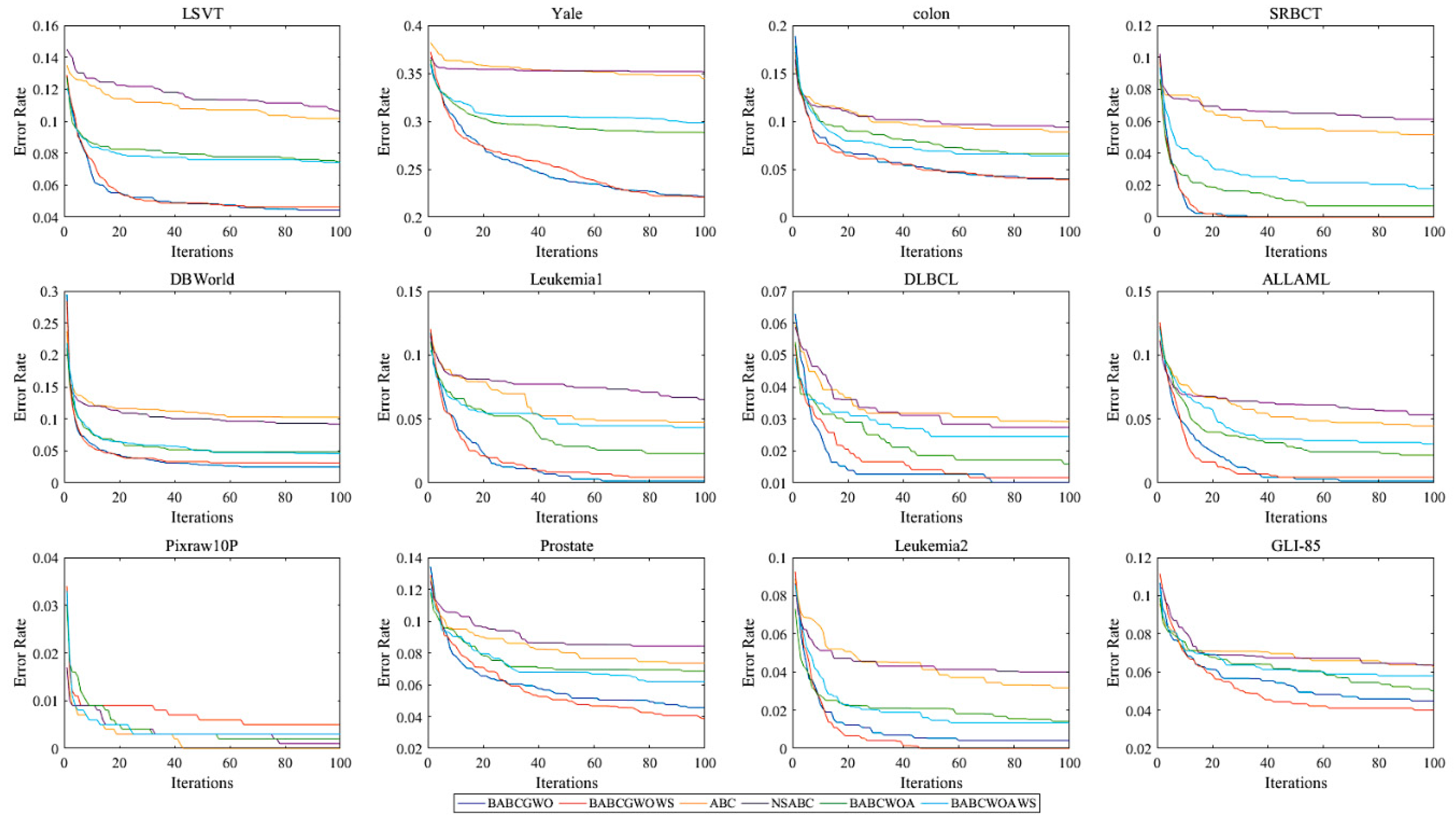
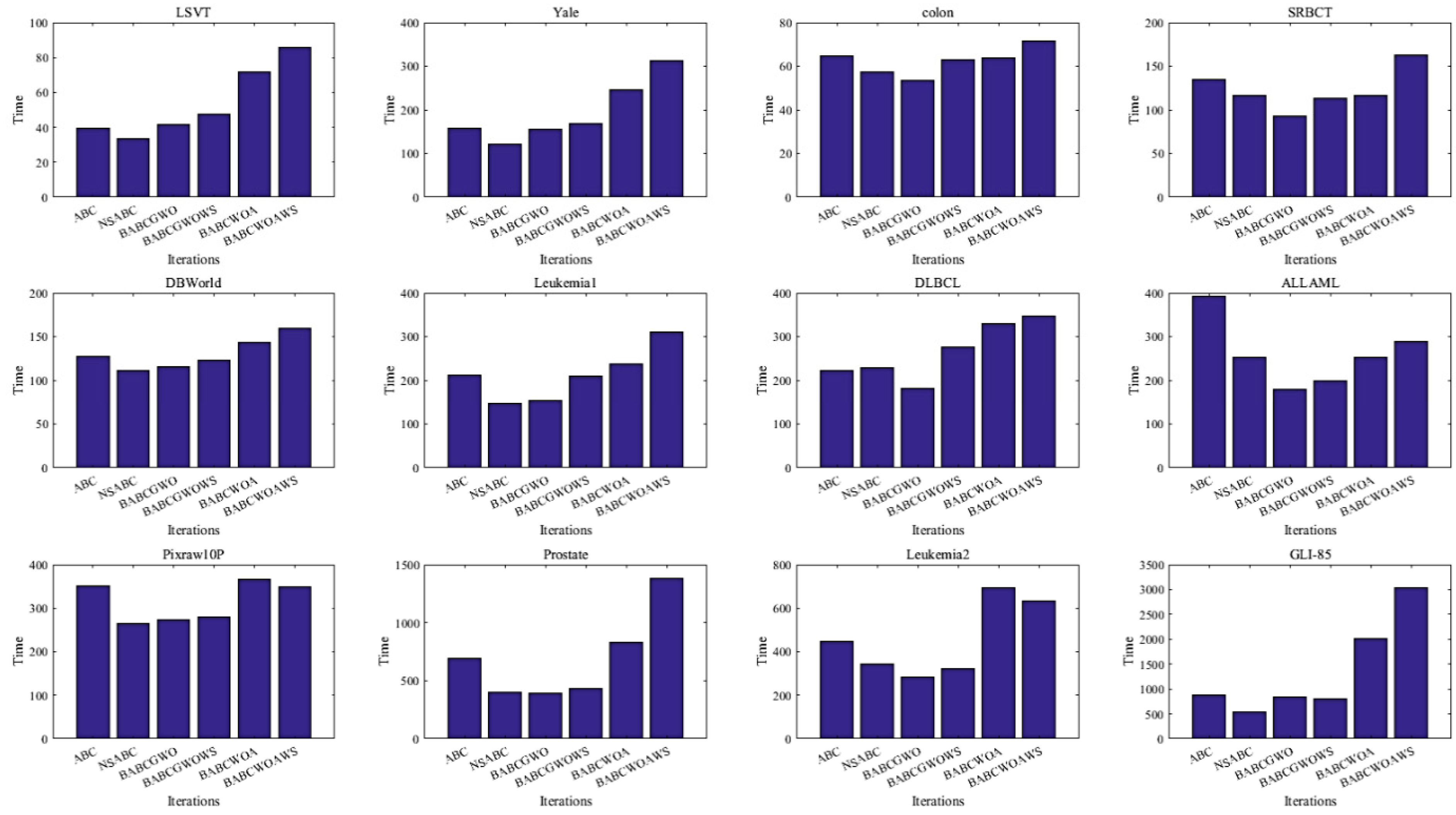
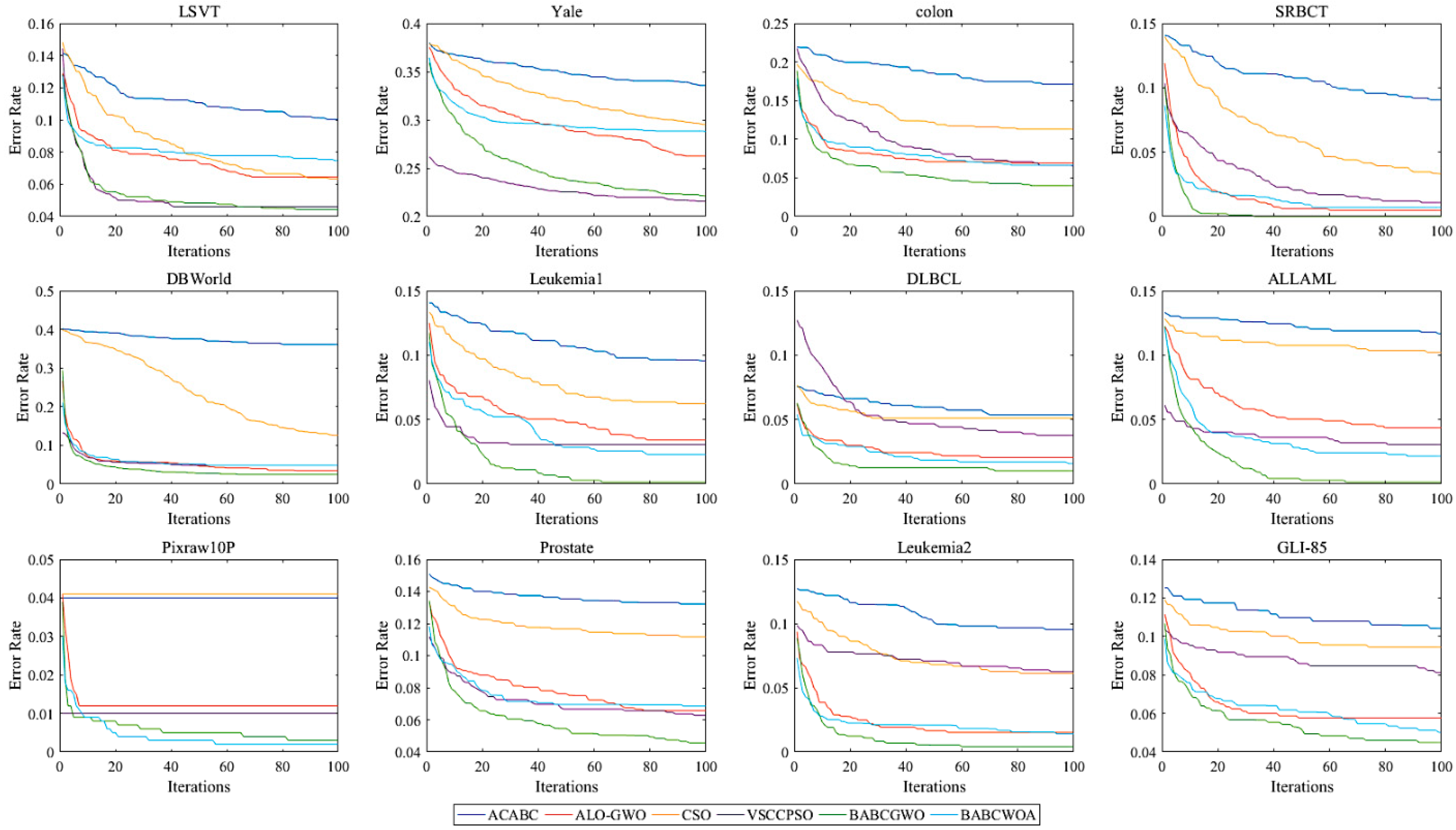
5.2. Experimental Results and Analysis
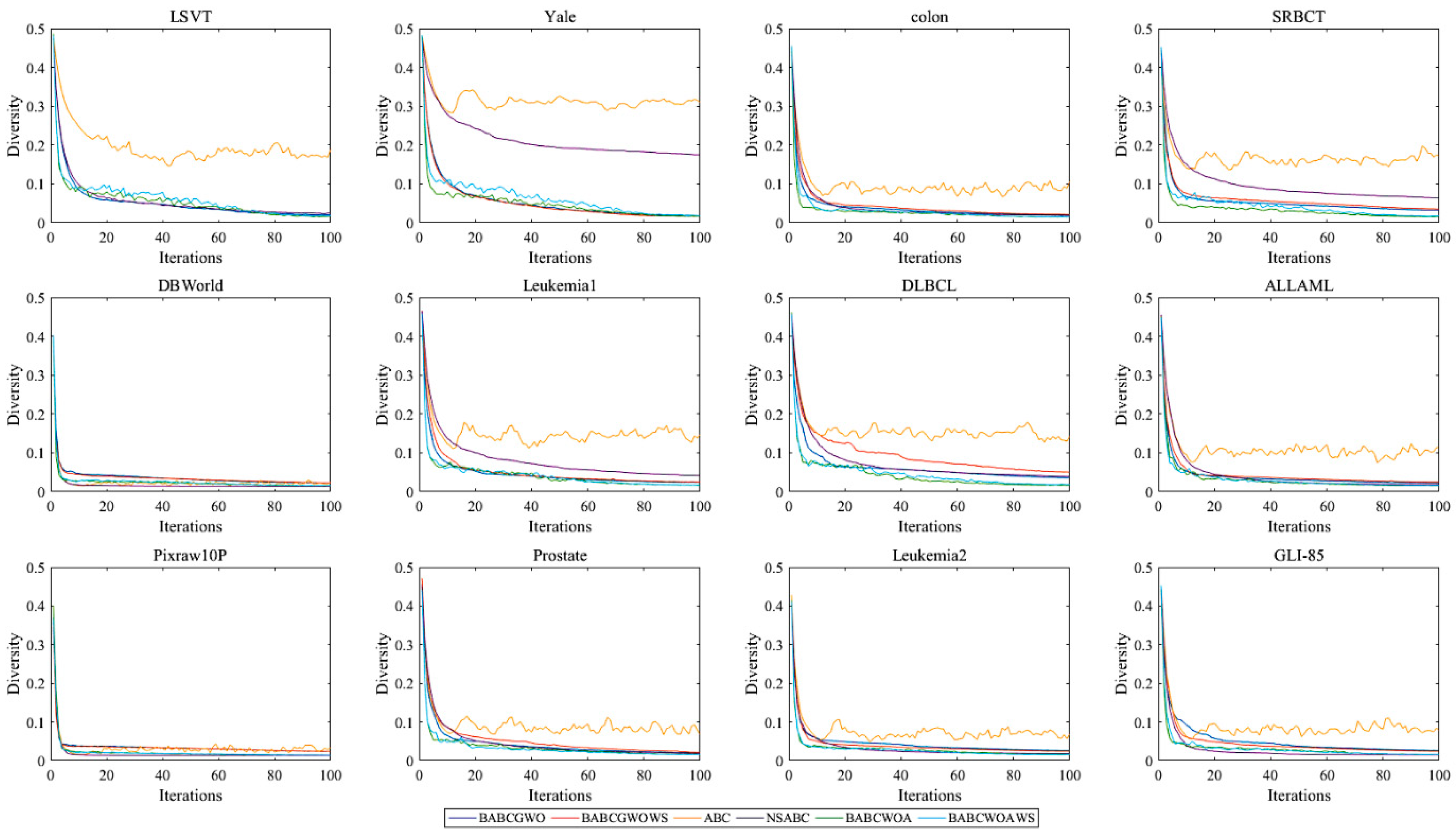
6. Further Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dash, M.; Liu, H. Feature selection for classification. Intell. Data Anal. 1997, 1, 131–156. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Mafarja, M.M.; Mirjalili, S. Hybrid Whale Optimization Algorithm with simulated annealing for feature selection. Neurocomputing 2017, 260, 302–312. [Google Scholar] [CrossRef]
- Gao, W.F.; Liu, S.Y.; Huang, L.L. A global best artificial bee colony algorithm for global optimization. J. Comput. Appl. Math. 2012, 236, 2741–2753. [Google Scholar] [CrossRef] [Green Version]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Zhang, Q. Differential evolution with composite trial vector generation strategies and control parameters. IEEE Trans. Evol. Comput. 2011, 15, 55–66. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Xue, B.; Zhang, M.; Browne, W.N.; Yao, X. A survey on evolutionary computation approaches to feature selection. IEEE Trans. Evol. Comput. 2015, 20, 606–626. [Google Scholar] [CrossRef] [Green Version]
- Djellali, H.; Djebbar, A.; Zine, N.G.; Azizi, N. Hybrid artificial bees colony and particle swarm on feature selection. In Proceedings of the International Conference on Computational Intelligence and Its Applications, Oran, Algeria, 8–10 May 2018; Springer: Cham, Switzerland, 2018; pp. 93–105. [Google Scholar]
- Zorarpacı, E.; Özel, S.A. A hybrid approach of differential evolution and artificial bee colony for feature selection. Expert Syst. Appl. 2016, 62, 91–103. [Google Scholar] [CrossRef]
- Al-Tashi, Q.; Kadir, S.J.A.; Rais, H.M.; Mirjalili, S.H. Alhussian, Binary Optimization Using Hybrid Grey Wolf Optimization for Feature Selection. IEEE Access 2019, 7, 39496–39508. [Google Scholar] [CrossRef]
- Shi, Y.; Pun, C.M.; Hu, H.; Gao, H. An improved artificial bee colony and its application. Knowl. Based Syst. 2016, 107, 14–31. [Google Scholar] [CrossRef]
- Garg, D.P.; Kumar, M. Optimization techniques applied to multiple manipulators for path planning and torque minimization. Eng. Appl. Artif. Intell. 2002, 15, 241–252. [Google Scholar] [CrossRef] [Green Version]
- Roberge, V.; Tarbouchi, M.; Labonté, G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning. IEEE Trans. Ind. Inform. 2012, 9, 132–141. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.-W.; Zhang, J.-H. Robot path planning in uncertain environment using multi-objective particle swarm optimization. Neurocomputing 2013, 103, 172–185. [Google Scholar] [CrossRef]
- Oh, I.-S.; Lee, J.-S.; Moon, B.-R. Hybrid genetic algorithms for feature selection. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1424–1437. [Google Scholar]
- Palanisamy, S.; Kanmani, S. Artificial bee colony approach for optimizing feature selection. Int. J. Comput. Sci. Issues 2012, 9, 432. [Google Scholar]
- Tran, B.; Xue, B.; Zhang, M. Improved PSO for feature selection on high-dimensional datasets. In Proceedings of the Asia-Pacific Conference on Simulated Evolution and Learning, Dunedin, New Zealand, 15–18 December 2014; Springer: Cham, Switzerland, 2014; pp. 503–515. [Google Scholar]
- Liang, Y.; Leung, K.-S. Genetic algorithm with adaptive elitist-population strategies for multimodal function optimization. Appl. Soft Comput. 2011, 11, 2017–2034. [Google Scholar] [CrossRef]
- Mirjalili, S.; Hashim, S.Z.M. A new hybrid PSOGSA algorithm for function optimization. In Proceedings of the 2010 International Conference on Computer and Information Application, Tianjin, China, 3–5 December 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 374–377. [Google Scholar]
- Pan, Q.-K.; Sang, H.-Y.; Duan, J.-H.; Gao, L. An improved fruit fly optimization algorithm for continuous function optimization problems. Knowl. Based Syst. 2014, 62, 69–83. [Google Scholar] [CrossRef]
- Clerc, M. Discrete particle swarm optimization, illustrated by the traveling salesman problem. In New Optimization Techniques in Engineering; Springer: Berlin/Heidelberg, Germany, 2004; pp. 219–239. [Google Scholar]
- Kan, J.M.; Zhang, Y. Application of an improved ant colony optimization on generalized traveling salesman problem. Energy Procedia 2012, 17, 319–325. [Google Scholar]
- Mahi, M.; Baykan, Ö.K.; Kodaz, H. A new hybrid method based on particle swarm optimization, ant colony optimization and 3-opt algorithms for traveling salesman problem. Appl. Soft Comput. 2015, 30, 484–490. [Google Scholar] [CrossRef]
- Li, A.-D.; Xue, B.; Zhang, M. Improved binary particle swarm optimization for feature selection with new initialization and search space reduction strategies. Appl. Soft Comput. 2021, 106, 107302. [Google Scholar] [CrossRef]
- Gao, W.F.; Liu, S.Y.; Jiang, F. An improved artificial bee colony algorithm for directing orbits of chaotic systems. Appl. Math. Comput. 2011, 218, 3868–3879. [Google Scholar] [CrossRef]
- Hancer, E.; Xue, B.; Karaboga, D.; Zhang, M. A binary ABC algorithm based on advanced similarity scheme for feature selection. Appl. Soft Comput. 2015, 36, 334–348. [Google Scholar] [CrossRef]
- Gaidhane, P.J.; Nigam, M.J. A hybrid grey wolf optimizer and artificial bee colony algorithm for enhancing the performance of complex systems. J. Comput. Sci. 2018, 27, 284–302. [Google Scholar] [CrossRef]
- Chao, X.Q.; Li, W. Feature selection method optimized by artificial bee colony algorithm. J. Front. Comput. Sci. Technol. 2019, 13, 300–309. [Google Scholar]
- Shunmugapriya, P.; Kanmani, S. A hybrid algorithm using ant and bee colony optimization for feature selection and classification (AC-ABC Hybrid). Swarm Evol. Comput. 2017, 36, 27–36. [Google Scholar] [CrossRef]
- Shunmugapriya, P.; Kanmani, S.; Supraja, R.; Saranya, K. Feature selection optimization through enhanced Artificial Bee Colony algorithm. In Proceedings of the 2013 International Conference on Recent Trends in Information Technology (ICRTIT), Chennai, India, 25–27 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 56–61. [Google Scholar]
- Zhu, G.; Kwong, S. Gbest-guided artificial bee colony algorithm for numerical function optimization. Appl. Math. Comput. 2010, 217, 3166–3173. [Google Scholar] [CrossRef]
- Singh, A.; Deep, K. Exploration–exploitation balance in Artificial Bee Colony algorithm: A critical analysis. Soft Comput. 2019, 23, 9525–9536. [Google Scholar] [CrossRef]
- Hong, P.N.; Ahn, C.W. Fast artificial bee colony and its application to stereo correspondence. Expert Syst. Appl. 2016, 45, 460–470. [Google Scholar] [CrossRef]
- Emary, E.; Zawba, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Tu, Q.; Chen, X.C.; Liu, X.C. Multi-strategy ensemble grey wolf optimizer and its application to feature selection. Appl. Soft Comput. 2019, 76, 16–30. [Google Scholar] [CrossRef]
- Long, W.; Jiao, J.J.; Liang, X.M.; Tang, M.Z. An exploration-enhanced grey wolf optimizer to solve high-dimensional numerical optimization. Eng. Appl. Artif. Intell. 2018, 68, 63–80. [Google Scholar] [CrossRef]
- Liao, Y.; Vemuri, V.R. Use of K-Nearest Neighbor classifier for intrusion detection. Comput. Secur. 2002, 21, 439–448. [Google Scholar] [CrossRef]
- Gu, S.K.; Cheng, R.; Jin, Y.C. Feature selection for high-dimensional classification using a competitive swarm optimizer. Soft Comput. 2018, 22, 811–822. [Google Scholar] [CrossRef] [Green Version]
- Song, X.-F.; Zhang, Y.; Guo, Y.-N.; Sun, X.-Y.; Wang, Y.-L. Variable-Size Cooperative Coevolutionary Particle Swarm Optimization for Feature Selection on High-Dimensional Data. IEEE Trans. Evol. Comput. 2020, 24, 882–895. [Google Scholar] [CrossRef]
- Zawbaa, H.M.; Emary, E.; Grosan, C.; Snasel, V. Large-dimensionality small-instance set feature selection: A hybrid bio-inspired heuristic approach. Swarm Evol. Comput. 2018, 42, 29–42. [Google Scholar] [CrossRef]
- El-Kenawy, E.M.; Eid, M.M.; Saber, M.; Ibrahim, A. MbGWO-SFS: Modified Binary Grey Wolf Optimizer Based on Stochastic Fractal Search for Feature Selection. IEEE Access 2020, 8, 107635–107649. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 196–202. [Google Scholar]
| Datasets | Features | Samples | Classes |
|---|---|---|---|
| LSVT | 310 | 126 | 2 |
| Yale | 1024 | 165 | 15 |
| colon | 2000 | 62 | 2 |
| SRBCT | 2308 | 83 | 4 |
| DBWorld | 4702 | 64 | 2 |
| Leukemia1 | 5327 | 72 | 3 |
| DLBCL | 5469 | 77 | 2 |
| ALLAML | 7129 | 72 | 2 |
| Pixraw10P | 10,000 | 100 | 10 |
| Prostate | 10,509 | 102 | 2 |
| Leukemia2 | 11,225 | 72 | 3 |
| GLI_85 | 22,283 | 85 | 2 |
| Datasets | Index | Algorithms | |||||
|---|---|---|---|---|---|---|---|
| ABC | NSABC | BABCWOA | BABCWOAWS | BABCGWO | BABCGWOWS | ||
| LSVT | worst | 0.112 | 0.121 | 0.103 | 0.104 | 0.056 | 0.064 |
| mean ± std | 0.102 ± 0.01 | 0.106 ± 0.01 | 0.075 ± 0.02 | 0.074 ± 0.02 | 0.044 ± 0.01 | 0.046 ± 0.01 | |
| best | 0.087 | 0.089 | 0.047 | 0.047 | 0.031 | 0.031 | |
| Yale | worst | 0.357 | 0.370 | 0.326 | 0.345 | 0.238 | 0.240 |
| mean ± std | 0.345 ± 0.01 | 0.351 ± 0.01 | 0.288 ± 0.03 | 0.299 ± 0.04 | 0.220 ± 0.01 | 0.220 ± 0.01 | |
| best | 0.327 | 0.327 | 0.241 | 0.243 | 0.210 | 0.207 | |
| colon | worst | 0.112 | 0.1 | 0.112 | 0.083 | 0.064 | 0.064 |
| mean ± std | 0.089 ± 0.02 | 0.094 ± 0.01 | 0.066 ± 0.02 | 0.064 ± 0.02 | 0.037 ± 0.02 | 0.038 ± 0.02 | |
| best | 0.0643 | 0.081 | 0.05 | 0.048 | 0.014 | 0.014 | |
| SRBCT | worst | 0.063 | 0.071 | 0.024 | 0.046 | 0.000 | 0.000 |
| mean ± std | 0.052 ± 0.01 | 0.061 ± 0.01 | 0.007 ± 0.01 | 0.018 ± 0.02 | 0.000 | 0.000 | |
| best | 0.022 | 0.047 | 0.000 | 0.000 | 0.000 | 0.000 | |
| DBWorld | worst | 0.121 | 0.110 | 0.093 | 0.074 | 0.033 | 0.048 |
| mean ± std | 0.103 ± 0.01 | 0.092 ± 0.01 | 0.048 ± 0.02 | 0.046 ± 0.02 | 0.025 ± 0.01 | 0.031 ± 0.01 | |
| best | 0.088 | 0.079 | 0.017 | 0.029 | 0.014 | 0.014 | |
| Leukemia1 | worst | 0.068 | 0.086 | 0.043 | 0.071 | 0.014 | 0.029 |
| mean ± std | 0.047 ± 0.02 | 0.065 ± 0.01 | 0.023 ± 0.02 | 0.043 ± 0.02 | 0.001 ± 0.01 | 0.004 ± 0.01 | |
| best | 0.027 | 0.039 | 0.000 | 0.014 | 0.000 | 0.000 | |
| DLBCL | worst | 0.039 | 0.0518 | 0.041 | 0.041 | 0.025 | 0.038 |
| mean ± std | 0.029 ± 0.01 | 0.027 ± 0.02 | 0.016 ± 0.01 | 0.025 ± 0.01 | 0.010 ± 0.01 | 0.012 ± 0.01 | |
| best | 0.025 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| ALLAML | worst | 0.057 | 0.071 | 0.070 | 0.068 | 0.014 | 0.014 |
| mean ± std | 0.045 ± 0.01 | 0.053 ± 0.01 | 0.022 ± 0.03 | 0.030 ± 0.03 | 0.001 ± 0.01 | 0.004 ± 0.01 | |
| best | 0.029 | 0.029 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Pixraw10P | worst | 0.000 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 |
| mean ± std | 0.000 | 0.001 ± 0.00 | 0.002 ± 0 | 0.003 ± 0 | 0.003 ± 0.01 | 0.005 ± 0.01 | |
| best | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Prostate | worst | 0.089 | 0.089 | 0.089 | 0.078 | 0.060 | 0.060 |
| mean ± std | 0.074 ± 0.01 | 0.084 ± 0.00 | 0.069 ± 0.02 | 0.062 ± 0.01 | 0.044 ± 0.01 | 0.039 ± 0.01 | |
| best | 0.049 | 0.078 | 0.040 | 0.049 | 0.029 | 0.020 | |
| Leukemia2 | worst | 0.043 | 0.070 | 0.043 | 0.039 | 0.027 | 0.000 |
| mean ± std | 0.032 ± 0.01 | 0.040 ± 0.01 | 0.014 ± 0.01 | 0.013 ± 0.01 | 0.004 ± 0.01 | 0.000 | |
| best | 0.014 | 0.013 | 0.000 | 0.000 | 0.000 | 0.000 | |
| GLI_85 | worst | 0.081 | 0.079 | 0.074 | 0.082 | 0.061 | 0.061 |
| mean ± std | 0.062 ± 0.01 | 0.064 ± 0.01 | 0.050 ± 0.01 | 0.058 ± 0.02 | 0.045 ± 0.01 | 0.040 ± 0.01 | |
| best | 0.046 | 0.047 | 0.033 | 0.025 | 0.035 | 0.035 | |
| Datasets | Index | Algorithms | |||||
|---|---|---|---|---|---|---|---|
| ABC | NSABC | BABCWOA | BABCWOAWS | BABCGWO | BABCGWOWS | ||
| LSVT | worst | 20 | 15 | 167 | 157 | 65 | 64 |
| mean ± std | 8.9 ± 4.58 | 6.8 ± 3.88 | 83.7 ± 50.61 | 104.5 ± 34.07 | 30.0 ± 16.83 | 33.4 ± 15.07 | |
| best | 4 | 3 | 27 | 61 | 15 | 16 | |
| Yale | worst | 147 | 284 | 421 | 477 | 126 | 124 |
| mean ± std | 96.9 ± 46.24 | 122.6 ± 88.40 | 245.6 ± 97.77 | 347.9 ± 103.06 | 102.4 ± 14.55 | 97.9 ± 21.37 | |
| best | 30 | 37 | 127 | 210 | 86 | 55 | |
| colon | worst | 30 | 40 | 266 | 532 | 112 | 169 |
| mean ± std | 18.5 ± 6.69 | 20.3 ± 8.53 | 142.8 ± 68.85 | 155.1 ± 138.18 | 80.4 ± 17.39 | 105.9 ± 28.05 | |
| best | 12 | 12 | 46 | 61 | 58 | 76 | |
| SRBCT | worst | 584 | 104 | 497 | 829 | 233 | 353 |
| mean ± std | 121.2 ± 166.69 | 64.8 ± 27.37 | 109.4 ± 254.02 | 394.5 ± 191.01 | 164.6 ± 45.35 | 204.0 ± 86.09 | |
| best | 25 | 21 | 112 | 151 | 107 | 116 | |
| DBWorld | worst | 44 | 40 | 484 | 423 | 297 | 263 |
| mean ± std | 32.3 ± 5.25 | 31.7 ± 5.08 | 249.4 ± 112.93 | 317.7 ± 99.99 | 216.2 ± 59.40 | 205.6 ± 52.63 | |
| best | 23 | 22 | 92 | 154 | 109 | 119 | |
| Leukemia1 | worst | 147 | 676 | 1694 | 1247 | 692 | 410 |
| mean ± std | 71.6 ± 30.28 | 149 ± 210.69 | 648.2 ± 504.44 | 741.6 ± 324.58 | 277.4 ± 156.79 | 300.5 ± 73.80 | |
| best | 42 | 30 | 237 | 305 | 160 | 182 | |
| DLBCL | worst | 128 | 695 | 1029 | 1484 | 1427 | 1413 |
| mean ± std | 59.4 ± 30.28 | 126.1 ± 202.79 | 545.3 ± 314.94 | 811.6 ± 532.06 | 458.4 ± 358.90 | 684.7 ± 464.70 | |
| best | 32 | 28 | 230 | 143 | 228 | 190 | |
| ALLAML | worst | 97 | 82 | 646 | 1168 | 370 | 444 |
| mean ± std | 66.5 ± 19.17 | 50.9 ± 11.54 | 386.4 ± 144.24 | 500.4 ± 286.34 | 276.4 ± 54.91 | 305.7 ± 87.46 | |
| best | 45 | 42 | 168 | 217 | 198 | 156 | |
| Pixraw10P | worst | 115 | 88 | 294 | 370 | 405 | 349 |
| mean ± std | 73.7 ± 17.81 | 66.8 ± 8.34 | 196.1 ± 56.32 | 200.4 ± 74.22 | 218.5 ± 76.059 | 253.5 ± 63.50 | |
| best | 52 | 58 | 137 | 121 | 157 | 159 | |
| Prostate | worst | 146 | 103 | 1454 | 1505 | 624 | 897 |
| mean ± std | 91.3 ± 32.66 | 76.9 ± 15.57 | 1055.4 ± 362.08 | 797.8 ± 314.48 | 444.5 ± 129.06 | 569.6 ± 227.40 | |
| best | 56 | 55 | 442 | 445 | 199 | 250 | |
| Leukemia2 | worst | 295 | 124 | 1300 | 1246 | 1036 | 844 |
| mean ± std | 115.8 ± 66.71 | 88.9 ± 18.75 | 876.4 ± 303.41 | 661.4 ± 273.88 | 582.6 ± 234.36 | 425.7 ± 153.55 | |
| best | 68 | 70 | 318 | 329 | 357 | 311 | |
| GLI_85 | worst | 248 | 173 | 5716 | 6691 | 2920 | 1453 |
| mean ± std | 161.8 ± 32.20 | 150.1 ± 12.05 | 1576.3 ± 1508.28 | 1553.6 ± 1840.90 | 1204.4 ± 674.09 | 1099.2 ± 272.00 | |
| best | 138 | 131 | 437 | 520 | 697 | 681 | |
| Datasets | Index | Algorithms | |||||
|---|---|---|---|---|---|---|---|
| CSO | VSCCPSO | ALO_GWO | ACABC | BABCWOA | BABCGWO | ||
| LSVT | worst | 0.081 | 0.064 | 0.078 | 0.080 | 0.075 | 0.056 |
| mean ± std | 0.063 ± 0.01 | 0.046 ± 0.01 | 0.065 ± 0.04 | 0.065 ± 0.01 | 0.075 ± 0.02 | 0.044 ± 0.01 | |
| best | 0.055 | 0.024 | 0.054 | 0.056 | 0.047 | 0.031 | |
| Yale | worst | 0.320 | 0.230 | 0.309 | 0.315 | 0.326 | 0.238 |
| mean ± std | 0.295 ± 0.02 | 0.216 ± 0.01 | 0.273 ± 0.02 | 0.288 ± 0.02 | 0.288 ± 0.03 | 0.220 ± 0.01 | |
| best | 0.268 | 0.200 | 0.254 | 0.266 | 0.241 | 0.210 | |
| colon | worst | 0.176 | 0.081 | 0.088 | 0.157 | 0.112 | 0.064 |
| mean ± std | 0.113 ± 0.03 | 0.065 ± 0.01 | 0.069 ± 0.01 | 0.119 ± 0.02 | 0.066 ± 0.02 | 0.037 ± 0.02 | |
| best | 0.081 | 0.048 | 0.064 | 0.095 | 0.050 | 0.014 | |
| SRBCT | worst | 0.049 | 0.024 | 0.025 | 0.063 | 0.024 | 0.000 |
| mean ± std | 0.033 ± 0.02 | 0.011 ± 0.01 | 0.005 ± 0.01 | 0.035 ± 0.01 | 0.007 ± 0.01 | 0.000 | |
| best | 0.000 | 0.000 | 0.000 | 0.022 | 0.000 | 0.000 | |
| DBWorld | worst | 0.255 | 0.091 | 0.062 | 0.198 | 0.093 | 0.033 |
| mean ± std | 0.126 ± 0.05 | 0.048 ± 0.01 | 0.034 ± 0.01 | 0.139 ± 0.03 | 0.048 ± 0.02 | 0.025 ± 0.01 | |
| best | 0.062 | 0.026 | 0.017 | 0.093 | 0.017 | 0.014 | |
| Leukemia1 | worst | 0.084 | 0.056 | 0.057 | 0.07 | 0.043 | 0.014 |
| mean ± std | 0.062 ± 0.01 | 0.031 ± 0.01 | 0.034 ± 0.02 | 0.058 ± 0.01 | 0.023 ± 0.02 | 0.001 ± 0.01 | |
| best | 0.039 | 0.028 | 0.000 | 0.041 | 0.000 | 0.000 | |
| DLBCL | worst | 0.075 | 0.091 | 0.038 | 0.064 | 0.041 | 0.025 |
| mean ± std | 0.051 ± 0.01 | 0.038 ± 0.02 | 0.021 ± 0.01 | 0.038 ± 0.02 | 0.016 ± 0.01 | 0.010 ± 0.01 | |
| best | 0.038 | 0.026 | 0.000 | 0.013 | 0.000 | 0.000 | |
| ALLAML | worst | 0.113 | 0.056 | 0.082 | 0.121 | 0.070 | 0.014 |
| mean ± std | 0.102 ± 0.01 | 0.031 ± 0.01 | 0.044 ± 0.03 | 0.103 ± 0.01 | 0.022 ± 0.03 | 0.001 ± 0.01 | |
| best | 0.093 | 0.014 | 0.000 | 0.082 | 0.000 | 0.000 | |
| Pixraw10P | worst | 0.050 | 0.010 | 0.040 | 0.040 | 0.010 | 0.010 |
| mean ± std | 0.041 ± 0.00 | 0.010 | 0.012 ± 0.01 | 0.040 | 0.002 ± 0 | 0.003 ± 0.01 | |
| best | 0.040 | 0.010 | 0.000 | 0.040 | 0.000 | 0.000 | |
| Prostate | worst | 0.126 | 0.078 | 0.079 | 0.117 | 0.089 | 0.060 |
| mean ± std | 0.112 ± 0.01 | 0.063 ± 0.01 | 0.066 ± 0.01 | 0.106 ± 0.01 | 0.069 ± 0.02 | 0.044 ± 0.01 | |
| best | 0.089 | 0.049 | 0.049 | 0.087 | 0.040 | 0.029 | |
| Leukemia2 | worst | 0.082 | 0.097 | 0.029 | 0.095 | 0.043 | 0.027 |
| mean ± std | 0.061 ± 0.01 | 0.063 ± 0.02 | 0.015 ± 0.01 | 0.054 ± 0.02 | 0.014 ± 0.01 | 0.004 ± 0.01 | |
| best | 0.041 | 0.028 | 0.000 | 0.027 | 0.000 | 0.000 | |
| GLI_85 | worst | 0.129 | 0.106 | 0.071 | 0.150 | 0.074 | 0.061 |
| mean ± std | 0.094 ± 0.02 | 0.074 ± 0.02 | 0.058 ± 0.01 | 0.109 ± 0.02 | 0.050 ± 0.01 | 0.045 ± 0.01 | |
| best | 0.081 | 0.047 | 0.047 | 0.082 | 0.033 | 0.035 | |
| Datasets | CSO | VSCCPSO | ALO_GWO | ACABC | ||||
|---|---|---|---|---|---|---|---|---|
| BABCGWO | BABCWOA | BABCGWO | BABCWOA | BABCGWO | BABCWOA | BABCGWO | BABCWOA | |
| LSVT | 0(+) | 0.04(−) | 0.68(=) | 0(−) | 0(+) | 0.08(=) | 0(+) | 0.10(=) |
| Yale | 0(+) | 0.57(=) | 0.52(=) | 0(−) | 0(+) | 0.20(=) | 0(+) | 0.97(=) |
| colon | 0(+) | 0(+) | 0(+) | 0.47(=) | 0(+) | 0.09(=) | 0(+) | 0(+) |
| SRBCT | 0(+) | 0(+) | 0(+) | 0.55(=) | 0.08(=) | 0.62(=) | 0(+) | 0(+) |
| DBWorld | 0(+) | 0(+) | 0(+) | 0.84(=) | 0.06(=) | 0.11(=) | 0(+) | 0(+) |
| Leukemia1 | 0(+) | 0(+) | 0(+) | 0.72(=) | 0(+) | 0.17(=) | 0(+) | 0(+) |
| DLBCL | 0(+) | 0(+) | 0(+) | 0.01(+) | 0(+) | 0.44(=) | 0(+) | 0.01(+) |
| ALLAML | 0(+) | 0(+) | 0(+) | 0.16(=) | 0(+) | 0.05(=) | 0(+) | 0(+) |
| Pixraw10P | 0(+) | 0(+) | 0.10(=) | 0.01(+) | 0.01(+) | 0(+) | 0(+) | 0(+) |
| Prostate | 0(+) | 0(+) | 0(+) | 0.38(=) | 0(+) | 0.73(=) | 0(+) | 0(+) |
| Leukemia2 | 0(+) | 0(+) | 0(+) | 0(+) | 0.02(+) | 0.82(=) | 0(+) | 0(+) |
| GLI_85 | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0.10(=) | 0(+) | 0(+) |
| Datasets | Index | Algorithms | |||||
|---|---|---|---|---|---|---|---|
| CSO | VSCCPSO | ALO_GWO | ACABC | BABCWOA | BABCGWO | ||
| LSVT | Subsets | 151.5 | 37.5 | 102.5 | 150.9 | 83.7 | 30.0 |
| Time | 55.5 | 83.4 | 89.6 | 172.1 | 71.7 | 41.9 | |
| Yale | Subsets | 504.1 | 150.1 | 240.6 | 506.3 | 245.6 | 102.4 |
| Time | 147.2 | 482.0 | 291.2 | 464.6 | 245.6 | 156.0 | |
| colon | Subsets | 983.0 | 194.0 | 261.2 | 995.6 | 142.8 | 80.4 |
| Time | 55.8 | 153.4 | 287.6 | 271.7 | 63.8 | 53.4 | |
| SRBCT | Subsets | 1127.1 | 205.8 | 408.3 | 1136.2 | 109.4 | 164.6 |
| Time | 101.5 | 275.0 | 311.0 | 381.8 | 116.9 | 93.2 | |
| DBWorld | Subsets | 2316.2 | 601.4 | 446.5 | 2338.0 | 249.4 | 216.2 |
| Time | 268.7 | 419.9 | 841.0 | 901.8 | 144.1 | 115.5 | |
| Leukemia1 | Subsets | 2664.6 | 721.2 | 867.4 | 2645.6 | 648.2 | 277.4 |
| Time | 417.7 | 549.0 | 774.6 | 1257.0 | 238.1 | 153.9 | |
| DLBCL | Subsets | 2737.6 | 625.6 | 1097.8 | 2733.1 | 545.3 | 458.4 |
| Time | 436.2 | 631.8 | 1259.8 | 2409.6 | 330.4 | 182.1 | |
| ALLAML | Subsets | 3563.3 | 1248.9 | 846.5 | 3537.0 | 386.4 | 276.4 |
| Time | 646.2 | 828.0 | 780.6 | 2954.4 | 252.0 | 180.3 | |
| Pixraw10P | Subsets | 5015.6 | 2366.7 | 882.1 | 5006.7 | 196.1 | 218.5 |
| Time | 1647.9 | 3417.9 | 1428.1 | 4187.3 | 367.0 | 253.3 | |
| Prostate | Subsets | 5246.2 | 1558.7 | 1440.3 | 5194.9 | 1055.4 | 444.5 |
| Time | 1418.7 | 2261.7 | 2435.9 | 8370.3 | 829.8 | 391.0 | |
| Leukemia2 | Subsets | 5627.1 | 2091.2 | 1336.5 | 5608.7 | 876.4 | 582.6 |
| Time | 852.6 | 1820.4 | 2342.9 | 2722.6 | 693.8 | 282.9 | |
| GLI_85 | Subsets | 11,157.5 | 5167.9 | 2971.2 | 11,682.5 | 1576.3 | 1204.4 |
| Time | 3996.3 | 3872.9 | 3013.8 | 9230.0 | 2023.4 | 836.3 | |
| Datasets | CSO | VSCCPSO | ALO_GWO | ACABC | ||||
|---|---|---|---|---|---|---|---|---|
| BABCGWO | BABCWOA | BABCGWO | BABCWOA | BABCGWO | BABCWOA | BABCGWO | BABCWOA | |
| LSVT | 0(+) | 0(+) | 0.10(=) | 0.03(−) | 0(+) | 0.33(=) | 0(+) | 0(+) |
| Yale | 0(+) | 0(+) | 0(+) | 0.57(=) | 0(+) | 0.05(=) | 0(+) | 0(+) |
| colon | 0(+) | 0(+) | 0(+) | 0.03(+) | 0(+) | 0.02(+) | 0(+) | 0(+) |
| SRBCT | 0(+) | 0(+) | 0.04(+) | 0.16(=) | 0(+) | 0.01(+) | 0(+) | 0(+) |
| DBWorld | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0.01(+) | 0(+) | 0(+) |
| Leukemia1 | 0(+) | 0(+) | 0(+) | 0.05(=) | 0(+) | 0.04(+) | 0(+) | 0(+) |
| DLBCL | 0(+) | 0(+) | 0.01(+) | 0.34 | 0(+) | 0.01(+) | 0(+) | 0(+) |
| ALLAML | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) |
| Pixraw10P | 0(+) | 0(+) | 0(+) | 0(+) | 0.03(+) | 0.02(+) | 0(+) | 0(+) |
| Prostate | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0.19(=) | 0(+) | 0(+) |
| Leukemia2 | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) |
| GLI_85 | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) |
| Datasets | CSO | VSCCPSO | ALO_GWO | ACABC | ||||
|---|---|---|---|---|---|---|---|---|
| BABCGWO | BABCWOA | BABCGWO | BABCWOA | BABCGWO | BABCWOA | BABCGWO | BABCWOA | |
| LSVT | 0(+) | 0.91(=) | 0(+) | 0.43(=) | 0(+) | 0.24(=) | 0(+) | 0(+) |
| Yale | 0.19(=) | 0(−) | 0(+) | 0(+) | 0(+) | 0.03(+) | 0(+) | 0(+) |
| colon | 0(+) | 0.06(=) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) |
| SRBCT | 0.12(=) | 0.03(−) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) |
| DBWorld | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) |
| Leukemia1 | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) |
| DLBCL | 0(+) | 0.03(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) |
| ALLAML | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) |
| Pixraw10P | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) |
| Prostate | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) |
| Leukemia2 | 0(+) | 0.14(=) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) |
| GLI_85 | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) | 0(+) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, J.; Li, X.; Huang, S.; Wang, X. Feature Selection for High-Dimensional Datasets through a Novel Artificial Bee Colony Framework. Algorithms 2021, 14, 324. https://doi.org/10.3390/a14110324
Zhang Y, Wang J, Li X, Huang S, Wang X. Feature Selection for High-Dimensional Datasets through a Novel Artificial Bee Colony Framework. Algorithms. 2021; 14(11):324. https://doi.org/10.3390/a14110324
Chicago/Turabian StyleZhang, Yuanzi, Jing Wang, Xiaolin Li, Shiguo Huang, and Xiuli Wang. 2021. "Feature Selection for High-Dimensional Datasets through a Novel Artificial Bee Colony Framework" Algorithms 14, no. 11: 324. https://doi.org/10.3390/a14110324
APA StyleZhang, Y., Wang, J., Li, X., Huang, S., & Wang, X. (2021). Feature Selection for High-Dimensional Datasets through a Novel Artificial Bee Colony Framework. Algorithms, 14(11), 324. https://doi.org/10.3390/a14110324






