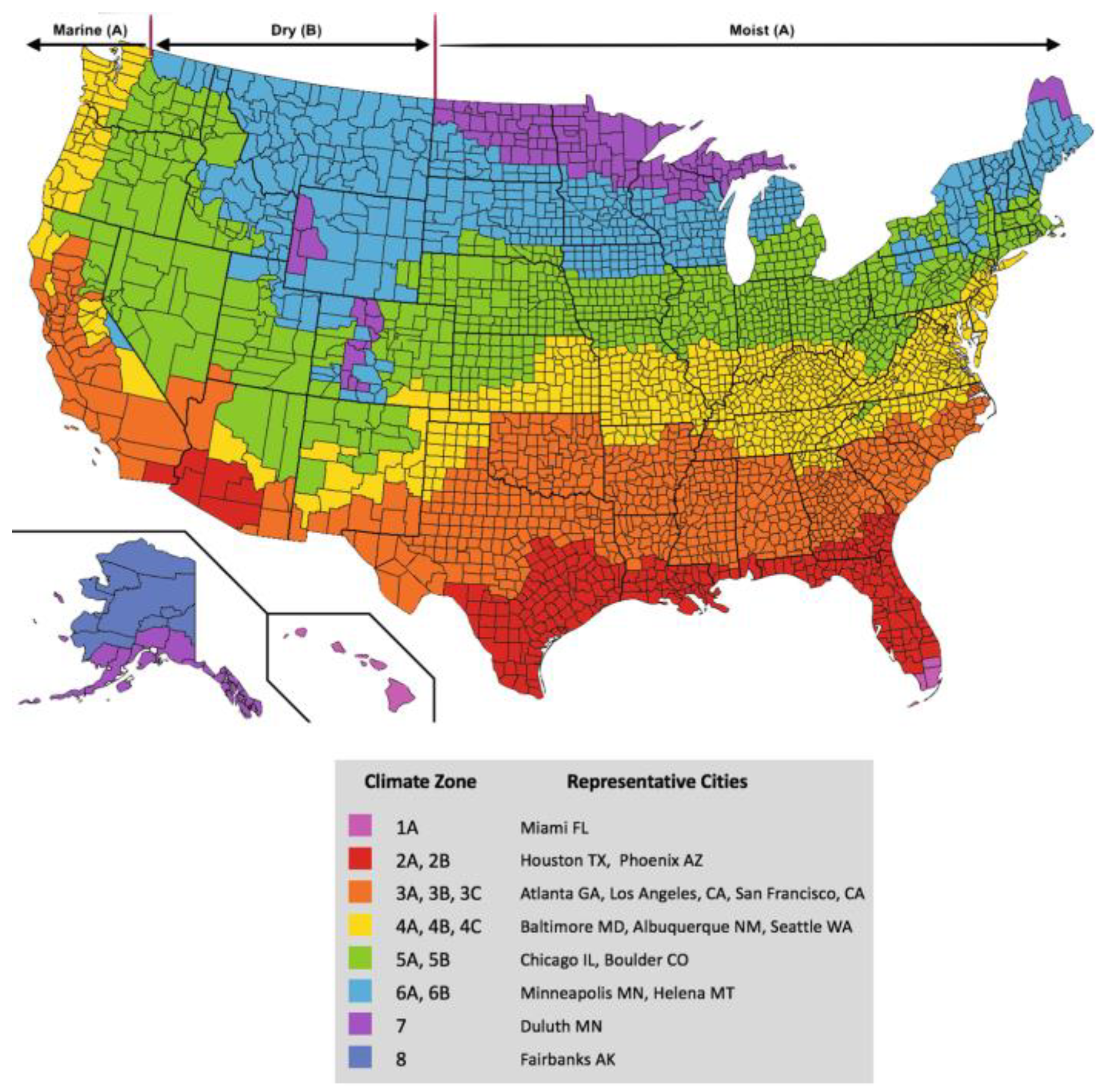
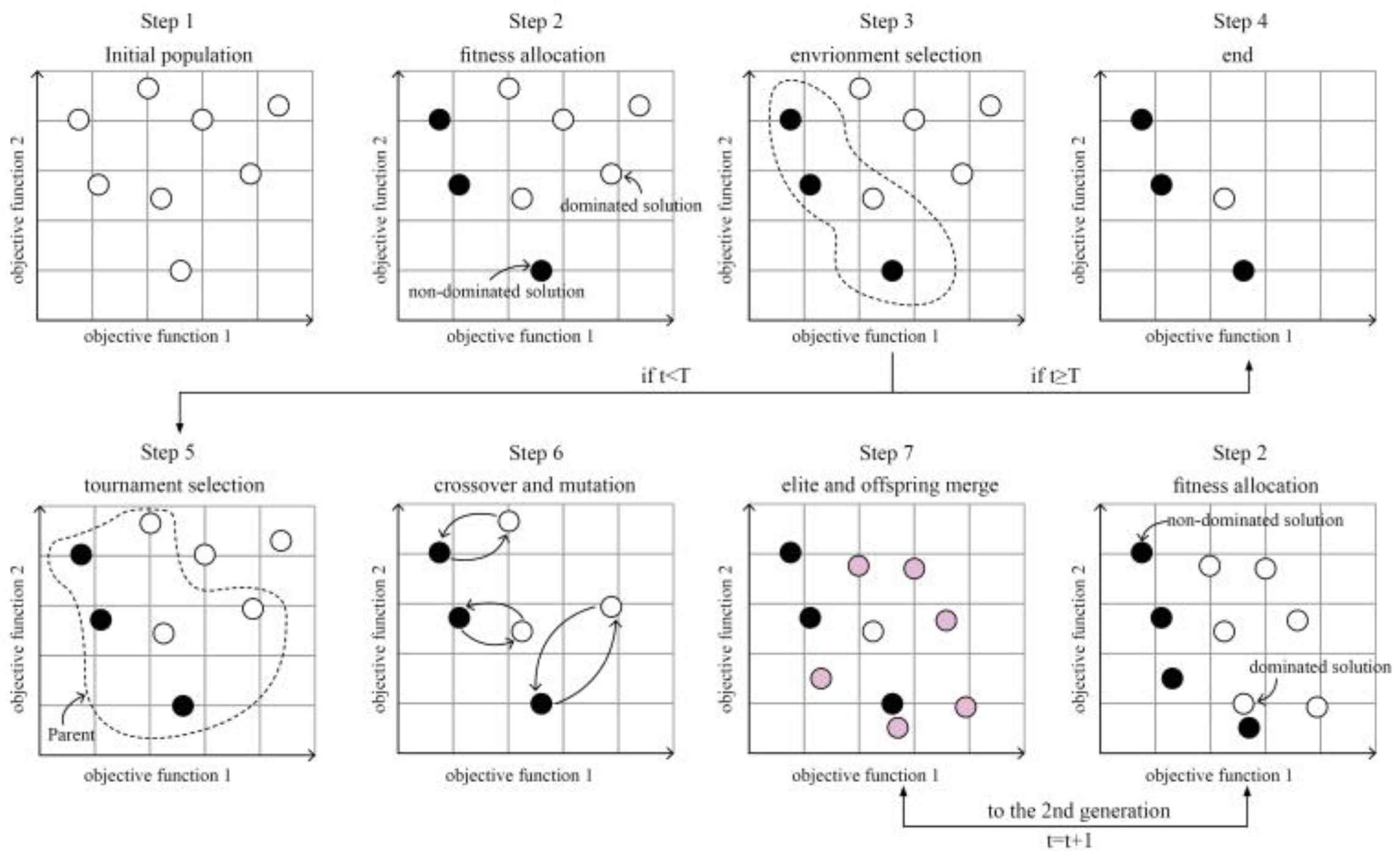
Based on the above multi-objective optimization logic, this section conducts climate responsive optimization analysis for typical cities in six different climate regions in the United States. As above mentioned, the objective functions are discomfort hours percentage (DH) for thermal environment evaluation, building energy demand (BED), and building life cycle global cost (GC). The optimized parameter results and performance indicators of residential buildings in various U.S climate zones are compared and discussed.
4.1. Optimization Results of Residential Buildings in Typical American Cities
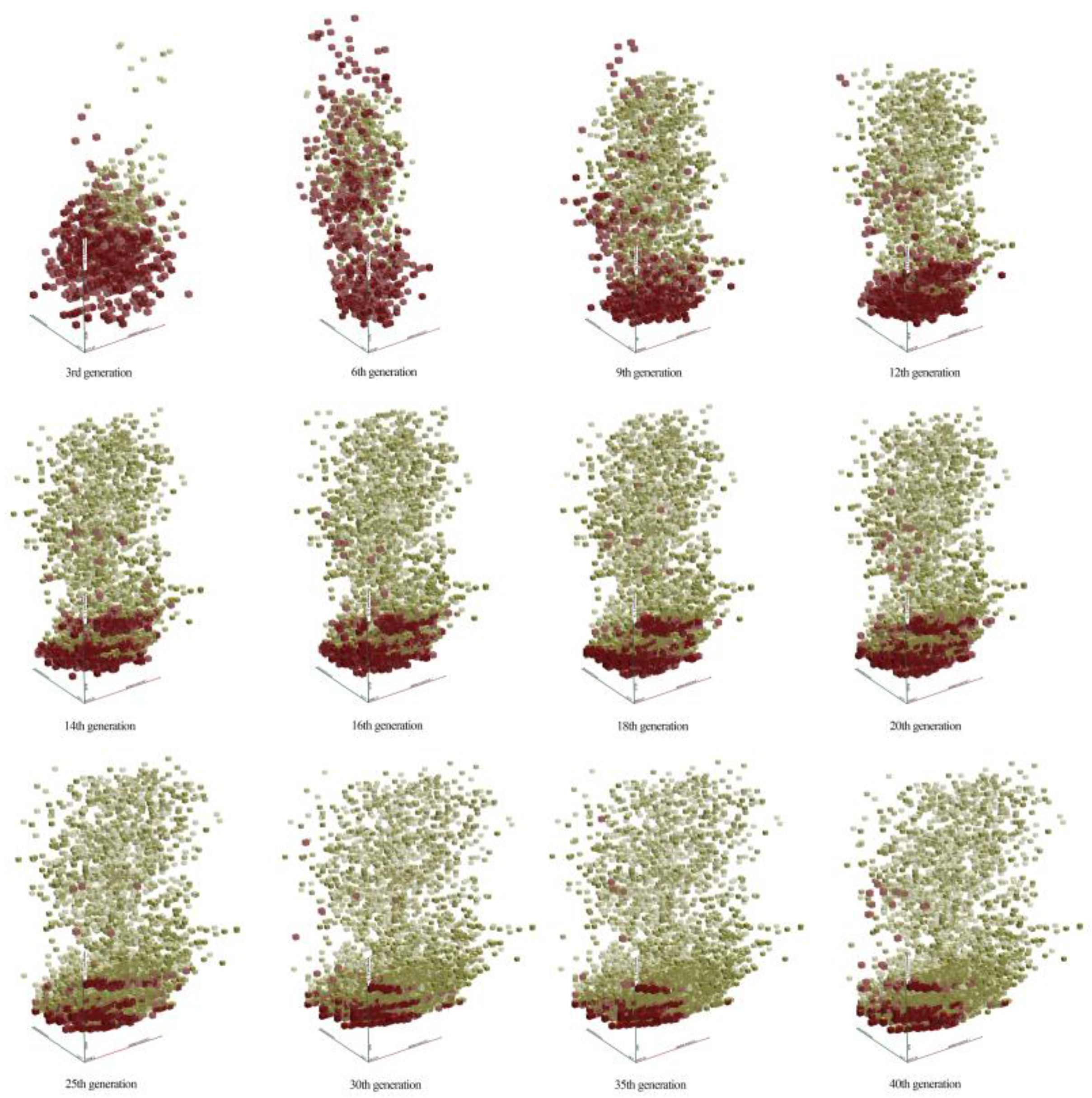
Figure 13 shows the optimization process with Duluth as an example. From the figure, it can be seen that the Pareto frontier of multi-objective optimization is more and more dense before the 9th generation, and then gradually begins to converge until the 30th generation. After 30 generations, the Pareto front has hardly changed.
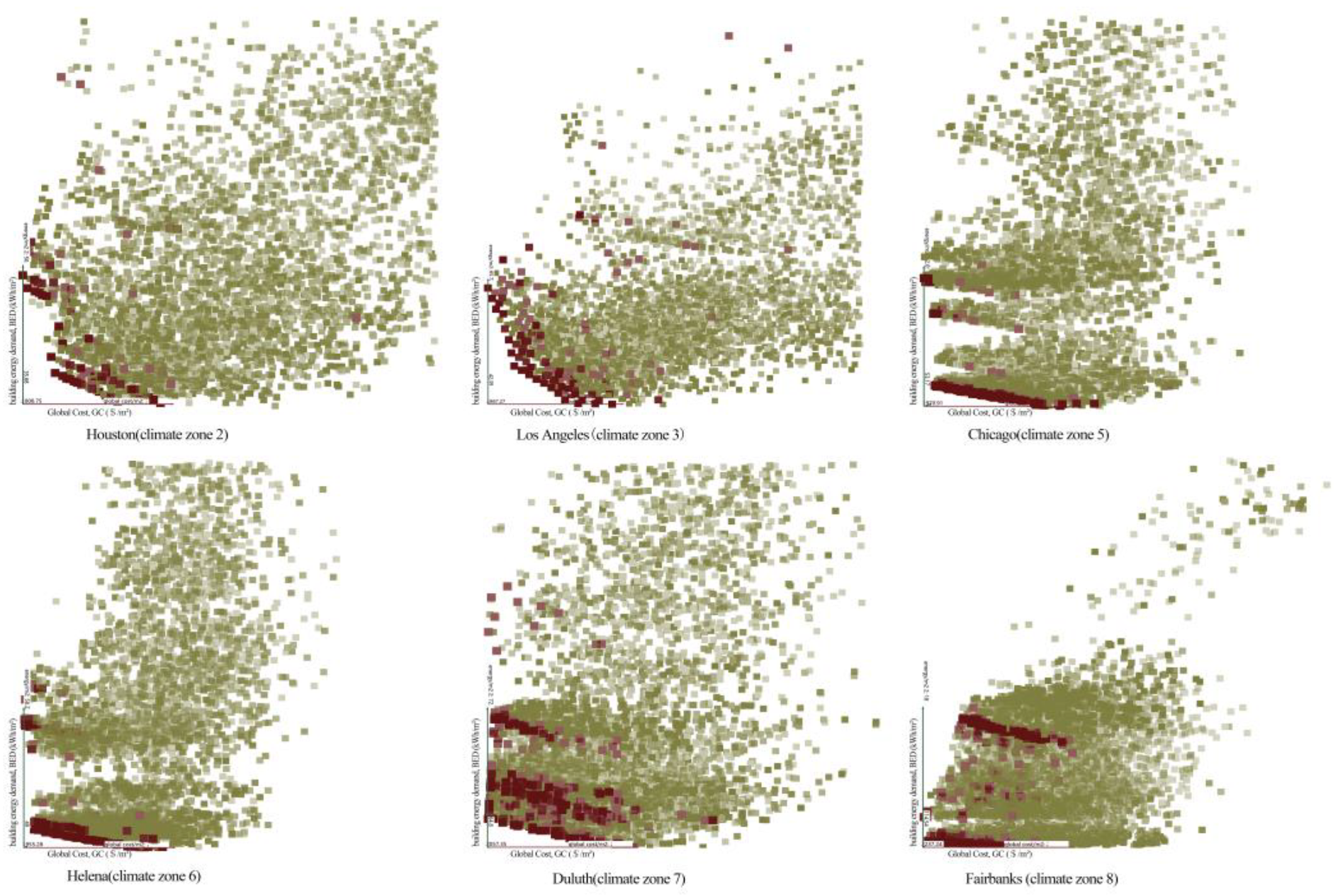
Figure 14 shows the optimization results of different climatic zones. In the three-dimensional space, all of Pareto non-dominated solutions with BED (building energy demand), GC (global cost), and DH (discomfort hour percentage) as objective functions are generated. These solutions represent trade-offs in design, because no other solution can improve (i.e., reduce) these three objectives at the same time. In order to better describe the optimization parameters, the three-dimensional solution is projected on the two-dimensional plane BED (horizontal axis)-GC (vertical axis) in
Figure 15.
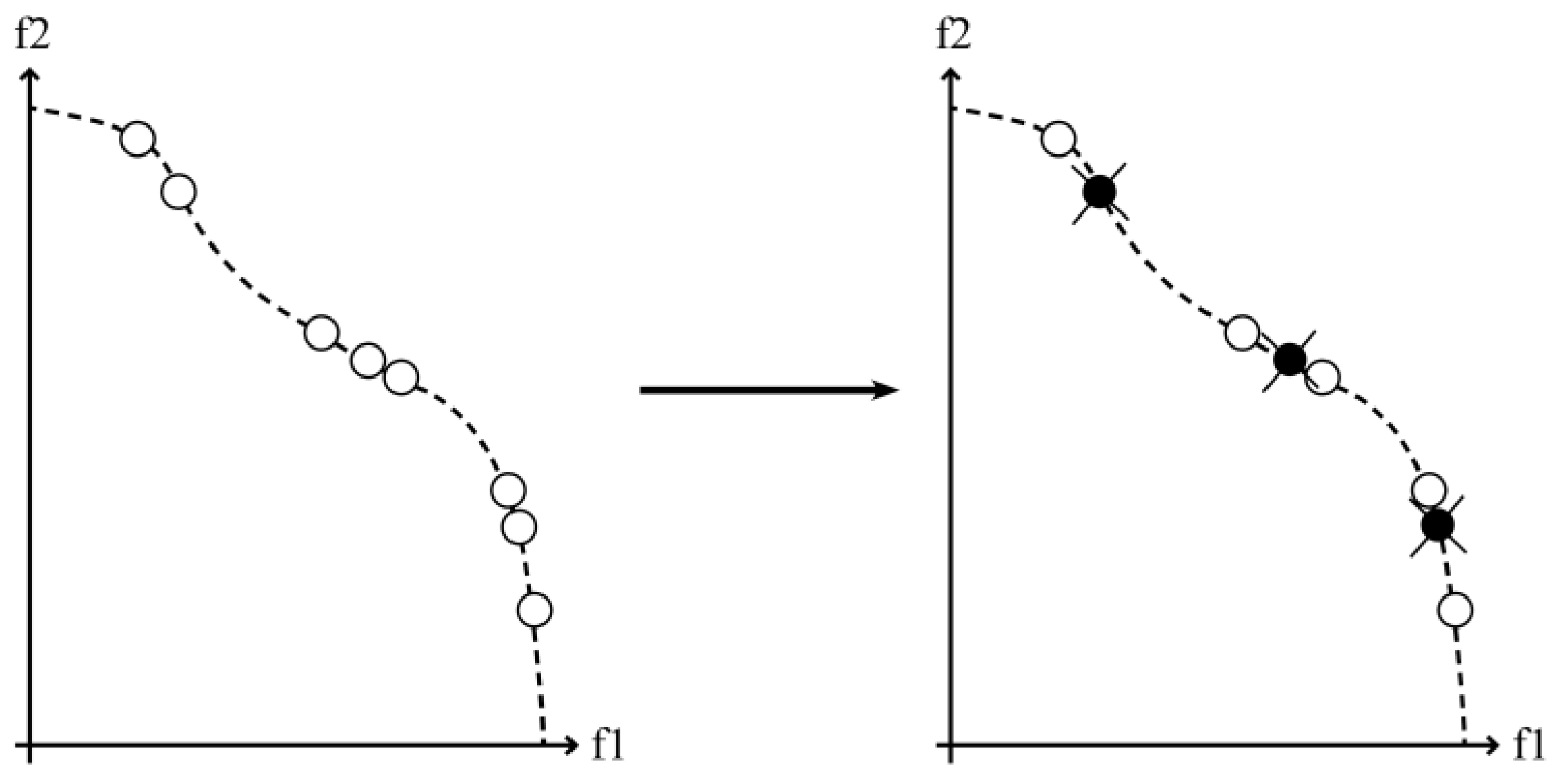
The study provides two optimal solutions, namely the energy-saving optimal solution (nZEB optimal) that minimizes building energy demand and the cost optimal solution (C-O optimal solution) that minimizes global costs. These two optimal solutions correspond to two different goals of public demand and private demand. In general, the main goal of the public social sector is to vigorously reduce energy consumption and pollution emissions, while the goal of private households is mainly to save costs and achieve indoor thermal comfort. Therefore, in
Figure 14. BED-GC non-dominated solutions focus on analyzing the minimization of BED and GC. These solutions are part of the 3D non-dominated solution because there is no other solution to improve (i.e., reduce) BED and GC at the same time. Through the BED-GC Pareto Frontier, it is easy to know:
- -
“Energy-saving optimal (nZEB) solution,” that is, BED is minimized in all non-dominated solutions, located at the right end of the 2D Pareto frontier of
Figure 15. Although this solution is expressed as nZEB, it does not mean it meets the specific nZEB standard, but because this solution is a non-dominant solution with the lowest energy demand, and its performance is closest to the nZEB standard.
- -
“Cost optimal (C-O) solution,” that is, the GC is minimized among all non-dominated solutions, located at the left end of the 2D Pareto frontier of
Figure 15.
- -
”nZEB’ solution,” when neither “energy-saving optimal (nZEB) solution” and “cost optimal (CO) solution” can meet the requirements of comprehensive indicators, in order to obtain a compromise result, it is necessary to introduce “nZEB’ Solution,” compared to the reference design, “nZEB’ solution” has lower GC and BED values (see
Figure 16).
When the Pareto front in
Figure 15 moves from left to right, the cost-effectiveness of the non-dominated solution gradually deteriorates, but the energy-saving effect gradually improves.
Table 12,
Table 13 and
Table 14 list the optimized values of the design parameters and corresponding performance indicators, specifically,
Table 12 lists the optimized values of the design parameters for each city in different climate zones, and
Table 13 lists the corresponding building envelope heating transmittance (U value),
Table 14 lists the performance indicator of the objective function under the optimized parameters and the investment cost.
From the analysis of the optimal objective function value in
Table 14, it can be seen that except Los Angeles, from warm climate zone to cold climate zone, the BED value gradually increases, because in the calculation of energy demand, heating demand is higher than cooling demand. Specifically, in nZEB optimal solution, BED in Houston is 36.20 kWh/m
2, GC is 286.97
$/m
2, DH is 29.17%, whereas in Fairbanks, BED is 114.54 kWh/m
2, GC is 418.76
$/m
2, DH is 53.33%. In C-O optimal solution, BED in Houston is 53.45 kWh/m
2, GC is 256.26
$/m
2, DH is 41.67%, whereas in Fairbanks, BED is 162.55 kWh/m
2, GC is 347.76
$/m
2, DH is 61.67%. Whereas in Los Angeles, because of its climate characteristic, the energy demand is relatively lower than other cities.
According to nZEB and C-O optimal solutions,
Table 12 lists the design parameters of residential buildings in different climate zones. In all optimization schemes, the best building orientation is the east–west orientation (0°), in order to facilitate the building to make maximum use of solar radiation in the colder season. As far as the optimization of the envelope parameters is concerned, the solar absorbance of the roof and external wall gradually increases from the warmer climate zone to the colder climate zone to maximize the utilization of solar radiation. For example, the solar absorbance of the roof and external wall in Houston residential building that is located in the south of the United States, is between 0.1 and 0.2, while that in Duluth and Fairbanks which are in the north of the United States are between 0.75 and 0.9.
The change in the thickness of envelope insulation is also related to the latitude of the city. The optimal solution for the US climatic zone 2 and climatic zone 3 represented by Houston and Los Angeles respectively does not recommend the use of insulation layers on roofs, external walls, and ground floors because these cities are in the southern United States. Compared with thermal insulation, it pays more attention to heat dissipation in summer. Therefore, the nZEB optimal solution in Houston and Los Angeles recommends the use of bricks with larger heat capacity on the building envelope. The thermal conductivity and density of the roof and ground floor bricks are 0.72 W/mK and 1800 Kg/m3, 0.9 W/mK, and 2000 Kg/m3 in Houston. The thermal conductivity and density of the external wall and ground floor bricks are 0.9 W/mK and 2000 Kg/m3, while for roof are 0.72 W/mK and 1800 Kg/m3 in Los Angeles. This helps the building absorb solar radiation during the day and delay solar energy entering the room, then at night when these heat-capacity materials release the solar energy absorbed during the day, heat is taken out of the room through night ventilation. With the exception of Houston and Los Angeles, the recommended values for the insulation thickness of external walls, roofs, and ground floors of the nZEB optimal for residential buildings in almost all cities are 0.12 m. The C-O optimal is quite different. Specifically, the thickness of the insulation layer on the external wall, roof and ground floor of the residential building in Chicago is 0.03 m, 0.04 m, and 0.03 m, respectively, making the U value of envelope slightly higher than that in the nZEB optimal, and the uncomfortable hours throughout the year is higher. In the Duluth C-O optimal solution, the thickness of the insulation layer of the external wall and roof is slightly lower than that of the nZEB optimal solution, which is 0.08 m and 0.1 m, respectively. But the block thermal conductivity and density of the roof and the ground floor in the C-O optimal solution are lower than the values in the nZEB optimal solution, which compensates for the lower thickness of the external wall and roof insulation layer, making the C-O optimal solution’s building energy demand value (BED) and the annual discomfort hours (DH) is not much different from that in the nZEB optimal solution, and reduces the global cost (GC) to some extent. In the Fairbanks C-O optimal solution, the recommended value of the insulation layer thickness of the external wall is 0.04 m, but the block thermal conductivity and density of the roof, external wall, and the ground floor of the C-O optimal solution and the nZEB optimal solution are the same, making the BED and DH values of the C-O optimal solution much higher than that in the nZEB optimal solution. Thus, a compromised nZEB’ solution is proposed, which uses the same insulation thickness of the roof, external wall, and ground floor, while only reducing the block thickness of roof and ground floor. The results show that the nZEB’ solution is able to achieve lower BED and DH values while reducing the global cost (GC), therefore, from the perspective of comprehensive indicators, it has better benefits. In general, when a thick insulation layer is installed in the envelope, the U value of it generally remains at a low value, between 0.15–0.18 W/m2K, when the insulation is not used, the U value of envelope is related to block thickness, thermal conductivity, and density. For example, the nZEB optimal solution and the C-O optimal solution in Houston are not recommended to install insulation on the external walls, roofs, and ground floors, however, the thermal conductivity and density of the roof and ground floor recommended by the C-O optimal solution are much lower than the nZEB optimal solution, leading to the U value of roof and ground floor in C-O optimal solution (0.87 W/m2K and 0.71 W/m2K) much lower than that in nZEB optimal solution (2.04 W/m2K and 1.45 W/m2K).
It can also be seen from the nZEB optimal solution that the block thickness of the external walls, roofs and ground floors gradually increases from the warmer climate zone to the colder climate zone. For example, the block thickness of the external wall and roof of residential buildings in Houston is 0.3 m and 0.25 m. In Los Angeles, the block thickness of that are 0.25 m, and ground floor is 0.4 m. The remaining cities are 0.4 m, while the block thickness of ground floor in Houston, Chicago, and Helena is 0.25 m, and that in Duluth and Fairbanks is 0.3 m. In addition, except Houston, Los Angeles, and Helena, the block thermal conductivity and density of the external wall and roof of residential buildings in various cities are always maintained between 0.25~0.3 W/mK and 600~800 kg/m3. For example, the block thermal conductivity and density for the roof of residential buildings in Houston and Helena are 0.72 W/mK, 1800 kg/m3, and 0.36 W/mK, 1000 kg/m3 respectively. In Los Angeles, the block thermal conductivity and density for the roof are 0.72 W/mK, 1800 kg/m3, and for external wall and ground floor are 0.9 W/mK, 2000 kg/m3. It is clear to see that the block thermal conductivity and density are gradually decreasing from south to north. For example, the thermal conductivity and density of ground floor in Houston and Chicago residential buildings are both 0.9 W/mK and 2000 kg/m3, while the corresponding values of Helena and Fairbanks residential buildings are 0.43 W/mK, 1200 kg/m3 and 0.25 W/mK, 600 kg/m3 respectively. It can be seen from the C-O optimal solution that the envelope block thermal conductivity and density in most typical cities’ residential buildings remained between 0.25 ~ 0.3 W/mK and 600 ~ 800 kg/m3.
For the transparent component of the envelope (i.e., windows), the triple-glazed with argon-filling, low-e coating, PVC frame window types are more common (i.e., type 7), for example, Chicago, Helena, Duluth, and Fairbanks nZEB optimal solution, Duluth C-O optimal solution, and Fairbanks nZEB’ optimal solution, although the price of this type of window is slightly high, but it has the best insulation performance. Houston’s nZEB optimal solution recommends the use of tinted double-glazed with argon-filling, low-e coating, PVC frame window (i.e., type 5), and the C-O optimal solution recommends the use of tinted double-glazed with air-filling, low-e coating, PVC frame window (i.e., type 2), this type of window has a low SHGC value of 0.38, which can effectively reduce excessive solar radiation entering the room. In Los Angeles, double-glazed with air-filling, low-e coating, aluminum frame window (type 1) is recommended in both nZEB optimal solution and C-O optimal solution, probably because it has the lowest price and will not increase the energy demand too much. Chicago, Helena, and Fairbanks C-O optimal solutions recommend double-glazed with argon-filling, low-e coating, PVC frame window (i.e., type 4). This type of window is cheaper and has a higher U value than other alternatives, which is 1.90 W/m2K, and the window SHGC is also high, which is 0.69, thus it can make better use of solar radiation, thereby greatly reducing the space heating energy.
4.2. Comparison of Optimization Results with Reference Buildings
Finally, the proposed optimal solution is compared with the climate-related reference design defined in the previous
Table 11 and
Table 15 shows the differences between BED, GC, IC, and DH.
In Houston, compared to the reference design, the BED of the nZEB optimal solution is reduced by approximately 20.55 kWh/m2, the global cost GC is reduced by approximately 36.55 $/m2, the initial investment cost is reduced by 25.22 $/m2, and the DH is reduced by 29.16%. In the CO optimal solution, although the value of GC decreased significantly, it was 67.26 $/m2, which was due to the low initial investment, which reduced to 65.4 $/m2; but the reduction in BED was very small, only 3.3 kWh/ m2, and the reduction of DH is not as effective as the nZEB program, which is 16.66% less than the reference building, making the uncomfortable hours of the year still 41.67%, so the applicability of this program in actual practice is not as good as nZEB optimal solution.
In Los Angeles, the energy demand of the reference building is very low, which is only 7.28 kWh/m
2, thus the nZEB optimal solution cannot improve it a lot. From the
Table 15, it can be seen that the BED in nZEB optimal solution is only improved by 5.24 kWh/m
2, but DH is increased by 45.84%, meanwhile the IC is also increased by 13.7
$/m
2. Compared with nZEB optimal solution, the C-O optimal solution decreases the GC by 92.98
$/m
2 and IC by 91.71
$/m
2, while only increasing DH by 8.34%. Therefore, in this climate zone, C-O optimal solution is more practical than nZEB optimal solution.
Compared with the reference design, the climate zone 5 represented by Chicago has reduced the BED in the nZEB optimal solution by approximately 20.45 kWh/m2 and DH by 13.17%, but increased the global cost by a small amount, the GC increased by approximately 14.71 $/m2, which is due to an increase in IC of approximately 25.94 $/m2. Compared with nZEB optimal, CO optimal greatly reduced the GC about 79.68 $/m2 and the IC about 82.54 $/m2, but at the expense of building energy demand and thermal environment comfort. Specifically, BED increased by 5.21 kWh/m2, DH remains the same as the reference building in 59.17%, thus compared to the C-O optimal solution, the nZEB optimal solution is more suitable for facilitating the actual design.
In the climate zone 6 represented by Helena, although the nZEB optimal solution has reduced BED by 22.32 kWh/m2 and DH by 12.5%, the cost has increased by 61.99 $/m2, which is due to the increase in IC (74.64 $/m2). The CO optimal solution reduces the building energy demand and improves the indoor thermal environment comfort, meanwhile, it also reduces the global investment cost. Specifically, BED is reduced by 18.8 kWh/m2, DH is reduced by 8.34%, GC and IC are reduced by 13.81 $/m2 and 6.27 $/m2, respectively. Therefore, the design parameters of the C-O optimal solution can be used as reference values for energy-saving design of residential buildings in climate zone 5 cities such as Chicago.
In Duluth, compared to the reference building, the BED in the nZEB optimal solution decreased by approximately 28.32 kWh/m2, and the DH decreased by 8.75%, but the GC and IC increased 28.71 $/m2 and 44.24 $/m2 respectively. Compared with the nZEB optimal solution, the GC and IC optimization of the C-O optimal solution did not come at the expense of the degradation of BED and DH. In the C-O optimal solution, BED decreased by approximately 20.43 kWh/m2, DH decreased by 6.25%, GC and IC decreased by 38.68 $/m2 and 27.47 $/m2, respectively. Therefore, from the perspective of comprehensive indicators, the design parameters of the C-O optimal solution can be used as the reference value for energy-saving design of residential buildings in Duluth.
In the climate zone 8 represented by Fairbanks, the BED of the nZEB optimal solution decreased by approximately 55.23 kWh/m2, the GC decreased by 56.97 $/m2, the IC decreased by 26.65 $/m2, and the DH decreased by 8.97%. Whereas in the C-O optimal solution, BED only decreased by about 7.22 kWh/m2, GC decreased by 127.97 $/m2, IC decreased by 106.12 $/m2, and DH decreased by 0.63%. From the aspects of building energy demand and global cost, the improvement of these two optimal solutions are not large, so a compromise nZEB’ optimal solution is proposed. In the nZEB’ optimal solution, BED is reduced by 52.37 kWh/m2, GC is reduced by 111.66 $/m2, IC is reduced by 82.91 $/m2, DH is reduced by 14.05%, the comprehensive indicator is better than nZEB optimal solution and CO optimal solution, thus it can be used as a reference value for residential buildings energy efficiency design in Fairbanks.
As can be seen from the comparison of different optimal solutions with reference buildings, the optimal design reference value of some typical cities in the United States can take the recommended value of the nZEB optimal solution, such as Houston and Chicago, because the nZEB optimal solution of these cities is superior to the CO optimal solution. While the optimal design parameters of Los Angeles, Helena and Duluth should take the recommended value of the C-O optimal solution, because in the C-O optimal solution, the best GC are able to be achieved without increasing BED, from an economic point of view, it is more suitable as an actual project reference value. Unlike the above cities, the optimal design parameters of Fairbanks should refer to the recommended value of nZEB’, because the comprehensive index of the nZEB’ solution is better than the nZEB optimal solution and the C-O optimal solution.
It can be seen from the comparison between the optimized design results and the reference building design that the best solution provides different guidelines for the energy-saving design of residential buildings in typical cities in the United States. Mainly as follows:
The best building orientation is 0°, i.e., from east to west;
In terms of external wall energy-saving design parameters, the solar absorbance of the external wall of residential buildings in the warm climate zone (Houston) can be lower (0.1), while cities in the colder climate zone require a higher solar absorbance. Besides, if the wall uses insulation in a typical city other than Houston and Los Angeles, the optimal thickness should be 0.10–0.12 m, much higher than that in the reference building (the reference building insulation thickness is 0.03–0.05 m). Moreover, the external wall is recommended to use low density and low thermal conductivity materials.
Similar to the external wall, the solar absorbance of the roof of residential buildings in the warm climate zone (Houston) can be lower (0.1), and that in the cold climate zone should be higher, the best roof insulation thickness should be 0.10–0.12 m which are similar to the reference buildings. It is recommended to use high thermal mass materials for roofs in warm climate zones, and low thermal mass materials for roofs in cold climate zones.
The ground floor is different from the external walls and roofs, as there is no direct solar radiation, the solar absorbance ranges are not predefined. However, the optimal insulation thickness of the ground floor in colder areas (except Houston and Los Angeles) should be 0.10–0.12 m, which is higher than that of the reference buildings (0.03–0.06 m), while residential buildings in Houston and other warmer areas are not recommended to use insulation, but it is recommended to use high thermal mass materials.
For windows, some cities (such as Chicago, Duluth, and Fairbanks) reference buildings that are filled with double-glazed argon-filling, low-e coating, PVC frame windows (type 4) can be replaced with triple-glazed with argon-filling, low-e coating, PVC frame windows (type 7).