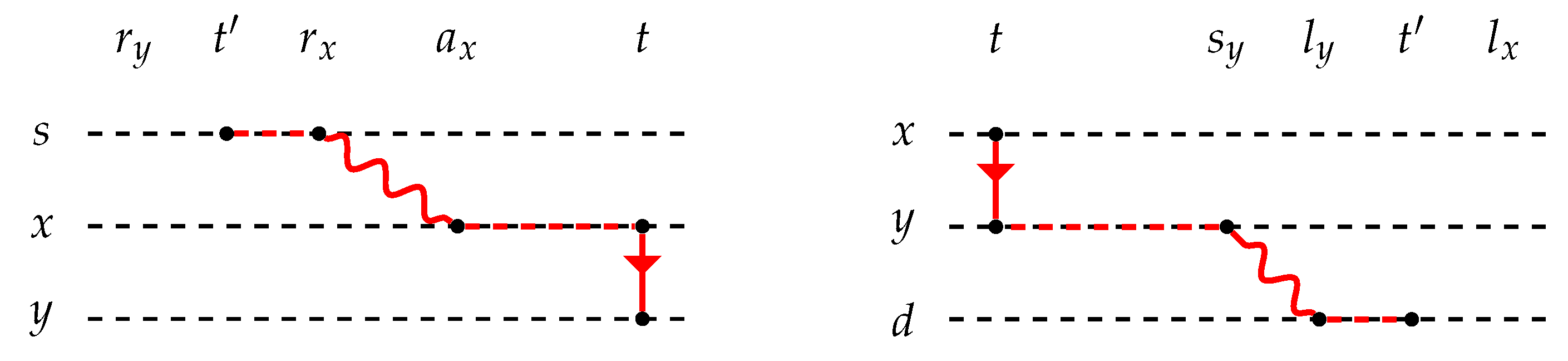1. Introduction
Determining indices capable of capturing the importance of a node in a complex network has been an active research area since the end of the forties, especially in the field of social network analysis where the ultimate goal has always been to develop theories “to explain the human behavior” [
1]. After observing “that centrality is an important structural attribute of social networks”, and that there “is certainly no unanimity on exactly what centrality is or on its conceptual foundations”, in [
2] the author proposed such a conceptual foundation of centrality by making use of graph theory concepts. The node indices proposed in that paper (that is, the degree centrality, the betweenness centrality, and the closeness centrality) have become quite standard notions in complex network analysis. For two of them in particular, that is, closeness and betweenness, a quite large amount of literature has been devoted to the design, analysis and experimental validation of efficient algorithms for computing them, either exactly (e.g., the well-celebrated Brandes’ algorithm for computing the betweenness [
3]) or approximately (e.g., the sampling approximation algorithm for estimating the closeness [
4]), especially after that very large network data have become available, thus making the searching of very efficient algorithms a necessity. Reporting all the results obtained in this direction is clearly out of the scope of this paper: we refer the interested reader to one of the several surveys that appeared in the literature (such as [
5]), to one of the several more conceptual works (such as [
6]), or to the excellent periodic table of network centrality shown in [
7].
In this paper, we focus our attention to the closeness centrality measure, which associates to each node of a graph its average distance from all the other nodes (since we will deal with unweighted graphs only, the distance between two nodes
u and
v is simply the number of edges included in the shortest path from
u to
v). In order to deal with the case of (weakly connected) directed graphs, two main alternatives are available when formally defining this measure: one approach assumes that the number of nodes reachable from a node
u is known (see, for example, [
8]), while the other, which is also called harmonic centrality, uses the inverse of the distances in order to deal with disconnected pairs of nodes (see, for example, [
9]). Since in this paper we will use the temporal analogue of the second alternative, we limit ourselves to give the following formal definition. Given a directed graph
, the (harmonic) closeness of a node
is defined as
, where
denotes the number of edges included in the shortest path from
u to
v (by convention,
if there is no path connecting
u to
v). The harmonic closeness of a node is a value between 0 and 1: the closer is
to 1, the more important the node
u is usually considered. For instance, in a directed star with
n nodes, there is one node whose closeness is equal to 1, while all other nodes have closeness equal to 0. On the contrary, in a directed cycle with
n nodes, all nodes have closeness
, where
denotes the
k-th harmonic number (that is, the sum of the reciprocals of the first
k natural numbers).
Computing the closeness of a node
u in a directed (unweighted) graph is simple: we just have to perform a breadth-first search starting from
u and sum the inverse of the distances to all the nodes reached by the search. This requires
time and
space, where
n denotes the number of nodes and
m denotes the number of edges. However, we are usually interested in comparing the closeness of all the nodes of the graph in order to rank them according to their centrality. This implies that we have to perform a breadth-first search starting from each node of the graph, thus requiring time
. This computational time is unavoidable (as shown in [
10]), unless the strong exponential time hypothesis [
11] fails. However, in the case of real-world complex networks, the number of nodes and of edges is typically so large that this algorithm is practically useless. For this reason, several approaches have been followed in order to deal with huge graphs, such as computing an approximation of the closeness centrality (see, for example, [
4,
12]) or limiting ourselves to find the top-
k nodes with respect to the closeness centrality [
10]. These algorithms turn out to be so effective and efficient that several of them are already included in well-known and widespread used network analysis software libraries (such as [
13,
14]).
So far, we have talked about static graphs, that is, graphs whose topology does not change over time. In this paper, however, we will focus on (directed) relationships which have timestamps. This led the research community to the definition of temporal graphs, that is, (unweighted) graphs in which edges are active at specific time instants: for this reason, we call them temporal edges and we denote them by triples , where t is the appearing time of the temporal edge connecting u and v. Temporal graphs are ubiquitous in real life: phone call networks, physical proximity networks, protein interaction networks, stock exchange networks, and public transportation networks are all examples of temporal graphs, in which the nodes are related to each other at different time instants. Until recently, the time dimension has been often neglected by aggregating the contacts between vertices to (possibly weighted) edges, even in cases when detailed information on the temporal sequences of contacts or interactions would have been easily available. For example, almost all collaboration networks (such as the scientific or professional collaboration networks) have been almost always analyzed without taking into account the time of the collaboration, even when this information was easily available (such as in the case of the information given by the DBLP computer science bibliography web site).
However, if the temporal information is just ignored, we can lose important properties of the graph and we can even deduce wrong consequences. For example, in the case of the temporal undirected graph shown in the left part of
Figure 1, if we ignore the temporal information associated with the edges, we can erroneously conclude that there exists a path starting from node
a, arriving at node
c, and visiting the other node
b. However, this path does not correspond to a temporally-feasible path, since the edge connecting node
a to node
b appears after the edge connecting
b to
c: in other words, when we arrive in
b it is too late to take the edge towards
c. It is then important to analyze temporal graph properties by taking into account the temporal information concerning the time intervals in which specific edges appear in the graph. For this reason, the community has rethought several classical definitions of graph theory in terms of temporal graphs [
15,
16,
17].
One of such definition is the one of closeness centrality, which has been repeatedly reconsidered in the case of temporal graphs [
18,
19,
20,
21,
22,
23,
24,
25,
26,
27]. In several of these papers, the authors refer to the classical definition of closeness centrality (that is, the one based on the average temporal distance), but in many cases, they actually consider the temporal analogue of the harmonic closeness centrality. In both cases, however, the first step to perform in order to rethink the definition of closeness in terms of temporal graphs consists of defining the temporal distance between two nodes. Even if different notions of distance have been introduced while working with temporal graphs (see, for example, [
28]), in this paper, we will focus only on one specific distance definition, which is, in our opinion, one of the most natural ones: that is, the time duration of the earliest arrival path starting no earlier than a specific time instant. This definition is motivated, for example, by the following typical query one could pose to a public transport network: if I want to leave no earlier than time
t, how long does it take to me to go from a (bus/metro/train) station to another station?
More precisely, for any time instant
t, a temporal
t-path (also called
t-journey) is a sequence of edges such that the first edge appears no earlier than
t and each edge appears later than the edges preceding it. Its arrival time is the appearing time of its last edge and its duration is the difference between its arrival time and
t (plus one in order to include the traveling time along the last edge). The
t-distance
from a node
u to a node
v is then the minimum duration of any temporal
t-path connecting
u to
v and having the smallest arrival time (once again, if there is no
t-path from
u to
v, we will assume that
). For instance, in the case of the temporal triangle in the left part of
Figure 1, we have that
, while
: indeed, if we insist in leaving after time 1, we cannot arrive at
a before time 4. Note that, for any
,
, since there are no temporal edges incident to
b with appearing time greater than 2.
Once we have a definition of distance from a node to another node, we can define the notion of temporal closeness centrality of a node
u at a given time instant
t by simply applying the harmonic definition of closeness in the case of a static graph (see, for example, [
9]). Note that we refer to the harmonic closeness centrality, since, as in the case of weakly connected directed graphs, this definition allows us to deal with the fact that two nodes might not be connected by a temporal path. More precisely, the
t-closeness of a node
u is defined as
. In [
22], the evolution of
was analysed in the case of two social networks (an e-mail graph and a contact graph). To this aim, the authors used an algorithm (inspired by [
29]) for computing the
t-closeness of a node of a temporal graph, whose time complexity is linear in the number
m of temporal edges and whose space complexity is linear in the number
n of nodes. For example, we can apply this algorithm to analyse and compare the evolution of the
t-closeness in the case of two actors, by referring to the IMDB collaboration graph, where the nodes are the actors and the temporal edges correspond to collaborations in the same (non TV) movie (the appearing time of an edge is the year of the movie). In the left part of
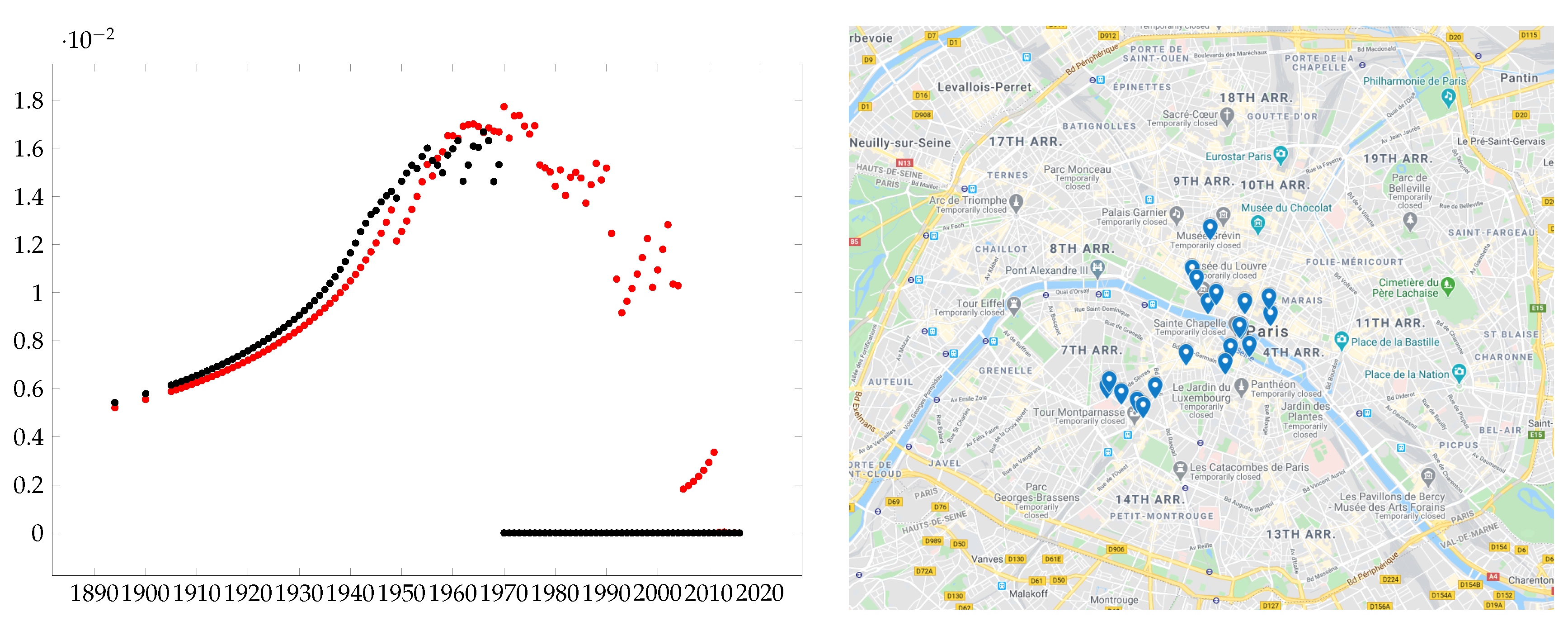
Figure 2, we show the evolution of the
t-closeness of Christopher Lee and Eleanor Parker (two actors who were alive approximately in the same period) (Note that the
t-closeness is greater than zero even when
t is less than the birth year of the corresponding actor. This is not a contradiction, since, in general, a temporal edge may contribute to the
t-closeness of a node for all
t preceding the appearing time of the temporal edge itself). As can be seen, the two plots are quite similar until the end of the sixties (even if the plot of Parker has a smaller peak). Successively, Parker drastically reduced her activity (indeed, after
The sound of music in 1965, she participated to only six not very successful movies), while Lee had two other growing periods (most likely, the second one is related to his participation to the
Star Wars and the
The Lord of the Rings sagas). The figure thus suggests that Lee has been more “important” than Parker.
In order to capture this idea formally, we introduce a global temporal closeness centrality of a node
u in a given time interval
which is based on computing the integral of
over that interval. That is, for any node
u in the graph, we compute and analyse the temporal closeness
of
u, which is defined as
(intuitively,
can be seen as the Area Under Curve (AUC) value of the function
). This is similar to what is done in [
18] for the betweenness centrality (which is connected to the number of shortest paths that pass through a node): since their betweenness definition depends on the time at which a node is considered, they average it to obtain a global value. Here the integral is the natural equivalent of the average, for a continuous function. For example, the closeness of Christopher Lee is approximately equal to 0.005, while the closeness of Eleanor Parker is approximately equal to 0.003, thus confirming the previous intuition that Lee is more central than Parker. The right part of
Figure 2, instead, shows the top 20 nodes in the public transport temporal graph of Paris with respect to the temporal closeness centrality measure (the used graph is derived by the data set published in [
30], and successively adapted to the temporal graph framework in [
31]).
1.1. Our Results
Our first contribution is the design and analysis of an algorithm for computing the temporal closeness of a node of a temporal graph in a given time interval, whose time complexity is linear in the number
m of temporal edges and whose space complexity is linear in the number
n of nodes. This algorithm, which is an appropriate modification of the one used in [
22] and adapted from [
29], can be seen as a temporal version of the classical breadth-first search algorithm. Computing the temporal closeness of all nodes in order to compare them and find the nodes with highest temporal closeness can, hence, be done in time
, by applying
n times the algorithm for computing the temporal closeness of a node. This time complexity, however, is much too high in the case of large temporal graphs.
Our second and more important contribution is showing that the algorithm for computing the temporal closeness of a node can be modified in order to obtain a backward version of the algorithm itself, which allows us to compute the “contribution”
of a specific node
d to the temporal closeness of any other node
u. By using this algorithm (which is inspired by the earliest arrival profile algorithms of [
32]), we can then implement a temporal version of the sampling algorithm introduced in [
4] in order to approximate the closeness in static graphs. In particular, for a temporal graph with
n nodes and
m temporal edges, we can compute an estimate of the temporal closeness of all its nodes whose absolute error is bounded by
in time
, which significantly improves over the time complexity of applying
n times the algorithm for computing the temporal closeness of a node, that is,
.
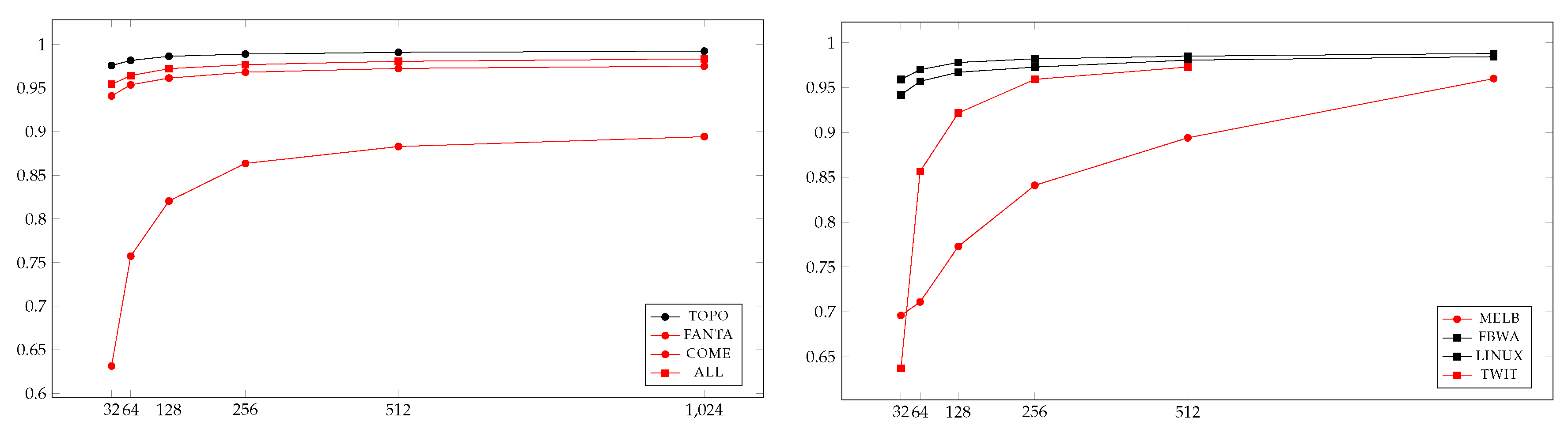
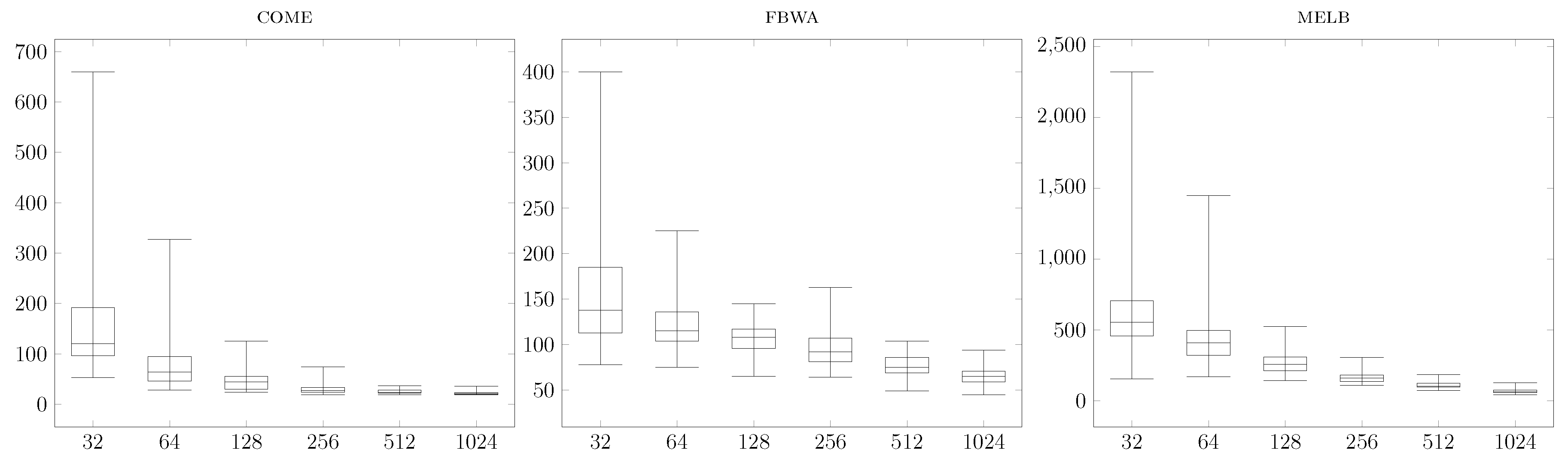
There is a natural way of using this temporal closeness estimation to empirically find the exact top-k nodes according to our temporal closeness metric. This approach simply consists in running our estimate temporal closeness computation algorithm, in finding the top-K nodes for the estimated temporal closeness, with , and in computing the exact temporal closeness of these nodes. Our third contribution is an extensive experimental validation of this approach with a dataset of 45 medium/large temporal graphs. Indeed, we show empirically that using this method we can retrieve the actual top-100 nodes of all large graphs we have considered by choosing , that is (with a little abuse of notation), in time , which is between 10 and 100 times faster than computing the temporal closeness of all nodes.
1.2. Other Related Work
Besides the references given above, our paper is related to all work on the definition and computation of different temporal centrality measures, such as the temporal betweenness centrality defined in [
33], the
f-PageRank centrality defined in [
34], or the temporal reachability used in [
35], just to mention some recent ones. The authors of [
36], instead, study the evolution of the closeness centrality for static graphs and propose efficient algorithms for computing it. In the case of static graphs, an approach based on the sampling approximation algorithm of [
4], in order to select the candidates for which computing the exact closeness, was proposed in [
37]: its complexity is, however, still quite high, that is,
(under the rather strong assumption that closeness values are uniformly distributed between 0 and the diameter). Still, in the case of static graphs, in [
38] the authors identify the candidates by looking for central nodes with respect to a “simpler” centrality measure (for instance, degree of nodes).
1.3. Structure of the Paper
In the rest of this section, we give all the necessary definitions concerning temporal paths, temporal distances and temporal closeness (these definitions are mostly inspired by [
16,
28,
39]). In
Section 2 we introduce and analyze our algorithm for computing the temporal closeness of a node of a temporal graph in a given time interval, while in
Section 3 we describe and analyze the backward version of this algorithm and we show how this version can be used in order to obtain an error-guaranteed estimate of the temporal closeness of all the nodes of a temporal graph. In these two sections, we assume that the temporal edges have all distinct appearing times: in
Section 4, we show how our algorithms can be adapted (without worsening the time and space complexity) to the more general and more realistic case in which multiple edges can appear at the same time. In
Section 5 we experimentally validate our approximation algorithm and we show how it can be applied to the problem of finding the top nodes in real-world medium/large temporal graphs. Finally, in
Section 6 we conclude by suggesting some research directions and possibly other applications of our backward temporal breadth-first search algorithm.
1.4. Definitions and Notations
A temporal graph is a pair , where V is the set of nodes and E is the set of temporal edges. A temporal edge is a triple , where are the source and destination nodes of the edge, respectively, and is the appearing time of the edge. If the temporal edges are bidirectional, then can be also written as . Let (respectively, ) denote the minimum (respectively, maximum) appearing time of a temporal edge in E. The time horizon of a temporal graph G is the interval of real numbers no smaller than and no greater than . In this paper, we will assume that the temporal edges are given to the algorithms one after the other (similarly, to the streaming model) either in non-decreasing or in non-increasing order with respect to the appearing time.
A temporal path
(also called a temporal walk [
17]) in a temporal graph
from a node
to a node
is a sequence of temporal edges
such that
,
, and, for each
i with
,
and
. The length of a temporal path is the number of temporal edges included in it. The starting time (respectively, ending time) of a temporal path
, denoted by
(respectively,
), is equal to the appearing time of the first (respectively, last) temporal edge in the path. Given a time
and two nodes
u and
v, we will denote by
the set of all temporal paths
from
u to
v such that
. Among all these temporal paths, in this paper we will distinguish the ones which allow us to arrive as early as possible.
Definition 1. Given a temporal graph , two nodes u and v in V, and a time , a path is said to be an earliest arrival t-path if .
Given a time and two nodes u and v, the t-duration of a path is defined as . Hence, an earliest arrival t-path is also a path in with minimum t-duration. For this reason, we will also call these paths the shortest t-paths from u to v.
Definition 2. Given a temporal graph , two nodes u and v in V, and a time , the t-distance from u to v is equal to the t-duration of any shortest t-path from u to v (by convention, if , then we set ).
Once we have introduced the notion of t-distance, we can also define the analog of the harmonic closeness centrality in static graphs as follows.
Definition 3. Given a temporal graph , a node u, and a time , the t-closeness of u is defined as The (temporal) closeness of u in is then defined as An Example
Let us consider the temporal graph shown in the left part of
Figure 1. In this case,
,
, and
. As shown in the right part of the figure, for any
, the duration of a shortest
t-path from node
a to node
b is equal to
, while, for any
, this duration is infinity since there is no
t-path from node
a to node
b. On the other hand, for any
, the duration of a shortest
t-path from node
a to node
c is equal to
. Hence, the closeness of node
a is equal to
Analogously, we can verify that the closeness of node b is , and that the closeness of node c is .
2. Computing the Closeness
In this section, we propose an algorithm for computing exactly the closeness of a node u of a temporal graph G. This algorithm can be seen as a temporal version of the breadth-first search algorithm starting from a source node s, in which the temporal edges are scanned in non-decreasing order with respect to their appearing time. In the following, we assume that the appearing times of all temporal edges are distinct: the algorithm can be adapted to the case in which this assumption is not satisfied, as we will see below. Moreover, we assume that the temporal graph is directed: if this is not the case, we simply have to examine each edge twice by inverting the source and the destination.
The algorithm maintains, for each node x of G, a triple , which indicates that, for any time instant t in , any earliest arrival t-path from s to x has ending time equal to (see Algorithm 1). At the beginning, we do not know anything about the reachability of a node x from s: hence, we set the arrival time of x equal to ∞ for an arbitrary time interval (for example, ) preceding (line 1). When we read a new temporal edge , we first set , since, clearly, the source node is always reachable even before the appearance of the edge (line 2). Let and be the two triples associated with x and y, respectively. If , then we add to the closeness of s the contribution of node y corresponding to the interval (line 3) and we update the triple associated with y by setting (line 4). This update is justified by Lemma 1. When all temporal edges have been read, we add to the closeness of s the contribution of a node x corresponding to the interval (line 5), which is the last interval for which the earliest arrival time has been computed. The way of computing the contribution to the closeness of s (lines 3 and 5) is justified by the proof of Theorem 1.
Lemma 1. Let be a temporal graph and . For any with , let be the sequence of triples such that , , , and, for , is the triple assigned to at the i-th execution of line 4 with during the running of Algorithm 1 with input G and s (note that if this line is never executed with ). Then, for any with , the intervals , for , form a partition of the interval , and, for any , | Algorithm 1: Algorithm for computing the closeness of a node |
![Algorithms 13 00211 i001 Algorithms 13 00211 i001]() |
Proof. We prove the lemma by induction on the number
k of temporal edges that have been read. In particular, for any
k with
, let
be the following statement.
For any with , let be the prefix of containing the triples assigned to at line 4 with after having read k edges. The intervals , for , form a partition of the interval , and, for any , if then .
We now prove by induction on
k that
is true for any
k with
.
Base case. . In this case, no edge has been read yet and, hence, line 4 has never been executed with . We then have that, for any with , , with , and, hence, . Moreover, the interval is empty and the condition on the t-distances is “vacuosly” true. Hence, is true.
Induction step. Given
k with
, suppose that
is true. We now prove that
is also true. Let
be the
k-th temporal edge read by the algorithm. Clearly, this edge has no influence on any other node than
y (since the graph is directed). Hence, we have just to prove that the value of
is correctly updated. By the induction hypothesis, we know that the current value of
is such that, for any
, the ending time of any earliest arrival
-path from
s to
y is at most
. Hence, the edge
e cannot improve these ending times since its appearing time is
t. Analogously, we know that the current value of
is such that
is the ending time of any earliest arrival
-path from
s to
x with
. If
, the edge
e does not add any information for the node
y, since we already know the ending time of any earliest arrival
-path from
s to
y, for any
. On the contrary (see the left part of
Figure 3), if
, then, for any time instant
(for which we did not know yet the corresponding ending time of any earliest arrival
-path from
s to
y), we can now say that we can first reach
x (at time
with
), and then wait until the temporal edge
e appears to move to
y at time
t: hence, for all these time instants, the earliest arrival time at
y can now be set equal to
t, that is, the value of
becomes
(note that subsequent edges cannot improve this value since their appearing times are greater than
t). Hence, if
, we have that
with
and
. By induction hypothesis, the intervals
, for
, form a partition of the interval
: by adding the triple
, we obtain a partition of the interval
(since
and
). From the previous argument, it also follows that, for any
, if
then
. We have thus proved that
is satisfied.
The lemma follows from the fact that its statement is exactly equivalent to . □
Theorem 1. Let be a temporal graph and . Algorithm 1 with input G and s correctly computes the closeness of s in G. If the temporal edges are already ordered in increasing order with respect to their appearing time, then the complexity of the algorithm is time and space.
Proof. From Lemma 1, it follows that, with respect to the node
u, the interval
is partitioned into
intervals
, such that, for any
, if
, then
. That is, each time instant
contributes to the closeness of
s with the value
. Hence, the closeness of
s is equal to
Note that we used the maximum function in order to deal with the first interval whose left extreme is smaller than and whose right extreme can also be smaller than (whenever u is not reachable from s in the interval ). Observe that the interval might be non empty: however, if this the case, then we can conclude that if we start from s at time t in this interval, then we cannot reach u. That is, for any and, hence, this interval does not contribute to the closeness of s. Hence, Algorithm 1 correctly computes the closeness of node s.
The time complexity of the algorithm is clearly , since each temporal edge is analyzed one time only, and the update operation requires constant time. The space complexity is linear in the number of nodes, since (apart from the value C), for each node u, we have to maintain just three numbers corresponding to the current value of . □
From the previous theorem, it follows that if we want to compute the closeness of all nodes, this would take time
, since we have to execute Algorithm 1 for each source node
s. This time complexity may turn out to be not acceptable in the case of real-world large size temporal graphs. That is why in the next section, we propose an analog of the sampling algorithm used for approximating the closeness in the case of static graphs [
4], based on an appropriate modification of Algorithm 1.
3. Approximating the Closeness
In order to approximate the closeness in temporal graphs, we first need to introduce the notion of the latest starting path. To this aim, given a time and two nodes u and v, we will denote by the set of all temporal paths from u to v such that .
Definition 4. Given a temporal graph , two nodes u and v in V, and a time , a path is said to be the latest starting t-path if .
Moreover, we need to define the contribution of a destination node d to the closeness of another node u.
Definition 5. Given a temporal graph and two distinct nodes d and u, the contribution of d to the closeness of u is defined as By convention, we also set , for any node .
We now introduce a sort of backward version of Algorithm 1 (which can be seen as an adaptation of the earliest arrival profile algorithms proposed in [
32]), which has to be applied to a destination node
d, and that will allows us to compute, for any other node
x, the contribution of
d to the closeness of
x (that is,
) and, hence, to adapt to temporal graphs the well-known sampling technique already used in the case of classical graphs. Differently from the case of Algorithm 1, we assume that the temporal edges are scanned in non-increasing order with respect to their appearing times. Once again, we assume that the appearing times of all temporal edges are distinct (we will see in the next section how the algorithm can be adapted to the case in which this assumption is not satisfied), and that the temporal graph is directed (if this not the case, we simply have to examine each edge twice by inverting the source and the destination). The algorithm maintains, for each node
x of
G, a triple
, which indicates that, for any time instant
t in
, any latest starting
t-path
from
x to
d has starting time
equal to
(see Algorithm 2). At the beginning, we do not know anything about the reachability of
d from a node
x: hence, we set the starting time of
x equal to
∞ for an arbitrary time interval (for example,
) following
(line 1). When we read a new temporal edge
, we first set
, since, clearly, the destination node can always reach itself even starting after the appearance of the edge (line 2). Let
and
be the two triples associated with
x and
y, respectively. If
, then we add to
the contribution corresponding to the interval
(line 3) and we update the triple associated with
x by setting
(line 4). This update is justified by Lemma 2. When all temporal edges have been read, for each node
x, we add to
the contribution corresponding to the interval
and to the interval
(line 5), which are the last intervals for which the latest starting time has been computed. The way of computing the contribution to
(lines 3 and 5) is justified by the proof of Theorem 2.
| Algorithm 2: Algorithm for computing the closeness contribution of a node to all the others |
![Algorithms 13 00211 i002 Algorithms 13 00211 i002]() |
Lemma 2. Let be a temporal graph and . For any with , let be the sequence of triples such that , , , and, for , is the triple assigned to at the -th execution of line 4 with during the running of Algorithm 2 with input G and d (note that if this line is never executed with ). Then, for any with , the intervals , for , form a partition of the interval , and, for any , Proof. We prove the lemma by induction on the number
k of temporal edges that have been read. In particular, for any
k with
, let
be the following statement.
For any with , let be the suffix of containing the triples assigned to at line 4 with after having read k edges. The intervals , for , form a partition of the interval , and, for any , if then .
We now prove by induction on
k that
is true for any
k with
.
Base case. . In this case, no edge has been read yet and, hence, line 4 has never been executed with . We then have that, for any with , , with , and, hence, . Moreover, the interval is empty and the condition on the t-distances is “vacuosly” true. Hence, is true.
Induction step. Given
k with
, suppose that
is true. We now prove that
is also true. Let
be the
k-th temporal edge read by the algorithm. Clearly, this edge has no influence on any other node than
x (since the graph is directed). Hence, we have just to prove that the value of
is correctly updated. By the induction hypothesis, we know that the current value of
is such that, for any
, the starting time of any latest starting
-path from
x to
d is at least
. Hence, the edge
e cannot improve these starting times since its appearing time is
t. Analogously, we know that the current value of
is such that
is the starting time of any latest starting
-path from
y to
d with
. If
, the edge
e does not add any information for the node
x, since we already know the starting time of any latest starting
-path from
x to
d, for any
. On the contrary (see the right part of
Figure 3), if
, then, for any time instant
(for which we did not know yet the corresponding latest starting time from
x), we can now say that we can first reach
y (at time
t with
by using the temporal edge
e), and then wait until starting the path from
y to
d at time
: hence, for all these time instants, the latest starting time at
x can now be set equal to
t, that is, the value of
becomes
(note that subsequent edges cannot improve this value since their appearing times are smaller than
t). Hence, if
, we have that
with
and
. By the induction hypothesis, the intervals
, for
, form a partition of the interval
: by adding the triple
, we obtain a partition of the interval
(since
and
). From the previous argument, it also follows that, for any
, if
then
. We have thus proved that
is satisfied.
The lemma follows from the fact that its statement is exactly equivalent to . □
Theorem 2. Let be a temporal graph and . Algorithm 2 with input G and d correctly computes, for any with , the value . If the temporal edges are already ordered in decreasing order with respect to their appearing time, then the complexity of the algorithm is time and space.
Proof. From Lemma 2, it follows that, with respect to the node
u, the interval
is partitioned into
intervals
, such that, for any
, if
, then
. That is, each time instant
contributes to
with the value
. Hence, we have that
Note that we used the minimum function in order to deal with the last interval whose right extreme is greater than and whose left extreme can also be greater than (whenever u cannot reach d in the interval ). Note also that the interval might be non empty: if this the case, then we can conclude that if we start from u at time t in this interval, then we cannot reach d before . That is, for any and, hence, this interval contributes to with the first integral in the previous equation. Hence, Algorithm 2 correctly computes the contribution of node d to the closeness of node u.
The time complexity of the algorithm is clearly , since each temporal edge is analyzed once only, and the update operation requires constant time. The space complexity is linear in the number of nodes, since, for each node u, we have to maintain (apart from the value C) just four numbers corresponding to the current value of and to the starting value of the previous tuple. □
From the definition of closeness and of
, it follows that
This formula immediately suggests the following definition of an estimator of the closeness of a node.
Definition 6. Given a temporal graph , a node u, and a (multi)set of vertices in V, we define the closeness X-estimator of u in as Theorem 3. Let be a temporal graph and be a randomly chosen (multi)set of h nodes in G. If , then, for any node , with high probability.
The proof of the above theorem uses the same techniques of [
4], and is very similar to the one given in [
40] to analyze the absolute error of a sampling-based algorithm for computing distance distribution approximations in static graphs. For the sake of completeness, we give the complete proof. As a first step, the following lemma shows that the closeness estimator is unbiased.
Lemma 3. Given a temporal graph and a uniformly randomly chosen node , the expected value of is equal to .
Proof. Since
x has been randomly chosen in a uniform way, we have that
From the definition of the estimator and from the fact that
, it follows that
The lemma is thus proved. □
In order to prove Theorem 3, we make use of the following application of the Hoeffding’s inequality (see, for example, [
41]).
Theorem 4. If are independent random variables such that and, for each i, , then, for any , Proof Theorem 3. Given a temporal graph
, a node
u, and a randomly chosen (multi)set
X of nodes in
V with
, we apply the above theorem by setting
, for each
i with
. From Lemma 3, it follows that
Moreover, from the definition of the estimator and from the fact that we can assume that the number
n of nodes is at least equal to 2, we have that, for each
i with
,
Finally, we also have that
Hence, from Theorem 4, it follows that, for any
,
By choosing
, we then have that
and the theorem thus follows. □
Finding Top-K Nodes
Theorem 3 states that we can approximate the closeness centrality of all nodes of a temporal graph by using a sample of size
h, which is logarithmic with respect to the number of nodes. In
Section 5, we will show how this approximation method works particularly well for nodes with a high closeness. Based on this observation, a natural strategy for finding the top-
k nodes consists of: (a) compute the approximated temporal closeness for all nodes, using a sample size
h; (b) rank the nodes according to this estimation and select the top-
K nodes, with
; and (c) compute the exact closeness of these
K nodes, then rank them and select the top-
k nodes. As we will see in
Section 5, in practice choosing
has worked in all cases we have investigated for finding the top-100 nodes. This leads to a total cost proportional to
, which is a quite small (between
and
) fraction of the cost that would be needed to compute the exact closeness for all nodes.
4. How to Deal with Multiple Edges
In the previous sections, we have assumed that, for each time , there exists at most one edge whose appearing time is equal to t. Clearly, this assumption is not realistic since, in the vast majority of real-world temporal graphs, many edges can appear at the same time. In this section, we show how we can modify Algorithm 2, in order to deal with this more general case (the modification of Algorithm 1 is similar). For the sake of clarity of exposition, we will assume that, for each node u, the algorithm maintains a list of triples (instead of just one triple): it is not difficult to show that only the last two triples are really necessary at each iteration of the algorithm, thus assuring that the algorithm itself has linear space complexity.
Let us suppose that a new temporal edge arrives, and that the last triple inserted in (respectively, ) is (respectively, ). This implies that that if we want to arrive at the destination d in the interval (respectively, ), then we cannot start from x (respectively, y) later than (respectively, ). Remember that, in Algorithm 2, the temporal edges are scanned in non-increasing order with respect to their appearing times: hence, we know that (respectively, ). We now distinguish the following cases.
. In this case, neither x nor y has yet used an edge at time t. Hence, we can update the set of intervals as we did in the case of edges with distinct appearing times. That is, if , then add to the triple .
. In this case, y has already “encountered” an edge at time t. Let be the triple just before in (note that and that ). If , then we add to the triple : indeed, since , we now know that, to arrive at d in the interval , we can start from u at time t (by using the edge e), wait until time , and then follow the journey from y to d.
. In this case, x has already “encountered” an edge at time t. If , then we extend to the left the triple of x until : indeed, since , we now know that, even to arrive at d in the interval , we can start at time t (by using the edge e), wait until time , and then follow the journey from y to d.
. In this case, both x and y have already “encountered” an edge at time t. Let be the triple just before in (note that and ). Similarly to the previous case, if , then we extend to the left the triple of x until .
Note that the modification of the contribution to has to be done only in the first two cases (and at the end of the while loop, in order to deal with the leftmost intervals). Note also that the four above cases require constant time, in order to be implemented: hence, the time complexity of the modified algorithm is still linear in the number of temporal edges.