Hierarchical and Unsupervised Graph Representation Learning with Loukas’s Coarsening
Abstract
1. Introduction
2. Related Work
3. Definitions and Background
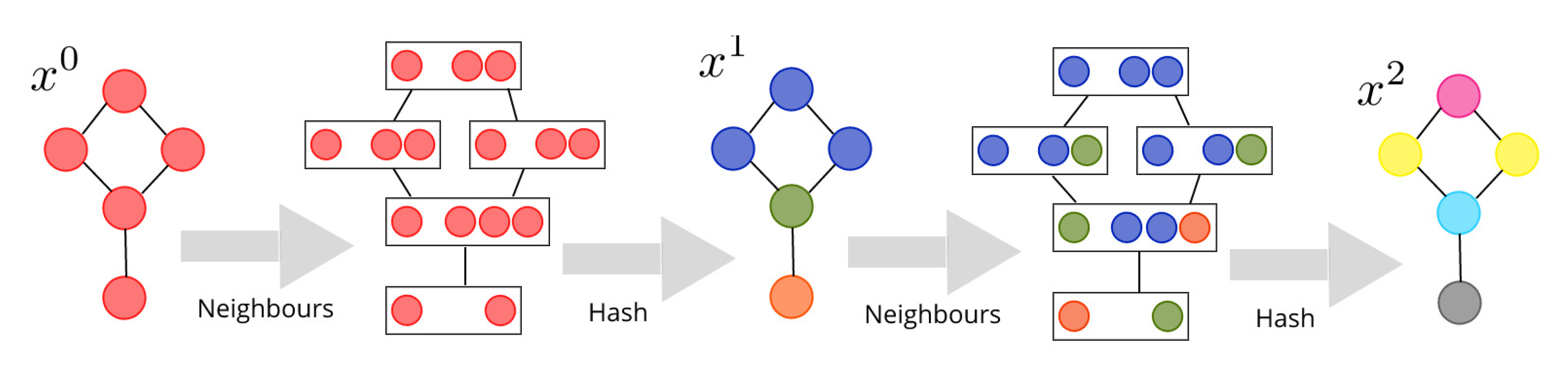
3.1. Weisfeiler–Lehman Procedure (WL)
3.2. Negative Sampling and Mutual Information
3.3. Graph2Vec
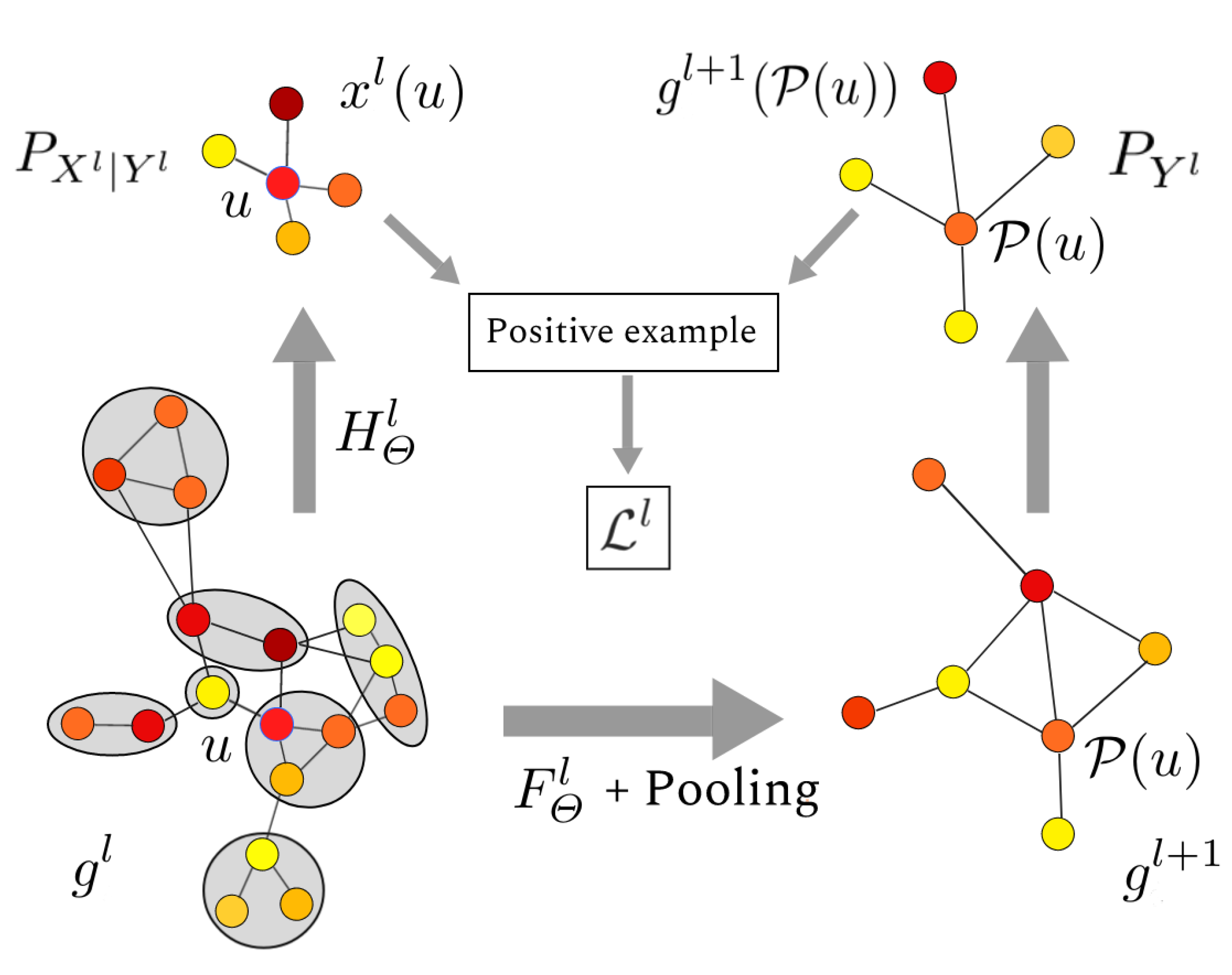
4. Contribution: Hierarchical Graph2Vec (HG2V)
- We first show that WL fails to capture global scale information, which is hurtful for many tasks;
- We then show that such flaw can be corrected by the use of graph coarsening. In particular, Loukas’s coarsening exhibits good properties in this regard;
- We finally show that the advantage of GNN over WL is to be continuous functions in node features. They are robust to small perturbations.
- The training is unsupervised. No label is required. The representation can be used for different tasks.
- The model is inductive, trained once for all with the graphs of the dataset in linear time. The training dataset is used as a prior to embed new graphs, whatever their underlying distribution.
- It handles continuous nodes attributes by replacing the hash function in WL procedure by a Convolutional Graph NN. It can be combined with other learning layers, serving as pre-processing step for feature extraction.
- The model is end-to-end differentiable. Its input and its output can be connected to other deep neural networks to be used as building block in a full pipeline. The signal of the loss can be back-propagated through the model to train feature extractors, or to retrain the model in transfer learning. For example, if the node features are rich and complex (images, audio), a CNN can be connected to the input to improve the quality of representation.
- The structures of the graph at all scales are summarized using Loukas coarsening. The embedding combines local view and global view of the graph.
| Algorithm 1: High-level version of the Hierarchical Graph2Vec (HG2V) algorithm |
 |
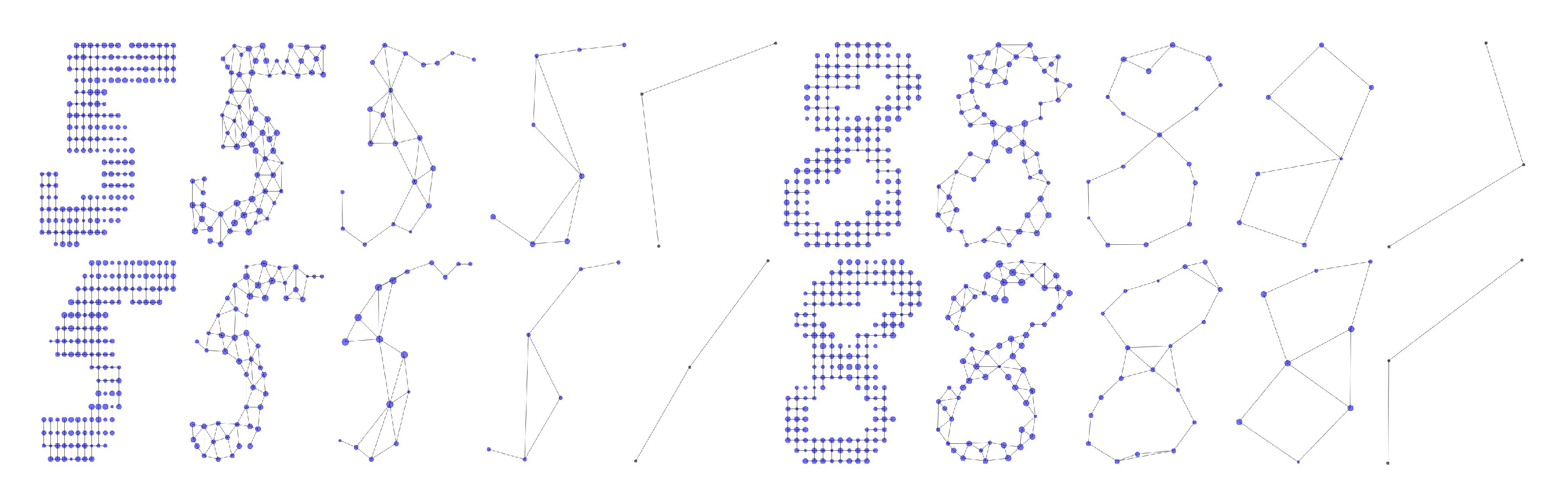
4.1. Loukas’s Coarsening
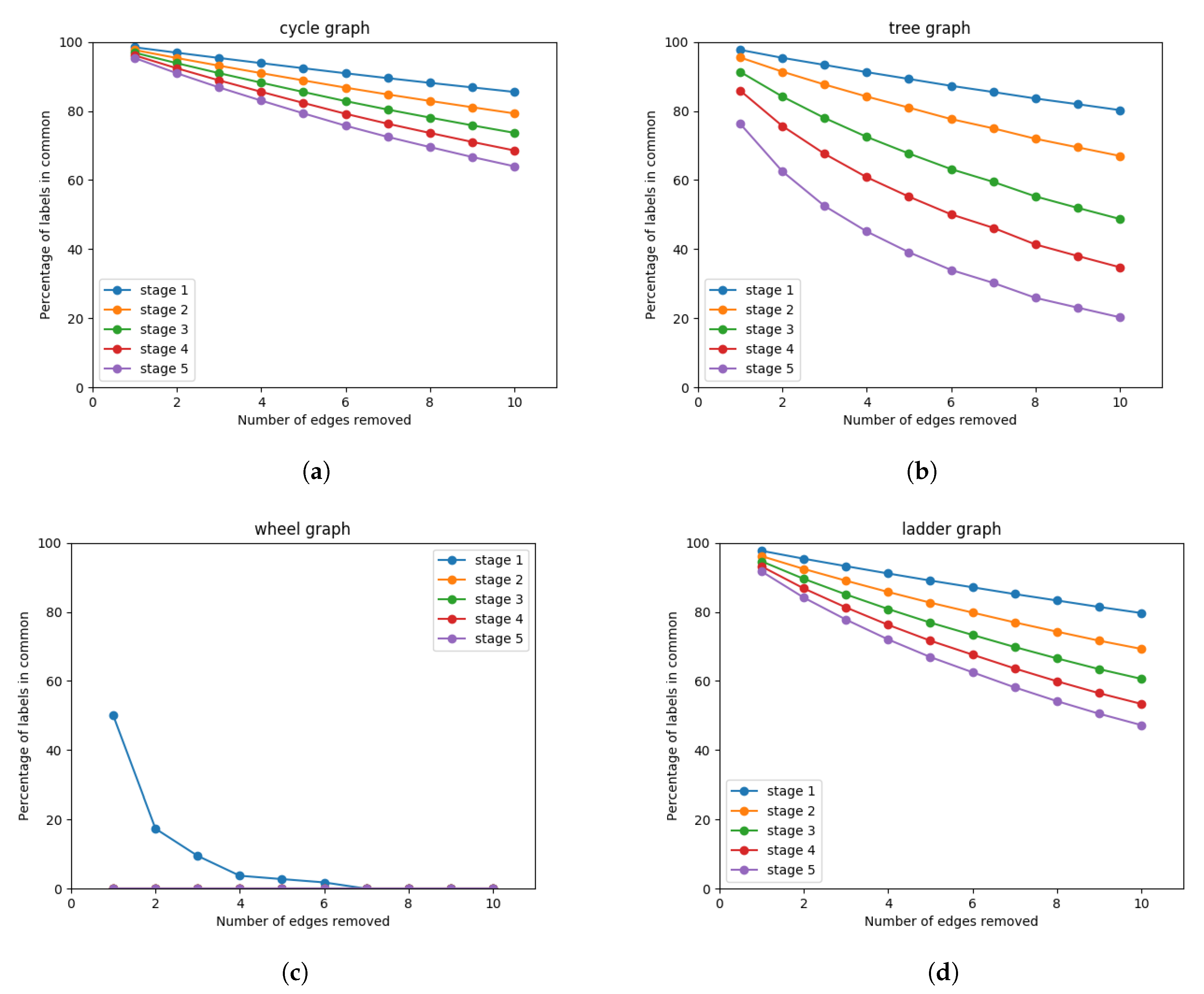
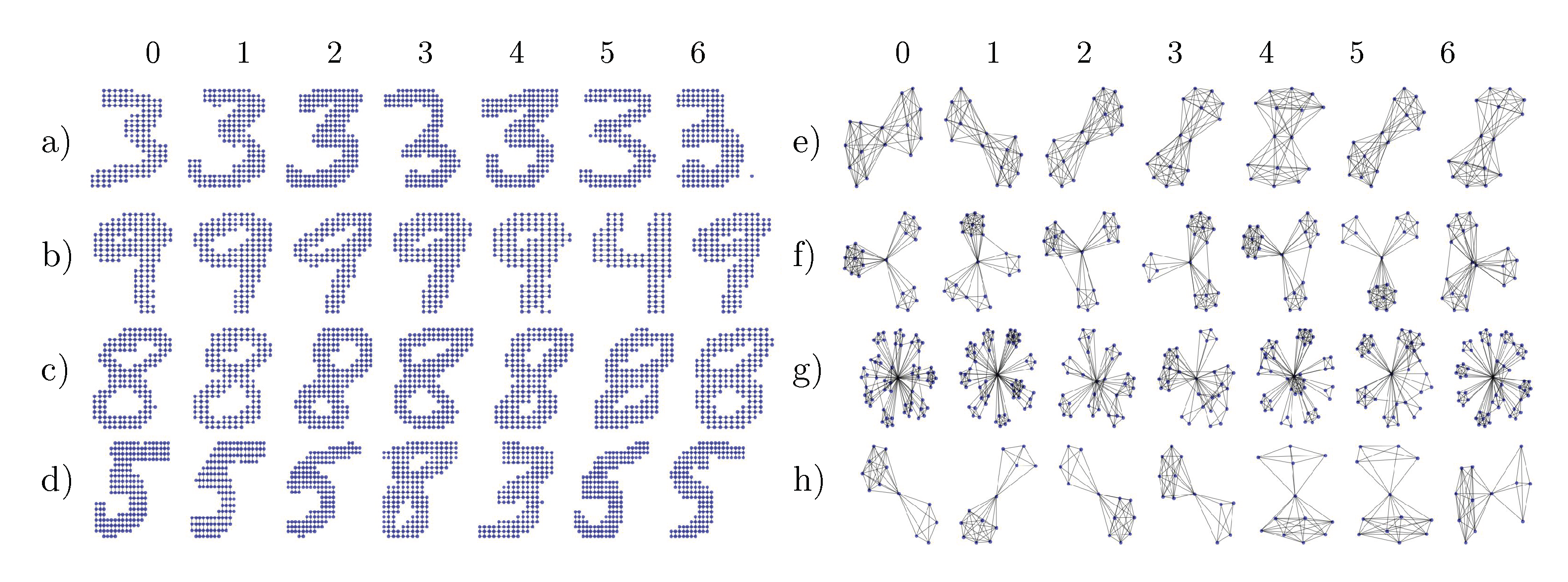
4.1.1. Wesfeiler-Lehman Sensibility to Structural Noise
4.1.2. Robustness to Structural Noise with Loukas’s Coarsening
4.2. Hierarchy of Neighborhoods
4.3. Handling Continuous Node Attributes with Truncated Krylov
4.4. Hierarchical Negative Sampling
Complexity
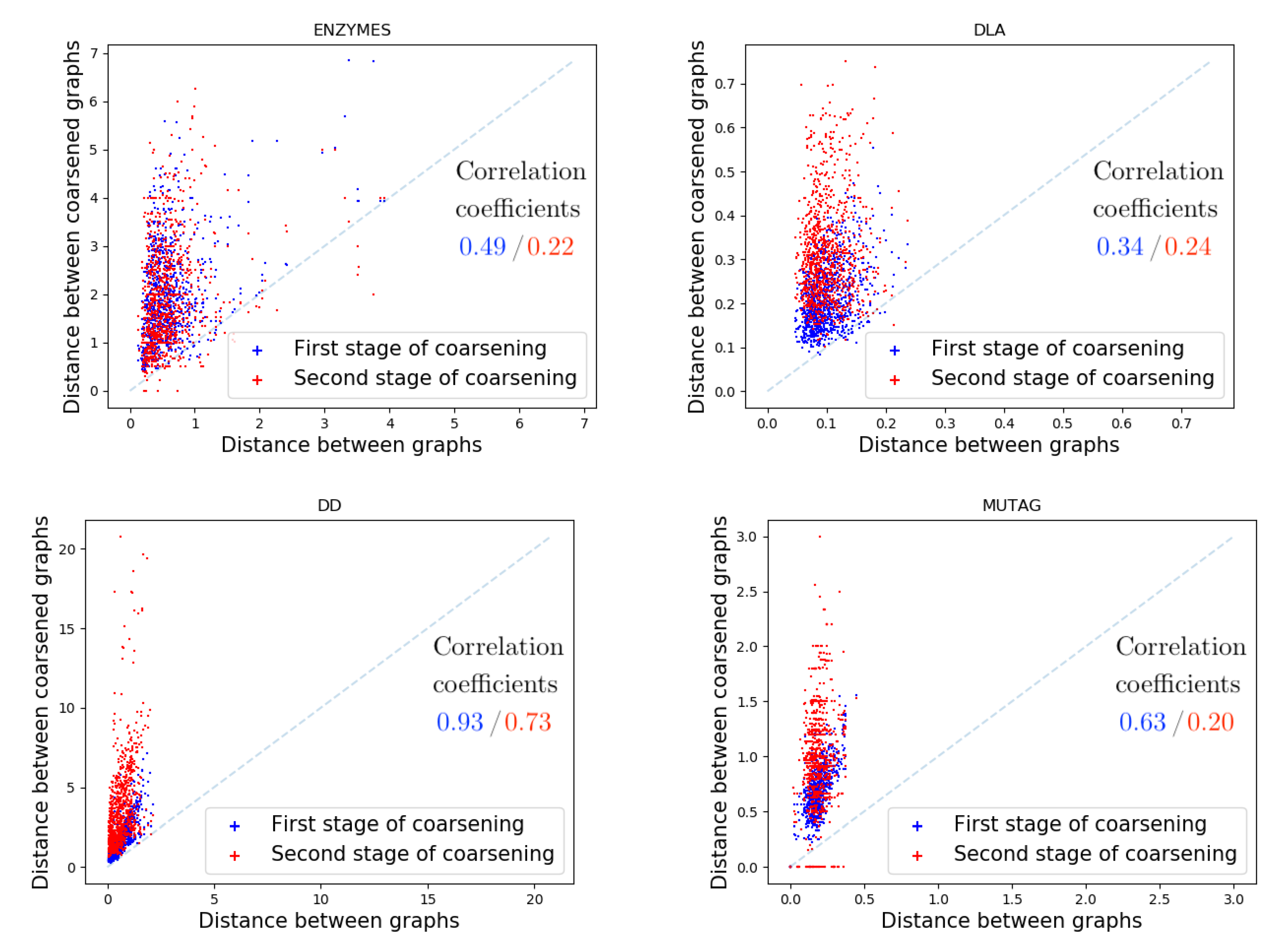
5. Evaluation
5.1. Datasets
5.2. Supervised Classification
5.2.1. Training Procedure
5.2.2. Model Selection
5.2.3. Baselines
5.2.4. Results
5.2.5. Computation Time
5.3. Inductive Learning
Results
5.4. Ablative Studies
Results
5.5. Latent Space
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proofs
Appendix B. Additional Visualizations of the Embeddings

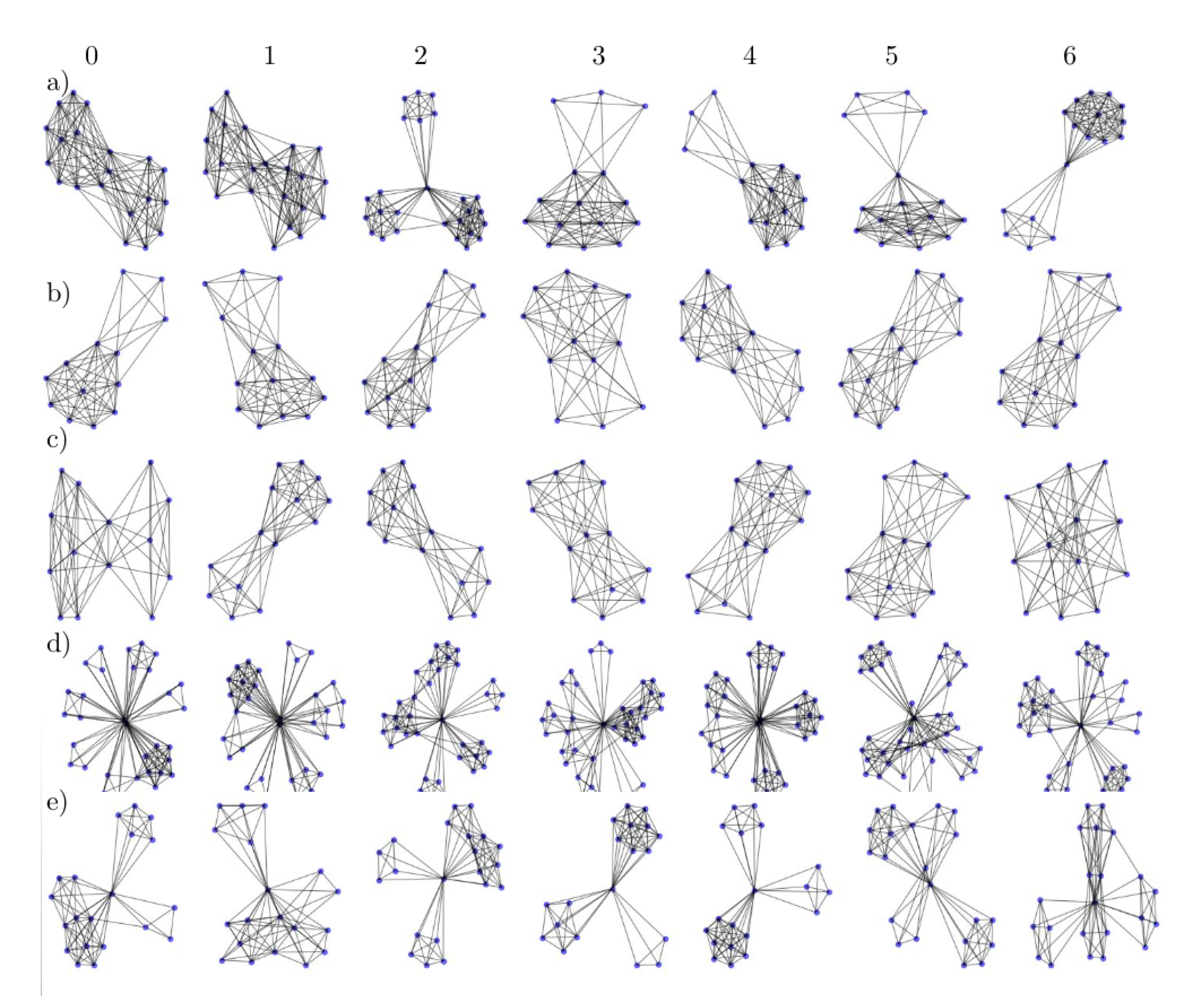
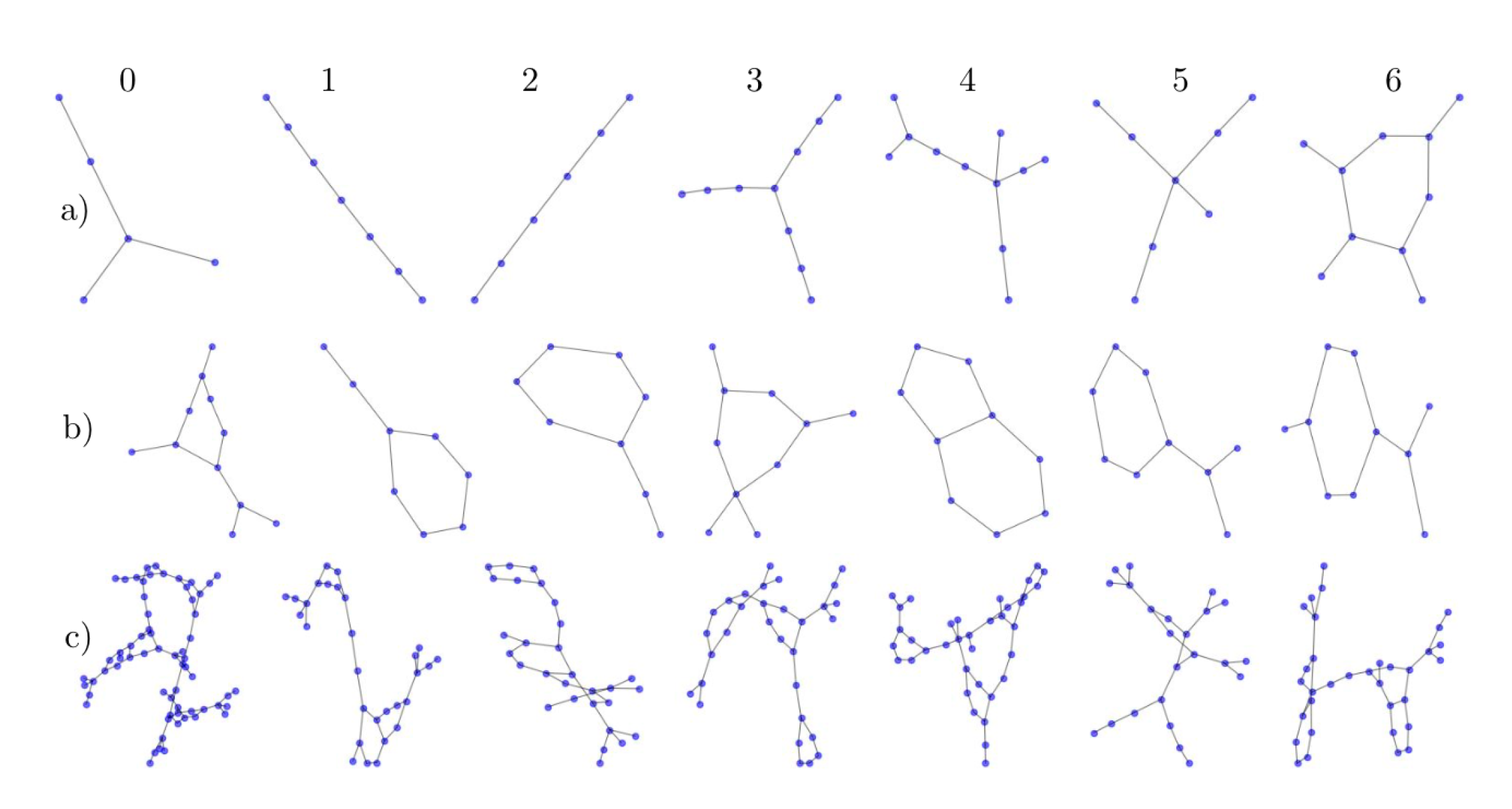
Appendix C. Details about the Datasets
Appendix C.1. DLA
Appendix C.2. MNIST and USPS
References
- Hamilton, W.L.; Ying, R.; Leskovec, J. Representation learning on graphs: Methods and applications. arXiv 2017, arXiv:1709.05584. [Google Scholar]
- Narayanan, A.; Chandramohan, M.; Venkatesan, R.; Chen, L.; Liu, Y.; Jaiswal, S. graph2vec: Learning distributed representations of graphs. arXiv 2017, arXiv:1707.05005. [Google Scholar]
- Loukas, A. Graph reduction with spectral and cut guarantees. J. Mach. Learn. Res. 2019, 20, 1–42. [Google Scholar]
- Togninalli, M.; Ghisu, E.; Llinares-López, F.; Rieck, B.; Borgwardt, K. Wasserstein weisfeiler-lehman graph kernels. In Proceedings of the Annual Conference on Neural Information Processing Systems 2019, Vancouver, BC, Canada, 8–14 December 2019; pp. 6439–6449. [Google Scholar]
- Vishwanathan, S.V.N.; Schraudolph, N.N.; Kondor, R.; Borgwardt, K.M. Graph kernels. J. Mach. Learn. Res. 2010, 11, 1201–1242. [Google Scholar]
- Shervashidze, N.; Borgwardt, K.M. Fast subtree kernels on graphs. In Proceedings of the 23rd Annual Conference on Neural Information Processing Systems 2009, Vancouver, BC, Canada, 7–10 December 2009; pp. 1660–1668. [Google Scholar]
- Shervashidze, N.; Schweitzer, P.; Leeuwen, E.J.V.; Mehlhorn, K.; Borgwardt, K.M. Weisfeiler-lehman graph kernels. J. Mach. Learn. Res. 2011, 12, 2539–2561. [Google Scholar]
- Feragen, A.; Kasenburg, N.; Petersen, J.; De Bruijne, M.; Borgwardt, K. Scalable kernels for graphs with continuous attributes. In Proceedings of the 27th Annual Conference on Neural Information Processing Systems 2013, Lake Tahoe, NV, USA, 5–8 December 2013; pp. 216–224. [Google Scholar]
- Kriege, N.; Mutzel, P. Subgraph matching kernels for attributed graphs. arXiv 2012, arXiv:1206.6483. [Google Scholar]
- Morris, C.; Kriege, N.M.; Kersting, K.; Mutzel, P. Faster kernels for graphs with continuous attributes via hashing. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016. [Google Scholar]
- Veličković, P.; Fedus, W.; Hamilton, W.L.; Liò, P.; Bengio, Y.; Hjelm, R.D. Deep graph infomax. In Proceedings of the ICLR, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; pp. 1024–1034. [Google Scholar]
- Sun, F.Y.; Hoffman, J.; Verma, V.; Tang, J. Infograph: Unsupervised and semi-supervised graph-level representation learning via mutual information maximization. In Proceedings of the ICLR, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Bianchi, F.M.; Grattarola, D.; Livi, L.; Alippi, C. Hierarchical representation learning in graph neural networks with node decimation pooling. arXiv 2019, arXiv:1910.11436. [Google Scholar]
- Dorfler, F.; Bullo, F. Kron reduction of graphs with applications to electrical networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 150–163. [Google Scholar] [CrossRef]
- Bravo Hermsdorff, G.; Gunderson, L. A unifying framework for spectrum-preserving graph sparsification and coarsening. In Proceedings of the Annual Conference on Neural Information Processing Systems 2019, Vancouver, BC, Canada, 8–14 December 2019; pp. 7736–7747. [Google Scholar]
- Ying, Z.; You, J.; Morris, C.; Ren, X.; Hamilton, W.; Leskovec, J. Hierarchical graph representation learning with differentiable pooling. In Proceedings of the Annual Conference on Neural Information Processing Systems 2018, Montreal, QC, Canada, 3–8 December 2018; pp. 4800–4810. [Google Scholar]
- Bianchi; Maria, F.; Grattarola, D.; Alippi, C. Spectral clustering with graph neural networks for graph pooling. In Proceedings of the 37th International Conference on Machine Learning, Online Event, 12–18 July 2020. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Networks Learn. Syst. 2020, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Proceedings of the Annual Conference on Neural Information Processing Systems 2016, Barcelona, Spain, 5–10 December 2016; pp. 3844–3852. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the ICLR, Toulon, France, 24–26 April 2017. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph attention networks. In Proceedings of the ICLR, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Luan, S.; Zhao, M.; Chang, X.W.; Precup, D. Break the ceiling: Stronger multi-scale deep graph convolutional networks. In Proceedings of the Annual Conference on Neural Information Processing Systems 2019, Vancouver, BC, Canada, 8–14 December 2019; pp. 10945–10955. [Google Scholar]
- Loukas, A. What graph neural networks cannot learn: Depth vs. width. In Proceedings of the ICLR, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Gama, F.; Marques, A.G.; Leus, G.; Ribeiro, A. Convolutional neural network architectures for signals supported on graphs. IEEE Trans. Signal Process. 2019, 67, 1034–1049. [Google Scholar] [CrossRef]
- Weisfeiler, B.; Lehman, A.A. A reduction of a graph to a canonical form and an algebra arising during this reduction. Nauchno-Tech. Informatsia 1968, 2, 12–16. [Google Scholar]
- Kriege, N.M.; Giscard, P.L.; Wilson, R. On valid optimal assignment kernels and applications to graph classification. In Proceedings of the Annual Conference on Neural Information Processing Systems 2016, Barcelona, Spain, 5–10 December 2016; pp. 1623–1631. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. In Proceedings of the 27th Annual Conference on Neural Information Processing Systems 2013, Lake Tahoe, NV, USA, 5–8 December 2013; pp. 3111–3119. [Google Scholar]
- Hjelm, R.D.; Fedorov, A.; Lavoie-Marchildon, S.; Grewal, K.; Bachman, P.; Trischler, A.; Bengio, Y. Learning deep representations by mutual information estimation and maximization. In Proceedings of the ICLR, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Nowozin, S.; Cseke, B.; Tomioka, R. f-gan: Training generative neural samplers using variational divergence minimization. In Proceedings of the Annual Conference on Neural Information Processing Systems 2016, Barcelona, Spain, 5–10 December 2016; pp. 271–279. [Google Scholar]
- Melamud, O.; Goldberger, J. Information-theory interpretation of the skip-gram negative-sampling objective function. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Short Papers), Vancouver, BC, Canada, 30 July–4 August 2017; Volume 2, pp. 167–171. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? In Proceedings of the ICLR, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Hagberg, A.; Swart, P.; S Chult, D. Exploring network structure, dynamics, and function using NetworkX. In Proceedings of the 7th Python in Science Conference (SciPy2008), Pasadena, CA, USA, 19–24 August 2008; Varoquaux, G., Vaught, T., Millman, J., Eds.; 2008; pp. 11–15. [Google Scholar]
- Maron, H.; Ben-Hamu, H.; Serviansky, H.; Lipman, Y. Provably powerful graph networks. In Proceedings of the Annual Conference on Neural Information Processing Systems 2019, Vancouver, BC, Canada, 8–14 December 2019; pp. 2156–2167. [Google Scholar]
- Morris, C.; Ritzert, M.; Fey, M.; Hamilton, W.L.; Lenssen, J.E.; Rattan, G.; Grohe, M. Weisfeiler and leman go neural: Higher-order graph neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4602–4609. [Google Scholar] [CrossRef]
- Vayer, T.; Chapel, L.; Flamary, R.; Tavenard, R.; Courty, N. Optimal Transport for structured data with application on graphs. In Proceedings of the ICML 2019—36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Kersting, K.; Kriege, N.M.; Morris, C.; Mutzel, P.; Neumann, M. Benchmark Data Sets for Graph Kernels. 2016. Available online: https://chrsmrrs.github.io/datasets/docs/datasets/ (accessed on 20 August 2020).
- Orsini, F.; Frasconi, P.; DeRaedt, L. Graph invariant kernels. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015; pp. 3756–3762. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Nikolentzos, G.; Siglidis, G.; Vazirgiannis, M. Graph kernels: A survey. arXiv 2019, arXiv:1904.12218. [Google Scholar]
- Errica, F.; Podda, M.; Bacciu, D.; Micheli, A. A Fair Comparison of Graph Neural Networks for Graph Classification. arXiv 2019, arXiv:1912.09893. [Google Scholar]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural Message Passing for Quantum Chemistry. arXiv 2017, arXiv:1704.01212. [Google Scholar]
- Witten, T.A., Jr.; Sander, L.M. Diffusion-limited aggregation, a kinetic critical phenomenon. Phys. Rev. Lett. 1981, 47, 1400. [Google Scholar] [CrossRef]
- Witten, T.A.; Sander, L.M. Diffusion-limited aggregation. Phys. Rev. B 1983, 27, 5686. [Google Scholar] [CrossRef]
| Method | Continuous Attributes | Complexity (Training) | Complexity (Inference) | End-to-End Differentiable | Supervised |
|---|---|---|---|---|---|
| Kernel methods, e.g., WL-OA [27], WWL [4] | ✓ | * | * | ✗ | ✗ |
| Graph2Vec [2] | ✗ | ✗ | ✗ | ✗ | |
| GIN [32], DiffPool [17], MinCutPool [18] | ✓ | ✓ | ✓ | ||
| HG2V (Section 4), Infograph [13] | ✓ | ✓ | ✗ |
| DATASET | #graphs | #nodes | HG2V (Ours) | Graph2Vec | Infograph | DiffPool (Supervised) | GIN (Supervised) | MinCutPool (Supervised) | WL-OA (Kernel) | WWL (Kernel) |
|---|---|---|---|---|---|---|---|---|---|---|
| IMDB-m | 1500 | 13 | ✗ | ✗ | ✗ | |||||
| PTC_FR | 351 | 15 | ✗ | ✗ | ✗ | ✗ | ✗ | |||
| FRANK. | 4337 | 17 | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ||
| MUTAG | 188 | 18 | ✗ | ✗ | ✗ | |||||
| IMDB-b | 1000 | 20 | ✗ | ✗ | ||||||
| NCI1 | 4110 | 30 | ✗ | ✗ | ||||||
| NCI109 | 4127 | 30 | ✗ | ✗ | ✗ | ✗ | ✗ | |||
| ENZYMES | 600 | 33 | ✗ | ✗ | ||||||
| PROTEINS | 1113 | 39 | ✗ | |||||||
| MNIST | 10000 | 151 | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ||
| D&D | 1178 | 284 | ✗ | |||||||
| REDDIT-b | 2000 | 430 | ✗ | |||||||
| DLA | 1000 | 501 | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ||
| REDDIT-5K | 4999 | 509 | ✗ | ✗ | ✗ |
| Training Set | Inference Set | Accuracy (Inference) | Delta with baseline (see Table 2) |
|---|---|---|---|
| MNIST | USPS | 94.86 | ✗ |
| USPS | MNIST | 93.68 | −2.40 |
| REDDIT-b | REDDIT-5K | 55.00 | −0.48 |
| REDDIT-5K | REDDIT-b | 91.00 | −0.15 |
| REDDIT-b | IMDB-b | 69.00 | −2.25 |
| REDDIT-5K | IMDB-b | 69.50 | −1.75 |
| MNIST | FASHION MNIST | 83.35 | ✗ |
| HG2V | Graph2Vec + GNN | Graph2Vec + Loukas | Graph2Vec | |||||
|---|---|---|---|---|---|---|---|---|
| DATASET | #nodes | Accuracy | Delta | Accuracy | Delta | Accuracy | Delta | |
| IMDB-b | 20 | 70.85 | +7.75 | 70.70 | +7.60 | 57.5 | −5.60 | 63.10 |
| NCI1 | 30 | 77.97 | +4.75 | 75.40 | +2.18 | 65.45 | −7.77 | 73.22 |
| MNIST | 151 | 95.83 | +39.56 | 91.05 | +34.78 | 72.5 | +16.23 | 56.27 |
| D&D | 284 | 78.01 | +19.37 | 79.26 | +13.16 | 66.10 | +7.45 | 58.64 |
| REDDIT-B | 430 | 91.95 | +16.23 | OOM | ✗ | 82.50 | +6.78 | 75.72 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Béthune, L.; Kaloga, Y.; Borgnat, P.; Garivier, A.; Habrard, A. Hierarchical and Unsupervised Graph Representation Learning with Loukas’s Coarsening. Algorithms 2020, 13, 206. https://doi.org/10.3390/a13090206
Béthune L, Kaloga Y, Borgnat P, Garivier A, Habrard A. Hierarchical and Unsupervised Graph Representation Learning with Loukas’s Coarsening. Algorithms. 2020; 13(9):206. https://doi.org/10.3390/a13090206
Chicago/Turabian StyleBéthune, Louis, Yacouba Kaloga, Pierre Borgnat, Aurélien Garivier, and Amaury Habrard. 2020. "Hierarchical and Unsupervised Graph Representation Learning with Loukas’s Coarsening" Algorithms 13, no. 9: 206. https://doi.org/10.3390/a13090206
APA StyleBéthune, L., Kaloga, Y., Borgnat, P., Garivier, A., & Habrard, A. (2020). Hierarchical and Unsupervised Graph Representation Learning with Loukas’s Coarsening. Algorithms, 13(9), 206. https://doi.org/10.3390/a13090206





