Abstract
This paper provides an overview of the field of parameterized parallel complexity by surveying previous work in addition to presenting a few new observations and exploring potential new directions. In particular, we present a general view of how known techniques, such as bounded search trees, color coding, kernelization, and iterative compression, can be modified to produce fixed-parameter parallel algorithms.
1. Introduction
Similarly to how computational problems are classified according to their tractability or whether efficient algorithms exist for them, problems are also classified according to whether efficient parallel algorithms exist to solve them. The class and the corresponding hierarchy have been used to classify “efficiently parallelizable” problems that lie in the class P. With the rise of parameterized complexity theory and the notion of fixed-parameter tractability (), the class was introduced as analogous to the class in the field of parameterized complexity. This notion was then extended to introduce the class fixed-parameter parallelizable () in [1]. More recently, a refined version of , dubbed fixed-parameter parallel tractable () was also introduced in [2].
Since the introduction of the notion of parameterized parallel complexity, a few articles have been published to study a variety of parameterized problems. Typically, a problem is either shown to be efficiently parallelizable or impossible to efficiently parallelize with respect to various parameters such as the solution size (or natural parameter), tree-width, modular-width, etc. In this paper, we survey the existing complexity classes and algorithmic methodologies, and we provide a number of observations about the various techniques and classes.
Throughout this paper we mainly consider parameterized problems. An instance of a parameterized problem is of the form where X is the problem input and k is the parameter, which is often a bound on the size of a desired solution. A parameterized problem is fixed-parameter tractable (FPT): if it can be solved in time where n is the input size () and c is a fixed constant, independent of n and k [3].
From a classical parallel complexity standpoint, the class , or Nick’s class, is known to be analogous to the class P (in sequential complexity). In short, a parallel problem is in if it can be solved in time using processors, where and are constants [4]. To convert this notion into a parameterized definition that we can use (or relate to) later, and following the same assumptions of [1], we consider a parameterized problem to be in if it is in for any given value of the parameter. By this definition, a problem parameterized by k (independent of n) is in if it is solvable in time using processors, where , being functions of k, are independent of n and are considered in this case constants with respect to n to abide by the original definition above.
The first parameterized parallel complexity class, defined in [5] and viewed as the parameterized analog to NC, is . Membership in PNC requires the problem to be solvable in using processors. The more restrictive class of fixed-parameter parallel () problems was defined by Cesati and Ianni in [1] where a strictly poly-logarithmic factor in the running time is required, by replacing with a constant. More recently, it was observed in [6] that the function in the number of processors is redundant. A corresponding refined version of was defined in [2] under the (also refined) name: fixed-parameter parallel tractable, or . In this paper we survey the various methods used in the area of parameterized parallel complexity and present the results known so far for all the studied problems in this area. Relations between the various complexity classes are also presented along with new observations and results. In particular we overview the methods used for obtaining a parameterized parallel algorithm from a known sequential fixed-parameter algorithm.
2. Preliminaries
We assume familiarity with basic graph-theoretic terminology such as the notions described in [7]. In particular, given a simple undirected graph and a vertex we denote by the set of neighbors of v and we define by the closed neighborhood of v in G. For a subset S of V we denote by the set , and we set . Moreover, the subgraph induced by S (i.e., the graph obtained by deleting all the elements of is denoted by . S is a clique in G if is a complete subgraph (i.e., any two elements of S are adjacent in G). A clique on t vertices is denoted by . On the other hand, S is said to be independent or stable in G if no two elements of S are adjacent in G.
One of the most studied parameterized problems is Vertex Cover which, for a given graph and a parameter k, asks for a subset C of V of cardinality at most k whose complement is independent. In other words, every edge of G has at least one endpoint in C. Vertex Cover is among the first classical problems shown to be fixed-parameter tractable [3]. A closely related problem is Clique, which for a given graph G and a parameter k, asks whether G has a clique of size at least k. From a parameterized complexity standpoint, Clique is equivalent to Independent Set due a straightforward transformation of the input, without changing the parameter. Both problems are -complete.
One of the reasons why Vertex Cover is popular, and not as “hard” as other parameterized problems, stems from the fact that it is a special case of many (more general) problems. It is a (i) deletion into maximum-degree d where , (ii) deletion into connected components of size p where , and (iii) deletion into -free graphs for , among other generalizations. A closely related problem is deletion into cycle-free graphs: in the Feedback Vertex Set (FVS) problem we ask for a subset C of V of cardinality at most k such that has no cycles. is fixed-parameter tractable.
A tree decomposition of a given graph is a tree T, whose nodes are subsets of V. To avoid confusion, vertices of G and T are referred to as vertices and nodes, respectively. Let the set of nodes of T be , the following properties should hold:
- (i)
- Every vertex of G is present in at least one node in T. Moreover .
- (ii)
- The nodes of T containing some vertex v form a connected subtree. In other words, if and both contain a vertex v, then every node along the unique path between and must contain v.
- (iii)
- All edges of G must be represented in the subsets. For every edges of G, there is at least one node in T that contains both u and v.
The width of a tree decomposition is one less the cardinality of the largest node of T (as subset of vertices of G). The treewidth of G, denoted by , is the minimum width of a tree decomposition of G. It is easy to show that the treewidth of a tree is one while the treewidth of a simple cycle is two. In fact, the graphs of treewidth two are exactly those that exclude in the minor order [8].
This transformation from a graph to a tree, via tree decomposition, has proven to be a powerful technique in the design of algorithms for parametrized problems. In fact, several computationally intractable problems can be solved in polynomial time on graphs of bounded treewidth. It would thus be interesting to try to utilize the tree-like structure to design fixed-parameter algorithms for problems parameterized by treewidth, whenever possible.
Another parameter that has been recently used in the design of parameterized parallel algorithms is modular-width, which is related to the modular decomposition of a graph, introduced in [9]. In a modular decomposition, the graph is decomposed into modules, also called autonomous, homogeneous, or partitive sets. A module X in a graph G satisfies: . The notion of a module obviously generalizes that of a connected component, but it should be noted that modules can be subsets of each other. A modular decomposition is a recursive division of the graph into modules, in which 4 steps defined in [9] are applied recursively to the graph, where steps can generate modules, until a tree of modules is obtained with one-element sets as its leaves. Modular width was defined in [10] as the maximum degree of the optimal modular decomposition tree.
Modular width was first used in [10] as auxiliary parameter and used to obtain fixed-parameter algorithms for coloring and path-partitioning problems (mainly Hamiltonian Path and Cycle). These problems are -hard with respect to other auxiliary graph parameters like shrub-depth.
The parallel complexity class is defined above in its general form. It is, however, divided into sub-classes, denoted by for , where is the set of problems that can be solved in time using a polynomial number of processors [4]. The relation between sub-classes of the -hierarchy is given by , where the question of whether the class is proper (whether or ) remains open, so far. It was shown in [4] that if for some , then the equality holds for every . This would result in the collapse of the -hierarchy from j onward into a single class .
A decision problem X is said to be P-complete is it belongs to the class P (of problems solvable in polynomial-time) and every problem in P can be reduced to X in time using a polynomial number of processors. It is well known, and easy to see, that is a subset of P, but it is strongly believed that the containment is proper.
The class , on the other hand, is the class of problems or languages recognized by Boolean circuits of logarithmic depth that use a polynomial number of unbounded fan-in AND and OR gates. A sub-class contains the set of languages recognized by Boolean circuits of depth and that use a polynomial number of AND and OR gates [11,12]. The lowest class is , where the Boolean circuit is of constant depth, and it can be shown that .
The relation between the -hierarchy and the -hierarchy is given by for , as noted in [11], since the circuit can be represented as a tree of logarithmic depth and a polynomial number of nodes.
3. Parameterized Parallel Complexity Classes
The notion of parameterized parallel complexity was first introduced in [1], where the concepts of and were formally defined. More recently, the class was defined in [2] as a refined version of . Formal definitions of these complexity classes follow.
Definition 1.
A parameterized problem is in if it can be solved by a parallel deterministic algorithm whose running time is in using processors, where f, g, and h are arbitrary computable functions, and β is a constant independent of n and k.
Definition 2.
A problem is fixed-parameter parallel (FPP) if it can be solved in time using processors, where and are independent fixed constants.
Definition 3.
A problem is fixed-parameter parallel tractable (FPPT) if it can be solved in time using processors, where and are independent fixed constants.
It was shown in [1] that is a subset of and that is a subset of . It was also shown that an problem can be if the work done at every step (of a corresponding algorithm) can be performed in -time. In fact, it is clear from the definitions that and . What still needs to be clarified is whether some classes are proper subsets of, or equal to, their successors.
3.1. PNC and NC
Cesati and Ianni proved in [1] that . Moreover, it is believed that because some problems, such as k-Clique, belong to the class but do not (seem to) belong to the class . In fact, the k-Clique problem is unlikely to be , being -hard [3], and therefore it is unlikely to be in or . To see why the problem falls in the class, take any value of k (given that k is independent of ), and note that we can use processors where every processor handles a subgraph of order k and can check in whether this subgraph induces a clique. Therefore, the problem is in since for any given value of k (independent of ), it is in .
3.2. PNC and FPT
It can be easily shown that is a proper subset of . To see this, assume (since we already know ). It follows that (since ). Therefore, , which is highly unlikely. As such, any problem in P that cannot be efficiently parallelized would be a counter example to .
3.3. FPP and PNC
The first -complete problem presented in [1] was the Bounded Size-Bounded Depth-Circuit Value problem (BS-BD-CVP), which was defined as follows:
Given a constant , three functions , a Boolean circuit C with n input lines, an input vector x, and an integral parameter k. the problem asks to decide whether the circuit C (size and depth ) accepts x.
Assume that this problem is in , then one can decide a circuit of depth in time, where is a constant. Then the same problems that belong to would belong to , since , and thus every problem in is also in for any i and j. As this is highly unlikely, it is safe to assume as long as there are hierarchies in the class . Moreover, unless the hierarchy collapses, a Boolean circuit of depth and gates (AND and OR) cannot be resolved in .
3.4. FPP and FPPT
It was also shown in [2] that since the work of processors can be simulated on processors, where each processor’s work or time is multiplied by , making the algorithm . The class could be preferred over since it makes the exponent of the logarithmic factor a constant independent of k (as with ), and it rids the required number of processors from a potentially large function of k which could possibly make the parallel algorithm more practical.
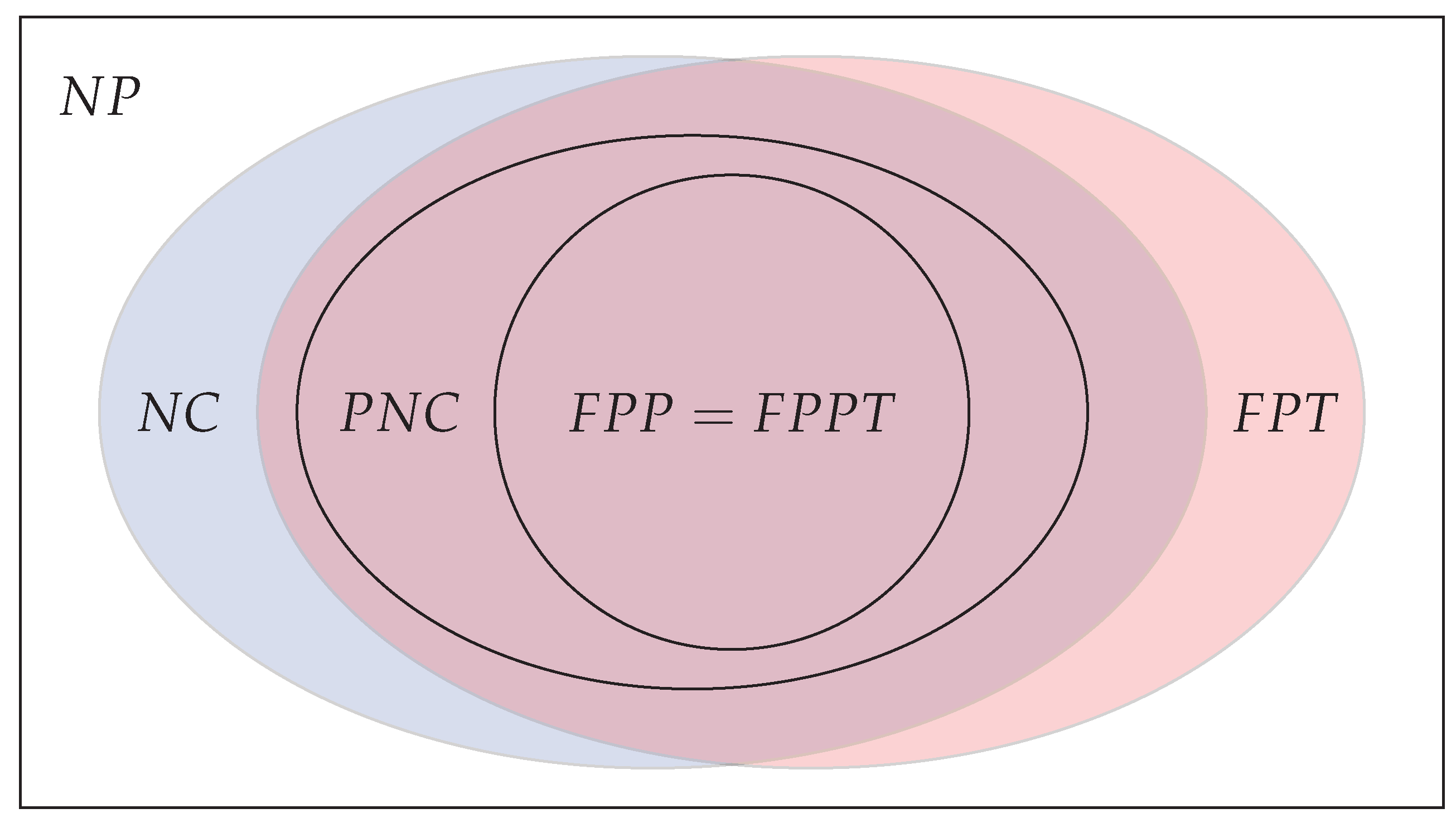
The currently known relationship between the various parameterized parallel complexity classes is depicted in Figure 1 below. It is still open at this point whether there exists a problem in that is not in , and whether there exists an problem that is not efficiently parallelizable.
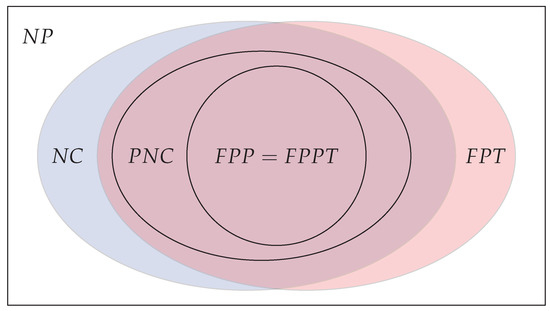
Figure 1.
and .
As the classes and are equivalent, we will use instead in the sequel.
3.5. Parameterized Parallel Intractability
It is natural when discussing complexity classes and membership to these classes to also discuss intractability and non-membership to the classes. This was discussed briefly in [1], where the notion of parameterized parallel intractability was first brought up. To prove a parameterized problem not in or not efficiently parallelizable, it is enough to show that for some value of the parameter, the problem is not in [1].
Consequently, one can use the known notion of reductions (namely, poly-time reductions to prove membership in P or ) to prove problems , , or not . Therefore, one can define reductions (similarly for reductions) to be reductions preserving membership to the class (, respectively).
4. Key Results and Methods
Since the emergence of the notion of parameterized parallel complexity and even before that, limited has been the scope of research on the topic, apart from experimental work that basically focused on scalability of parallel parameterized algorithms [13,14]
To the best of our knowledge, the first algorithm dates back to 1988 and showed that the Feedback Vertex Set problem, on cyclically reducible digraphs, can be solved in time using processors [15]. Of course, the notion of fixed-parameter parallelism was not known at that time. In addition, the problem at hand was not -hard, as is the case with common modern algorithms. In fact, when parameterized parallel complexity was introduced in [1] (ten years later), it was shown that some known problems can be or even if operations at every step are performed in - or -time respectively. Examples include Vertex Cover and Max Leaf Spanning Tree, among others.
The approach used for these problems was kernelization, where each step is performed in -time, and no more than k steps are performed, then a regular sequential algorithm is applied to the kernel. The aim was to prove and rather than achieving a most-efficient algorithm. The classical Vertex Cover kernel of [16] was used at the time, as a proof of concept, where all vertices of degree greater than the solution size k are removed in -time, leaving a No instance or a kernel of order quadratic in k.
Using this notion of kernelization followed by a sequential algorithm on the kernel, Abu-Khzam et al. [2] achieved a more efficient algorithm for Vertex Cover. Crown reduction through maximal matching was used to obtain a kernel that is linear in k and an algorithm for Vertex Cover using a polynomial number of processors.
In addition to kernelization, color coding was applied, in an attempt to produce algorithms. It was shown in [17] that a universal coloring family for a given input can be generated in constant parallel time. This coloring was then used to prove that several graph embedding, packing, covering, and clustering problems can be solved in efficient parallel time depending on the parameter k. The algorithms were certainly not efficient or best-possible; however, they were enough to prove several problems and .
A third approach consisted of choosing an auxiliary parameter that is different form the solution size (which is often called the natural parameter). This work was mainly based on the work if Bodlaender and Hagerup in [5], who showed that one can construct, in -time, a tree decomposition of minimum width or decide that the tree-width is greater than the parameter k. This paved the way for Cesati and Ianni [1] to prove several problems when restricted to graphs of tree-width bounded by some parameter k. Such problems are listed in [1] and include Hamiltonian Circuit, Hamiltonian Path, Chordal Graph Completion (fixed k), Dominating Set, Feedback Vertex Set, Feedback Arc Set, Longest Path, etc. The Feedback Vertex Set problem, for example, is in since YES instance have a tree-width bounded by the parameter k.
More recently, the work reported in [18] adopted the graph modular width as auxiliary parameter. The Weighted Maximum Clique and the Maximum Matching problems were shown to be solvable in using processors, when the modular-width is bounded by k.
Along with proving problems , some problems were proved to be not in or . The work reported in [1] showed how problems can be -complete with respect to reductions. The Bounded Size-Bounded Depth-Circuit Value problem (BS-BD-CVP), defined above, was used as a -complete problem. Problems like the k-Clique were proved to be in but not in to show these classes are not equal.
Another approach for classifying parameterized parallel problems was recently introduced in [17] where parallel algorithms are studied through circuit complexity, depth, and size. Several complexity classes were defined and used, diverging from the known classes like and . Para- is defined for all as the class with circuits of depth and size at most , where c is a constant. Para- is defined for all as the class with circuits of depth . Both definitions follow the standard base of not-, or-, and and-gates, the last two of which may have unlimited fan-in [19]. We will use and whenever possible.
Taking all the above pioneering work into consideration, we can classify the main methods used (thus far) to design fixed-parameter parallel algorithms into the following:
- -
- Applying branching (i.e., parallel bounded search tree algorithms);
- -
- Applying reductions to kernelize a problem instance before applying a general sequential (possibly branching) algorithm.
- -
- Coloring the input graph (in graph-theoretic problems) with a number of colors that is dependent on the parameter to reduce the problem into one solvable in -time.
- -
- Choosing the right auxiliary parameters for which the problem falls in the class .
5. Implementation Aspects
When discussing parameterized parallel complexity, several implementation aspects are overlooked, especially those related to input representation, access, and manipulation. A simple input query or modification operation may prove to be serial or linear in the input size, which could make the whole algorithm invalid. We present here a way to represent input, query it, and manipulate it in -time, so that when discussing algorithms later, we can safely assume that input operations are . This will ensure that any later algorithm or approach described that can be performed in a logarithmic number of steps using a polynomial number of processors, remain when considering the basic input operations since they also can be performed in .
In the following, we will assume that memory locations can be read in parallel, while the writing is exclusive. This is also important, as writing a memory location by n processors with locking is also not , as the writing is performed sequentially in this case.
5.1. Input Representation
If we assume the input is a collection of at most n sets, drawn from a universal set of size m, then most (if not all) required operations on the input instance are in given processors, by assigning processors to each of the given sets. We use the two parameters n and m here for simplicity; however, in reality, each is a function of the other. A graph can be seen as a collection of n sets of size n for the adjacency matrix representation, or m sets of size n for the incidence matrix representation. The input to problems like Set Cover, Set Packing, and others is also of any of those two forms. The values stored in the two-dimensional array representation can either be binary values or counting values as in weighted graphs. Several graph representations can be found in [20], in addition to other papers such as [21] which aimed at speeding up graph modification operations to allow for faster recursive backtracking. Since we follow a rather generalized approach in this paper, we will stick to the above-mentioned classical (generic) representations. Of course, some operations will not require more than or processors, but again, in this section we are more concerned about generality rather than optimality.
5.2. Input Queries
Checking whether some set S of the input contains some element x can be done in constant time by checking the corresponding index. In general, we can efficiently check whether some set S of the input contains as a subset some given set T. The operation is using processors, just as in the case of a single element. In fact, for each set of the input, the processors assigned to this set will check whether T is a subset. This can be done in constant time since the universe of elements is of size m, so there exists a processor for every element of the universe that checks whether this element is present in both T and S. An element not in T is ignored. The m processors for a given set forward their results in a binary reduction tree manner in logarithmic time. If no processor has detected an element in T that is not in S, then the set contains T as a subset. The results from all sets are then combined in a similar reduction tree approach in logarithmic time.
This means that finding if some element or set of elements exists in a particular set of the input is . Note that we can also count the occurrences, that is how many sets contain a particular subset, and this helps in a variety of problems that perform reduction or branching rules. For example, the classical d-Hitting Set kernelization finds elements or subsets of elements that are present above a certain limit and deals with them until the obtained instance is a kernel (i.e., cannot be further reduced by the used kernelization procedure). For (3-Hitting Set), subsets of elements of size 2 that are present in more than k sets are included in the solution. Then, elements that are present in more than sets are also dealt with. There will be at most sets of size 2 and m elements to check, and we have seen that checking the occurrences of each of these sets is . It is just the number of processors needed that has to be multiplied by to achieve the mentioned kernelization. To find a subset of elements of constant size d that is present in at least k sets, we can consider every possible combination of d elements from the universe as an element. This will require additional processors; however, the upper bound of shows that the query is .
Finally, computing the number of occurrences of every element in all sets is also clearly . For a given element, the are n processors, each in a set, allocated for this element, These processors can check for the presence of the element in their sets and combine their results in logarithmic time.
5.3. Input Modification
Adding or removing an element of the universe to or from a set is a constant time operation since the corresponding cell has to be updated. Doing this operation for all sets or for a group of sets is also since we have processors, one for each cell. Adding or deleting a set of elements can be done in a similar manner.
Changing the universe, however, is different. Deleting an element or set of elements from the universe of elements requires just ignoring the processors and cells related to these elements. On the other hand, adding elements to the universe requires creating new columns in the input representation for the introduced elements. These new cells will also require additional processors to handle them. If the number of introduced elements remains linear in m, then the existing processors can handle a constant number of cells and simulate the work of a constant number of additional processors. The same applies to adding a new set to the collection of sets in the input. A new row will be required in this case, in addition to new processors. However, a simple observation can solve this case and the previous one. We should also note that composition of addition and deletion operations are also by following the same steps.
It is safe to assume that the number of sets and number of elements will not exceed polynomial functions of n and m (say and ), respectively. If we initially know an upper bound for and , which is generally the case, then we can assume the input initially has sets and elements, and the algorithm will remain with as many processors as needed since the number of processors () is polynomial. If there is no polynomial bound for how large the input can grow, then the algorithm is not in the first place, therefore it cannot be .
Many algorithms tend to have the above input modification features (of deletion or addition to the input). Examples include the well known Vertex Cover algorithm, where vertices included in the solution are deleted. Other modification methods may employ reductions that consist of adding vertices to the input to transform it into an instance of another problem, before applying an FPP algorithm.
5.4. Avoiding Excessive Use of Successive Operations
Although a single operation on a given instance is , a combination of or such operations will not result in an algorithm, unless they occur simultaneously in parallel. Consider for example that we are given a graph G and a reduction rule that deletes a pendant vertex unless the graph is empty or until the minimum degree is two, as in the Feedback Vertex Set algorithm of [22] or the kernelization algorithm in [23]. Applying the rule once is ; however, in the worst case, when G is a tree or path, n operations are needed until the graph is completely consumed.
Of course this does not mean there exists no solution for trees, but that the algorithm must account for this case and find other ways of dealing with certain operations. Therefore, it is important to note that after a constant number of operations, or even after operations, k should be decremented to guarantee an overall -time.
6. Common FPT Methods
In this section we outline the most known approaches used to design fixed-parameter algorithms for problems parameterized by solution size. These techniques will be used later to show how to produce corresponding algorithms.
6.1. Bounded Search Trees
The notion of a bounded search tree appeared in the initial work of Downey and Fellows on parameterized complexity theory [24]. According to [25], a Bounded Search Tree algorithm is one that, in each step, reduces an instance I, with some measure (a function of the parameter k), into l smaller instances such that .
In every invocation of the algorithm, we identify in polynomial time a subset S of the elements of I (or actions on the elements, as in coloring or editing problems), such that every feasible solution to the problem should contain at least one element of S. Then, we proceed by branching on the elements of S, producing instances or subproblems, each of which has a reduced measure (often a smaller value of k). Of course, is assumed to be bounded by a function of k. This general approach yields algorithms.
6.2. Kernelization
The notion of kernelization plays a central role in parameterized complexity theory. In general, a kernelization algorithm takes an arbitrary instance of a problem that is parameterized by k, as input, and produces as output an equivalent instance such that for some function g that is independent of the input size (depends only on the parameter k). The instance is often called a problem kernel.
When a kernelization algorithm exists for a parameterized problem X we say X is kernelizable. The importance of kernelization in this field also stems from the fact that a problem is fixed-parameter tractable if and only if it is kernelizable [26]. Of course the interest is in achieving a smallest possible kernel, and it is natural to further classify problems based on whether kernels of polynomial-size can be obtained (in polynomial-time). For example, while Vertex Cover admits a kernel of size bounded by , the Connected Vertex Cover problem is unlikely to have a polynomial kernel unless unless [27].
A kernelization algorithm is usually based on identifying certain structures in the input instance and then dealing with them, to reduce the instance in size, successively until the instance no longer has such favorable structures to reduce. After that, the instance should be of bounded size in terms of the parameter.
6.3. Color Coding
An -universal coloring family is defined as a set of functions such that of size and , there is at least one function with . In other words, an -universal coloring guarantees that every subset of elements can be colored with all possible colors by at least one coloring.
Color coding, introduced in [28,29], is a de-randomization technique in which patterns can be detected in -time. A universal coloring family is generated that enumerates all possible colorings of the input that could represent the sought solution. If verifying each coloring can be done in -time, and since the size of this set is polynomial in the input size n, then overall it takes -time to generate all colorings and verify them. This method has been used to design algorithms for many problems including Longest Path and Subgraph Isomorphism on graphs of bounded degree (see [25] for more details).
6.4. Iterative Compression
Iterative compression algorithms are mainly applied to some minimization problems when it is possible to construct a feasible solution whose size is slightly larger than the target solution size k, which is the parameter in this case. Once such a solution is found, exhaustive search is applied to compress it into a solution of size k. This “compression” procedure is typically applied “iteratively” to a graph problem as follows. Start by finding a subgraph for which a solution of size k is easily found. Then, at every step/iteration, some element is added and a new solution of size k is computed for the new instance (after the element addition) using the compression procedure. As computing the new solution of size k takes -time, every iteration up to n runs in -time, making the whole approach (see [25] for more details and examples).
7. Parallel Algorithms Using FPT Methods
Since every problem is , it is reasonable to try to convert known techniques into analogues ones. Of course it is not possible to find a general conversion from any algorithm into a corresponding algorithm, especially since . The most common algorithms for problems parameterized in terms of the solution size k can be categorized into the four techniques described in the previous Section. We present, for each of them, methods to achieve efficient parallel algorithms, stating the conditions or limitations associated with each approach. Some of these methods are not based on previous work (i.e., introduced in this paper).
7.1. Bounded Search Trees
The idea behind our approach is that a fixed-parameter algorithm that is based on the bounded search tree approach will always run in -time while branching, and could only violate the condition when querying and updating the input, simply because a bounded search tree has a total number of nodes that is bounded by a function of the parameter. Typically, a bounded search tree algorithm would have a number of options, or possible branches, at each search-tree node. In most cases, and in what we shall assume in this section, this can be interpreted as a branching set S that is of size bounded by some constant.
In the parallel algorithm, we set a master process to do the branching, while each of the other processes can supply the master with the needed set of elements to branch on. Since there are sets of size , we need processors, each of which will handle a set. A processor can identify its set simply by its rank.
The approach entails keeping a global solution array of size bounded by some function of the parameter k, usually linear in (or exactly equal to) k if we want a solution of size at most or at least k. The solution array is kept in the master, and upon adding or removing an element from the solution, the other processes are informed by a reduction tree in logarithmic time, and that way all processes will always have the current solution stored locally.
Depending on the problem in question, every process is responsible for a some subset of elements and some condition for any of the elements to be in the solution. The process should forward the set of elements needed to satisfy the condition. If some elements cannot be forwarded due possibly to conflicts with the current (global) solution set, then only the valid elements are forwarded. An empty set is forwarded if the set is no longer valid as a branching set.
By using a reduction tree method, we reduce the various sets of elements into one set. At step i, starting from , a process whose index j is congruent to zero modulo receives from the process whose index is . Therefore, we have established that each process will be responsible for a potential branching set of size in such a way that each such subset of the input is included. These processes will be notified of which element was included in the solution set at each branch. Without loss of generality, in the case of d-Hitting Set (where d is a constant), each process will be responsible for a set of the input of size at most d, while there would be a global solution set of size at most k. At each branch, the process can check in time whether its set has been hit by the existing solution set. If not, then this process forwards its set in a reduction tree manner along with other such processes. Eventually, the master process will either receive no set (or empty set) meaning that all input sets are covered by the existing solution set. The master may also receive a set that is not hit by the existing solution to branch on this set. In this manner, the master branching would always run in -time since it is a bounded search tree algorithm. Querying the input sets, finding a set, and updating the input after including an element into the solution set are all since each process is handling a specific input set.
To generalize, if a process already has its set uncovered, then it forwards its set instead of the other process’s set. This procedure repeats for steps where is the number of processes, n is the input size, and c is a fixed constant. We can also apply certain comparison rules in order to return a set with given properties. We may, for example, return the largest or smallest set. In this case, all the master process has to do is to define a comparator method which the slaves will use to produce a final set for branching. The master then performs -time branching and checks after k steps whether a solution exists or not by invoking a similar procedure in the slave nodes. If a set is returned, then the solution is incorrect and should be discarded; otherwise, if an empty set is returned, the solution is correct and should be returned.
The algorithm can be easily modified for maximization problems. If the solution size reaches k, return the solution. Otherwise, query for a set to branch on, and if there is no set returned, then the current branch does not entail a valid solution.
The whole procedure of querying the input—for a set to branch on and branching on this set once found—is . This approach, as described, applies to problems where the branching set size is bounded by a constant, to allow the usage of polynomial number of processors to cover all sets. Problems that fall into this category include the d-Hitting Set problem (when d is constant), which brings to mind the Vertex Cover problems as a special case. In addition, problems on d-degenerate graphs (d constant), often have a branching set equal to , such as Independent Set and Dominating Set. Independent Set on planar graphs also lies in this category as planar graphs are 5-degenerate.
Another family of problems for which this approach is applicable consists of problems where the branching set S is some (constant-size) forbidden structure. A typical example is the Cluster Editing problem, which requires transforming a given input graph into a disjoint union of cliques by performing a number of edge editing (addition/deletion) operations that does not exceed some parameter k. In this case, the branching set consists of any three vertices that induce a path of length two (known as a conflict triple), as described in [30]. Our approach thus proves that Cluster Editing is . It would also be interesting to extend this algorithm further to other variants of Cluster Editing (see, for example, [31,32,33]).
7.2. Kernelization
Another common approach for designing algorithms, introduced in [1], is based on the use of kernelization. This technique was also used in [2] where reductions are used to kernelize Vertex Cover instances using the crown reduction technique [34,35,36,37].
If all steps of the kernelization algorithm take -time, when the instance becomes a kernel of size bounded by a function of k, any subsequent fixed-parameter algorithm applied on this kernel would run in -time, resulting in a global -time algorithm. Since modifying the input instance is -time, what remains is to ensure that the number of modifications done to kernelize the instance is a function of the parameter k only. We can even make use of the above color coding techniques to find a particular structure in the input instance.
The simplest Vertex Cover kernel, for example, is obtained by removing all vertices of degree more than k [16]. Each such operation takes -time (refer to the input representation discussion above), and these will iterate for at most k times, after which the solution size would exceed k (obviously resulting in a NO instance). All isolated vertices can be removed simultaneously. Overall, the kernelization takes -time and either determines the instance to be a NO instance, or results in a graph of order . Whatever algorithm applied to this new instance will therefore take -time. In fact, even a brute force algorithm would solve the problem in time. Moreover, the verification of Vertex Cover (which has to consider the original input) takes -time as it was shown earlier.
We note that fast, and more effective, kernelization algorithms exist, as the one in [2], where maximal matching is used to perform crown reduction and obtain a kernel for an arbitrary Vertex Cover instance. It is also shown that maximum matching parameterized by an upper bound on the matching size is and can be performed in using processors for a graph with n vertices and m edges. This allows for a crown reduction that produces a kernel, which leads to better results when a regular sequential algorithm is applied later.
7.3. Color Coding
It was shown in [17] that an -universal color coding can be achieved in using a polynomial number of processors, by generating a set of hash functions, bounded above by this number. Given n processors, we can apply any coloring in constant time, where every processor can compute the color of its element based on the hash function that is currently examined. This means that the coloring step in color coding takes -time, so if other operations of a color coding algorithm can be efficiently parallelized, then the whole algorithm would run in -time.
The above result was used to prove multiple problems in [17], especially graph packing problems such as parameterized Matching; k-Triangle Packing, which is nothing but finding k vertex-disjoint 3-cliques; and -Cycle Packing, which requires finding k vertex-disjoint cycles of length l each. In fact, it was shown that any problem that requires finding k vertex-disjoint copies of a graph H in an arbitrary graph G is in as long as the order of H is constant or bounded by some parameter other than the order of G. Formally, given an arbitrary graph G of order n and a “fixed” graph H of order h, where h is a constant independent of n. The question is whether G contains k disjoint subgraphs isomorphic to H, where k is a parameter independent of n. We shall describe how color coding is used (mainly in [17]) to obtain an algorithm for the problem.
First, determining whether a graph of order contains a subgraph isomorphic to of constant-order can be done in constant time using processors, as there are at most that much subgraph of that have order . Every processor checks in a constant time whether its subgraph is isomorphic to (since is a constant and querying the input as noted above is ).
Now, to find at least k disjoint subgraphs isomorphic to H in G, we will need color coding. Since the solution is of size k, then exactly vertices will be involved. In addition, if there is a solution, then an coloring family will contain at least one coloring where every subgraph of the k subgraphs in the solution is completely colored with a unique color. Generating the hash functions for the coloring and coloring the graph G with every possible coloring can be done in -time, as mentioned above.
For every coloring, and for every color of the k colors, check whether the subgraph of G induced by the vertices of this color (keep G as is, but only consider the vertices of one color) contains a subgraph isomorphic to H. As shown previously, this takes -time, so the overall algorithm becomes . The correctness of the algorithm follows from the fact that every coloring partitions G into k disjoint subgraphs. Hence, whenever a coloring function generates a valid solution, stop and return it; otherwise, continue to try all colorings, and report a NO instance if none gives a solution.
Therefore, finding whether an arbitrary graph G contains at least k disjoint subgraphs isomorphic to some fixed, constant graph H is and the algorithm described above runs in time using processors.
A related problem that is amenable to the color coding method is (Induced) Subgraph Isomorphism. Consider an arbitrary graph G of order n, and another arbitrary graph H of order k (where k is a parameter independent of n) along with a tree decomposition for H. It was shown in [17] that when H is of bounded treewidth, checking whether G has a subgraph (or induced subgraph) isomorphic to H can be done in time using processors by coloring the vertices of H uniquely and computing a -coloring of G. In this case, is not more than k, so this algorithm takes -time. This proves that the Subgraph Isomorphism and Induced Subgraph Isomorphism problems are in this particular case.
Finally, some clustering problems can also be solved using the color coding technique. For example, the -Cluster Editing problem was shown in [17] to be solvable in para- time (the class proposed in the same paper that is a subset of ). The -Cluster Editing problem asks whether deleting or adding at most k edges yields l disjoint cliques. In fact, at most, vertices can be affected by the allowed modifications, and there are at most l vertices representing the vertices of least index that are unmodified in each cluster. By using an coloring, one can identify the edges to add or remove and the clusters that are to be obtained. There is a little subtlety, however, regarding the complexity of traversing the graph, since graph traversal has not yet been proved to be in the class . A para- algorithm is also presented for the k-Cluster Editing problem, where the number of clusters is unknown. The observation here is that after eliminating the isolated cliques present initially, the number of clusters newly formed after the edge editing operations cannot exceed , so the problem becomes similar to the preceding one with l at most .
7.4. Iterative Compression
Iterative compression is inherently serial, as elements of the input are added one at a time. Therefore, escaping the n factor in the time complexity of a parallel algorithm would be impossible in classical iterative compression algorithms regardless of the number of processors used.
A workaround to escape the n factor is to apply some approximation scheme before the actual search for a solution begins. Assume there exists some -factor approximation algorithm [38] (for any constant ) for a problem which we require a solution of size at most k for (maximization problems also apply similarly). Applying this algorithm will produce a solution of size t, knowing that (where is the minimum possible solution size). If , then the instance is a No-instance since in this case.
After this simple trick, we can start with a (feasible) solution of size at most , and our objective is to reduce it to a solution of size at most k.
Let us consider Vertex Cover as an example, and use the well known factor-two approximation algorithm, based on maximal matching, to obtain a solution of size at most . For every vertex in the solution, it may either remain in the solution, or it leaves the solution with all its neighbors being inside the solution. It is possible to generate all choices, and, for each, check in -time whether it results in a valid solution of smaller size. Observe that all vertices that left the solution will be removed from the graph while all their neighbors are marked in the solution and deleted as well. There will be no more than removals, and no more than k vertices can be in the solution, so all the described changes can be performed in -time. Every potential solution can be verified in time using processors (where m is the number of edges in the graph) simply by checking whether at least one edge endpoint is among the k vertices.
This demonstrates how iterative compression, an inherently serial approach, can be made by making use of an initial approximate solution. The key is that, once an element is removed from the solution, some other set of elements is forced to be in the solution.
8. Problems not Fixed-Parameter Parallel Tractable
In this section we discuss, with examples, problems that fall in the class but are not in the subclasses or .
8.1. Problems that Are NC but not FPT (so neither PNC nor FPP)
By the definition of , most problems for which a solution of size k is required are in for any particular value of k, given that k is independent of the input size n. We now consider problems that are in for any fixed value of the parameter k, but not . Many problems fall in this class. Examples include k-Clique, k-Independent Set, and k-Dominating Set. In all of these cases, we can assign processors, where every processor handles some subset of k elements from the input of size n. Using a number of processors that is polynomial in n, we can verify whether a subset of k elements forms a valid solution. We reemphasize that, as far as the definition is concerned, the value of k is treated as a constant since it is independent of n.
In fact, the above discussion is based on (and can be generalized into) the following simple observation: a problem parameterized by the solution size k is always in as long as, given a solution to the problem, it can be verified in -time.
8.2. Problems that Are FPT but not NC (also neither PNC nor FPP)
Problems in this category are parameterized problems that can be solved in polynomial time but are not in for some value of the parameter. In fact, any P-complete problem serves as an example, such as the Circuit Value Problem, Linear Programming, Lexicographically First Depth First Search Ordering.
8.3. Problems that Are NC and FPT But Not PNC (So Not FPP)
Currently, we are not aware of any problems in this category. Problems like the Feedback Vertex Set are and , but no solution is known yet for such problems. We believe this particular class (or sub-class of NC) is non-empty based on the description provided above regarding the complexity classes.
9. Conclusions
In this paper we presented a brief survey of parameterized parallel complexity along with new observations about the various parameterized parallel complexity classes. Key known results from the literature are highlighted and described in detail, with a trial to abstract the common approaches in the design of algorithms.
We showed how classical techniques for sequential algorithms, such as bounded search trees, kernelization, iterative compression, and color coding, can be used to obtain algorithms for problems parameterized by solution size. To the best of our knowledge, some of the presented techniques, especially bounded search trees and iterative compression, are introduced or at least developed for the first time in this paper.
Subtleties about implementation aspects are also introduced, including how the input can be effectively represented, accessed, and manipulated to guarantee -time. Finally, problems that are intractable in the sense were discussed briefly, mainly to highlight some of the most classical examples.
Author Contributions
The two authors have contributed equally to the writing of this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cesati, M.; Di Ianni, M. Parameterized parallel complexity. In Proceedings of the European Conference on Parallel Processing, Southampton, UK, 1–4 September 1998; Springer: Cham, Switzerland, 1998; pp. 892–896. [Google Scholar]
- Abu-Khzam, F.N.; Li, S.; Markarian, C.; Heide, F.M.A.D.; Podlipyan, P. On the Parameterized Parallel Complexity and the Vertex Cover Problem. In Lecture Notes in Computer Science, Proceedings of the Combinatorial Optimization and Applications, Hong Kong, China, 16–18 December 2016; Springer: Cham, Switzerland, 2016; pp. 477–488. [Google Scholar] [CrossRef]
- Downey, R.G.; Fellows, M.R.; Stege, U. Computational tractability: The view from mars. Bull. EATCS 1999, 69, 73–97. [Google Scholar]
- Papadimitriou, C. Section 15.3: The class NC. In Computational Complexity, 1st ed.; Addison Wesley: Boston, MA, USA, 1993; pp. 375–381. [Google Scholar]
- Bodlaender, H.L.; Hagerup, T. Parallel algorithms with optimal speedup for bounded treewidth. SIAM J. Comput. 1998, 27, 1725–1746. [Google Scholar] [CrossRef]
- Abu-Khzam, F.N.; Li, S.; Markarian, C.; auf der Heide, F.M.; Podlipyan, P. Efficient parallel algorithms for parameterized problems. Theor. Comput. Sci. 2019, 786, 2–12. [Google Scholar] [CrossRef]
- Diestel, R. Graph Theory. Grad. Texts Math. 2017, 173. [Google Scholar] [CrossRef]
- Bodlaender, H.L. Dynamic programming on graphs with bounded treewidth. In Proceedings of the Automata, Languages and Programming, Tampere, Finland, 11–15 July 1988; Lepistö, T., Salomaa, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1988; pp. 105–118. [Google Scholar]
- Gallai, T. Transitiv orientierbare graphen. Acta Math. Hung. 1967, 18, 25–66. [Google Scholar] [CrossRef]
- Gajarskỳ, J.; Lampis, M.; Ordyniak, S. Parameterized algorithms for modular-width. In Proceedings of the International Symposium on Parameterized and Exact Computation, Sophia Antipolis, France, 4–6 September 2013; Springer: Cham, Swizterland, 2013; pp. 163–176. [Google Scholar]
- Arora, S.; Barak, B. Computational Complexity: A Modern Approach; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Clote, P.; Kranakis, E. Boolean Functions and Computation Models; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Abu-Khzam, F.N.; Langston, M.A.; Shanbhag, P.; Symons, C.T. Scalable Parallel Algorithms for FPT Problems. Algorithmica 2006, 45, 269–284. [Google Scholar] [CrossRef]
- Abu-Khzam, F.N.; Daudjee, K.; Mouawad, A.E.; Nishimura, N. On scalable parallel recursive backtracking. J. Parallel Distrib. Comput. 2015, 84, 65–75. [Google Scholar] [CrossRef]
- Bovet, D.P.; De Agostino, S.; Petreschi, R. Parallelism and the feedback vertex set problem. Inf. Process. Lett. 1988, 28, 81–85. [Google Scholar] [CrossRef]
- Buss, J.F.; Goldsmith, J. Nondeterminism within P. SIAM J. Comput. 1993, 22, 560–572. [Google Scholar] [CrossRef]
- Bannach, M.; Stockhusen, C.; Tantau, T. Fast Parallel Fixed-parameter Algorithms via Color Coding. In Proceedings of the 10th International Symposium on Parameterized and Exact Computation (IPEC 2015), Patras, Greece, 16–18 September 2015; Husfeldt, T., Kanj, I., Eds.; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2015; Volume 43, pp. 224–235. [Google Scholar] [CrossRef]
- Abu-Khzam, F.N.; Li, S.; Markarian, C.; Heide, F.M.A.D.; Podlipyan, P. Modular-Width: An Auxiliary Parameter for Parameterized Parallel Complexity. In Lecture Notes in Computer Science, Proceedings of the Frontiers in Algorithmics, Chengdu, China, 23–25 June 2017; Springer: Cham, Switzerand, 2017; pp. 139–150. [Google Scholar] [CrossRef]
- Bannach, M.; Tantau, T. Computing kernels in parallel: Lower and upper bounds. arXiv 2018, arXiv:1807.03604. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; The MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Abu-Khzam, F.N.; Langston, M.A.; Mouawad, A.E.; Nolan, C.P. A hybrid graph representation for recursive backtracking algorithms. In Proceedings of the International Workshop on Frontiers in Algorithmics, Wuhan, China, 11–13 September 2010; Springer: Cham, Switzerland, 2010; pp. 136–147. [Google Scholar]
- Dehne, F.; Fellows, M.; Langston, M.; Rosamond, F.; Stevens, K. An O (2 O (k) n 3) FPT algorithm for the undirected feedback vertex set problem. Theory Comput. Syst. 2007, 41, 479–492. [Google Scholar] [CrossRef]
- Thomassé, S. A 4k2 kernel for feedback vertex set. ACM Trans. Algorithms (TALG) 2010, 6, 32. [Google Scholar]
- Downey, R.G.; Fellows, M.R. Parameterized computational feasibility. In Feasible mathematics II; Springer: Berlin/Heidelberg, Germany, 1995; pp. 219–244. [Google Scholar]
- Cygan, M.; Fomin, F.V.; Kowalik, L.; Lokshtanov, D.; Marx, D.; Pilipczuk, M.; Pilipczuk, M.; Saurabh, S. Parameterized Algorithms; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Downey, R.G.; Fellows, M.R.; Stege, U. Parameterized complexity: A framework for systematically confronting computational intractability. In Contemporary Trends in Discrete Mathematics: From DIMACS and DIMATIA to the Future; American Mathematical Society: Providence, RI, USA, 1999; Volume 49, pp. 49–99. [Google Scholar]
- Lokshtanov, D.; Panolan, F.; Ramanujan, M.S.; Saurabh, S. Lossy Kernelization. In Proceedings of the STOC 2017 49th Annual ACM SIGACT Symposium on Theory of Computing, Montreal, QC, Canada, 19–23 June 2017; ACM: New York, NY, USA, 2017; pp. 224–237. [Google Scholar] [CrossRef]
- Alon, N.; Yuster, R.; Zwick, U. Color-coding: A New Method for Finding Simple Paths, Cycles and Other Small Subgraphs Within Large Graphs. In Proceedings of the STOC’94 Twenty-Sixth Annual ACM Symposium on Theory of Computing, Montreal, QC, Canada, 23–25 May 1994; ACM: New York, NY, USA, 1994; pp. 326–335. [Google Scholar] [CrossRef]
- Alon, N.; Yuster, R.; Zwick, U. Color-coding. J. ACM 1995, 42, 844–856. [Google Scholar] [CrossRef]
- Gramm, J.; Guo, J.; Hüffner, F.; Niedermeier, R. Graph-Modeled Data Clustering: Exact Algorithms for Clique Generation. Theory Comput. Syst. 2005, 38, 373–392. [Google Scholar] [CrossRef]
- Abu-Khzam, F.N. On the complexity of multi-parameterized cluster editing. J. Discret. Algorithms 2017, 45, 26–34. [Google Scholar] [CrossRef]
- Komusiewicz, C.; Uhlmann, J. Cluster editing with locally bounded modifications. Discret. Appl. Math. 2012, 160, 2259–2270. [Google Scholar] [CrossRef]
- Heggernes, P.; Lokshtanov, D.; Nederlof, J.; Paul, C.; Telle, J.A. Generalized Graph Clustering: Recognizing (p, q)-Cluster Graphs. In Lecture Notes in Computer Science, Proceedings of the Graph Theoretic Concepts in Computer Science—36th International Workshop, WG 2010, Zarós, Crete, Greece, 28–30 June 2010; Revised Papers; Thilikos, D.M., Ed.; Spring: Cham, Switzerland, 2010; Volume 6410, pp. 171–183. [Google Scholar] [CrossRef]
- Chor, B.; Fellows, M.; Juedes, D.W. Linear Kernels in Linear Time, or How to Save k Colors in O(n2) Steps. In Lecture Notes in Computer Science, Proceedingsof the Graph-Theoretic Concepts in Computer Science, 30th International Workshop, WG 2004, Bad Honnef, Germany, 21–23 June 2004; Revised Papers; Hromkovic, J., Nagl, M., Westfechtel, B., Eds.; Spring: Cham, Switzerland, 2004; Volume 3353, pp. 257–269. [Google Scholar] [CrossRef]
- Abu-Khzam, F.N.; Langston, M.A.; Suters, W.H. Fast, effective vertex cover kernelization: A tale of two algorithms. In Proceedings of the 2005 ACS/IEEE International Conference on Computer Systems and Applications (AICCSA 2005), Cairo, Egypt, 3–6 January 2005; IEEE Computer Society: Washington, DC, USA, 2005; p. 16. [Google Scholar] [CrossRef]
- Abu-Khzam, F.N.; Fellows, M.R.; Langston, M.A.; Suters, W.H. Crown Structures for Vertex Cover Kernelization. Theory Comput. Syst. 2007, 41, 411–430. [Google Scholar] [CrossRef]
- Chlebík, M.; Chlebíková, J. Crown reductions for the Minimum Weighted Vertex Cover problem. Discret. Appl. Math. 2008, 156, 292–312. [Google Scholar] [CrossRef][Green Version]
- Williamson, D.P.; Shmoys, D.B. The Design of Approximation Algorithms; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).