Abstract
The open-domain Frame Problem is the problem of determining what features of an open task environment need to be updated following an action. Here we prove that the open-domain Frame Problem is equivalent to the Halting Problem and is therefore undecidable. We discuss two other open-domain problems closely related to the Frame Problem, the system identification problem and the symbol-grounding problem, and show that they are similarly undecidable. We then reformulate the Frame Problem as a quantum decision problem, and show that it is undecidable by any finite quantum computer.
1. Introduction
The Frame Problem (FP) was introduced by McCarthy and Hayes [1] as the problem of circumscribing the set of axioms that must be deployed in a first-order logic representation of a changing environment. From an operational perspective, it is the problem of circumscribing the set of (object, property) pairs that need to be updated following an action. In a fully-circumscribed domain comprising a finite set of objects, each with a finite set of properties, the FP is clearly solvable by enumeration; in such domains, it is merely the problem of making the enumeration efficient. Fully-circumscribed domains are, however, almost by definition artificial [2]. In open domains, including task environments of interest for autonomous robotics, the ordinary world of human experience, or the universe as a whole, the FP raises potentially-deep questions about the representation of causality and change, particularly the representation of unobserved changes, e.g., leading to unanticipated side-effects. Interest in these questions in the broader cognitive science community led to broader formulations of the FP as the problem of circumscribing (generally logical) relevance relations [3,4], a move vigorously resisted by some AI researchers [5,6]. The FP in its broader formulation appears intractable; we have previously argued that it is in fact intractable on the basis of time complexity [7]. However, general discussion of the FP has remained largely qualitative (e.g., References [8,9,10,11,12,13,14]; see References [15,16] for recent reviews) and the question of its technical tractability in a realistic, uncircumscribed operational setting remains open. Practical solutions to the FP, particularly in robotics, remain heuristic (e.g., References [17,18,19]).
Here we show that in a fully-general, operational setting, the open-domain FP (hereafter, “FP”) is equivalent to the Halting Problem (HP). The HP is the problem of constructing an oracle , a an algorithm and i an input, such that if a given i halts in finite time and otherwise. That no such oracle can be implemented by a finite Turing machine (TM) was demonstrated by Turing [20]. The HP has since been widely regarded as the canonical undecidable problem; proof of equivalence to the HP is proof of (finite Turing) undecidability. The FP is, therefore, undecidable and hence strictly unsolvable by finite means. This same result can also be obtained via Rice’s Theorem [21]: supposing that a set of programs solving the FP exists, membership in that set is undecidable.
If identity over time is regarded as a property of an object or more generally, a system, the problem of re-identifying objects or systems as persistent individuals is equivalent to the FP [22]. If the denotation of a symbol is a persistent object or set of objects, the symbol grounding problem is equivalent to the object identification problem [23] and hence to the FP. Undecidability of the FP renders these problems undecidable. To further investigate these issues, we here reformulate the FP as a quantum decision problem (the “QFP”) faced by a finite-dimensional quantum computer, and show that this quantum version is also undecidable. We then show that the construction of a two-prover interactive proof system in which the provers share an entangled state [24] requires a solution to the QFP, which given its unsolvability can only be heuristic or “FAPP” (for all practical purposes; see Reference [25] where “FAPP” was introduced as a pejorative term). Given the recent proof of Ji et al. that MIP* = RE [26], MIP* indicating languages decidable by a multiprover interactive proof system with shared entanglement and RE the recursively enumerable languages, we here conjecture that the QFP is not only strictly harder than the HP, but that it is outside RE.
The FP being unsolvable by finite systems, whether classical or quantum, renders computational models of relevance, causation, identification, and communication equally intractable. It tells us that multiple realizability (i.e., platform independence) is a fundamental feature of the observable universe.
2. Results
We show in this section that the FP and the HP are equivalent: undecidability of one entails undecidability of the other.
2.1. Notation and Operational Set-Up
Consider an agent A that interacts with an environment E. We intend A to be a physically-realizable agent, so we demand that A’s state space have only finite dimension . We can, for the present purposes, consider A to be a classical agent with a classical state space; we extend the model to the quantum case in Section 3.3 below. For simplicity, we consider only computational states of A, each of which we require to be finitely specifiable, that is, without loss of generality, specifiable as a finite bit string. Hence A has finite computational resources, expends finite energy, and generates finite waste heat [27].
The environment E with which A interacts is by stipulation open; we also assume that E is “large”, that is, that it has dimension . All realistic non-artificial task environments are both large and open: these include practical robotic task environments including human interaction [28], undersea [29] and planetary [30] exploration as well as the general human environment. Robotic or other AI systems operating in such environments all face the FP; as noted earlier, practical FP solutions in such environments are heuristic and hence subject to unpredictable failure.
What is of interest in characterizing E is the ability of A to extract information from E by interaction. As A is limited to finite, finite-resolution interaction with E, we have:
Lemma 1
(No Full Access lemma). A finite observer A can access only a finite proper component of a large open environment E.
Proof.
A can allocate at most some proper subset of its state space to memory, hence it can represent at most some components of the state space of E. □
As an obvious corollary, A cannot determine .
Given the No Full Access lemma, we can without loss of generality represent the problem set-up as shown in Figure 1. We assume that A has observational access to some finite-dimensional proper component of E, but no access to the remainder ; , , where ⊔ indicates disjoint union. We assume that A has a perception module obtaining input from , an action module supplying input to E, and a problem-solving module with access to two generative models, one of E and one of A. We take the model of E to be constructed entirely on the basis of A’s inputs from ; this loses no generality, as any finite agent capable of encoding the model a priori would be subject to the same in-principle access restrictions as A. The model of E has a proper component that models based on observational outcomes obtained; the remainder models via (deductive, inductive, or abductive) inferences executed by the problem solving module. This model of may be radically incomplete, containing many “unknown unknowns”; given A’s inability to determine , these cannot be circumscribed. The inferences employed to construct the model of cannot, moreover, be subjected to experimental tests except via their predicted consequences for the behavior of . For any physically-realizable agent, the models of and are clearly both finite and of finite resolution; similarly A’s “self” model must be both finite and of finite resolution.
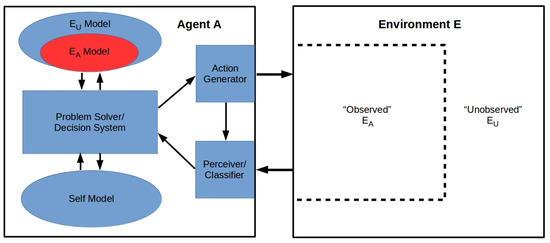
Figure 1.
General set-up for the Frame Problem (FP): a finite agent A interacts with an environment E. The agent has perception and action modules and a problem solver. The problem solver has access to two generative models, one of the environment and the other a “self” model of its own problem-solving capabilities. The environment is divided into a part to which A has observational access and a remainder to which A does not have observational access.
We can, clearly, think of A as a Turing machine with finite processing and input/output (I/O) tapes. We can, however, also think of A as a hierarchical Bayesian or other predictive-processing agent (e.g., References [31,32]) or as an artificial neural network with weights stored in the E and self models. Agent architectures such as ACT-R [33], LIDA [34], or CLARION [35] can all be represented in the form of Figure 1.
2.2. The FP as an Operational Problem
While the FP is sometimes considered an abstract, logical problem as discussed above, in any practical setting it is an operational problem. We can state it in full generality as follows.
The task of any agent in a real environment is to predict appropriate next behaviors. In the notation of Figure 1, the informational resources available to A to solve this problem are (1) current perceptual input from and (2) the , and self models. Let us make the simplifying assumption that A knows its own algorithm, that is, that its self model consists of a copy of its complete program. Given our assumption that A learns by observation, its program implements a learning algorithm; we can also assume that it specifies A’s action repertoire and any other internal functionality. This assumption is enormously generous, as no system can learn its own algorithm by observation, even if given a partial representation of its algorithm a priori [36].
The operational problem faced by A is, therefore, to predict at each time t its own next state (at ) from (1) its current input from , (2) its model of , and (3) its knowledge of its own algorithm. This is the FP: A must accurately predict both the current and next states of , which A cannot observe, in order to predict the next state of , which determines A’s next input and hence A’s next state. To do this reliably, A must have a complete “theory” of , including in particular a theory of how and interact; even reasonably probable success requires a robust theory of the - interaction. If A’s theory is stated in first-order logic, it requires a set of axioms; hence the original formulation of the FP as the problem of circumscribing this set. Given the potential for unknown unknowns, and hence a radically incomplete model of in any open environment, the impossibility of circumscribing a sufficient set of axioms a priori is already evident (cf. References [3,4,7]).
2.3. Equivalence of the FP and HP
We can now state our main result—not only does the known undecidability of the HP show that the FP is undecidable, but the reverse holds as well.
Theorem 1.
The Frame Problem (FP) and the Halting problem (HP) are equally hard.
Proof:
- FP →
- HP: Let a = the algorithm that generates the next state of and let i be some instantaneous state of . Let A’s state be , and the states of and be and respectively. Consistent with the above, we assume A knows but not , and knows one component of a, namely the algorithm implemented by A. Now assume the FP is undecidable: A cannot deduce the state of at from knowledge of and at t. In this case, A cannot deduce either i or a. In this case A cannot build an oracle that decides whether a halts on i and cannot recognize such an oracle if it exists a priori. Hence the HP is also undecidable by A. Since A is a generic finite agent, the HP is undecidable by any such agent.
- HP →
- FP: Assume that the HP is undecidable (as shown in Reference [20]) and hence that no oracle exists. In this case, A cannot deduce, even if given all of i at the current step t, that A’s next state (at ) is not a halting state. Hence A cannot deduce even its own next state at , let alone the full state . Hence the FP is undecidable. □
As the FP centrally concerns what an agent can deduce, it is also of interest to formulate it as an instance of Rice’s Theorem. The latter states that the problem of determining what programs compute a given, non-trivial function is equivalent to the HP, and is therefore undecidable. Suppose then that there is a set S of programs that, given an action on an open environment E, compute all (object, property) pairs that must be updated in consequence of the action. The FP is then the problem of deciding whether for any given program P. This problem is, by Rice’s Theorem, undecidable.
3. Discussion
Here we consider the relationship between the FP and two other problems that straddle the borders between AI, general cognitive science, and philosophy: the system identification problem and the symbol-grounding problem. We then reformulate the FP in a quantum setting as the QFP, and show that it is also undecidable.
3.1. The System Identification Problem
The system identification problem arises in classical cybernetics, taking two related forms [36]:
- Given a system in the form of a black box (BB) allowing finite input-output interactions, deduce a complete specification of the system’s machine table (i.e., algorithm or internal dynamics).
- Given a complete specification of a machine table (i.e., algorithm or internal dynamics), recognize any BB having that description.
That finite observers cannot solve the system identification problem in either form was shown by Moore [36] over 60 years ago. A quantum-theoretic formulation has also been investigated, and is likewise unsolvable [37].
The system identification problem is easily seen to be an instance of the FP. Consider any system S having, at some time t, a complete, finite, uniquely-identifying description . On encountering a system at some , what is required to determine whether ? Even if is taken to be given a priori, and contra [36,37] an oracle capable of deciding whether satisfies is assumed to be available, is it possible to decide whether actions taken on systems between t and have altered one or more properties of S, or one or more properties of some other system, so that no longer describes, or no longer uniquely describes, S at ? This is the FP [22]. Hence the undecidability of the FP renders the system identification problem undecidable even given a previous complete description and an oracle. This result can, once again, also be formulated in terms of Rice’s theorem.
The question of system identification is clearly closely related to the question of multiple realizability of algorithms and hence of platform independence. Given its undecidability, the specification of the “bottom layer” of a virtual machine (VM) stack, even if it is a “hardware” layer, can only be considered stipulative. The undecidability of system identification also implies that the question of whether two implementations on “the same” VM stack implement the same algorithm is undecidable. Here the connection to Rice’s theorem as well as the HP is obvious.
3.2. The Symbol-Grounding Problem
It is a commonplace that symbols, including nouns in natural languages and mental representations, for example, of visual scenes, refer to objects, that is, to localized, bounded physical systems. Determining the reference of a symbol and hence “grounding” it on the object(s) to which it refers requires identifying the referred-to object(s). If system identification is undecidable, the question of what object(s) ground any particular symbol is likewise undecidable [23]. While this has long been suspected on philosophical grounds [38], here we see it as a consequence of fundamental physical and information-theoretic considerations.
3.3. Undecidability of the QFP
The FP has been considered above in completely classical terms; the systems A and E in Figure 1, for example, are there considered classical systems. What is the status of the FP, however, if we allow quantum computation instead of classical computation?
Considered broadly, the FP is the problem of deciding about relevance in an open domain. From a formal perspective, x and y are mutually relevant if they are statistically connected, that is, if they have a joint probability distribution. While the limiting case of connection in classical statistics is perfect correlation, the limiting case of connection is quantum theory is (monogamous) entanglement, that is, a joint state with an entanglement entropy of unity (and hence von Neumann entropy of zero). Such states are not separable, that is, . Suppose then that the environment E in Figure 1 is a quantum system. In this case, predicting the next state of requires knowing both the classical correlation between and and the entanglement entropy of the joint state . Hence we can formulate the QFP in general form as:
QFP: Given a quantum agent A interacting with a quantum environment E, how does an action of A on E at t affect the entanglement entropy of E at ?
We can now ask: Is the QFP decidable by a finite quantum agent (i.e., a finite quantum computer) A? The answer to this question is known, and is negative:
Theorem 2.
The QFP is undecidable by finite quantum agents.
Proof.
The QFP can only be stated for agents that are separable from the systems with which they interact; in the notation of Figure 1, the joint state must be separable as and hence have entanglement entropy of identically zero. In this case, Theorem 1 of Reference [39] applies, showing that (1) the communication channel between A and E is classical, and (2) the information communicated is limited to finite, bit-string representations of the eigenvalues of the Hamiltonian operator that physically implements the A-E interaction. This Hamiltonian is, however, independent of the internal self-interactions and , and even of the dimensions of the Hilbert spaces and provided that they are sufficiently large. Its eigenvalues, in particular, reveal nothing about tensor decompositions of or their entanglement entropies. □
As A is in-principle ignorant of the entanglement entropy of E, changes in that entanglement entropy are clearly unpredictable. Indeed A cannot determine, solely on the basis of finite observations, that E is not a classical computer (see Reference [40] for the needed extension of classical probability theory to include “quantum” contextuality).
The undecidability of the QFP has immediate consequences for the construction of multi-prover interactive proof systems in which the provers are assumed to share quantum resources, for example, entangled states [24]. A two-prover set-up is illustrated in Figure 2, using the canonical labels A and B for the provers. This set-up obviously replicates a canonical Bell/EPR experiment [41,42] with the verifier playing the role of the third observer, Charlie, who is able to communicate classically with Alice and Bob. Hence it replicates many real experimental set-ups, beginning with that of Aspect et al. in 1982 [43]. Any such experiment requires that the “detectors” A and B be identifiable by the verifier, who must also be capable of establishing that A and B share the entangled state . Hence the verifier must solve both the FP (to identify A and B) and the QFP (to determine the entanglement entropy of the joint system ). Theorems 1 and 2 show that neither can be accomplished by finite observation. A heuristic solution—effectively, an a priori stipulation—is therefore required.
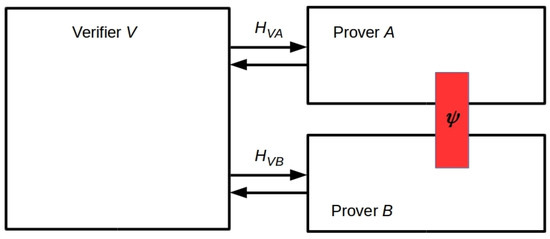
Figure 2.
An interactive proof system with two otherwise noninteracting provers (A and B) that share an entangled state (red rectangle). The verifier interacts separately with the two provers. This is the set-up used in Reference [26] to prove Multiprover Interactive Proof* (MIP*) = RE, and hence that the Halting Problem (HP) can be solved by interactive proof with entanglement as a resource.
Ji et al. have recently proved that the set of problems solvable by a multi-prover interactive proof system in which the provers share entanglement (the set MIP*) is identical to the set RE of recursively-enumerable languages [26]. Hence the HP can be decided (with high probability) by the set-up in Figure 2. As a solution to the QFP must be assumed to operationalize this set-up, we can conjecture that the QFP is strictly harder than the HP, and indeed, that it is not in RE.
4. Conclusions
The FP was originally formulated [1] as a problem for AI systems that employed logic programming. In its open-domain form, it is considered primarily a problem for robots or other autonomous systems [15]. We are, however, everywhere confronted with the real-world consequences of human failures to solve the FP, in the form of failures to adequately anticipate the unintended side-effects of actions. Climate change, widespread antibiotic resistance, and the current Covid-19 pandemic are timely examples. We have shown here that these are not anomalies. Both the FP and the QFP are undecidable by finite agents, including human agents. All “solutions” of either are necessarily heuristic, and hence subject to unpredictable failure.
While computer science is often viewed as a technical discipline, in this case computer science tells us something very deep about what the observable universe is like. It is open in principle. This openness cannot, as we show in Theorem 2, be resolved or controlled by replacing classical computers with quantum computers. If the QFP ∉ RE as we conjecture here, the “unknown unknowns” of the observable universe cannot even be considered to be emergent from the knowns.
Author Contributions
Conceptualization, Formal analysis and writing—review and editing, E.D. and C.F.; writing—original draft preparation, C.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACT-R | Adaptive Control of Thought-Rational |
| AI | Artificial intelligence |
| BB | Black Box |
| CLARION | Connectionist Learning with Adaptive Rule Induction On-line |
| EPR | Einstein-Podolsky-Rosen |
| FAPP | For all practical purposes |
| FP | Frame problem |
| HP | Halting problem |
| I/O | Input/Output |
| LIDA | Learning Intelligent Distribution Agent |
| MIP* | Multiprover Interactive Proof* |
| QFP | Quantum Frame problem |
| RE | Recursively enumerable |
| VM | Virtual machine |
References
- McCarthy, J.; Hayes, P.J. Some philosophical problems from the standpoint of artificial intelligence. In Machine Intelligence; Michie, D., Meltzer, B., Eds.; Edinburgh University Press: Edinburgh, UK, 1969; pp. 463–502. [Google Scholar]
- Fields, C.; Dietrich, E. Engineering artificial intelligence applications in unstructured task environments: Some methodological issues. In Artificial Intelligence and Software Engineering; Partridge, D., Ed.; Ablex: Norwood, UK, 1991; pp. 369–381. [Google Scholar]
- Dennett, D. Cognitive wheels: The frame problem of AI. In Minds, Machines and Evolution: Philosophical Studies; Hookway, C., Ed.; Cambridge University Press: Cambridge, UK, 1984; pp. 129–151. [Google Scholar]
- Fodor, J.A. Modules, frames, fridgeons, sleeping dogs, and the music of the spheres. In The Robot’s Dilemma; Pylyshyn, Z.W., Ed.; Ablex: Norwood, UK, 1987; pp. 139–149. [Google Scholar]
- Hayes, P.J. What the frame problem is and isn’t. In The Robot’s Dilemma; Pylyshyn, Z.W., Ed.; Ablex: Norwood, UK, 1987; pp. 123–137. [Google Scholar]
- McDermott, D. We’ve been framed: Or, why AI is innocent of the frame problem. In The Robot’s Dilemma; Pylyshyn, Z.W., Ed.; Ablex: Norwood, UK, 1987; pp. 113–122. [Google Scholar]
- Dietrich, E.; Fields, C. The role of the frame problem in Fodor’s modularity thesis: A case study of rationalist cognitive science. In The Robot’s Dilemma Revisited; Ford, K.M., Pylyshyn, Z.W., Eds.; Ablex: Norwood, UK, 1996; pp. 9–24. [Google Scholar]
- Fodor, J.A. The Language of Thought Revisited; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Wheeler, M. Cognition in context: Phenomenology, situated cognition and the frame problem. Int. J. Philos. Stud. 2010, 16, 323–349. [Google Scholar] [CrossRef]
- Samuels, R. Classical computationalism and the many problems of cognitive relevance. Stud. Hist. Philos. Sci. Part A 2010, 41, 280–293. [Google Scholar] [CrossRef]
- Chow, S.J. What’s the problem with the Frame problem? Rev. Philos. Psychol. 2013, 4, 309–331. [Google Scholar] [CrossRef]
- Ransom, M. Why emotions do not solve the frame problem. In Fundamental Issues in Artificial Intelligence; Müller, V., Ed.; Springer: Cham, Switzerland, 2016; pp. 355–367. [Google Scholar]
- Nobandegani, A.S.; Psaromiligkos, I.N. The causal Frame problem: An algorithmic perspective. Preprint 2017, arXiv:1701.08100v1 [cs.AI]. Available online: https://arxiv.org/abs/1701.08100 (accessed on 19 July 2020).
- Nakayama, Y.; Akama, S.; Murai, T. Four-valued semantics for granular reasoning towards the Frame problem. In Proceedings of the 2018 Joint 10th International Conference on Soft Computing and Intelligent Systems (SCIS) and 19th International Symposium on Advanced Intelligent Systems (ISIS), Toyama, Japan, 5–8 December 2018; pp. 37–42. [Google Scholar]
- Shanahan, M. The frame problem. In The Stanford Encyclopedia of Philosophy, Spring 2016 Edition; Zalta, E.M., Ed.; Stanford University: Palo Alto, CA, USA, 2016. [Google Scholar]
- Dietrich, E. When science confronts philosophy: Three case studies. Axiomathes 2020, in press. Available online: https://link.springer.com/article/10.1007/s10516-019-09472-9 (accessed on 19 July 2020). [CrossRef]
- Oudeyer, P.-Y.; Baranes, A.; Kaplan, F. Intrinsically motivated learning of real world sensorimotor skills with developmental constraints. In Intrinsically Motivated Learning in Natural and Artificial Systems; Baldassarre, G., Mirolli, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 303–365. [Google Scholar]
- Alterovitz, R.; Koenig, S.; Likhachev, M. Robot planning in the real world: Research challenges and opportunities. AI Mag. 2016, 37, 76–84. [Google Scholar] [CrossRef]
- Raza, A.; Ali, S.; Akram, M. Immunity-based dynamic reconfiguration of mobile robots in unstructured environments. J. Intell. Robot. Syst. 2019, 96, 501–515. [Google Scholar] [CrossRef]
- Turing, A. On computable numbers, with an application to the Entscheid. Proc. Lond. Math. Soc. Ser. 2 1937, 42, 230–265. [Google Scholar] [CrossRef]
- Rice, H.G. Classes of recursively enumerable sets and their decision problems. Trans. Am. Math. Soc. 1953, 74, 358–366. [Google Scholar] [CrossRef]
- Fields, C. How humans solve the frame problem. J. Expt. Theor. Artif. Intell. 2013, 25, 441–456. [Google Scholar] [CrossRef]
- Fields, C. Equivalence of the symbol grounding and quantum system identification problems. Information 2014, 5, 172–189. [Google Scholar] [CrossRef]
- Cleve, R.; Hoyer, P.; Toner, B.; Watrous, J. Consequences and limits of nonlocal strategies. In Proceedings of the 19th IEEE Annual Conference on Computational Complexity, Amherst, MA, USA, 24 June 2004; pp. 236–249. [Google Scholar]
- Bell, J. Against ‘measurement’. Phys. World 1990, 3, 33–41. [Google Scholar] [CrossRef]
- Ji, Z.; Natarajan, A.; Vidick, T.; Wright, J.; Yuen, H. MIP* = RE. Preprint 2020, arXiv:2001.04383 [quant-ph] v1. Available online: https://arxiv.org/abs/2001.04383 (accessed on 19 July 2020).
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–195. [Google Scholar] [CrossRef]
- Dautenhahn, K. Socially intelligent robots: Dimensions of human–robot interaction. Philos. Trans. R. Soc. B 2007, 362, 679–704. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud Zadeh, S.; Powers, D.M.W.; Bairam Zadeh, R. Advancing autonomy by developing a mission planning architecture (Case Study: Autonomous Underwater Vehicle). In Autonomy and Unmanned Vehicles. Cognitive Science and Technology; Springer: Singapore, 2019; pp. 41–53. [Google Scholar]
- Schuster, M.J.; Brunner, S.G.; Bussman, K.; Büttner, S.; Dömel, A.; Hellerer, M.; Lehner, H.; Lehner, P.; Porges, O.; Reill, J.; et al. Toward autonomous planetary exploration. J. Intell. Robot. Syst. 2019, 93, 461–494. [Google Scholar] [CrossRef]
- Friston, K.J.; Kiebel, S. Predictive coding under the free-energy principle. Philos. Trans. R. Soc. Lond. B 2009, 364, 1211–1221. [Google Scholar] [CrossRef]
- Clark, A. Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behav. Brain Sci. 2013, 36, 181–204. [Google Scholar] [CrossRef]
- Anderson, J.R.; Bothell, D.; Byrne, M.D.; Douglass, S.; Lebiere, C.; Qin, Y. An integrated theory of the mind. Psych. Rev. 2004, 111, 1036–1060. [Google Scholar] [CrossRef]
- Franklin, S.; Madl, T.; D’Mello, S.; Snaider, J. LIDA: A systems-level architecture for cognition, emotion and learning. IEEE Trans. Auton. Ment. Dev. 2014, 6, 19–41. [Google Scholar] [CrossRef]
- Sun, R. The importance of cognitive architectures: An analysis based on CLARION. J. Expt. Theor. Artif. Intell. 2007, 19, 159–193. [Google Scholar] [CrossRef]
- Moore, E.F. Gedankenexperiments on sequential machines. In Autonoma Studies; Shannon, C.W., McCarthy, J., Eds.; Princeton University Press: Princeton, NJ, USA, 1956; pp. 129–155. [Google Scholar]
- Fields, C. Some consequences of the thermodynamic cost of system identification. Entropy 2018, 20, 797. [Google Scholar] [CrossRef]
- Quine, W.V.O. Word and Object; MIT Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Fields, C.; Marcianò, A. Holographic screens are classical information channels. Quant. Rep. 2020, 2, 326–336. [Google Scholar] [CrossRef]
- Dzhafarov, E.N.; Kon, M. On universality of classical probability with contextually labeled random variables. J. Math. Psychol. 2018, 85, 17–24. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein-Podolsky-Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Mermin, D. Hidden variables and the two theorems of John Bell. Rev. Mod. Phys. 1993, 65, 803–815. [Google Scholar] [CrossRef]
- Aspect, A.; Grangier, P.; Roger, G. Experimental realization of Einstein-Podolsky-Rosen-Bohm gedankenexperiment: A new violation of Bell’s inequalities. Phys. Rev. Lett. 1982, 49, 91–94. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).