Equivalence of the Frame and Halting Problems
Abstract
1. Introduction
2. Results
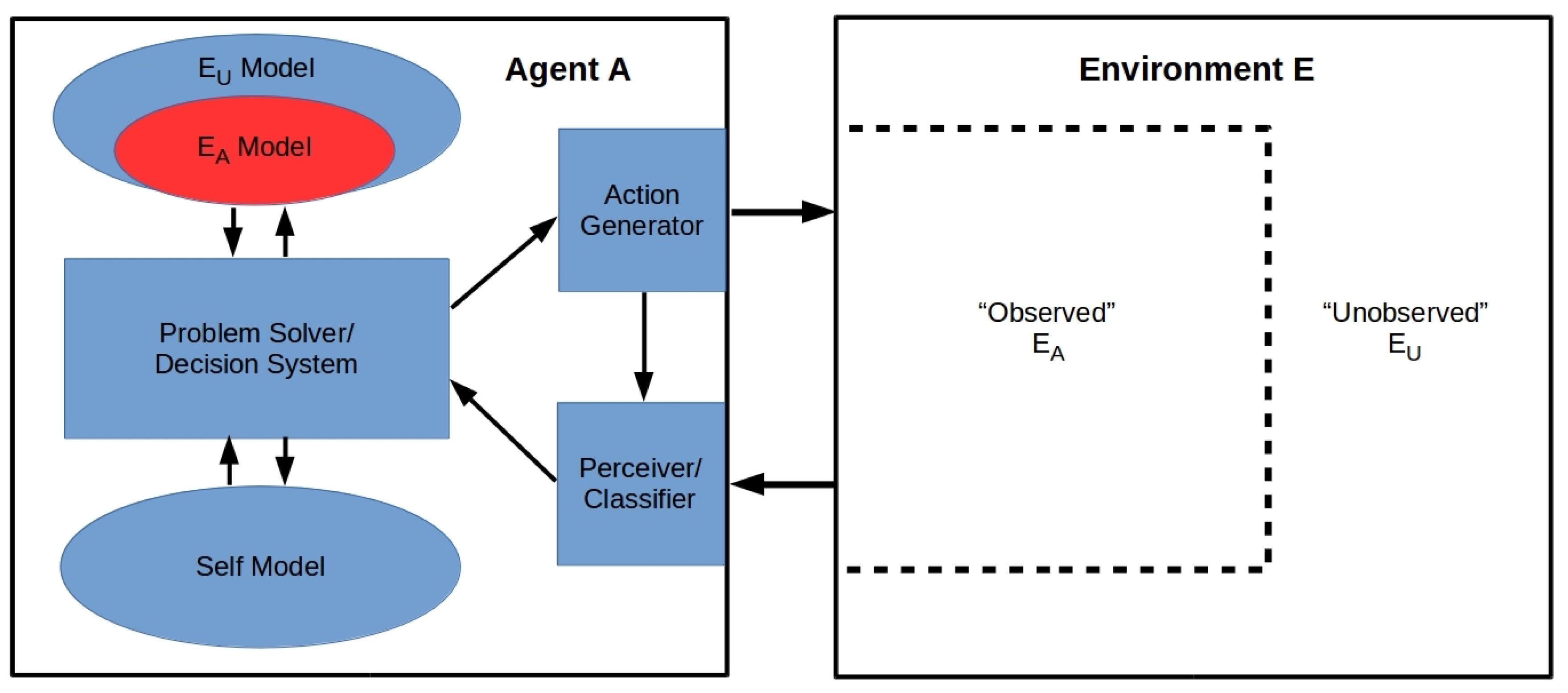
2.1. Notation and Operational Set-Up
2.2. The FP as an Operational Problem
2.3. Equivalence of the FP and HP
- FP →
- HP: Let a = the algorithm that generates the next state of and let i be some instantaneous state of . Let A’s state be , and the states of and be and respectively. Consistent with the above, we assume A knows but not , and knows one component of a, namely the algorithm implemented by A. Now assume the FP is undecidable: A cannot deduce the state of at from knowledge of and at t. In this case, A cannot deduce either i or a. In this case A cannot build an oracle that decides whether a halts on i and cannot recognize such an oracle if it exists a priori. Hence the HP is also undecidable by A. Since A is a generic finite agent, the HP is undecidable by any such agent.
- HP →
- FP: Assume that the HP is undecidable (as shown in Reference [20]) and hence that no oracle exists. In this case, A cannot deduce, even if given all of i at the current step t, that A’s next state (at ) is not a halting state. Hence A cannot deduce even its own next state at , let alone the full state . Hence the FP is undecidable. □
3. Discussion
3.1. The System Identification Problem
- Given a system in the form of a black box (BB) allowing finite input-output interactions, deduce a complete specification of the system’s machine table (i.e., algorithm or internal dynamics).
- Given a complete specification of a machine table (i.e., algorithm or internal dynamics), recognize any BB having that description.
3.2. The Symbol-Grounding Problem
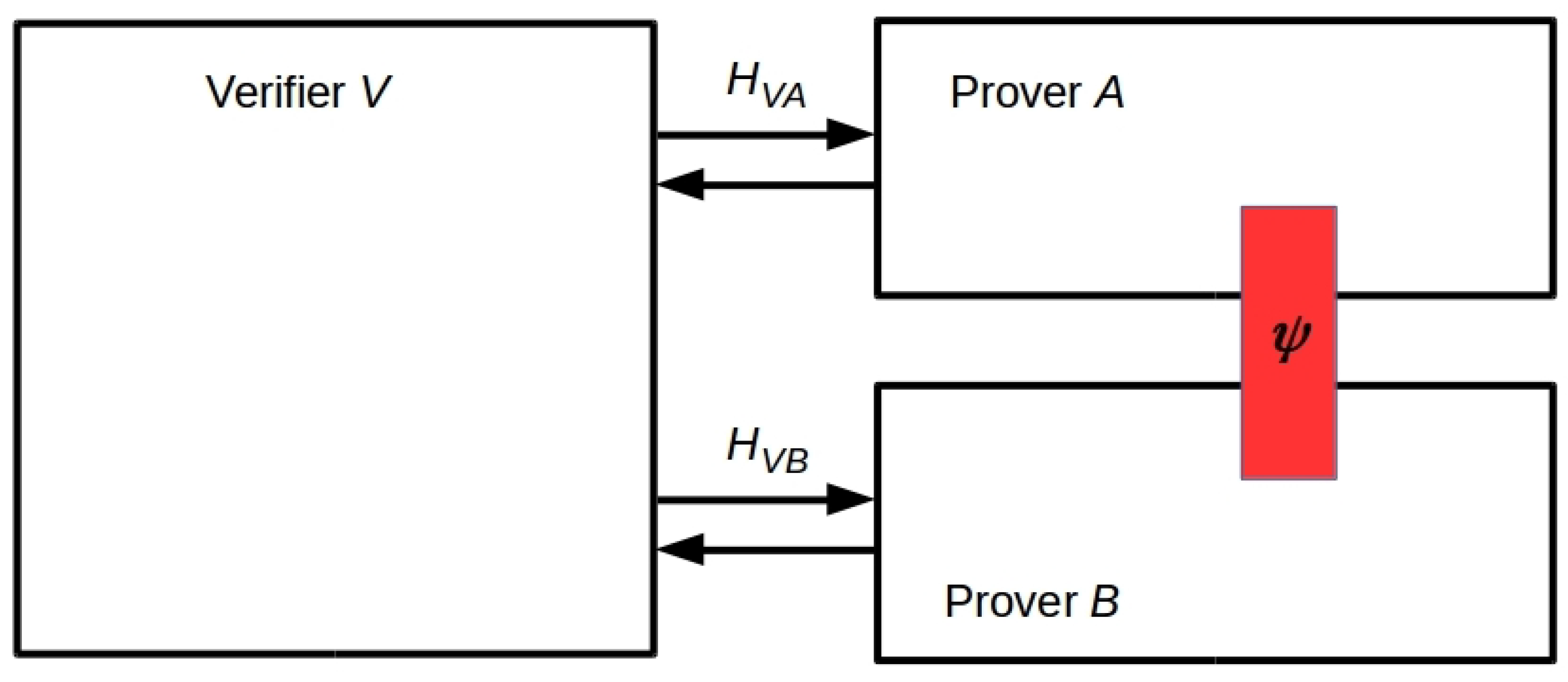
3.3. Undecidability of the QFP
QFP: Given a quantum agent A interacting with a quantum environment E, how does an action of A on E at t affect the entanglement entropy of E at ?
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ACT-R | Adaptive Control of Thought-Rational |
| AI | Artificial intelligence |
| BB | Black Box |
| CLARION | Connectionist Learning with Adaptive Rule Induction On-line |
| EPR | Einstein-Podolsky-Rosen |
| FAPP | For all practical purposes |
| FP | Frame problem |
| HP | Halting problem |
| I/O | Input/Output |
| LIDA | Learning Intelligent Distribution Agent |
| MIP* | Multiprover Interactive Proof* |
| QFP | Quantum Frame problem |
| RE | Recursively enumerable |
| VM | Virtual machine |
References
- McCarthy, J.; Hayes, P.J. Some philosophical problems from the standpoint of artificial intelligence. In Machine Intelligence; Michie, D., Meltzer, B., Eds.; Edinburgh University Press: Edinburgh, UK, 1969; pp. 463–502. [Google Scholar]
- Fields, C.; Dietrich, E. Engineering artificial intelligence applications in unstructured task environments: Some methodological issues. In Artificial Intelligence and Software Engineering; Partridge, D., Ed.; Ablex: Norwood, UK, 1991; pp. 369–381. [Google Scholar]
- Dennett, D. Cognitive wheels: The frame problem of AI. In Minds, Machines and Evolution: Philosophical Studies; Hookway, C., Ed.; Cambridge University Press: Cambridge, UK, 1984; pp. 129–151. [Google Scholar]
- Fodor, J.A. Modules, frames, fridgeons, sleeping dogs, and the music of the spheres. In The Robot’s Dilemma; Pylyshyn, Z.W., Ed.; Ablex: Norwood, UK, 1987; pp. 139–149. [Google Scholar]
- Hayes, P.J. What the frame problem is and isn’t. In The Robot’s Dilemma; Pylyshyn, Z.W., Ed.; Ablex: Norwood, UK, 1987; pp. 123–137. [Google Scholar]
- McDermott, D. We’ve been framed: Or, why AI is innocent of the frame problem. In The Robot’s Dilemma; Pylyshyn, Z.W., Ed.; Ablex: Norwood, UK, 1987; pp. 113–122. [Google Scholar]
- Dietrich, E.; Fields, C. The role of the frame problem in Fodor’s modularity thesis: A case study of rationalist cognitive science. In The Robot’s Dilemma Revisited; Ford, K.M., Pylyshyn, Z.W., Eds.; Ablex: Norwood, UK, 1996; pp. 9–24. [Google Scholar]
- Fodor, J.A. The Language of Thought Revisited; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Wheeler, M. Cognition in context: Phenomenology, situated cognition and the frame problem. Int. J. Philos. Stud. 2010, 16, 323–349. [Google Scholar] [CrossRef]
- Samuels, R. Classical computationalism and the many problems of cognitive relevance. Stud. Hist. Philos. Sci. Part A 2010, 41, 280–293. [Google Scholar] [CrossRef]
- Chow, S.J. What’s the problem with the Frame problem? Rev. Philos. Psychol. 2013, 4, 309–331. [Google Scholar] [CrossRef]
- Ransom, M. Why emotions do not solve the frame problem. In Fundamental Issues in Artificial Intelligence; Müller, V., Ed.; Springer: Cham, Switzerland, 2016; pp. 355–367. [Google Scholar]
- Nobandegani, A.S.; Psaromiligkos, I.N. The causal Frame problem: An algorithmic perspective. Preprint 2017, arXiv:1701.08100v1 [cs.AI]. Available online: https://arxiv.org/abs/1701.08100 (accessed on 19 July 2020).
- Nakayama, Y.; Akama, S.; Murai, T. Four-valued semantics for granular reasoning towards the Frame problem. In Proceedings of the 2018 Joint 10th International Conference on Soft Computing and Intelligent Systems (SCIS) and 19th International Symposium on Advanced Intelligent Systems (ISIS), Toyama, Japan, 5–8 December 2018; pp. 37–42. [Google Scholar]
- Shanahan, M. The frame problem. In The Stanford Encyclopedia of Philosophy, Spring 2016 Edition; Zalta, E.M., Ed.; Stanford University: Palo Alto, CA, USA, 2016. [Google Scholar]
- Dietrich, E. When science confronts philosophy: Three case studies. Axiomathes 2020, in press. Available online: https://link.springer.com/article/10.1007/s10516-019-09472-9 (accessed on 19 July 2020). [CrossRef]
- Oudeyer, P.-Y.; Baranes, A.; Kaplan, F. Intrinsically motivated learning of real world sensorimotor skills with developmental constraints. In Intrinsically Motivated Learning in Natural and Artificial Systems; Baldassarre, G., Mirolli, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 303–365. [Google Scholar]
- Alterovitz, R.; Koenig, S.; Likhachev, M. Robot planning in the real world: Research challenges and opportunities. AI Mag. 2016, 37, 76–84. [Google Scholar] [CrossRef]
- Raza, A.; Ali, S.; Akram, M. Immunity-based dynamic reconfiguration of mobile robots in unstructured environments. J. Intell. Robot. Syst. 2019, 96, 501–515. [Google Scholar] [CrossRef]
- Turing, A. On computable numbers, with an application to the Entscheid. Proc. Lond. Math. Soc. Ser. 2 1937, 42, 230–265. [Google Scholar] [CrossRef]
- Rice, H.G. Classes of recursively enumerable sets and their decision problems. Trans. Am. Math. Soc. 1953, 74, 358–366. [Google Scholar] [CrossRef]
- Fields, C. How humans solve the frame problem. J. Expt. Theor. Artif. Intell. 2013, 25, 441–456. [Google Scholar] [CrossRef]
- Fields, C. Equivalence of the symbol grounding and quantum system identification problems. Information 2014, 5, 172–189. [Google Scholar] [CrossRef]
- Cleve, R.; Hoyer, P.; Toner, B.; Watrous, J. Consequences and limits of nonlocal strategies. In Proceedings of the 19th IEEE Annual Conference on Computational Complexity, Amherst, MA, USA, 24 June 2004; pp. 236–249. [Google Scholar]
- Bell, J. Against ‘measurement’. Phys. World 1990, 3, 33–41. [Google Scholar] [CrossRef]
- Ji, Z.; Natarajan, A.; Vidick, T.; Wright, J.; Yuen, H. MIP* = RE. Preprint 2020, arXiv:2001.04383 [quant-ph] v1. Available online: https://arxiv.org/abs/2001.04383 (accessed on 19 July 2020).
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–195. [Google Scholar] [CrossRef]
- Dautenhahn, K. Socially intelligent robots: Dimensions of human–robot interaction. Philos. Trans. R. Soc. B 2007, 362, 679–704. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud Zadeh, S.; Powers, D.M.W.; Bairam Zadeh, R. Advancing autonomy by developing a mission planning architecture (Case Study: Autonomous Underwater Vehicle). In Autonomy and Unmanned Vehicles. Cognitive Science and Technology; Springer: Singapore, 2019; pp. 41–53. [Google Scholar]
- Schuster, M.J.; Brunner, S.G.; Bussman, K.; Büttner, S.; Dömel, A.; Hellerer, M.; Lehner, H.; Lehner, P.; Porges, O.; Reill, J.; et al. Toward autonomous planetary exploration. J. Intell. Robot. Syst. 2019, 93, 461–494. [Google Scholar] [CrossRef]
- Friston, K.J.; Kiebel, S. Predictive coding under the free-energy principle. Philos. Trans. R. Soc. Lond. B 2009, 364, 1211–1221. [Google Scholar] [CrossRef]
- Clark, A. Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behav. Brain Sci. 2013, 36, 181–204. [Google Scholar] [CrossRef]
- Anderson, J.R.; Bothell, D.; Byrne, M.D.; Douglass, S.; Lebiere, C.; Qin, Y. An integrated theory of the mind. Psych. Rev. 2004, 111, 1036–1060. [Google Scholar] [CrossRef]
- Franklin, S.; Madl, T.; D’Mello, S.; Snaider, J. LIDA: A systems-level architecture for cognition, emotion and learning. IEEE Trans. Auton. Ment. Dev. 2014, 6, 19–41. [Google Scholar] [CrossRef]
- Sun, R. The importance of cognitive architectures: An analysis based on CLARION. J. Expt. Theor. Artif. Intell. 2007, 19, 159–193. [Google Scholar] [CrossRef]
- Moore, E.F. Gedankenexperiments on sequential machines. In Autonoma Studies; Shannon, C.W., McCarthy, J., Eds.; Princeton University Press: Princeton, NJ, USA, 1956; pp. 129–155. [Google Scholar]
- Fields, C. Some consequences of the thermodynamic cost of system identification. Entropy 2018, 20, 797. [Google Scholar] [CrossRef]
- Quine, W.V.O. Word and Object; MIT Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Fields, C.; Marcianò, A. Holographic screens are classical information channels. Quant. Rep. 2020, 2, 326–336. [Google Scholar] [CrossRef]
- Dzhafarov, E.N.; Kon, M. On universality of classical probability with contextually labeled random variables. J. Math. Psychol. 2018, 85, 17–24. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein-Podolsky-Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Mermin, D. Hidden variables and the two theorems of John Bell. Rev. Mod. Phys. 1993, 65, 803–815. [Google Scholar] [CrossRef]
- Aspect, A.; Grangier, P.; Roger, G. Experimental realization of Einstein-Podolsky-Rosen-Bohm gedankenexperiment: A new violation of Bell’s inequalities. Phys. Rev. Lett. 1982, 49, 91–94. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dietrich, E.; Fields, C. Equivalence of the Frame and Halting Problems. Algorithms 2020, 13, 175. https://doi.org/10.3390/a13070175
Dietrich E, Fields C. Equivalence of the Frame and Halting Problems. Algorithms. 2020; 13(7):175. https://doi.org/10.3390/a13070175
Chicago/Turabian StyleDietrich, Eric, and Chris Fields. 2020. "Equivalence of the Frame and Halting Problems" Algorithms 13, no. 7: 175. https://doi.org/10.3390/a13070175
APA StyleDietrich, E., & Fields, C. (2020). Equivalence of the Frame and Halting Problems. Algorithms, 13(7), 175. https://doi.org/10.3390/a13070175




