Embedded Bayesian Network Contribution for a Safe Mission Planning of Autonomous Vehicles
Abstract
1. Introduction
- a simple (friendly) way to generate their BN specifications
- a design methodology to elaborate the efficient BN implementation on parallel FPGA support
- a practical way to incorporate the BN monitors into the decision-making mechanism for the mission management of an autonomous vehicle.
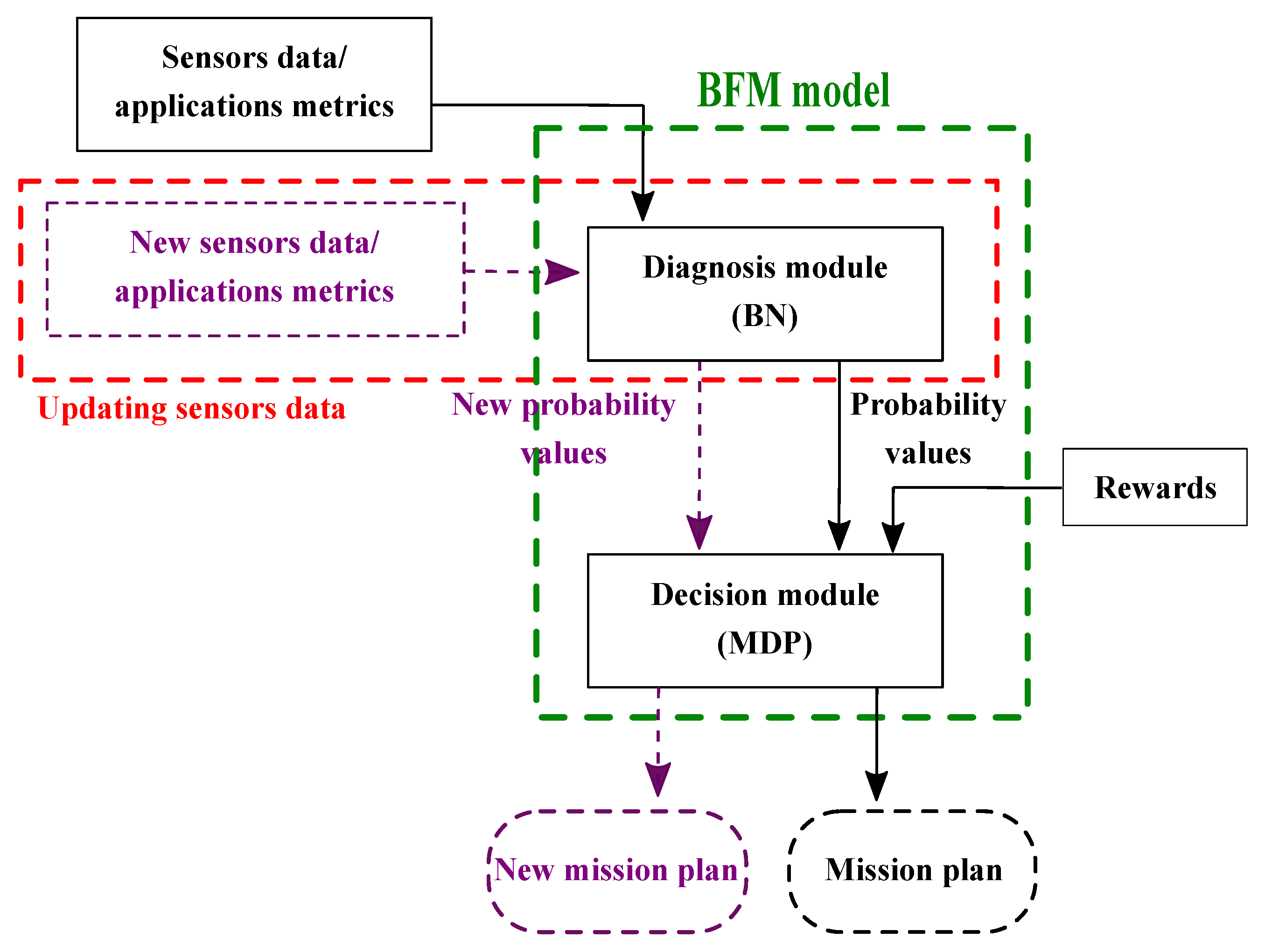
2. BN Model for the Monitoring and the Error Recovery
2.1. Diagnosis with BN
2.2. Error Mitigation with BN
2.3. Integration of the Embedded System Constraints
3. Methodology for an Automatic BN Generation and Its Embedded Implementation
3.1. Pattern Driven Approach
3.1.1. The Pattern
3.1.2. The Pattern
3.1.3. The Pattern
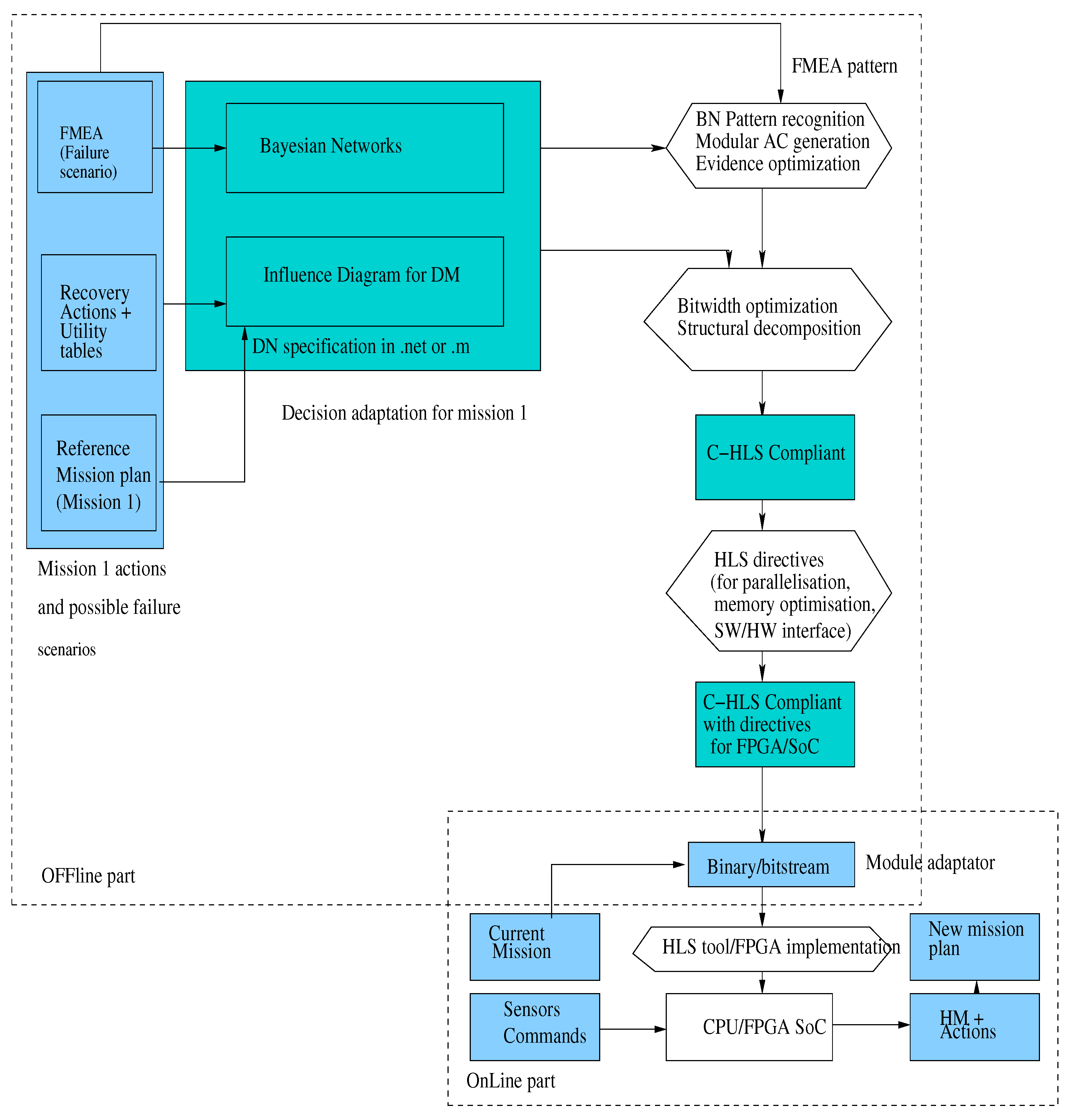
3.2. Design Flow for an Embedded Version of BN Diagnosis
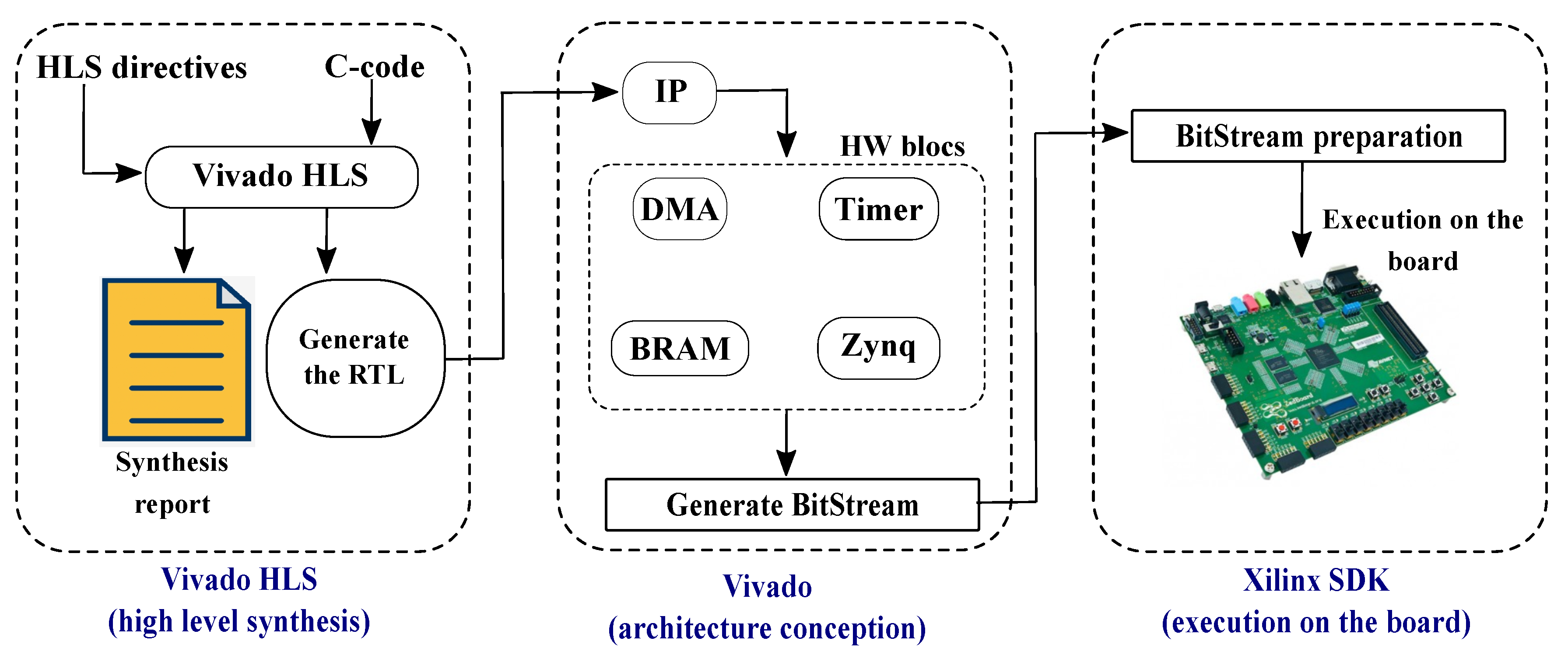
- two kinds of high-level transformations: one dedicated to BN compilation and one more classical related to the structural (or hierarchical) decomposition and to the bitwidth optimization. The first category includes the compilation into an Arithmetic Circuit (AC) form, the evidence optimization. This step provides an C-code (C-HLS Compliant) that can feed HLS tool such as Vivado-HLS from Xilinx.
- HLS directives proposal for the C-code in order to generate efficient implementation onto FPGA (C-HLS Compliant with directives). These directives are proposed to guide the management of the parallelism for the resource usage, the management of the memory and the management of SW/HW interface. These directives are defined in Pragma form using the Vivado-HLS tool [23].
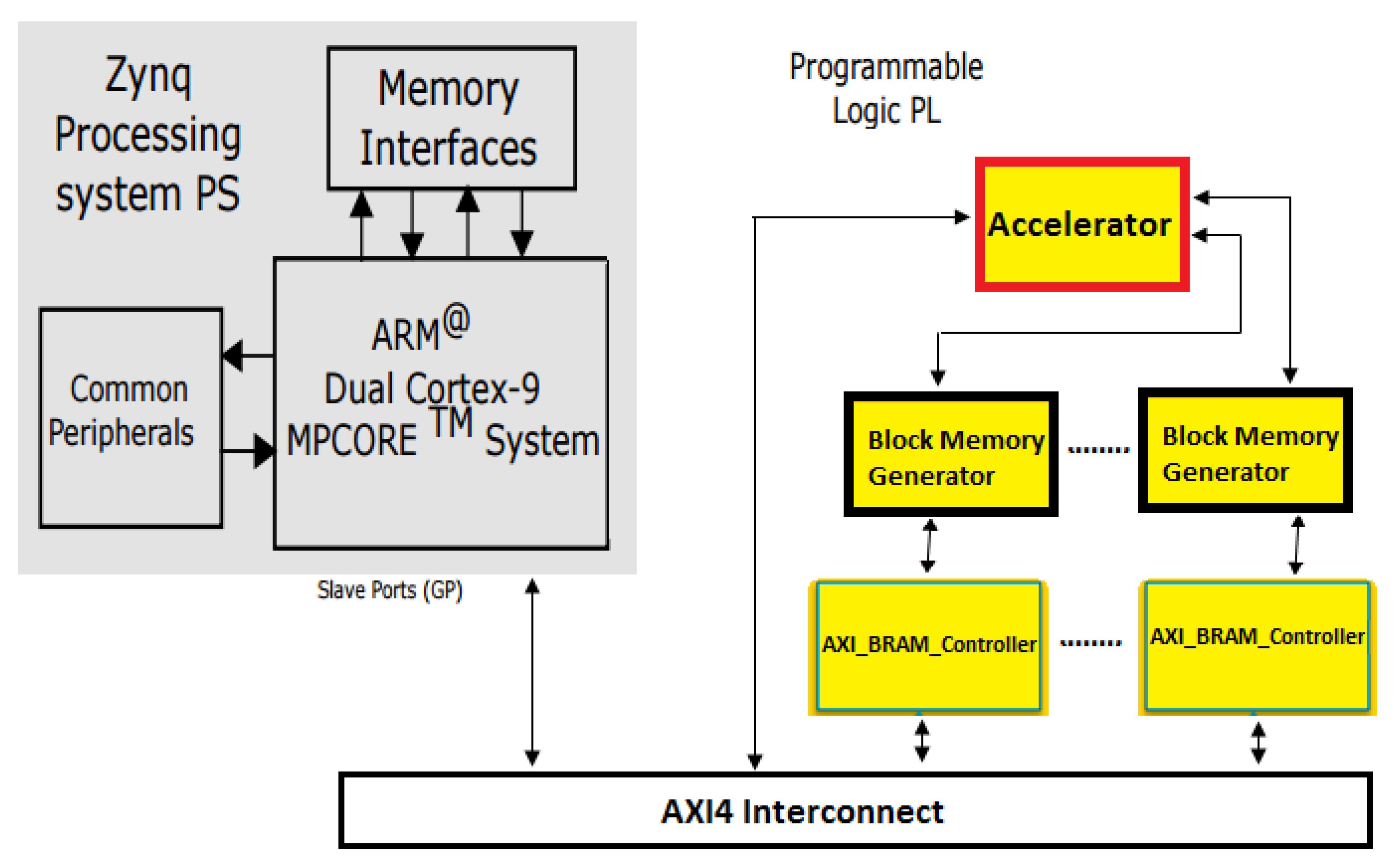
- Integration to HLS tool such as Vivado-HLS whose flow towards a FPGA-SoC board is illustrated in Figure 12. From the implementation on an hybrid FPGA-SoC, different types of interfaces can be used to import the evidence values from the sensors or the parameters of the BN (DMA interface or BRAM interface) via (see Figure 24).
3.3. Dedicated Optimizations for an Efficient Implementation of BN
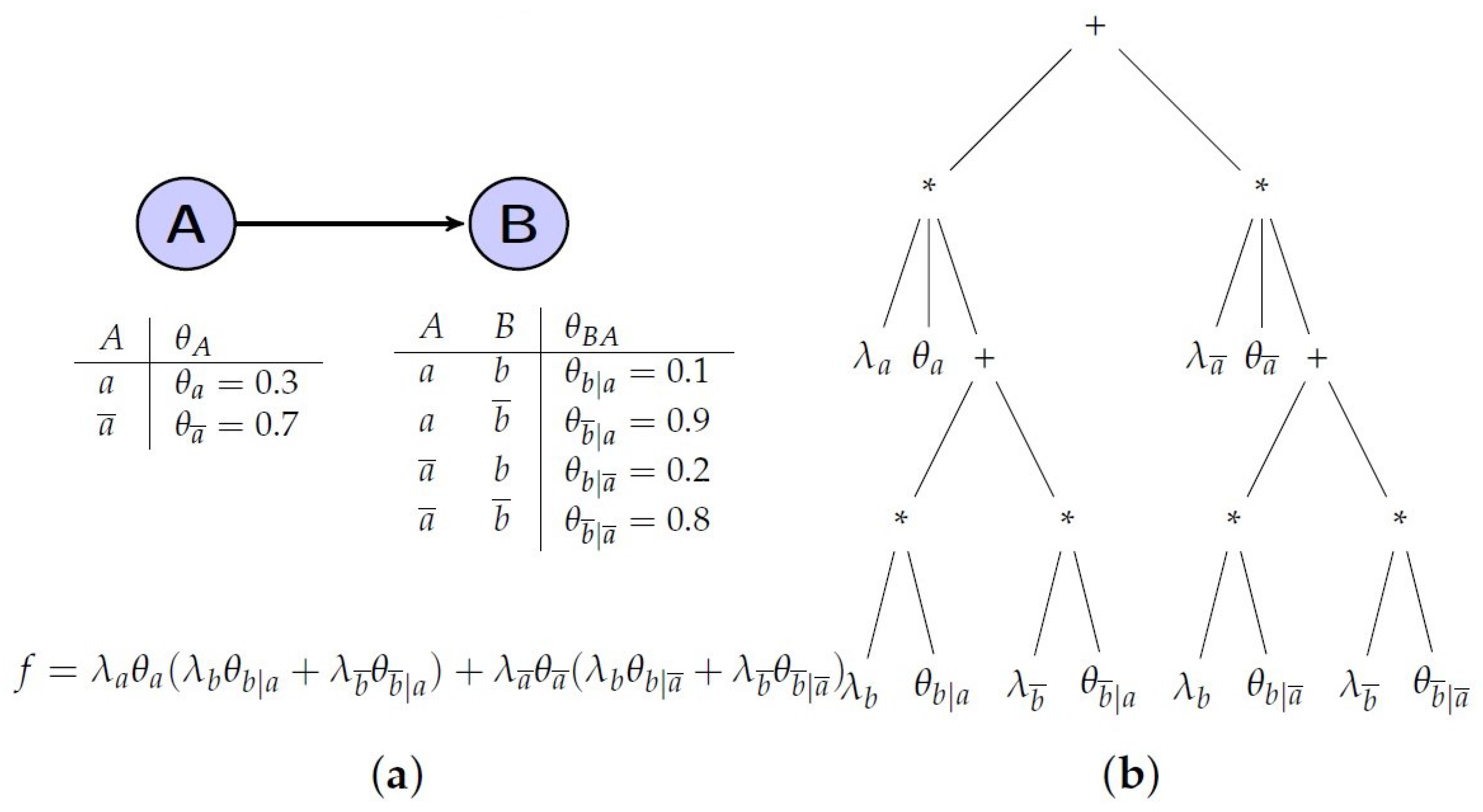
3.3.1. AC Compilation
| Algorithm 1 to C-code |
| Require: Evidence indicators and Network parameters for each s state of the node U do Compute SubAC for all states () end for Multiply all by network parameters of U node related to s (1) for each s state of the U node do Compute SubAC for system monitor () with the new parameters obtained by (1) end for Compute the probability of the system Health node Ensure: Health probability of the system |
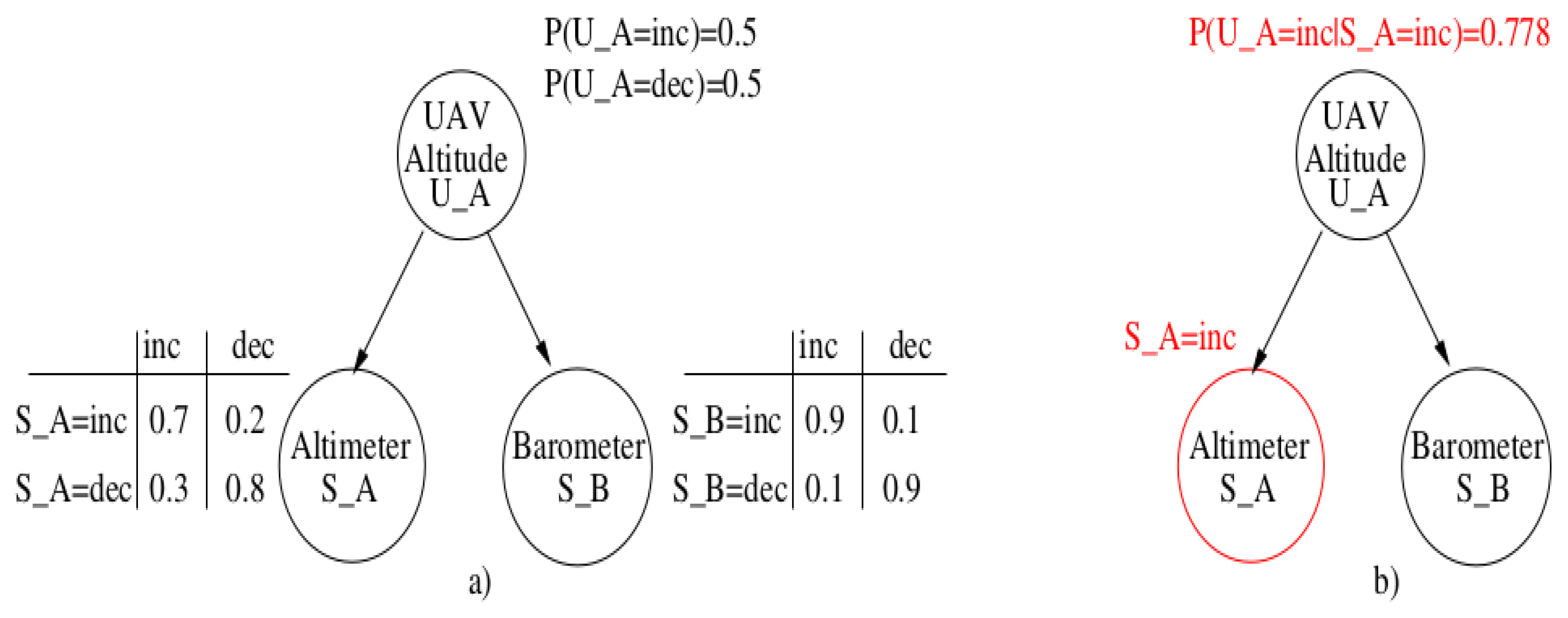
3.3.2. Evidence Optimization
- when there is no observation on the variable X,
- when the evidence is on the variable X and the observation is x,
- when the evidence is on the variable X and the observation is .
- Delete the left (or right) topmost branch containing a C (or an H) node, and in all sub-branches where C (or H) appears, replace the probability parameters by a choice between the right or left value. We can simplify here, because the value of of these nodes is never equal to 1 at the same time,
- Repeat this procedure for all C and H nodes,
- Fix all the values for the unobservable nodes at .
4. Methodology for the BN Integration at the Mission Manager Level
4.1. Decision Networks (DN)
4.1.1. Mission Planning Description with DN
4.1.2. The DN Design Tool for an Embedded Implementation
- In the first layer, a friendly front-end interface to generate the Bayesian Network model from FMEA-like analysis and incorporate to decision process for a DN definition. The DN specifications can be expressed in format or format in order to be compatible with other tools such as Genie [26], BNT [27] tool for Matlab.
- In the second layer, the Bayesian core tool takes a DN as input. First a series of dedicated high-level transformations are proposed for the BN part: AC compilation based on model patterns, evidence optimization. Then optimizations on the whole DN part are proposed such as bitwidth optimization and a functional/structural decomposition based on the choice of the elementary function for a hierarchical decomposition before the generation of the C-code.
- In the second layer, a refinement of C-code is proposed by introduction of HLS directives for code parallelization, memory and interface management. This latter C-HLS compliant code is tailored for a complete FPGA implementation on ZedBoard.
4.2. Markov Decision process (MDP)
- Navigation functionality (BFM navigation): considers all the applications needed to achieve navigation phase. These applications are for example take-off, path planning, obstacle avoidance, etc.
- Safety functionality (BFM safety): consists of a set of application that used for mission and autonomous system safety. These applications are landing, obstacle detection and avoidance, emergency search landing area, etc.
- Application functionality (BFM application): consists of a set of applications using to achieve the mission aim like target detection, tracking, indoor/outdoor mapping, etc.
Example of Mission Planning with BFM Model
- For the BFM-navigation: the MDP of the navigation phase includes 9 states (ex: waypoints states, obstacle detection state, etc.) and 7 actions (example: take-off, obstacle detection, follow trajectory, etc.) which involves 7 transition matrices of size 9 × 9 and a rewards matrix of size 9 × 7.
- For the BFM-landing: the MDP contains 10 states (landing state, found landing area state, etc.) and 6 actions (search landing area, landing, etc.). This gives 6 transition matrices of size 10 × 10 and a rewards matrix of size 10 × 6 generated for the landing phase.
- For the BFM-tracking: the MDP contains 12 states (target detection state, tracking states, etc.) and 10 actions (target detection, tracking, stabilization, etc.). Thus, its gives 10 transitions matrices of 12 × 12 size and a rewards matrix of size 12 × 10.
5. Study Cases
5.1. BN Generation Examples
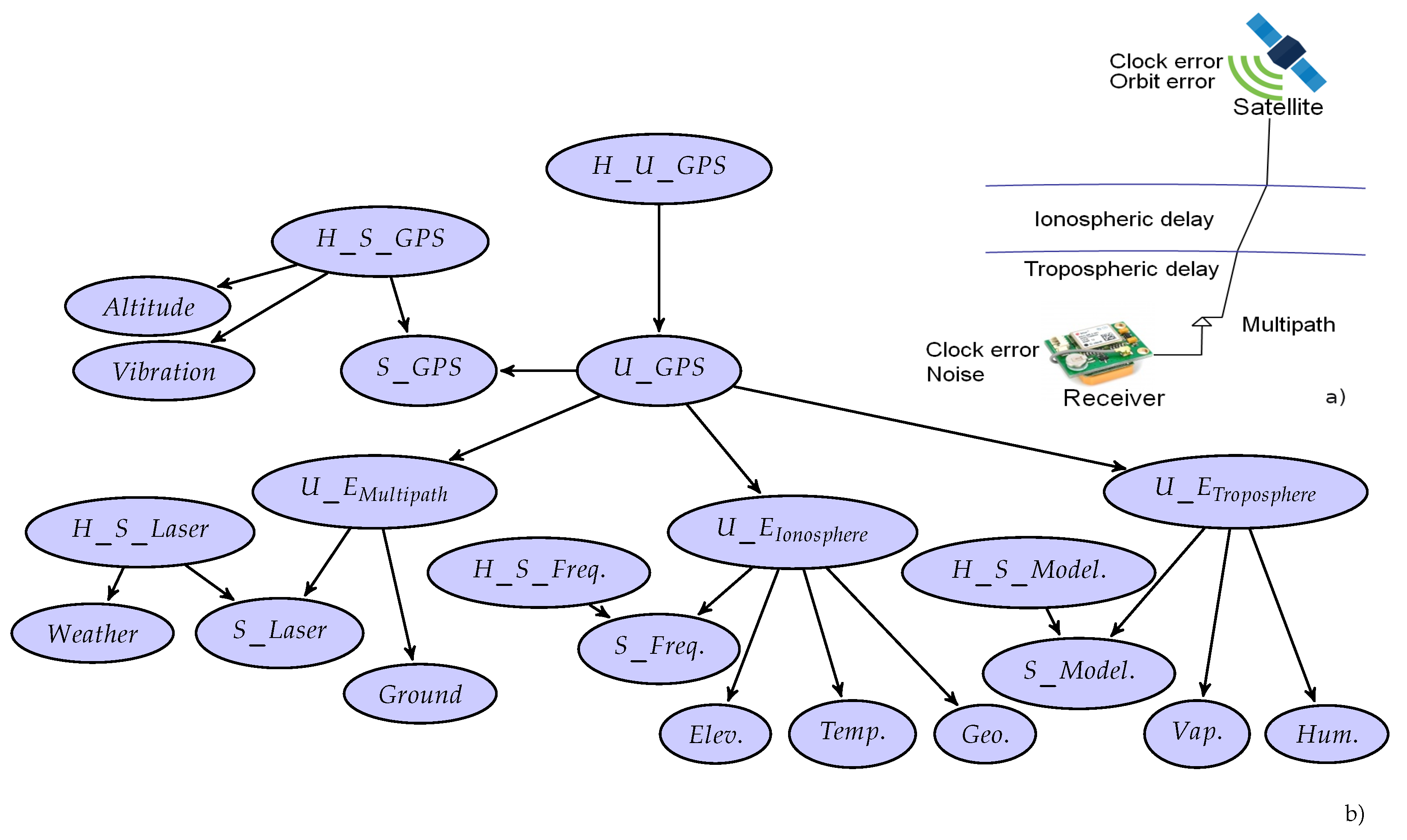
5.1.1. Example 1 Sensors Monitoring: GPS Example
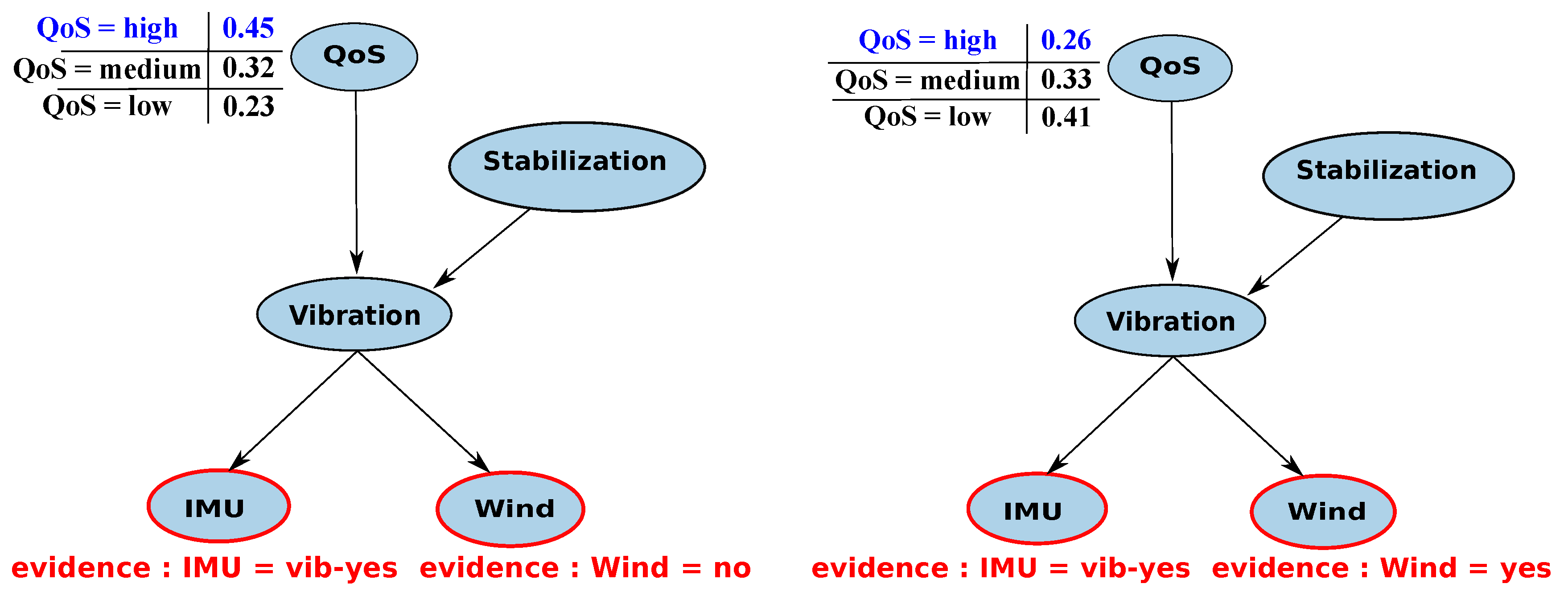
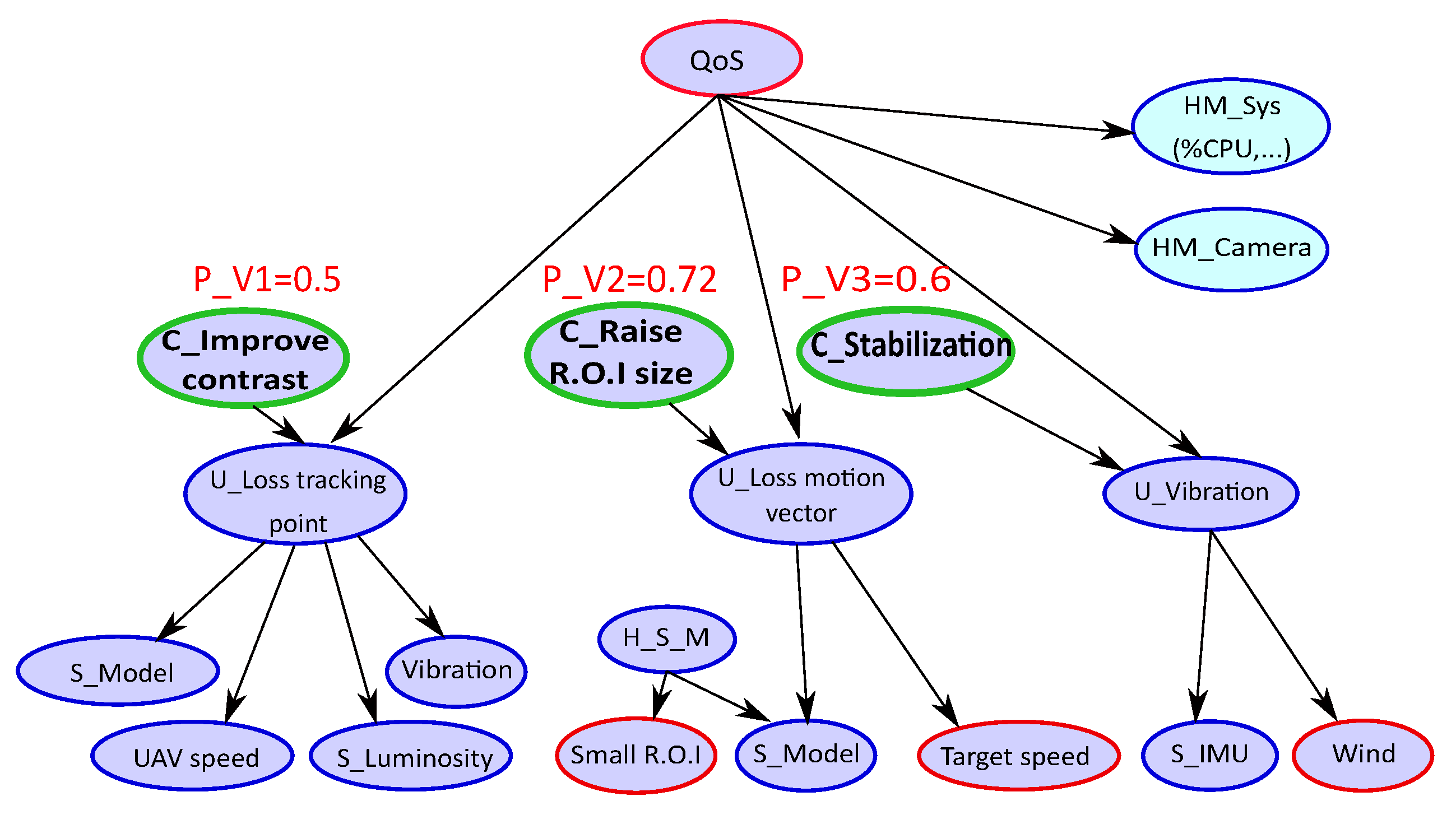
5.1.2. Example 2 Application Monitoring with Mitigation: Tracking Application Example
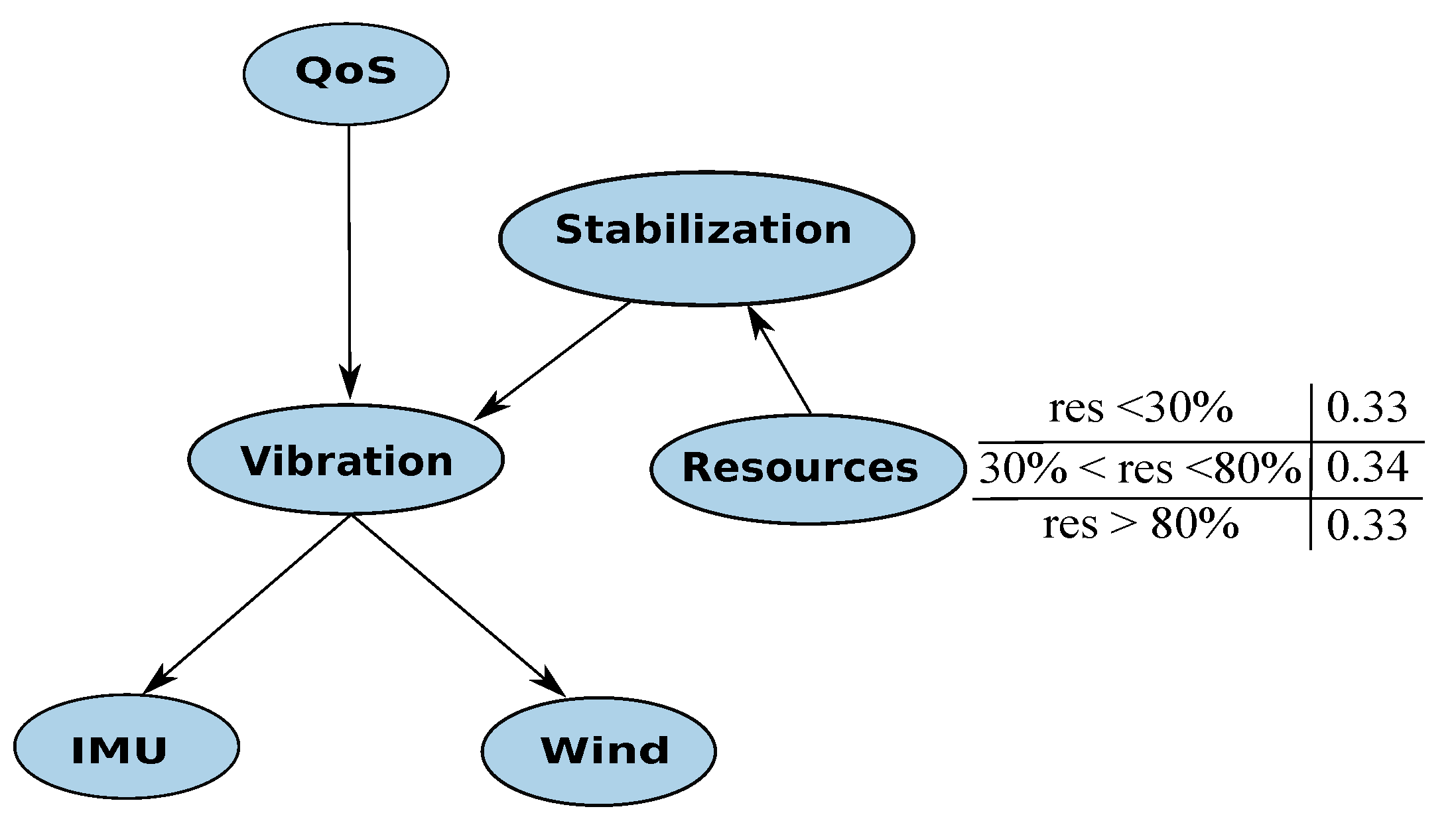
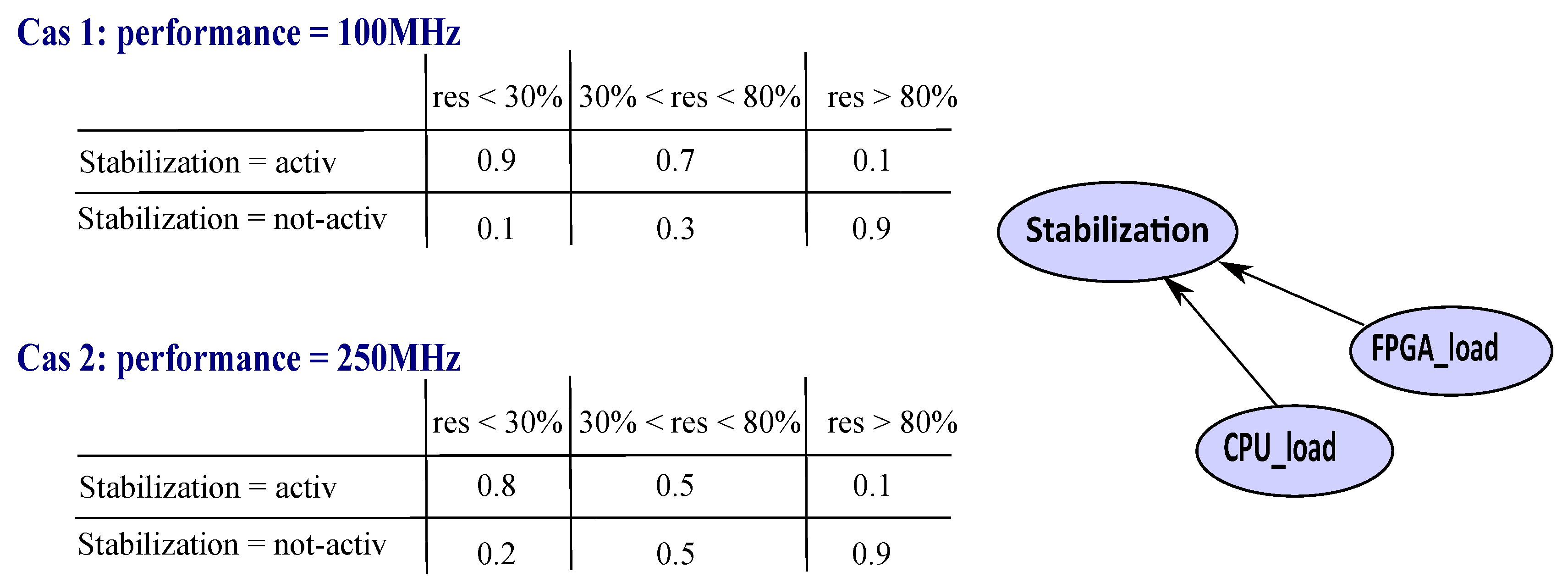
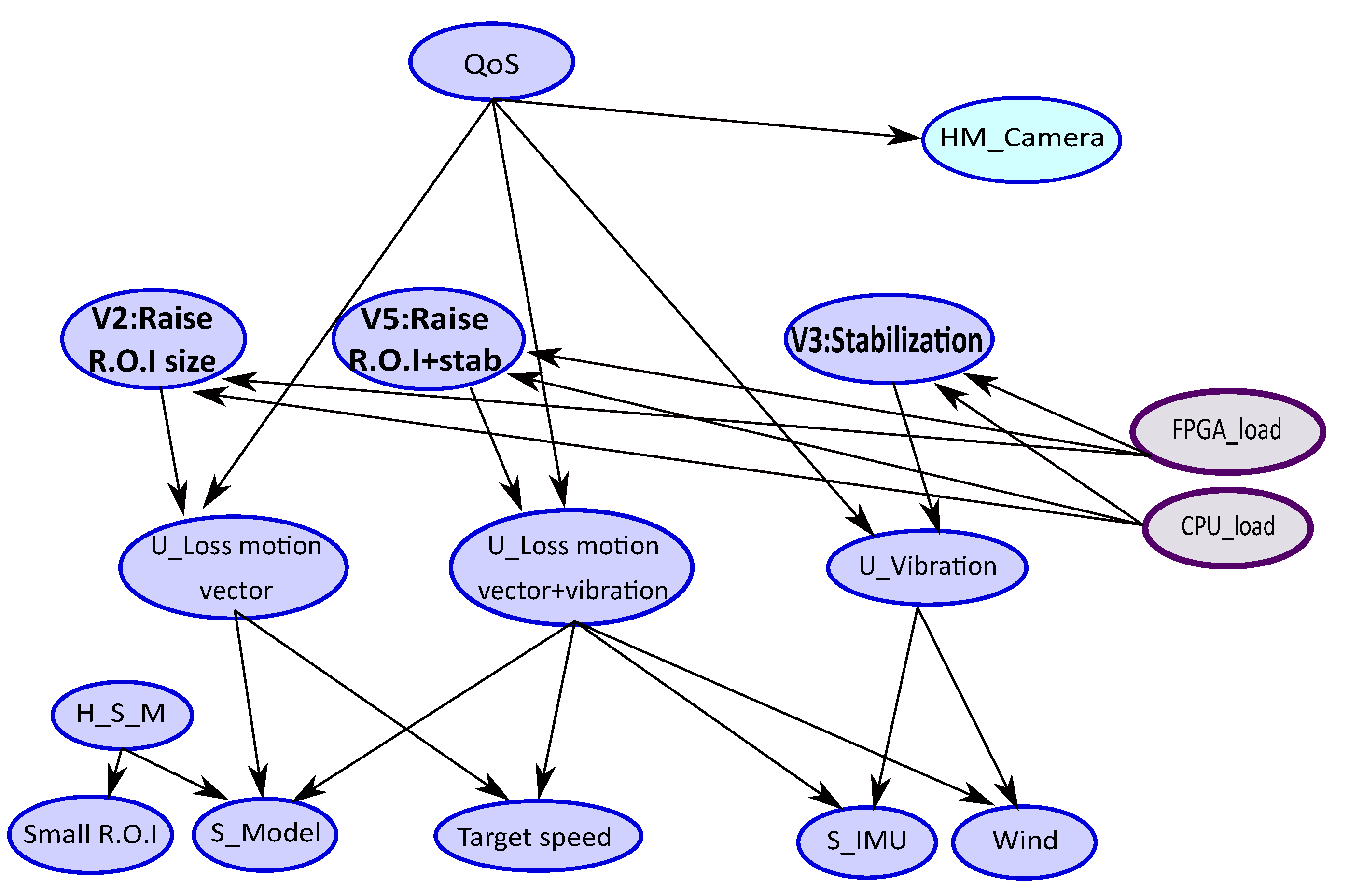
5.1.3. Example 3 Resource-Aware Monitoring for the Tracking Application
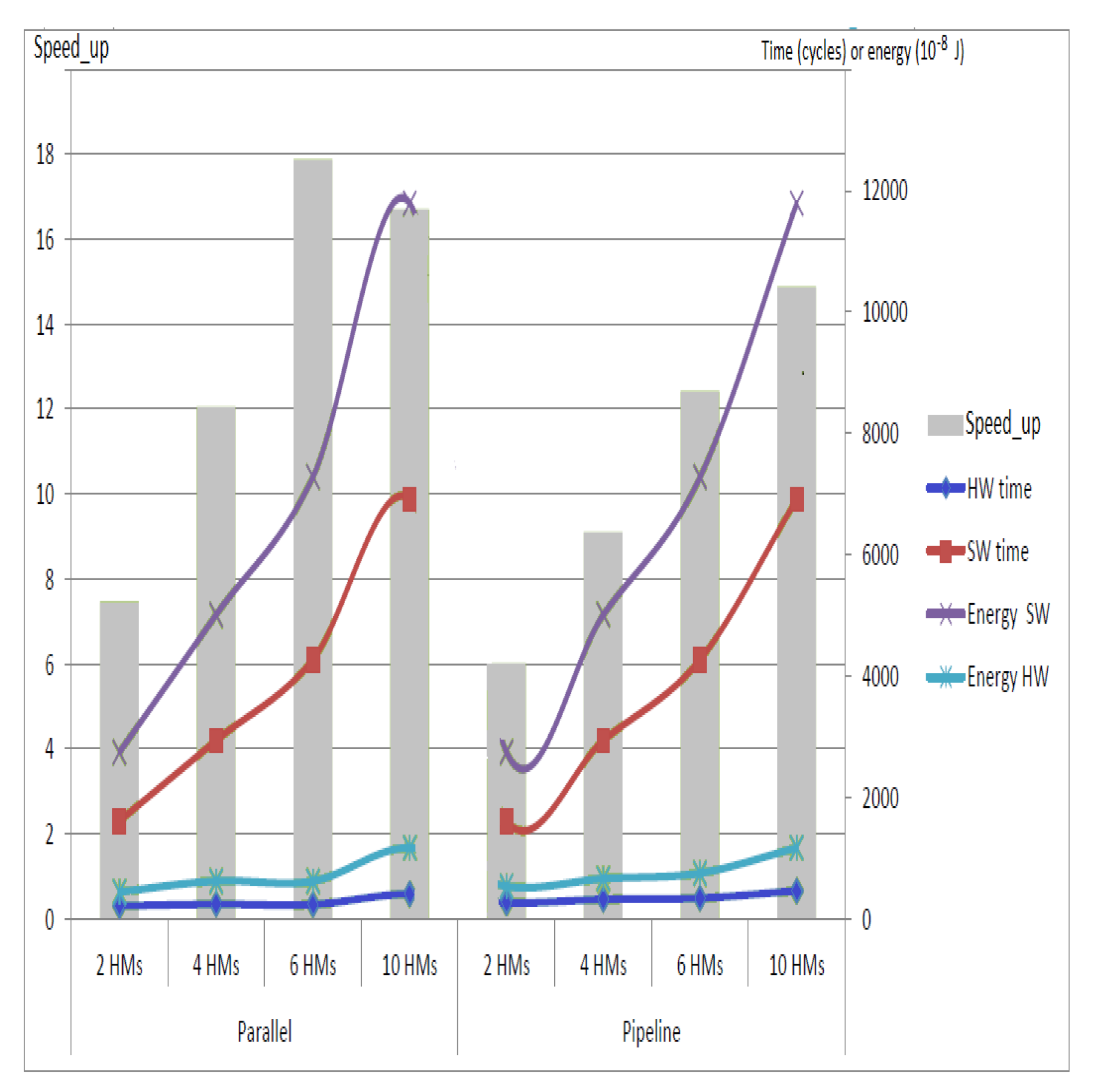
5.2. Experiment on FPGA-SoC Based on FMEA_HM Pattern
5.3. HW Exploration for DN
6. Discussion
6.1. BN Parameter Issue
6.1.1. Description of EM Algorithm
- Step E (expectation): estimate the missing values from the current parameters . For each BN node V and for each sample of the incomplete database, we compute the conditional probability P(|) (Equation (5)). The computation of these probabilities is based on the inference process using generally the junction tree algorithm.where indicates the evidence of the whole measured data and pa() = represent the status of the parent node of . is the conditional probability at time t of and its parent knowing the value of the observation about V and . Finally, N represents the sum of the probabilities of all the instances of node .
- Step M (maximization): re-estimate the parameters from the results obtained from step E by applying the maximum likelihood or the maximum a posteriori approaches. The most used approach is the maximum likelihood. Therefore, the probability at the next time step is equal to the occurrence of divided by the sum of all the occurrences of across the whole database (Equation (5)).
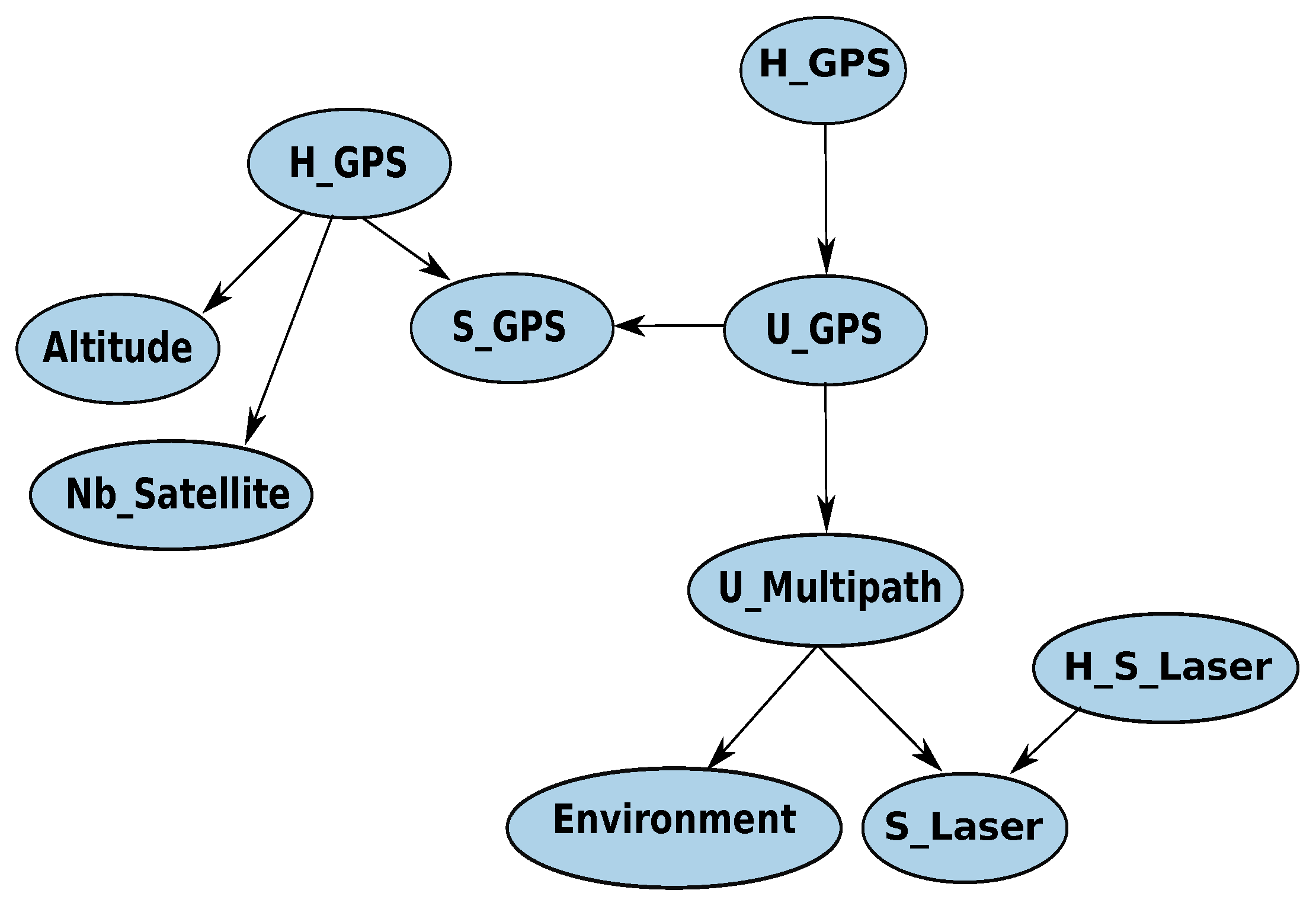
6.1.2. BN Parameter Learning: GPS Case Study
- H_GPS: represents the health of the GPS.
- H_S_GPS: represents the health of the GPS receiver.
- U_GPS: indicates the internal GPS type error node.
- S_GPS: represents the GPS receiver sensor.
- U_Multipath: indicates the multipath type error.
- S_Laser: laser sensor node.
- H_S_Laser: represents the health of of laser sensor.
- Nb_Satellite: indicates the number of the visible satellites.
- Altitude: indicates the altitude.
- Environment: represents the appearance context of multipath error.
- Altitude correspond to ‘altitude’ node.
- Deviation correspond to ‘H_GPS’ node.
- Distance correspond to ‘S_laser’ node.
- Satellite correspond to ‘nb_satellite’ node.
- Accuracy correspond to ‘S_GPS’ node.
6.2. HW/SW Implementation of Decision-Making Mechanism Based on BN
HW Exploration of the MDP Model
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Avizienis, A.; Laprie, J.C.; Randell, B.; Landwehr, C. Basic concepts and taxonomy of dependable and secure computing. IEEE Trans. Dependable Secur. Comput. 2004, 1, 11–33. [Google Scholar] [CrossRef]
- Marzat, J.; Piet-Lahanier, H.; Damongeot, F.; Walter, E. Model-based fault diagnosis for aerospace systems: A survey. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 226, 1329–1360. [Google Scholar] [CrossRef]
- Wander, A.; Förstner, R. Innovative Fault Detection, Isolation and Recovery Strategies on-Board Spacecraft: State of the Art and Research Challenges; Deutsche Gesellschaft für Luft-und Raumfahrt-Lilienthal-Oberth eV: Bonn, Germany, 2013. [Google Scholar]
- Khakzad, N.; Khan, F.; Amyotte, P. Dynamic risk analysis using bow-tie approach. Reliab. Eng. Syst. Saf. 2012, 104, 36–44. [Google Scholar] [CrossRef]
- Khakzad, N.; Khan, F.; Amyotte, P. Safety analysis in process facilities: Comparison of fault tree and Bayesian network approaches. Reliab. Eng. Syst. Saf. 2011, 96, 925–932. [Google Scholar] [CrossRef]
- Bobbio, A.; Portinale, L.; Minichino, M.; Ciancamerla, E. Improving the analysis of dependable systems by mapping fault trees into Bayesian networks. Reliab. Eng. Syst. Saf. 2001, 71, 249–260. [Google Scholar] [CrossRef]
- Schumann, J.M.; Rozier, K.Y.; Reinbacher, T.; Mengshoel, O.J.; Mbaya, T.; Ippolito, C. Towards real-time, on-board, hardware-supported sensor and software health management for unmanned aerial systems. Int. J. Progn. Health Manag. 2015, 6, 021. [Google Scholar]
- Portinale, L.; Codetta-Raiteri, D. Arpha: An Fdir Architecture for Autonomous Spacecrafts Based On Dynamic Probabilistic Graphical Models. In Proceedings of the IJCAI workshop on AI on Space, Barcelona, Spain, 16–22 July 2011. [Google Scholar]
- Codetta-Raiteri, D.; Portinale, L. Dynamic Bayesian networks for fault detection, identification, and recovery in autonomous spacecraft. Syst. Man Cybern. Syst. IEEE Trans. 2015, 45, 13–24. [Google Scholar] [CrossRef]
- Schumann, J.; Moosbrugger, P.; Rozier, K.Y. R2U2: Monitoring and Diagnosis of Security Threats for Unmanned Aerial Systems; Springer: Cham, Switzerland, 2015; pp. 233–249. [Google Scholar]
- Muniraj, D.; Farhood, M. A framework for detection of sensor attacks on small unmanned aircraft systems. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1189–1198. [Google Scholar]
- Daly, R.; Shen, Q.; Aitken, S. Learning Bayesian networks: Approaches and issues. Knowl. Eng. Rev. 2011, 26, 99–157. [Google Scholar] [CrossRef]
- Grossman, D.; Domingos, P. Learning Bayesian Network Classifiers by Maximizing Conditional Likelihood. In Proceedings of the Twenty-first International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; p. 46. [Google Scholar] [CrossRef]
- Friedman, N. The Bayesian Structural EM Algorithm. In Proceedings of the Fourteenth Conference on Uncertainty in Artificial Intelligence, Madison, WI, USA, 24–26 July 1998; pp. 129–138. [Google Scholar]
- Chenini, H.; Heller, D.; Dezan, C.; Diguet, J.P.; Campbell, D. Embedded real-time localization of UAV based on an hybrid device. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 1543–1547. [Google Scholar]
- Schumann, J.; Mengshoel, O.; Mbaya, T. Integrated Software and Sensor Health Management for Small Spacecraft. In Proceedings of the 2011 IEEE Fourth International Conference on Space Mission Challenges for Information Technology, Pasadena, CA, USA, 19–23 August 2011; pp. 77–84. [Google Scholar] [CrossRef]
- Geist, J.; Rozier, K.Y.; Schumann, J. Runtime Observer Pairs and Bayesian Network Reasoners On-board FPGAs: Flight-Certifiable System Health Management for Embedded Systems. In Proceedings of the Runtime Verification—5th International Conference, RV 2014, Toronto, ON, Canada, 22–25 September 2014; pp. 215–230. [Google Scholar] [CrossRef]
- Darwiche, A. A differential approach to inference in Bayesian networks. J. ACM 2003, 50, 280–305. [Google Scholar] [CrossRef]
- Cowell, R.G. Probabilistic Networks and Expert Systems: Exact Computational Methods for Bayesian Networks; Springer Science & Business: Medford, MA, USA, 2006. [Google Scholar]
- Zermani, S.; Dezan, C.; Hireche, C.; Euler, R.; Diguet, J.P. Embedded context aware diagnosis for a UAV SoC platform. Microprocess. Microsyst. 2017, 51, 185–197. [Google Scholar] [CrossRef]
- Zermani, S.; Dezan, C.; Diguet, J.; Euler, R. Bayesian Network-Based Framework for the design of Reconfigurable Health Management Monitors. In Proceedings of the NASA/ESA Conference on Adaptive Hardware and systems (AHS-15), Zhangjiajie, China, 18–20 November 2015. [Google Scholar]
- Zermani, S.; Dezan, C.; Chenini, H.; Diguet, J.; Euler, R. FPGA implementation of Bayesian network inference for an embedded diagnosis. In Proceedings of the 2015 IEEE Conference on Prognostics and Health Management (PHM), Austin, TX, USA, 22–25 June 2015; pp. 1–10. [Google Scholar]
- Xilinx. Available online: https://www.xilinx.com/support/documentation/sw_manuals/ug998-vivado-intro-fpga-design-hls.pdf. (accessed on 30 April 2020).
- Chavira, M.; Darwiche, A. Compiling Bayesian Networks with Local Structure. Available online: https://www.ijcai.org/Proceedings/05/Papers/0931.pdf (accessed on 30 April 2020).
- Tipaldi, M.; Glielmo, L. A survey on model-based mission planning and execution for autonomous spacecraft. IEEE Syst. J. 2017, 12, 3893–3905. [Google Scholar] [CrossRef]
- Druzdzel, M.J. SMILE: Structural Modeling, Inference, and Learning Engine and GeNIe: A Development Environment for Graphical Decision-Theoretic Models. Available online: https://www.aaai.org/Papers/AAAI/1999/AAAI99-129.pdf (accessed on 30 April 2020).
- Murphy, K. The Bayes Net Toolbox for MATLAB. Comput. Sci. Stat. 2001, 33, 2001. [Google Scholar]
- Kolobov, A. Planning with Markov decision processes: An AI perspective. Synth. Lect. Artif. Intell. Mach. Learn. 2012, 6, 1–210. [Google Scholar]
- Hireche, C.; Dezan, C.; Diguet, J.P.; Mejias, L. BFM: A Scalable and Resource-Aware Method for Adaptive Mission Planning of UAVs. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 6702–6707. [Google Scholar]
- Hireche, C.; Dezan, C.; Mocanu, S.; Heller, D.; Diguet, J.P. Context/Resource-Aware Mission Planning Based on BNs and Concurrent MDPs for Autonomous UAVs. Sensors 2018, 18, 4266. [Google Scholar] [CrossRef] [PubMed]
- Zermani, S.; Dezan, C.; Hireche, C.; Euler, R.; Diguet, J.P. Embedded and probabilistic health management for the GPS of autonomous vehicles. In Proceedings of the 2016 5th Mediterranean Conference on Embedded Computing (MECO), Bar, Montenegro, 12–16 June 2016. [Google Scholar]
- Langley, R.B. The GPS error budget. GPS World 1997, 8, 51–56. [Google Scholar]
- Salós, D.; Macabiau, C.; Martineau, A.; Bonhoure, B.; Kubrak, D. Nominal GNSS pseudorange measurement model for vehicular urban applications. In Proceedings of the Position Location and Navigation Symposium (PLANS), 2010 IEEE/ION, Indian Wells, CA, USA, 4–6 May 2010; pp. 806–815. [Google Scholar]
- Dovis, F.; Muhammad, B.; Cianca, E.; Ali, K. A Run-Time Method Based on Observable Data for the Quality Assessment of GNSS Positioning Solutions. Sel. Areas Commun. IEEE J. 2015, 33, 2357–2365. [Google Scholar] [CrossRef]
- Drevelle, V.; Bonnifait, P. Reliable positioning domain computation for urban navigation. Intell. Transp. Syst. Mag. IEEE 2013, 5, 21–29. [Google Scholar] [CrossRef]
- Kalal, Z.; Mikolajczyk, K.; Matas, J. Tracking-Learning-Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1409–1422. [Google Scholar] [CrossRef] [PubMed]
- ZedBoard. Available online: http://zedboard.org/product/zedboard. (accessed on 30 April 2020).
- Tembo, S.R.; Vaton, S.; Courant, J.L.; Gosselin, S. A tutorial on the EM algorithm for Bayesian networks: Application to self-diagnosis of GPON-FTTH networks. In Proceedings of the 2016 International Wireless Communications and Mobile Computing Conference (IWCMC), Paphos, Cyprus, 5–9 September 2016; pp. 369–376. [Google Scholar]
- Hireche, C.; Dezan, C.; Diguet, J.P. Online diagnosis updates for embedded health management. In Proceedings of the 2017 6th Mediterranean Conference on Embedded Computing (MECO), Bar, Montenegro, 11–15 June 2017; pp. 1–5. [Google Scholar]
- Lauritzen, S.L. The EM algorithm for graphical association models with missing data. Comput. Stat. Data Anal. 1995, 19, 191–201. [Google Scholar] [CrossRef]




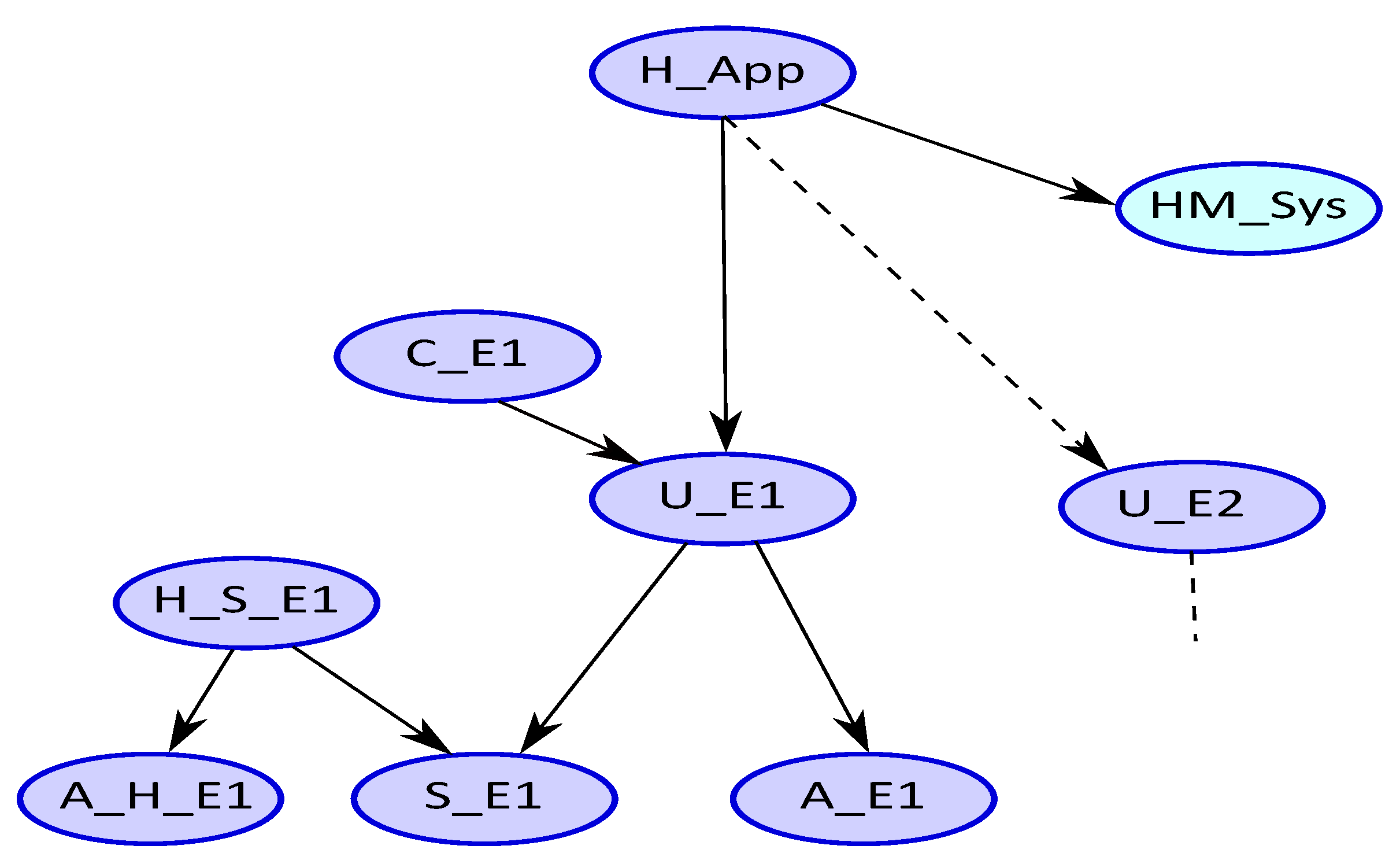
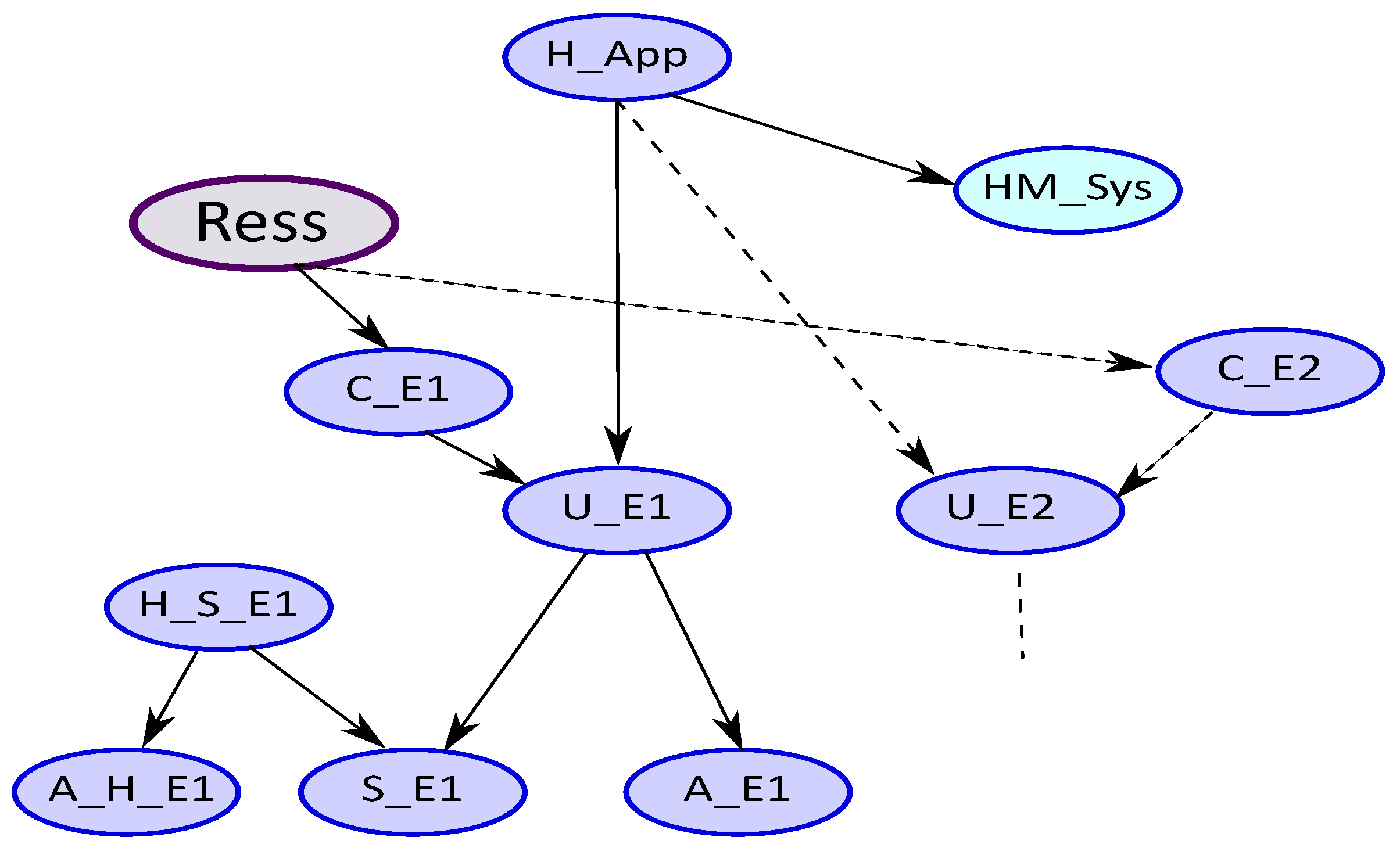






| Error Type | Monitoring | Appearance Contexts (Error Type) | Appearance Contexts (Monitoring) |
|---|---|---|---|
| Error Type | Monitoring | Appearance Contexts | Mitigation |
|---|---|---|---|
| U_Ei | S_Ei | A_Ei | C_Ei |
| Error Type | Monitoring | Appearance Contexts | Mitigation | Resources | Performance |
|---|---|---|---|---|---|
| U_Ei | S_Ei | A_Ei | C_Ei | Ress_min | Perf_min, Perf_max |
| UAV | inc | dec | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alt. | ||||||||||||
| () | ||||||||||||
| Battery | ok | bad | ok | bad | ||||||||
| () | ||||||||||||
| Actions | SU | SD | EL | SU | SD | EL | SU | SD | EL | SU | SD | EL |
| (A) | ||||||||||||
| U | 100 | 0 | 0 | 0 | 0 | 100 | 0 | 100 | 0 | 0 | 0 | 100 |
| Error Types | Monitoring | Appearance Context (Error Types or Monitor) |
|---|---|---|
| Ionosphere | Dual frequency measurement | - Low elevation satellites - Solar storm - Proximity to geomagnetic equator/poles |
| Troposphere | Model based on: - temperature - relative humidity - satellite elevation angle | - Dryness - Vapor |
| Multipath | Obstacle detection (laser sensor, software) | - Urban terrain - Weather (laser monitor) |
| Receiver (internal monitor) | Comparison with the calculated position | - High altitude - Vibration |
| Errors | Possible Monitoring | Appearances Context | Solution (Algorithms) |
|---|---|---|---|
| Vibration | IMU (Inertial Measurement Unit) Vibration sensor | Wind Vibration | Activate the stabilization |
| Tracking point lost | Model based on: number of features detected (Harris) [36] | Drone speed variations of luminosity | Improve the contrast |
| Motion vector lost | Model based on: motion vector between 2 images [36] | Target speed Small R.O.I (Region Of Interest) | Raise the R.O.I size |
| Resource | Latency | Speed-Up | Conso. | ||||||
|---|---|---|---|---|---|---|---|---|---|
| BRAM | DSP | LUT | FF | (cycles) | (J) | ||||
| 2 Bayesian networks (54 nodes) | 2 Actions | All in HW | 14% | 14% | 23% | 12% | 310 | 5.96 | 6.33 |
| Mixed | 14% | 6% | 20% | 11% | 528 | 3.50 | 10.50 | ||
| 10 Actions | All in HW | 14% | 24% | 32% | 16% | 355 | 7.33 | 7.56 | |
| Mixed | 14% | 6% | 20% | 11% | 1328 | 1.96 | 26.42 | ||
| 10 Bayesian networks (270 nodes) | 2 Actions | All in HW | 61% | 41% | 78% | 34% | 6001 | 11.12 | 170.42 |
| Mixed | 60% | 6% | 44% | 24% | 60,370 | 1.10 | 1521.32 | ||
| 10 Actions | All in HW | 80% | 60% | 80% | 40% | 11025 | 21.3 | 330.84 | |
| Mixed | 60% | 6% | 44% | 23% | 232,475 | 1.02 | 5835.12 |
| Collected Data | Corresponding BN Node Status |
|---|---|
| Deviation > 3 m | H_GPS = not_ok |
| Distance > 10 | S_laser = not_ok |
| Accuracy > 3 | S_GPS = not_ok |
| Altitude > 40 m | Altitude = high |
| Nb_satellite > 4 | Nb_satellite = sup4 |
| MDP-Navigation | MDP-Landing | MDP-Tracking | |
|---|---|---|---|
| Speed up | 2.86 | 1.22 | 1.14 |
| Execution time (SW clock frequency 1 GHz) | 2.7 ms | 3.1 ms | 8.6 ms |
| Execution time (HW clock frequency 100 MHz) | 0.9 ms | 2.6 ms | 7.6 ms |
| MDP-Navigation | MDP-Landing | MDP-Tracking | |
|---|---|---|---|
| BRAM | |||
| DSP | |||
| FF | |||
| LUT |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dezan, C.; Zermani, S.; Hireche, C. Embedded Bayesian Network Contribution for a Safe Mission Planning of Autonomous Vehicles. Algorithms 2020, 13, 155. https://doi.org/10.3390/a13070155
Dezan C, Zermani S, Hireche C. Embedded Bayesian Network Contribution for a Safe Mission Planning of Autonomous Vehicles. Algorithms. 2020; 13(7):155. https://doi.org/10.3390/a13070155
Chicago/Turabian StyleDezan, Catherine, Sara Zermani, and Chabha Hireche. 2020. "Embedded Bayesian Network Contribution for a Safe Mission Planning of Autonomous Vehicles" Algorithms 13, no. 7: 155. https://doi.org/10.3390/a13070155
APA StyleDezan, C., Zermani, S., & Hireche, C. (2020). Embedded Bayesian Network Contribution for a Safe Mission Planning of Autonomous Vehicles. Algorithms, 13(7), 155. https://doi.org/10.3390/a13070155





