4.1. Augmented Graph
4.1.1. Graph Model
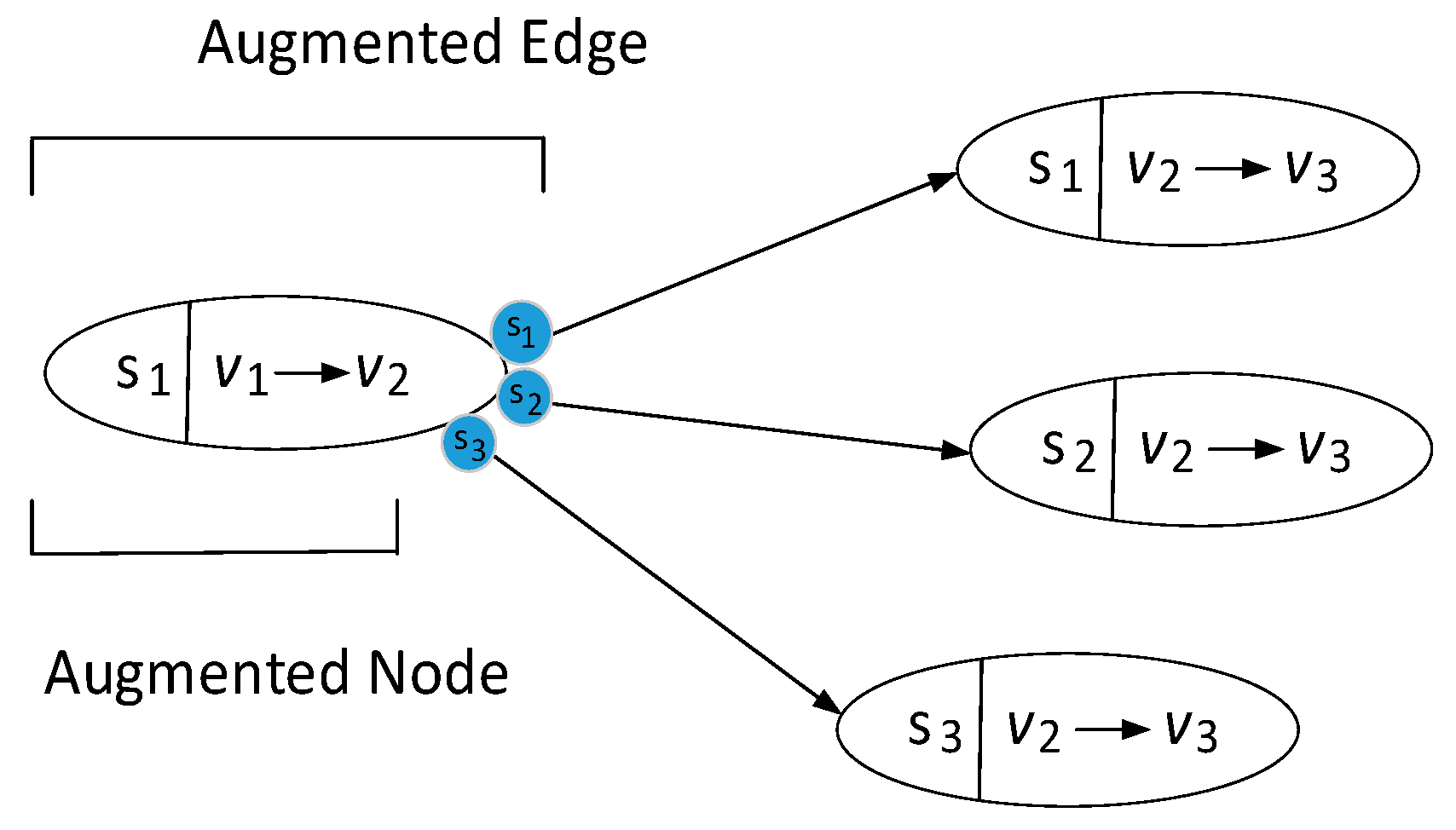
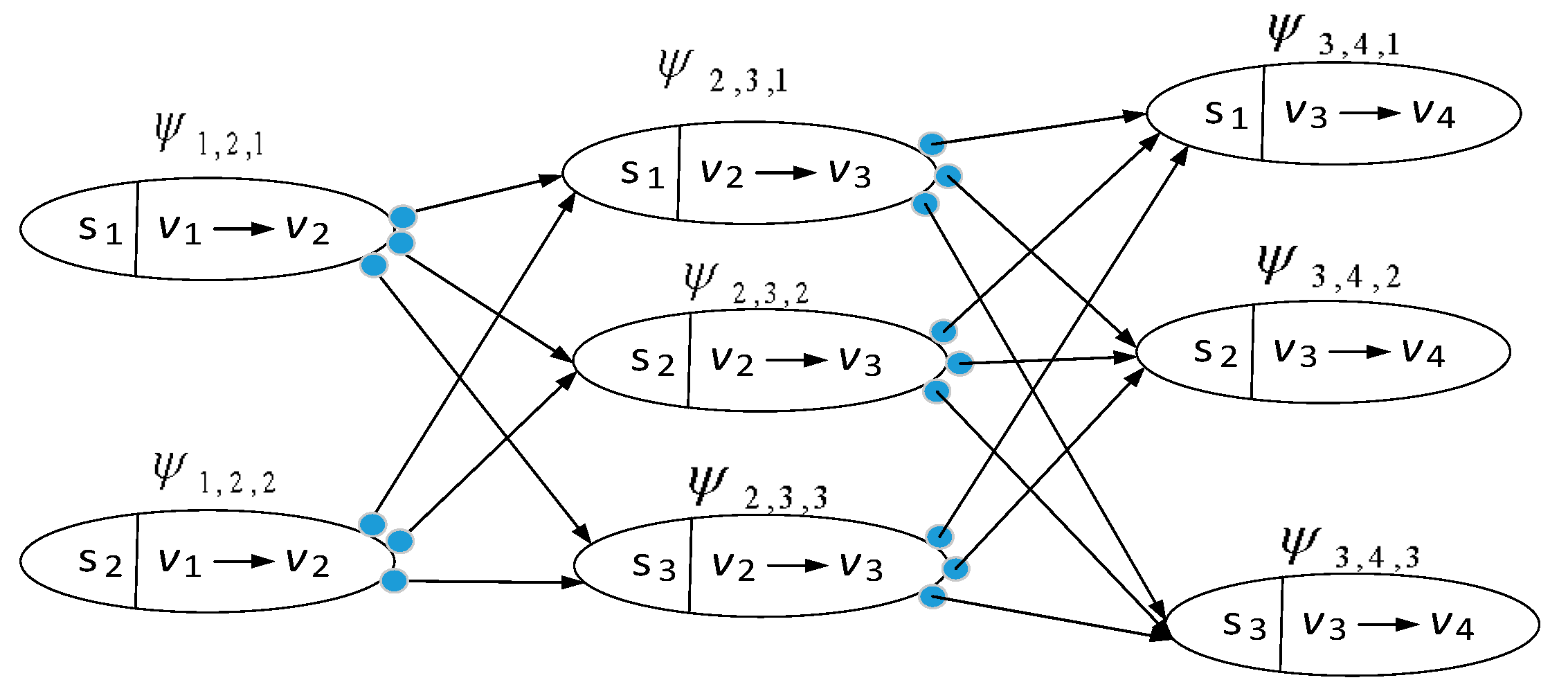
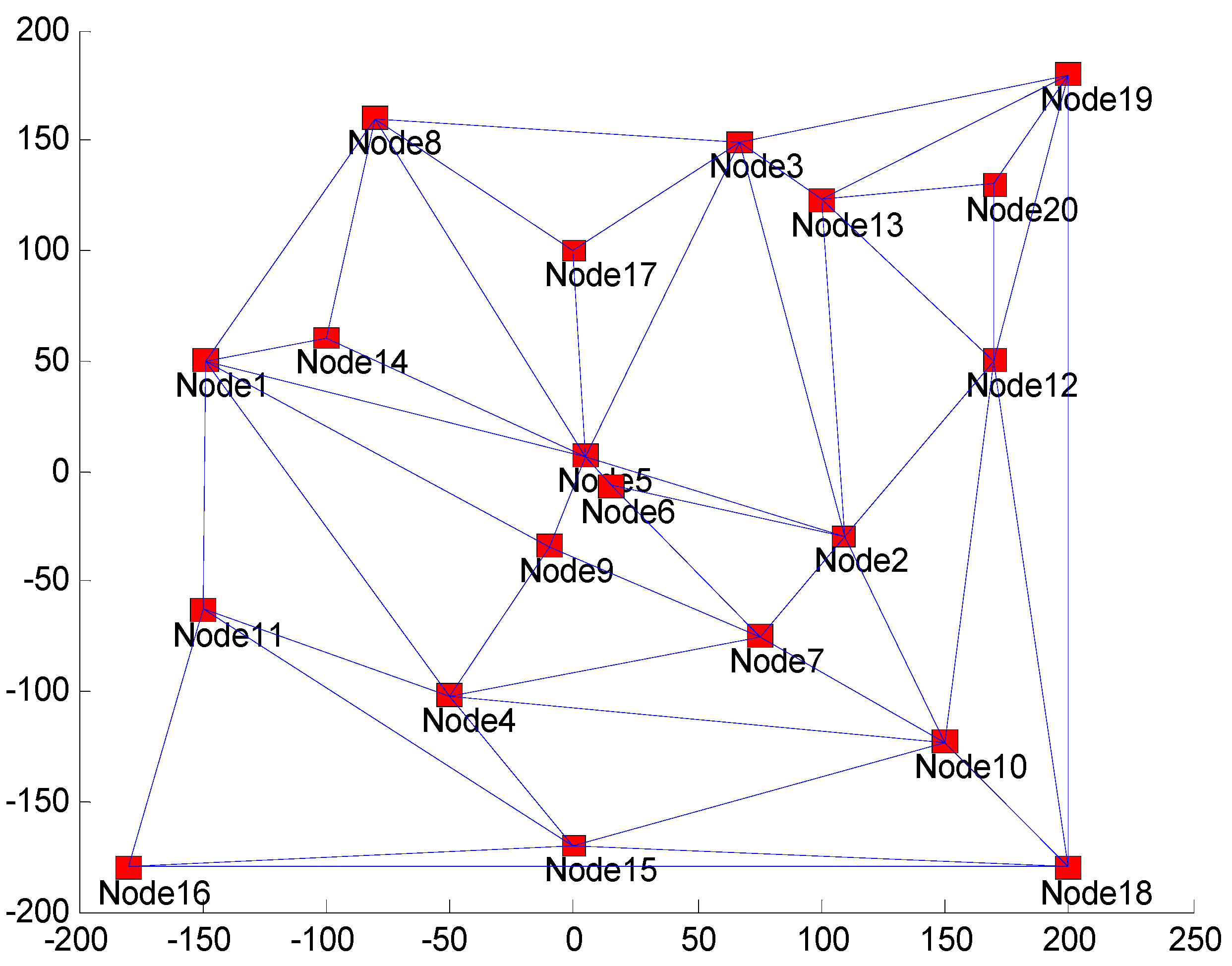
Solving the problem described in (1) is difficult by using typical graph , since there is no information about the arrival time of each vehicle at each node. Consequently, the inter-vehicle collision problem is unable to solve. To address such a problem, instead of using typical graph , we developed a novel structure of the graph, which is called an augmented graph, denoted by . The augmented node can be constructed from the typical graph . Let be an augmented graph, where , as long as , and }, is defined as a set of augmented nodes and , where is augmented edge, i.e., start and end connected sub-trajectories pairs and . Note that the notation implies that must be a successor of . Therefore, it is required that .
Figure 1 visualizes the proposed
,
, and
.
expands the typical
from the node-to-node relation into transition-to-transition relation. In the typical graph
, the edges are weighted by node-to-node distance
while in the augmented graph
, the augmented edges are weighted by acceleration, whose formulation is conducted using start and final speeds the node-to-node distance (see Equation (5)).
Figure 2 shows that, for a node-to-node trajectory, there are some speed alternatives to apply. Therefore, the augmented edge between any pair of augmented nodes can represent information of acceleration and traveling time, for instance, the transition from
to
. The applied initial and target speeds at the endpoint of
are
and
, respectively. Therefore, the uniform acceleration
along the augmented edge is formulated as following:
where
is the length of the edge
, and it is plotted to the transition from
to
.
Furthermore, the traveling time,
, related to the acceleration in Equation (2) is formulated as follows:
4.1.2. Additional Adjacency Matrix
We introduced some supporting matrices to support the proposed algorithm. First of all, we introduced
edge matrix, denoted as
, whose dimension is the same with the adjacency matrix
. Let
, where
q is the identifier of an edge whose value can be determined by Algorithm 1, be defined as the edge identifier of each element of
, i.e.,
that has the value of 1. Therefore, we get the following:
where
.
| Algorithm 1 Determine the index of edge matrix |
| 1: Input: B |
| 2: ; |
| 3: For to |
| 4: For to |
| 5: If and , then q = q +1 and . |
| 6: End |
| 7: End |
| 8: Output: all . |
For instance, suppose that we have the following adjacency matrix of a graph
whose number of nodes is 5, as follows.
Therefore, by using (4), we have the following:
.
Furthermore, we use the index of
, i.e.,
as the index of row of another adjacency matrix named
trajectory adjacency matrix, denoted as
. Each row and each column of this matrix represent edge
and speed
, respectively. Let
be the element of
, where we have the following:
and
are defined in (4). Suppose that we apply three-speed options; therefore,
. From the adjacency matrix example in Equation (5) and its respective edge matrix in (6), we have the elements of
as follows: For edge
, we have three trajectories, i.e.,
,
, and
. Since from Equations (5) to (7),
represents
, then
,
, and
represent
,
, and
, respectively. Similarly,
represents
. By using (10), we have trajectories
,
, and
. Therefore, according to Equations (5)–(7),
,
, and
represent
,
, and
, respectively.
The last adjacency matrix is the
augmented-edge adjacency matrix, denoted by
, where the row and column are indexed by the index of
, i.e.,
. Let
be the element of
, whose value is not zero and be associated to
by applying Algorithm 2.
| Algorithm 2 Determining the index of : |
| 1: Inputs: |
| 2: Output: , |
| 3: h = 0 |
| 4: For i = 1,…,// loop for all rows |
| 5: For j=1,…, // loop for all columns |
| 6: = ; = |
| 7: If |
| 8: If = |
| 9: h=h+1 |
| 10: |
| 11: |
| 12: Else |
| 13: |
| 14: End |
| 15: Else |
| 16: |
| 17: End if |
| 18: End for |
| 19: End for |
The functions , , and return the row index belonged to the row in containing x, the indexes of start and end node in , respectively. In the previous example, there are ten edges and three speed options. The number of trajectories is 30 and the dimension of . Until this step, we have the following adjacency matrices:, , and . Suppose that we are given ; then, by using the map described in , we obtain and , where and are the indexes of the row and column of associated to . After that, we check the map in , and we obtain the edge and speed option for each and .
4.2. Ant Colony Optimization
Ant Colony Optimization (ACO) was first introduced in Reference [
28]. This algorithm is powerful for routing problems such as traveling salesman problem (TSP), vehicle routing problem (VRP), and their variants [
17,
27]. The algorithm mimics the behavior of a colony of ants in foraging activities. Suppose that, at the beginning, the colony has no information about the location of the food source. An ant system (AS) consists of a set of artificial ants which perform foraging activities, from their nest to a food source. Some ants begin to move randomly to any direction and deposit a chemical called “pheromone”, whose trails will be traced by other ants. This process is iterated such that the optimal route is that with the maximum number of pheromone trails.
In this study, we used an ACO algorithm for finding trajectories for a multiple-vehicle system. The algorithm is different from the typical ones. It involves more than one species of ants whose pheromone the others cannot detect trails of. In the cases of CFMTSP, a species represents a vehicle. We develop an algorithm such that each species performs a collision-free trajectory, i.e., all species can prevent collision with each other. In this study, we assume that any two species are not colliding with each other if the difference of their arrival times exceeds a minimum allowable value.
Suppose that there exist
ant species. Each species consists of
ants. The
r-th ant of the
k-th species, denoted by
,
,
, represents the
k-th vehicle. Each ant is assumed to be able to recognize only the trails produced by ants of the same species. Therefore, if there exists a large concentration of pheromone in a sub-route, if it comes from different species, then it is less possible for the ant to choose that sub-route as a choice. As the typical ACO algorithms, as one ant passes a sub-route, it leaves pheromone trails along the sub-routes. From now on, the others will smell the trails, and based on the largest amount of pheromones, it will choose the sub-route. Even though there are pheromones produced by other different ant species, the ant cannot recognize them. This behavior is similar to the behavior of some colonies of ants in the real world, that is, they cannot recognize the trail of other different ant species, as reported in Reference [
40]. Researchers in that study have discovered that a species of ants, i.e.,
Lasius nigers (
La. nigers), is unable to recognize the pheromone trails produced by
Novomessor cockerelli (
N. cockerelli) and
Linepithema humilis (
Li. humilis). The reason is that their pheromone trails are constructed by different chemicals.
In this model, we applied the amount of pheromone applied to the proposed augmented graph
to augmented edges
. Define
,
, and
as the iteration, the total amount of pheromone left by the
k-th ant species on augmented edges
, and the increase of pheromone amount left by each
r-th ant of the
k-th ant species, respectively. We formulate
as follows.
if a solution is found and the
i-th and
j-th nodes are the part of the augmented edge passed through by the
k-th ant species, and
where
is defined as evaporation rate, if the search fails to find a solution. Furthermore,
is formulated as follows:
where
is the total distance traveled by the
r-th ant from the
k-th species, and
is a positive constant.
We apply the probability of selecting
, i.e.,
as follows:
Note that the selection of trajectories of more than one vehicle leads to a consequence of inter-vehicle collision-checking. Therefore, a procedure for checking the collision is developed.
Before describing the main algorithm, we define a number of variables: and are the initial position and speed, respectively. , , , , and are the lists of unvisited nodes, collection of edges, collection of trajectories, and collection of augmented-edges, the sequence of selected augmented-edges from the start to end nodes, respectively. is a collection for each node that stores information of the k-th vehicle that has visited the node and its associated arrival time, . is the best trajectory performed by the k-th species.
In Line 1 of Algorithm 3, the input is the graph , initial positions , and speed of each r-ant of the k-th ant species. Note that r also represents the index of iteration. Consequently, represents the number of iterations. In Lines 3 and 4, all the required adjacency matrices are constructed, and for all ant species is set to be empty.
The searching process starts from Line 5. For each iteration, trajectories are constructed for each species. In Line 7, some required initializations are performed, such as the initial amount of pheromones. The values are set randomly small to prevent division-by-zero at the beginning at the process. The next processes are focused on identifying the augmented edge of the current occupied node, .
The function CreateEdgeList() is purposed to extract all edges in whose start nodes are . In this process, the edge matrix is used. The resulted is then pushed to .
The next step is to extract the sub-trajectories, , whose edges are . However, two conditions make the extraction fail. First, it is possible that the end node of the edge , i.e., ), was visited. Therefore, the availability of the end node of the edge must be checked (Line 13). Second, even though ) is available, if there exists another ant occupying the node such that the second constraint is violated, then the process is continued to the next edge. This process is revealed in Lines 14–16.
If the end node of the edge
has not been visited yet and has no collision issue, then the function
CreateTrajectoriesList(
,
) is executed (Line 18). The
CreateTrajectoriesList(
,
) uses trajectory adjacency matrix
as reference to find the correct trajectories that are spanned by the
q-th edge in
. If the end node of the edge
has been visited previously, the process will check the other edges. If there is no edge available, then it can be concluded that a complete trajectory is failed to found. Therefore, the process is continued to new iteration (Lines 29–32). In Line 30, the amount of pheromone trails is reduced by calling
ReducePheromoneTrailsAmount(
), which applies Equation (12).
| Algorithm 3 Main Algorithm |
| 1: Inputs: , , , for all ,, |
| 2: Perform , , and . |
| 3: , for all . |
| 4: , for all . |
| 5: For r = 1 to |
| 6: |
| 7: Initialize(, ); |
| 8: , , , , , . |
| 9: For each k-th ant species |
| 10: While |
| 11: CreateEdgeList(). |
| 12: For each edge in , i.e., , |
| 13: If , |
| 14: If IsCollided(, ) is TRUE |
| 15: continue; |
| 16: End |
| 17: CreateSubTrajectoriesList(,). |
| 18: . |
| 19: For each p-th trajectory in i.e., , |
| 20: CreateAugmentedEdgesList(, ). |
| 21: End |
| 22: SelectAugmentedEdge(). |
| 23: CalculateMaxArrivalTime(). |
| 24: Remove(). |
| 25: Else |
| 26: continue. |
| 27: End |
| 28: End |
| 29: If |
| 30: ReducePheromoneTrailsAmount() |
| 31: go to Line 5. |
| 32: End |
| 33: . |
| 34: End //end while |
| 35: End // end for |
| 36: CalculatePheromoneTrailsAmount(), for all . |
| 37: = CalculateProbability(), for all . |
| 38: = min() |
| 39: |
| 40: End |
| 41: Outputs: with = , for all . |
In Lines 19–21, the function CreateAugmentedEdgesList (, ) is used to extract the augmented edges that is spanned by the p-th trajectory in . This function uses augmented-edge adjacency matrix as a reference to find the correct augmented edge that is spanned by the p-th trajectory in . The result is and is pushed to , and we select the augmented edge, whose probability, calculated using Equation (11), is the largest. The selected augmented edge is then pushed into (Line 22). In addition, the maximum traveling time, , is calculated in Line 23. Here, the final value of is the traveling time of the slowest ant species. Moreover, the member of that is the same to ) is removed (Line 24), since the ) is selected to be visited.
After all ants from all species complete their routes, the pheromone trails on all augmented edges are updated in Line 31 by using Equation (11). By using the current pheromone trails, the probability of all augmented edges in , is calculated by using CalculateProbability() in Line 37. The global minimum, , is then calculated in Line 38. Finally, the output is with = , for all .