Efficient Probabilistic Joint Inversion of Direct Current Resistivity and Small-Loop Electromagnetic Data
Abstract
1. Introduction
2. Methodology
2.1. Frequency-Domain Electromagnetics
2.2. Vertical Electrical Sounding
2.3. Bayesian Inference and the Kalman Ensemble Generator
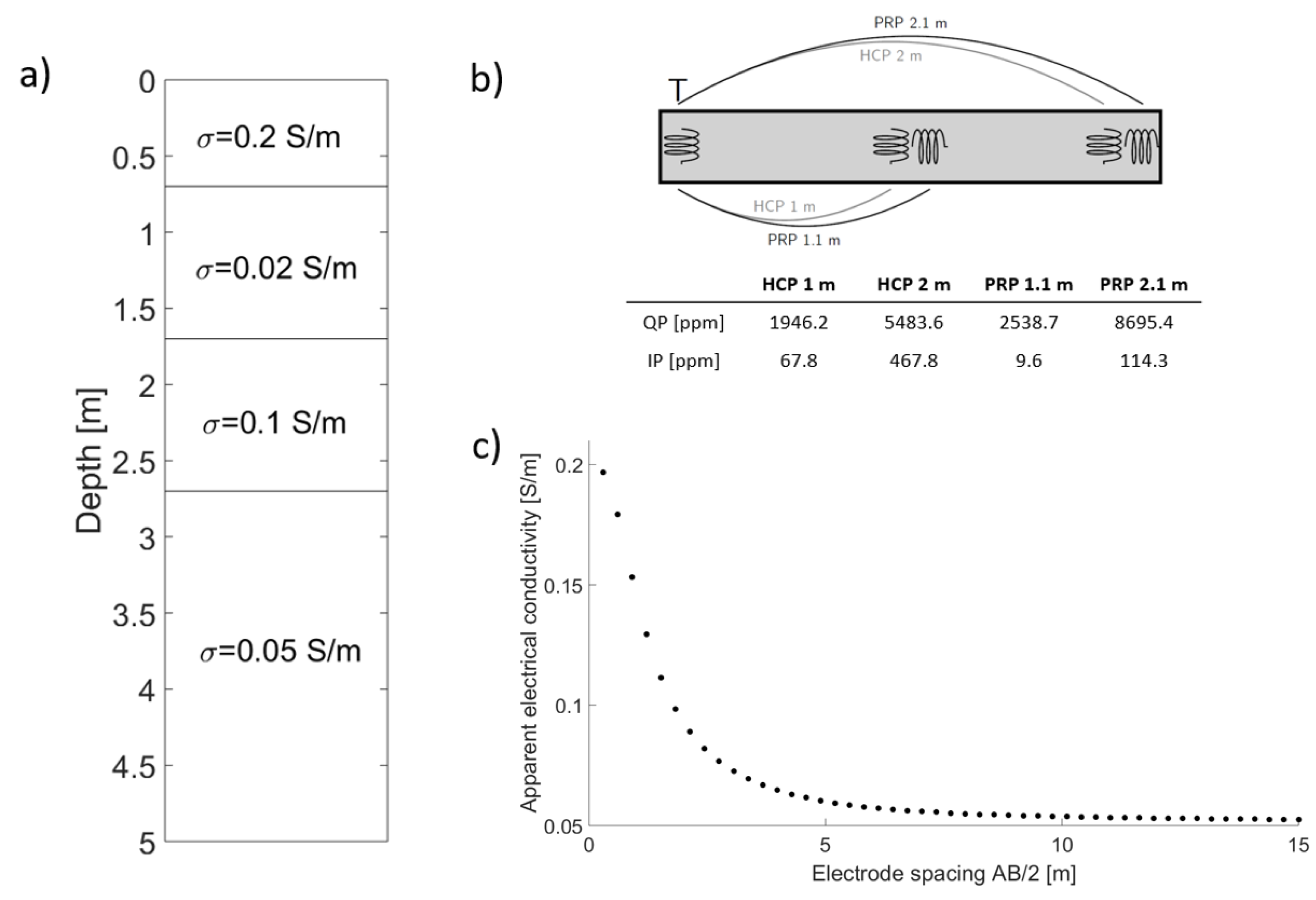
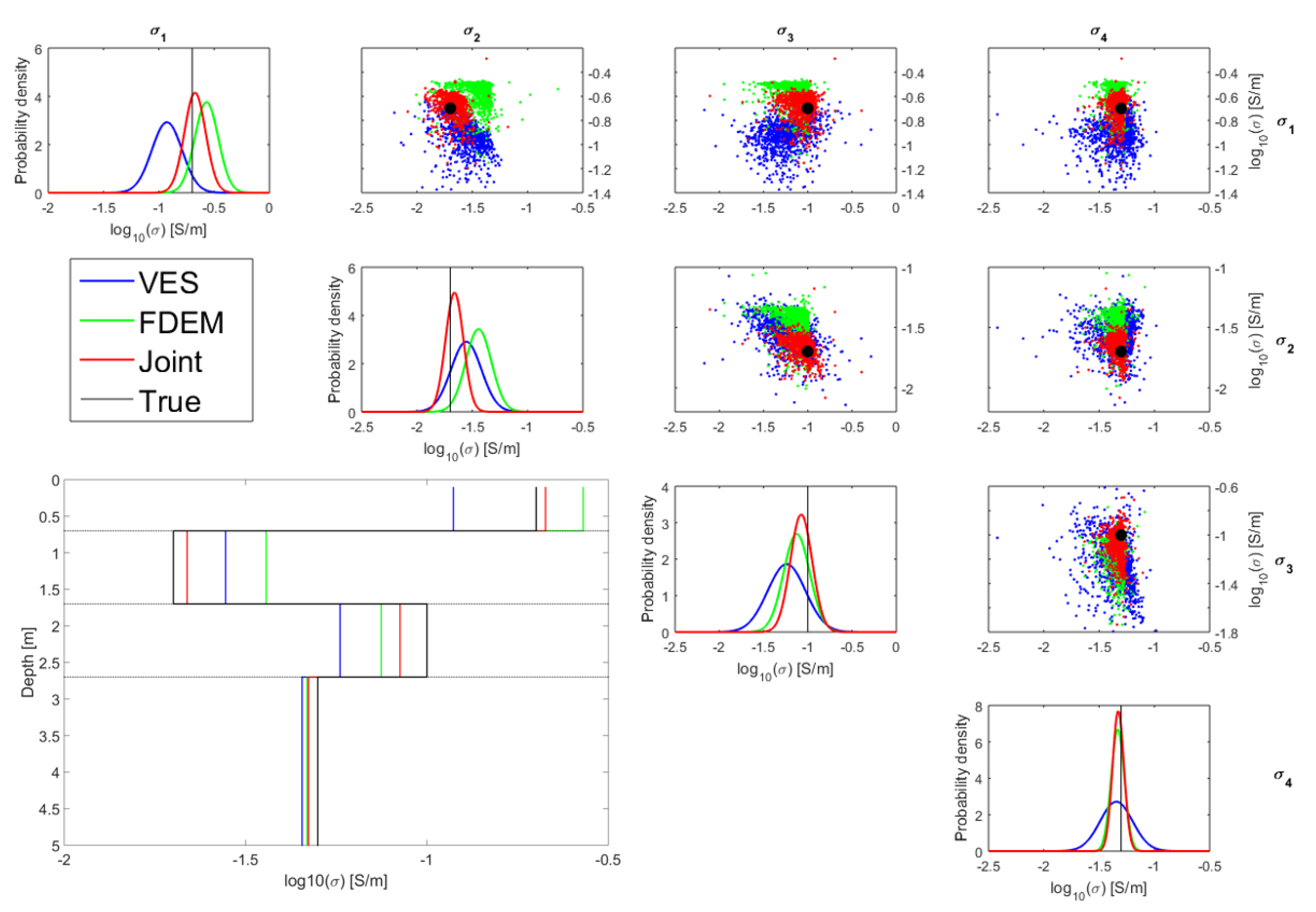
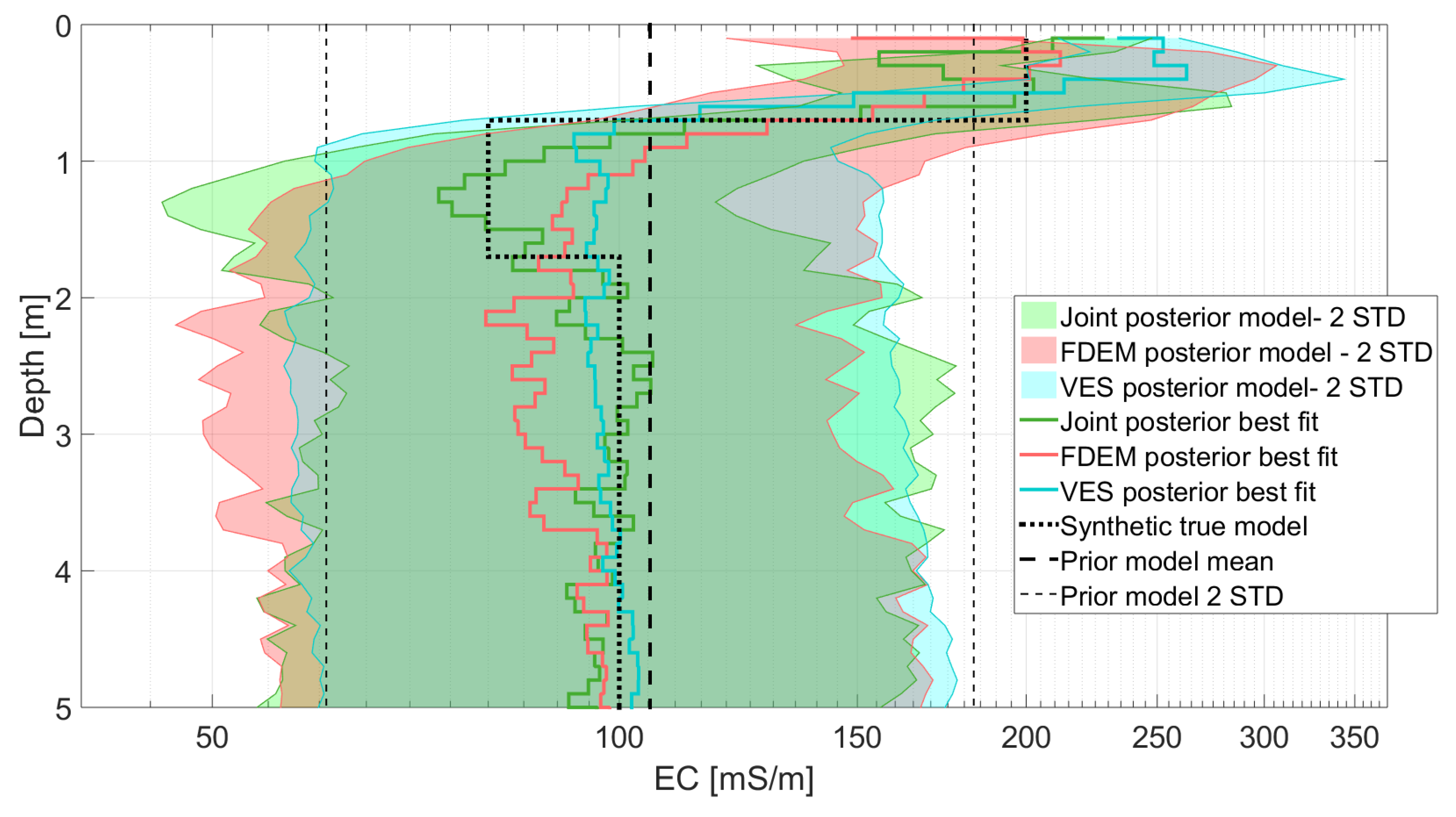
3. Synthetic Cases
3.1. Four-Layer Inversion
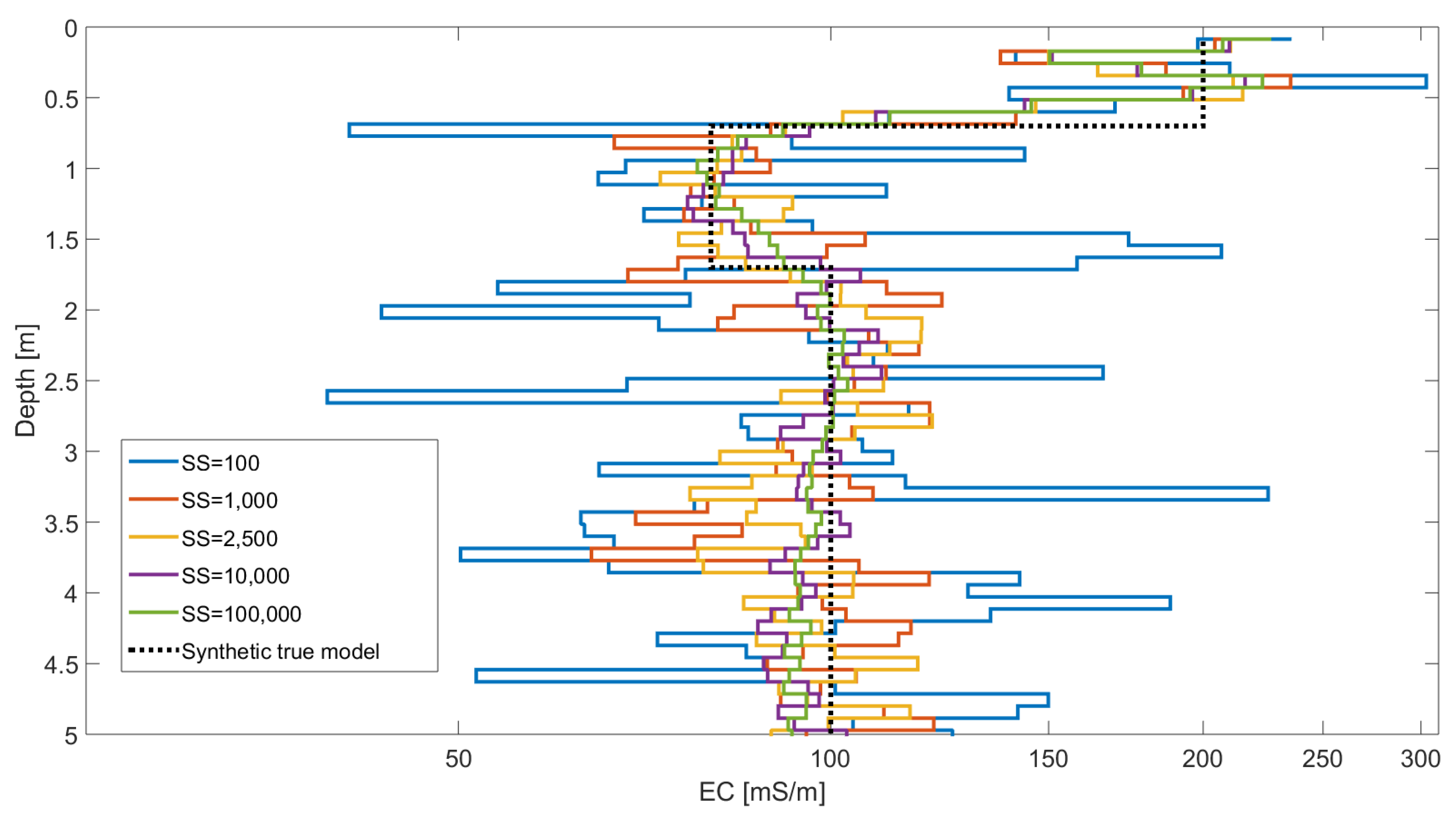
3.2. Multi-Layer Inversion
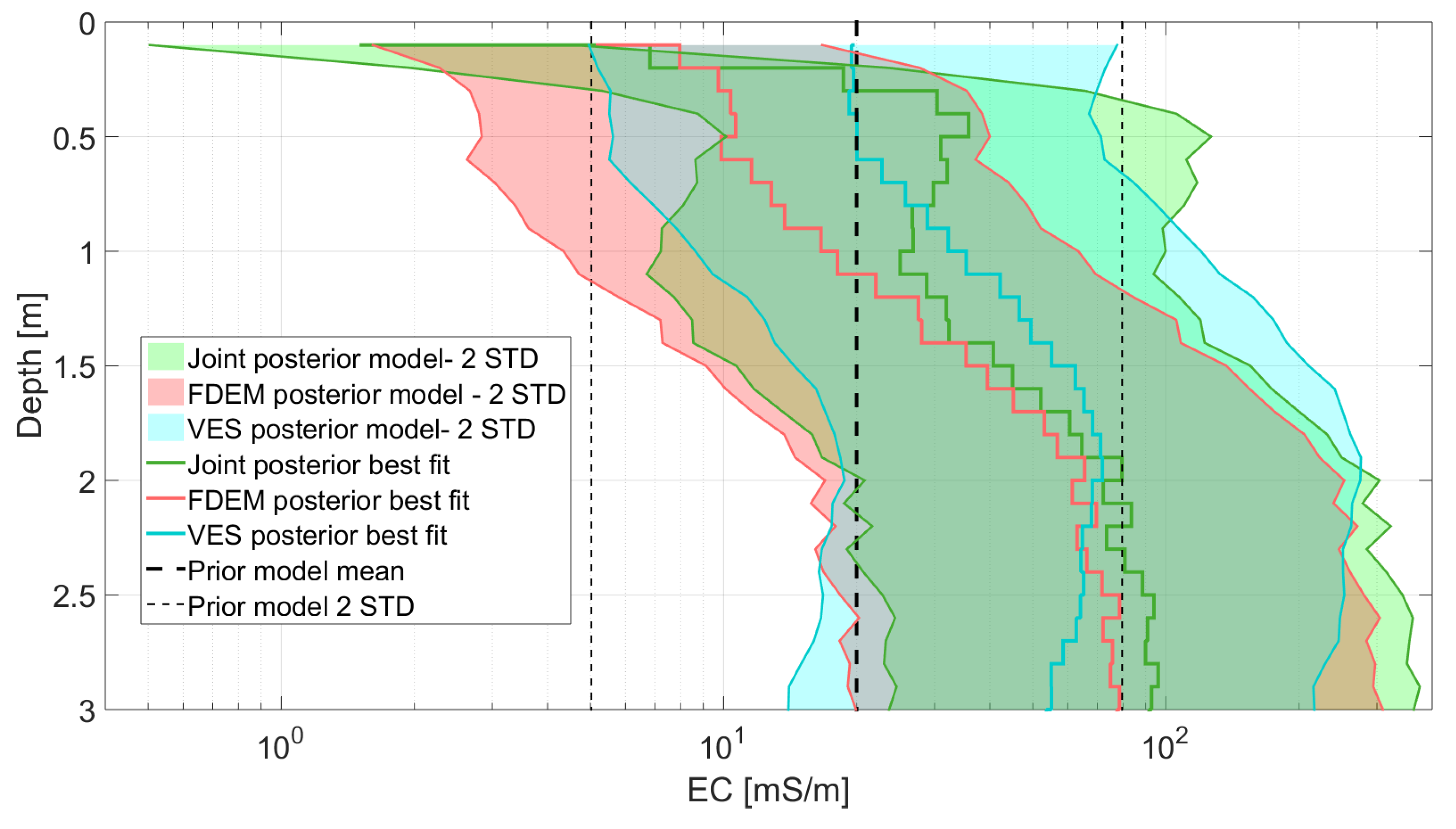
4. Field Data Case
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; SIAM: Philadelphia, PA, USA, 2005. [Google Scholar]
- Moorkamp, M. Integrating electromagnetic data with other geophysical observations for enhanced imaging of the earth: A tutorial and review. Surv. Geophys. 2017, 38, 935–962. [Google Scholar] [CrossRef]
- Gomez-Trevino, E.; Edwards, R. Electromagnetic soundings in the sedimentary basin of southern Ontario—A case history. Geophysics 1983, 48, 311–330. [Google Scholar] [CrossRef]
- Raiche, A.; Jupp, D.; Rutter, H.; Vozoff, K. The joint use of coincident loop transient electromagnetic and Schlumberger sounding to resolve layered structures. Geophysics 1985, 50, 1618–1627. [Google Scholar] [CrossRef]
- Sharma, S.; Kaikkonen, P. Appraisal of equivalence and suppression problems in 1D EM and DC measurements using global optimization and joint inversion. Geophys. Prospect. 2003, 47, 219–249. [Google Scholar] [CrossRef]
- Yi, M.J.; Sasaki, Y. 2-D and 3-D joint inversion of loop–loop electromagnetic and electrical data for resistivity and magnetic susceptibility. Geophys. J. Int. 2015, 203, 1085–1095. [Google Scholar] [CrossRef][Green Version]
- Koefoed, O. Geosounding Principles, 1. Resistivity Sounding Measurements; Elsevier Science Publishing Co.: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Aster, R.C.; Borchers, B.; Thurber, C.H. Parameter Estimation and Inverse Problems; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Commer, M.; Newman, G.A. Three-dimensional controlled-source electromagnetic and magnetotelluric joint inversion. Geophys. J. Int. 2009, 178, 1305–1316. [Google Scholar] [CrossRef]
- Malinverno, A.; Briggs, V.A. Expanded uncertainty quantification in inverse problems: Hierarchical Bayes and empirical Bayes. Geophysics 2004, 69, 1005–1016. [Google Scholar] [CrossRef]
- Sambridge, M.; Mosegaard, K. Monte Carlo methods in geophysical inverse problems. Rev. Geophys. 2002, 40, 3-1–3-29. [Google Scholar] [CrossRef]
- Bobe, C.; Van De Vijver, E.; Keller, J.; Hanssens, D.; Van Merivenne, M.; De Smedt, P. Probabilistic 1-D inversion of frequency-domain electromagentic data using a Kalman ensemble generator. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3287–3297. [Google Scholar] [CrossRef]
- Michel, H.; Nguyen, F.; Kremer, T.; Elen, A.; Hermans, T. 1D geological imaging of the subsurface from geophysical data with Baeysian Evidential Learning. Comput. Geosci. 2020, 138, 104456. [Google Scholar] [CrossRef]
- Nowak, W. Best unbiased ensemble linearization and the quasi-linear Kalman ensemble generator. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Reynolds, J.M. An Introduction to Applied and Environmental Geophysics; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ward, S.H.; Hohmann, G.W. Electromagnetic theory for geophysical applications. Electromagn. Methods Appl. Geophys. 1988, 1, 131–311. [Google Scholar]
- Hanssens, D.; Delefortrie, S.; De Pue, J.; Van Meirvenne, M.; De Smedt, P. Frequency-Domain Electromagnetic Forward and Sensitivity Modeling: Practical Aspects of Modeling a Magnetic Dipole in a Multilayered Half-Space. IEEE Geosci. Remote Sens. Mag. 2019, 7, 74–85. [Google Scholar] [CrossRef]
- Sasaki, Y.; Son, J.S.; Kim, C.; Kim, J.H. Resistivity and offset error estimations for the small-loop electromagnetic method. Geophysics 2008, 73, F91–F95. [Google Scholar] [CrossRef]
- Bobe, C.; Van De Vijver, E. Offset errors in probabilistic inversion of small-loop frequency-domain electromagnetic data: A synthetic study on their influence on magnetic susceptibility estimation. In Proceedings of the International Workshop on Gravity, Electrical & Magnetic Methods and Their Applications, Xi’an, China, 19–22 May 2019; Society of Exploration Geophysicists: Tulsa, OK, USA, 2019; pp. 312–315. [Google Scholar]
- Binley, A.; Kemna, A. DC resistivity and induced polarization methods. In Hydrogeophysics; Springer: Dordrecht, Switzerland, 2005; pp. 129–156. [Google Scholar]
- Everett, M.E. Near-Surface Applied Geophysics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Blatter, D.; Key, K.; Ray, A.; Gustafson, C.; Evans, R. Bayesian joint inversion of controlled source electromagnetic and magnetotelluric data to image freshwater aquifer offshore New Jersey. Geophys. J. Int. 2019, 218, 1822–1837. [Google Scholar] [CrossRef]
- Gelman, A.; Stern, H.S.; Carlin, J.B.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC: London, UK, 2013. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Burgers, G.; Jan van Leeuwen, P.; Evensen, G. Analysis scheme in the ensemble Kalman filter. Mon. Weather Rev. 1998, 126, 1719–1724. [Google Scholar] [CrossRef]
- MATLAB. MATLAB and Statistics Toolbox Release; The MathWorks Inc.: Natick, MA, USA, 2012. [Google Scholar]
- Zhou, H.; Gomez-Hernandez, J.J.; Franssen, H.J.H.; Li, L. An approach to handling non-Gaussianity of parameters and state variables in ensemble Kalman filtering. Adv. Water Resour. 2011, 34, 844–864. [Google Scholar] [CrossRef]
- Cassidy, N.J. Electrical and magnetic properties of rocks, soils and fluids. In Ground Penetrating Radar: Theory and Applications; Jol, H., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; Volume 2, Chapter 2; pp. 41–72. [Google Scholar]


| VES | FDEM | Joint | |
|---|---|---|---|
| RMSE [mS/m] | 18.32 | 15.05 | 11.89 |
| SS | RMS |
|---|---|
| 100 | 0.201 |
| 1000 | 0.086 |
| 2500 | 0.081 |
| 10,000 | 0.069 |
| 100,000 | 0.067 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bobe, C.; Hanssens, D.; Hermans, T.; Van De Vijver, E. Efficient Probabilistic Joint Inversion of Direct Current Resistivity and Small-Loop Electromagnetic Data. Algorithms 2020, 13, 144. https://doi.org/10.3390/a13060144
Bobe C, Hanssens D, Hermans T, Van De Vijver E. Efficient Probabilistic Joint Inversion of Direct Current Resistivity and Small-Loop Electromagnetic Data. Algorithms. 2020; 13(6):144. https://doi.org/10.3390/a13060144
Chicago/Turabian StyleBobe, Christin, Daan Hanssens, Thomas Hermans, and Ellen Van De Vijver. 2020. "Efficient Probabilistic Joint Inversion of Direct Current Resistivity and Small-Loop Electromagnetic Data" Algorithms 13, no. 6: 144. https://doi.org/10.3390/a13060144
APA StyleBobe, C., Hanssens, D., Hermans, T., & Van De Vijver, E. (2020). Efficient Probabilistic Joint Inversion of Direct Current Resistivity and Small-Loop Electromagnetic Data. Algorithms, 13(6), 144. https://doi.org/10.3390/a13060144







