1. Introduction
More applications of dynamic networks have arisen in recent years, for example, wireless mobile ad hoc, transportation, inter vehicle, or social networks and so on, more important the researches about the dynamic networks have got. A network is
dynamic if its topology may change with time (due to various reasons, e.g., faults or movements of nodes). In a dynamic network, existing methods designed for static networks (the topologies of which do not change with time) might no longer work. For this reason, the researchers have started to consider several problems on dynamic networks [
1].
The exploration which requires a mobile entity called an agent (e.g., a software agent, a robot, or a vehicle) to visit all the nodes of the network is one of the most fundamental problems. The exploration is useful for solving fundamental tasks on the networks such as broadcast or network maintenance. It has been well-studied for static networks [
2] and recently been studied for dynamic networks. In the previous works about the exploration of dynamic networks, two extreme cases are considered: an agent has the a priori complete knowledge about changes of all the links for all the future time steps [
3,
4,
5,
6,
7]; or an agent can only see whether the links adjacent to its current node are present or not at the moment [
8,
9,
10,
11,
12]. The former one models the situation where the network changes are completely predictable as the public transportation networks in which the network changes are introduced by totally scheduled movements of the nodes. The latter one models the situation where the network changes are caused by unscheduled events, for example, faults or unscheduled movements of the nodes.
Although the above two models are plausible and also theoretically important, the intermediate model, i.e., an agent with partial information or, in other words, capability to know link changes within some distance in the near future should be considered due to the following reasons: even in the totally scheduled situation (if exists), computing all the future changes often costs computation time and it is desirable to compute only the necessary information to solve a problem to save computing time or memories; the ability of an agent to monitor whether there are faults or environmental changes roughly depends on the quality (or costs) of its sensor and it can save some costs to compute only the necessary information for a problem. Moreover, such a model is so interesting from a theoretical viewpoint: how the amount of information available for an agent influences the solvability or the time complexity of problems.
In this paper, we consider the exploration of dynamic networks by a single agent with partial information about network changes. To the best of our knowledge, this is the very first work to investigate the exploration using such partial information. As a first step in this research direction, we focus on 1-interval connected rings as dynamic networks in this paper. To formalize the concept of partial information and analyze its influences, in this paper, we first propose the
view such that the agent with the view can see the
link scheduling (when and which links disappear or appear) of the links within
H hops from its location for
S time steps from the current time. Then, we consider how the value of
H or
S influences the solvability or the time complexity of the exploration by a single agent of
1-interval connected rings in which at most one link is missing at each time step. While the 1-interval connected rings are probably too restrictive from a practical point of view, they are adequate targets to investigate in the novel direction as investigated in many works (e.g., in the field of mobile agents on dynamic networks, [
7,
10,
13,
14,
15] consider 1-interval connected rings).
1.1. Related Works
To see various settings and exploration algorithms on static networks, there is a good survey [
2], for example, a network with distinct node labeling or without node labeling (an anonymous network), exploration with termination or perpetual exploration, and from the point of the number of agents, exploration by a single agent or by multiple agents.
The literature of dynamic networks are surveyed in [
1,
16].
The recent works about mobile agents (or robots) on dynamic networks are summarized in [
17] including exploration;
gathering on 1-interval connected rings [
13] which requires all the agents to gather at one node or at adjacent two nodes;
dispersion [
18] which stipulates that every node must be occupied by exactly one agent where the number of agents is the same as that of nodes on
permuting rings in which the nodes may be permuted at each time step, i.e., the neighbors of a node may change at each time step while the topologies are rings or paths at each time step.
The following works consider the exploration of dynamic networks by multiple agents (or robots) without the knowledge of a link scheduling (or only with the ability to detect whether the adjacent links are present or not at the moment). In [
10], the exploration for 1-interval connected rings is considered. The
perpetual exploration (i.e., the exploration without termination) on
connected-over-time rings is considered in [
8,
9]. In [
11], the perpetual exploration on two kinds of temporal networks with arbitrary footprints is considered:
connected-over-time graphs and
1-interval connected graphs with bounded missing links. The difference between with or without the ability to detect whether the adjacent links are present or not at the moment (called the
link presence detection) is considered in [
12] for an
dynamic torus which consists of
n horizontal rings and
m vertical rings each of which is a 1-interval connected ring. It is shown that the minimum number of agents with the link presence detection to explore the networks is a half of the minimum number of agents without the one to explore.
The following works consider the exploration of dynamic networks by an agent with the full knowledge of a link scheduling, i.e., the information about when and which links disappear or appear. In [
7], the exploration is considered on
T-interval connected rings where at most one link is missing at each time step and for any
T successive time steps, there exists a common spanning connected component. It is shown that the optimal exploration time is
when
where
n is the network size. In [
6], the exploration on
1-interval connected cactuses is considered. They show that the graphs can be explored in
time which is much less than the known upper bound for the general graph,
. In [
3], the authors reveal the existence of the 1-interval connected graphs which have the exploration time
, proving the exploration time of arbitrary 1-interval connected graphs is
. In [
5], it is shown that when the maximum degree at each time step is upper-bounded by
d, the exploration time is reduced to
. In [
4], the authors prove that the exploration time is reduced to
if an agent can move two hops in each time step.
Other problems are also considered on dynamic networks;
patrolling on 1-interval connected rings [
14] which requires the maximum length of the interval between two visits to a node to be minimized;
compacting on 1-interval connected rings [
15] which stipulates that all the agents in a network must be located in a continuous part of the ring and at each node there exists at most one agent.
1.2. Our Contributions
In this paper, we consider the exploration of 1-interval connected rings by a single agent with the
view (formalizing the proofs and the pseudo codes and extending the results given in [
19]). Remind that the agent with the
view can see the link scheduling of the links within
H hops (
) from its location for
S time steps from the current time. To the best of our knowledge, this is the first work to generalize the agent capacity to see a link scheduling.
The results are summarized in
Table 1. For the proposed model, we show that
and
(
n is the size of networks) are the necessary and sufficient conditions to explore 1-interval connected rings by a single agent. We also show that in the case where the above conditions holds, the exploration can be achieved within
time if
or otherwise
time where
. This is a new addition to the contributions of the previous work [
19]. Moreover, we show that when
, the exploration time can be reduced to
. This leads to
time when
. Finally, we show a lower bound of the exploration time,
, for any
S. This implies that we have tight bound
when
,
, and
H is
and when
and
.
2. Models and Terminologies
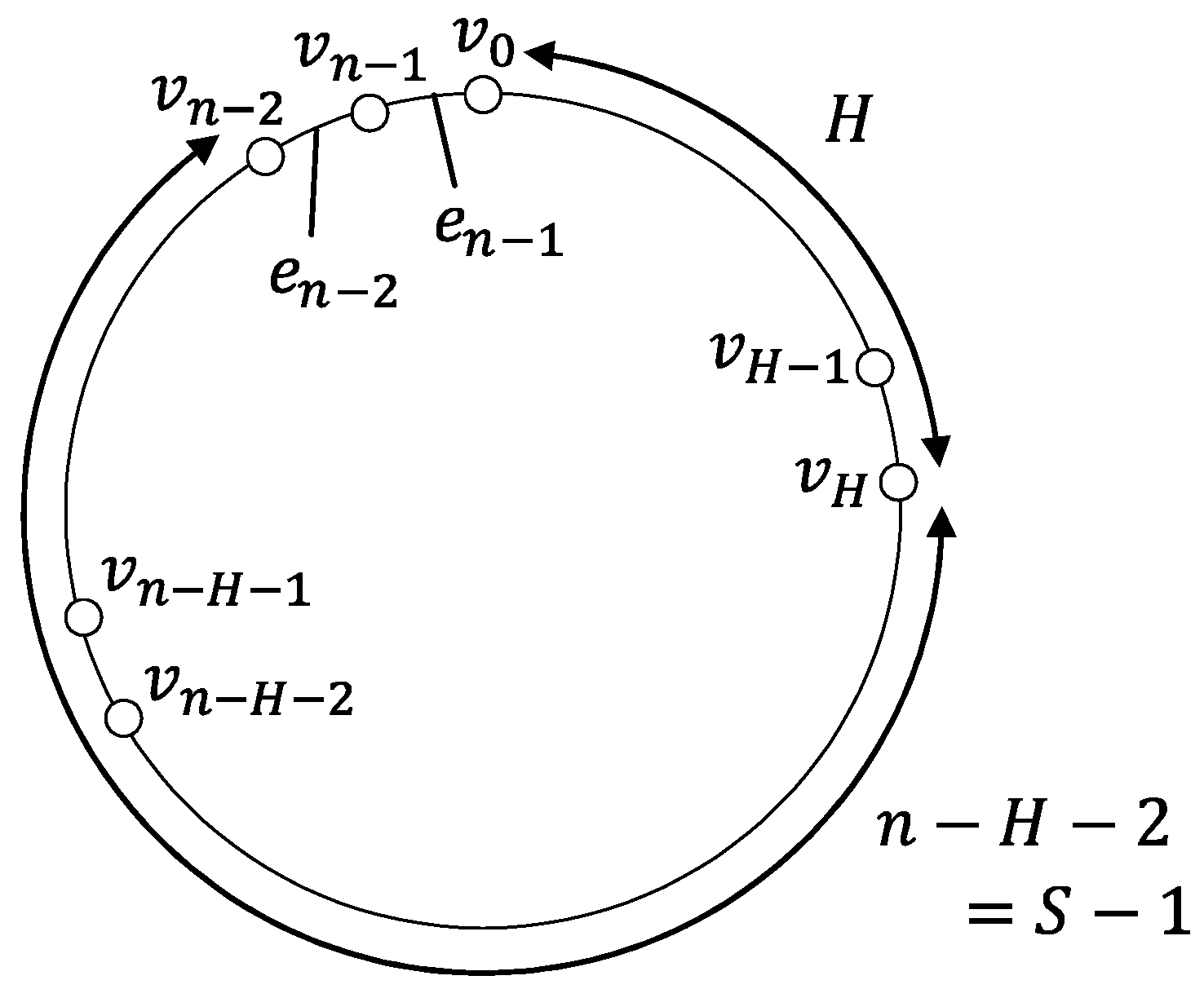
We consider a time variant ring where is a ring network, i.e., is a set of n nodes and is a set of n links such that . The nodes of the network are anonymous. For simplicity, we omit in the following. A function is called a link presence function such that is 1 (resp., 0) if link e is present (resp., missing) at time step (or step) . A network at each step t is denoted as where . We assume that is 1-interval connected, i.e., at each step t, a network is connected. In other words, at each step t, there is at most one missing link such that .
We say the ascending (resp., descending) order of node indices is the right (resp., left) direction. Each port of has a globally consistent label at and which gives an entity on the ring a global direction (the right direction at and the left direction at ) of the ring. Given a connected component , the right (resp., left) extremity of is the node such that (resp., ). If , the unique node in is both the right extremity and the left extremity of .
In the network, a single agent A is operational. Agent A knows the network size n, has computation capacity and its own memory, and can traverse at most one link in each step. In addition to them, A can get the view which contains information of presence of nearby links in near future as defined later. In a step t, A at a node, say , first decides which direction it moves and updates its memory depending on the current content of its memory and the view from . If the corresponding link is present at t, A succeeds to move and reaches a neighbor of by the end of t. Otherwise, A fails to move and stays at .
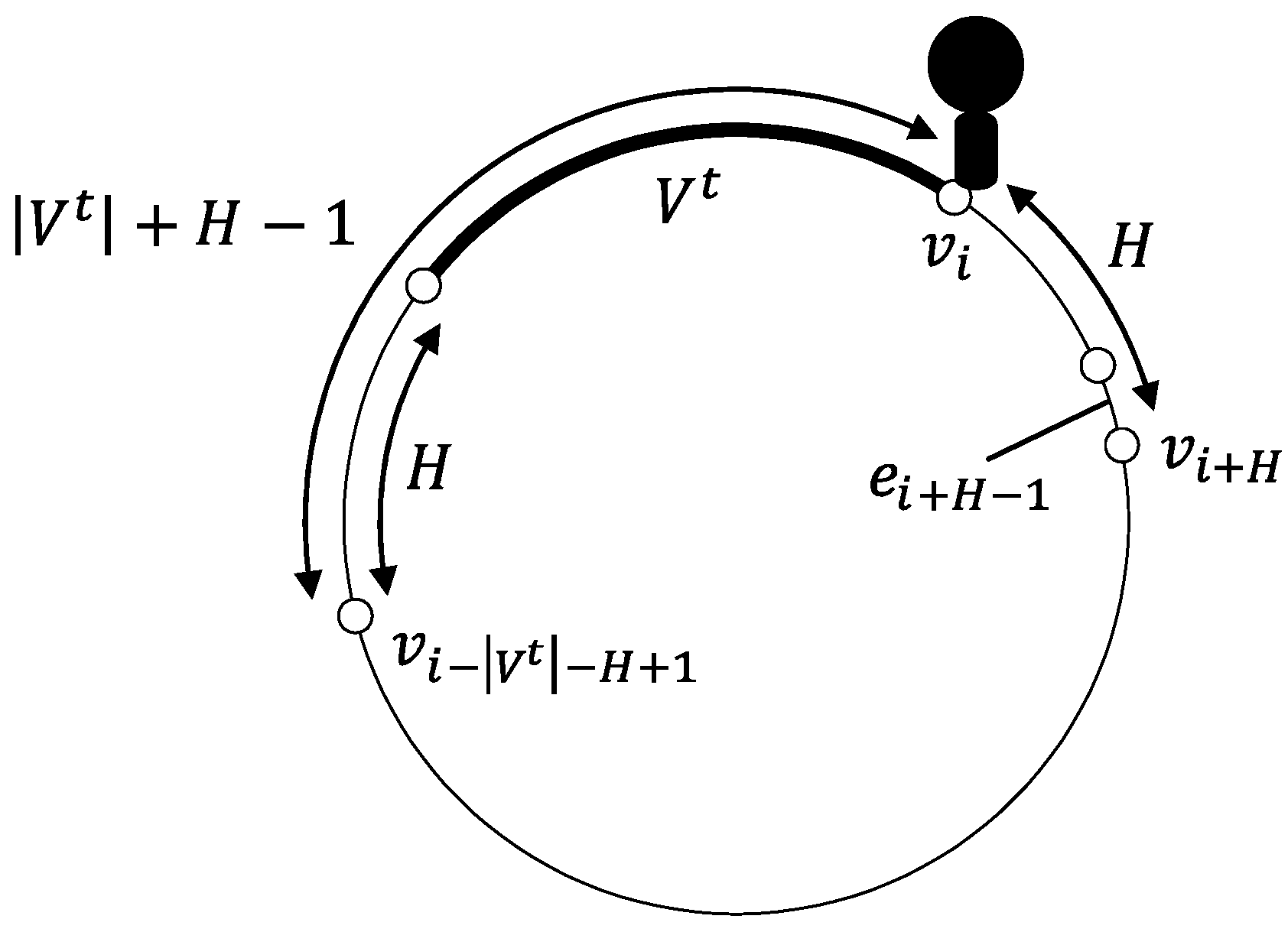
Informally speaking, the view that agent A can get shows which link is missing within H hops from the current node and within S steps in the future including the current step. Formally speaking, for and , A gets the view when A exists on at step s. For example, when , , and A exists on at step 5, A can see . When no confusion arises, we simply write the view instead of writing the “ view”.
It is assumed that a link scheduling (or for every and every step ) is decided by the adversary. The adversary knows the algorithm of A, has infinite computation capacity, and tries to prevent A from exploring the ring.
In this paper, we consider the exploration problem by a single agent A: A is required to visit all the nodes in the ring. A node is said to be explored by (resp., at) the t-th step when it is visited by A at the end of the ()-th step or earlier (resp., at the end of the ()-th step for the first time). In the similar manner, we say that A reaches a node at the t-th step when A visits the node at the end of the ()-th step and that A explores a node v at the t-th step if v is unexplored at the start of the ()-th step and A reaches v at the t-th step. The set of explored (resp., unexplored) nodes at the start of the t-th step is denoted by (resp., ). Without loss of generality, we assume A starts the exploration from .
In the following, we use “to move to right (resp., left)” instead of “to move in the right (resp., left) direction” for simplicity.
3. Impossibility Result
We show an impossibility result in this section. Specifically, we show that the exploration is impossible when or holds.
Lemma 1. If or , a deterministic single agent with the view cannot explore 1-interval connected rings.
Proof. We first consider the condition . We assume . It suffices to show that the exploration is impossible when . We assume for contradiction, that there is an algorithm by which A can explore any ring under any link scheduling when . Since A can explore the ring, A starting from eventually reaches (no matter whether the exploration is completed or not).
The adversary decides a link scheduling so that (resp., ) is missing when A exists on (resp., ). The adversary first keeps showing a link scheduling where is kept deleted for S steps from the current step until A moves to . If A does not move to and stays for , is kept deleted and A cannot reach (A must pass through or to reach from ), which is a contradiction. Thus, A eventually reaches at some step, say t.
Then, the adversary deletes from the ()-th step (the ()-th step) until A moves to . By the scheduling, since A reaches at earliest at the ()-th step (the ()-th step) from , starts to disappear when (or before) A reaches and keeps disappearing unless A moves to . Thus, if A does not move to , A cannot reaches . This is a contradiction.
This means that A moves to after the t-th step. However, by the similar way, the adversary can prevent A from reaching . This is a contradiction. Hence, when , a single agent cannot explore 1-interval connected rings.
Secondly, we consider the condition and . It is sufficient to show that A cannot explore the ring when for since from the conditions. Again, we assume for contradiction, that there is an algorithm by which A can explore any ring under any link scheduling. Since A can explore the ring, A starting from eventually reaches (no matter whether the exploration is completed or not).
The adversary first keeps showing a link scheduling where
is kept deleted for
S steps from the current step until
A moves to
. If
A does not move to
and stays at
for
,
is kept deleted and
A cannot reach
, which is a contradiction. Thus,
A eventually reaches
at some step, say
t. After step
t, depending on whether
A reaches
before
or not, the missing link is decided (
Figure 1). Note that since
,
and there exists a node
such that
. Moreover,
A can see neither
nor
in its view when existing at
for
.
If A reaches before , the adversary keeps deleting . By the link scheduling, unless A decides to reach from , is kept deleted and A cannot reach , which is a contradiction. This means that A eventually reaches . Let be the last step before A reaches such that A exists at at the start of .
When A leaves at the -th step, the adversary makes a scheduling so that starts and keeps disappearing from the ()-th step until A comes back to . This does not conflict with the link scheduling in the past view of A since at the -th step, is scheduled to be deleted for the next steps and for the next steps at the ()-th step.
Since it takes at least steps to reach from , A reaches at earliest at the ()-th step. However, at the ()-th step, is missing and the adversary keeps deleting until A reaches . Then, A cannot reach unless moving to . However, by the similar way, the adversary can prevent A from reaching . This is a contradiction. Hence, when or , a single agent cannot explore 1-interval connected rings. □
4. Possibility Result and Upper Bounds of Exploration Time
In this section, we prove the exploration is possible when and by giving an exploration algorithm by a single agent. In the following, we use . The algorithm also gives upper bounds of the exploration time, if or otherwise . Note that since and .
We first introduce two operations ExpH and EXPONE that are used as building blocks to construct the exploration algorithm.
In the algorithms, Extremity is a function which returns right if v is the right extremity of , left if v is the left extremity, or otherwise nil. Variable dir is used to store the direction and denotes the other direction (e.g., if dir is right, is left).
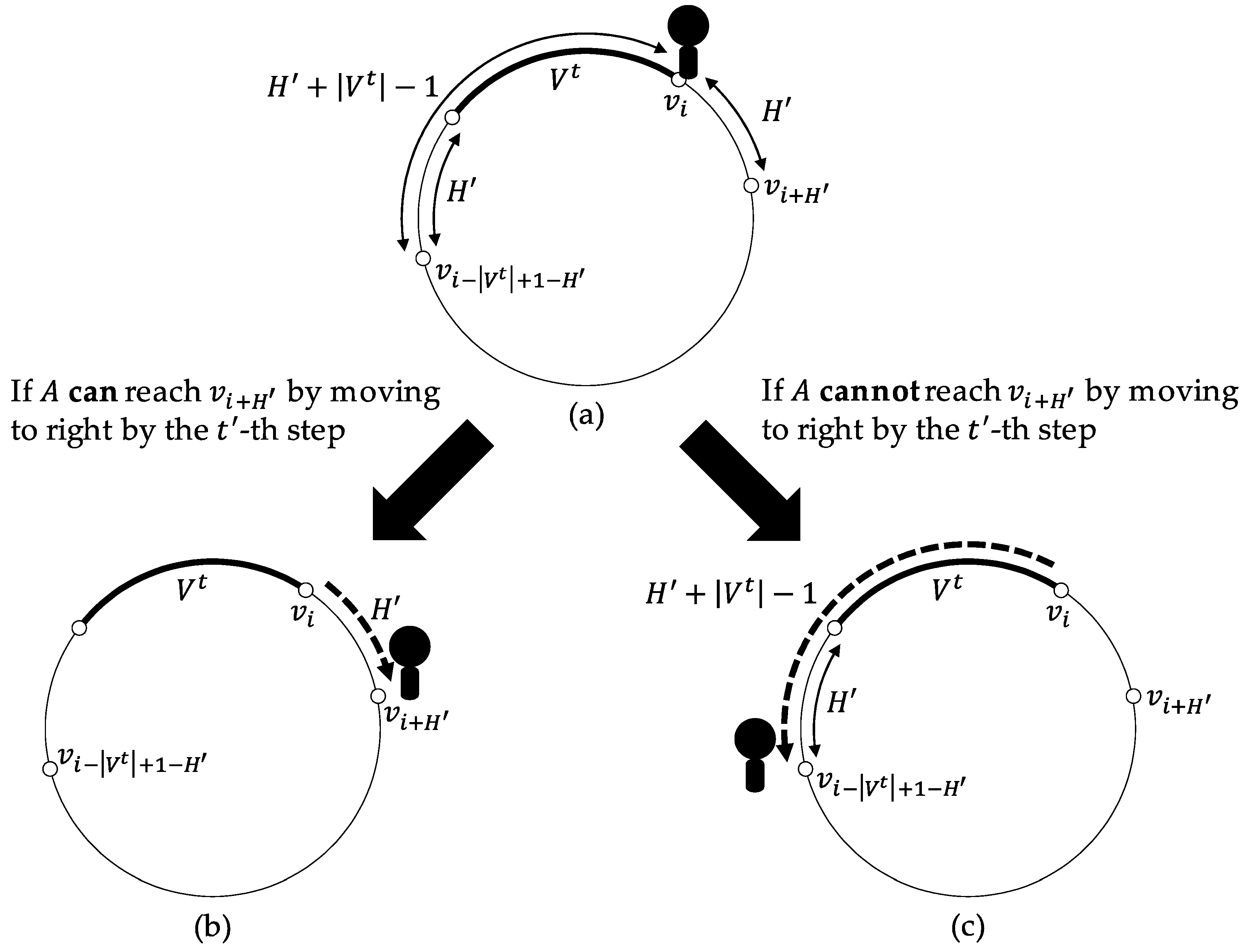
ExpH. ExpH described in Algorithm 1 is an algorithm by which A explores nodes when A starts ExpH from at the t-th step under the assumption that is the right or left extremity of and . Note that in the following, when A executes ExpH, A is always on the right or left extremity of .
When starting the algorithm,
A first sees if
is the right extremity or the left one and stores
right if
is the right extremity or otherwise
left in
dir. If
A can move
hops to
dir by the (
)-th step according to the view,
A does so (
Figure 2b). Otherwise,
A moves
hops to
(
Figure 2c). Notice that
A can decide this condition because
and
.
| Algorithm 1 ExpH |
1: 2: if A can move hops to dir by the -th step then 3: Move hops to dir 4: else 5: Move hops to 6: Wait until the ()-th step |
Lemma 2. Suppose that at the t-th step, A exists at the right or left extremity, say , of and starts ExpH. If , A explores nodes by the -th step (the end of ExpH) and exists on the right or left extremity of at the -th step where .
Proof. Without loss of generality, we assume is the right extremity of . Let , , and . Note that since and , .
Now, consider the move of A. Since , i.e., , A can see whether it can move hops to right by the -th step or not.
If A can, A moves hops to right and thus the lemma holds.
Otherwise, A can move at most hops to right by the ()-th step, which means during the steps, there exists at least steps at each of which one of the links in is missing. Since at most one link is missing at each step and , every link in exists at each of the steps. Thus, A succeeds to move hops to left and the lemma holds. □
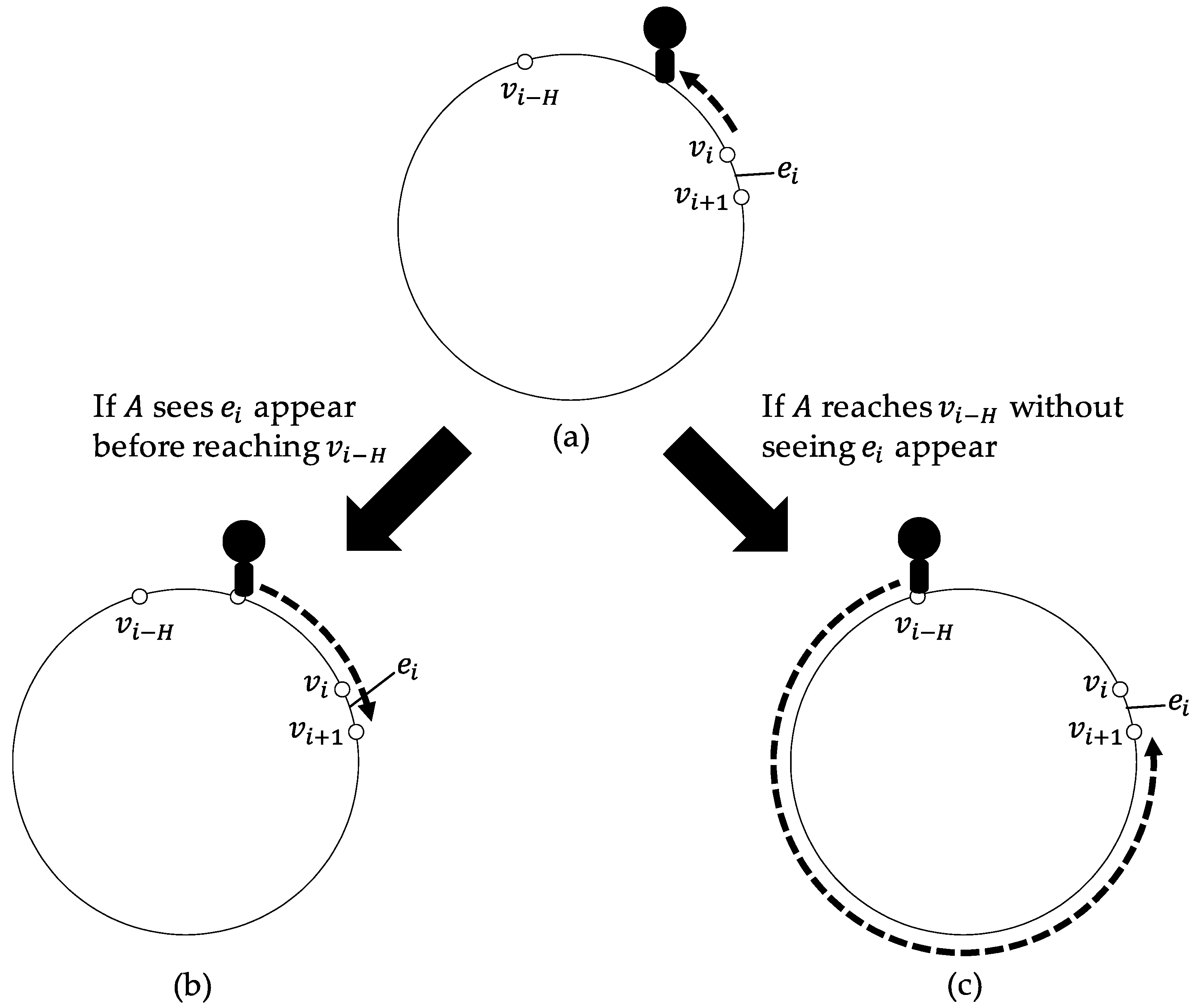
EXPONE. EXPONE described in Algorithm 2 is an algorithm by which A explores at least one node or completes the exploration when A starts EXPONE from at the t-th step under the assumption that is the right or left extremity of . Note that in the following, when A executes EXPONE, A is always on the right or left extremity of .
When starting the algorithm, A first sees if is the right extremity or the left one and stores the direction in dir. Variables and are used to remember the dir neighbor of and the dir incident edge of respectively, e.g., (resp., ) if dir is right (resp., left). Then, A stores to which is not larger than S and is used instead of S in the algorithm.
After that, if
appears by the (
)-th step,
A waits at
until
appears and moves to
when
appears. Otherwise, for each
,
A moves one hop to
at the (
)-th step if
is missing at the (
)-th step in its view (
Figure 3a). If
A sees
appear at the (
)-th step in its view at the (
)-th step, then
A starts to move
dir from the (
)-th step, returns to
, waits at
until
appears, and reaches
through
(
Figure 3b). When
d reaches
H, i.e.,
A moves
H hops to
and
is no longer included in the view of
A,
A starts to keep moving to
until reaching
and the exploration finishes when reaching
(
Figure 3c).
| Algorithm 2 ExpOne |
1: 2: if dir is right then 3: , 4: else 5: , 6: 7: 8: while ) do 9: if is always missing until the ()-th step then 10: Move one hop to 11: 12: else 13: Move d hops to dir (reach ) 14: Wait for to appear and pass through as soon as it appears 15: Exit from the while loop 16: if () then 17: Move hops to (reach ) 18: Wait until the ()-th step |
Lemma 3. Suppose that at the t-th step, A exists at the right (resp., left) extremity, say , of and starts EXPONE. Then, A completes the exploration or reaches (resp., ) by the ()-th step (the end of EXPONE). In addition to that, A exists on the right or left extremity of at the ()-th step when the exploration has not been completed.
Proof. Without loss of generality, we assume is the right extremity of . As in Algorithm 2, let . We first show the lemma for the case appears by the ()-th step in A’s view at the -th step for .
For , A can clearly reach by the ()-th step.
For , when A sees appear for the first time at the ()-th step in its view at the ()-th step, must appear at the ()-th step and be missing at the -th step for by the construction. This means that all the other links than are present at the -th step (), and thus A can move for steps from to right without interference by missing links until reaching .
Since and , A always reaches by the ()-th step at which appears. Then, A reaches as soon as appears. Since A moves at most hops to left, appears steps after A starts to move to right, and from , A reaches through by the ()-th step.
We then show for the other case, i.e., A reaches at the ()-th step. When this happens, must be deleted for at least steps from the ()-th step and all the other links than are present in the steps. Thus, A can move for steps from to left without interference by missing links until reaching since . Since , A reaches after steps, i.e., at the ()-th step, and the exploration is completed at the same time. □
Exploration algorithm. Algorithm 3 describes the exploration algorithm. Let
. The algorithm repeats E
xpH
for
times (lines 2-6) and EXPONE
for
times (lines 7-13). We call the part repeating E
xpH
(lines 2-6)
the first part and the part repeating EXPONE
the second part (lines 7-13). In the first part,
nodes are explored and, in the second part, the remaining
nodes are explored.
| Algorithm 3 Exploration algorithm for |
1: 2: //starting the first part 3: while () do 4: Let t be the current step and be the current node 5: ExpH 6: 7: //starting the second part 8: while () do 9: Let t be the current step and be the current node 10: EXPONE 11: if Exploration is completed then 12: Exit from the while loop 13: |
Theorem 1. For and , the exploration time of 1-interval connected rings by a single agent with the view is upper-bounded by if or otherwise it is upper-bounded by .
Proof. It suffices to show that A with the view completes exploration within steps if or otherwise steps by executing Algorithm 3 when and .
We first consider the case where . In this case, since , the first part is executed at least once. Consider the first part. Let be the step when A starts the p-th ExpH.
We show by induction that for , and A explores nodes by ExpH.
For the base case, i.e., , is clearly . This leads to that . Then, by Lemma 2, A explores nodes by ExpH.
Now, for , assume that and A explores nodes by ExpH. Then, clearly . Since , and . Thus, A explores nodes by ExpH.
By Lemma 2,
, and
, the exploration time of the first part is
We then consider the second part. By Lemma 2, A exists at the right or left extremity of and at the start of the second part. Thus, since A explores one node within n steps by Lemma 3, the exploration time of the second part is .
As a result, the exploration time of Algorithm 3 is when .
When , the first part is never executed and then the number of remaining nodes at the start of the second part is . Thus, in this case, the exploration time of Algorithm 3 is . □
From Lemma 1 and Theorem 1, the following theorem holds.
Theorem 2. If and only if and , a single agent with the view can explore of 1-interval connected rings within finite time steps.
5. Upper Bound of Exploration Time for
In this section, we consider the upper bound of the exploration time when . We show that the upper bound of the exploration time is reduced to in this case by giving an exploration algorithm.
We first introduce a new operation ExpHalf that is used as a building block to construct the exploration algorithm.
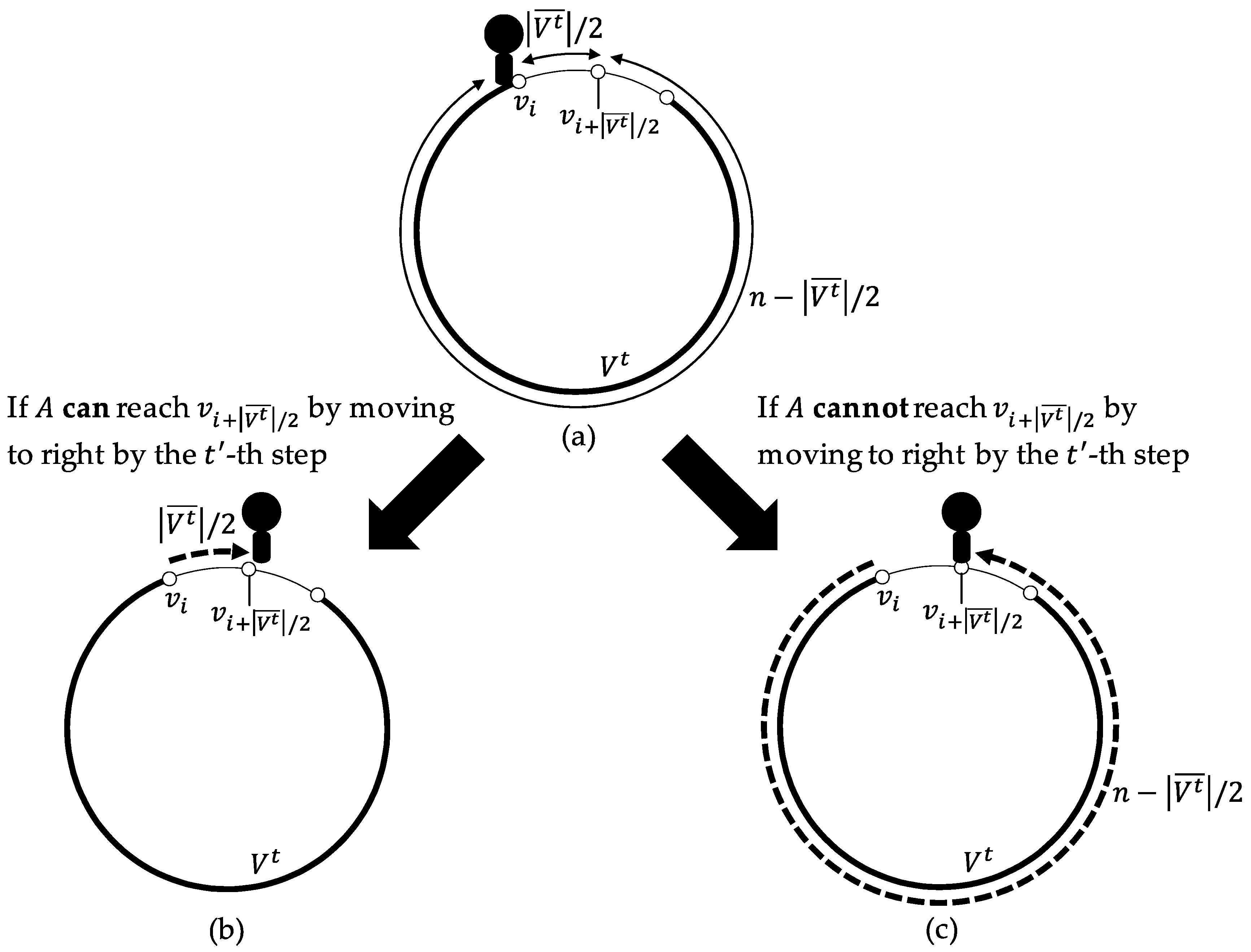
ExpHalf. ExpHalf described in Algorithm 4 is an algorithm by which A explores nodes when A starts ExpHalf from at the t-th step under the assumption that is the right or left extremity of , , and . Note that in the following, when A executes ExpHalf, A is always on the right or left extremity of .
When starting the algorithm,
A first sees if
is the right extremity or the left one and stores
right if
is the right extremity or otherwise
left in
dir. If
A can move
hops to
dir by the (
)-th step according to the view,
A does so (
Figure 4b). Otherwise,
A moves
hops to
(
Figure 4c).
| Algorithm 4 ExpHalf |
1: 2: if A can move hops to dir by the ()-th step then 3: Move hops to dir 4: else 5: Move hops to 6: Wait until the ()-th step |
Lemma 4. Suppose that at the t-th step, A exists at the right or left extremity, say , of and starts ExpHalf. If and , A can explore at least nodes by the -th step (the end of ExpHalf) and exists on the right or left extremity of at the -th step where .
Proof. Without loss of generality, we assume is the right extremity of . Let , , and .
Now, consider the move of A. Since and , A can see whether it can move hops to right by the ()-th step or not.
If A can move hops, A moves hops to right and thus the lemma holds.
Otherwise, A can move at most hops to right by the ()-th step, which means during the steps, there exist at least steps at each of which one of the links in is missing. Since at most one link is missing at each step and , every link in exists at each of the steps. By this and , A succeeds to reach by moving to left, which means at least nodes are explored. □
Exploration algorithm. Algorithm 5 describes the exploration algorithm. The algorithm repeats E
xpH
for
times (lines 1–5) and E
xpH
alf for
times (lines 6–10). We call the part repeating E
xpH
(lines 1-5)
the first part and the part repeating E
xpH
alf the second part (lines 6–10). In the first part,
nodes are explored and, in the second part, the remaining
nodes are explored.
| Algorithm 5 Exploration algorithm for |
1: //starting the first part 2: while () do 3: Let t be the current step and be the current node 4: ExpH 5: 6: //starting the second part 7: while () do 8: Let t be the current step and be the current node 9: ExpHalf 10: |
Theorem 3. For , the exploration time of 1-interval connected rings by a single agent with the view is upper-bounded by .
Proof. It suffices to show that A completes exploration within steps by Algorithm 5 when . It is proven that the total exploration time of the first part is and that of the second part is .
We first consider the first part. Note that, since , and thus the first part is always executed at least once. Let be the step when A starts the p-th ExpH. We can show that for , A can explore nodes by ExpH by induction and the exploration time of the first part is as in the proof of Lemma 2.
We then consider the second part. By Lemma 2, A exists at the right or left extremity of and at the start of the second part. Thus, since A explores a half of within steps by Lemma 4, the exploration time of the second part is . As a result, the exploration time of Algorithm 3 is . □