Late Acceptance Hill-Climbing Matheuristic for the General Lot Sizing and Scheduling Problem with Rich Constraints
Abstract
1. Introduction
- We investigate the relationship between the original formulation of the general lot sizing and scheduling problem (GLSP) and the GLSP-RP by providing a comprehensive discussion of both problems.
- For solving the GLSP-RP, we propose the Late Acceptance Hill-climbing Matheuristic (LAHCM) as a general solution framework, which is inspired by and integrates the LAHC strategy with the exact approaches, i.e., the solution of optimization models for reduced problems configured in the spirit of the LAHC. To assess its performance, we evaluate it over a set of well-defined instances. The computational results indicate that by means of our approach we are able to improve the objective function values for several instances where a general-purpose solver such as CPLEX (https://www.ibm.com/nl-en/analytics/cplex-optimizer) is not able to find optimal solutions in the given time limit of 1800 s.
2. Literature Review
2.1. The General Lot Sizing and Scheduling Problem
2.2. Solution Approaches and Model Extensions
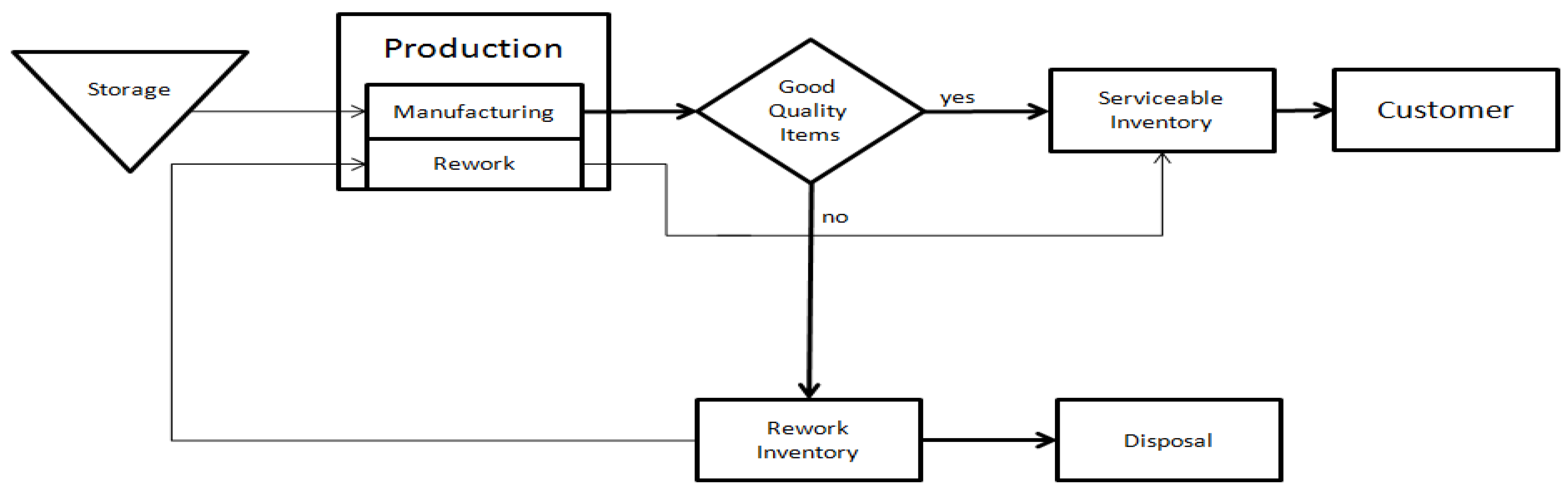
3. The GLSP with Rework and Lifetime Constraint for Defective Items
4. Late Acceptance Hill-Climbing Matheuristic Template
4.1. Initial Solution
| Algorithm 1: Matheuristic Late Acceptance Hill-Climbing algorithm (LAHCM) |
 |
4.2. Mathematical Programming-Based Neighborhood
- Strategy 1 (): The variables are fixed except for those regarding a product j selected at random.
- Strategy 2 ():The variables are fixed except for those regarding two products j and selected at random and where .
- Strategy 3 ():The variables are fixed except for those regarding three products j, , and selected at random and where .
| Algorithm 2: Fix and Solve algorithm for the GLSP-RP |
 |
4.3. Illustrative Example of the Functioning of the LAHCM for the GLSP-RP
5. Computational Results
5.1. Data Set
5.2. Algorithm Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Goerler, A.; Pahl, J.; Voß, S. Simultaneous Lot Sizing and Scheduling for Contamination Sensitive Items with Rework Options; Working Paper; Institute of Information Systems, University of Hamburg: Hamburg, Germany, 2017. [Google Scholar]
- Maniezzo, V.; Stützle, T.; Voß, S. Matheuristics: Hybridizing Metaheuristics and Mathematical Programming. In Annals of Information Systems 10; Springer: New York, NY, USA, 2009. [Google Scholar]
- Meira, W.H.T.; Magatão, L.; Relvas, S.; Barbosa-Póvoa, A.P.; Neves, F., Jr.; Arruda, L.V. A matheuristic decomposition approach for the scheduling of a single-source and multiple destinations pipeline system. Eur. J. Oper. Res. 2018, 268, 665–687. [Google Scholar] [CrossRef]
- Lalla-Ruiz, E.; Voß, S. A popmusic approach for the multi-depot cumulative capacitated vehicle routing problem. Optim. Lett. 2019, 14, 671–691. [Google Scholar] [CrossRef]
- Caserta, M.; Voß, S. Accelerating mathematical programming techniques with the corridor method. Int. J. Prod. Res. 2020. [Google Scholar] [CrossRef]
- Lalla-Ruiz, E.; Voß, S. POPMUSIC as a matheuristic for the berth allocation problem. Ann. Math. Artif. Intell. 2016, 76, 173–189. [Google Scholar] [CrossRef]
- Archetti, C.; Speranza, M.G. A survey on matheuristics for routing problems. EURO J. Comput. Optim. 2014, 2, 223–246. [Google Scholar] [CrossRef]
- Burke, E.K.; Bykov, Y. A late acceptance strategy in hill-climbing for exam timetabling problems. In Proceedings of the PATAT 2008 Conference, Montreal, QC, Canada, 18 August 2008. [Google Scholar]
- Terzi, M.; Arbaoui, T.; Yalaoui, F.; Benatchba, K. Solving the Unrelated Parallel Machine Scheduling Problem with Setups Using Late Acceptance Hill Climbing. In Proceedings of the Asian Conference on Intelligent Information and Database Systems, Phuket, Thailand, 23–26 March 2020; pp. 249–258. [Google Scholar]
- Zhu, X.; Wilhelm, W. Scheduling and lot sizing with sequence-dependent setup: A literature review. IIE Trans. 2006, 38, 987–1007. [Google Scholar] [CrossRef]
- Copil, K.; Wörbelauer, M.; Meyr, H.; Tempelmeier, H. Simultaneous lotsizing and scheduling problems: A classification and review of models. OR Spectr. 2017, 39, 1–64. [Google Scholar] [CrossRef]
- Fleischmann, B.; Meyr, H. The general lotsizing and scheduling problem. OR Spectr. 1997, 19, 11–21. [Google Scholar] [CrossRef]
- Meyr, H. Simultaneous lotsizing and scheduling by combining local search with dual reoptimization. Eur J. Oper. Res. 2000, 120, 311–326. [Google Scholar] [CrossRef]
- Koçlar, A.; Süral, H. A note on The general lot sizing and scheduling problem. OR Spectr. 2005, 27, 145–146. [Google Scholar] [CrossRef]
- Haase, K. Lotsizing and Scheduling for Production Planning; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin, Germany, 1994; Volume 408. [Google Scholar]
- Haase, K. Capacitated Lot-Sizing with Sequence Dependent Setup Costs. OR Spectr. 1996, 18, 51–59. [Google Scholar] [CrossRef]
- Meyr, H. Simultaneous lotsizing and scheduling on parallel machines. Eur. J. Oper. Res. 2002, 139, 277–292. [Google Scholar] [CrossRef]
- Meyr, H. Simultane Losgrößen- und Reihenfolgeplanung bei mehrstufiger kontinuierlicher Fertigung. Z. Betriebswirtschaft 2004, 74, 585–610. [Google Scholar]
- Seeanner, F.; Meyr, H. Multi-stage simultaneous lot-sizing and scheduling for flow line production. Spectrum 2013, 35, 33–73. [Google Scholar] [CrossRef]
- Toledo, C.; Kimms, A.; França, P.; Morabito, R. A Mathematical Model for the Synchronized and Integrated Two-Level Lot Sizing and Scheduling Problem; Working Paper; University of Campinas: Campinas, Brazil, 2006. [Google Scholar]
- Toledo, C.; França, P.; Rosa, K. Meta-heuristic approaches for a soft drink industry problem. In Proceedings of the ACM Symposium on Applied Computing, Ceara, Brazil, 16–20 March 2008; pp. 1777–1781. [Google Scholar]
- Toledo, C.; de Jesus Filho, J.; França, P. Meta-heuristic approaches for a soft drink industry problem. In Proceedings of the 2008 IEEE International Conference on Emerging Technologies and Factory Automation, Hamburg, Germany, 18 September 2008; pp. 1384–1391. [Google Scholar]
- Toledo, C.; França, P.; Morabito, R.; Kimms, A. Multi-population genetic algorithm to solve the synchronized and integrated two-level lot sizing and scheduling problem. Int. J. Prod. Res. 2009, 47, 3097–3119. [Google Scholar] [CrossRef]
- Ferreira, D.; Morabito, R.; Rangel, S. Solution approaches for the soft drink integrated production lot sizing and scheduling problem. Eur. J. Oper. Res. 2009, 196, 697–706. [Google Scholar] [CrossRef]
- Ferreira, D.; Morabito, R.; Rangel, S. Relax and fix heuristics to solve one-stage one-machine lot-scheduling models for small-scale soft drink plants. Comput. Oper. Res. 2010, 37, 684–691. [Google Scholar] [CrossRef]
- Ferreira, D.; Clark, A.; Almada-Lobo, B.; Morabito, R. Single-stage formulations for synchronised two-stage lot sizing and scheduling in soft drink production. Int. J. Prod. Econ. 2012, 136, 255–265. [Google Scholar] [CrossRef]
- Toledo, C.; de Oliveira, L.; de Freitas Pereira, R.; França, P.; Morabito, R. A genetic algorithm/mathematical programming approach to solve a two-level soft drink production problem. Comput. Oper. Res. 2014, 48, 40–52. [Google Scholar] [CrossRef]
- Baldo, T.; Santos, M.; Almada-Lobo, B.; Morabito, R. An optimization approach for the lot sizing and scheduling problem in the brewery industry. Comput. Ind. Eng. 2014, 72, 58–71. [Google Scholar] [CrossRef]
- Taillard, E.; Voß, S. POPMUSIC Partial Optimization Metaheuristic Under Special Intensification Conditions. In Essays and Surveys in Metaheuristics; Ribeiro, C., Hansen, P., Eds.; Kluwer: Alphen aan den Rijn, The Netherlands, 2002; pp. 613–629. [Google Scholar] [CrossRef]
- Fandel, G.; Stammen-Hegene, C. Simultaneous lot sizing and scheduling for multi-product multi-level production. Int. J. Prod. Econ. 2006, 104, 308–316. [Google Scholar] [CrossRef]
- Mohammadi, M.; Fatemi Ghomi, S.; Karimi, B.; Torabi, S. Rolling-horizon and fix-and-relax heuristics for the multi-product multi-level capacitated lotsizing problem with sequence-dependent setups. J. Intell. Manuf. 2010, 21, 501–510. [Google Scholar] [CrossRef]
- Mohammadi, M. Integrating lotsizing, loading, and scheduling decisions in flexible flow shops. Int. J. Adv. Manuf. Technol. 2010, 50, 1165–1174. [Google Scholar] [CrossRef]
- Mohammadi, M.; Torabi, S.; Fatemi Ghomi, S.; Karimi, B. A new algorithmic approach for capacitated lot-sizing problem in flow shops with sequence-dependent setups. Int. J. Adv. Manuf. Technol. 2010, 49, 201–211. [Google Scholar] [CrossRef]
- Toso, E.; Morabito, R.; Clark, A. Lot sizing and sequencing optimisation at an animal-feed plant. Comput. Ind. Eng. 2009, 57, 813–821. [Google Scholar] [CrossRef]
- Lang, J. Production and Inventory Management with Substitutions; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin, Germany, 2010. [Google Scholar]
- Almeder, C.; Almada-Lobo, B. Synchronisation of scarce resources for a parallel machine lotsizing problem. Int. J. Prod. Res. 2011, 49, 7315–7335. [Google Scholar] [CrossRef]
- Transchel, S.; Minner, S.; Kallrath, J.; Löhndorf, N.; Eberhard, U. A hybrid general lot-sizing and scheduling formulation for a production process with a two-stage product structure. Int. J. Prod. Res. 2011, 49, 2463–2480. [Google Scholar] [CrossRef]
- Camargo, V.; Toledo, F.; Almada-Lobo, B. Three time-based scale formulations for the two-stage lot sizing and scheduling in process industries. J. Oper. Res. Soc. 2012, 63, 1613–1630. [Google Scholar] [CrossRef]
- Camargo, V.; Toledo, F.; Almada-Lobo, B. HOPS Hamming-Oriented Partition Search for production planning in the spinning industry. Eur. J. Oper. Res. 2014, 234, 266–277. [Google Scholar] [CrossRef]
- Santos, M.; Almada-Lobo, B. Integrated pulp and paper mill planning and scheduling. Comput. Ind. Eng. 2012, 63, 1–12. [Google Scholar] [CrossRef]
- Figueira, G.; Santos, M.; Almada-Lobo, B. A hybrid VNS approach for the short-term production planning and scheduling: A case study in the pulp and paper industry. Comput. Oper. Res. 2013, 40, 1804–1818. [Google Scholar] [CrossRef]
- Furlan, M.; Almada-Lobo, B.; Santos, M.; Morabito, R. Unequal individual genetic algorithm with intelligent diversification for the lot-scheduling problem in integrated mills using multiple-paper machines. Comput. Oper. Res. 2015, 59, 33–50. [Google Scholar] [CrossRef]
- Wolter, A.; Helber, S. Simultaneous Production and Maintenance Planning for a Single Capacitated Resource Facing Both a Dynamic Demand and Intensive Wear and Tear; Hannover Economic Papers (HEP); Leibniz Universität Hannover, Wirtschaftswissenschaftliche Fakultät: Hannover, Germany, 2013. [Google Scholar]
- Mohammadi, M.; Poursabzi, O. A rolling horizon-based heuristic to solve a multi-level general lot sizing and scheduling problem with multiple machines (MLGLSP_MM) in job shop manufacturing system. Uncertain Supply Chain Manag. 2014, 2, 167–178. [Google Scholar] [CrossRef]
- Rohaninejad, M.; Kheirkhah, A.; Fattahi, P. Simultaneous lot-sizing and scheduling in flexible job shop problems. Int. J. Adv. Manuf. Technol. 2015, 78, 1–18. [Google Scholar] [CrossRef]
- Pahl, J.; Voß, S.; Woodruff, D.L. Discrete Lot-Sizing and Scheduling with Sequence-Dependent Setup Times and Costs Including Deterioration and Perishability Constraints. In Proceedings of the Hawaiian International Conference on Systems Sciences (HICSS), Kauai, HI, USA, 4–7 January 2011; pp. 1–10. [Google Scholar]
- Alem, D.; Curcio, E.; Amorim, P.; Almada-Lobo, B. A computational study of the general lot-sizing and scheduling model under demand uncertainty via robust and stochastic approaches. Comput. Oper. Res. 2018, 90, 125–141. [Google Scholar] [CrossRef]
- Alipour, Z.; Jolai, F.; Monabbati, E.; Zaerpour, N. General lot-sizing and scheduling for perishable food products. RAIRO-Oper. Res. 2020, 54, 913–931. [Google Scholar] [CrossRef]
- Goerler, A.; Voß, S. Dynamic lot-sizing with rework of defective items and minimum lot-size constraints. Int. J. Prod. Res. 2016, 54, 2284–2297. [Google Scholar] [CrossRef]
- Alzaqebah, M.; Abdullah, S. An adaptive artificial bee colony and late-acceptance hill-climbing algorithm for examination timetabling. J. Sched. 2014, 17, 249–262. [Google Scholar] [CrossRef]
- Goerler, A.; Schulte, F.; Voß, S. An Application of Late Acceptance Hill-Climbing to the Traveling Purchaser Problem; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2013; pp. 173–183. [Google Scholar]
- Yuan, B.; Zhang, C.; Shao, X. A late acceptance hill-climbing algorithm for balancing two-sided assembly lines with multiple constraints. J. Intell. Manuf. 2015, 26, 159–168. [Google Scholar] [CrossRef]
- Tierney, K. Late acceptance hill climbing for the liner shipping fleet repositioning problem. In Proceedings of the 14th EU/ME Workshop, Hamburg, Germany, 1 March 2013; pp. 21–27. [Google Scholar]
- Burke, E.K.; Bykov, Y. The late acceptance Hill-Climbing heuristic. Eur. J. Oper. Res. 2017, 258, 70–78. [Google Scholar] [CrossRef]
- Lobo, F.G.; Bazargani, M.; Burke, E.K. A cutoff time strategy based on the coupon collector’s problem. Eur. J. Oper. Res. 2020, 286, 101–114. [Google Scholar] [CrossRef]
- Frøseth, G.T.; Rönnquist, A. Finding the train composition causing the greatest fatigue damage in railway bridges by Late Acceptance Hill Climbing. Eng. Struct. 2019, 196, 109342. [Google Scholar] [CrossRef]
| Indices | |
|---|---|
| Products with | |
| Denoting the last micro-period of a macro-period t | |
| m | Micro-periods with |
| Set of micro-periods m within macro-period t | |
| t | Macro-periods with |
| Parameters | |
| Available capacity in macro-period t in time units | |
| Demand of product j in period t | |
| Sequence-dependent setup costs for a change over from product i to j | |
| Inventory holding cost factor for product j | |
| Minimum lot size amount of product j | |
| Fixed number of micro-periods within a macro-period t | |
| setup times for a change over from product i to j | |
| Process time per unit of product j | |
| M | big number, e.g., |
| Variables | |
| Inventory of product j in period t | |
| Binary setup variable, 1 if product j is set up for production | |
| in micro-period m, 0 otherwise | |
| Production amount of product j in micro-period m | |
| Changeover variable, 1 if production is changed from product i to j | |
| in micro-period m, 0 otherwise |
| Parameters | |
|---|---|
| Inventory holding cost factor for defective items of product j | |
| Disposal cost for one perished item of product j | |
| Lifetime of product j in micro-periods | |
| Proportion of defective items of product j in t | |
| Process time for reworking a defective item per unit of product j | |
| Variables | |
| Number of defective items of product j produced in micro-period m | |
| Number of perished items of rework inventory of product j | |
| in micro-period m | |
| Number of defective items stored in rework inventory of product j | |
| in micro-period m | |
| Binary joint-setup variable, 1 if product j is set up for production and/or rework | |
| in micro-period m, 0 otherwise | |
| Quantity of defective items of product j reworked in micro-period m | |
| Production amount of good-quality items of product j in micro-period m |
| GLSP | t: | 1 | 2 | 3 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |||
| j = 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |||
| j = 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | |||
| j = 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |||
| j = 1 | 96 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 90 | 0 | 0 | 108 | 0 | 0 | |||
| j = 2 | 0 | 79 | 0 | 0 | 0 | 0 | 0 | 0 | 159 | 0 | 0 | 0 | 0 | 58 | 0 | |||
| j = 3 | 0 | 0 | 113 | 0 | 0 | 0 | 144 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 93 | |||
| j = 1 | 1 | 0 | 0 | |||||||||||||||
| j = 2 | 79 | 0 | 0 | |||||||||||||||
| j = 2 | 6 | 0 | 0 | |||||||||||||||
| GLSP-RP | t: | 1 | 2 | 3 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |||
| j = 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |||
| j = 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | |||
| j = 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |||
| j = 1 | 137 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 50 | 107 | 0 | 0 | 0 | 0 | |||
| j = 2 | 0 | 149 | 0 | 0 | 0 | 0 | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 50 | 0 | |||
| j = 3 | 0 | 0 | 10 | 97 | 0 | 243 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| j = 1 | 137 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 49 | 105 | 0 | 0 | 0 | 0 | |||
| j = 2 | 0 | 148 | 0 | 0 | 0 | 0 | 0 | 0 | 99 | 0 | 0 | 0 | 0 | 49 | 0 | |||
| j = 3 | 0 | 0 | 10 | 97 | 0 | 243 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| j = 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 0 | 0 | 0 | 0 | |||
| j = 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | |||
| j = 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| j = 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 0 | 0 | 0 | |||
| j = 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| j = 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| j = 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| j = 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | |||
| j = 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| j = 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 0 | 0 | 0 | 0 | |||
| j = 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| j = 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| j = 1 | 42 | 0 | 0 | |||||||||||||||
| j = 2 | 148 | 9 | 0 | |||||||||||||||
| j = 2 | 0 | 93 | 0 | |||||||||||||||
| GLSP | t: | 1 | 2 | 3 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |||
| j = 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |||
| j = 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | |||
| j = 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |||
| GLSP | t: | 1 | 2 | 3 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |||
| j = 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| j = 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| j = 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |||
| GLSP-RP | t: | 1 | 2 | 3 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |||
| j = 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | |||
| j = 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||
| j = 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |||
| GLSP-RP | t: | 1 | 2 | 3 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |||
| j = 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | |||
| j = 2 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||
| j = 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |||
| Parameter | Class A | Class B | Class C |
|---|---|---|---|
| # of instances | 50 | 50 | 50 |
| # of products (j) | 5 | 4 | 6 |
| # of macro-periods (t) | 4 | 3 | 2 |
| # of micro-periods within t () | 7 | 6 | 8 |
| [0;40,120] | [0;40,120] | [0;600,1000] | |
| [100,400] | [100,400] | [100,400] | |
| /10 | /10 | [10,40] | |
| 1 | 1 | 1 | |
| 0.5 | 0.5 | 0.75 | |
| [10,20] | [10,20] | [1,5] | |
| / | / | (/)*0.75 | |
| 10 | 10 | 50 | |
| 1000 | 1000 | 1000 | |
| 3 | 3 | 2 | |
| [0;0.005,0.03] | [0;0.005,0.03] | [0;0.005,0.03] | |
| Class A | CPLEX | LAHCM () | LAHCM () | LAHCM () | LAHCM () | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Instance | Objective | Time | Objective | Time | Iterations | Objective | Time | Iterations | Objective | Time | Iterations | Objective | Time | Iterations | |||||
| 1 | 6049.71 | 1800 s | 15535.14 | 106 s | 5 | 5749.71 | 568 s | 37 | 5749.71 | 548 s | 52 | 5799.71 | 665 s | 69 | |||||
| 2 | 6099.29 | 1800 s | 11273.29 | 101 s | 3 | 6646.57 | 229 s | 27 | 5392.71 | 255 s | 50 | 5443.85 | 508 s | 88 | |||||
| 3 | 4597.86 | 1800 s | 9076.71 | 241 s | 8 | 3902.43 | 204 s | 13 | 3902.43 | 208 s | 29 | 4295.85 | 800 s | 120 | |||||
| 4 | 10941.60 | 1800 s | 8799.86 | 235 s | 4 | 8477.86 | 922 s | 38 | 8318.14 | 1128 s | 57 | 8088.00 | 1558 s | 94 | |||||
| 5 | 6332.86 | 1800 s | 14586.85 | 119 s | 4 | 5803.00 | 407 s | 36 | 5733.50 | 655 s | 45 | 5715.71 | 849 s | 57 | |||||
| 6 | 7872.14 | 1800 s | 7422.14 | 121 s | 4 | 7372.14 | 322 s | 19 | 7372.14 | 622 s | 46 | 7249.28 | 1172 s | 76 | |||||
| 7 | 5074.14 | 1800 s | 14331.85 | 102 s | 7 | 5363.71 | 286 s | 30 | 4875.57 | 280 s | 39 | 4674.14 | 543 s | 65 | |||||
| 8 | 7044.71 | 1800 s | 10723.57 | 125 s | 7 | 6157.85 | 293 s | 34 | 7118.43 | 407 s | 39 | 6367.85 | 669 s | 86 | |||||
| 9 | 7846.14 | 1800 s | 9596.28 | 116 s | 5 | 8243.28 | 722 s | 31 | 8048.57 | 619 s | 28 | 7763.42 | 1434 s | 112 | |||||
| 10 | 5972.00 | 1800 s | 6290.29 | 239 s | 11 | 5884.85 | 605 s | 39 | 6032.57 | 452 s | 45 | 5884.85 | 935 s | 86 | |||||
| 11 | 5030.00 | 1800 s | 6050.71 | 137 s | 5 | 4780.00 | 529 s | 44 | 4685.71 | 501 s | 35 | 4529.42 | 543 s | 78 | |||||
| 12 | 4625.00 | 1800 s | 4628.28 | 144 s | 9 | 4297.28 | 251 s | 32 | 4347.29 | 304 s | 41 | 4185.57 | 316 s | 74 | |||||
| 13 | 5176.00 | 1800 s | 5909.57 | 168 s | 7 | 4179.85 | 263 s | 18 | 3925.71 | 364 s | 44 | 3957.71 | 389 s | 65 | |||||
| 14 | 6927.00 | 1800 s | 7077.00 | 289 s | 12 | 7043.29 | 318 s | 13 | 6526.99 | 280 s | 27 | 6327.00 | 450 s | 54 | |||||
| 15 | 5316.14 | 1800 s | 5450.43 | 137 s | 6 | 5252.85 | 321 s | 22 | 4966.14 | 343 s | 34 | 5152.85 | 408 s | 61 | |||||
| 16 | 7428.86 | 1800 s | 8962.29 | 160 s | 10 | 6831.43 | 376 s | 20 | 7167.00 | 1085 s | 70 | 6627.71 | 764 s | 84 | |||||
| 17 | 5168.00 | 1800 s | 10950.85 | 103 s | 4 | 5178.00 | 385 s | 17 | 4878.00 | 376 s | 47 | 4859.14 | 705 s | 71 | |||||
| 18 | 4793.71 | 1800 s | 8443.43 | 105 s | 4 | 4019.86 | 293 s | 21 | 4069.85 | 362 s | 56 | 4119.85 | 330 s | 75 | |||||
| 19 | 6122.14 | 1800 s | 7208.71 | 409 s | 7 | 5606.57 | 721 s | 42 | 6222.14 | 590 s | 33 | 5318.85 | 1714 s | 105 | |||||
| 20 | 6858.00 | 1800 s | 9694.43 | 120 s | 5 | 6396.29 | 669 s | 61 | 6096.71 | 548 s | 49 | 6061.28 | 946 s | 91 | |||||
| 21 | 5355.57 | 1800 s | 8035.28 | 114 s | 3 | 5455.57 | 530 s | 36 | 5455.57 | 259 s | 59 | 5455.57 | 1066 s | 105 | |||||
| 22 | 5983.86 | 1800 s | 6472.57 | 118 s | 6 | 6026.14 | 229 s | 24 | 5477.71 | 615 s | 49 | 5477.71 | 612 s | 72 | |||||
| 23 | 7784.29 | 1800 s | 14793.29 | 141 s | 5 | 6427.71 | 875 s | 33 | 6384.28 | 979 s | 71 | 6876.14 | 965 s | 98 | |||||
| 24 | 4834.86 | 1800 s | 5756.00 | 131 s | 4 | 4913.71 | 156 s | 23 | 5325.71 | 344 s | 42 | 4715.14 | 652 s | 76 | |||||
| 25 | 7774.29 | 1800 s | 7876.29 | 146 s | 3 | 7086.29 | 272 s | 18 | 7186.29 | 223 s | 27 | 7230.57 | 1040 s | 59 | |||||
| 26 | 4199.57 | 1800 s | 7983.57 | 106 s | 4 | 3674.43 | 226 s | 31 | 3854.43 | 260 s | 39 | 3656.42 | 443 s | 87 | |||||
| 27 | 6020.71 | 1800 s | 9443.57 | 127 s | 3 | 5218.00 | 170 s | 28 | 5370.71 | 466 s | 55 | 5218.00 | 1031 s | 121 | |||||
| 28 | 6260.29 | 1800 s | 7497.14 | 133 s | 4 | 5775.43 | 234 s | 20 | 6956.29 | 298 s | 24 | 5624.28 | 512 s | 70 | |||||
| 29 | 9204.29 | 1800 s | 8537.71 | 134 s | 8 | 7157.14 | 705 s | 36 | 7157.14 | 809 s | 57 | 7157.14 | 1542 s | 122 | |||||
| 30 | 3922.71 | 1800 s | 4428.43 | 113 s | 7 | 3572.71 | 172 s | 24 | 3572.71 | 229 s | 36 | 3572.71 | 528 s | 61 | |||||
| 31 | 7513.14 | 1800 s | 15084.29 | 102 s | 3 | 5958.00 | 403 s | 34 | 5770.00 | 649 s | 47 | 5770.00 | 1800 s | 115 | |||||
| 32 | 6869.14 | 1800 s | 7081.57 | 259 s | 7 | 6673.43 | 253 s | 21 | 6233.28 | 1210 s | 59 | 6137.14 | 1157 s | 84 | |||||
| 33 | 4902.71 | 1800 s | 8331.71 | 142 s | 4 | 4502.14 | 306 s | 29 | 4502.14 | 671 s | 71 | 4704.42 | 1110 s | 110 | |||||
| 34 | 5602.86 | 1800 s | 9533.86 | 133 s | 4 | 5488.57 | 316 s | 30 | 5638.57 | 598 s | 24 | 5576.14 | 904 s | 61 | |||||
| 35 | 8134.57 | 1800 s | 13257.86 | 202 s | 5 | 6821.86 | 700 s | 37 | 6571.85 | 706 s | 42 | 6571.85 | 1589 s | 111 | |||||
| 36 | 3811.86 | 1800 s | 5019.71 | 164 s | 7 | 3667.29 | 208 s | 33 | 3720.71 | 244 s | 31 | 3517.29 | 363 s | 72 | |||||
| 37 | 6487.71 | 1800 s | 8290.29 | 131 s | 7 | 6637.29 | 410 s | 32 | 6588.71 | 477 s | 38 | 6637.28 | 1037 s | 74 | |||||
| 38 | 8037.43 | 1800 s | 9030.29 | 179 s | 3 | 6831.14 | 533 s | 21 | 6831.14 | 827 s | 57 | 6831.14 | 1345 s | 62 | |||||
| 39 | 7095.43 | 1800 s | 7939.00 | 131 s | 4 | 6696.29 | 272 s | 27 | 6053.71 | 593 s | 50 | 5928.85 | 653 s | 72 | |||||
| 40 | 4176.00 | 1800 s | 9561.14 | 107 s | 5 | 4226.00 | 202 s | 28 | 4274.29 | 237 s | 48 | 4174.28 | 538 s | 98 | |||||
| 41 | 4141.71 | 1800 s | 4058.57 | 139 s | 4 | 3974.29 | 170 s | 15 | 4031.43 | 173 s | 31 | 3931.43 | 453 s | 81 | |||||
| 42 | 4625.00 | 1800 s | 7156.71 | 103 s | 5 | 5435.00 | 145 s | 17 | 4337.43 | 585 s | 71 | 4437.43 | 839 s | 91 | |||||
| 43 | 9968.57 | 1800 s | 9535.99 | 602 s | 9 | 8421.99 | 604 s | 49 | 8622.00 | 701 s | 38 | 8542.14 | 1333 s | 81 | |||||
| 44 | 4851.29 | 1800 s | 9972.42 | 105 s | 5 | 4497.14 | 263 s | 27 | 4669.14 | 406 s | 31 | 4597.14 | 449 s | 64 | |||||
| 45 | 5191.14 | 1800 s | 10550.71 | 101 s | 4 | 3649.57 | 184 s | 20 | 3599.57 | 250 s | 25 | 3601.71 | 474 s | 92 | |||||
| 46 | 7982.71 | 1800 s | 14014.29 | 101 s | 3 | 7749.57 | 510 s | 19 | 6879.29 | 629 s | 45 | 7059.28 | 1304 s | 89 | |||||
| 47 | 7434.43 | 1800 s | 8172.43 | 131 s | 4 | 6610.43 | 313 s | 26 | 6214.00 | 514 s | 30 | 6490.42 | 865 s | 57 | |||||
| 48 | 8093.57 | 1800 s | 8817.57 | 139 s | 4 | 8958.99 | 266 s | 48 | 7449.14 | 490 s | 34 | 6791.85 | 1423 s | 83 | |||||
| 49 | 6721.14 | 1800 s | 6426.29 | 140 s | 7 | 6304.29 | 325 s | 21 | 5825.71 | 385 s | 33 | 5725.71 | 863 s | 82 | |||||
| 50 | 6238.43 | 1800 s | 8563.86 | 247 s | 8 | 6304.43 | 475 s | 24 | 4960.85 | 550 s | 51 | 4960.85 | 1208 s | 103 | |||||
| avg. | 6289.89 | 1800.00 s | 8864.68 | 157.96 s | 5.52 | 5838.03 | 382.22 s | 28.50 | 5698.86 | 506.08 s | 43.62 | 5587.84 | 875.92 s | 83.28 | |||||
| Gap to CPLEX (in %) | +40.9% | −91.2% | - | −7.2% | −78.8% | - | −9.4% | −71.9% | - | −11.2% | −51.3% | - | |||||||
| # of better sol. found* | 6 | 37 | 40 | 48 | |||||||||||||||
| Class B | CPLEX | LAHCM () | LAHCM () | LAHCM () | LAHCM () | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Instance | Objective | Time | Objective | Time | Iterations | Objective | Time | Iterations | Objective | Time | Iterations | Objective | Time | Iterations | |||||
| 1 | 1620.00 | 107 s | 2187.83 | 31 s | 4 | 1818.17 | 65 s | 32 | 1620.00 | 94 s | 43 | 1620.00 | 114 s | 60 | |||||
| 2 | 1957.33 | 66 s | 2057.33 | 23 s | 5 | 2003.67 | 58 s | 18 | 1957.33 | 83 s | 24 | 1957.33 | 159 s | 54 | |||||
| 3 | 1386.00 | 21 s | 1386.00 | 16 s | 5 | 1386.00 | 17 s | 12 | 1386.00 | 28 s | 22 | 1386.00 | 57 s | 65 | |||||
| 4 | 3474.33 | 332 s | 4319.99 | 24 s | 6 | 3554.66 | 128 s | 37 | 3474.33 | 324 s | 33 | 3474.33 | 404 s | 69 | |||||
| 5 | 2344.50 | 45 s | 4440.83 | 20 s | 5 | 2344.49 | 43 s | 25 | 2344.50 | 48 s | 33 | 2344.49 | 94 s | 63 | |||||
| 6 | 2170.17 | 56 s | 4037.17 | 10 s | 3 | 2170.16 | 26 s | 13 | 2387.66 | 122 s | 33 | 2170.17 | 106 s | 58 | |||||
| 7 | 4153.33 | 313 s | 7189.66 | 35 s | 3 | 4304.99 | 146 s | 24 | 4153.33 | 320 s | 59 | 4153.33 | 334 s | 62 | |||||
| 8 | 2591.67 | 341 s | 2591.66 | 57 s | 4 | 2591.66 | 93 s | 17 | 2591.67 | 127 s | 28 | 2591.66 | 322 s | 73 | |||||
| 9 | 1699.50 | 33 s | 6009.00 | 13 s | 7 | 1699.50 | 38 s | 14 | 1699.50 | 60 s | 24 | 1699.49 | 122 s | 68 | |||||
| 10 | 3156.83 | 97 s | 4114.00 | 56 s | 5 | 3156.83 | 110 s | 24 | 3164.66 | 119 s | 30 | 3156.83 | 225 s | 62 | |||||
| 11 | 2203.17 | 27 s | 2203.17 | 13 s | 5 | 2203.17 | 30 s | 17 | 2203.16 | 59 s | 24 | 2203.16 | 98 s | 54 | |||||
| 12 | 3401.00 | 757 s | 3401.00 | 72 s | 5 | 3602.33 | 169 s | 24 | 3401.00 | 167 s | 52 | 3401.00 | 229 s | 58 | |||||
| 13 | 2395.50 | 64 s | 2645.50 | 36 s | 7 | 2395.50 | 80 s | 17 | 2464.83 | 118 s | 28 | 2395.50 | 179 s | 69 | |||||
| 14 | 2594.00 | 32 s | 6585.67 | 27 s | 4 | 2594.00 | 79 s | 23 | 2593.90 | 75 s | 32 | 2593.99 | 185 s | 110 | |||||
| 15 | 2806.67 | 146 s | 4688.33 | 17 s | 6 | 2806.67 | 168 s | 22 | 2806.66 | 94 s | 45 | 2806.66 | 146 s | 55 | |||||
| 16 | 2042.17 | 78 s | 2359.33 | 32 s | 4 | 2359.33 | 37 s | 14 | 2359.33 | 51 s | 30 | 2042.16 | 214 s | 97 | |||||
| 17 | 2843.33 | 112 s | 2993.33 | 26 s | 4 | 2843.33 | 56 s | 13 | 2843.33 | 73 s | 23 | 2843.33 | 191 s | 55 | |||||
| 18 | 3975.17 | 1061 s | 4219.33 | 20 s | 4 | 4126.33 | 56 s | 15 | 4055.99 | 313 s | 32 | 3975.16 | 304 s | 56 | |||||
| 19 | 2787.33 | 44 s | 4090.17 | 25 s | 4 | 2787.33 | 29 s | 16 | 3390.50 | 93 s | 40 | 2787.33 | 192 s | 72 | |||||
| 20 | 1514.00 | 33 s | 2137.33 | 29 s | 4 | 1514.00 | 41 s | 27 | 1514.00 | 74 s | 38 | 1514.00 | 109 s | 94 | |||||
| 21 | 3339.50 | 233 s | 4865.83 | 65 s | 5 | 3339.50 | 68 s | 13 | 3339.50 | 151 s | 45 | 3339.50 | 227 s | 91 | |||||
| 22 | 2790.00 | 173 s | 3770.67 | 29 s | 3 | 3341.99 | 53 s | 13 | 2789.99 | 97 s | 38 | 2790.00 | 146 s | 70 | |||||
| 23 | 3647.00 | 175 s | 9462.00 | 42 s | 4 | 3879.67 | 107 s | 12 | 3879.66 | 194 s | 28 | 3647.00 | 319 s | 62 | |||||
| 24 | 3951.00 | 427 s | 4719.99 | 46 s | 5 | 3998.66 | 138 s | 22 | 4065.33 | 393 s | 47 | 3951.00 | 251 s | 58 | |||||
| 25 | 1794.00 | 27 s | 1794.00 | 16 s | 5 | 1794.00 | 36 s | 15 | 1794.00 | 61 s | 26 | 1794.00 | 92 s | 61 | |||||
| 26 | 2578.50 | 89 s | 3168.00 | 34 s | 3 | 2679.16 | 68 s | 34 | 2578.50 | 154 s | 47 | 2578.50 | 128 s | 69 | |||||
| 27 | 2530.67 | 241 s | 8331.33 | 13 s | 3 | 2803.17 | 44 s | 22 | 2803.16 | 55 s | 32 | 2530.66 | 152 s | 64 | |||||
| 28 | 983.50 | 18 s | 1083.50 | 20 s | 4 | 983.49 | 27 s | 17 | 983.50 | 49 s | 46 | 983.50 | 53 s | 58 | |||||
| 29 | 2951.50 | 156 s | 3154.33 | 42 s | 5 | 3154.33 | 51 s | 13 | 3154.33 | 83 s | 23 | 2951.49 | 93 s | 53 | |||||
| 30 | 2552.00 | 144 s | 2551.99 | 37 s | 4 | 2555.66 | 48 s | 20 | 2552.00 | 80 s | 23 | 2697.16 | 127 s | 58 | |||||
| 31 | 2697.17 | 136 s | 3527.83 | 38 s | 7 | 2697.17 | 41 s | 18 | 2697.17 | 33 s | 24 | 2697.17 | 173 s | 77 | |||||
| 32 | 3377.83 | 1003 s | 3377.83 | 34 s | 5 | 3377.83 | 38 s | 13 | 3377.83 | 87 s | 34 | 3377.83 | 200 s | 84 | |||||
| 33 | 3554.33 | 231 s | 4337.16 | 51 s | 5 | 3554.33 | 128 s | 25 | 3554.33 | 195 s | 56 | 3554.33 | 202 s | 81 | |||||
| 34 | 3710.50 | 234 s | 4192.33 | 61 s | 5 | 4010.33 | 183 s | 15 | 3715.33 | 119 s | 28 | 3710.50 | 187 s | 59 | |||||
| 35 | 2675.50 | 179 s | 3330.83 | 36 s | 6 | 2875.50 | 67 s | 13 | 2675.50 | 62 s | 28 | 2675.50 | 149 s | 54 | |||||
| 36 | 2157.17 | 86 s | 3549.83 | 41 s | 6 | 2157.17 | 40 s | 27 | 2157.17 | 90 s | 39 | 2157.17 | 61 s | 53 | |||||
| 37 | 3296.17 | 229 s | 4998.50 | 20 s | 6 | 3495.33 | 38 s | 13 | 3345.33 | 71 s | 29 | 3296.17 | 178 s | 67 | |||||
| 38 | 3107.50 | 95 s | 1942.67 | 27 s | 6 | 3248.66 | 96 s | 26 | 3236.17 | 66 s | 23 | 3107.49 | 138 s | 63 | |||||
| 39 | 1892.67 | 26 s | 1892.67 | 25 s | 5 | 1942.66 | 26 s | 20 | 1942.66 | 35 s | 23 | 1892.66 | 59 s | 56 | |||||
| 40 | 2297.83 | 39 s | 2347.83 | 21 s | 5 | 2347.83 | 29 s | 12 | 2347.83 | 42 s | 25 | 2347.83 | 58 s | 58 | |||||
| 41 | 4051.67 | 1800 s | 5854.49 | 39 s | 5 | 4051.66 | 53 s | 16 | 4051.67 | 192 s | 28 | 4051.67 | 306 s | 53 | |||||
| 42 | 2572.50 | 110 s | 6122.17 | 24 s | 5 | 2572.50 | 47 s | 12 | 2572.49 | 75 s | 37 | 2572.50 | 111 s | 60 | |||||
| 43 | 1973.17 | 18 s | 2065.17 | 21 s | 6 | 2173.16 | 31 s | 19 | 1973.17 | 48 s | 32 | 1973.17 | 76 s | 66 | |||||
| 44 | 1350.67 | 22 s | 1500.67 | 14 s | 4 | 1350.67 | 14 s | 14 | 1500.66 | 42 s | 25 | 1350.66 | 38 s | 54 | |||||
| 45 | 2153.00 | 17 s | 2402.99 | 20 s | 3 | 2153.00 | 33 s | 17 | 2152.99 | 54 s | 26 | 2153.00 | 117 s | 67 | |||||
| 46 | 2071.83 | 48 s | 2071.83 | 31 s | 5 | 2071.83 | 36 s | 13 | 2071.83 | 60 s | 23 | 2071.83 | 131 s | 56 | |||||
| 47 | 2604.67 | 143 s | 3536.33 | 39 s | 6 | 3342.33 | 74 s | 13 | 2704.67 | 89 s | 34 | 2604.67 | 163 s | 55 | |||||
| 48 | 2963.33 | 235 s | 3265.50 | 41 s | 7 | 3451.33 | 69 s | 17 | 2963.33 | 145 s | 43 | 2963.33 | 224 s | 72 | |||||
| 49 | 3089.50 | 277 s | 7007.00 | 30 s | 3 | 3141.83 | 106 s | 17 | 3141.83 | 163 s | 39 | 3089.50 | 204 s | 74 | |||||
| 50 | 3379.17 | 233 s | 4937.99 | 30 s | 4 | 3379.17 | 129 s | 13 | 3379.17 | 95 s | 29 | 3379.17 | 259 s | 70 | |||||
| avg. | 2664.20 | 212.18 s | 3776.40 | 31.38 s | 4.78 | 2763.72 | 67.74 s | 18.36 | 2718.26 | 110.44 s | 33.06 | 2668.10 | 168.12 s | 65.54 | |||||
| Gap to CPLEX (in %) | +41.7% | −85.2% | - | +3.7% | −68.1% | - | +2.0% | −48.0% | - | +0.1% | −20.8% | - | |||||||
| # of better sol. found* | 10 | 26 | 32 | 48 | |||||||||||||||
| Class C | CPLEX | LAHCM () | LAHCM () | LAHCM () | LAHCM () | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Instance | Objective | Time | Objective | Time | Iterations | Objective | Time | Iterations | Objective | Time | Iterations | Objective | Time | Iterations | |||||
| 1 | 30064.10 | 1800 s | 40243.62 | 106 s | 4 | 29964.50 | 156 s | 72 | 30064.50 | 128 s | 36 | 29964.50 | 160 s | 65 | |||||
| 2 | 11761.90 | 689 s | 12110.75 | 109 s | 10 | 18239.13 | 119 s | 15 | 11810.75 | 133 s | 36 | 11761.90 | 174 s | 106 | |||||
| 3 | 24294.50 | 630 s | 62634.50 | 101 s | 7 | 35088.87 | 118 s | 17 | 24694.50 | 137 s | 53 | 24294.50 | 142 s | 88 | |||||
| 4 | 33426.10 | 1800 s | 47853.88 | 96 s | 3 | 34167.63 | 124 s | 43 | 34017.63 | 177 s | 97 | 33426.10 | 184 s | 97 | |||||
| 5 | 21528.40 | 935 s | 27950.75 | 102 s | 4 | 22300.63 | 115 s | 32 | 21578.37 | 130 s | 64 | 21528.38 | 194 s | 128 | |||||
| 6 | 63558.00 | 1800 s | 82703.50 | 106 s | 4 | 64818.37 | 129 s | 26 | 63558.00 | 145 s | 45 | 63557.99 | 190 s | 100 | |||||
| 7 | 31807.30 | 311 s | 32314.75 | 104 s | 5 | 32257.25 | 140 s | 46 | 31857.25 | 140 s | 71 | 31807.25 | 152 s | 91 | |||||
| 8 | 6384.75 | 352 s | 7195.63 | 103 s | 6 | 6435.38 | 114 s | 29 | 6585.38 | 121 s | 42 | 6384.75 | 153 s | 137 | |||||
| 9 | 26849.50 | 467 s | 27050.00 | 111 s | 7 | 27050.00 | 119 s | 28 | 26850.00 | 131 s | 64 | 26849.50 | 139 s | 76 | |||||
| 10 | 10713.00 | 965 s | 33008.75 | 105 s | 3 | 11163.00 | 114 s | 17 | 10847.00 | 115 s | 32 | 10713.00 | 74 s | 163 | |||||
| 11 | 41102.00 | 1800 s | 45801.63 | 108 s | 6 | 41102.00 | 119 s | 30 | 41102.00 | 142 s | 62 | 40701.99 | 179 s | 111 | |||||
| 12 | 38239.10 | 855 s | 55782.00 | 105 s | 3 | 38339.13 | 119 s | 24 | 38289.12 | 143 s | 51 | 38239.10 | 145 s | 66 | |||||
| 13 | 57119.40 | 1800 s | 61553.00 | 103 s | 4 | 60370.13 | 113 s | 17 | 58023.25 | 147 s | 40 | 57219.00 | 276 s | 171 | |||||
| 14 | 36329.90 | 1800 s | 36879.88 | 99 s | 10 | 36968.13 | 113 s | 20 | 36418.00 | 154 s | 77 | 36579.87 | 150 s | 56 | |||||
| 15 | 54449.60 | 1800 s | 54595.87 | 105 s | 4 | 53984.13 | 122 s | 20 | 54486.63 | 142 s | 33 | 53884.13 | 309 s | 153 | |||||
| 16 | 18046.10 | 1450 s | 27043.75 | 105 s | 6 | 18395.75 | 104 s | 13 | 18046.10 | 122 s | 44 | 18046.10 | 175 s | 141 | |||||
| 17 | 65550.50 | 1800 s | 65748.25 | 109 s | 7 | 65598.25 | 115 s | 19 | 65700.50 | 138 s | 47 | 65398.25 | 184 s | 87 | |||||
| 18 | 18158.50 | 93 s | 37458.25 | 102 s | 3 | 18658.50 | 106 s | 13 | 18158.50 | 125 s | 37 | 18158.50 | 147 s | 89 | |||||
| 19 | 70202.50 | 1800 s | 89141.88 | 112 s | 7 | 70302.50 | 143 s | 38 | 70202.49 | 182 s | 66 | 70202.49 | 204 s | 117 | |||||
| 20 | 13960.90 | 148 s | 34704.50 | 103 s | 4 | 13960.87 | 108 s | 30 | 13960.88 | 121 s | 58 | 13960.88 | 122 s | 59 | |||||
| 21 | 22345.40 | 720 s | 23208.50 | 103 s | 5 | 22659.13 | 142 s | 44 | 22345.38 | 157 s | 45 | 22445.37 | 217 s | 145 | |||||
| 22 | 29961.80 | 1800 s | 37861.75 | 107 s | 7 | 30061.75 | 111 s | 20 | 29911.75 | 123 s | 24 | 29911.75 | 180 s | 93 | |||||
| 23 | 39030.30 | 1800 s | 47525.75 | 85 s | 6 | 39608.87 | 100 s | 21 | 39509.25 | 123 s | 46 | 39180.24 | 152 s | 71 | |||||
| 24 | 16223.30 | 1800 s | 25611.50 | 102 s | 4 | 17571.50 | 112 s | 30 | 16473.87 | 137 s | 35 | 16223.24 | 165 s | 87 | |||||
| 25 | 8436.00 | 35 s | 10938.00 | 101 s | 3 | 8636.00 | 105 s | 18 | 8736.00 | 115 s | 38 | 8435.99 | 116 s | 53 | |||||
| 26 | 8741.13 | 273 s | 17349.13 | 102 s | 5 | 16237.38 | 121 s | 31 | 8991.13 | 124 s | 39 | 8741.13 | 151 s | 123 | |||||
| 27 | 19510.63 | 1800 s | 51356.99 | 103 s | 5 | 19710.63 | 124 s | 24 | 19610.63 | 152 s | 42 | 19510.63 | 180 s | 70 | |||||
| 28 | 34204.00 | 1800 s | 36959.62 | 107 s | 5 | 37209.63 | 113 s | 14 | 34204.00 | 141 s | 38 | 34204.00 | 252 s | 57 | |||||
| 29 | 22248.75 | 310 s | 26831.63 | 104 s | 5 | 22460.75 | 136 s | 54 | 22598.75 | 125 s | 26 | 22248.75 | 173 s | 111 | |||||
| 30 | 55401.50 | 1800 s | 76742.25 | 115 s | 4 | 55012.00 | 123 s | 31 | 55451.50 | 192 s | 78 | 55201.49 | 198 s | 117 | |||||
| 31 | 36470.38 | 1503 s | 57020.25 | 108 s | 4 | 37525.25 | 128 s | 29 | 37374.88 | 155 s | 54 | 36470.37 | 175 s | 100 | |||||
| 32 | 31585.25 | 1800 s | 33886.37 | 106 s | 9 | 31862.63 | 137 s | 24 | 31585.25 | 169 s | 57 | 31585.24 | 163 s | 74 | |||||
| 33 | 17730.25 | 1612 s | 22179.75 | 101 s | 4 | 17730.25 | 116 s | 40 | 18030.25 | 123 s | 40 | 17730.25 | 150 s | 98 | |||||
| 34 | 38211.63 | 1800 s | 38782.00 | 104 s | 4 | 38458.63 | 132 s | 38 | 38382.00 | 133 s | 24 | 38408.63 | 265 s | 78 | |||||
| 35 | 23770.88 | 827 s | 31775.13 | 101 s | 3 | 23870.87 | 115 s | 33 | 23920.87 | 115 s | 29 | 23770.87 | 174 s | 65 | |||||
| 36 | 18219.50 | 1800 s | 19472.50 | 103 s | 8 | 18669.50 | 120 s | 38 | 18453.50 | 135 s | 34 | 18219.50 | 168 s | 99 | |||||
| 37 | 45210.25 | 1800 s | 46334.25 | 113 s | 7 | 48069.50 | 127 s | 27 | 44249.75 | 162 s | 56 | 44278.75 | 211 s | 80 | |||||
| 38 | 16696.50 | 1363 s | 16945.88 | 104 s | 7 | 16995.88 | 116 s | 27 | 16845.88 | 125 s | 52 | 16696.50 | 182 s | 133 | |||||
| 39 | 38395.13 | 1800 s | 39751.75 | 106 s | 5 | 40036.88 | 126 s | 24 | 38295.13 | 137 s | 37 | 38245.13 | 166 s | 64 | |||||
| 40 | 5876.00 | 186 s | 8229.25 | 101 s | 5 | 6240.50 | 110 s | 22 | 6240.50 | 117 s | 42 | 5976.00 | 163 s | 73 | |||||
| 41 | 23764.38 | 1800 s | 35347.63 | 105 s | 5 | 24364.38 | 116 s | 25 | 24071.00 | 138 s | 39 | 23871.00 | 170 s | 88 | |||||
| 42 | 38450.13 | 1800 s | 53822.38 | 103 s | 4 | 38700.12 | 138 s | 31 | 38550.13 | 170 s | 45 | 38650.13 | 308 s | 132 | |||||
| 43 | 49706.63 | 1800 s | 53004.37 | 106 s | 4 | 52854.38 | 140 s | 32 | 50056.38 | 128 s | 34 | 49706.63 | 204 s | 84 | |||||
| 44 | 31453.00 | 1800 s | 31956.50 | 106 s | 4 | 31553.00 | 125 s | 18 | 31953.00 | 124 s | 31 | 31553.00 | 199 s | 86 | |||||
| 45 | 22222.75 | 1800 s | 23462.13 | 105 s | 4 | 22774.75 | 118 s | 17 | 22672.75 | 161 s | 46 | 22222.75 | 172 s | 71 | |||||
| 46 | 47763.75 | 1800 s | 48213.75 | 105 s | 6 | 48113.75 | 122 s | 22 | 47963.75 | 116 s | 23 | 47763.75 | 180 s | 73 | |||||
| 47 | 29746.13 | 1800 s | 29996.13 | 99 s | 4 | 29952.75 | 119 s | 20 | 30008.25 | 145 s | 41 | 29701.25 | 271 s | 171 | |||||
| 48 | 47663.50 | 1800 s | 49409.88 | 101 s | 5 | 49409.88 | 109 s | 13 | 48163.63 | 128 s | 33 | 47663.50 | 173 s | 75 | |||||
| 49 | 52298.00 | 1800 s | 65293.49 | 105 s | 9 | 56111.87 | 138 s | 34 | 55961.87 | 162 s | 67 | 55961.88 | 187 s | 75 | |||||
| 50 | 19509.25 | 1800 s | 20109.25 | 108 s | 6 | 20570.75 | 129 s | 42 | 19759.25 | 162 s | 55 | 19509.25 | 185 s | 68 | |||||
| avg. | 31287.84 | 1354.48 s | 39223.06 | 104.26 s | 5.26 | 32443.94 | 121.56 s | 27.84 | 31532.42 | 139.34 s | 46.10 | 31335.30 | 182.06 s | 96.30 | |||||
| Gap to CPLEX (in %) | +25.4% | −92.3% | - | +3.7% | −91.0% | - | +0.8% | −89.7% | - | +0.2% | −86.6% | - | |||||||
| # of better sol. found* | 0 | 6 | 12 | 40 | |||||||||||||||
| CPLEX | LAHCM () | ||||
|---|---|---|---|---|---|
| Instance | Objective | Time | Objective | Time | Iterations |
| Class A | |||||
| 21 | 5355.57 | 1800 s | 5355.57 | 843 s | 141 |
| 37 | 6487.71 | 1800 s | 6387.71 | 1017 s | 140 |
| Class B | |||||
| 30 | 2552.00 | 144 s | 2552.00 | 209 s | 113 |
| 40 | 2297.83 | 39 s | 2297.83 | 189 s | 202 |
| Class C | |||||
| 13 | 57,119.40 | 1800 s | 57,119.40 | 313 s | 253 |
| 14 | 36,329.90 | 1800 s | 36,329.90 | 233 s | 191 |
| 21 | 22,345.40 | 720 s | 22,345.40 | 240 s | 169 |
| 23 | 39,030.30 | 1800 s | 39,180.24 | 225 s | 190 |
| 34 | 38,211.63 | 1800 s | 38,211.63 | 220 s | 120 |
| 40 | 5876.00 | 186 s | 5876.00 | 142 s | 132 |
| 41 | 23,764.38 | 1800 s | 23,871.00 | 241 s | 256 |
| 42 | 38,450.13 | 1800 s | 38,450.13 | 233 s | 121 |
| 44 | 31,453.00 | 1800 s | 31,453.00 | 253 s | 173 |
| 49 | 52,298.00 | 1800 s | 52,298.00 | 260 s | 224 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goerler, A.; Lalla-Ruiz, E.; Voß, S. Late Acceptance Hill-Climbing Matheuristic for the General Lot Sizing and Scheduling Problem with Rich Constraints. Algorithms 2020, 13, 138. https://doi.org/10.3390/a13060138
Goerler A, Lalla-Ruiz E, Voß S. Late Acceptance Hill-Climbing Matheuristic for the General Lot Sizing and Scheduling Problem with Rich Constraints. Algorithms. 2020; 13(6):138. https://doi.org/10.3390/a13060138
Chicago/Turabian StyleGoerler, Andreas, Eduardo Lalla-Ruiz, and Stefan Voß. 2020. "Late Acceptance Hill-Climbing Matheuristic for the General Lot Sizing and Scheduling Problem with Rich Constraints" Algorithms 13, no. 6: 138. https://doi.org/10.3390/a13060138
APA StyleGoerler, A., Lalla-Ruiz, E., & Voß, S. (2020). Late Acceptance Hill-Climbing Matheuristic for the General Lot Sizing and Scheduling Problem with Rich Constraints. Algorithms, 13(6), 138. https://doi.org/10.3390/a13060138





