6.1. Simulated/Artificial Data
The results for the simulated datasets are presented
Figure 3,
Figure 4,
Figure 5,
Figure 6,
Figure 7 and
Figure 8. In particular,
Figure 4,
Figure 5,
Figure 6,
Figure 7 and
Figure 8 refer to dataset (f)—Manufacturing, while
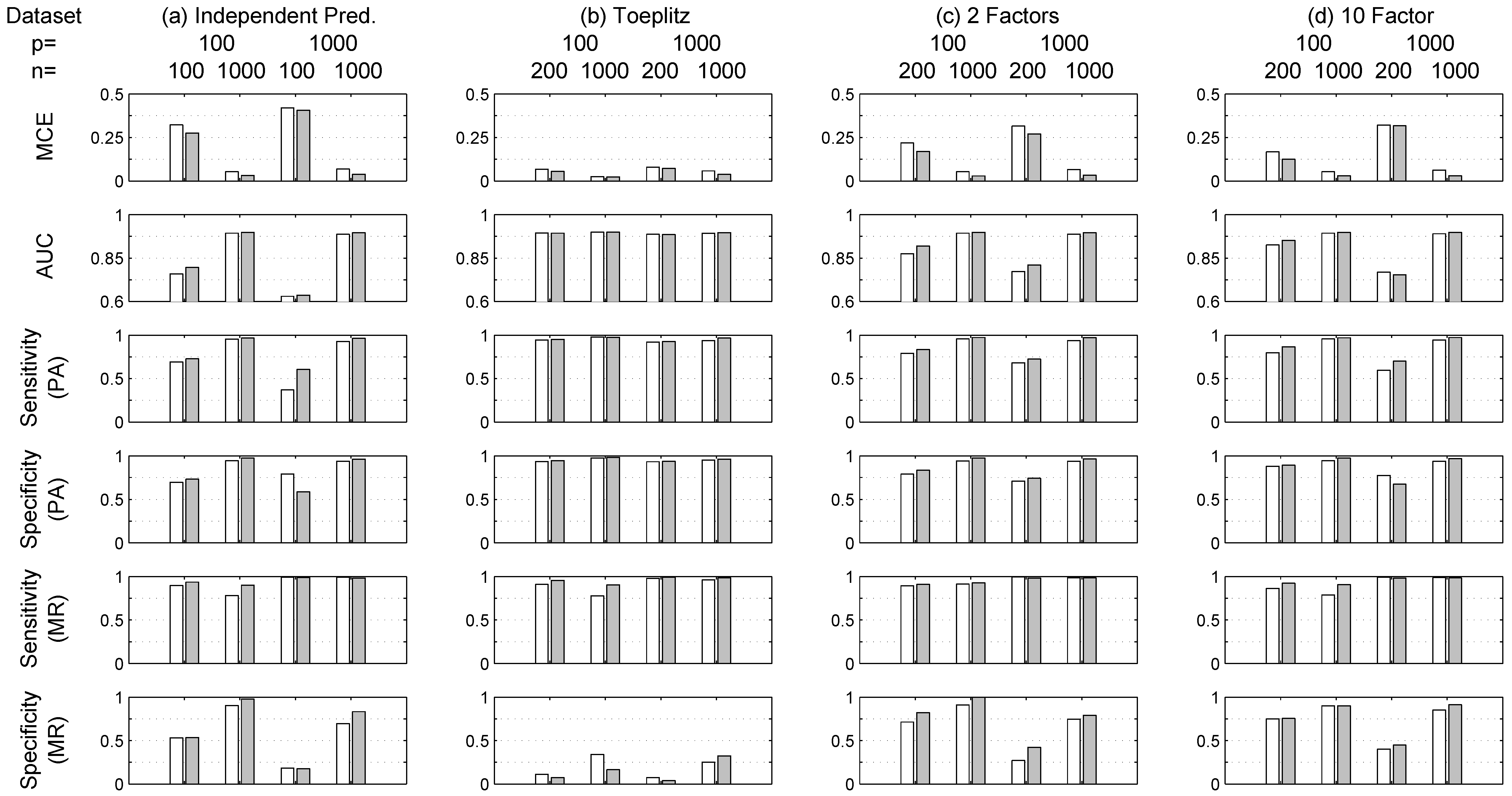
Figure 3 refers to other datasets (a)–(e). As expected, in general, the performance for all indicators improves for both methods with increasing values of
n, for example the MCE in
Figure 5 for dataset (f) decreases as
n increases. Moreover,
Figure 3 shows that, in general, for the same value of
n, the lower the value of
p the better the performance. RVM outperforms LASSO when
in terms of MCE and AUC. Increasing Prediction Accuracy (PA) is obtained for both methods when
p and
n are comparable with respect to the case
. For example,
Figure 3 shows a drop for simulation (a) in terms of average MCE from 30% to 5% for LASSO and from 25% to 3% for RVM when
and
respectively. Similar performance improvements are obtained for simulations (b)–(d) as can be seen from
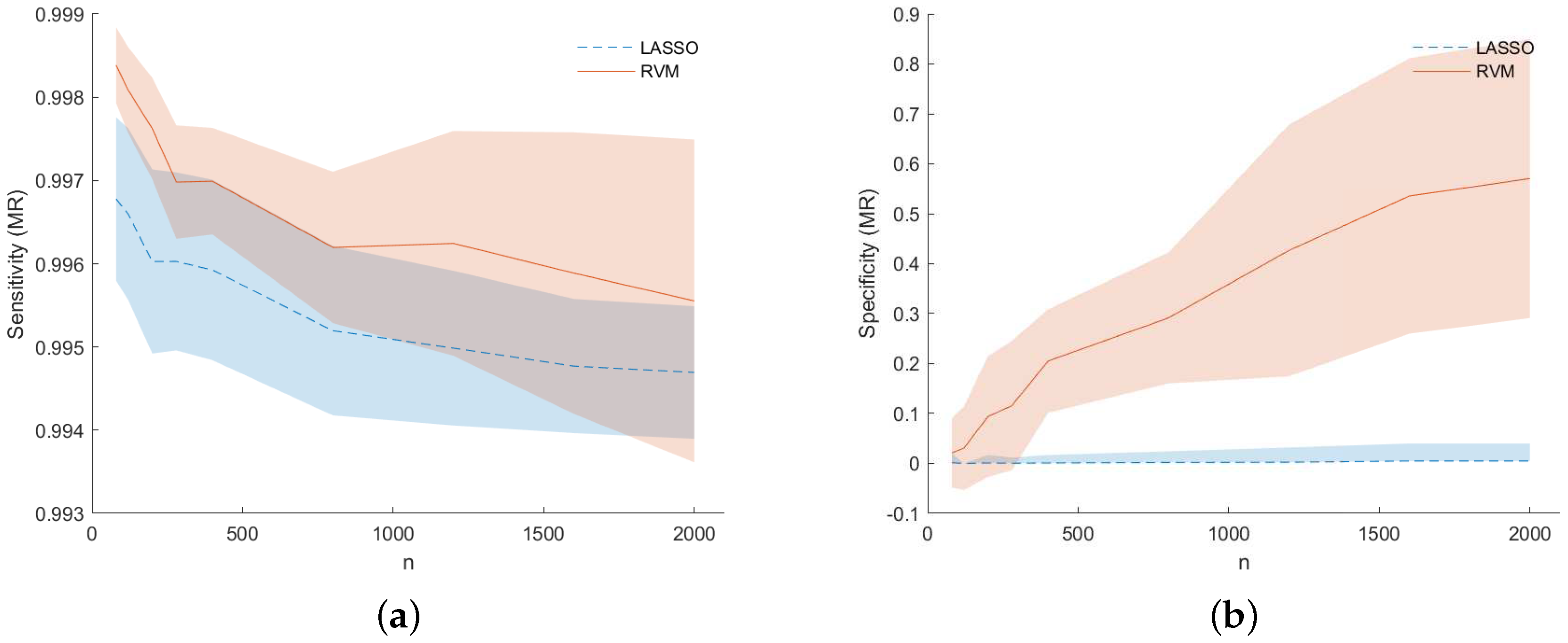
Figure 3. Additionally, the same figure shows that RVM tends to outperform LASSO in the estimation of the true model structure (or Model Recovery—MR) in terms of Sensitivity, i.e., True Positive rate, and Specificity, i.e., True Negative rate.
The set of simulations (e), basically the same as (a)–(d) but repeated for
, whose results are also shown in
Figure 3, confirm that RVM tends to outperform LASSO in all situations, although in a few cases results are comparable, especially when
.
In this situation (
), the structure discovery ability of the RVM degenerates. This can be due to the fact that the hyperparameters for RVM are optimized with an iterative procedure (see
Section 3.2) that does not guarantee the cost function minimum is reached. On the other hand, the LASSO problem is convex and thus the coordinate descent algorithm is more likely to reach the minimum of the cost function.
Several studies have been conducted in the literature studying the selection consistency property of the LASSO estimator. A necessary condition for the LASSO to recover the true model structure is the so-called Irrepresentable Condition (IC) [
54,
55] calculated as:
where the subscript ”
S“ indicated the set of variables whose coefficients are different from zero, while
N identifies the
k variables with
. If this condition is violated, the recovery of the true model is not guaranteed.
Table 2 collects the IC values obtained for the simulated datasets (a)–(f). Interestingly, observing
Figure 3 and
Table 2 it is possible to notice that the lower the IC, the higher the Specificity values in model recovery (MR) for LASSO, and specificity values are also higher for RVM when
n is large. It can be also noticed that the irrepresentable condition (
17) occasionally fails when the IC value is greater than 1; in these cases, the structure recovery provided by LASSO is not suitable according to (
17).
With regard to LASSO, in
Table 2 it can be noticed that for increasing values of
n, in general, the IC value improves, i.e., is lower, even though condition (
17) is not satisfied for several cases in which the LASSO structure recovery capability fails. It is pointed out that several approaches exist in the literature as alternatives to LASSO with regard to model recoveries, such as the smoothly clipped absolute deviation (SCAD) and the adaptive lasso [
29], but they are not used here in order to keep the focus on the two methods mentioned: LASSO and RVM, whose variable selection capabilities are embedded within the logistic model estimation phase.
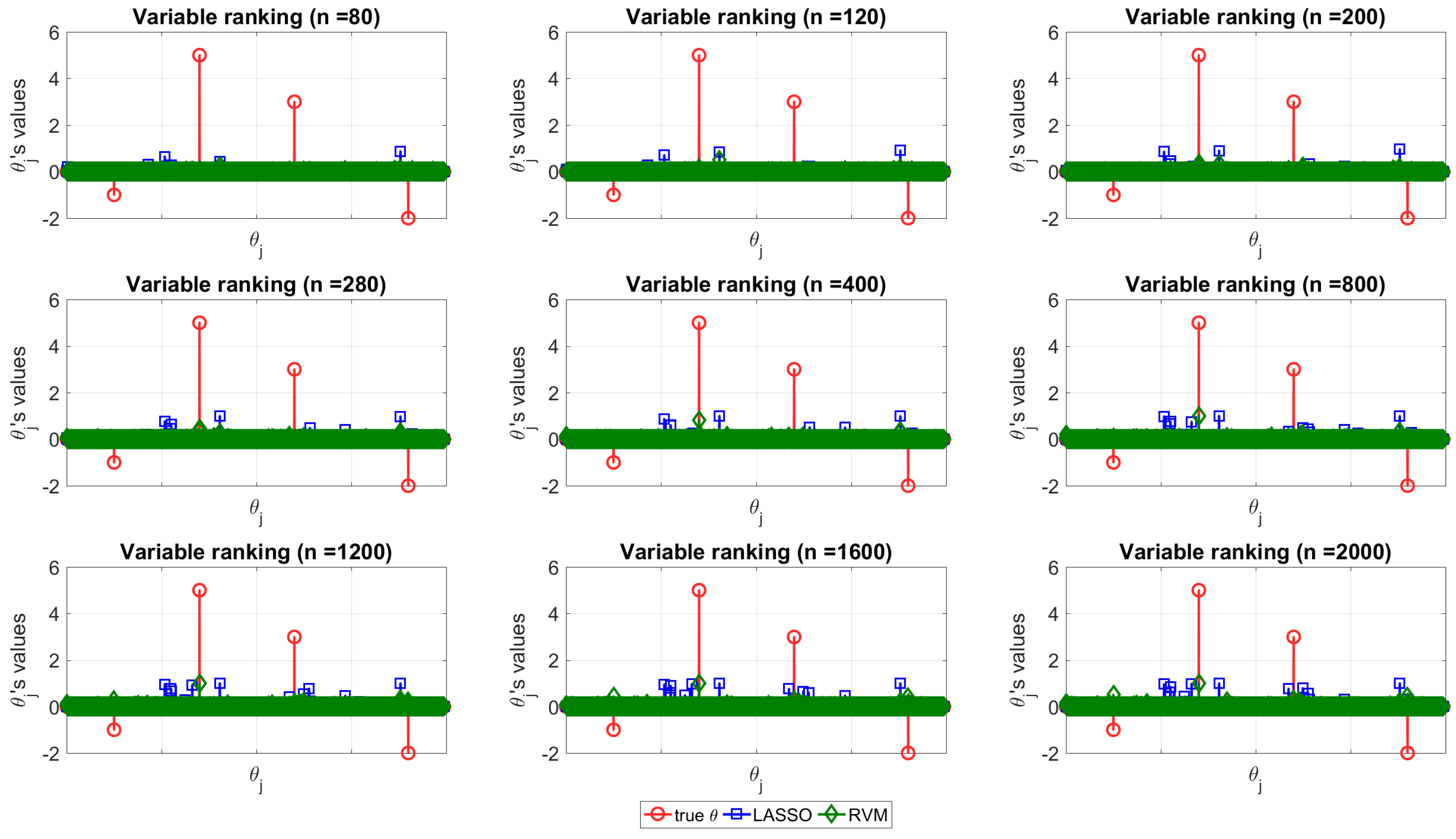
The structure discovery ability of the two techniques is depicted in
Figure 4 for dataset (f), where the true vector
(red circle) is compared with the normalized distribution obtained with the MC simulation with LASSO (blue square) and RVM (green diamond) for increasing values of
n (from top left to bottom right).
Figure 4 can be used to appreciate the capability of each of the two techniques in terms of structure recovery in a specific case study (dataset (f)). In this case, the predictors with more impact on the model are known in advance and are depicted in red (circle) in the figure. In this scenario, one method is better than the other if its estimates tend to overlap the real coefficient, i.e., if the stem plots of the real coefficients and estimates show nonzero values for the same indices. It can be seen that, neither RVM, nor LASSO are able to reveal the correct predictors when
n is small, instead, as
n increases, both of the methods tend to provide more reliable coefficients as expected.
The important fact observed and pointed out here is that RVM seems to be more powerful for model recovery than LASSO when
n is large, because when it shows nonzero coefficients, they match the real ones. In order to improve the readability of the picture, the reader can consider it together with
Table 3 and
Figure 8a which show the same conclusions for the same data quantifying the differences. In particular,
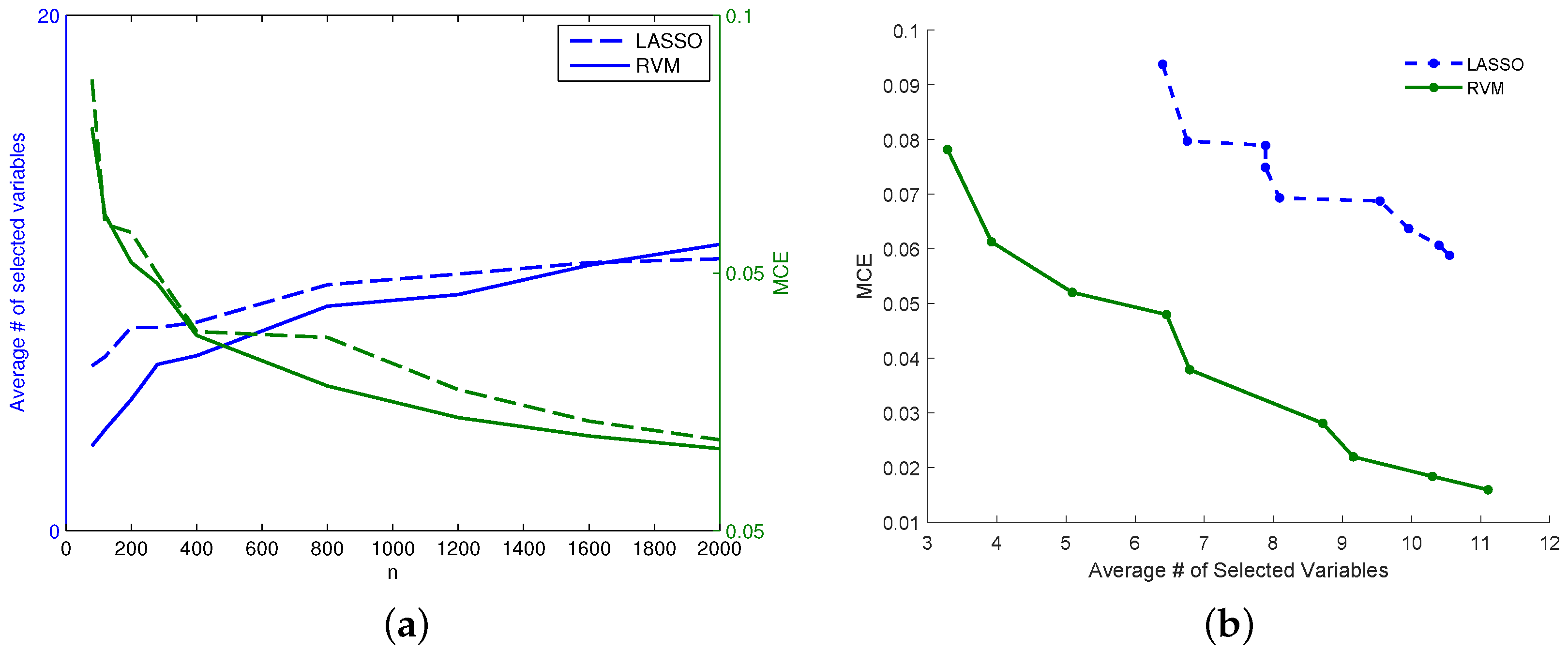
Figure 8a represents how the number of selected (nonzero) variables tends to be lower for RVM as
n increases. On the other hand,
Table 3 shows the matches between the selected variables and the real ones in percentage for each method. RVM appears more effective for model recovery in this case study; nevertheless, it is noteworthy to consider that this dataset presents high collinearity among variables, as already stated, and LASSO suffers somewhat from the multi-collinearity problem [
33]. It turns out that, for increasing values of
n, the RVM performs better than LASSO identifying the true
, namely those that are used to predict the output class.
Considering
Table 2, the reader can notice that the LASSO Irrepresentable Condition fails also for increasing values of
n, so it is not surprising that better results for model recovery, in this case, are obtained with the other technique.
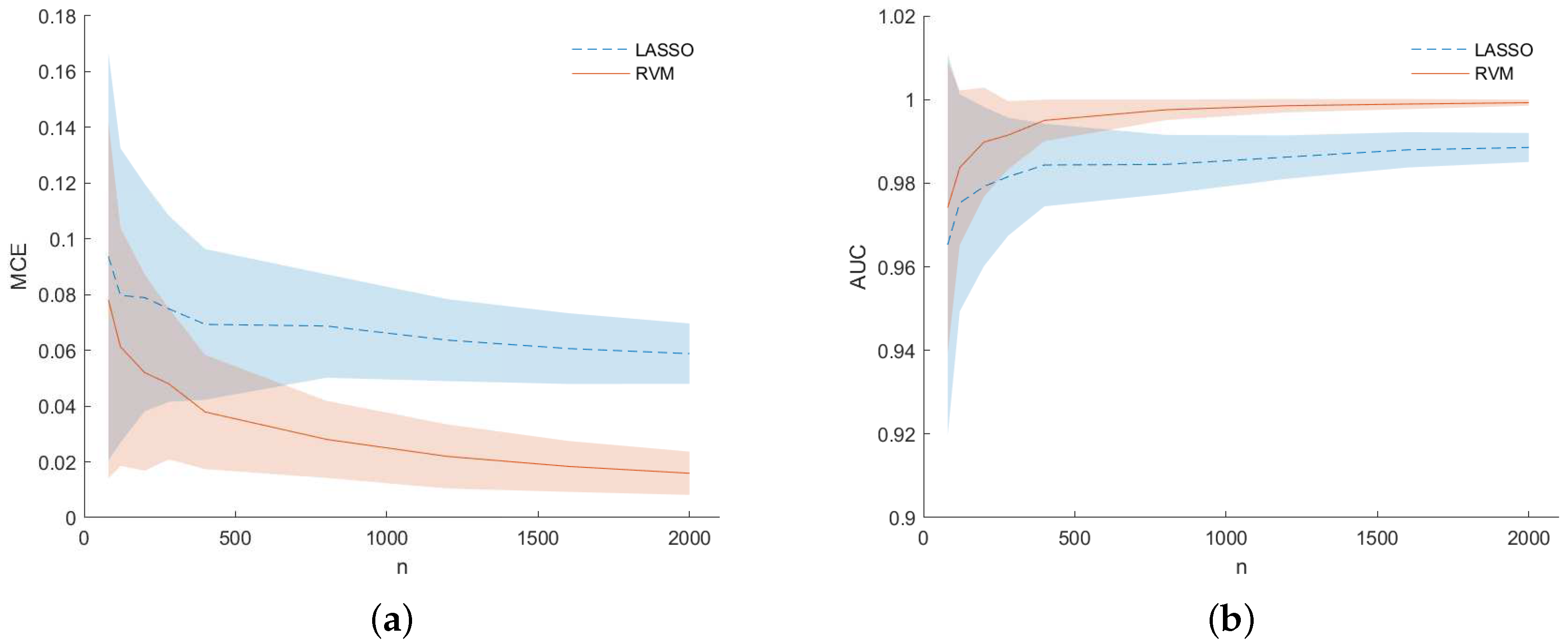
Figure 5 shows results in terms of MCE (left) and AUC (right) for dataset (f). They are presented as a function of the number of samples
n used to build the dataset at each MC iteration. The RVM models (solid line) outperform the LASSO one (dashed line) as
n increases to a value approximately equal to
p. For low values of
n, i.e., when
, results for the LASSO and RVM became comparable as happened for simulations (b) in
Figure 3. However, analyzing
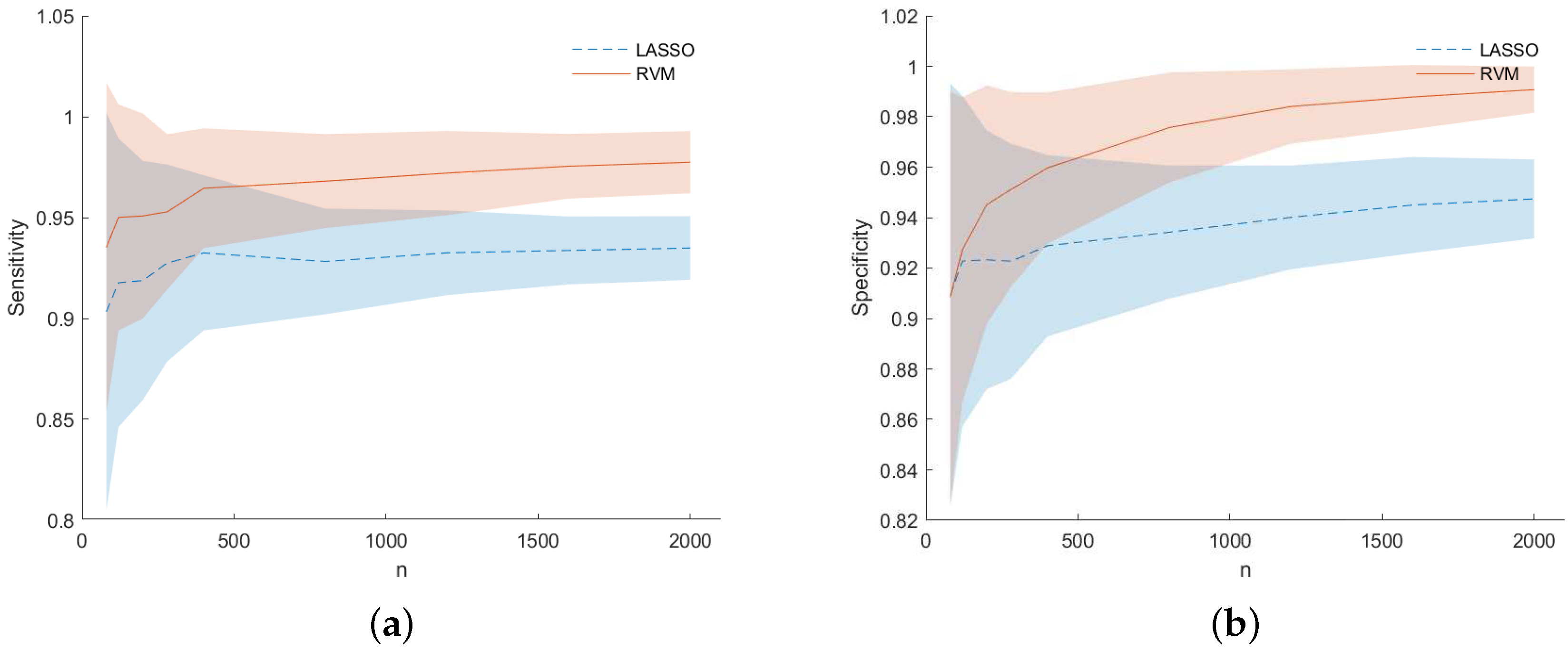
Figure 6 for dataset (f), one can see that RVM still outperforms the LASSO in terms of sensitivity (left) and specificity (right) for prediction accuracy (PA) considering the predicted output for the two models during the MC simulation.
Figure 7 shows for dataset (f) the TP (or sensitivity) and TN (or specificity) rates for the model recovery capability of the two studied models. Not only LASSO often selects the wrong variables, but the selected variables are spread around the true ones (observing
Figure 7 together with
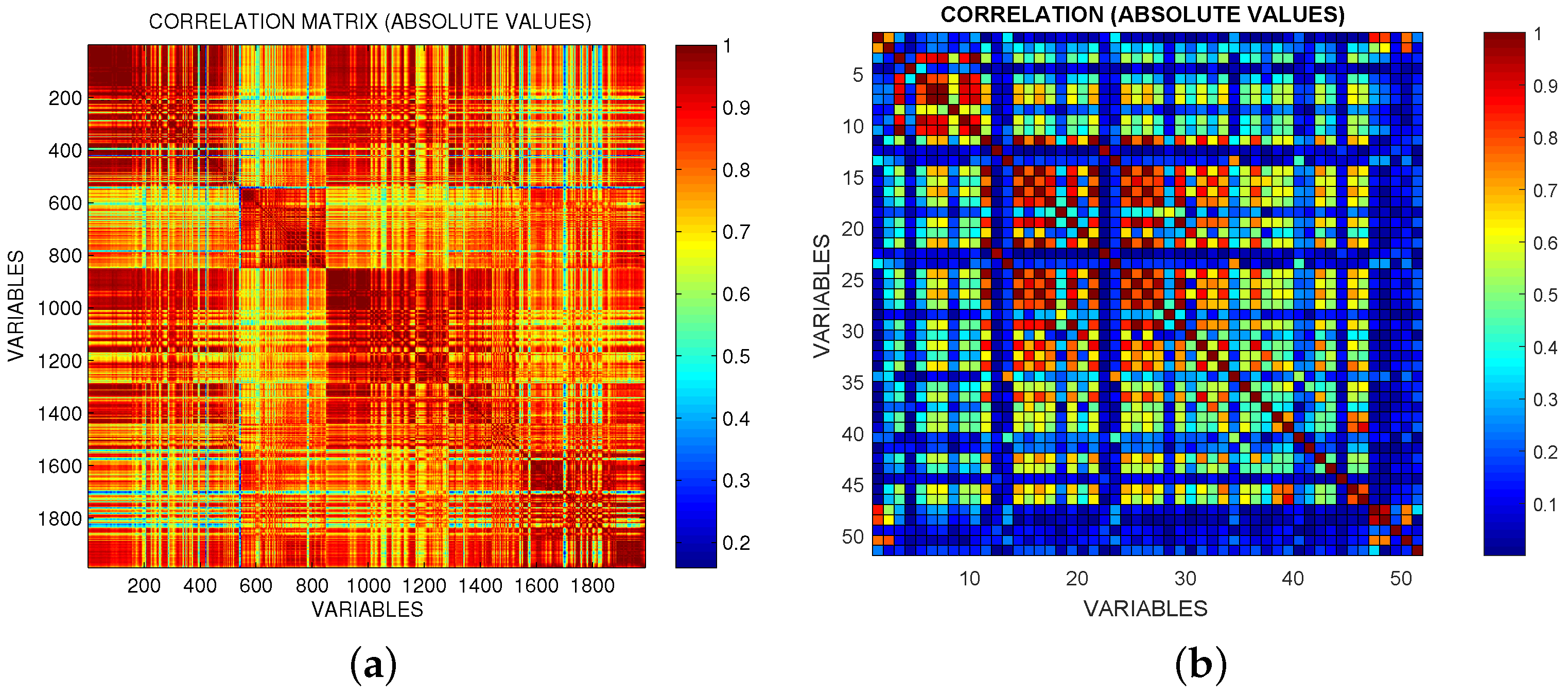
Figure 4). This is an example of the so-called grouping effect affecting the LASSO, namely, if there is a group of highly correlated variables, LASSO tends to select only one of them from the group and does not care which one is selected. The data under analysis are actually highly correlated in some occasions as can be seen from
Figure 2 which shows the heat-map matrix of the absolute correlations between the OES dataset variables (dataset (f)). As can be seen from
Figure 8 for dataset (f), while for the lower
n RVM selects fewer variables than LASSO, the situation changes for increasing values of
n. Despite this behavior in the sparsity of the two models, the RVM model still outperforms the LASSO in terms of MCE (continuous decreasing line in
Figure 8a compared with dashed decreasing line). In particular,
Figure 8b for dataset (f) shows that for an equal number of active variables in the two models, RVM achieves better prediction performance.
6.2. Real Data
Results for the real datasets are presented only in terms of prediction accuracy since the true underlying model is unknown.
Table 4 shows that, in general, as regards prediction accuracy, RVM and LASSO are numerically equivalent, i.e., there is no absolute winner in terms of MCE and AUC. Some considerations could be made on results considering
Table 4,
Figure 1 and the prior knowledge on available data, in particular:
RVM tends to be better as n increases (and the ratio is far from 1);
The Madelon dataset is known to be highly non-linear and dataset Fabric Care Appliance is a further example of a non-linear dataset. This leads to suggest the use of LASSO if, somehow, the non-linear structure of data is known in advance for the problem at hand; however, this consideration should be supported by other similar cases;
The Gisette dataset is very noisy and this is due to the intrinsic difficulty of separating the digits “4” and “9”; also in this case LASSO turns out to be better than RVM;
For the Arcene dataset where , RVM slightly outperforms LASSO in terms of MCE, but LASSO is better in terms of AUC.
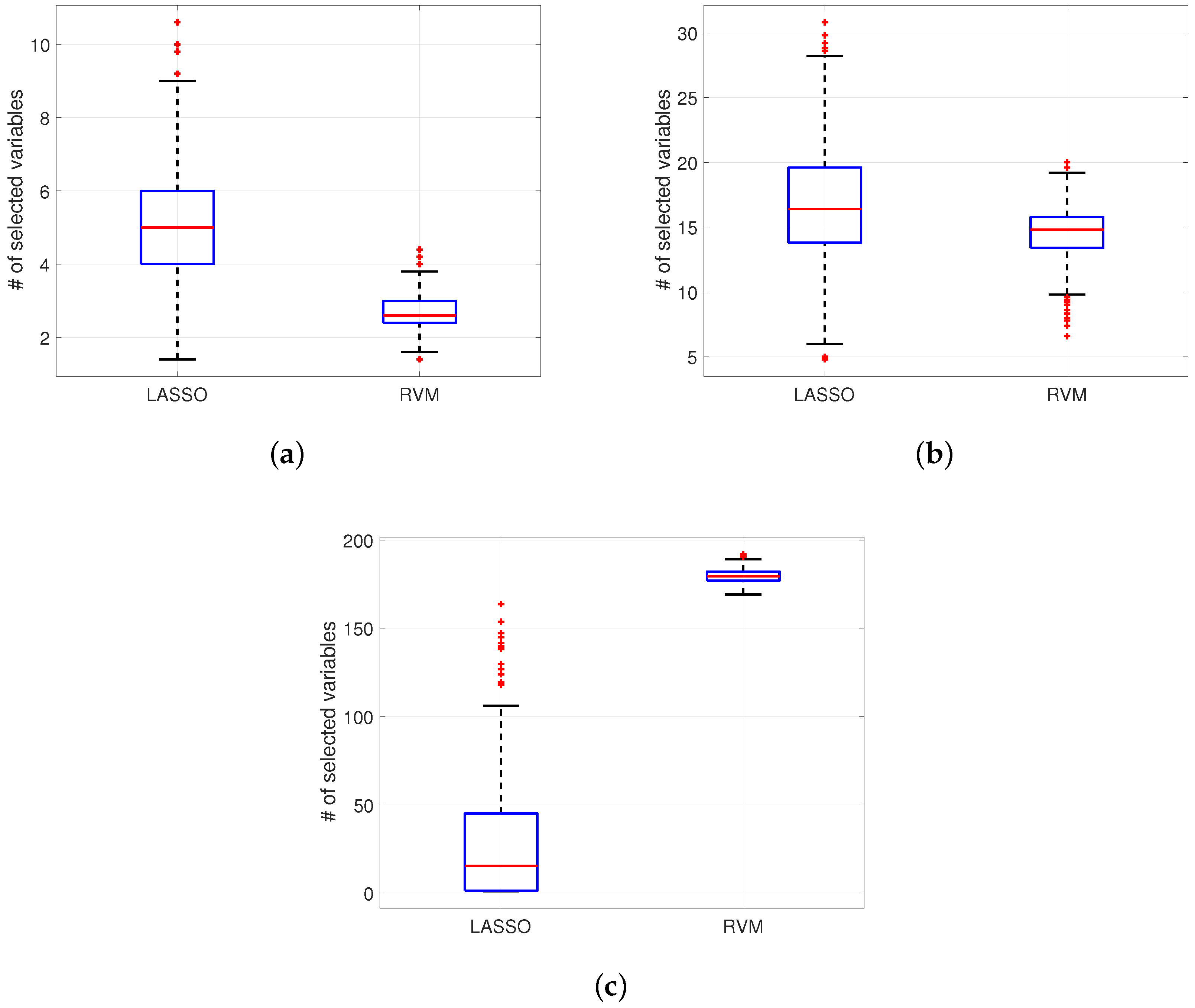
Concerning the structure recovery of the two algorithms using real datasets, some examples are depicted in
Figure 9. With the Semiconductor dataset in
Figure 9a RVM gives a distribution of nonzero variables in cross-validations which is less than the one provided by LASSO (for example the mean is
for RVM and
for LASSO). The same situation, applies for the Arcene dataset (
Figure 9b) where
, i.e.,
mean for RVM and
for LASSO. In contrast, for the highly nonlinear dataset Madelon in
Figure 9c, the difference between the mean number of selected variables in cross-validations is much higher with RVM than with LASSO (
versus
). As a result, the use of LASSO can be recommended in general when dataset is non-linear (or even more when there is no a priori knowledge about the structure).
For real data case the same set of implementation details was kept, i.e., in terms of number of Cross-Validation, percentage of training and test data, etc. (as explained in
Section 6.1).
6.3. Computational Considerations
Both implementations of the linear logistic model considered in this work are based on iterative algorithms. Thus, the time required for model parameter estimation depends on thresholds and the number of iterations specified by the user.
The update of parameters in the RVM implementation requires the inversion of a matrix to compute the posterior weight covariance matrix, an operation with complexity
and memory requirement
([
33,
42]). The algorithm implementation described in [
44] does not start by including all variables in the model but rather incrementally adds or deletes variables as appropriate. Moreover, as already noted, complexity is automatically determined.
The LASSO algorithm consists of several steps. The coordinate descent algorithm requires
([
33]), but additional complexity is due to the calculation of the quadratic approximation by the Newton algorithm.
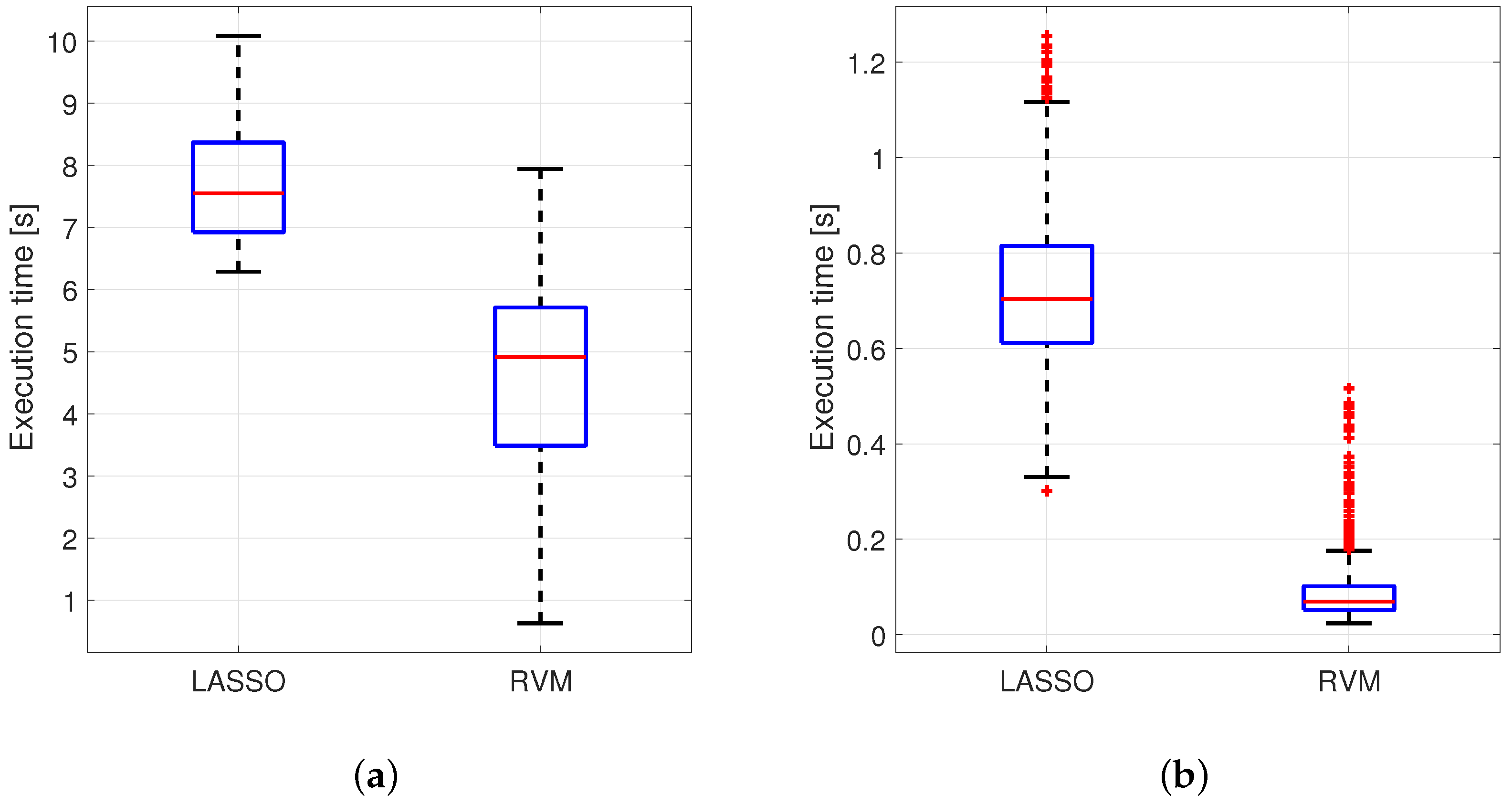
An example of comparison in terms of execution time performance has been provided in
Figure 10 for 2 real cases introduced before: Arcene, and Fabric Care Appliance. These two case studies have been chosen in this case among all the others because of their
ratio which is very different from one to other.
Figure 10 shows distributions of the execution times obtained for each MCCV iteration for each method. The elapsed time for each execution was measured by using tic-toc command available in MATLAB. This couple of instructions was used to tag the beginning and the end of the key code for each method so that the difference in time between the two tags indicates the desired execution time. More specifically, the tic function records the current time, and the toc function uses the recorded value to calculate the elapsed time (source:
https://www.mathworks.com/help/matlab/ref/tic.html). The main steps related to the implementation of the two procedures have been summarized in
Table 5 for the sake of clarity. These steps affect the execution time and are useful to stress the methodological differences between the two strategies as well. As the reader can notice, only LASSO performs the choice of the optimal regularization parameter with a dedicated inner procedure that turns out to be particularly demanding considering the entire set of iterations. On the other hand, RVM determines the model complexity automatically by the data through ARD as already stated in
Section 3.2.
Step I in
Table 5 refers to the code used in the glmnet LASSO implementation to determine the optimal regularization parameter lambda at a grid of values via Coordinate Descent algorithm. This part is obtained in LASSO with a nested loop (another cross-validation level for LASSO) while II provides the coefficients using the best hyperparameters fixed at the previous step.
Figure 10 shows that RVM provides an advantage in terms of execution time and this is mainly due to the fact that it does not require the estimation of a regularization parameter like LASSO. In terms of the entire code, it turns out that, for the latter, the computational effort is higher (quoted values were obtained on an Intel Core i7-4510U CPU @ 2.60GHz under Windows 10).


 LASSO results;
LASSO results;  RVM results.
RVM results.
 LASSO results;
LASSO results;  RVM results.
RVM results.