1. Introduction
Nuclear magnetic resonance (NMR) is an important biochemical technique for the in vitro determination of protein structure and protein-drug interaction studies [
1,
2], which is also being widely used in the field of in-cell NMR [
3,
4,
5,
6]. Magnetic resonance spectroscopy (MRS), which is based on NRM principles, is widely being used along with magnetic resonance imaging (MRI) to acquire detailed information about the tissue structures for medical diagnosis [
7,
8,
9]. MRS non-invasively provides information on the brain’s metabolites concentrations, which aids the early detection of neurodegenerative diseases [
10,
11,
12] The current developed techniques and software packages for MRS signal processing retain significant variance in the absolute metabolite quantification. Magnetic resonance (MR) spectra analysis methods can be classified as either black box (data-driven) or basis sets methods [
8]. Basis set methods incorporate prior knowledge of metabolites chemical structures in both in-vivo NMR (e.g., LC Model
TM [
13], TARQUIN [
14]), and in-vitro NMR [
15], while the black box does not incorporate prior knowledge, and are completely data-driven, such as QUEST [
16].
The black box methods decompose the free induction decay (FID) signals in the time domain, and then quantify the metabolites by modeling the decomposed FID signal. Black box methods have been shown effective on sparse data, and long echo time (TE) acquisition; however, the main drawback of black box methods is impracticable results for complex data, such as short TE, due to not including prior knowledge [
14,
17]. The number of detected peaks in MR spectra increases using short TE scanning, which allows for the precise quantification of metabolites with short T
2 relaxation time [
18]; thus, the pattern complexity of some metabolites increases. Therefore, modeling the metabolites basis sets with a series of single peaks is difficult using existing black box methods.
The basis sets method match basis sets models developed in the laboratory with the MR spectra of the scanned data in the frequency domain. It has been shown that basis sets methods are more operative for complex data when compared with black box methods. However, one of the shortcomings of the basis sets methods is the existence of unknown components in the complex in vivo data, as a consequence of using basis sets that were developed in laboratory environments [
8,
19]. Therefore, the possibility of accuracy loss increases.
In this study we address the abovementioned issues, by the integration of the truncated HSVD and K-means clustering with centroids initialized using prior knowledge of basis sets developed in the laboratory environments. We used a phantom to generate a ground truth data to compare the accuracy of the proposed algorithm and TARQUIN. Two different brain regions of four subjects were scanned at Texas Tech Neuro-imaging Institute (TTNI) in order to provide in vivo data, allowing for a comparison of proposed approach and TARQUIN.
2. Materials and Methods
The FID signal consists of both real and imaginary terms corresponding to the
x and
y components of rotating magnetization, which is perpendicular to the magnetization vector in the z-axis [
20]. The FID is a detectable NMR signal that generates a process known as Larmor precession [
21]. The complex notation is used to represent the FID signal due to its suitability for further mathematical operations.
The algorithm consists of two main steps: preprocessing and modeling. Preprocessing steps include zero-filling, signal smoothing, and noise filtering [
22], eddy current correction [
23], water peak removal, phase correction, and baseline correction. The modeling steps include decomposition, clustering, peak matching, and quantification. Truncated HSVD is utilized to decompose the FID signal in time domain into single tone FIDs, and each tone generates a single peak in the frequency domain. K-means clustering with initialized centroids was employed to cluster the single peaks as the metabolites basis sets. The diagram of the proposed approach is shown in the
Figure 1 and the details of each step are described in the following sections.
2.1. Preprocessing
In this section, we only describe those preprocessing blocks that we modified or developed. Other preprocessing blocks, such as signal smoothing, noise filteration, and eddy current correction, were applied exactly the same as described in [
22,
23].
2.1.1. Water Peak Removal
The water suppressed MR spectra still contains a residual water peak in the frequency range of
[
14]. This residual peak can be filtered out while using the maximum-phase pass-band FIR filter from [
24], which is more accurate than the HSVD that is used in the TARQUIN for water peak removal. A FIR filter is a weighted sum of the most recent input values of the filter [
24,
25] to suppress all of the water components in the specified frequency region, while maintaining the other frequency regions with minimal distortion.
2.1.2. Phase Correction
MR spectra are not always in absorption mode, due to the misadjustment of the reference phase relative to the receiver phase detector, amplifier dead time, and phase shift from the digital filter employed to reduce noise [
26]. The phase correction operation is automatically performed through application of reference [
27], which combines “coarse tuning” and “fine tuning”. In the former procedure, the position of the tail ends of each peak is determined with a baseline, and then the preliminary phase spectra are obtained by minimizing the height difference between tail ends. After the coarse tuning, peaks are classified as: positive, negative, or distorted. A custom negative penalty function is generated to neglect the negative and distorted peaks. Ultimately, the phase spectra are obtained by minimizing the generated negative penalty function.
2.1.3. Baseline Correction
Separating macromolecules (MM) from the metabolites in the MR spectra, which is essential for reducing variability in the metabolite quantification, is applied through a process called baseline correction [
1]. To detect the baseline and subtract it from the MR spectra, the automatic baseline correction algorithm of [
7] is used. This process detects the local minima of the MR spectra to not include sharp metabolites peaks, and then iteratively generates envelopes to estimate a baseline for the MR spectra. Afterward, the estimated baseline is subtracted from the MR spectra to obtain metabolites-only MR spectra.
2.1.4. Spectrum Referencing
The inhomogeneity of the rotating magnetic field often causes a chemical shift in the MR spectra and, therefore, the selection of an identifiable reference peak to adjust the MR spectra is implemented. For in vivo
1H MRS, it is standard to define the chemical shift scale vector, ppm, as follows:
where
fR represents the static magnetic field in hertz and
ref is the chemical shift value at the center of the spectrum (typically 4.7 ppm for
1H MRS) [
25]. For spectrum allignment, the NAA singlet peak was fixed at 2.01 ppm.
2.2. FID Decomposition
The first step to generate basis sets of data-driven modeling is decomposing the FID signal while using truncated Hankel singular value decomposition (HSVD), which decomposes the FID signal into time domain components [
8,
28]. The decomposition step is performed after the removal of the water peak with a time-domain FIR filter. The FID signal is described by four parameters, as depicted in Equation (2), below.
where parameters of the FID signal components are:
—amplitude of a single component,
—damping factor of a single component,
—frequency of a single component,
—sampling time,
—phase of single component, and
—is imaginary unit.
HSVD starts with arranging data in form of an
Hankel matrix.
L and
M must be chosen greater than the number of expected damped sinusoids,
K. The
L and
M summation must be equal to
N + 1, where
N is number of datapoints. It is recommended to pick
L and
M in a way that makes
SH matrix as square as possible [
8].
Subsequently, the Hankel matrix
is decomposed into a product of three matrices by the application of SVD.
where
U and
V are unitary matrixes and
is a diagonal matrix, whose main diagonal elements are the singular values of
. The next step is truncating
into
, where
K is the number of sinusoids, which is assumed to be necessary to model the FID signal, and it corresponds to the number of rows of matrix
and the number of columns of matrix
.
To estimate eigenvalues of the state matrix
corresponding to the model of (1), Equation (6), below, is formed. In (6),
, and
, matrices from
, by omitting the first and the last row, respectively.
When the Equation (6) is solved in the least squares sense, the
K eigenvalues of
lead to estimates of the damping coefficients
dk and frequencies
fk [
28].
Some of the eigenvalues are positive (driving coefficients) and others are negative (damping coefficients). Therefore, the eigenvectors that are associated with negative eigenvalues (damping coefficients) must be kept. In next step, estimates
can be filled in model equation and by the least squares fit of the model (2) to the measure NMR signal. The amplitude
and phase
can be estimated:
By substituting (8) in (2), we have:
In
Figure 2, we show MR spectrum of an in vivo data as an example of decomposing a FID signal while using truncated HSVD.
2.3. Clustering
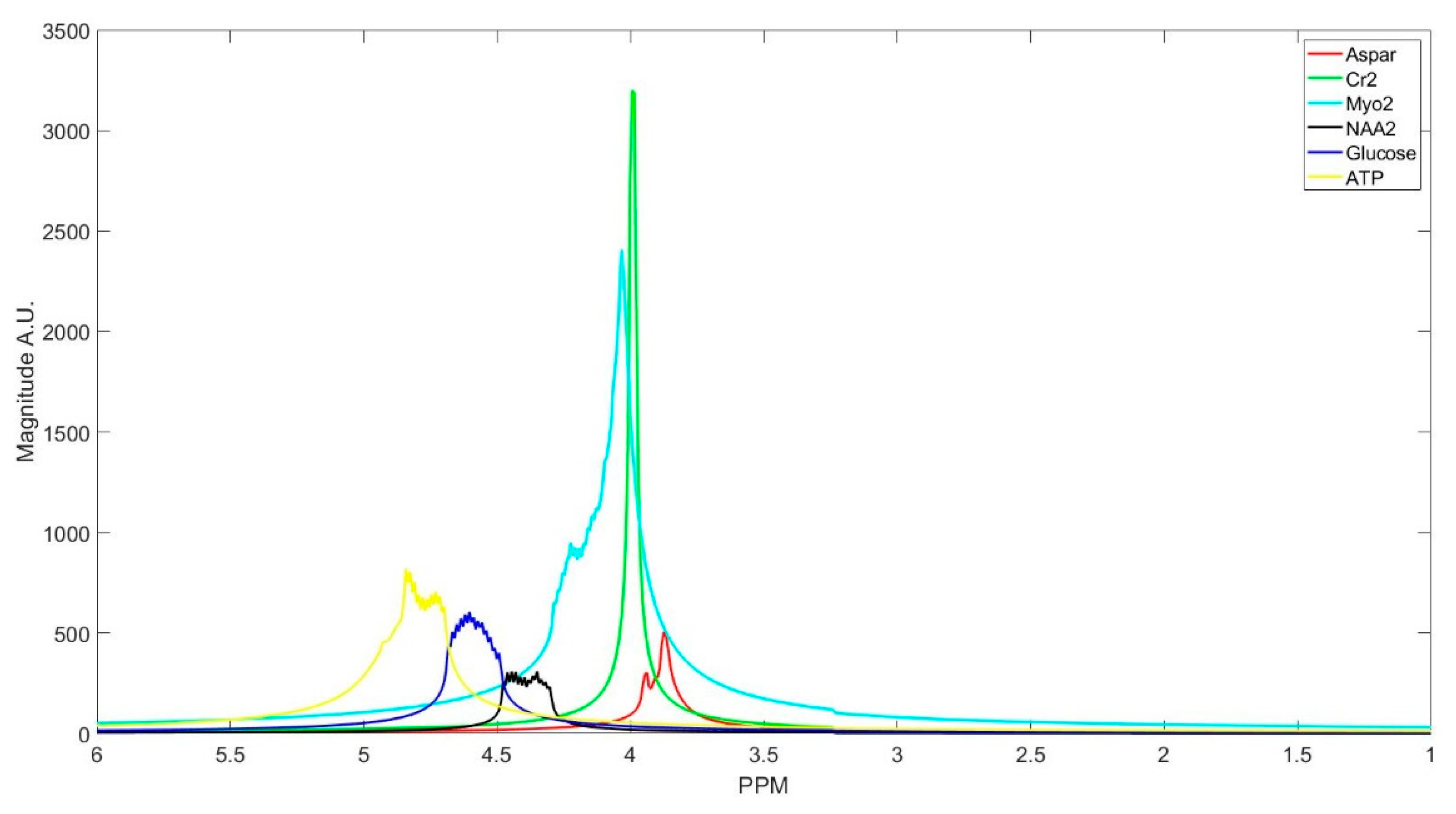
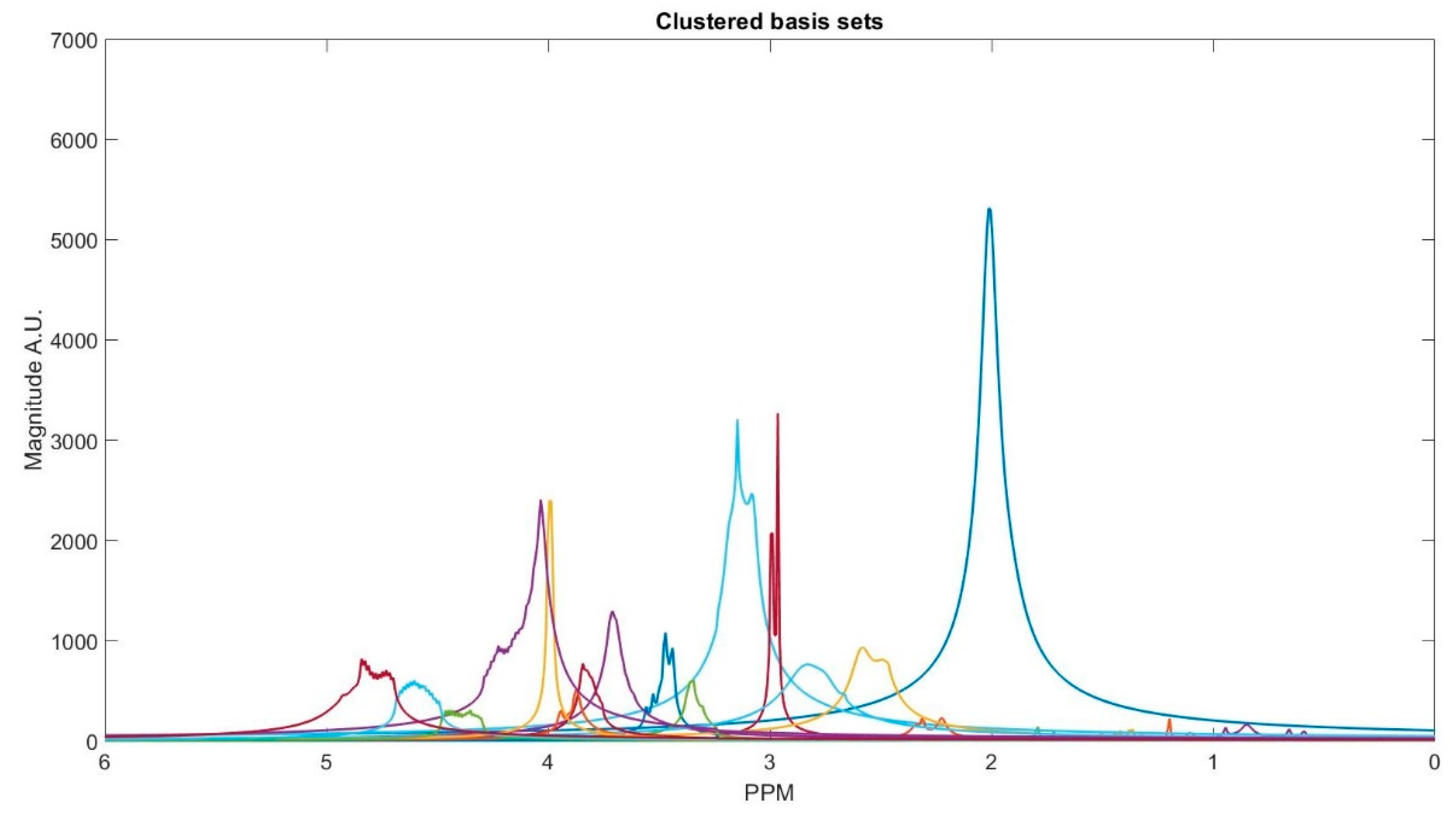
The number of decomposed FID components is larger than the number of metabolites in the FID signal. Hence, FID components need to be clustered into the number of interest metabolites. Initialized K-means is utilized to determine the cluster of components corresponding to each metabolite. K-means clustering partition number of observations; here are spectrum of the FID components, into number of clusters; here are number of metabolites, in which each component belongs to the metabolite with the nearest mean. To this end, first, the components are divided into three groups that are based on their maximum peak location in the parts per million (ppm) domain. The first group has the metabolites with peaks locations below 2.15 ppm, the second group between 2.16 and 3.85 ppm, and the third group has peaks above 3.86 ppm. Second, in each group, clusters centroids are initialized while using prior knowledge of each metabolite chemical structure, and their peak locations.
Table 1 details the initialized cluster centroids, as acquired from [
29].
Figure 3 shows the clustering result. The clustering process is done subject-wise, meaning that we do not learn cluster centroids from the dataset, and they are already learnt. A clustering process for one of the subjects (basis sets spectra is shown in the
Figure 2) is demonstrated, step-by-step, with figures in the
Appendix A.
Some of the metabolites (i.e., NAA, Creatine, Myo-inositol, and GABA) employ two cluster centroids, as shown in
Table 1. Creatine, Myo-inositol, and GABA have two strong peaks that are well removed from each other and, therefore, two cluster centers for each of them were used. NAA has one large peak and one small peak. If the small peak is neglected, then the components of that peak will be picked up by other cluster centroids, and the error in calculating the metabolites concentrations of those clusters increases.
2.4. Peak Matching
The clusters are modified to address minor differences in the line shapes, frequency bins, and the peak magnitudes of the clustered components to generate the ultimate metabolites’ basis set. The linear least square was applied constrained to full width half maximum (FWHM) of each metabolite to adjust the clustered components to make the model more closely represent the observed MR spectra. Mathematically, this approach finds a θ by solving the following problem:
where, in Equation (10),
and
are the MR spectra and the estimate of constructed metabolite spectra, respectively. The difference between each metabolite model and the observed MR spectra is only considered over the FWHM for the peak of that metabolite. The FWHM constraint was applied to omit the data points of the MR spectra with little or no information content for the chosen metabolite. In Equation (9),
is the basis set of metabolites, which is generated by the clustered components, and
is the weight vector that corresponds to each specific metabolite. The basis set is not orthogonal, because metabolite peaks overlap and, thus, the solution is iterative. The process is iterative until all of the metabolites’ spectra match with the pre-processed MR spectra.
2.5. Quantification
The water signal was used as the internal reference to quantify metabolite concentrations in the volume of interest (VOI) of the tissue. The internal reference is more stable than the external reference, as it is not associated with considerable large inter-individual variability [
30,
31]. The internal reference spectra must be generated by the same brain VOI that generates the metabolite spectra [
25,
32]. Water reference is a very strong signal that can be quickly acquired, even though it must be done without water suppression in a separate scan [
33]. The area under the water MR spectra is calculated and multiplied to a correction factor to calculate water intensity:
where,
is the area under the water peak, TE and TR are the echo time and the repetition time, respectively, and
T1
w and
T2
w are the water relaxation times. Equation (2) was obtained from [
34].
The metabolite concentrations are calculated, while using area of a peak by integrating over a fitted basis model function for that metabolite. Specifically, the intensity of a peak,
p, of metabolite,
m, from MRS data derived from a PRESS pulse sequence is given by:
where [
m] is the concentration of metabolite,
m;
is the intensity of metabolite
m in peak
p;
Nm,p is the number of hydrogens in the molecular group of m that gives rise to peak,
p,
K is a scale factor that takes into account the MR machine,
TE and
TR are the echo and repetition times of the PRESS sequence; and,
T1m,p and
T2m,p are the longitudinal and transverse relaxation times of the hydrogen in the molecular group of m that gives rise to peak,
p. Hence, the absolute quantification of metabolite concentration is achievable using a water reference concentration, yielding:
where all of the water quantities are denoted by the W and the sum is over all resolvable peaks. Equations (12)–(14) are from [
1,
29,
35].
2.6. Data Acquisition for Methodology Validation
MR spectroscopy signals from both in vitro (phantom) data and in vivo (subject) data are acquired with the Siemens 3T Skyra scanner at the TTNI by a Point RESolved Spectroscopy (PRESS) sequence. Each data scan was acquired with the following pulse sequence parameters: TE/TR = 30/2000 ms, voxel size = 2 × 2 × 2 cm
3, sampling frequency for the phantom data = 2000 Hz, and in vivo data sampling frequency = 1200 Hz. For both in vitro and in vivo cases, both water suppressed, and water unsuppressed data were acquired. The phantom data contain nine different metabolites, with their concentrations are listed in
Table 2. Five different MR spectra were scanned from five different regions of the same phantom.
The in vivo MRS and MRI data were collected from two different regions of four healthy volunteers. Two brain regions of each subject that are commonly affected by Alzheimer’s disease, the Inferior Precuneus (IP) and the Posterior Cingulate Cortex (PCC), were scanned [
36,
37]. For one of the subjects, in addition to PCC and IP, three other regions (left and right hippocampus, as well as ventral posterior cingulate gyrus) were also scanned, in order to assess water concentration variability in different brain regions of an individual.
3. Results
Figure 4a shows TARQUIN model fits and the baseline of the phantom data MR spectra while using a short TE PRESS sequence with a customized setting, where the reference signals are NAA, Creatine, Choline. In this customized setting, we only used the basis set of the existing metabolites of the phantom. The existing metabolites’ basis set must be selected, because TARQUIN, by default, uses basis set of 26 metabolites and macromolecules to fit the MR spectra. Therefore, if the default setting is used for fitting the non-existing metabolites, it will cause over or under estimation of existing metabolites concentration and might report some metabolites concentrations that do not exist in the phantom. Even with this modified setting, TARQUIN may not e properly stimate the existing metabolite properly. For instance, as it is shown in the
Figure 4, TARQUIN overestimates the baseline in two regions, where the peak of Glutathione and Glutamate is located. Thus, this overestimation leads to mis-quantification of these two metabolites. On the other hand, the creatine and NAA peaks are not detected properly and consequently did not match perfectly due to misalignment of their peaks with the basis sets. Therefore, NAA and Creatine are underestimated for the specific example that is provided in the
Figure 4.
Figure 4b shows the fit of the proposed approach model to the phantom data and the estimated baseline. In the proposed approach, the estimated baseline is very smooth as compared to the TARQUIN estimation. In contract with TARQUIN, we model the baseline as a preprocessing step prior to model each metabolite MR spectra, while TARQUIN models the metabolite first and then considers the residual as the baseline. The subtraction of the baseline prior to modeling leads to more accurate estimation of the metabolite’s MR spectra, as is shown in the
Figure 4b. The main peaks including the NAA, Creatine, Choline, and Myo-inositol are matched more accurately with the MR spectra. More specifically, TARQUIN tries to detect the metabolites using basis sets matching, and then separates the baseline and the residue from the remaining part of the MR spectra, and, therefore, the detected metabolites overlap with the estimated baseline, and they are prone to over/under quantification.
The metabolite concentrations of the phantom data in the five different regions are calculated and compared with TARQUIN; the average results along with their 95% confidence interval are provided, as shown in
Table 3. The mean squared error (MSE) of each quantification method calculated using the provided ground truth of the phantom data in the
Table 3. The proposed approach MSE is 0.34 while the MSE associated with the TARQUIN for the phantom data is 0.94. It is notable to mention that the proposed approach provides more accurate estimation of the six out of nine metabolites concentration.
Water signal was used as the internal reference to calculate brain metabolite concentrations [
25,
38,
39]. Water intensities of all five different brain regions of one subject were compared to investigate the possibility of reducing the scanning time. The maximum and minimum water intensities were
and
in arbitrary unit, respectively. Therefore, one cannot expect to scan the water unsuppressed signal for one of the brain’s region and consider that measurement provides a constant internal reference across the whole brain. Hence, for accurate metabolite concentration calculation, one must scan both waters, suppressed and unsuppressed, for each selected voxel.
For the brain regions, (IP and PCC), metabolite concentrations were calculated while using both the proposed approach and the TARQUIN. For each metabolite average and 95% confidence interval over each region were calculated and compared. Based on our observation, TARQUIN does not calculate some of the metabolite’s concentration (e.g., glycerol, valine, taurine and ATP) and also underestimates some other metabolites (e.g., glucose, Scylla-inositol, alanine, and glutamine). In the latter case, the metabolites concentration is either zero or very close to zero. Therefore, comparing the results for those metabolites is not possible.
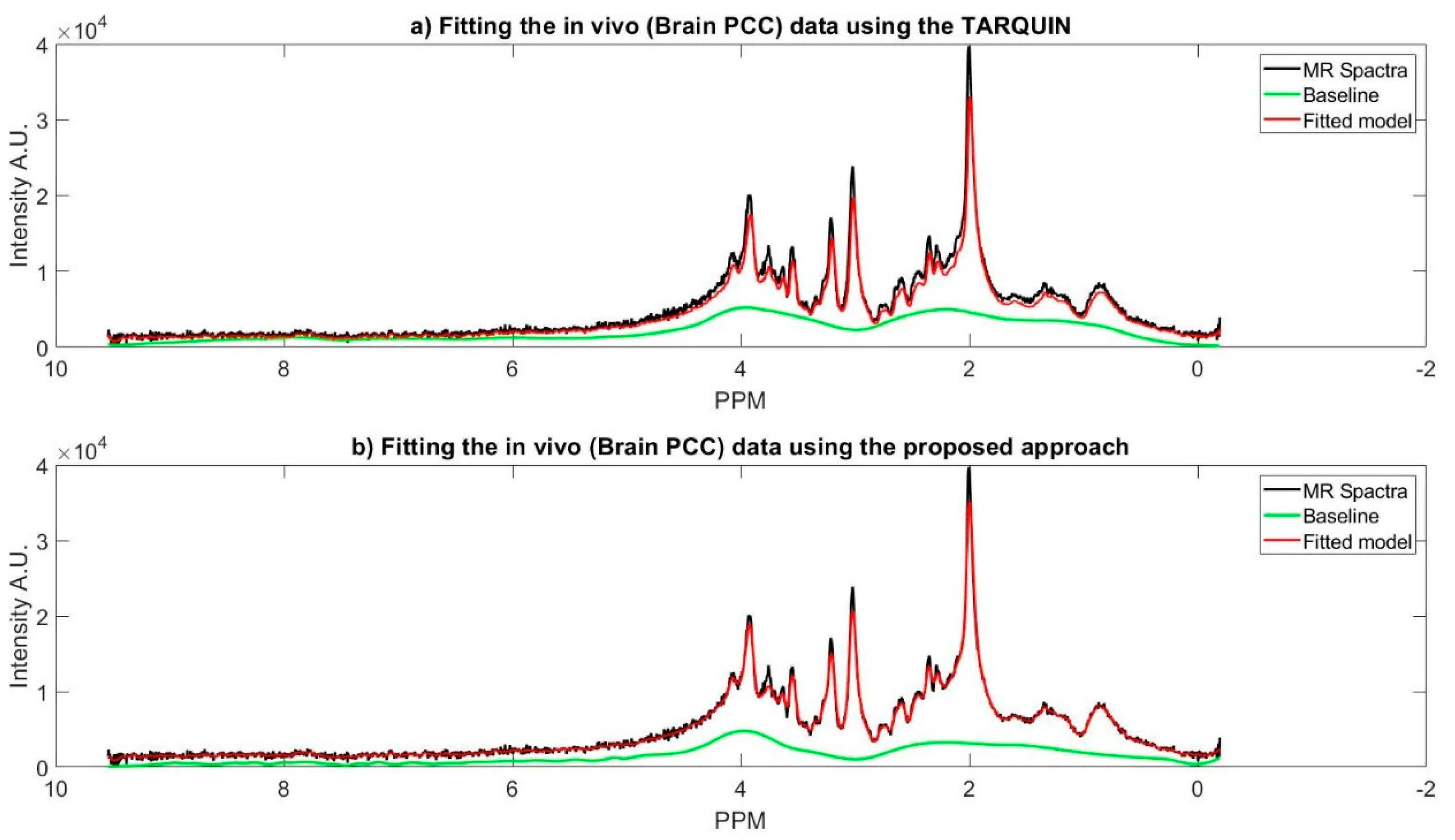
Figure 5 represents MR spectra of the one of the subjects’ brain (PCC region), and the fitted model of the proposed approach along with the TARQUIN model.
In
Table 4, a comparison between our results and TARUQIN is provided. For each metabolite mean and 95% confidence interval of its concentration over all subjects within each selected brain are shown. For those metabolites with relatively high concentration, (i.e., NAA or creatine), the confidence interval is larger, relatively. Confidence interval can be a criterion to measure the consistency of the results because no ground truth is available for an in vivo data. The confidence intervals and the means are not unalike, except for Glutamate, as shown in
Table 4. The TARQUIN results for glutamate vary significantly from our approach. One possible resolution can be the GLX metabolite concentration (i.e., Glutamate, Glutathione, and Glutamine). Because TARQUIN reports a very small concentration for Glutamine for all the subjects; therefore, its concentration might be assigned under the umbrella of GLX.
Full width half maximum (FWHM) also can be considered as another comparison criterion. FWHM for metabolites should be less than 0.1 ppm [
9]. This fact is considered as a peak matching criterion, such that large FWHM indicates poor peak matching. The FWHM for all of the metabolites are calculated while using both the proposed approach and TARQUIN. The average of FWHM for TARQUIN and the proposed approach are 0.0375 and 0.0404 ppm, respectively.
4. Discussion
In this paper, a new data-driven algorithm for MRS signal analysis is proposed, which decomposes the FID signal in the time domain and clusters the decomposed components in the frequency domain while using prior knowledge of the chemical structure of different metabolites within the selected voxel. Although the algorithm is generalized, we have focused on the analyzing short TE 1H MRS data, due to its popularity in clinical application of MRS. We have compared against TARQUIN, as a freely available automatic software package that is widely used in MRS signal analysis applications with better claimed accuracy than the LCModelTM.
The complexity of metabolites spectra varies according to their chemical structure. For instance, the NAA spectrum frequently contains one peak that is assumed to N-acetyl aspartate [
40]. The Cr peak corresponds to superposition of creatine and phosphocreatine. The PCh spectrum is more complex, containing a contribution from phosphocholine, glycerophosphocholine, free choline, acetylcholine, phosphatidylcholine, and choline-plasminogen [
29]. The myo-inositol peak includes phosphatidylinositol, inositol polyphosphatide, and inositol monophosphate [
30,
41]. Therefore, basis sets developed in the environment laboratories must consider all of these contributions carefully, before they can be used to model the MR spectra, through the basis sets methods of MRS signal analysis. One, reason for under/over estimation of metabolite concentration using these methods could be imperfect matching of subpeaks of the complex non-orthogonal basis sets with the corresponding metabolites in the MR spectra.
The fitted model using TARQUIN in
Figure 4a shows that the NAA and Creatine peaks are not properly detected. TARQUIN estimates the model using the basis sets and then estimates the baseline, which makes the modeling of the metabolite’s MR spectra an error prone task. In agreement with some literatures including [
1,
10], the baseline is a major source of variability, and therefore it must be detected and corrected before the peak matching step. On the other hand, TARQUIN has a fixed number of basis sets which will be fitted to a spectrum, even if that spectrum does not contain corresponding metabolites, which is a source of error in modeling and quantification of metabolites concentration of the in vitro data. In the proposed approach, the decomposing and clustering process are performed right after the water peak removal. The clustered components are then matched with the corrected MR spectra in the frequency domain. The comparison of TARQUIN results with the phantom data ground truth shows, our approach outperforms TARQUIN in quantifying the metabolite concentration.
Several important limitations must be considered. First, the metabolites relaxation times, T1 and T2, were not measured due to limited scan time; therefore, the values from other studies were used to quantify the metabolite’s concentrations [
42,
43], which provides a potential source of error. Second, generally, some uncertainty exists in the parameters that were used to calculate the correction factor from the internal reference, which might cause a systematic error that must be addressed in an independent study. Third, the number of subjects and their age range were too small to investigate age-related variances in the metabolite quantification process. Fourth, the study was conducted with a 3T scanner, and using MR scanner machines with higher field strength provides signals with better quality and SNR.
5. Conclusions
In this study, a robust fully automatic data-driven approach has been proposed that incorporates prior knowledge in modeling metabolites bases sets. It decomposes FID signal in the time domain, and then clusters the decomposed components in the frequency domain. When compared with TARQUIN, the proposed method on average provides more accurate metabolites concentration of phantom data. In this work, we focused on quantification of brain’s metabolites concentration using MRS, to be utilized in our future work in an early detection of neurodegenerative diseases studies, such as Alzheimer in West Texas. Additionally, since the brain’s metabolites spectrum are in a limited range, in our future works, we will develop our algorithm that is suitable for applications covers wider range of MR spectrum.