About Granular Rough Computing—Overview of Decision System Approximation Techniques and Future Perspectives
Abstract
1. Introduction
2. Granulation Techniques
- 2.0.1.
- First Step—GranulationWe begin with computation of granules around each training object using a selected method.
- 2.0.2.
- Second Step—The Process of CoveringThe training decision system is covered by selected granules.
- 2.0.3.
- Third Step—Building the Granular ReflectionsThe granular reflection of original training decision system is derived from the granules selected in step 2.We start with detailed description of the basic method—see [24].
2.1. Standard Granulation
Toy Example
2.2. Concept Dependent Granulation
Toy Example
2.3. Homogeneous Granulation
Toy Example
2.4. Layered Granulation
Toy Example
2.5. Epsilon Variants
–Modification of the Standard Rough Inclusion
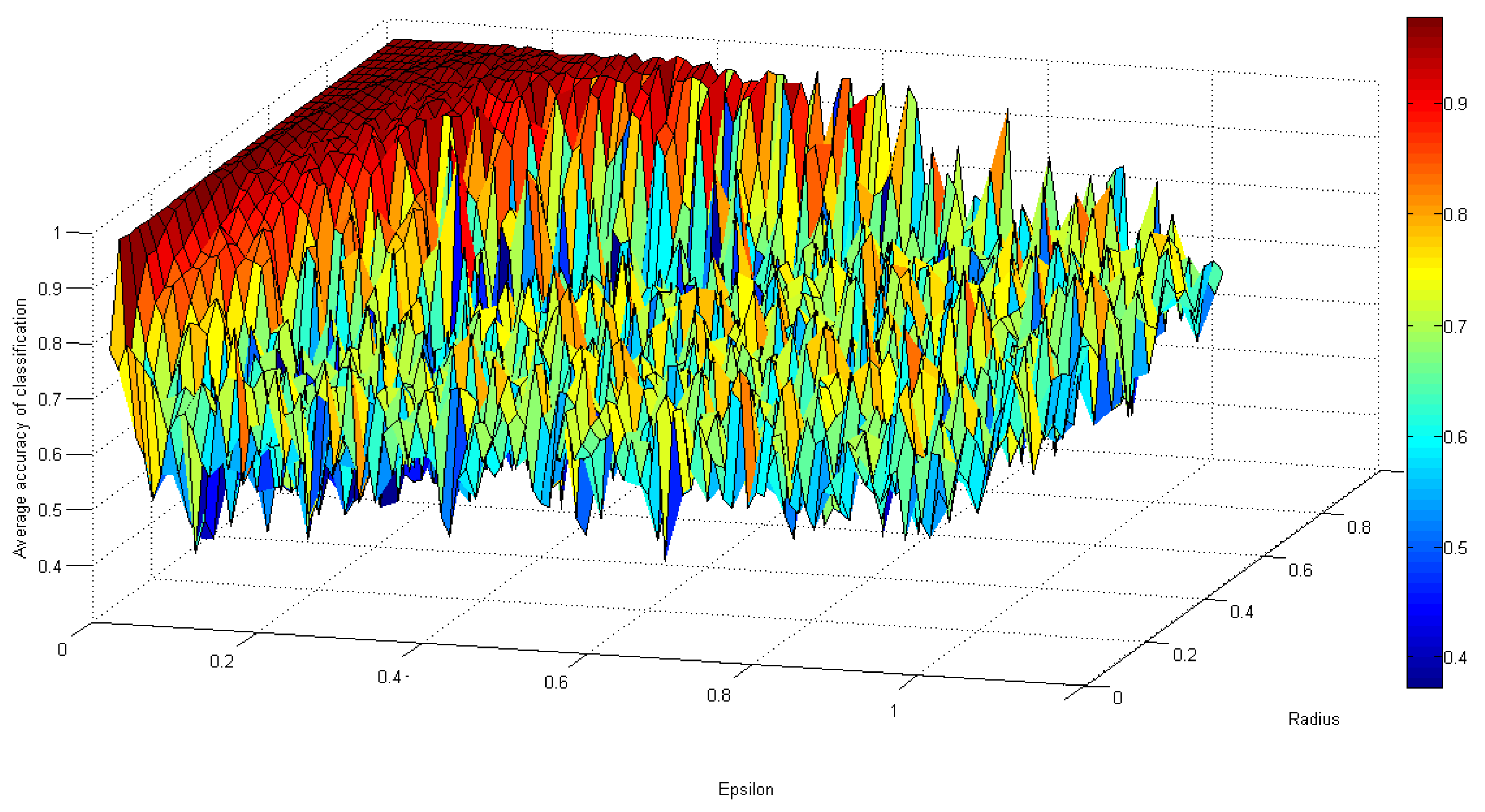
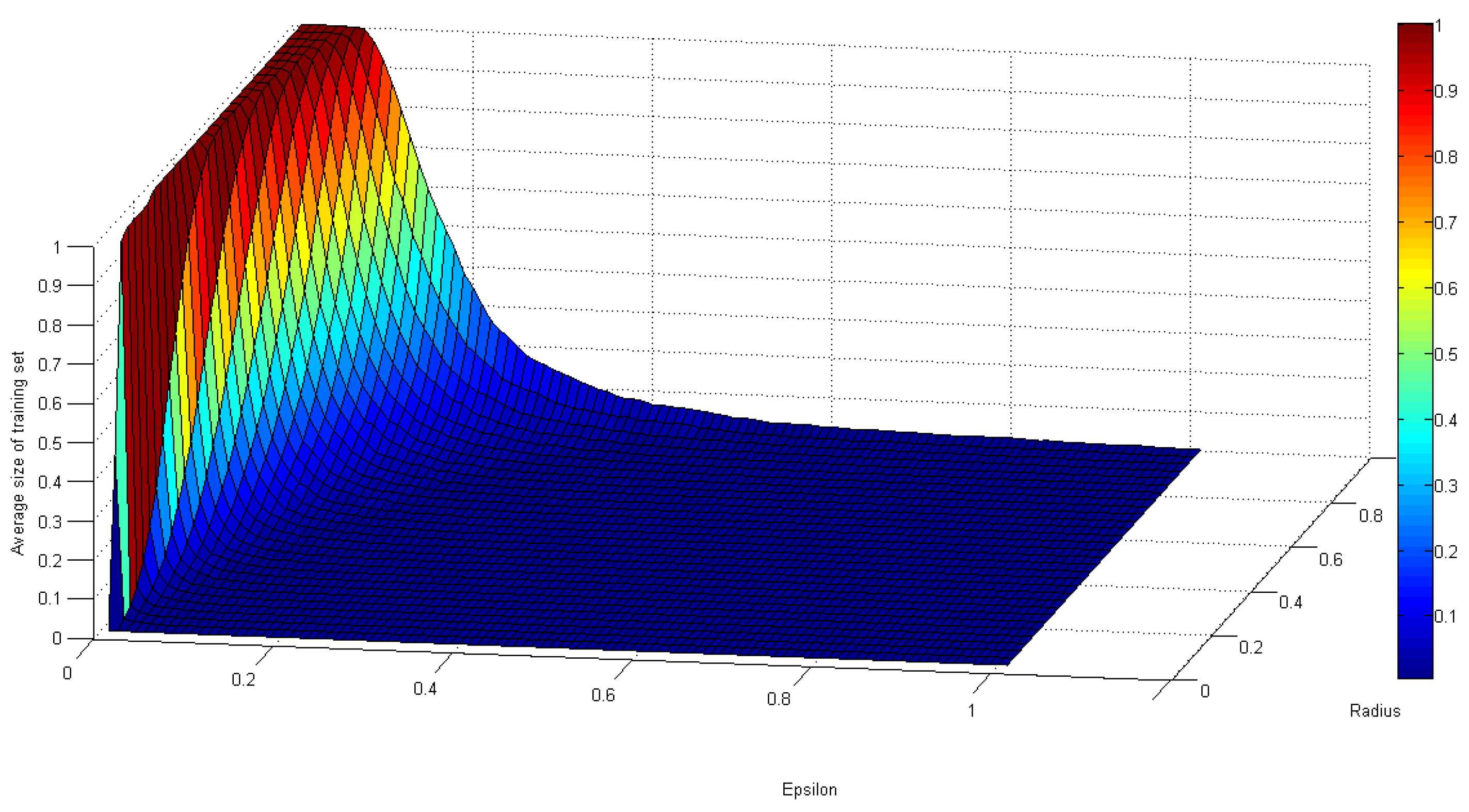
2.6. Epsilon Homogeneous Granulation
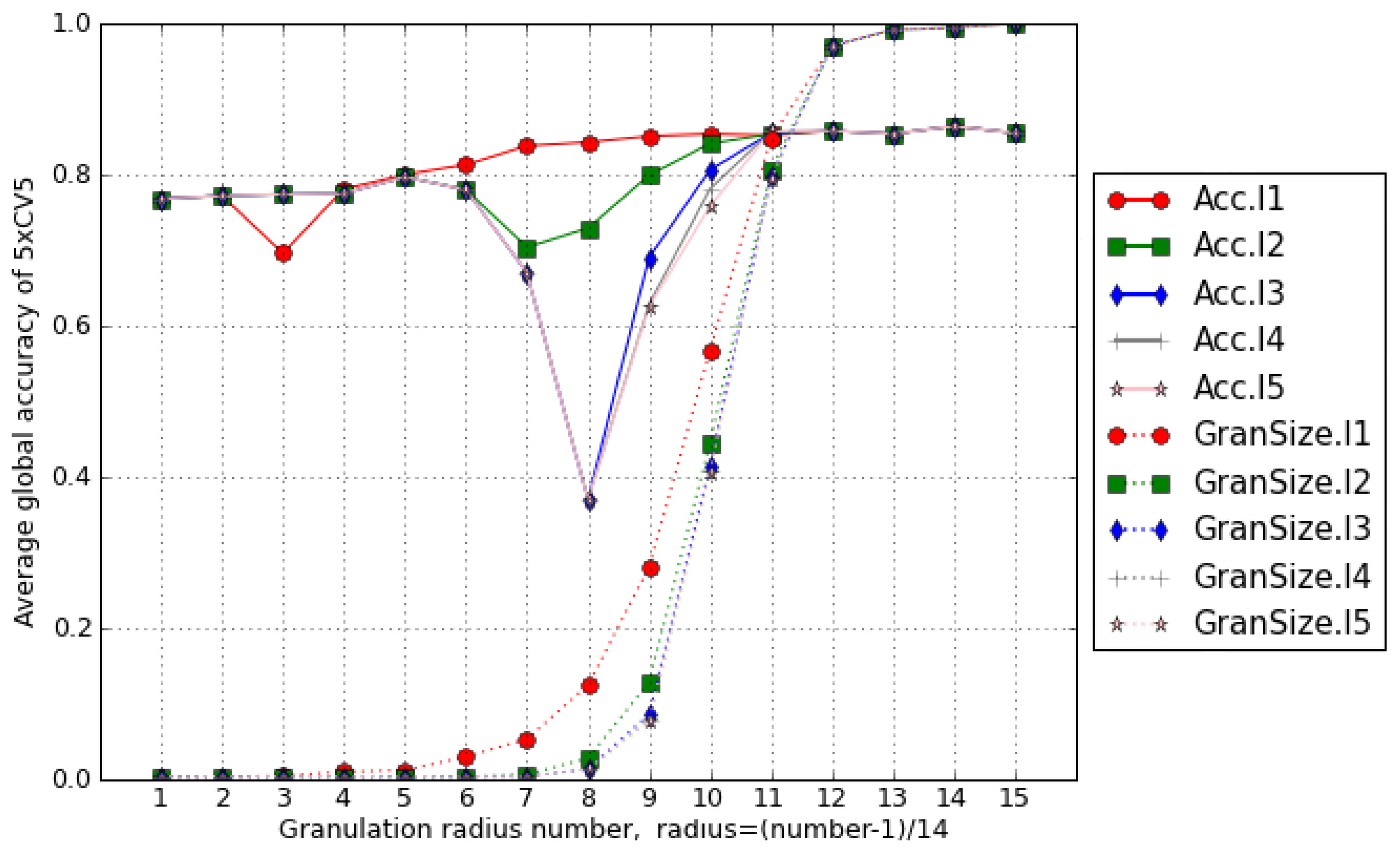
3. A Sample of the Experimental Work Results
4. Application of Selected Other Classifiers on Granular Data
- .
- .
- .
- .
5. Future Directions in Granular Computing Paradigm
6. Conclusions
Funding
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy Sets and Information Granularity. 1979. Available online: https://digitalassets.lib.berkeley.edu/techreports/ucb/text/ERL-m-79-45.pdf (accessed on 13 February 2020).
- Zadeh, L.A. Graduation and granulation are keys to computation with information described in natural language. In Proceedings of the 2006 IEEE International Conference on Granular Computing, Atlanta, GA, USA, 10–12 May 2006. [Google Scholar]
- Pawlak, Z. Rough sets. Int. J. Comput. Inform. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Skowron, A.; Polkowski, L. Synthesis of decision systems from data tables. In Rough Sets and Data Mining; Lin, T.Y., Cercone, N., Eds.; Springer: Boston, MA, USA, 1997; pp. 289–299. [Google Scholar]
- Lin, T.Y. Granular computing: Examples, intuitions and modeling. In Proceedings of the 2005 IEEE International Conference on Granular Computing, Beijing, China, 25–27 July 2005; Volume 1, pp. 40–44. [Google Scholar]
- Yao, Y.Y. Granular computing: Basic issues and possible solutions. In Proceedings of the 5th Joint Conference on Information Sciences, Atlantic, NJ, USA, 27 February 2000; Volume 1, pp. 186–189. [Google Scholar]
- Yao, Y. Information Granulation and Approximation in a Decision-Theoretical Model of Rough Sets. In Rough-Neural Computing; Pal, S.K., Polkowski, L., Skowron, A., Eds.; Springer: Berlin, Germany, 2004; pp. 491–516. [Google Scholar]
- Yao, Y. Perspectives of granular computing. In Proceedings of the 2005 IEEE International Conference on Granular Computing, Beijing, China, 25–27 July 2005; Volume 1, pp. 85–90. [Google Scholar]
- Skowron, A.; Stepaniuk, J. Information granules: Towards foundations of granular computing. Int. J. Intell. Syst. 2001, 16, 57–85. [Google Scholar] [CrossRef]
- Skowron, A.; Stepaniuk, J. Information Granules and Rough-Neural Computing. In Rough-Neural Computing; Pal, S.K., Polkowski, L., Skowron, A., Eds.; Springer: Berlin, Germany, 2004; pp. 43–84. [Google Scholar]
- Polkowski, L.; Semeniuk–Polkowska, M. On rough set logics based on similarity relations. Fund. Inform. 2005, 64, 379–390. [Google Scholar]
- Liu, Q.; Sun, H. Theoretical study of granular computing. In Rough Sets and Knowledge Technology; Wang, G.Y., Peters, J.F., Skowron, A., Yao, Y., Eds.; Springer: Berlin, Germany, 2006; Volume 4062, pp. 92–102. [Google Scholar]
- Cabrerizo, F.J.; Al-Hmouz, R.; Morfeq, A.; Martínez, M.A.; Pedrycz, W.; Herrera-Viedma, E. Estimating incomplete information in group decision-making: A framework of granular computing. Appl. Soft Comput. 2020, 86, 105930. [Google Scholar] [CrossRef]
- Hryniewicz, O.; Kaczmarek, K. Bayesian analysis of time series using granular computing approach. Appl. Soft Comput. 2016, 47, 644–652. [Google Scholar] [CrossRef]
- Martino, A.; Giuliani, A.; Rizzi, A. (Hyper) Graph Embedding and Classification via Simplicial Complexes. Algorithms 2019, 12, 223. [Google Scholar] [CrossRef]
- Martino, A.; Giuliani, A.; Todde, V.; Bizzarri, M.; Rizzi, A. Metabolic networks classification and knowledge discovery by information granulation. Comput. Biol. Chem. 2020, 84, 107187. [Google Scholar] [CrossRef] [PubMed]
- Pownuk, A.; Kreinovich, V. Granular approach to data processing under probabilistic uncertainty. In Granular Computing; Springer: Berlin, Germany, 2019; pp. 1–17. [Google Scholar]
- Zhong, C.; Pedrycz, W.; Wang, D.; Li, L.; Li, Z. Granular data imputation: A framework of granular computing. Appl. Soft Comput. 2016, 46, 307–316. [Google Scholar] [CrossRef]
- Leng, J.; Chen, Q.; Mao, N.; Jiang, P. Combining granular computing technique with deep learning for service planning under social manufacturing contexts. Knowl.-Based Syst. 2018, 143, 295–306. [Google Scholar] [CrossRef]
- Ghiasi, B.; Sheikhian, H.; Zeynolabedin, A.; Niksokhan, M.H. Granular computing-neural network model for prediction of longitudinal dispersion coefficients in rivers. Water Sci. Technol. 2020, 80, 1880–1892. [Google Scholar] [CrossRef] [PubMed]
- Capizzi, G.; Lo Sciuto, G.; Napoli, C.; Połap, D.; Woźniak, M. Small Lung Nodules Detection Based on Fuzzy-Logic and Probabilistic Neural Network with Bio-inspired Reinforcement Learning. 2019. Available online: https://ieeexplore.ieee.org/abstract/document/8895990 (accessed on 13 February 2020).
- Polkowski, L. Formal granular calculi based on rough inclusions. In Proceedings of the 2005 IEEE Conference on Granular Computing, Beijing, China, 25–27 July 2005; pp. 57–62. [Google Scholar]
- Polkowski, L. Approximate Reasoning by Parts. An Introduction to Rough Mereology; Springer: Berlin, Germany, 2011. [Google Scholar]
- Polkowski, L. A model of granular computing with applications. In Proceedings of the 2006 IEEE Conference on Granular Computing, Atlanta, GA, USA, 10 May 2006; pp. 9–16. [Google Scholar]
- Artiemjew, P. Classifiers from Granulated Data Sets: Concept Dependent and Layered Granulation. 2007. Available online: https://pdfs.semanticscholar.org/e46a/0e41d0833263220680aa1ec7ae9ed3edbb42.pdf#page=7 (accessed on 13 February 2020).
- Artiemjew, P.; Ropiak, K.K. On Granular Rough Computing: Handling Missing Values by Means of Homogeneous Granulation. Computers 2020, 9, 13. [Google Scholar] [CrossRef]
- Polkowski, L. Granulation of knowledge in decision systems: The approach based on rough inclusions. The method and its applications. In Rough Sets and Intelligent Systems Paradigms; Kryszkiewicz, M., Peters, J.F., Rybinski, H., Skowron, A., Eds.; Springer: Berlin, Germany, 2007; Volume 4585, pp. 69–79. [Google Scholar]
- Polkowski, L. Granulation of Knowledge: Similarity Based Approach in Information and Decision Systems. In Encyclopedia of Complexity and System Sciences; Meyers, R.A., Ed.; Springer: Berlin, Germany, 2009. [Google Scholar]
- Polkowski, L.; Artiemjew, P. On granular rough computing with missing values. In Rough Sets and Intelligent Systems Paradigms; Kryszkiewicz, M., Peters, J.F., Rybinski, H., Skowron, A., Eds.; Springer: Berlin, Germany, 2007; Volume 4585, pp. 271–279. [Google Scholar]
- Polkowski, L.; Artiemjew, P. Granular Computing in Decision Approximation - An Application of Rough Mereology; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Polkowski, L.; Artiemjew, P. On granular rough computing: Factoring classifiers through granular structures. In Rough Sets and Intelligent Systems Paradigms; Kryszkiewicz, M., Peters, J.F., Rybinski, H., Skowron, A., Eds.; Springer: Berlin, Germany, 2007; Volume 4585, pp. 280–290. [Google Scholar]
- Artiemjew, P.; Ropiak, K. A Novel Ensemble Model - The Random Granular Reflections. 2018. Available online: http://ceur-ws.org/Vol-2240/paper17.pdf (accessed on 13 February 2020).
- Ropiak, K.; Artiemjew, P. Homogenous Granulation and Its Epsilon Variant. Computers 2019, 8, 36. [Google Scholar] [CrossRef]
- Artiemjew, P. A Review of the Knowledge Granulation Methods: Discrete vs. Continuous Algorithms. In Rough Sets and Intelligent Systems - Professor Zdzisław Pawlak in Memoriam; Skowron, A., Suraj, Z., Eds.; Springer: Berlin, Germany, 2013; Volume 43, pp. 41–59. [Google Scholar]
- Polkowski, L. Rough Sets; Springer: Berlin, Germany, 2002. [Google Scholar]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Elsevier: New York, NY, USA, 2004. [Google Scholar]
- University of California, Irvine Machine Learning Repository. Available online: https://archive.ics.uci.edu/ml/index.php (accessed on 13 February 2020).
- Szypulski, J.; Artiemjew, P. The Rough Granular Approach to Classifier Synthesis by Means of SVM. In Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing; Yao, Y., Hu, Q., Yu, H., Grzymala-Busse, J., Eds.; Springer: Cham, Switzerland, 2015; Volume 9437, pp. 256–263. [Google Scholar]
- Ropiak, K.; Artiemjew, P. On a Hybridization of Deep Learning and Rough Set Based Granular Computing. Algorithms 2020, 13, 63. [Google Scholar] [CrossRef]

| Day | Outlook | Temperature | Humidity | Wind | Play.golf |
|---|---|---|---|---|---|
| Sunny | Hot | High | Weak | No | |
| Sunny | Hot | High | Strong | No | |
| Overcast | Hot | High | Weak | Yes | |
| Rainy | Mild | High | Weak | Yes | |
| Rainy | Cool | Normal | Weak | Yes | |
| Rainy | Cool | Normal | Strong | No | |
| Overcast | Cool | Normal | Strong | Yes | |
| Sunny | Mild | High | Weak | No | |
| Sunny | Cool | Normal | Weak | Yes | |
| Rainy | Mild | Normal | Weak | Yes | |
| Sunny | Mild | Normal | Strong | Yes | |
| Overcast | Mild | High | Strong | Yes | |
| Overcast | Hot | Normal | Weak | Yes | |
| Rainy | Mild | High | Strong | No |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | ||
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | |||
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | ||||
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | |||||
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | ||||||
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | |||||||
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | ||||||||
| 1 | 1 | 1 | 0 | 1 | 0 | |||||||||
| 1 | 1 | 0 | 1 | 1 | ||||||||||
| 1 | 1 | 0 | 1 | |||||||||||
| 1 | 0 | 1 | ||||||||||||
| 1 | 0 | |||||||||||||
| 1 |
| Play.golf | |||||
|---|---|---|---|---|---|
| Sunny | Hot | High | Weak | Yes | |
| Rainy | Mild | High | Weak | Yes | |
| Rainy | Cool | Normal | Weak | Yes | |
| Rainy | Mild | High | Strong | No |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | ||
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | |||
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | ||||
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | |||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||||||
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | ||||||||
| 1 | 1 | 1 | 0 | 1 | 0 | |||||||||
| 1 | 1 | 1 | 1 | 0 | ||||||||||
| 1 | 1 | 1 | 0 | |||||||||||
| 1 | 1 | 0 | ||||||||||||
| 1 | 0 | |||||||||||||
| 1 |
| Play.golf | |||||
|---|---|---|---|---|---|
| Overcast | Mild | Normal | Weak | Yes | |
| Sunny | Hot | High | Strong | No |
| Day | Outlook | Temperature | Humidity | Wind | Play Golf |
|---|---|---|---|---|---|
| Sunny | Hot | High | Weak | No | |
| Rainy | Mild | High | Weak | Yes | |
| Rainy | Cool | Normal | Strong | No | |
| Overcast | Cool | Normal | Strong | Yes | |
| Sunny | Mild | High | Weak | No | |
| Rainy | Cool | Normal | Weak | Yes | |
| Rainy | Mild | Normal | Weak | Yes | |
| Overcast | Mild | High | Strong | Yes | |
| Overcast | Hot | High | Weak | Yes | |
| Rainy | Mild | High | Strong | No |
| Day | Outlook | Temperature | Humidity | Wind | Play Golf |
|---|---|---|---|---|---|
| Sunny | Hot | High | Weak | No | |
| Sunny | Hot | High | Weak | No | |
| Overcast | Mild | High | Weak | Yes | |
| Rainy | Mild | High | Weak | Yes | |
| Rainy | Cool | Normal | Weak | Yes | |
| Rainy | Cool | Normal | Strong | No | |
| Overcast | Cool | Normal | Strong | Yes |
| Day | Outlook | Temperature | Humidity | Wind | Play Golf |
|---|---|---|---|---|---|
| Sunny | Hot | High | Weak | No | |
| Overcast | Mild | High | Weak | Yes | |
| Rainy | Mild | High | Weak | Yes | |
| Rainy | Cool | Normal | Weak | Yes | |
| Rainy | Cool | Normal | Strong | No |
| Day | Outlook | Temperature | Humidity | Wind | Play Golf |
|---|---|---|---|---|---|
| Sunny | Hot | High | Weak | No | |
| Overcast | Mild | High | Weak | Yes | |
| Rainy | Mild | High | Weak | Yes | |
| Rainy | Cool | Normal | Strong | No |
| Name | Attr No. | Obj No. | Class No. |
|---|---|---|---|
| Australian-credit | 15 | 690 | 2 |
| Car Evaluation | 7 | 1728 | 4 |
| Heartdisease | 14 | 270 | 2 |
| Hepatitis | 20 | 155 | 2 |
| Wisconsin Diagnostic Breast Cancer | 32 | 569 | 2 |
| AccSG | SizeSG | AccCDG | SizeCDG | |
|---|---|---|---|---|
| 0.84058 | 4.8 | |||
| 0.847826 | 51.2 | 0.845 | 71.64 | |
| 297 | ||||
| 1 | 552 | 552 |
| AccSG | SizeSG | AccCDG | SizeCDG | |
|---|---|---|---|---|
| 0.864 | 371.64 | |||
| AccSG | SizeSG | AccCDG | SizeCDG | |
|---|---|---|---|---|
| 11 | 0.819 | 16.76 | ||
| 0.833333 | 27 | |||
| 118 | ||||
| 210 | ||||
| 216 | 216 | |||
| 216 | 216 | |||
| 1 | 216 | 216 |
| AccSG | SizeSG | AccCDG | SizeCDG | |
|---|---|---|---|---|
| 2 | 2 | |||
| 2 | 2 | |||
| 2 | ||||
| 0.854 | 7.56 | |||
| 0.847742 | 11.28 | 0.875 | ||
| 121 | 121 | |||
| 122 | ||||
| 124 | 124 |
| Data Set | Acc | GS | TRN_size | TRN_red | Radii_range |
|---|---|---|---|---|---|
| 552 | |||||
| 1382 | |||||
| 216 | |||||
| 124 |
| Layer1 | Layer2 | Layer3 | Layer4 | |||||
|---|---|---|---|---|---|---|---|---|
| Acc | GranSize | Acc | GranSize | Acc | GranSize | Acc | GranSize | |
| 0 | 2 | 2 | 2 | 2 | ||||
| 2 | 2 | 2 | 2 | |||||
| 2 | 2 | 2 | ||||||
| 2 | 2 | 2 | ||||||
| 2 | 2 | 2 | ||||||
| 2 | 2 | 2 | ||||||
| 0.838 | 29.6 | |||||||
| 0.841 | 245.6 | |||||||
| 0.855 | 440 | 0.857 | 438.6 | |||||
| 1 | 552 | 552 | 552 | 552 | ||||
| Layer1 | Layer2 | Layer3 | Layer4 | |||||
|---|---|---|---|---|---|---|---|---|
| Acc | GranSize | Acc | GranSize | Acc | GranSize | Acc | GranSize | |
| 0 | 4 | 4 | 4 | 4 | ||||
| 4 | 4 | 4 | ||||||
| 44 | 7 | |||||||
| 0.865 | 370 | 0.841 | 199.8 | 137 | ||||
| 1 | ||||||||
| Layer1 | Layer2 | Layer3 | Layer4 | |||||
|---|---|---|---|---|---|---|---|---|
| Acc | GranSize | Acc | GranSize | Acc | GranSize | Acc | GranSize | |
| 0 | 2 | 2 | 2 | 2 | ||||
| 2 | 2 | 2 | 2 | |||||
| 3 | 2 | 2 | 2 | |||||
| 2 | 2 | 2 | ||||||
| 2 | 2 | 2 | ||||||
| 17 | 2 | 2 | ||||||
| 0.833 | 35.6 | 4 | ||||||
| 23 | ||||||||
| 171 | ||||||||
| 211 | 0.826 | 210.2 | 0.826 | 210 | 210 | |||
| 216 | 216 | 216 | 216 | |||||
| 216 | 216 | 216 | 216 | |||||
| 1 | 216 | 216 | 216 | 216 | ||||
| Layer1 | Layer2 | Layer3 | Layer4 | |||||
|---|---|---|---|---|---|---|---|---|
| Acc | GranSize | Acc | GranSize | Acc | GranSize | Acc | GranSize | |
| 0 | 2 | 2 | 2 | 2 | ||||
| 2 | 2 | 2 | 2 | |||||
| 2 | 2 | 2 | 2 | |||||
| 2 | 2 | 2 | 2 | |||||
| 2 | 2 | 2 | 2 | |||||
| 3 | 2 | 2 | 2 | |||||
| 2 | 2 | 2 | ||||||
| 2 | 2 | 2 | ||||||
| 2 | 2 | 2 | ||||||
| 0.871 | 12.4 | 2 | 2 | |||||
| 27 | ||||||||
| 67 | 0.865 | 54.6 | 0.865 | 52.6 | ||||
| 79 | ||||||||
| 121 | ||||||||
| 122 | 122 | 122 | 122 | |||||
| 1 | 124 | 124 | 124 | 124 | ||||
| Acc | |||
| HGS_size | |||
| TRN_size | 552 | 216 | 124 |
| HG_TRN_red | 50.3% | 49.4% | 62.7% |
| HG_r_range |
| Acc | GranSize | |||||||
|---|---|---|---|---|---|---|---|---|
| rgran | ||||||||
| 0.853 | 32.84 | |||||||
| 71 | ||||||||
| 157 | ||||||||
| 319 | ||||||||
| 536 | ||||||||
| 1 | 552 | 552 | 552 | 552 | ||||
| Acc | GranSize | |||||||
|---|---|---|---|---|---|---|---|---|
| rgran | ||||||||
| 1 | ||||||||
| Acc | GranSize | |||||||
|---|---|---|---|---|---|---|---|---|
| rgran | ||||||||
| 9 | ||||||||
| 0.824 | 16.6 | |||||||
| 216 | 216 | 216 | 216 | |||||
| 216 | 216 | 216 | 216 | |||||
| 1 | 216 | 216 | 216 | |||||
| Acc | GranSize | |||||||
|---|---|---|---|---|---|---|---|---|
| rgran | ||||||||
| 0.839 | 2 | 2 | 2 | 2 | ||||
| 2 | 2 | 2 | 2 | |||||
| 2 | 2 | 2 | ||||||
| 0.876 | 18.28 | |||||||
| 110 | 110 | |||||||
| 121 | 121 | 121 | 121 | |||||
| 122 | ||||||||
| 1 | 124 | 124 | 124 | 124 | ||||
| Gran_rad | No_of_gran_objects | Percentage_of_objects | Time_to_learn | Accuracy |
|---|---|---|---|---|
| Mean | Mean | Mean | Mean | |
| 283.8 | 0.8399 | |||
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Artiemjew, P. About Granular Rough Computing—Overview of Decision System Approximation Techniques and Future Perspectives. Algorithms 2020, 13, 79. https://doi.org/10.3390/a13040079
Artiemjew P. About Granular Rough Computing—Overview of Decision System Approximation Techniques and Future Perspectives. Algorithms. 2020; 13(4):79. https://doi.org/10.3390/a13040079
Chicago/Turabian StyleArtiemjew, Piotr. 2020. "About Granular Rough Computing—Overview of Decision System Approximation Techniques and Future Perspectives" Algorithms 13, no. 4: 79. https://doi.org/10.3390/a13040079
APA StyleArtiemjew, P. (2020). About Granular Rough Computing—Overview of Decision System Approximation Techniques and Future Perspectives. Algorithms, 13(4), 79. https://doi.org/10.3390/a13040079





