1. Introduction
Nowadays, porous media have attracted multidisciplinary attention due to their notable properties, which have broadened their applications in the petroleum [
1] and chemical industries [
2], hydrology [
3], etc. This increased interest makes the accurate analysis of the microstructural behavior of the examined porous media a great field of research. To accurately measure the transport properties of a porous material, e.g., diffusivity, permeability, and conductivity, the 3D material structure needs to be known. However, the acquisition of the 3D structure of a material requires microscopes of high technology and high cost, as well as a high processing time.
Alternatively, the 3D material structure can be derived by applying a computational reconstruction technique that uses a single 2D image of the material that is acquired using conventional imaging equipment [
4]. The first reconstruction method was proposed quite early by Quiblier [
5] in the years when imaging systems were limited and displayed marginal performance. Lately, Adler et al. [
6] generalized Quiblier’s method to measure the flow in porous media, while Bentz and Martys [
7] proposed a simplified version of Quiblier’s method, which is free of filter parameter calculations but adds a significant computational overhead. Since then, several algorithms have been proposed [
8,
9,
10,
11] aiming to improve the reconstruction accuracy. Almost all algorithms make use of specific correlation functions for measuring the morphology of the material’s microstructure. The spatial correlation functions [
12], such as auto-correlation functions, have proved to be good descriptors of the porous space morphology, while their simplicity accelerates the overall reconstruction procedure.
More recent attempts to develop a reliable 3D reconstruction of porous media from a single 2D image were targeted toward investigating the connectivity of the flow paths by utilizing reconstruction approaches using multiple-point statistics [
13,
14,
15], cross-correlation functions [
16,
17,
18], spatial correlation functions [
19], and multiple statistical functions [
20]. The majority of these approaches consist of several simple processing steps in an iterative manner, where the 3D material is reconstructed layer by layer through repetitive comparisons with the 2D slice reference image. Of course, the reconstruction accuracy is higher if more information is retrieved from the initial 2D image. Very recent works [
21,
22,
23] have tried to utilize the advantages of the deep learning models to represent some initial information (2D thin image) with massive abstract features and to generate possible 3D reconstructions as adversarial images of the input information. However, these approaches are time-consuming and need many annotated samples from the same material for model training, which in most cases are difficult to collect.
Among the reconstruction methods presented in the literature, the work of Yeong and Torquato [
9,
10] exhibits some remarkable properties relative to its simplicity and efficiency. In their work Yeong and Torquato tackled the reconstruction procedure as an optimization problem, which they solved by applying the simulated annealing (SA) algorithm. Of course, the main weakness of this method is the high computation time stemming from the low convergence time of the SA algorithm. Motivated by the method of Yeong and Torquato [
9,
10], in this study, we examine the reconstruction performance of porous media when several traditional, as well as recently proposed, nature-inspired optimization algorithms are used instead of SA. The application of the standard genetic algorithm (GA) [
24], particle swarm optimization (PSO) [
25], differential evolution (DE) [
26], firefly algorithm (FA) [
27], artificial bee colony (ABC) [
28], and gravitational search algorithm (GSA) [
29] optimization evolutionary algorithms showed some important advantages: (1) they could provide a global solution to the problem via exploitation and exploration of the solution space, (2) they were free from complex mathematics, (3) they did not require the objective function being optimized to have specific mathematical properties, (4) they provided flexibility in combining multiple objectives, (5) they had a parallel nature and could be executed very fast by applying high-performance computing frameworks (GPU, Spark, etc.).
The contributions of this work are as follows:
- (1)
The 3D porous media reconstruction was formulated as a generic optimization problem described using a multi-objective function that was able to incorporate any type and any combination of statistical functions, alleviating the restrictions of the past techniques that used a single statistical measure.
- (2)
For the first time, the nature-inspired algorithms were applied in 3D porous media reconstruction.
- (3)
A novel and efficient material data representation that enabled the reliable deployment of the evolutionary algorithms with a fast execution rate was proposed.
- (4)
The emergence of the existing auto-correlation functions’ weaknesses and the highlight of the needs for more descriptive auto-correlation functions.
It is worth mentioning that although the standard versions of the abovementioned evolutionary algorithms were applied in this study, the generic nature of the derived optimization problem permitted the application of more sophisticated and advanced evolutionary algorithms [
30,
31,
32,
33,
34].
The paper is organized as follows:
Section 2 reviews the main principles of porous media 3D reconstruction and briefly describes the theory of some popular and efficient nature-inspired optimization algorithms.
Section 3 presents the problem formulation in terms of optimization and illustrates the scheme of the proposed reconstruction methodology.
Section 4 evaluates the reconstruction performance of the applied optimization algorithms.
Section 5 summarizes the main conclusions derived from the previous experimental study, while future research directions are defined toward the development of a more efficient porous media 3D reconstruction technique.
2. Material and Methods
2.1. 3D Porous Media Reconstruction
To study the macroscopic behavior of a porous media, the geometry and topology of the pore space need to be determined. However, the acquisition of the porous media microstructure requires the application of specialized and expensive equipment (TEM, GEM, etc.) that can accurately capture the distribution of the pores in a short time. Another, less equipment-demanding way to derive the 3D porous media structure is to apply a 3D reconstruction algorithm, utilizing the material information enclosed in a single 2D thin slice of the material, which can be captured easily using a conventional microscope.
Mainly, there are two categories of 3D material reconstruction algorithms: (1) statistical/stochastic methods that apply linear and non-linear filters to an uncorrelated Gaussian distribution [
5,
7,
8,
35] and (2) optimization-based methods that tackle the reconstruction process as an optimization problem [
9,
10]. The former methods are characterized by lower accuracy and higher computation time compared to the latter ones. However, both types of algorithms use the same measures for encoding the porous space and describing the morphological properties of the material, such as multiple-point and auto-correlation functions [
36]. These functions are capable of statistically describing the microstructures of the 2D slice of porous media and thus can be used to construct 3D models with the same statistical properties.
A recent work investigating the role of the correlation function in 3D material reconstruction [
37] has shown that among the diverse number of correlation functions, the following two-point auto-correlation function exhibits a high reconstruction performance:
where
is the vector of the coordinates of each image pixel,
is the distance vector,
is the average operator, and
is the phase function defined as:
Moreover, corresponds to the porosity of the material.
It is worth noting that when calculating the auto-correlation function of the 2D slice image, the method of periodic boundaries is applied for the coordinates lying outside the image’s dimensions. The porosity and the auto-correlation function of Equation (1) corresponds to the first two statistical moments of the 2D image, which describe the distribution of the pixel values inside the material image space.
In this study, the 3D reconstruction of a material using an algorithm belonging to the second abovementioned category was examined. The defined optimization problem was solved by applying several nature-inspired optimization algorithms discussed in the next section.
2.2. Nature-Inspired Optimization Algorithms
It is well known that for the optimization of a specific procedure/function, a common practice is to apply a gradient-based algorithm [
38], e.g., Newton’s method. However, the gradient-based optimization algorithms have two significant limitations: (1) can be trapped at a local minimum and (2) require that the function being minimized is differentiable. These limitations do not make the gradient-based optimization algorithms applicable in complex problems where the analytical definition of the objective function is not easy to derive.
To handle the abovementioned limitations of the traditional optimization algorithms, the nature-inspired algorithms were proposed. These algorithms use a population of candidate solutions, where their fitness to solve the problem under investigation were examined in parallel, while a set of operators inspired by several natural processes were applied in each algorithm’s iteration. Some of the most popular, as well as modern, nature-inspired optimization algorithms are briefly discussed in the next section and are applied in the 3D reconstruction of porous media in the experimental section.
2.2.1. Genetic Algorithm (GA)
A simple genetic algorithm (GA) is a stochastic method that searches in wide search spaces, subject to some probability values. For these reasons, it can converge to the global minimum or maximum, depending on the specific application, and can skip possible local minima or maxima. Genetic algorithms were proposed by Holland [
24] who tried to find a method to mimic the evolutionary process that characterizes the evolution of living organisms. This theory is based on the mechanism representing the survival of the fittest individuals over a population. Genetic algorithms have been widely applied to several disciplines, such as feature selection [
39], biomedicine [
40], mechanical systems [
41], etc.
Initially, a population of candidate solutions (chromosomes), satisfying the constraints of the problem, is randomly constructed. In each iteration (generation) of the algorithm, a fitness is assigned to each chromosome, which is a real number value that indicates how suitable the solution for the problem under consideration is. In each generation, a set of operators, aiming to produce new unexplored solutions, is applied to the entire population. The most popular operators are:
Selection is an operator applied to the current population like the one used by natural selection found in biological systems. The fitter individuals are promoted to the next population and poorer individuals are discarded.
Crossover is the second operator and follows selection. This operator allows for solutions to exchange information that the living organisms use to reproduce themselves. Specifically, two solutions are selected to exchange their substrings from a single point and after, according to a predefined probability . The resulting offsprings carry some information from their parents.
Mutation is the third operator and follows crossover. According to this operation, a small part of the chromosome is changed (e.g., a single bit of a binary string is flipped) according to a predefined probability .
Elitism is the procedure according to which a fraction of the fittest chromosomes in a generation is ensured to be maintained in the next generation.
After the application of the above operators to the current population, a new population is formed and the generational counter is increased by one. This process is repeated until a predefined number of generations is attained or some form of convergence criterion is met.
2.2.2. Particle Swarm Optimization (PSO)
Particle swarm optimization (PSO) was proposed by Kennedy and Eberhart [
25] as a new optimization method based on swarming theory, such as bird flocking and fish schooling. Similar to a genetic algorithm, a population of potential solutions (particles) is created randomly. Each particle is characterized by its position
and velocity
. In each iteration, the velocity and position of the particle
are defined as follows:
where
[
27] are the learning parameters;
are random numbers;
is the current best of particle
; and
is the current global best of the entire population.
From the above equations, it is obvious that the movements of the particles are guided by their own best-known position in the search space, as well as the entire swarm’s best-known position. This algorithm is simpler than the GA since it does not apply any advanced operator; instead, some simple mathematical calculations are incorporated.
2.2.3. Differential Evolution (DE)
According to the differential evolution (DE) algorithm [
26], a population (with NP size) of candidate solutions (agents) is initially randomly selected. New solutions are produced by adding the weighted difference between two population agents
to a third one
. This operation is called mutation and its mathematical expression is as follows:
where
are randomly selected and
is called the differential weight, which controls the amplification of the differential variation of Equation (5). Next, a crossover operator is applied to the resultant mutant agent subject to a crossover
, according to the following rule:
where
is the trial solution in the n-dimensional search space,
is a random number, and
is a random index. Finally, the produced solution
is compared with its value in the previous iteration (generation)
with respect to the objective function being minimized. If the new solution yields a smaller objective function value than its old value, then
is set to
; otherwise, the old value
is retained.
The main advantages of the DE algorithm are its simplicity (few control parameters and simple operators) and the fast convergence to the global optimum.
2.2.4. Firefly Algorithm (FA)
The firefly algorithm (FA) was recently proposed by Yang [
27] as an alternative population-based optimization method that mimics the natural process of the flashing behavior of the fireflies. It is known that the flashing light of the fireflies is used to attract mating partners and potential prey. The variation of light intensity (light intensity decreases with the distance increase because the air absorbs the light) and the formulation attractiveness are the main functional principles of FA that need to be handled. The movement of a firefly
toward another attractive one
is determined by:
where
(usually equal to 1) corresponds to the attractiveness,
(usually between 0.1 and 10) is the absorption coefficient,
is the Euclidean distance between fireflies
and
,
is the step size, and
is a random vector drawn from a Gaussian or normal distribution. It is worth noting that the light intensity is associated with the objective function that needs to be optimized, while the entire population tends to be attracted by the brightest firefly during the algorithm.
2.2.5. Artificial Bee Colony (ABC)
The artificial bee colony (ABC) algorithm is a heuristic optimization algorithm based on the intelligent behavior of a honey bee swarm, which was proposed by Karaboga and Basturk [
28]. In the ABC algorithm, the colony of artificial bees contains three groups of bees: employed bees (bees going to the food source visited by themselves previously), onlookers (bees waiting to decide on a food source), and scouts (bees carrying out a random search). In the ABC algorithm, the first half of the colony consists of employed artificial bees and the second half consists of onlookers. For every food source (a possible solution), there is only one employed bee (the number of employed bees is equal to the number of food sources around the hive). Each cycle of the search consists of three steps: sending the employed bees to the food sources and then measuring their nectar amounts, selection of the food sources by the onlookers after the information is shared by the employed bees and determining the nectar amount of the foods, and determining the scout bees and then sending them to possible food sources [
28,
42]. The colony has to optimize the overall efficiency of nectar collection, where each possible solution has a specific amount of nectar. An artificial employed or onlooker bee probabilistically produces a modification on the position (solution) in her memory for finding a new food source and tests the nectar amount (fitness value) of the new source (new solution).
An onlooker bee
evaluates the nectar information taken from all the employed bees and chooses a food source with a probability related to its nectar amount according to the following definition:
where
is the fitness value of the
th solution. This probabilistic selection is equal to a roulette wheel selection mechanism.
Each employed bee
generates a new candidate solution (food position) in the neighborhood of its present position according to the following rule:
where
and
,
are randomly chosen indexes,
is the number of employed bees, and
is a random number.
2.2.6. Gravitational Search Algorithm (GSA)
The gravitational search algorithm (GSA) is a new nature-inspired optimization algorithm proposed by Rashedi et al. [
29] based on the law of gravity and mass interactions. The GSA emulates a small artificial world of masses obeying the Newtonian laws of gravitation and motion. According to the GSA algorithm, a population (with NP size) of candidate solutions (masses) is randomly initialized and the force acting to each other (from mass
to mass
at time
) is calculated based on the following equation:
where
is the active gravitational mass related to mass
,
is the passive gravitational mass related to mass
,
is a gravitational constant at time
,
is a small constant, and
is the Euclidean distance between the two masses
and
. The total force that acts on mass
is calculated as follows:
where
is a random number.
Based on the law of motion, the acceleration of mass
is defined as follows:
where
is the inertial mass of solution
.
The velocity and position of each mass of the population is calculated as follows:
where
is a random number.
It is worth noting that the gravitational and inertial masses are updated according to the following equations:
where
is the fitness of mass
, and
and
are the worst and best fitness of the entire population at time
, respectively.
2.2.7. Discussion
All the above-discussed nature-inspired optimization algorithms share some common properties even though each one applies different operators that control the method for producing better solutions. These common characteristics are summarized as follows:
- −
A set of candidate solutions (population) are examined in parallel by avoiding trapping in a local optimum.
- −
Several variants of each algorithm are proposed to handle real, integer, and binary unknowns (solutions).
- −
The diversity of the population should be retained during the algorithm execution to avoid its premature convergence to a local optimum.
- −
Each algorithm aims to compromise between exploration and exploitation of the search space.
- −
The cost (objective) non-differentiable function that measures the utility of each solution in the real problem under study needs to be determined carefully.
- −
The same termination criteria are applied, where either a fixed number of iterations is attained or a predefined accuracy is reached.
The nature-inspired optimization algorithms discussed in the previous section are used to solve the problem of 3D porous media reconstruction as long as it is defined in terms of optimization, as follows in the next section.
3. 3D Reconstruction as an Optimization Problem
The 3D reconstruction of a material by using statistical methods, such as the well-known Quiblier’s method [
5] and its variants [
7,
8,
35], has the following weaknesses:
The computation of the coefficients needed to define the linear and the non-linear filters is a laborious task.
Only one correlation function can be incorporated into the algorithm at a time to code the morphological properties of the material.
There is no proof of optimality for the resultant porous media distribution.
The need to binarize the computed 3D model to derive the final porous media distribution.
On the other hand, the nature-inspired, optimization-based 3D reconstruction algorithms exhibit the following properties, which alleviate the aforementioned limitations of the statistical methods:
There is no need to compute coefficients of any filter (they do not exist).
Several correlation functions can be used simultaneously in the same objective function and therefore the morphological properties of the material can be described more accurately.
Although there is no analytical proof, regarding the optimality of the solutions derived by the nature-inspired optimization algorithms, experience has shown that the solutions are near optimal.
There is no need to apply a binarization method in order to derive the final 3D model since the optimization algorithms can directly provide the solutions in a binary form.
To apply a nature-inspired optimization algorithm for reconstructing a 3D model of porous media, two important issues need to be addressed appropriately. First, the task of 3D reconstruction should be defined in terms of optimization, where the appropriate cost (objective) function needs to be defined to describe the fitness of each solution of the real system. Second, the solutions should be coded appropriately through an efficient data representation scheme such that the algorithm operates in the real search space with the lowest possible complexity. Both issues are hereafter discussed in detail.
3.1. Problem Formulation
Based on the previous analysis, it was concluded that the application of a nature-inspired optimization algorithm will significantly enhance the 3D reconstruction of porous media. However, the application of any nature-inspired optimization algorithm is highly dependent on the successful formulation of the optimization problem related to the definition of the cost (objective) function being minimized. A generic objective function consisting of multiple correlation functions was proposed in this work for the set of
N unknowns (the phases
of the 3D model’s pixels)
, according to the following form:
where
is the number of different functions (correlation and/or statistical) used to measure the morphological properties of the material;
and
are the
th function and its reference value (of the 2D slice image);
and
are the dimension and the normalization factor of the
function, respectively; and
is its weight defining its importance satisfying the following condition:
Based on the objective function of Equation (18), the 3D reconstruction optimization problem is defined as follows:
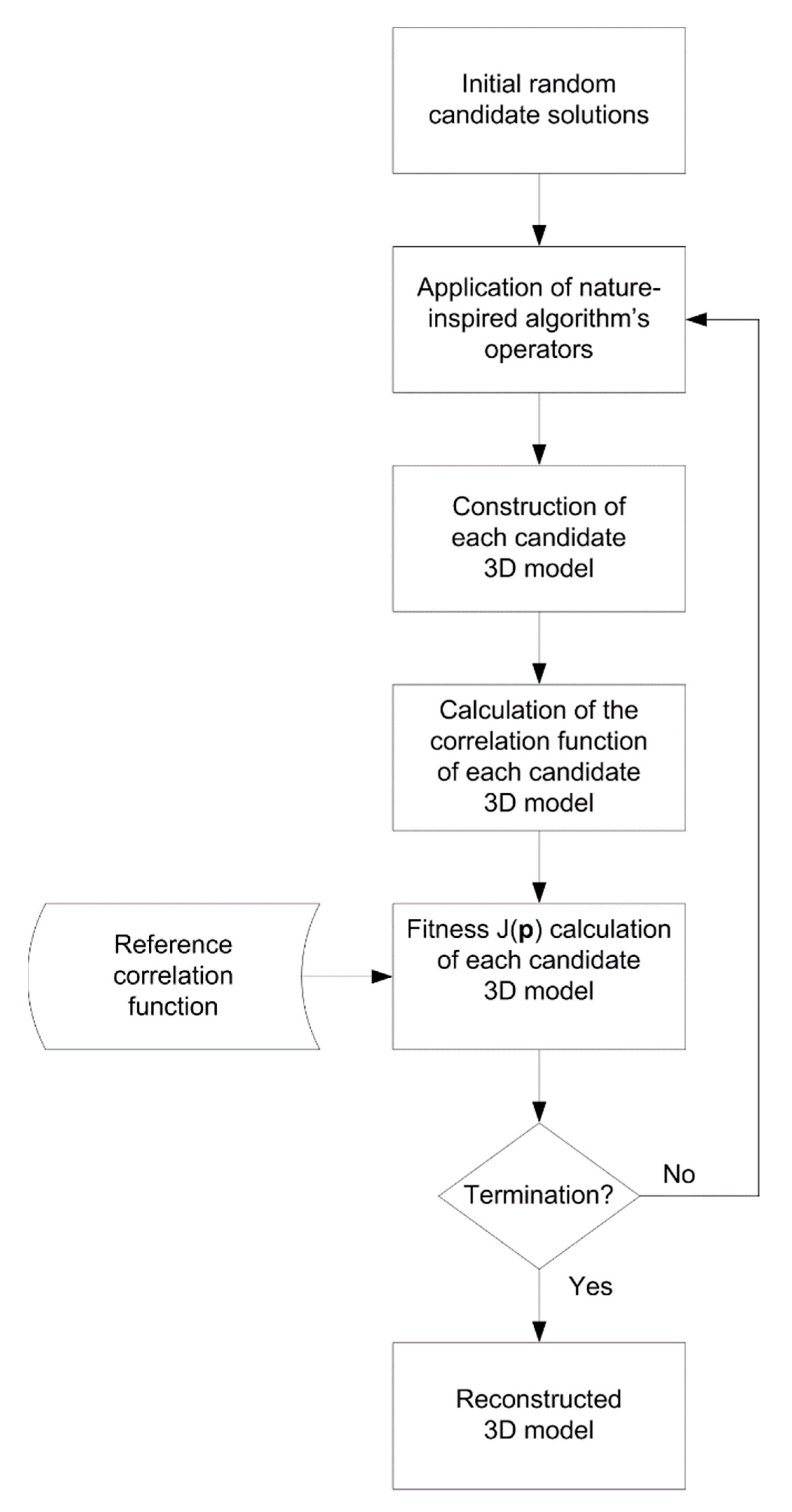
The flowchart of the proposed reconstruction methodology, applied for each one of the algorithms of
Section 2, is depicted in
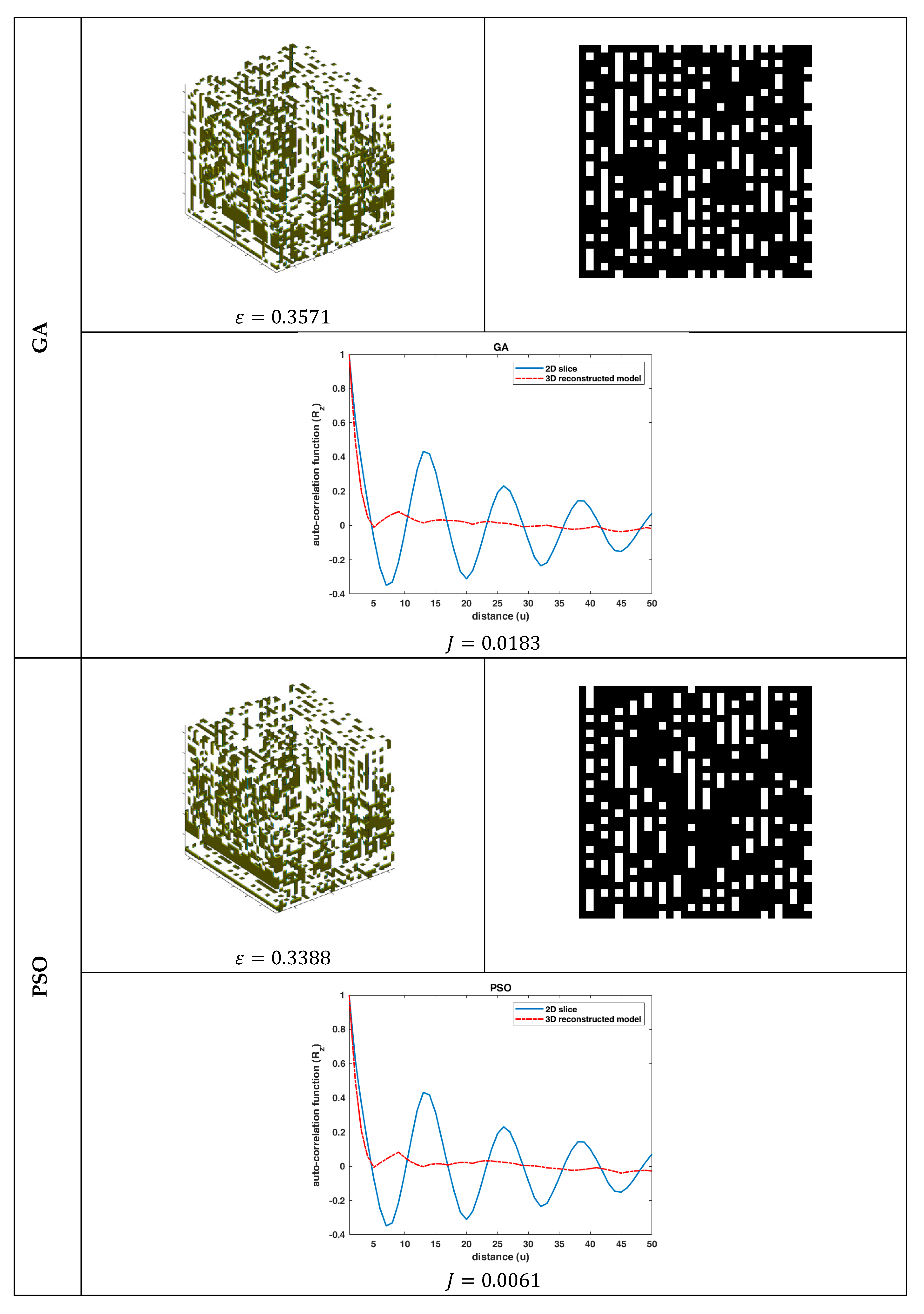
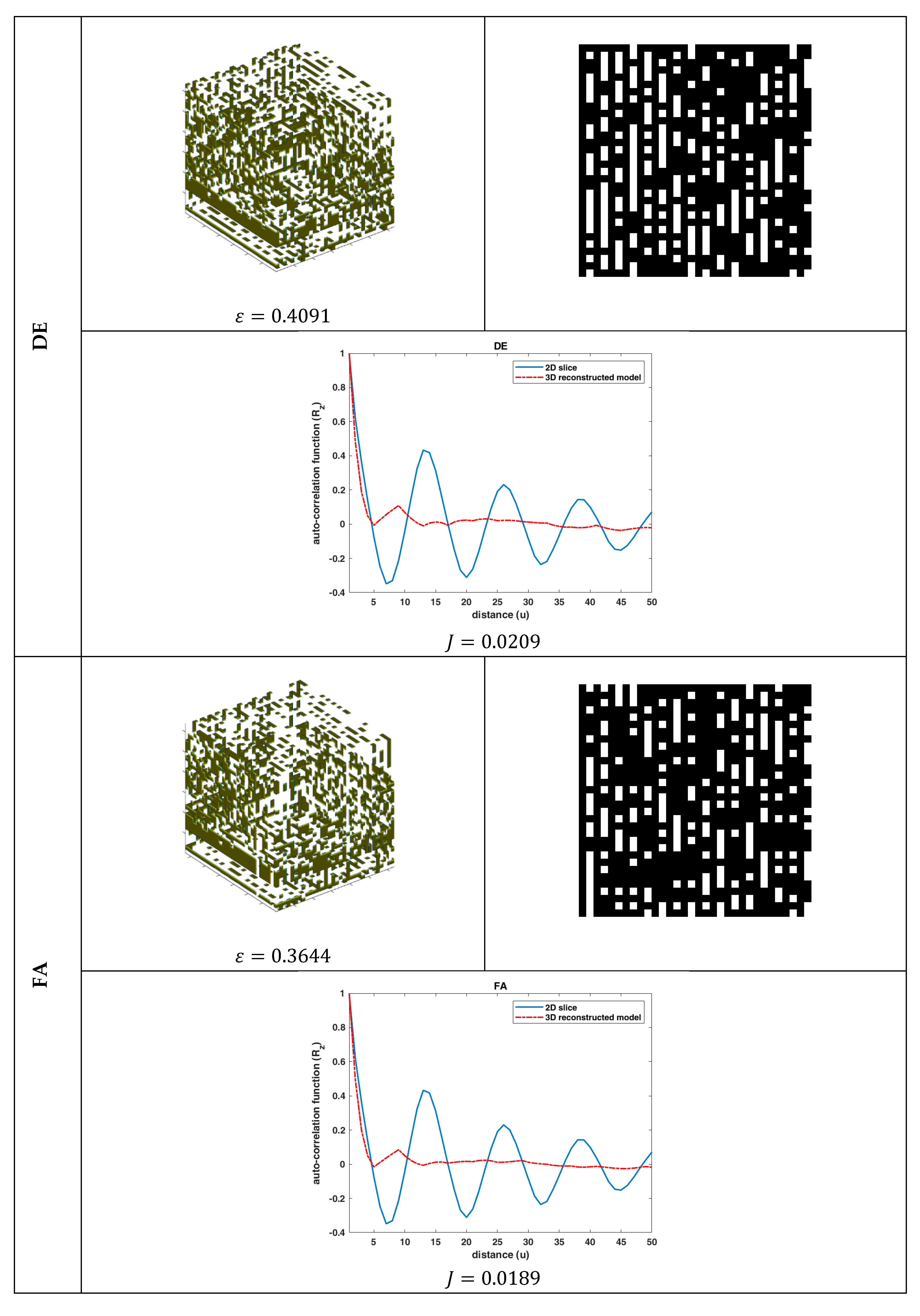
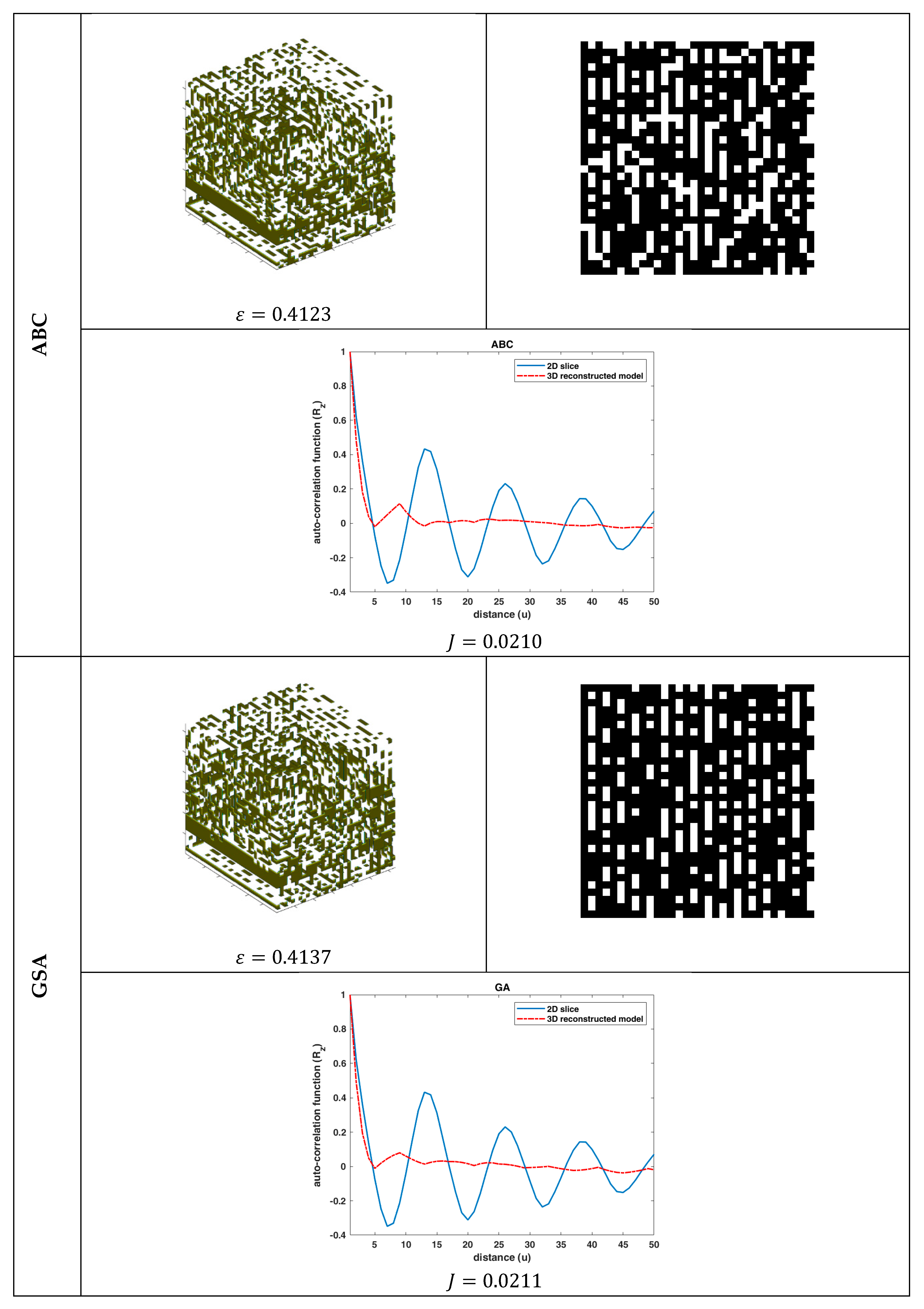
Figure 1. Based on this figure, the proposed 3D porous media reconstruction consists of the following phases: (1) initial random candidate solutions: in this phase, random material phases are generated and the proposed data representation scheme is applied to reduce the number of unknowns that need to be found by the evolutionary algorithm, (2) application of the specific operators of the applied evolutionary algorithm to produce solutions with higher fitnesses, (3) reconstruction of a 3D material model for each candidate solution, and (4) fitness calculation of each candidate solution using Equation (18). The execution of these four phases is repeated until a termination criterion is met. After the termination of the algorithm, the fittest solution corresponds to the reconstructed 3D porous media.
3.2. Data Representation
In the above-defined optimization problem, the unknowns that need to be found are the phase values of each material image pixel. Therefore, for an image of pixels in size, the number of unknowns is , and thus the corresponding search space where any nature-inspired algorithm needs to be executed is extremely complex. For example, if a 3D model of pixels size needs to be derived, a total of 2,097,152 unknowns should be found by the algorithm.
To overcome the above problem of high dimensional data, an efficient data representation is proposed in this work. For this purpose, the notion of the fundamental element (fe), which controls the representation accuracy of the reconstructed 3D material model, was introduced. Considering that the material is composed of homogenous cubic (all pixels of the cube have the same phase) elements of pixels in size, the number of unknowns can be reduced to , achieving a significant reduction in the problem’s dimension.
Moreover, considering the case of a two-phase porous media and without loss of generality, each cubic element can be decoded as a single bit. In this way, by using a 64-bit arithmetic representation, one can compactly encode the phase of 64 cubic elements in a single integer value. By applying the proposed data representation, the problem dimension is finally reduced to .
3.3. Complexity Analysis
The main overhead of the proposed methodology is the fitness computation of each candidate solution consisting of the 3D model construction and the computation of its auto-correlation function. However, the former process is of order of complexity, whereas the latter one is of . This improvement in the data representation decreases the solution space and accelerates the convergence of the deployed evolutionary algorithms.
5. Conclusion and Future Work
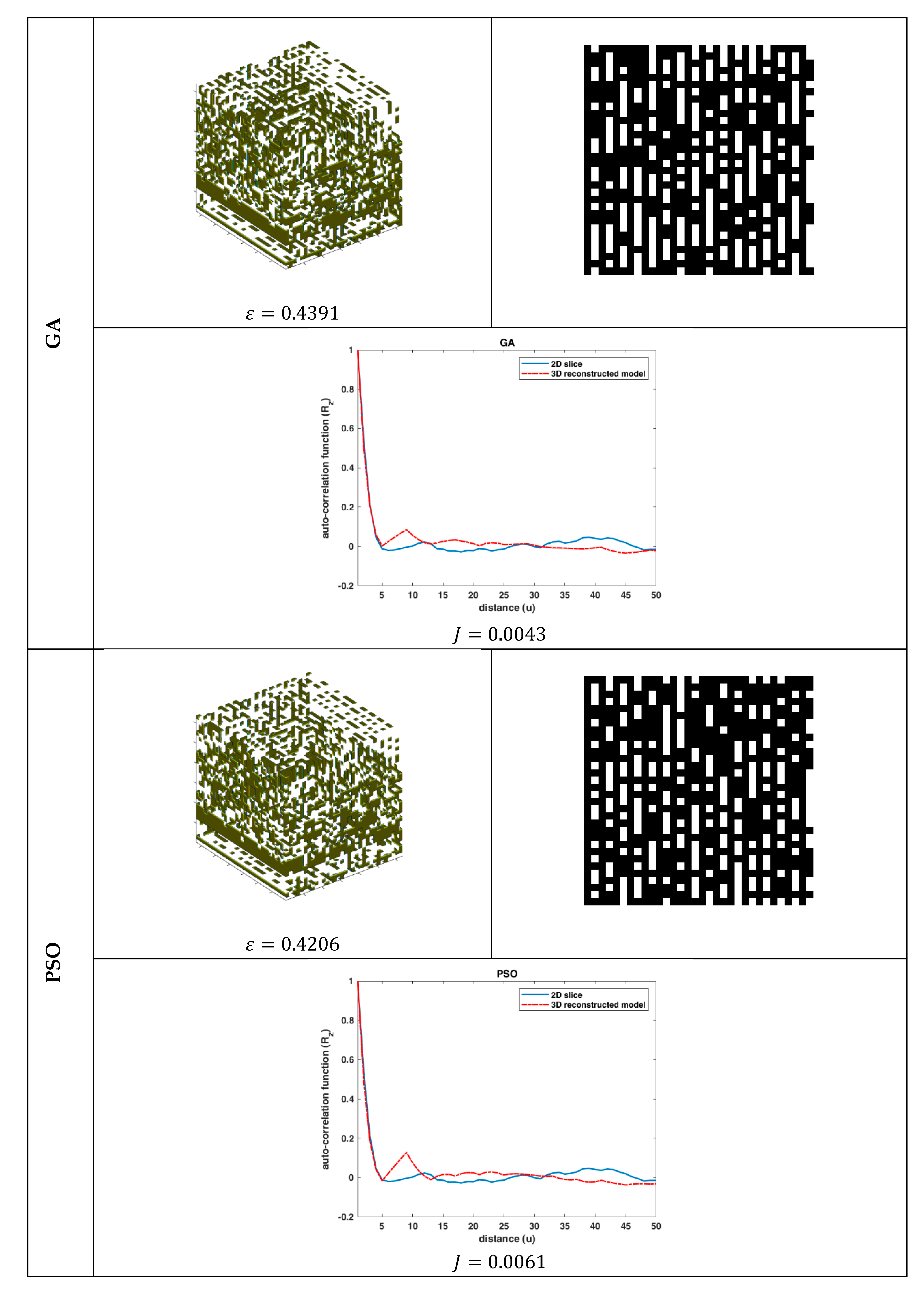
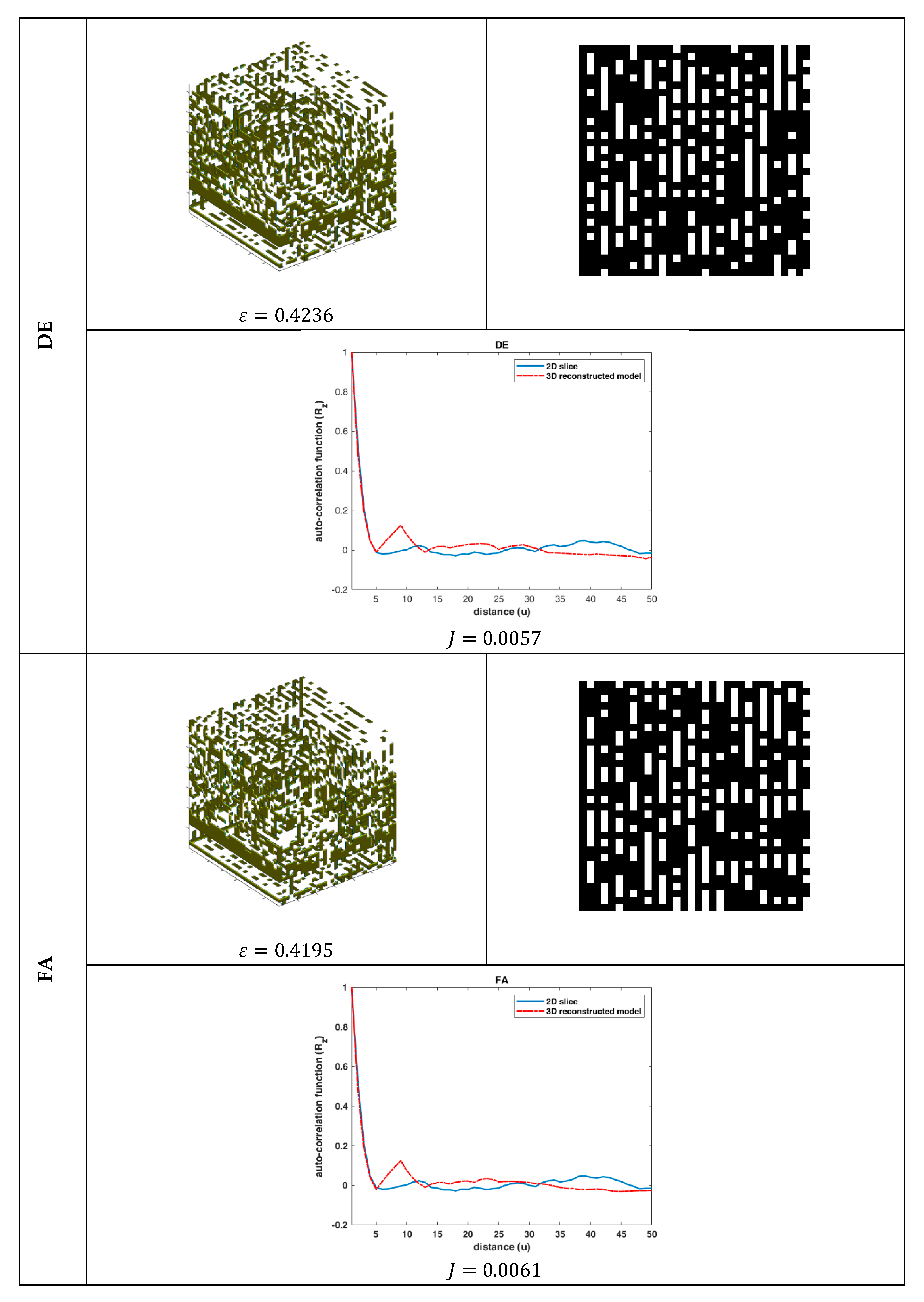
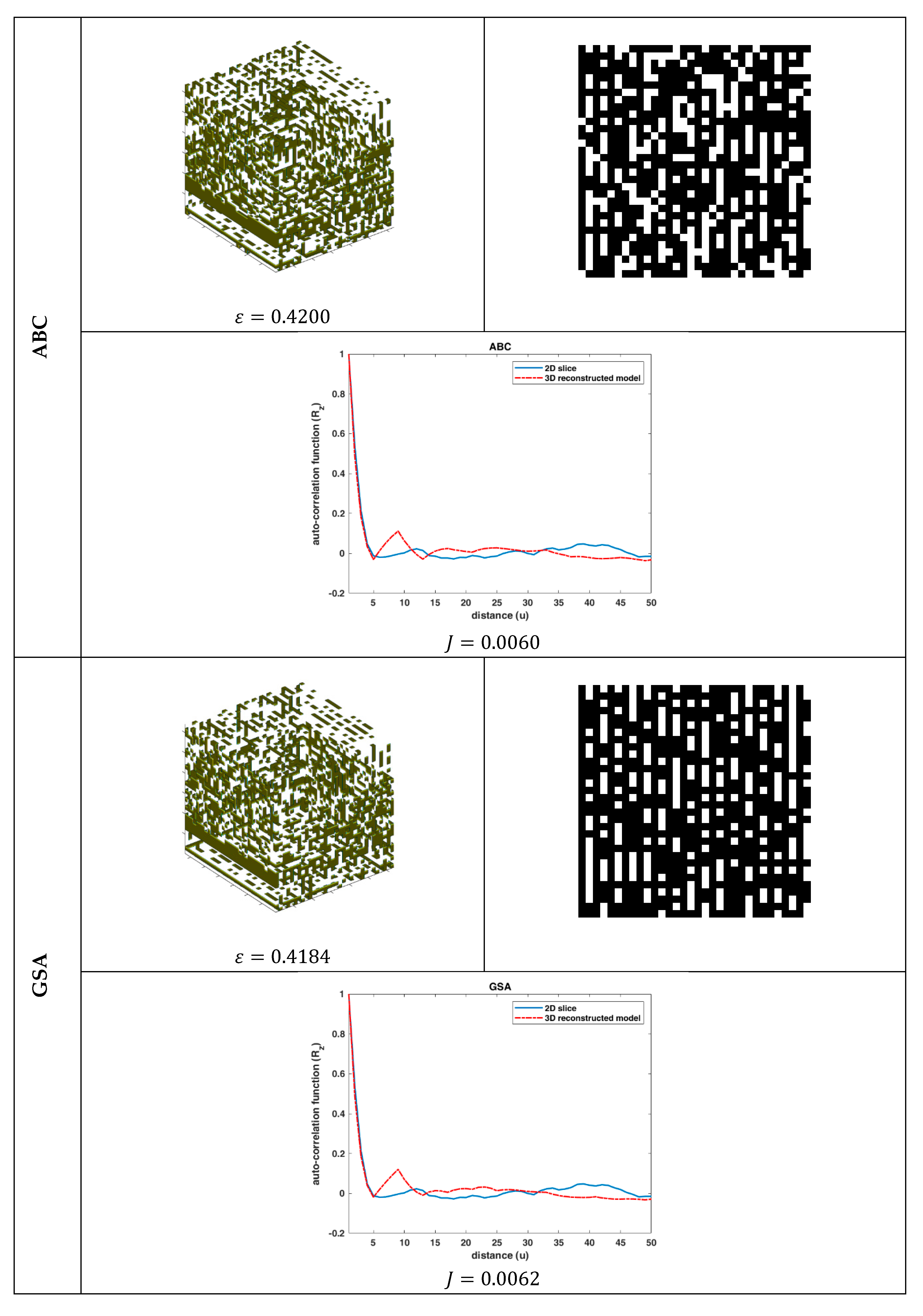
The problem of the 3D reconstruction of porous media from a single 2D material image using six nature-inspired optimization algorithms was studied. Although the reconstruction results were very accurate in terms of
MSE for the case of the
statistical functions, the visual representation deviated significantly from the desired materials’ microstructures. This contradiction between the numerical and visual performance of the reconstruction methodology was due to the existence of more than one different 3D microstructure having the same statistical properties
. Moreover, the suboptimal configuration of the algorithms also affected the numerical accuracy of the methodology, and a sensitivity analysis of the optimization algorithms regarding their free parameters is needed. However, this study sheds light on two important issues: (1) a nature-inspired algorithm could reconstruct the 3D porous media by applying an appropriate data representation scheme despite the complex search space and (2) there are needs for more descriptive and higher-order [
46,
47] functions for measuring the material’s phase distribution to increase the fidelity of the reconstructed microstructure. These outcomes pave the way for future research toward the development of an efficient reconstruction algorithm in terms of accuracy and processing time.
As far as the computation time is concerned, the high computational burden stemming from the sources described in
Section 3.3 can be reduced by applying modern parallel computing frameworks (e.g., MPI – Message Passing Interface, GPU programming, thread programming, MapReduce, SparK, cluster computing, and grid computing). For example, the high parallelism of all the nature-inspired algorithms enables the implementation of the algorithms (fitness computation) by utilizing the parallel computing capabilities of a GPU (graphics processing unit) Nvidia card within the CUDA architecture [
48]. The development of an accelerated nature-inspired algorithm in conjunction with the proposed data representation scheme will allow for the execution of an algorithm with a larger population size and more iterations that can increase the reconstruction accuracy.
Finally, additional research should be arranged toward the direction of applying higher-order statistics to describe the microstructure of the material uniquely. The proposed generic form of the objective function can help in this direction since it enables the incorporation of any number and type of functions with minimal modifications.