Multidimensional Group Recommendations in the Health Domain
Abstract
1. Introduction
- We demonstrate a multidimensional group recommendation model in the health domain, using collaborative filtering.
- We propose a novel semantic similarity function that takes into account, in addition to the patients medical problems, the education, the health literacy and the psycho-emotional status of the patients, showing its superiority over a traditional measure.
- We introduce a new aggregation method accumulating preference scores, called AccScores, showing that it dominates other aggregation methods and is able to produce fair recommendations to small groups of patients.
- We experimentally show the value of our approach, introducing the first synthetic dataset with such information for benchmarking works in the area.
2. Related Work
Recommendations in the Health Domain
3. Single User Recommendations
3.1. User Profiles
3.2. User Similarities
3.2.1. Similarity Based on Ratings
3.2.2. Similarity Based on Health Information
Overall Semantic Similarity Between Two Users
3.2.3. Similarity Based on Education and Health Literacy Level
3.2.4. Similarity Based on Psycho-Emotional Status
3.2.5. Similarity between Users
3.3. Single User Rating Model
4. Group Recommendations
4.1. Group Rating Model
4.2. Fairness in Group Recommendations
4.3. Aggregation Designs
| Algorithm 1: Fair Group Recommendations Algorithm |
 |
| Algorithm 2: AccScores Group Recommendations Algorithm |
 |
5. Dataset
- Document Corpus
- -
- Create document corpus. Initially, we generated documents for each node in the second level of the ontology tree that represents the ICD10 ontology. For each such document, we selected randomly words from the nodes descriptions in each subsequent subtree.
- -
- Assignment of Education and Health Literacy Levels. We divide the documents based on five percentage scores that correspond to the five different education levels. We assign to the documents in each subgroup their corresponding education level. We propose that a document cannot have a vastly different education and health literacy score. A document that has high education level is improbable to be for users with low literacy score and, similarly, a document with high health literacy is not probable to have a low education level. Therefore, with equal probability, we assign to each document a health literacy score that is the same, one highest or one lowest level than that of its education level.
- Rating Dataset
- -
- Divide the patients into groups. We assume that all patients have assigned ratings to documents. For doing so, we distinguish the patients between , , and . The users in each group gave few, average and a lot of ratings, respectively.
- -
- Assignment of Education and Health Literacy Levels. The procedure to assign education and health literacy levels to the patients is the same as the one to assign them to the documents.
- -
- Assignment of Anxiety and Cognitive Closure. Anxiety and cognitive closure scores are regularly measured for each patient since these tend to change rapidly. This is why in our methods we only take into account the most recent ones. Therefore, in our dataset, we generate one anxiety and cognitive closure score for each patient. We follow a similar method as the one for education and health literacy levels and divide the patients based on five percentage scores . However, now anxiety will be the score that will define cognitive closure. The more anxious a person is about their health problems the more he/she needs to understand them.
- -
- Simulate a power law rating distribution. When ranking documents with respect to real users preferences, the documents typically follow the power law distribution. To show this, we randomly chose documents and consider them as the most popular.
- -
- Generate documents to rate. For each patient, we distinguished the ratings that he/she will give between and . Given the assumption that patients are interested in both documents related to their health problems, as well as to other documents, we assigned ratings to both such groups of documents.
- -
- Generate ratings. Last, for each item generated above, we randomly assigned a rating from 1 to 5.
6. Evaluation
6.1. Evaluation Measures
6.2. Evaluation Results
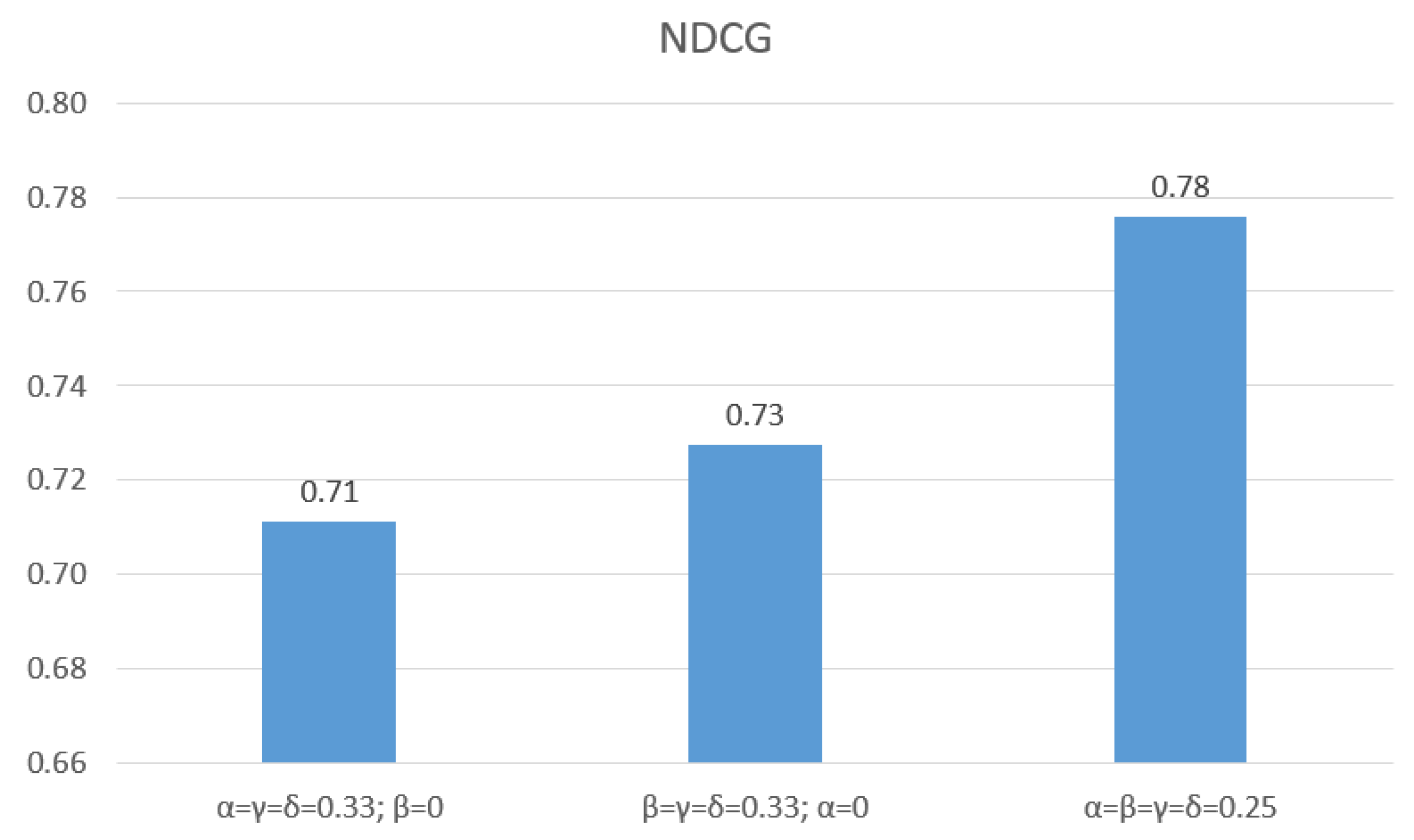
6.2.1. Evaluation of Similarity Functions
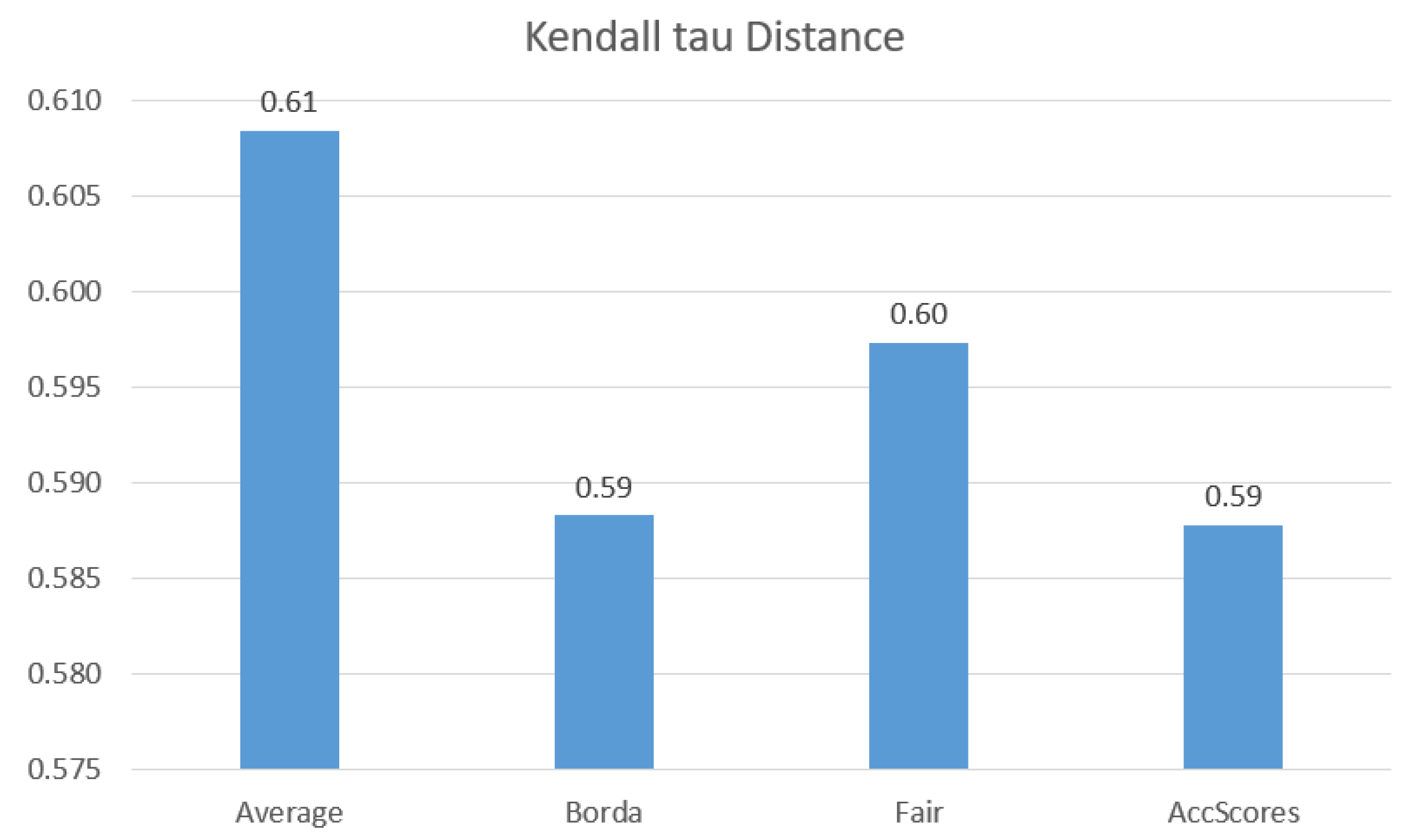
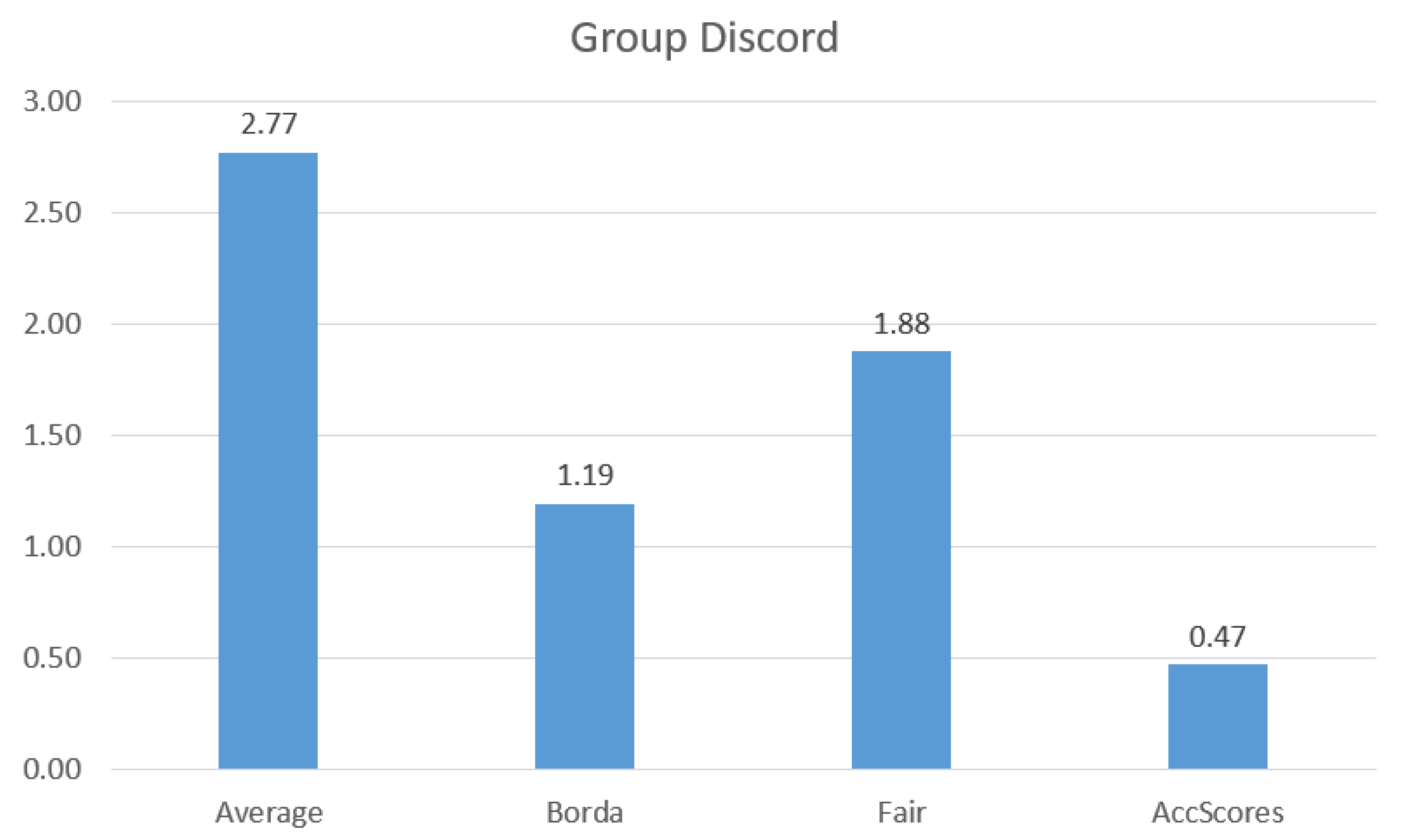
6.2.2. Evaluation of Aggregation Methods
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Berg, G.M.; Hervey, A.M.; Atterbury, D.; Cook, R.; Mosley, M.; Grundmeyer, R.; Acuna, D. Evaluating the quality of online information about concussions. J. Am. Acad. PAS 2014, 27, 1547–1896. [Google Scholar] [CrossRef] [PubMed]
- McMullan, M. Patients using the Internet to obtain health information: How this affects the patient-health professional relationship. Patient Educ. Couns. 2006, 63, 24–28. [Google Scholar] [CrossRef] [PubMed]
- Wiesner, M.; Pfeifer, D. Adapting recommender systems to the requirements of personal health record systems. In Proceedings of the ACM International Health Informatics Symposium, IHI 2010, Arlington, VA, USA, 11–12 November 2010; pp. 410–414. [Google Scholar]
- Brandon, I.; Daniel, K.; Patrice, C.; Nicholas, T. Testing the Efficacy of OurSpace, a Brief, Group Dynamics-Based Physical Activity Intervention: A Randomized Controlled Trial. J. Med. Internet Res. 2016, 18, e87. [Google Scholar]
- Cheung, D.Y.T.; Chan, H.C.H.; Lai, J.C.K.; Chan, V.W.F.; Wang, P.M.; Li, W.H.C.; Chan, C.S.S.; Lam, T.H. Using WhatsApp and Facebook Online Social Groups for Smoking Relapse Prevention for Recent Quitters: A Pilot Pragmatic Cluster Randomized Controlled Trial. J. Med. Internet Res. 2015, 17, e238. [Google Scholar] [CrossRef] [PubMed]
- Batenburg, A.; Das, E. Emotional Approach Coping and the Effects of Online Peer-Led Support Group Participation Among Patients With Breast Cancer: A Longitudinal Study. J. Med. Internet Res. 2014, 16, e256. [Google Scholar] [CrossRef]
- Serbos, D.; Qi, S.; Mamoulis, N.; Pitoura, E.; Tsaparas, P. Fairness in Package-to-Group Recommendations. In Proceedings of the 26th International Conference on World Wide Web (WWW), Perth, Australia, 3–7 April 2017. [Google Scholar]
- Machado, L.; Stefanidis, K. Fair Team Recommendations for Multidisciplinary Projects. In Proceedings of the IEEE/WIC/ACM International Conference on Web Intelligence (WI), Thessaloniki, Greece, 14–17 October 2019. [Google Scholar]
- Stratigi, M.; Kondylakis, H.; Stefanidis, K. Fairness in Group Recommendations in the Health Domain. In Proceedings of the 33rd IEEE International Conference on Data Engineering, ICDE 2017, San Diego, CA, USA, 19–22 April 2017; pp. 1481–1488. [Google Scholar]
- Stratigi, M.; Kondylakis, H.; Stefanidis, K. The FairGRecs Dataset: A Dataset for Producing Health-related Recommendations. In Proceedings of the First International Workshop on Semantic Web Technologies for Health Data Management, SWH@ISWC 2018, Monterey, CA, USA, 9 October 2018. [Google Scholar]
- Stratigi, M.; Kondylakis, H.; Stefanidis, K. FairGRecs: Fair Group Recommendations by Exploiting Personal Health Information. In Proceedings of the Database and Expert Systems Applications—29th International Conference, DEXA 2018, Regensburg, Germany, 3–6 September 2018; pp. 147–155. [Google Scholar]
- Kondylakis, H.; Bucur, A.; Crico, C.; Dong, F.; Graf, N.; Hoffman, S.; Koumakis, L.; Manenti, A.; Marias, K.; Mazzocco, K.; et al. Patient empowerment for cancer patients through a novel ICT infrastructure. J. Biomed. Inform. 2020, 101, 103342. [Google Scholar] [CrossRef]
- Kondylakis, H.; Koumakis, L.; Katehakis, D.G.; Kouroubali, A.; Marias, K.; Tsiknakis, M.; Simos, P.G.; Karademas, E. Developing a Data Infrastructure for Enabling Breast Cancer Women to BOUNCE Back. In Proceedings of the 32nd IEEE International Symposium on Computer-Based Medical Systems, CBMS 2019, Cordoba, Spain, 5–7 June 2019; pp. 652–657. [Google Scholar]
- Bobadilla, J.; Ortega, F.; Hernando, A.; Gutiérrez, A. Recommender systems survey. Knowl.-Based Syst. 2013, 46, 109–132. [Google Scholar] [CrossRef]
- Mooney, R.J.; Roy, L. Content-based book recommending using learning for text categorization. In Proceedings of the Fifth ACM Conference on Digital Libraries, San Antonio, TX, USA, 2–7 June 2000; pp. 195–204. [Google Scholar] [CrossRef]
- Konstan, J.A.; Miller, B.N.; Maltz, D.; Herlocker, J.L.; Gordon, L.R.; Riedl, J. GroupLens: Applying Collaborative Filtering to Usenet News. Commun. ACM 1997, 40, 77–87. [Google Scholar] [CrossRef]
- Lu, J.; Wu, D.; Mao, M.; Wang, W.; Zhang, G. Recommender system application developments: A survey. Decis. Support Syst. 2015, 74, 12–32. [Google Scholar] [CrossRef]
- Yin, Z.; Gupta, M.; Weninger, T.; Han, J. LINKREC: A unified framework for link recommendation with user attributes and graph structure. In Proceedings of the 19th International Conference on World Wide Web, WWW 2010, Raleigh, NC, USA, 26–30 April 2010. [Google Scholar]
- Eirinaki, M.; Abraham, S.; Polyzotis, N.; Shaikh, N. QueRIE: Collaborative Database Exploration. IEEE Trans. Knowl. Data Eng. 2014, 26, 1778–1790. [Google Scholar] [CrossRef]
- Koskela, M.; Simola, I.; Stefanidis, K. Open Source Software Recommendations Using Github. In Proceedings of the International Conference on Theory and Practice of Digital Libraries, Porto, Portugal, 10–13 September 2018. [Google Scholar]
- Ge, X.; Chrysanthis, P.K.; Pelechrinis, K. MPG: Not So Random Exploration of a City. In Proceedings of the 17th IEEE International Conference on Mobile Data Management (MDM), Porto, Portugal, 13–16 June 2016. [Google Scholar]
- Stratigi, M.; Nummenmaa, J.; Pitoura, E.; Stefanidis, K. Fair Sequential Group Recommendations. In Proceedings of the 35th ACM/SIGAPP Symposium on Applied Computing, SAC 2020, Brno, Czech Republic, 30 March–3 April 2020. [Google Scholar]
- Borges, R.; Stefanidis, K. Enhancing Long Term Fairness in Recommendations with Variational Autoencoders. In Proceedings of the 11th International Conference on Management of Digital EcoSystems, MEDES 2019, Limassol, Cyprus, 12–14 November 2019. [Google Scholar]
- Stefanidis, K.; Kondylakis, H.; Troullinou, G. On Recommending Evolution Measures: A Human-Aware Approach. In Proceedings of the 33rd IEEE International Conference on Data Engineering, ICDE 2017, San Diego, CA, USA, 19–22 April 2017; pp. 1579–1581. [Google Scholar]
- Troullinou, G.; Kondylakis, H.; Stefanidis, K.; Plexousakis, D. Exploring RDFS KBs Using Summaries. In Proceedings of the The Semantic Web—ISWC 2018—17th International Semantic Web Conference, Monterey, CA, USA, 8–12 October 2018; pp. 268–284. [Google Scholar]
- Gartrell, M.; Xing, X.; Lv, Q.; Beach, A.; Han, R.; Mishra, S.; Seada, K. Enhancing group recommendation by incorporating social relationship interactions. In Proceedings of the 2010 International ACM SIGGROUP Conference on Supporting Group Work, GROUP 2010, Sanibel Island, FL, USA, 6–10 November 2010; pp. 97–106. [Google Scholar]
- Castro, J.; Lu, J.; Zhang, G.; Dong, Y.; Martínez-López, L. Opinion Dynamics-Based Group Recommender Systems. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 2394–2406. [Google Scholar] [CrossRef]
- Amer-Yahia, S.; Roy, S.B.; Chawla, A.; Das, G.; Yu, C. Group Recommendation: Semantics and Efficiency. PVLDB 2009, 2, 754–765. [Google Scholar] [CrossRef]
- Ntoutsi, E.; Stefanidis, K.; Nørvåg, K.; Kriegel, H. Fast Group Recommendations by Applying User Clustering. In Proceedings of the Conceptual Modeling—31st International Conference ER 2012, Florence, Italy, 15–18 October 2012; pp. 126–140. [Google Scholar]
- Qi, S.; Mamoulis, N.; Pitoura, E.; Tsaparas, P. Recommending Packages to Groups. In Proceedings of the IEEE 16th International Conference on Data Mining, ICDM 2016, Barcelona, Spain, 12–15 December 2016; pp. 449–458. [Google Scholar]
- Pfeifer, D. Health Recommender Systems: Concepts, Requirements, Technical Basics and Challenges. Int. J. Environ. Res. Public Health 2014, 11, 2580–2607. [Google Scholar]
- Schäfer, H.; Hors-Fraile, S.; Karumur, R.P.; Valdez, A.C.; Said, A.; Torkamaan, H.; Ulmer, T.; Trattner, C. Towards Health (Aware) Recommender Systems. In Proceedings of the 2017 International Conference on Digital Health, London, UK, 2–5 July 2017; pp. 157–161. [Google Scholar]
- Hors-Fraile, S.; Romero, O.R.; Schneider, F.; Fernández-Luque, L.; Luna-Perejón, F.; Balcells, A.C.; de Vries, H. Analyzing recommender systems for health promotion using a multidisciplinary taxonomy: A scoping review. Int. J. Med Inform. 2018, 114, 143–155. [Google Scholar] [CrossRef]
- Agapito, G.; Calabrese, B.; Guzzi, P.H.; Cannataro, M.; Simeoni, M.; Care, I.; Lamprinoudi, T.; Fuiano, G.; Pujia, A. DIETOS: A recommender system for adaptive diet monitoring and personalized food suggestion. In Proceedings of the 2th IEEE International Conference on Wireless and Mobile Computing, Networking and Communications, WiMob 2016, New York, NY, USA, 17–19 October 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Espín, V.; Hurtado, M.V.; Noguera, M. Nutrition for Elder Care: A nutritional semantic recommender system for the elderly. Expert Syst. 2016, 33, 201–210. [Google Scholar] [CrossRef]
- Hors-Fraile, S.; Núñez-Benjumea, F.J.; Hernández, L.C.; Ruiz, F.O.; Fernández-Luque, L. Design of two combined health recommender systems for tailoring messages in a smoking cessation app. arXiv 2016, arXiv:1608.07192. [Google Scholar]
- Smileska, C.; Koceska, N.; Koceski, S.; Trajkovik, V. Development and Evaluation of Methodology for Personal Recommendations Applicable in Connected Health. In Enhanced Living Environments—Algorithms, Architectures, Platforms, and Systems; Lecture Notes in Computer Science; Ganchev, I., Garcia, N.M., Dobre, C., Mavromoustakis, C.X., Goleva, R., Eds.; Springer: New York, NY, USA, 2019; Volume 11369, pp. 80–95. [Google Scholar]
- Afolabi, A.O.; Toivanen, P.J. Integration of Recommendation Systems Into Connected Health for Effective Management of Chronic Diseases. IEEE Access 2019, 7, 49201–49211. [Google Scholar] [CrossRef]
- Hu, H.; Elkus, A.; Kerschberg, L. A Personal Health Recommender System incorporating personal health records, modular ontologies, and crowd-sourced data. In Proceedings of the 2016 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, ASONAM 2016, San Francisco, CA, USA, 18–21 August 2016; pp. 1027–1033. [Google Scholar]
- Torrent-Fontbona, F.; López, B. Personalized Adaptive CBR Bolus Recommender System for Type 1 Diabetes. IEEE J. Biomed. Health Inform. 2019, 23, 387–394. [Google Scholar] [CrossRef]
- Kim, J.; Lee, D.; Chung, K. Item recommendation based on context-aware model for personalized u-healthcare service. Multimed. Tools Appl. 2014, 71, 855–872. [Google Scholar] [CrossRef]
- Wang, S.; Chen, Y.; Kuo, A.M.; Chen, H.; Shiu, Y. Design and evaluation of a cloud-based Mobile Health Information Recommendation system on wireless sensor networks. Comput. Electr. Eng. 2016, 49, 221–235. [Google Scholar] [CrossRef]
- Kondylakis, H.; Koumakis, L.; Kazantzaki, E.; Chatzimina, M.; Psaraki, M.; Marias, K.; Tsiknakis, M. Patient Empowerment through Personal Medical Recommendations. In Proceedings of the MEDINFO 2015: EHealth-enabled Health—Proceedings of the 15th World Congress on Health and Biomedical Informatics, São Paulo, Brazil, 19–23 August 2015; p. 1117. [Google Scholar]
- Kondylakis, H.; Koumakis, L.; Psaraki, M.; Troullinou, G.; Chatzimina, M.; Kazantzaki, E.; Marias, K.; Tsiknakis, M. Semantically-enabled Personal Medical Information Recommender. In Proceedings of the ISWC 2015 Posters & Demonstrations Track co-located with the 14th International Semantic Web Conference (ISWC-2015), Bethlehem, PA, USA, 11 October 2015. [Google Scholar]
- Nores, M.L.; Blanco-Fernández, Y.; Pazos-Arias, J.J.; Gil-Solla, A. Property-based collaborative filtering for health-aware recommender systems. Expert Syst. Appl. 2012, 39, 7451–7457. [Google Scholar] [CrossRef]
- Qin, L.; Xu, X.; Li, J. A Real-Time Professional Content Recommendation System for Healthcare Providers’ Knowledge Acquisition. In Proceedings of the Big Data—BigData 2018—7th International Congress, Held as Part of the Services Conference Federation, SCF 2018, Seattle, WA, USA, 25–30 June 2018; pp. 367–371. [Google Scholar]
- Bermingham, A.; Caprani, N.; Collins, R.; Gurrin, C.; Irving, K.; O’Rourke, J.; Smeaton, A.F.; Yang, Y. Recommending Video Content for Use in Group-Based Reminiscence Therapy. In Health Monitoring and Personalized Feedback Using Multimedia Data; Springer: New York, NY, USA, 2015; pp. 215–244. [Google Scholar]
- Kondylakis, H.; Kazantzaki, E.; Koumakis, L.; Genitsaridi, I.; Marias, K.; Gorini, A.; Mazzocco, K.; Pravettoni, G.; Burke, D.; McVie, G. et al. Development of interactive empowerment services in support of personalised medicine. eCancer 2014, 8, 400. [Google Scholar] [CrossRef] [PubMed]
- Berkman, N.D.; Davis, T.C.; McCormack, L. Health Literacy: What Is It? J. Health Commun. 2010, 15, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Berkman, N.D.; DeWalt, D.A.; Pignone, M.; Sheridan, S.L.; Lohr, K.N.; Lux, L.; Sutton, S.F.; Swinson, T.; Arthur, J. Literacy and health outcomes. J. Gen. Intern. Med. 2004, 19, 1228–1239. [Google Scholar]
- Lillie, S.E.; Fu, S.S.; Fabbrini, A.E.; Rice, K.L.; Clothier, B.A.; Doro, E.; Melzer, A.C.; Partin, M.R. Does need for cognitive closure explain individual differences in lung cancer screening? A brief report. J. Health Psychol. 2018, 1359105317750253. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.B.; Amer-Yahia, S.; Chawla, A.; Das, G.; Yu, C. Space efficiency in group recommendation. VLDB J. 2010, 19, 877–900. [Google Scholar] [CrossRef]
- Emerson, P. The original Borda count and partial voting. Soc. Choice Welf. 2013, 40, 353–358. [Google Scholar] [CrossRef]
- Kartoun, U. A Methodology to Generate Virtual Patient Repositories. arXiv 2016, arXiv:1608.00570. [Google Scholar]
- Järvelin, K.; Kekäläinen, J. IR Evaluation Methods for Retrieving Highly Relevant Documents. SIGIR Forum 2017, 51, 243–250. [Google Scholar] [CrossRef]
- Kendall, M. Rank Correlation Methods; Griffin: London, UK, 1948. [Google Scholar]
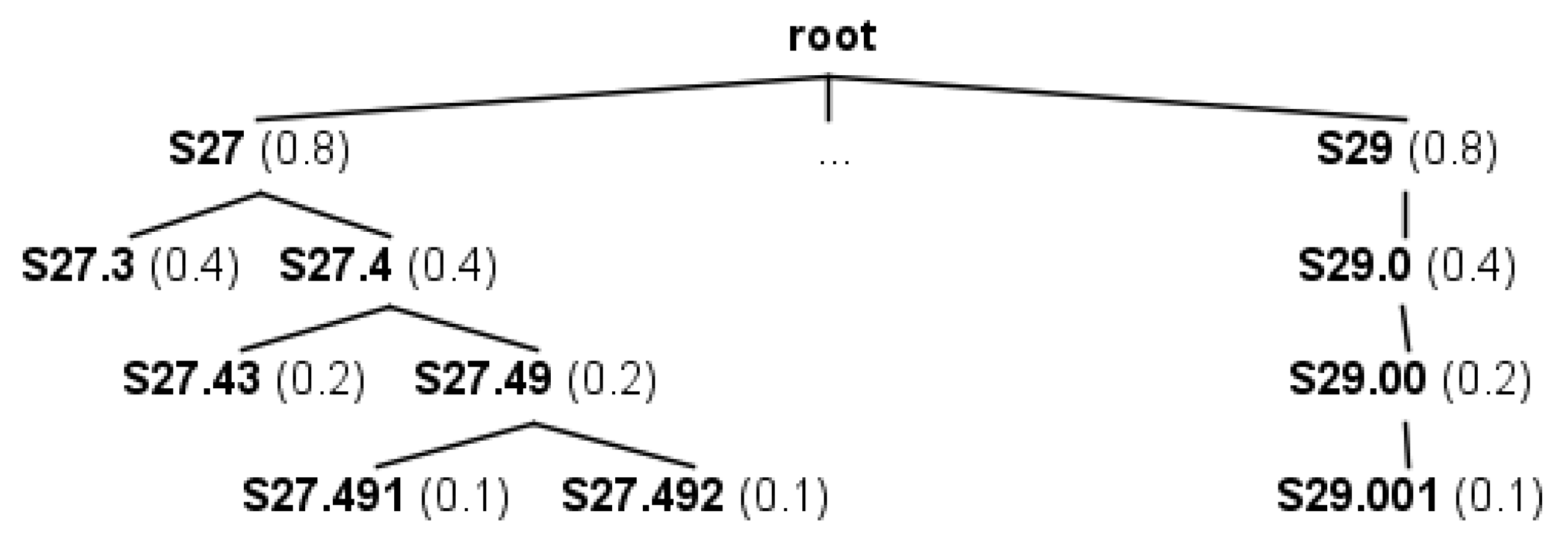
| Code ID | Description | Level |
|---|---|---|
| S27 | Injury of other and unspecified intrathoracic organs | 1 |
| S29 | Other and unspecified injuries of thorax | 1 |
| S27.3 | Other injury of bronchus, unilateral | 2 |
| S27.4 | Injury of bronchus | 2 |
| S27.43 | Laceration of bronchus | 3 |
| S27.49 | Other injury of bronchus | 3 |
| S27.491 | Other injury of bronchus, unilateral | 4 |
| S27.492 | Other injury of bronchus, bilateral | 4 |
| Node A | Node B | LCA(A,B) | simN(A,B) |
|---|---|---|---|
| S27.43 | S27.49 | S27.4 | |
| S27 | S29 | root | |
| S27.492 | S27.49 | S27.49 | |
| S27.3 | S27.49 | S27 | |
| S27.492 | S29.001 | root | |
| S27.491 | S27.492 | S27.49 |
| Parameter Name | Explanation | Value |
|---|---|---|
| numDocs | # of documents generated for each category of health problems. | 200 |
| numKeyWords | # of keywords appended to documents. | 10 |
| popularDocs | The # of the most popular documents in each category, for simulating a power law distribution. | 70 |
| Partitions | Parameter Name | Explanation | Value |
|---|---|---|---|
| Group Partition | Group | # of ratings given by patients in this group is 20 to 100 | 50% of all patients |
| Group | # of ratings given by patients in this group is 100 to 250 | 30% of all patients | |
| Group | # of ratings given by patients in this group is 250 to 500 | 20% of all patients | |
| Education Levels | Patients with Education Level 1 | 5% of all patients | |
| Patients with Education Level 2 | 10% of all patients | ||
| Patients with Education Level 3 | 40% of all patients | ||
| Patients with Education Level 4 | 30% of all patients | ||
| Patients with Education Level 5 | 15% of all patients | ||
| Anxiety Scores | Patients with Anxiety Score 1 | 30% of all patients | |
| Patients with Anxiety Score 2 | 40% of all patients | ||
| Patients with Anxiety Score 3 | 15% of all patients | ||
| Patients with Anxiety Score 4 | 10% of all patients | ||
| Patients with Anxiety Score 5 | 5% of all patients | ||
| Scores Partition | One | # of ratings that have as score 1 | 20% of all ratings |
| Two | # of ratings that have as score 2 | 10% of all ratings | |
| Three | # of ratings that have as score 3 | 30% of all ratings | |
| Four | # of ratings that have as score 4 | 20% of all ratings | |
| Five | # of ratings that have as score 5 | 20% of all ratings | |
| Ratings Partition | healthRelevant | # of relevant to some health problems documents each user will rate | 40% of ratings from each user |
| nonRelevant | # of non relevant to any health problems documents each user will rate. | 60% of ratings from each user |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stratigi, M.; Kondylakis, H.; Stefanidis, K. Multidimensional Group Recommendations in the Health Domain. Algorithms 2020, 13, 54. https://doi.org/10.3390/a13030054
Stratigi M, Kondylakis H, Stefanidis K. Multidimensional Group Recommendations in the Health Domain. Algorithms. 2020; 13(3):54. https://doi.org/10.3390/a13030054
Chicago/Turabian StyleStratigi, Maria, Haridimos Kondylakis, and Kostas Stefanidis. 2020. "Multidimensional Group Recommendations in the Health Domain" Algorithms 13, no. 3: 54. https://doi.org/10.3390/a13030054
APA StyleStratigi, M., Kondylakis, H., & Stefanidis, K. (2020). Multidimensional Group Recommendations in the Health Domain. Algorithms, 13(3), 54. https://doi.org/10.3390/a13030054






