Uncertainty Propagation through a Point Model for Steady-State Two-Phase Pipe Flow
Abstract
1. Introduction
2. Materials and Methods
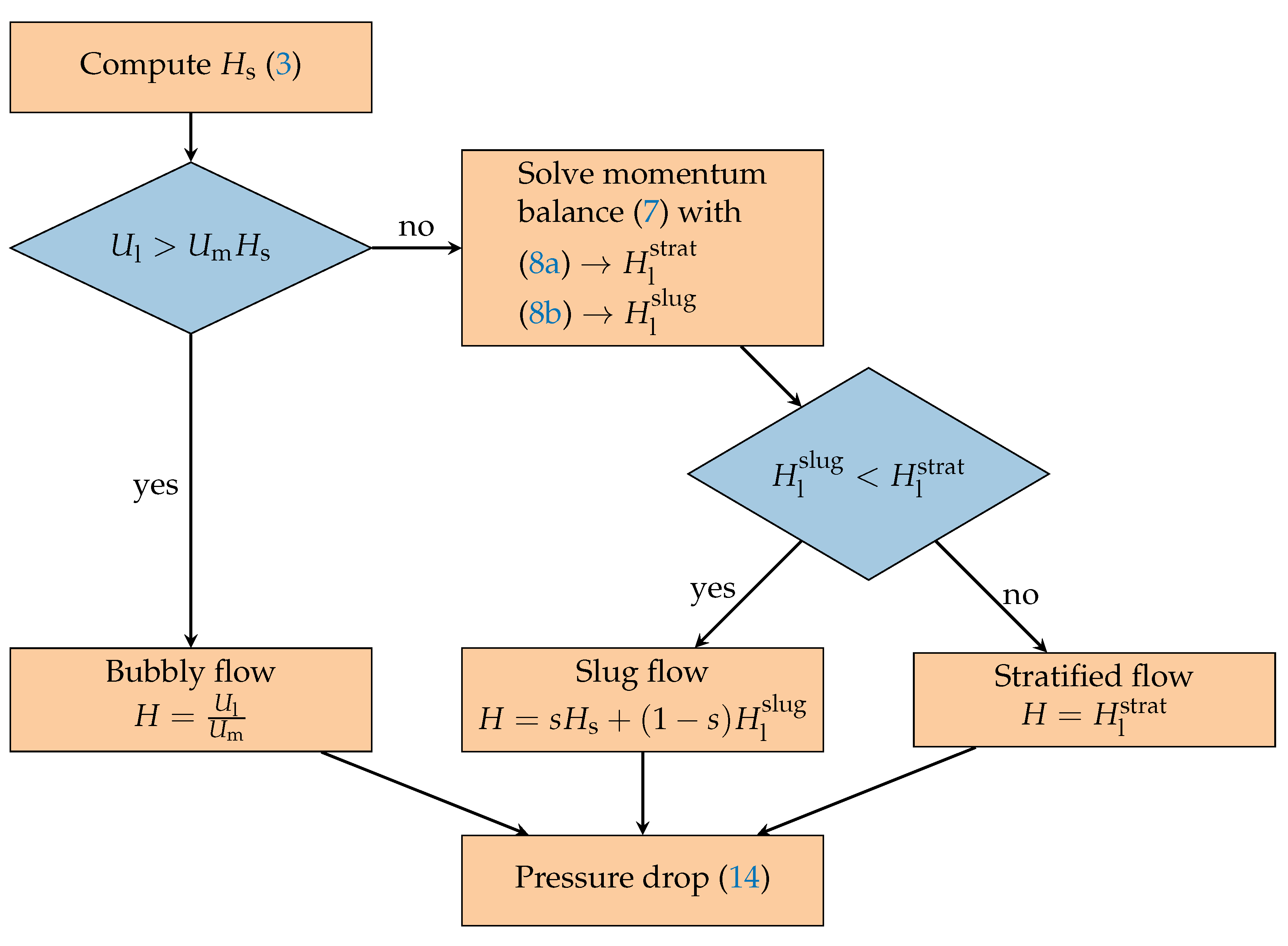
2.1. Flow Model
2.1.1. Slug Zone
2.1.2. Bubble Zone
2.1.3. Slug Fraction
2.1.4. Pressure Gradient
2.1.5. Interpolation by Reynolds Number
2.2. Uncertainty Quantification
2.2.1. Measurement error
2.2.2. Uncertainty Propagation
2.2.3. Input Sampling
2.2.4. Statistics
2.3. Monte Carlo Methods
2.4. Polynomial Chaos
2.5. Simulations
3. Results
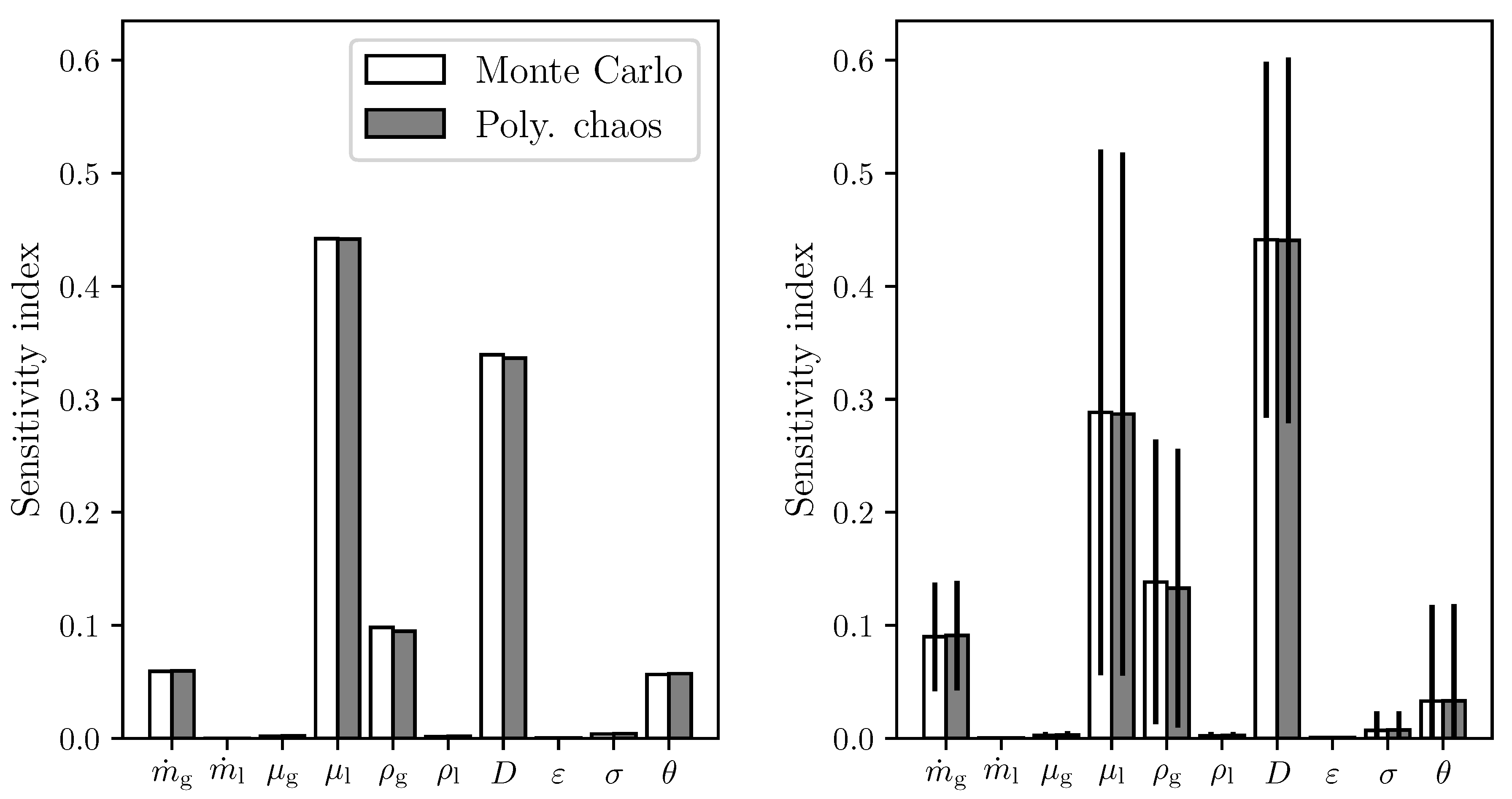
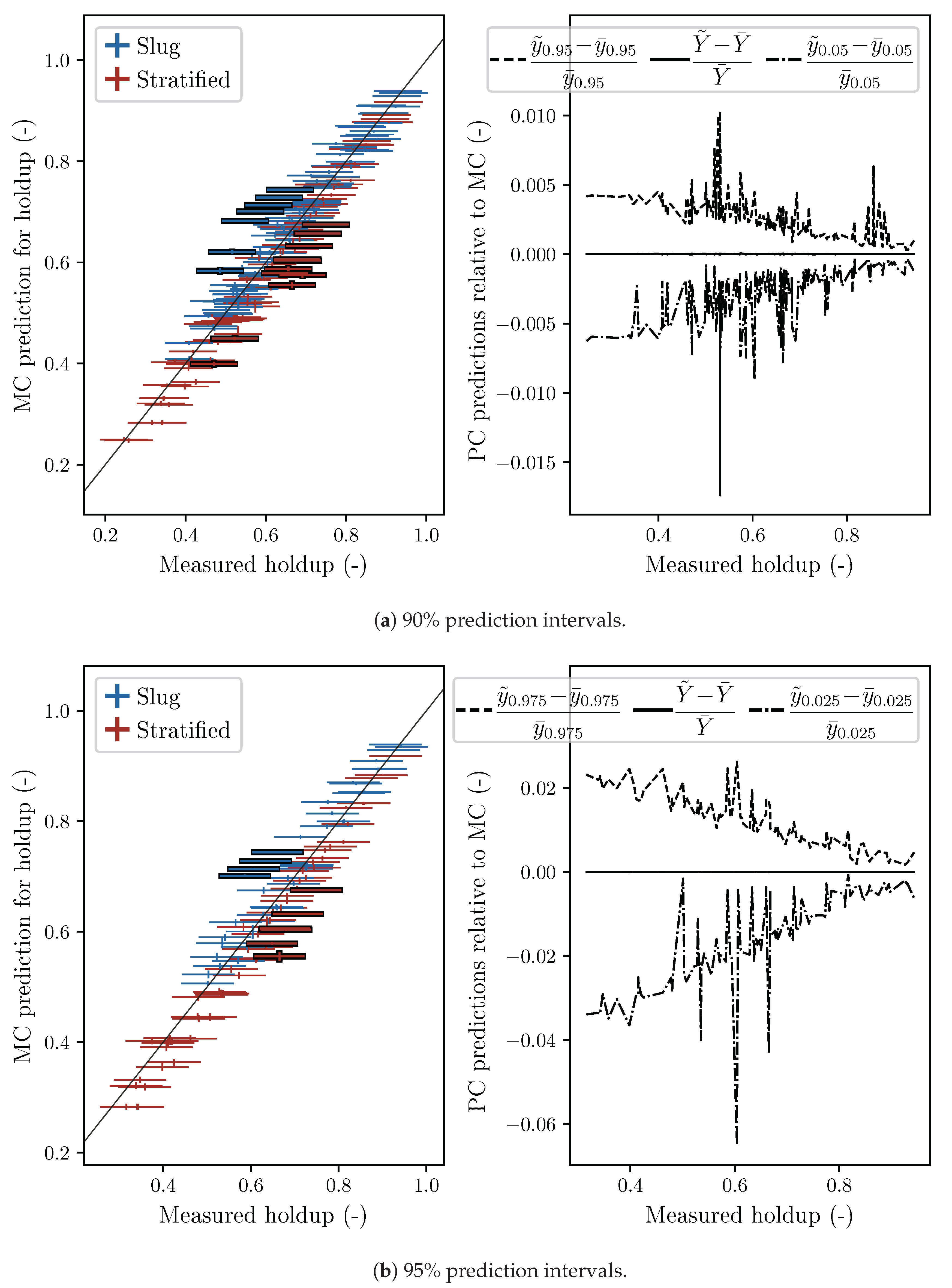
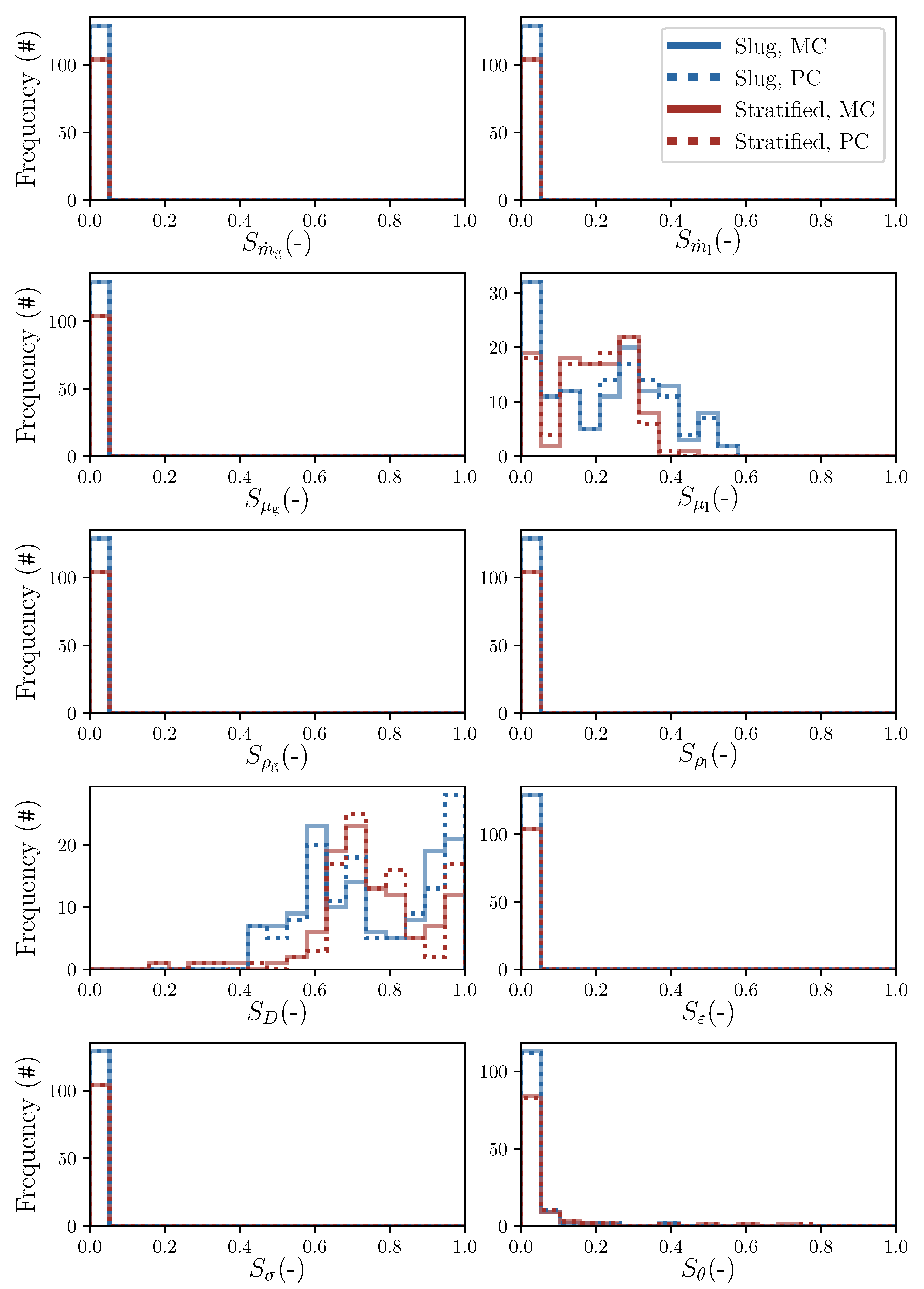
3.1. Holdup
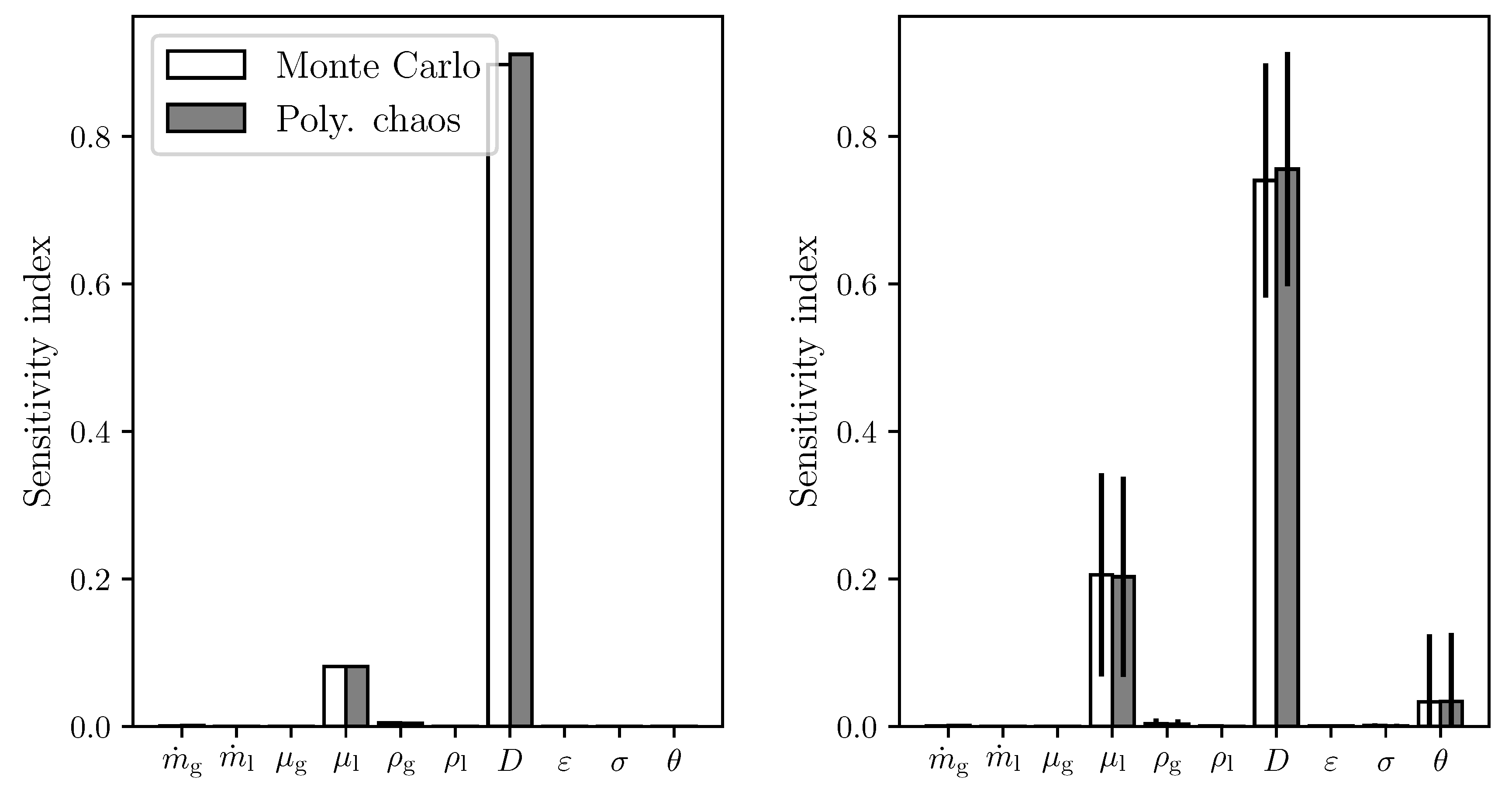
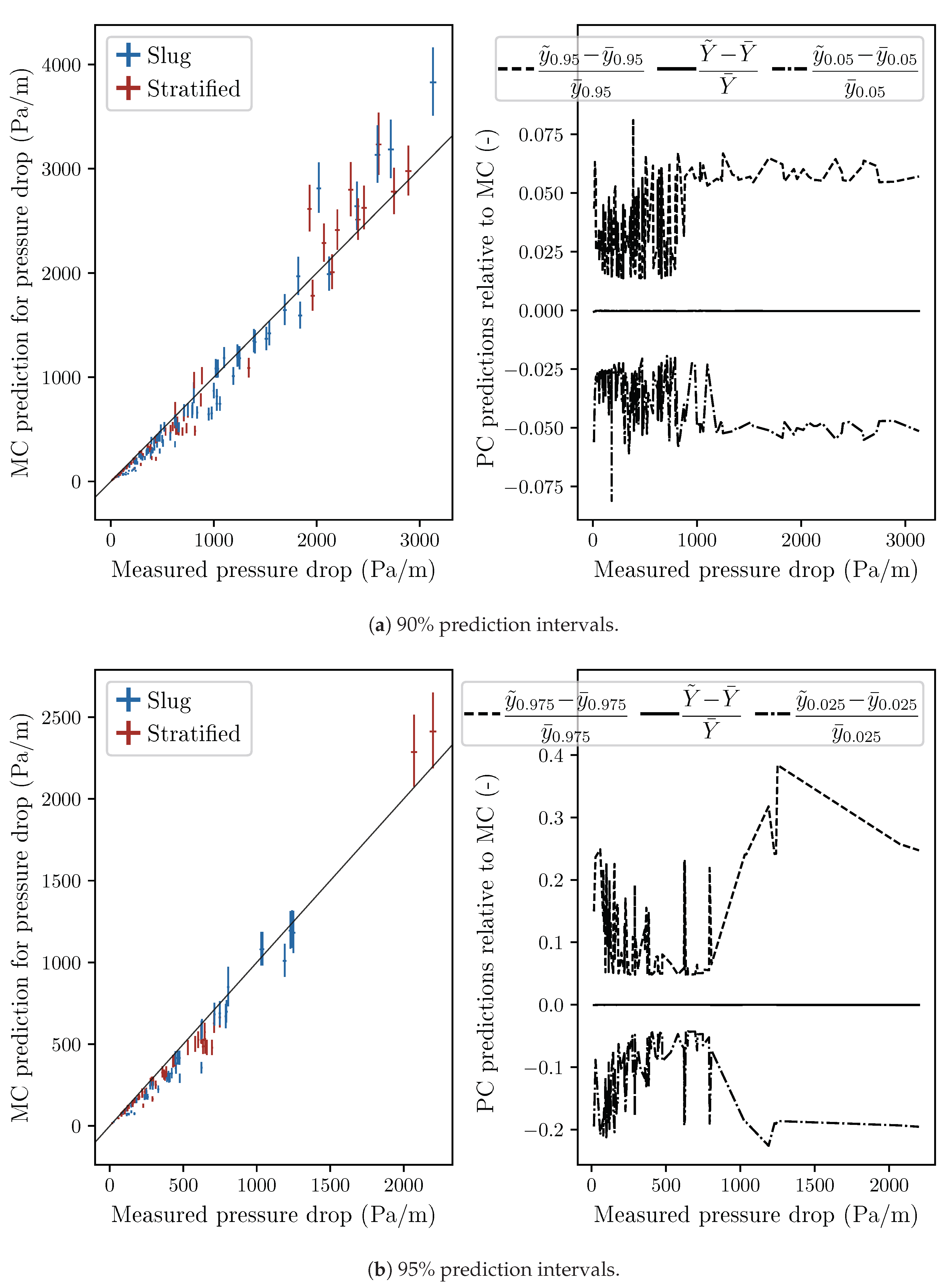
3.2. Pressure drop
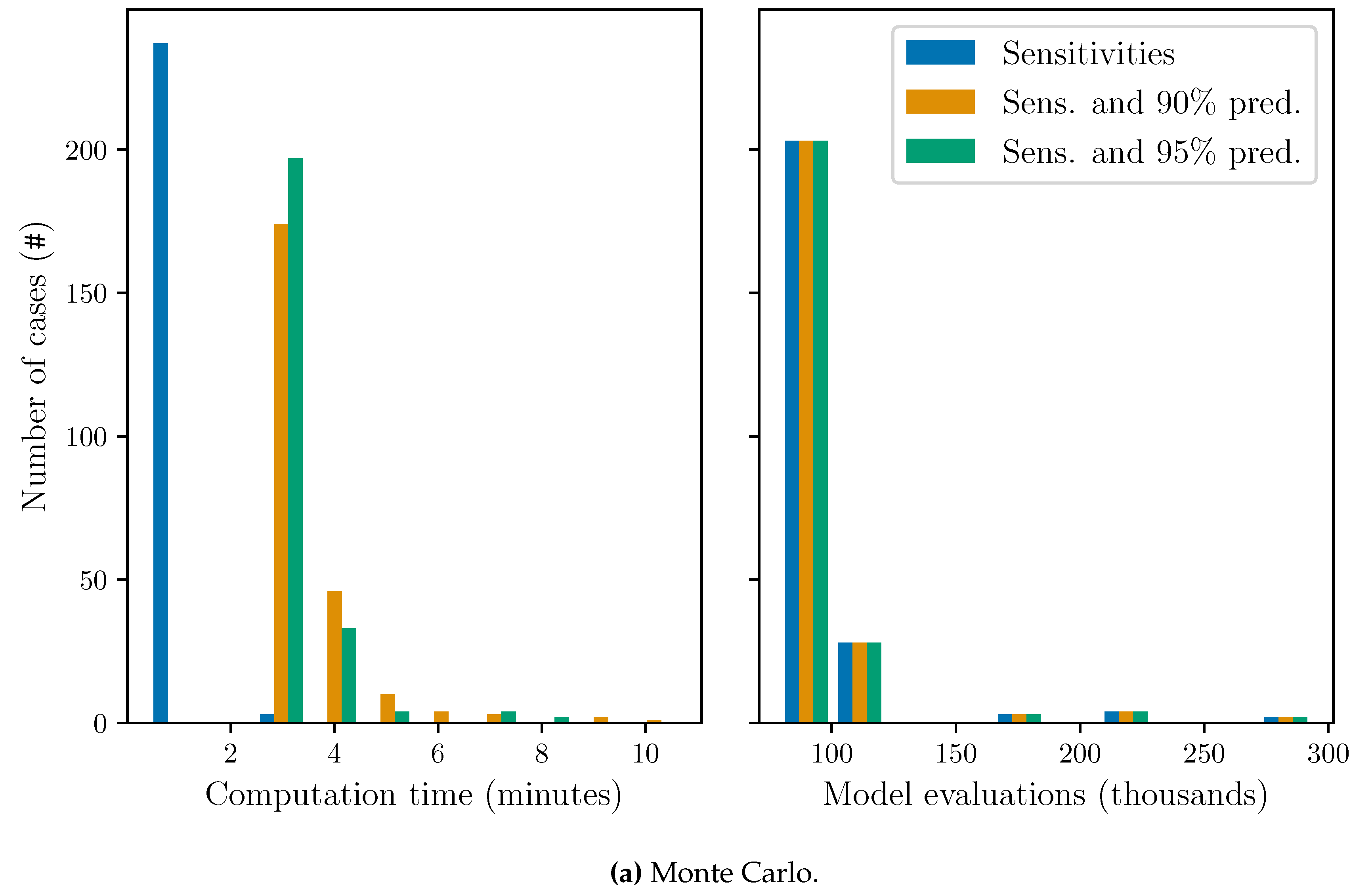
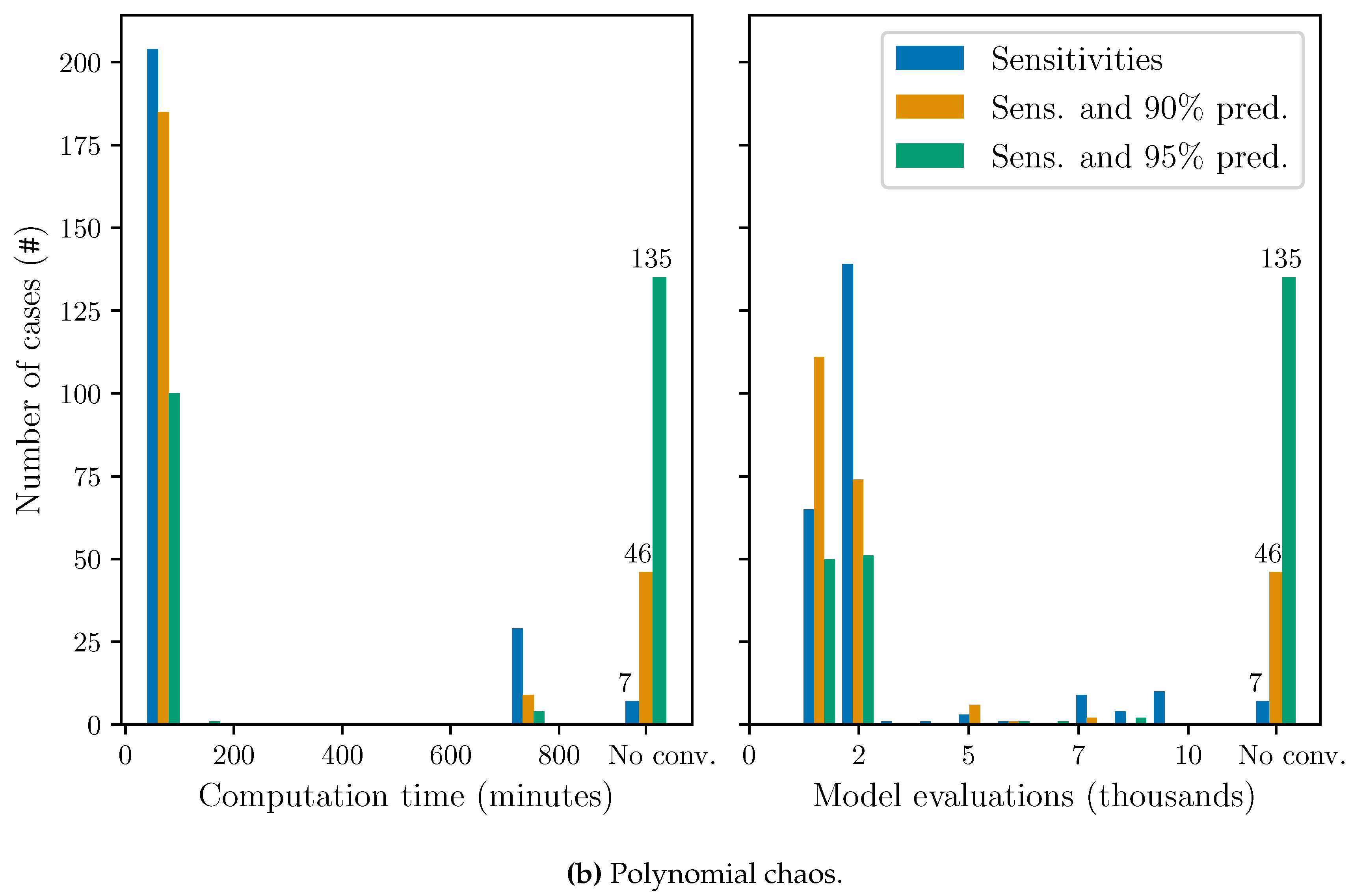
3.3. Computational Cost
4. Discussion
Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, S.H.; Chen, W. A comparative study of uncertainty propagation methods for black-box-type problems. Struct. Multidiscipl. Optim. 2009, 37, 239. [Google Scholar] [CrossRef]
- Cremaschi, S.; Kouba, G.E.; Subramani, H.J. Characterization of confidence in multiphase flow predictions. Energ. Fuel. 2012, 26, 4034–4045. [Google Scholar] [CrossRef]
- Holm, H.; Saha, P.; Suleymanov, V.; Vanvik, T.; Hoyer, N. Shtokman flow assurance challenges—A systematic approach to analyze uncertainties–Part 1. In Proceedings of the 15th International Conference on Multiphase Production Technology, Cannes, France, 15–17 June 2011. [Google Scholar]
- Holm, H.; Saha, P.; Suleymanov, V.; Vanvik, T.; Hoyer, N. Shtokman flow assurance challenges—A systematic approach to analyze uncertainties–Part 2. In Proceedings of the 15th International Conference on Multiphase Production Technology, Cannes, France, 15–17 June 2011. [Google Scholar]
- Hoyer, N.; Kirkedelen, M.; Biberg, D.; Johnson, G.; Valle, A.; Johansson, P.; Nossen, J. A structured approach for the evaluation of uncertainties in flow assurance systems. In Proceedings of the 16th International Conference on Multiphase Production Technology, Cannes, France, 12–14 June 2013. [Google Scholar]
- Klavetter, K.; Posluszny, D.; Warr, J.; Cremaschi, S.; Sarica, C.; Subramani, H. Uncertainty analysis of multiphase flow models: A comparison of three propagation approaches. In Proceedings of the 8th North American Conference on Multiphase Technology, Banff, AB, Canada, 20–22 June 2012. [Google Scholar]
- Keinath, B. Decision analysis in multiphase flow: Uncertainty, risk and application. In Proceedings of the 18th International Conference on Multiphase Production Technology, Cannes, France, 7–9 June 2017. [Google Scholar]
- Liu, Y.; Dinh, N.T.; Smith, R.C.; Sun, X. Uncertainty quantification of two-phase flow and boiling heat transfer simulations through a data-driven modular Bayesian approach. Int. J. Heat. Mass. Tran. 2019, 138, 1096–1116. [Google Scholar] [CrossRef]
- Picchi, D.; Poesio, P. Uncertainty quantification and global sensitivity analysis of mechanistic one-dimensional models and flow pattern transition boundaries predictions for two-phase pipe flows. Int. J. Multiphas. Flow 2017, 90, 64–78. [Google Scholar] [CrossRef]
- Klinkert, J. The characterization of Uncertainty for Steady State Multiphase Flow Models in Pipelines. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 19 January 2018. [Google Scholar]
- Lataniotis, C.; Marelli, S.; Sudret, B. Uqlab User Manual—The Input Module. 2015. Available online: https://www.researchgate.net/profile/Bruno_Sudret/publication/281232688_UQLab_user_manual_-_the_INPUT_module/links/55dc1df708ae9d6594937608.pdf (accessed on 26 February 2020).
- Smith, I.E.; Nossen, J.; Unander, T.E. Improved holdup and pressure drop predictions for multiphase flow with gas and high viscosity oil. In Proceedings of the 16th International Conference on Multiphase Production Technology, Cannes, France, 12–14 June 2013. [Google Scholar]
- Lichota, P.; Szulczyk, J.; Tischler, M.B.; Berger, T. Frequency Responses Identification from Multi-Axis Maneuver with Simultaneous Multisine Inputs. J. Guid. Contr. Dynam. 2019, 42, 2550–2556. [Google Scholar] [CrossRef]
- Lichota, P.; Noreña, D.A. A priori model inclusion in the multisine maneuver design. In Proceedings of the 17th International Carpathian Control Conference (ICCC), Tatranska Lomnica, Slovakia, 29 May–1 June 2016; pp. 440–445. [Google Scholar]
- Chen, S.; Wang, X.; Harris, C.J. NARX-based nonlinear system identification using orthogonal least squares basis hunting. IEEE Trans. Contr. Syst. Tech. 2007, 16, 78–84. [Google Scholar] [CrossRef]
- Efremov, A. System Identification Based on Stepwise Regression for Dynamic Market Representation. In Proceedings of the International Conference on Data Mining and Knowledge Engineering, Rome, Italy, 29 April 2010; Volume 4, pp. 28–30. [Google Scholar]
- Dukler, A.E.; Hubbard, M.G. A model for gas-liquid slug flow in horizontal and near horizontal tubes. Ind. Eng. Chem. Fund. 1975, 14, 337–347. [Google Scholar] [CrossRef]
- Gregory, G.; Nicholson, M.; Aziz, K. Correlation of the liquid volume fraction in the slug for horizontal gas-liquid slug flow. Int. J. Multiphas. Flow 1978, 4, 33–39. [Google Scholar] [CrossRef]
- Kora, C.; Sarica, C.; Zhang, H.q.; Al-Sarkhi, A.; Al-Safran, E. Effects of high oil viscosity on slug liquid holdup in horizontal pipes. In Proceedings of the Canadian Unconventional Resources Conference, Calgary, AB, Canada, 15–17 November 2011. [Google Scholar]
- Bendiksen, K.H. An experimental investigation of the motion of long bubbles in inclined tubes. Int. J. Multiphas. Flow 1984, 10, 467–483. [Google Scholar] [CrossRef]
- Jeyachandra, B.; Gokcal, B.; Al-Sarkhi, A.; Sarica, C.; Sharma, A. Drift-velocity closure relationships for slug two-phase high-viscosity oil flow in pipes. SPE J. 2012, 17, 593–601. [Google Scholar] [CrossRef]
- Nuland, S. Bubble front velocity in horizontal slug flow with viscous Newtonian, shear thinning and Bingham fluids. In Proceedings of the 3rd International Conference on Multiphase Flow (ICMF’98), Lyon, France, 8–12 June 1998. [Google Scholar]
- Hinze, J.O. Turbulence; McGraw-Hill: New York, NY, USA, 1975; Volume 2. [Google Scholar]
- Andreussi, P.; Persen, L. Stratified gas-liquid flow in downwardly inclined pipes. Int. J. Multiphas. Flow 1987, 13, 565–575. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Brkić, D.; Praks, P. Accurate and efficient explicit approximations of the Colebrook flow friction equation based on the Wright ω-function. Mathematics 2019, 7, 34. [Google Scholar] [CrossRef]
- Khaledi, H.A.; Smith, I.E.; Unander, T.E.; Nossen, J. Investigation of two-phase flow pattern, liquid holdup and pressure drop in viscous oil–gas flow. Int. J. Multiphas. Flow 2014, 67, 37–51. [Google Scholar] [CrossRef]
- ISO, I.; OIML, B. Guide to the Expression of Uncertainty in Measurement. 1995. Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf (accessed on 26 February 2020).
- Sobol, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Comm. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Comm. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Sobol, I.M.; Tarantola, S.; Gatelli, D.; Kucherenko, S.; Mauntz, W. Estimating the approximation error when fixing unessential factors in global sensitivity analysis. Reliab. Eng. Syst. Saf. 2007, 92, 957–960. [Google Scholar] [CrossRef]
- Jansen, M.J. Analysis of variance designs for model output. Comput. Phys. Comm. 1999, 117, 35–43. [Google Scholar] [CrossRef]
- Xiu, D. Numerical Methods for Stochastic Computations: A Spectral Method Approach; Princeton university press: Princeton, NJ, USA, 2010. [Google Scholar]
- Feinberg, J.; Langtangen, H.P. Chaospy: An open source tool for designing methods of uncertainty quantification. J. Comput. Sci. 2015, 11, 46–57. [Google Scholar] [CrossRef]
- Smith, I.E.; Nossen, J.; Kjølaas, J.; Lund, B. Development of a Steady-State Point Model for Prediction of Gas/Oil and Water/Oil Pipe Flow. J. Dispers. Sci. Technol. 2015, 36, 1394–1406. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E.; Westveld III, A.H.; Goldman, T. Calibrated probabilistic forecasting using ensemble model output statistics and minimum CRPS estimation. Mon. Weather Rev. 2005, 133, 1098–1118. [Google Scholar] [CrossRef]
Sample Availability: Code and data are available online: https://dataverse.no/dataset.xhtml?persistentId=doi:10.18710/OWKABR. |



| Symbol | Description | Unit |
|---|---|---|
| Mass rate | kg/s | |
| Viscosity | Pa s | |
| Density | Pa s | |
| D | Pipe diameter | m |
| Hydraulic roughness | m | |
| Surface tension | N/m | |
| Pipe inclination | rad |
| (a) Input | ||
|---|---|---|
| Variable | Unit | Uncertainty |
| kg/s | ||
| kg/s | ||
| Pa s | ||
| Pa s | ||
| kg/m3 | 0.2 kg/m3 | |
| kg/m3 | 1 kg/m3 | |
| D | m | |
| m | ||
| N/m | ||
| (b) Output | ||
| Variable | Unit | Uncertainty |
| H | − | |
| Pa/m | ||
| Variable | Polynomial Order | Unit | Flow Regime | ||
|---|---|---|---|---|---|
| 3 | 4 | 5 | |||
| 0.9961 | 0.9518 | 0.9882 | − | Bubbly/slug | |
| 0.4814 | 0.5044 | 0.5215 | − | Slug/stratified | |
| 24.214 | 24.906 | 25.196 | Slug/stratified | ||
| 28.301 | 29.042 | 31.399 | Slug/stratified | ||
| 217.10 | 291.76 | 269.55 | Slug/stratified | ||
| 514.15 | 528.26 | 521.32 | Slug/stratified | ||
| 5833.6 | 6555.0 | 6980.1 | Bubbly/slug | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strand, A.; Smith, I.E.; Unander, T.E.; Steinsland, I.; Hellevik, L.R. Uncertainty Propagation through a Point Model for Steady-State Two-Phase Pipe Flow. Algorithms 2020, 13, 53. https://doi.org/10.3390/a13030053
Strand A, Smith IE, Unander TE, Steinsland I, Hellevik LR. Uncertainty Propagation through a Point Model for Steady-State Two-Phase Pipe Flow. Algorithms. 2020; 13(3):53. https://doi.org/10.3390/a13030053
Chicago/Turabian StyleStrand, Andreas, Ivar Eskerud Smith, Tor Erling Unander, Ingelin Steinsland, and Leif Rune Hellevik. 2020. "Uncertainty Propagation through a Point Model for Steady-State Two-Phase Pipe Flow" Algorithms 13, no. 3: 53. https://doi.org/10.3390/a13030053
APA StyleStrand, A., Smith, I. E., Unander, T. E., Steinsland, I., & Hellevik, L. R. (2020). Uncertainty Propagation through a Point Model for Steady-State Two-Phase Pipe Flow. Algorithms, 13(3), 53. https://doi.org/10.3390/a13030053





