Approximation and Uncertainty Quantification of Systems with Arbitrary Parameter Distributions Using Weighted Leja Interpolation
Abstract
1. Introduction
2. Theory and Methodology
2.1. Stochastic Parametric Models
2.2. Univariate Interpolation Schemes
2.2.1. Univariate Lagrange Interpolation
2.2.2. Hierarchical Univariate Interpolation
2.2.3. Interpolatory Univariate Quadrature
2.3. Leja Interpolation Nodes
2.3.1. Unweighted Leja Nodes
2.3.2. Weighted Leja Nodes
2.4. Sparse Adaptive Leja Interpolation
2.4.1. Generalized Sparse Grid Interpolation
2.4.2. Adaptive Anisotropic Leja Interpolation

2.4.3. Post-Processing
3. Results
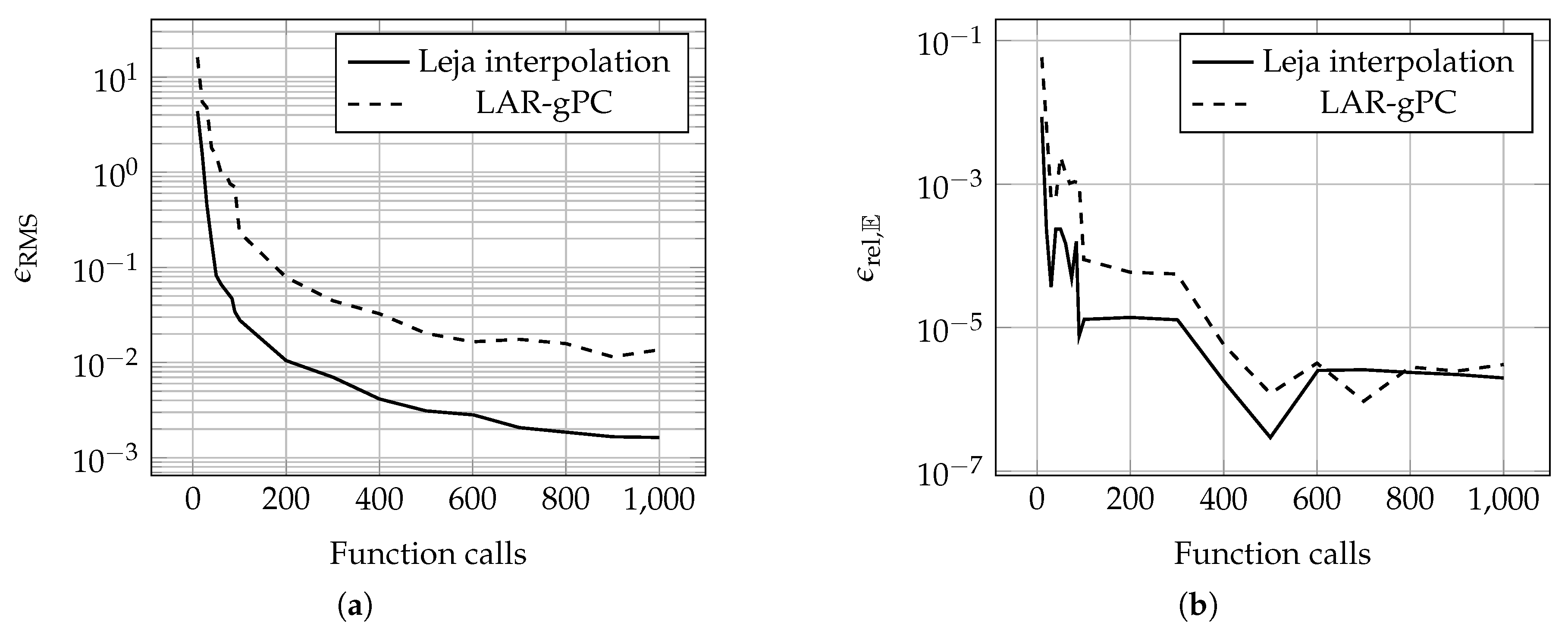
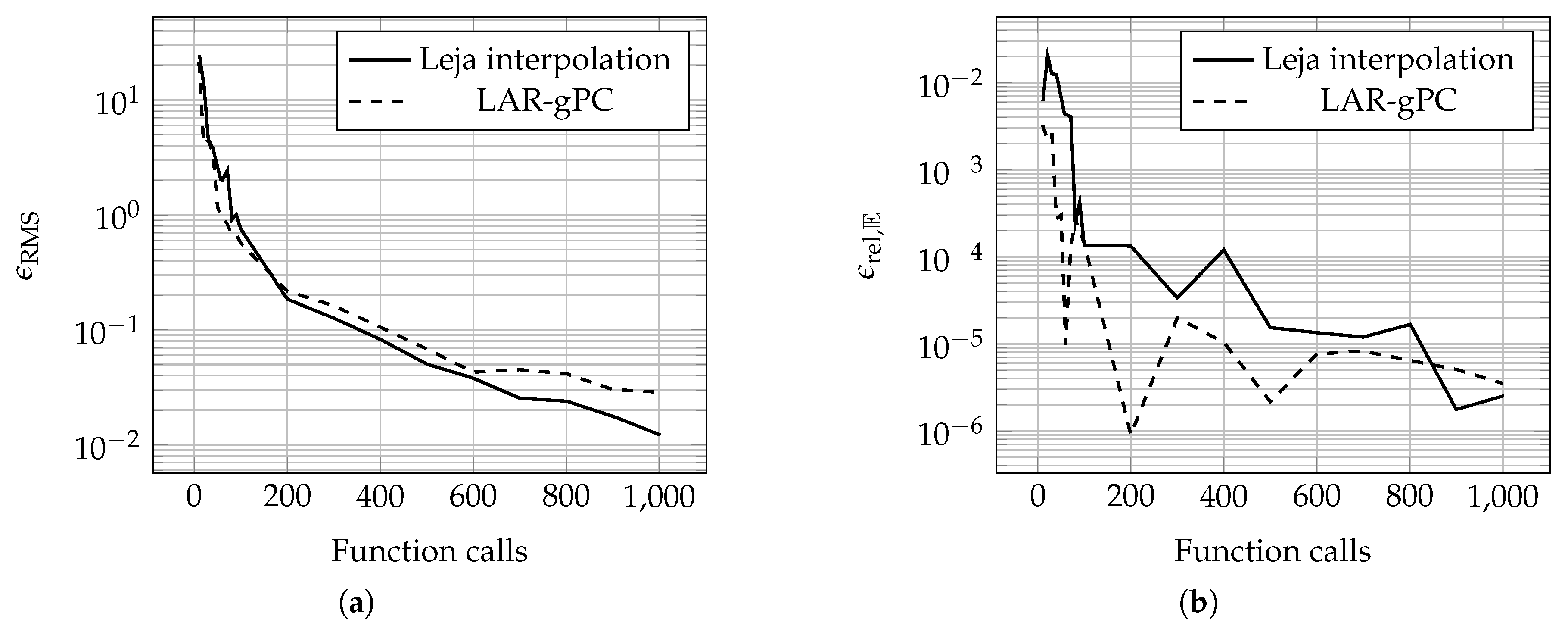
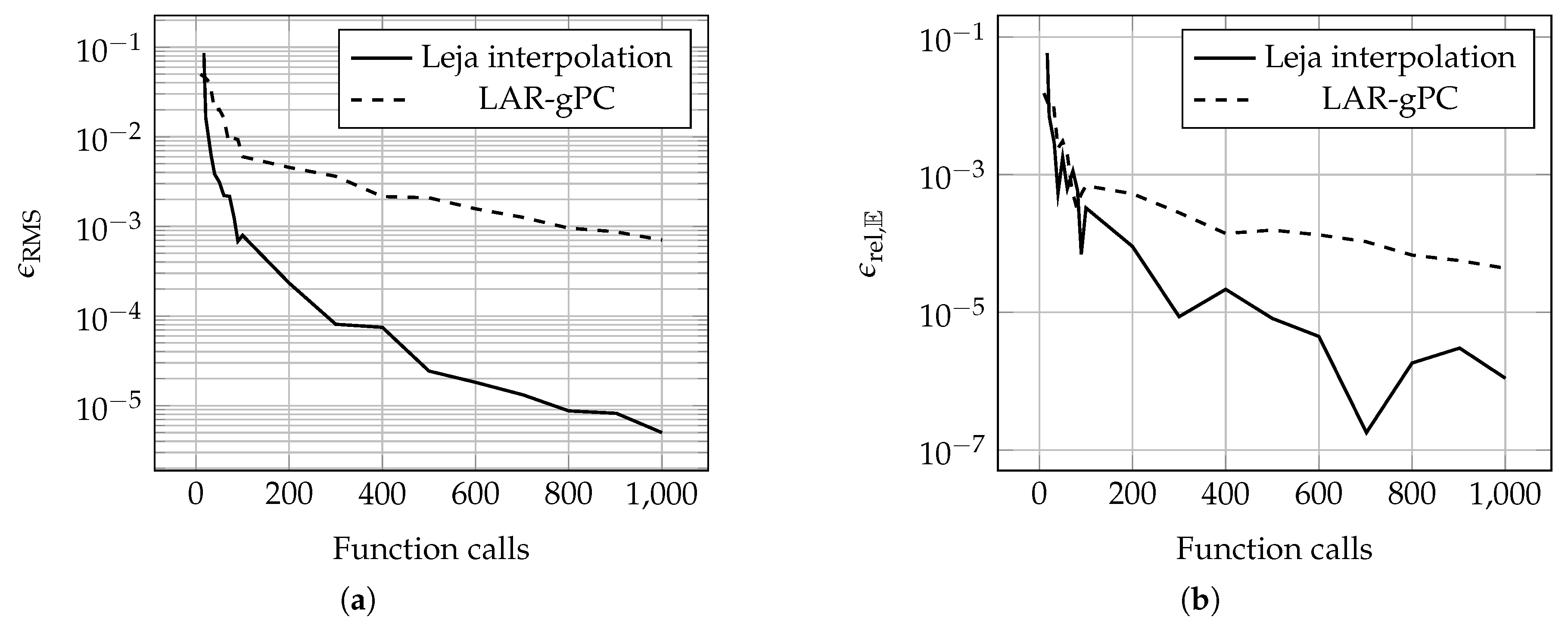
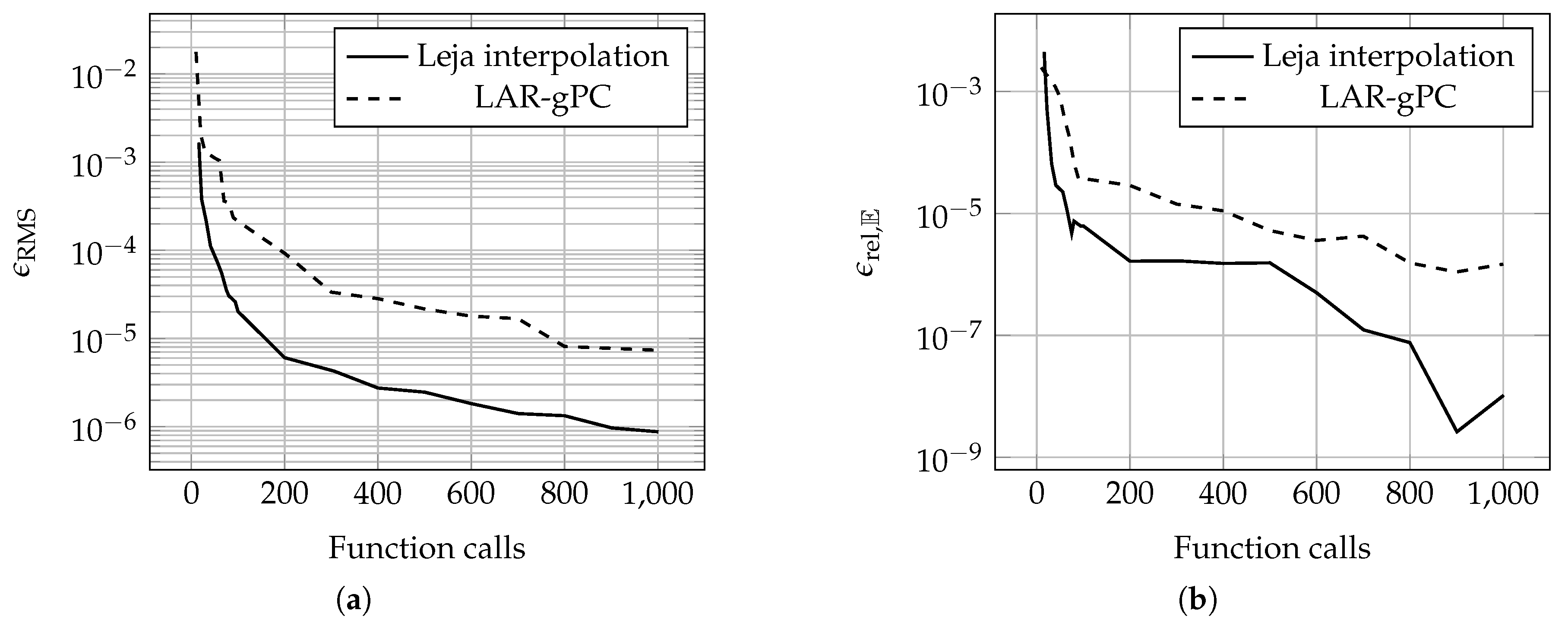
3.1. Error Metrics
3.2. Accuracy versus Costs
3.3. Borehole Model
- The parameter originally follows the normal distribution . The distribution is now truncated to the range ;
- The parameter r originally follows the log-normal distribution . Therefore, the parameter r has a mean value equal to and a variance equal to . The corresponding truncated normal distribution is defined by these mean and variance values, as well as by the truncation range l
- The remaining parameters are originally uniformly distributed, such that , , , , , and . Assuming a uniform distribution with support in , the corresponding truncated normal distribution is given as , i.e., the mean value and variance of the normal distribution correspond to those of the original uniform distribution, while the truncation limits coincide with the uniform distribution’s support boundaries.
3.4. Steel Column Limit State Function
3.5. Meromorphic Function
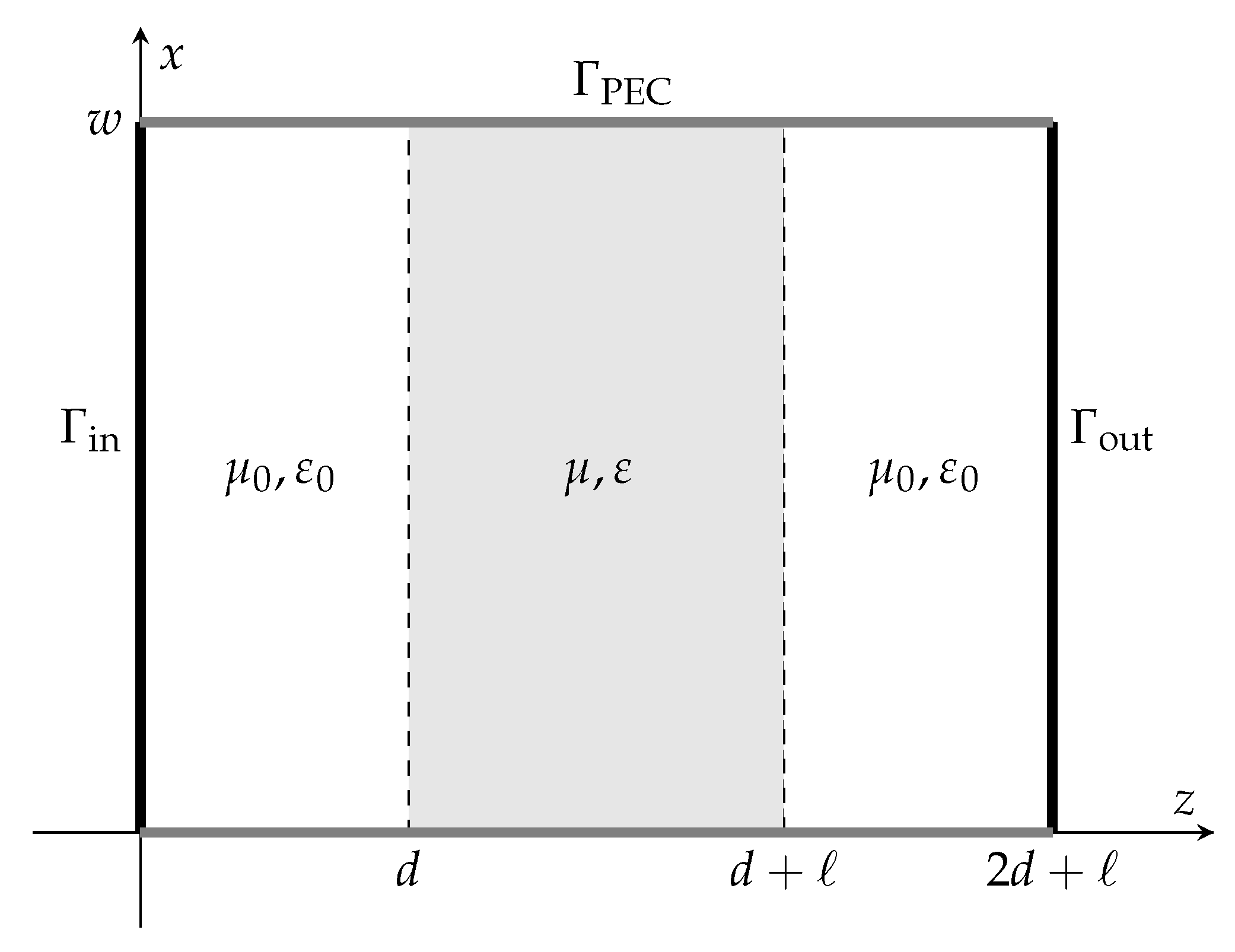
3.6. Dielectric Inset Waveguide
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Caflisch, R. Monte Carlo and quasi-Monte Carlo methods. Acta Numer. 1998, 7, 1–49. [Google Scholar] [CrossRef]
- Loh, W.L. On latin hypercube sampling. Ann. Stat. 1996, 24, 2058–2080. [Google Scholar] [CrossRef]
- Le Maître, O.P.; Knio, O.M. Spectral Methods for Uncertainty Quantification: With Applications to Computational Fluid Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Xiu, D. Numerical Methods for Stochastic Computations: A Spectral Method Approach; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Babuška, I.; Nobile, F.; Tempone, R. A stochastic collocation method for elliptic partial differential equations with random input data. SIAM Rev. 2010, 2, 317–355. [Google Scholar] [CrossRef]
- Barthelmann, V.; Novak, E.; Ritter, K. High dimensional polynomial interpolation on sparse grids. Adv. Comput. Math. 2000, 12, 273–288. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener-Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis. Probab. Eng. Mech. 2010, 25, 183–197. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. Adaptive sparse polynomial chaos expansion based on least angle regression. J. Comput. Phys. 2011, 230, 2345–2367. [Google Scholar] [CrossRef]
- Migliorati, G. Adaptive polynomial approximation by means of random discrete least squares. In Numerical Mathematics and Advanced Applications - ENUMATH 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 547–554. [Google Scholar]
- Conrad, P.R.; Marzouk, Y.M. Adaptive Smolyak Pseudospectral Approximations. SIAM J. Sci. Comput. 2013, 35, A2643–A2670. [Google Scholar] [CrossRef]
- Constantine, P.G.; Eldred, M.S.; Phipps, E.T. Sparse pseudospectral approximation method. Comput. Methods Appl. Mech. Eng. 2012, 229, 1–12. [Google Scholar] [CrossRef]
- Le Maître, O.P.; Knio, O.M.; Najm, H.N.; Ghanem, R.G. A Stochastic Projection Method for Fluid Flow: I. Basic Formulation. J. Comput. Phys. 2001, 173, 481–511. [Google Scholar] [CrossRef]
- Loukrezis, D.; De Gersem, H. Adaptive Sparse Polynomial Chaos Expansions via Leja Interpolation. arXiv 2019, arXiv:1911.08312. [Google Scholar]
- Bellman, R. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Chkifa, A.; Cohen, A.; Schwab, C. High-dimensional adaptive sparse polynomial interpolation and applications to parametric PDEs. Found. Comput. Math. 2014, 14, 601–633. [Google Scholar] [CrossRef]
- Nobile, F.; Tempone, R.; Webster, C.G. An anisotropic sparse grid stochastic collocation method for partial differential equations with random input data. SIAM J. Numer. Anal. 2008, 46, 2411–2442. [Google Scholar] [CrossRef]
- Stoyanov, M.; Webster, C.G. A dynamically adaptive sparse grids method for quasi-optimal interpolation of multidimensional functions. Comput. Math. Appl. 2016, 71, 2449–2465. [Google Scholar] [CrossRef]
- Ernst, O.; Sprungk, B.; Tamellini, L. Convergence of sparse collocation for functions with countably many Gaussian random variables. SIAM J. Numer. Anal. 2018, 56, 877–905. [Google Scholar] [CrossRef]
- Clenshaw, C.W.; Curtis, A.R. A method for numerical integration on an automatic computer. Numer. Math. 1960, 2, 197–205. [Google Scholar] [CrossRef]
- Genz, A.; Keister, B. Fully symmetric interpolatory rules for multiple integrals over infinite regions with Gaussian weight. J. Comput. Appl. Math. 1996, 71, 299–309. [Google Scholar] [CrossRef]
- Burkardt, J. The Truncated Normal Distribution, 2014. Department of Scientific Computing, Florida State University. Available online: https://people.sc.fsu.edu/~jburkardt/presentations/truncated_normal.pdf (accessed on 25 February 2020).
- Sommariva, A. Fast construction of Fejér and Clenshaw–Curtis rules for general weight functions. Comput. Math. Appl. 2013, 65, 682–693. [Google Scholar] [CrossRef]
- Soize, C.; Ghanem, R. Physical systems with random uncertainties: Chaos representations with arbitrary probability measure. SIAM J. Sci. Comput. 2004, 26, 395–410. [Google Scholar] [CrossRef]
- Wan, X.; Karniadakis, G.E. Beyond Wiener-Askey expansions: Handling arbitrary PDFs. J. Sci. Comput. 2006, 27, 455–464. [Google Scholar] [CrossRef][Green Version]
- Wan, X.; Karniadakis, G.E. Multi-element generalized polynomial chaos for arbitrary probability measures. SIAM J. Sci. Comput. 2006, 28, 901–928. [Google Scholar] [CrossRef]
- Eldred, M. Recent advances in non-intrusive polynomial chaos and stochastic collocation methods for uncertainty analysis and design. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 17th AIAA/ASME/AHS Adaptive Structures Conference 11th AIAA, Palm Springs, CA, USA, 4–7 May 2009. [Google Scholar]
- Eldred, M.; Burkardt, J. Comparison of non-intrusive polynomial chaos and stochastic collocation methods for uncertainty quantification. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Ng, L.W.T.; Eldred, M. Multifidelity uncertainty quantification using non-intrusive polynomial chaos and stochastic collocation. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 20th AIAA/ASME/AHS Adaptive Structures Conference 14th AIAA, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar]
- Narayan, A.; Jakeman, J.D. Adaptive Leja Sparse Grid Constructions for Stochastic Collocation and High-Dimensional Approximation. SIAM J. Sci. Comput. 2014, 36, A2952–A2983. [Google Scholar] [CrossRef]
- Ahlfeld, R.; Belkouchi, B.; Montomoli, F. SAMBA: Sparse approximation of moment-based arbitrary polynomial chaos. J. Comput. Phys. 2016, 320, 1–16. [Google Scholar] [CrossRef]
- Oladyshkin, S.; Nowak, W. Data-driven uncertainty quantification using the arbitrary polynomial chaos expansion. Reliab. Eng. Syst. Saf. 2012, 106, 179–190. [Google Scholar] [CrossRef]
- Ernst, O.; Sprungk, B.; Tamellini, L. On Expansions and Nodes for Sparse Grid Collocation of Lognormal Elliptic PDEs. arXiv 2019, arXiv:1906.01252. [Google Scholar]
- Georg, N.; Loukrezis, D.; Römer, U.; Schöps, S. Uncertainty quantification for nanoplasmonics with adjoint-based Leja adaptive collocation and conformal maps. arXiv 2019, arXiv:1807.07485. [Google Scholar]
- Nobile, F.; Tamellini, L.; Tempone, R. Comparison of Clenshaw-Curtis and Leja quasi-optimal sparse grids for the approximation of random PDEs. In Spectral and High Order Methods for Partial Differential Equations, ICOSAHOM 2014; Springer International Publishing: Cham, Switzerland, 2015; pp. 475–482. [Google Scholar]
- Schillings, C.; Schwab, C. Sparse, adaptive Smolyak quadratures for Bayesian inverse problems. Inverse Probl. 2013, 29, 065011. [Google Scholar] [CrossRef]
- Loukrezis, D.; Römer, U.; De Gersem, H. Assessing the performance of Leja and Clenshaw-Curtis collocation for computational electromagnetics with random input data. Int. J. Uncertain. Quantif. 2019, 9, 33–57. [Google Scholar] [CrossRef]
- Loukrezis, D. Adaptive Approximations for High-Dimensional Uncertainty Quantification in Stochastic Parametric Electromagnetic Field Simulations. Ph.D. Thesis, TU Darmstadt, Darmstadt, Germany, 2019. [Google Scholar]
- Feinberg, J.; Eck, V.G.; Langtangen, H.P. Multivariate Polynomial Chaos Expansions with Dependent Variables. SIAM J. Sci. Comput. 2018, 40, A199–A223. [Google Scholar] [CrossRef]
- Lebrun, R.; Dutfoy, A. A generalization of the Nataf transformation to distributions with elliptical copula. Probab. Eng. Mech. 2009, 24, 172–178. [Google Scholar] [CrossRef]
- Leja, F. Sur certaines suites liées aux ensembles plans et leur application à la représentation conforme. Ann. Pol. Math. 1957, 4, 8–13. [Google Scholar] [CrossRef]
- Taylor, R.; Totik, V. Lebesgue constants for Leja points. IMA J. Numer. Anal. 2010, 30, 462–486. [Google Scholar] [CrossRef]
- Marchi, S.D. On Leja sequences: some results and applications. Appl. Math. Comput. 2004, 152, 621–647. [Google Scholar] [CrossRef]
- Jantsch, P.; Webster, C.; Zhang, G. On the Lebesgue constant of weighted Leja points for Lagrange interpolation on unbounded domains. IMA J. Numer. Anal. 2019, 39, 1039–1057. [Google Scholar] [CrossRef]
- Bungartz, H.; Griebel, M. Sparse grids. Acta Numer. 2004, 13, 147–269. [Google Scholar] [CrossRef]
- Beck, J.; Tempone, R.; Nobile, F.; Tamellini, L. On the optimal polynomial approximation of stochastic PDEs by Galerkin and collocation methods. Math. Model. Methods Appl. Sci. 2012, 22, 1250023. [Google Scholar] [CrossRef]
- Gerstner, T.; Griebel, M. Dimension-adaptive tensor-product quadrature. Computing 2003, 71, 65–87. [Google Scholar] [CrossRef]
- Klimke, A.; Wohlmuth, B.I. Algorithm 847: Spinterp: Piecewise multilinear hierarchical sparse grid interpolation in MATLAB. ACM Trans. Math. Softw. 2005, 31, 561–579. [Google Scholar] [CrossRef]
- Buzzard, G.T. Efficient Basis Change for Sparse-Grid Interpolating Polynomials with Application to T-Cell Sensitivity Analysis. Comput. Biol. J. 2013, 2013. Available online: https://www.hindawi.com/journals/cbj/2013/562767/ (accessed on 25 February 2020). [CrossRef]
- Marelli, S.; Sudret, B. UQLab User Manual Polynomial Chaos Expansions, 2015. Available online: https://www.researchgate.net/profile/Bruno_Sudret/publication/279532922_UQLab_user_manual_-_Polynomial_chaos_expansions/links/5595b6c308ae793d137b26a5/UQLab-user-manual-Polynomial-chaos-expansions.pdf (accessed on 25 February 2020).
- Surjanovic, S.; Bingham, D. Virtual Library of Simulation Experiments: Test Functions and Datasets. Available online: http://www.sfu.ca/$\sim$ssurjano (accessed on 1 March 2019).
- Kuschel, N.; Rackwitz, R. Two basic problems in reliability-based structural optimization. Math. Methods Oper. Res. 1997, 46, 309–333. [Google Scholar] [CrossRef]
- Loukrezis, D.; Galetzka, A.; De Gersem, H. Robust Adaptive Least Squares Polynomial Chaos Expansions in High-Frequency Applications. Int. J. Numer. Model. El. 2020, e2725. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/jnm.2725 (accessed on 25 February 2020).
- Xu, J.; Koledintseva, M.Y.; Zhang, Y.; He, Y.; Matlin, B.; DuBroff, R.E.; Drewniak, J.L.; Zhang, J. Complex permittivity and permeability measurements and finite-difference time-domain simulation of ferrite materials. IEEE Trans. Electromagn. Compat. 2010, 52, 878–887. [Google Scholar] [CrossRef]
| Parameter | Distribution |
|---|---|
| B | |
| D | |
| H | |
| E | |
| L |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loukrezis, D.; De Gersem, H. Approximation and Uncertainty Quantification of Systems with Arbitrary Parameter Distributions Using Weighted Leja Interpolation. Algorithms 2020, 13, 51. https://doi.org/10.3390/a13030051
Loukrezis D, De Gersem H. Approximation and Uncertainty Quantification of Systems with Arbitrary Parameter Distributions Using Weighted Leja Interpolation. Algorithms. 2020; 13(3):51. https://doi.org/10.3390/a13030051
Chicago/Turabian StyleLoukrezis, Dimitrios, and Herbert De Gersem. 2020. "Approximation and Uncertainty Quantification of Systems with Arbitrary Parameter Distributions Using Weighted Leja Interpolation" Algorithms 13, no. 3: 51. https://doi.org/10.3390/a13030051
APA StyleLoukrezis, D., & De Gersem, H. (2020). Approximation and Uncertainty Quantification of Systems with Arbitrary Parameter Distributions Using Weighted Leja Interpolation. Algorithms, 13(3), 51. https://doi.org/10.3390/a13030051






