1. Introduction
The rapid proliferation of data is a major challenge in many scientific and business domains: data may often be gathered faster than it can currently be processed [
1]. This applies particularly in molecular biology, where sequencing costs have fallen exponentially since the initial public genome projects, with human genomes costing less than USD 1000 [
2] in 2019. This leads to a substantial bottleneck in storing and processing the data [
3]. Initial analysis, annotation and subsequent research—perhaps targeting disease mechanisms or drug targets—all rely crucially on rapid sequence comparison.
Sequence comparison is an active and long-established branch of bioinformatics research, and here we provide only a brief sketch of the field. Broadly speaking, sequence comparison algorithms utilize one of two main strategies, although the most commonly used approaches share a number of important ideas. The most widely used approaches are based on sequence alignment, with scoring based on a generalized edit distance between the strings, with calculations relying on dynamic programming [
4,
5] or a range of heuristics [
6,
7]. The principal alternatives are so-called alignment-free methods [
8] which usually involve some indexing of the substrings or k-mers which make up the sequence, most commonly based on a bag of words model. Our example in this paper follows this latter approach but avoids direct character comparison by embedding the sequences as elements of a binary vector space. There are many alternative methods available to generate this representation, with the simplest a straightforward bit vector indicating the presence or absence of a particular k-mer in the sequence lexicon. A full survey of these alternatives is beyond the scope of the present work, but these ideas are well-known. The application of Locality Sensitive Hashing (LSH) to sequence analysis is a natural extension of its familiar use in text processing and information retrieval. Binary signature encodings of this kind have a number of advantages over alternative methods, most pertinently here the ability to encode sequences of varying lengths to a representation of the same width to enable straightforward comparison and the availability of bit-level operations for rapid evaluation of the Hamming distance. The effectiveness of these methods in sequence comparison has been demonstrated in, e.g., [
9], and related work has been considered in [
10] and elsewhere. Here we are concerned with rapid, energy-efficient and scalable computation of a very large number of comparisons.
LSH was initially introduced by Indyk and Motwani [
11] for nearest neighbor search in high-dimensional spaces, and subsequently improved and generalized by Gionis [
12] to find the nearest or the
k-nearest neighbors to detect (near) duplicates. It has been widely used in applications such as web crawlers, ensuring that only pages that contain new information are added to an existing search index [
13]. The same can be achieved for any large collection of documents [
14].
As the name suggests, LSH uses specialized hash functions, which are optimized to maintain similarities between related input data by causing hash collisions. The outputs of the hash functions form the (binary) signatures mentioned above. In general, the signatures only have to be constructed once.
In [
9] Buckingham et al. showed that LSH provides a suitable representation to support comparison of sequences with large DNA databases and analysis of the content for similarity and variation. Given this representation, the basic Hamming distance [
15] between two signatures is sufficient to determine the similarity of the underlying DNA sequence. Equation (
1) depicts the definition of the Hamming distance.
The Hamming distance of two signatures
s1 and
s2 is defined as the number of bits that differ between
s1 and
s2. Therefore, we first compute
s1 xor s2. In the result, the
one bits indicate the positions at which
s1 and
s2 differ. Subsequently, the
one bits in the result are counted; this procedure is called
population count, which is essential for many other fields of applications such as error detection or even clustering of biological sequences [
16].
This work targets a simple but realistic scenario in which 100,000 signatures of partially sequenced genomes (m) are compared to an existing database of 100 million entries (n). In this work, we are concerned only with performance, and so it is sufficient to use synthetic data of the same dimension as the biologically derived signatures. Finding the matching or nearest neighbor signatures requires , 100 billion comparisons. On a state-of-the-art workstation CPU, this process takes a few minutes, using a highly optimized application and employing specialized intrinsic functions.
Since the calculation of Hamming distances between signatures can be executed in parallel, this work focuses on leveraging the inherent parallelism of Field Programmable Gate Arrays (FPGAs) to enable greater throughput. For the results of the comparisons often only the signature indices and the Hamming distance of the best x-results are of interest. These calculations can also be parallelized and performed very efficiently on FPGAs.
This work focuses on the implementation of a scalable architecture for binary string comparisons, optimized for high-throughput with configurable bit widths.
In general, the architecture is capable of supporting bit widths ranging from 16-bit to 2048-bit. In this work, only the most significant bit widths of 128-bit and 512-bit have been analyzed in detail. However, acceleration of a variety of applications such as Google simhash [
13], computing 64-bit Hamming distances or image duplicate retrieval [
17] with 128-bit comparisons are also possible with our design. This is also the case for the above-mentioned LSH for DNA sequence analysis, for which signature lengths of 512-bit and greater may allow the representation of longer sequences.
The architecture has been designed to make the calculation units for the string comparisons as easily interchangeable as possible, to support other algorithms besides the Hamming distance.
2. Related Work
A brief overview of sequence comparison in computational biology was provided in the introduction, and here we highlight only those questions pertinent to the present study. Sequence comparison has been dominated for many years by alignment-based methods, exact algorithms which rely on dynamic programming such as the Smith-Waterman algorithm [
4] for local alignments, or heuristics such as BLAST, the Basic Local Alignment Search Tool [
6], which relies on a series of hit extension and scoring heuristics to identify rapidly the most promising matches and is highly parallel. As discussed above, the dramatic rise in the availability of sequence data has led to an increasing demand for faster and more scalable alternatives.
We have earlier considered the division between alignment-based and alignment-free approaches, but we would emphasize that performance improvements in this domain have usually relied on two main strategies: (i) careful selection of the computations that need to be performed—and equally careful rejection of those that may be avoided, thereby, limiting the computational cost; and (ii) careful attention to the underlying representation of the sequence, thus, reducing the unit cost of each comparison. BLAST is a perfect example of the former strategy, with seed matches and score-based hit extensions dramatically limiting the regions to be explored. USearch [
7] takes these ideas even further, offering database searches potentially orders of magnitude faster than BLAST for a modest reduction in accuracy. The present work, based on binary embeddings of the sequence data, belongs more to the second camp, with these encodings allowing the pairwise Hamming distance-based comparisons to be implemented through bit-level operations, offering dramatic reductions in the time required for each computation. The remainder of this paper is concerned with supporting these rapid comparisons to allow exploration of extreme-scale collections. While our work remains motivated by embeddings obtained via LSH, we again note the more general utility of the approach, there exist numerous other methods leading to a binary representation of the sequence.
In general, there are three different approaches to accelerate these kinds of computationally intensive tasks. The first is the usage of CPUs in combination with, e.g., SIMD-instructions (Single instruction, multiple data), many-core CPUs or distributed computing [
18,
19]. The second is the usage of either high-performance compute or consumer-grade GPUs as accelerators [
20,
21]. The last approach is the usage of FPGA-accelerators which, although they are not as fast as systems based on high-performance GPUs, tend to be more energy-efficient [
22,
23,
24]. However, these systems have started to reach their limits in terms of performance, therefore, current research focuses on heterogeneous and cluster-based systems, e.g., multi-GPU clusters [
25] or CPU-GPU co-systems [
26].
As noted above, the use of Locality Sensitive Hashing allows us to represent sequences through a fixed-length binary signature and to replace alignment-based scoring with the Hamming distance. Moreover, methods of this nature are alignment-free [
8], offering some advantages in scalability to large collections, and greater robustness in the presence of structural re-arrangements in the sequences being compared.
While various implementations on CPU and FPGA target architectures for calculating Hamming distances have been described in the literature, the authors are not aware of any publications that analyze the suitability of GPU architectures for this purpose.
In [
27] Pappalardo et al. published results on the possible speed of Hamming distance calculations on CPUs. They used three different lookup table (LUT)-based calculation methods, implemented in ANSI C. For the evaluation
calculations with signature lengths up to 64-bit were performed on three different platforms, an Intel Xeon, an IBM Power 5 and an AMD Opteron. The best performance with up to 167 MH/s (Million Hamming distance calculations per second) was achieved on the AMD Opteron, using its intrinsic functions for population counting.
The publications from Pedroni [
28] and Parhami [
29] on Hamming weight comparators should be mentioned here, as both implementations were used as a basis for the presented FPGA-based solution. Pedroni proposed a Hamming weight comparator with
delay (logic gate levels) and
complexity. The optimizations by Parhami reduce the run-time to
using up/down counters, achieving a complexity of
. Additionally, for the comparison of Hamming weights, a sorting mechanism is used, and only the signatures with the highest or lowest similarity are determined. Therefore, these results cannot be compared to those in the current study as here we are concerned with the set of best matches returned.
In [
30] the authors developed a method to determine the population count of the Hamming distance calculations using an LUT-based counting network, based on a Xilinx Zynq XC7Z020. The proposed solutions are either using 8- or 36-bit input vectors for the calculation. In the case of an 8-bit input vector, two LUTs are required. For 36-bit inputs two LUT stages (with 6 and 3 LUTs) and two adder stages are used. The LUTs are configured with the predefined values and pipeline registers are located between all stages to achieve high-throughput. For longer signatures, several compute units with input vectors of 8 or 36-bit are combined and the intermediate results are summed up in further adder stages. For 512-bit signatures the lowest presented combinatorial path delay is approximately 8 ns (125 MHz); for 256-bit signatures, it is about 6 ns (166 MHz). Due to an exponentially increasing number of used slices, the authors decided to not continue the experiments for signatures >256-bit.
The design proposed in [
31] is based on a population count calculation on the Xilinx 7-series DSP (Digital Signal Processor) blocks. The authors state that DSP slices should be used because they are located on most modern FPGA-architectures, but are usually unused. In their design, only one signature, with a configurable length between 16 and 2048-bit, is processed at a time. The population count itself is realized in a parallel computation by DSP blocks, with 48-bit input each. To evaluate their design, the authors used a Nexys 4 prototyping board, containing a Xilinx Artix-7 XC7A100t-3 FPGA. This approach achieved a speed-up of about 10% compared to the LUT-based design using the same target architecture while requiring less LUT.
As a follow-up from the last two implementation variants, a mixed design based on lookup tables and DSP blocks was developed in [
32]. The focus of this work was to realize population counts for relatively large signatures widths between
and
-bit. The best results were achieved with a signature length of
-bit, with one computation requiring 22 544
s.
In
Table 1 the three approaches from Sklyarov and Skliarova using FPGAs as an accelerator for population counts are summarized. The given values were based on the maximum combinational path delays. The implementations focus on the population count itself, aiming for a short delay and low resource use and not for high-throughput, which is essential for our targeted application. Therefore, these results cannot be directly compared to the proposed architecture, which also includes the data management, the
xor calculation of two binary strings and the collection and storing of multiple results.
An accelerator for Hamming distance comparison is used as the core component of the duplicate image retrieval engine proposed in [
17]. The authors state that finding and calculating the minimum Hamming distance accounts for most of the execution time of their application. A peak performance of 40 GH/s has been achieved on an Altera Stratix V FPGA running at 200 MHz, using a design with 64 parallel processing elements for the calculation of 128-bit Hamming distances.
4. Design Architecture
The design was written in a generic manner to support different signature widths via VHDL generics at synthesis-time and has been optimized for the Xilinx Virtex UltraScale+ FPGA VCU1525 Acceleration Development Kit. All FPGA designs evaluated in this work were developed using the Xilinx Vivado Design Suite Version 2019.1.
The focus was to create a scalable design that could be applied and optimized for many possible use cases. Therefore, it should not only be capable of performing one specific distance calculation but be applicable for a range of other comparison and distance measuring algorithms.
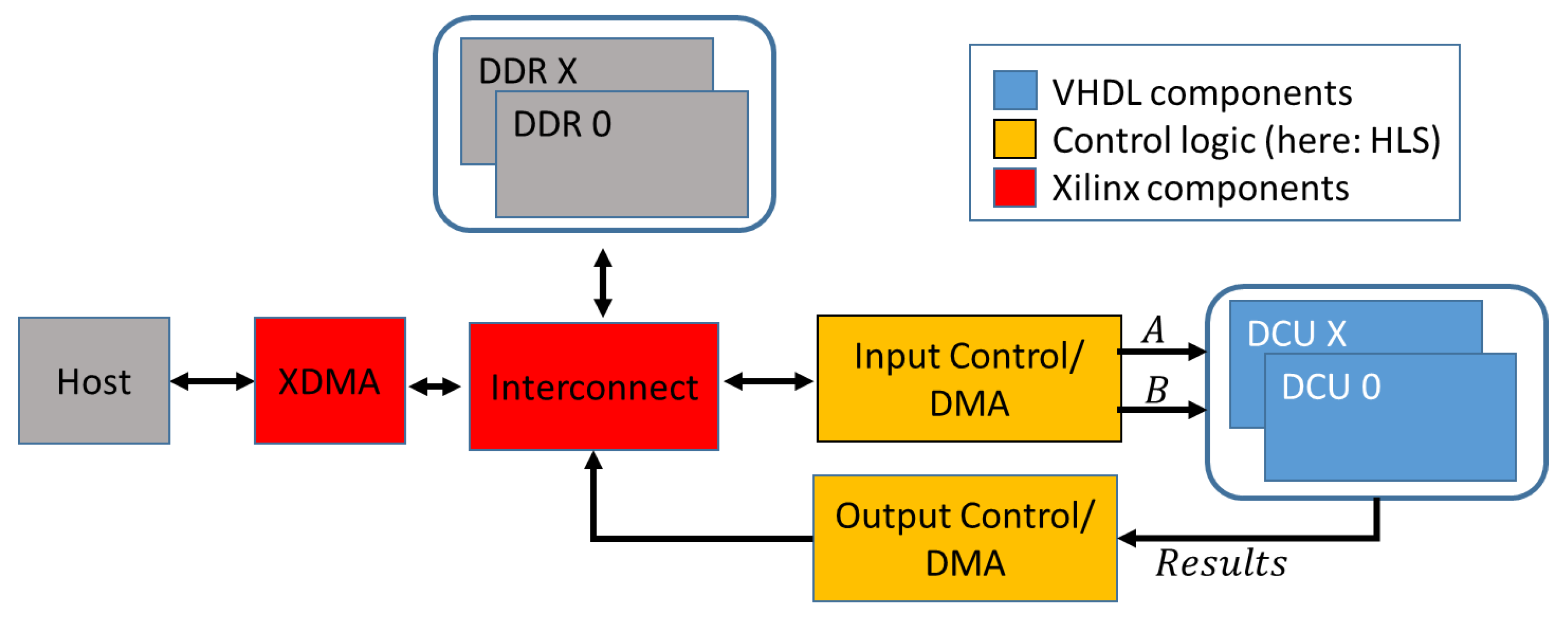
An overview of the basic design is shown in
Figure 1. The PCIe-based connection to the host is established using the Xilinx XDMA IP-Core. For optimal performance with large numbers of comparisons, the design works with streamed input signatures and results. Both, input signatures and the results can either be transmitted directly to and from the host via control units or buffered in DDR memory. Distance calculation units (DCUs) are the central calculation elements of the architecture. To ensure the best possible performance, the DCUs and all its components are completely hand-optimized and implemented in VHDL. The DCUs contain the processing elements (PE) that perform the distance calculation and result handling. For all contained components, 1547 lines of VHDL code (counted without comments and blank lines) were implemented. General parameters like signature length, number of used PE, buffer FIFO sizes and the number of combined results in every collector stage can be configured as generic parameters. The design will automatically adjust to the given values. Since the number of logic resources, and thus the maximum number of PEs on the FPGA is limited, it was decided to store one signature of the query locally in each available PE; these signatures are therefore called
static signatures in the following. The signatures of the database are streamed between the PE in every clock cycle and are called
dynamic signatures.
4.1. Distance Comparison Unit
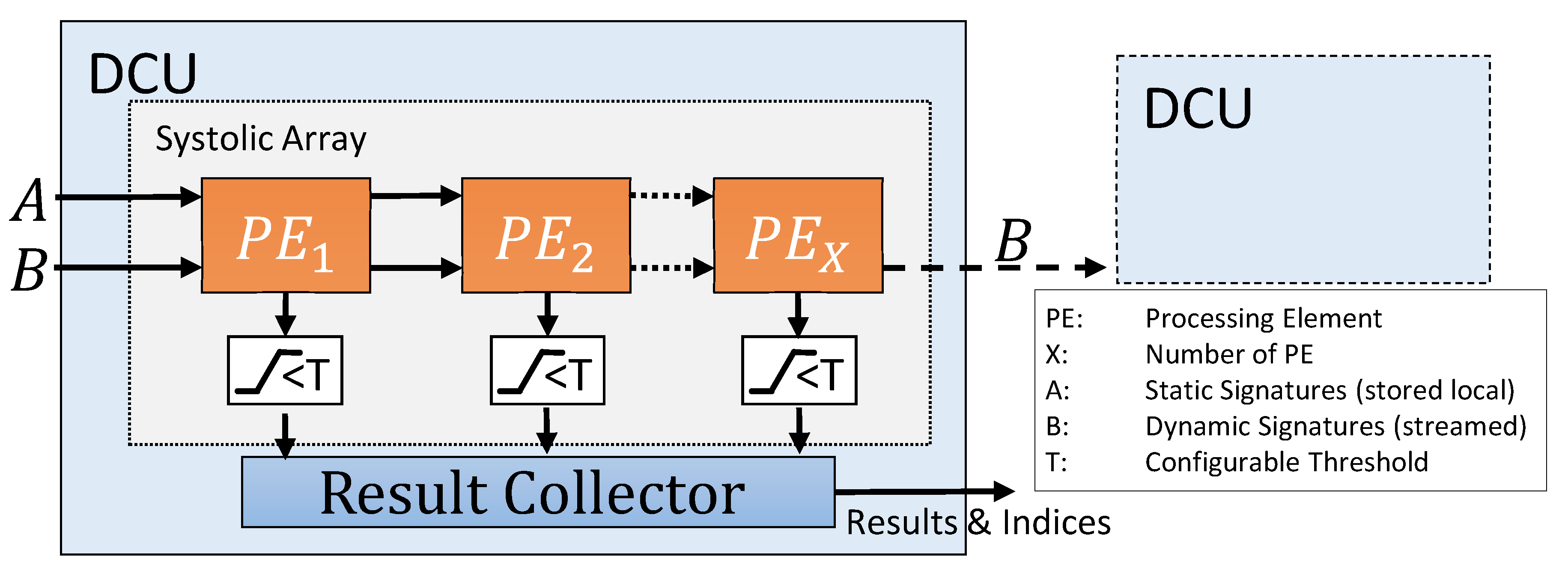
Every DCU contains a generic amount of processing elements, working in a systolic array. The results calculated by the PE can be filtered by a threshold checker and are then passed on to the result collector unit.
In the used streaming-based architecture, both signatures are only connected to the first PE of every DCU, shown as
in
Figure 2. However, static and dynamic signatures are treated differently during further processing. Static signatures are passed via shift register to the next PE until one signature is assigned to each PE and stored there locally. The dynamic signatures are also streamed to the first PE and sent from there to the next PE. Each time a dynamic signature is valid, the distance between it and the static signature of the PE is calculated. With this data flow concept, a new incoming dynamic signature can be processed by the design in each clock cycle. To avoid delays, a FIFO for the dynamic signatures is used to buffer the inputs.
To accommodate lots of PE instances on the FPGA, it was necessary to constrain the maximum fanout of the reset signal; otherwise, the routing of the design was failing quickly due to timing violations. Furthermore, the input clock for the PE is gated by a BUFGCE (BUFG with clock enable) from the AXI clock, to further improve the fanout. The enable for the BUFGCE is generated by the result collector unit and disabled when no further results can be handled and the design needs to stop producing new results.
Since the space for PE on the FPGA is limited it is likely that not all static signatures can be processed in one iteration. Therefore, the PEs have to be reinitialized when all calculations have finished and dynamic signatures have to be streamed again. This way the static signatures are partially processed, while the dynamic signatures are streamed multiple times. Despite the very limited local storage, the streaming-based design results in high-throughput, which directly depends on the number of parallel used PEs.
Using this technique it is possible to calculate all distances between a large number of signatures on one FPGA. Furthermore, multiple FPGAs can be used to work in parallel on the sequences. In such a setup, every FPGA would process different static signatures while the dynamic signatures are streamed between the FPGAs. This minimizes how often the dynamic signatures have to be streamed from the DDR. The DCU-based design also enables the partitioning of the design, e.g., for applying one DCU to every available super logic region (SLR) on an FPGA.
4.1.1. Processing Elements
The central components of the design are a generic number of processing elements, working in a systolic array. For the interconnection of the two signatures in the design and their associated indices, the data streams themself and shift ports are required. When the shift signal of the static signature is set, the signature and corresponding index is valid and stored locally in the PE. The previously stored value and index are transmitted to the next PE in the systolic array. The procedure is the same for the dynamic signature. In addition, a valid shift signal also triggers the calculation of the distance between the stored static and incoming dynamic signature.
The results are output simultaneously with the indexes of the signatures that produced the result. Currently, the size of one result is 64-bit, where 10-bit are used for the result and 27-bit each are used to store the index of the input signatures.
This design allows for the calculation function to be adjusted to any comparison between two binary strings, while the rest of the design can remain unchanged.
4.1.2. Use Case: Hamming Distance Processing Element
In this design, Hamming distance calculation was implemented inside the processing elements (see
Figure 3). While the
xor comparison between two signatures can be evaluated on the FPGA in one clock cycle, the more complex part is the counting of the ones bits in the
xor result, which gives the resulting Hamming distance. The implementation of this population count was inspired by the LUT-based Hamming weight counter, developed by Sklyarov and Skilarova in [
30]. Therefore, the calculation is performed in a generic adder tree structure, which is automatically adjusted to any given input signature length. The first tree stage was optimized to use the 6-Input LUTs of the Xilinx 7-Series FPGAs. In the next tree stages, two results are added together and transmitted to the subsequent tree stage; this flow is repeated until the final result is calculated. Pipeline registers are used between all tree stages to ensure optimal timing. In total
adder stages are used.
4.1.3. Threshold Checker
Since in practical applications only results with a low Hamming distance (highly similar signatures) are of interest, the threshold checker is used to filter the results by comparing them with a threshold value, which can be set at runtime. The advantage is that very long distances, which are not of interest, are omitted, saving memory and time when the results are read. The threshold can be set dynamically at runtime, which offers the possibility to read all results, e.g., for testing purposes.
4.1.4. Result Collector
Besides the calculation, another major challenge of the design is the collection and storage of results. After the results have been filtered by the threshold checker, they are forwarded to generic collector units that control the storage process. All relevant results from the PE are combined in a tree structure and at the end buffered in a single FIFO.
Since it depends on the input signatures and the applied threshold value, it is not possible to predict how many valid results will be found and need to be stored. To solve this problem a tree structure of collector units was implemented, each containing a priority arbitrator and a FIFO. In a standard configuration, each collector unit will combine the results of four units from the previous tree stage. Though, the number of combined results is easily adaptable by a generic parameter for optimizing designs. The first collector stage contains one input FIFO for every PE in the design to buffer the results from the threshold checker. Further stages with an automatically instantiated number of collecting elements are instantiated recursively until all results are merged into a single output FIFO.
As soon as a FIFO contains data, a request is sent to the connected priority arbiter of the next tree stage. The arbiter uses the
Round Robin [
35] scheduling to grant access to one of the requesting FIFOs from the previous stage. The results are read from the FIFO and written to the FIFO in the next collector stage (see
Figure 4). If a FIFO in the tree reaches the almost full state, a special priority request is sent to the arbiter. Priority requests will always be treated first from the arbiter to prevent a FIFO from running full. If more than one priority request is active, all of them will be scheduled as described above. If priority scheduling cannot prevent a FIFO from running full, the connected arbiter (same stage) that handles the input will be disabled. This way no further input can be written to the FIFO. This allows for parts of the tree to be disabled, propagating from bottom to top, until one of the FIFOs with a direct connection to the PE is running full. In this case, the entire calculation is stopped until there is enough space available to prevent data loss. The basic structure of the priority arbiter used was developed by Grigori Goronzy [
36] and has been published under the MIT License. For this design it was extended to include the mechanism of priority scheduling.
4.2. Control Logic
While it is possible to address the design components directly from the host via an AXI4 slave interface, it is recommended to store input signatures and results in a dedicated DDR memory. The communication overhead with the DDR is much lower than with the host. Thus, the static signatures in the processing elements can be easily managed and exchanged, while the dynamic signatures can be restreamed several times.
In this work, the Xilinx XDMA IP-Core is used to communicate with the board and to access the attached DDR. A High-Level Synthesis (HLS) core, configured by software, has been developed to transmit the input signatures from the DDR memory to the calculation units. In addition, the core also defines basic configurations, such as the threshold size. When all dynamic signatures have been streamed through the processing elements, the core automatically sends new static signatures and restreams the dynamic signatures. This is repeated until all available static signatures are processed.
Another HLS core was developed to handle the transfer of the results to the DDR. It reads the results from the result collector FIFO as soon as it contains data and transmits them to the connected DDR.
4.3. Connection/Design Options
The design has been constructed in a scalable way to enable an optimized implementation on different or multiple FPGAs and for several use cases.
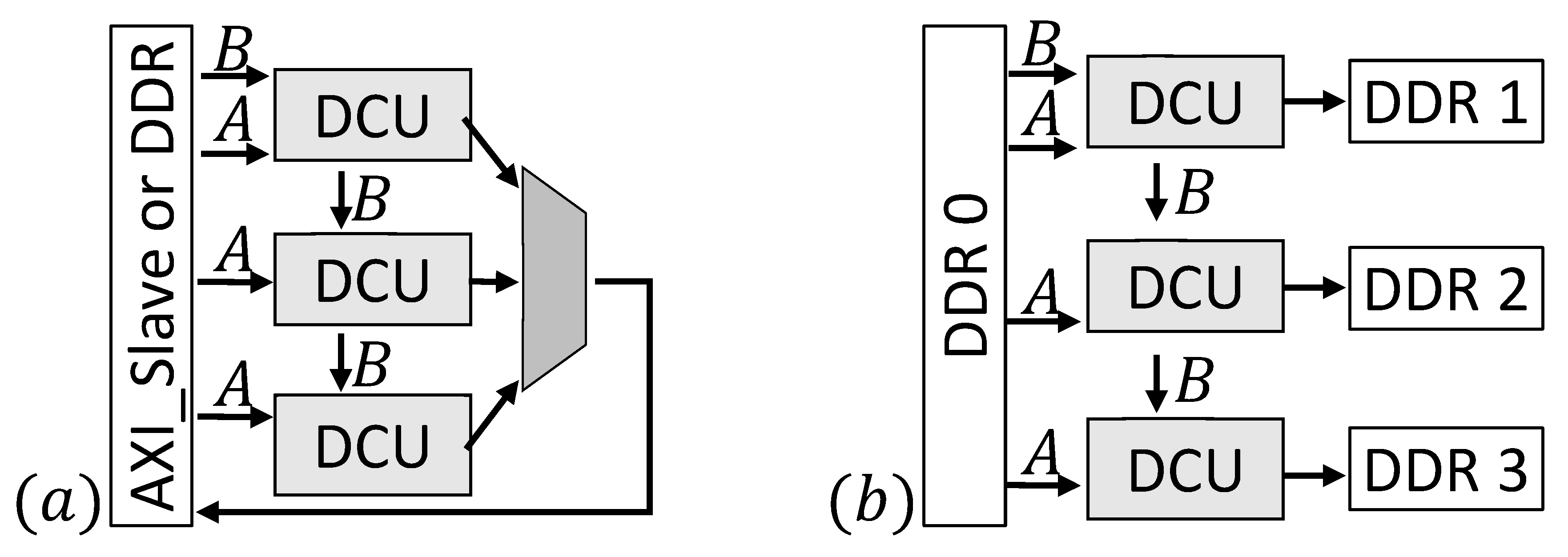
Figure 5 sketches two exemplary designs. Depending on the FPGA-architecture it can be useful to implement more than one DCU, e.g., for FPGAs containing SLRs. In this case (
Figure 5a), a part of the static signatures (one for every processing element) is sent to every DCU and the dynamic signature is streamed between the daisy chained units. This implementation also allows the use of a different number of processing elements for each DCU, e.g., to save more space for the control structure in one SLR. Input signatures are streamed directly via a custom AXI slave interface or from an onboard DDR. Results of all DCUs are combined and send back to the AXI slave or DDR. Furthermore, it is possible to use more than one DDR. In example (
b) (
Figure 5b), four DDRs are used to provide the input data and store the results. The input signatures are stored in one DDR while the remaining three DDRs are connected to one DCU each to store the results.
Example (b) is an appropriate solution for use cases where many results can be expected. To find only a few results in a huge database example (a) in combination with more DDRs to store the input signatures is a better choice. The design developed for this work uses one DDR and is connected similar to example (a).
4.4. Performance Considerations
All components of the architecture were designed for maximum throughput. For validation, the parameters of individual components, which influence the overall system performance, here initialization interval, latency, and throughput, have been determined using simulations on a register transfer level (see
Table 3). All components of a DCU allow for initializing one new computation per clock cycle, which is indicated as
Initialization Interval in
Table 3. Except for the population count, all components have a latency of 1 clock cycle. The population count is calculated in a tree structure and therefore, the latency depends on the signature width.
The number of results to be stored depends on the input data and the configured threshold value. Each valid 64-bit result of a PE, which passed the threshold check, is buffered in a FIFO and from there read by the first collector stage. In the used default configuration, each collector stage merges four result streams into one and passes them to the next collector stage until all results are combined into a single FIFO, from where it is written into the DDR. In the worst-case scenario, where all results pass the threshold check and only 8 results can be written to the DDR per clock cycle (512-bit per transfer), the collector is the bottleneck. In the considered use-case scenario, only a few results pass the threshold checker which is why the internal FIFOs do not run full and no pipeline stalls are triggered. In this case, the initialization interval is still one and the latency is determined by the pipeline depth to . The DDR memory controller of the design offers a 512-bit AXI interface, running at 300 MHz. Hence, the theoretical throughput of read and write transactions is . The practical achieved performance using Direct Memory Access (DMA) is with about 144 Gbit/s for sequential read and about 136 Gbit/s for sequential write transactions. Applied to the described use-case this means that 281 million signatures per second can be transferred from the DDR to the DCU and 2,125 billion results per second can be written to the DDR.
5. Results
The proposed generic system architecture for binary string comparisons allows quick adaptation via Vivado IP-Integrator to a variety of possible applications, with respect to parameters such as bit widths, the number of processing elements, clock frequency and internal buffer sizes. Today’s FPGAs, such as the Xilinx XCVU9P, used in this work, offer enough resources to integrate several hundred of the implemented processing elements. Since the synthesis times for complex designs increase significantly with the number of processing elements and can often take several hours, only selected configurations were created for this work to demonstrate the scalability of the system architecture. Depending on the configuration, synthesizing the design, presented in this work took between 2 h (1 DCU and 64 PE for 512-Bit signatures) and 5 h (3 DCU with 128 PE each for 512-Bit signatures).
5.1. Validation
After the hardware components of the design have been carefully verified by simulations on a functional level, the PCIe-based Xilinx VCU1525 card was used for testing and performance evaluation. The bitstreams have been generated using Vivado 2019.1 with all configurations for synthesis and implementation set to default. The Xilinx board was used in a bare-metal manner with a Xilinx XDMA as an x16 Gen3 PCIe endpoint. The workstation (Intel Core i7 CPU 870 @ 2.93GHz with 12 GByte DDR-3 RAM) communicates via the Xilinx XDMA Linux kernel module with the accelerator device. The test application supplies the proposed architecture, configured for Hamming distance calculation, with randomly generated signatures, configures the HLS-based management system, reads back the results, and compares them with a golden master computed by the CPU. The data sets used contain one million static and ten million dynamic signatures, resulting in a total of comparisons. Since the number of processing elements on the FPGA is limited, the static signatures must be processed in chunks, resulting in several calculation cycles. In each cycle, static signatures are loaded into the available processing elements and in each run, the dynamic signatures are streamed completely from the DDR, by the HLS-core. To cover many relevant test cases and especially trigger pipeline stalls caused by FIFOs running almost full in the collector stages, different thresholds ranging from 0 (only exact matches pass) and 512 (all results pass) have been tested.
5.2. Performance
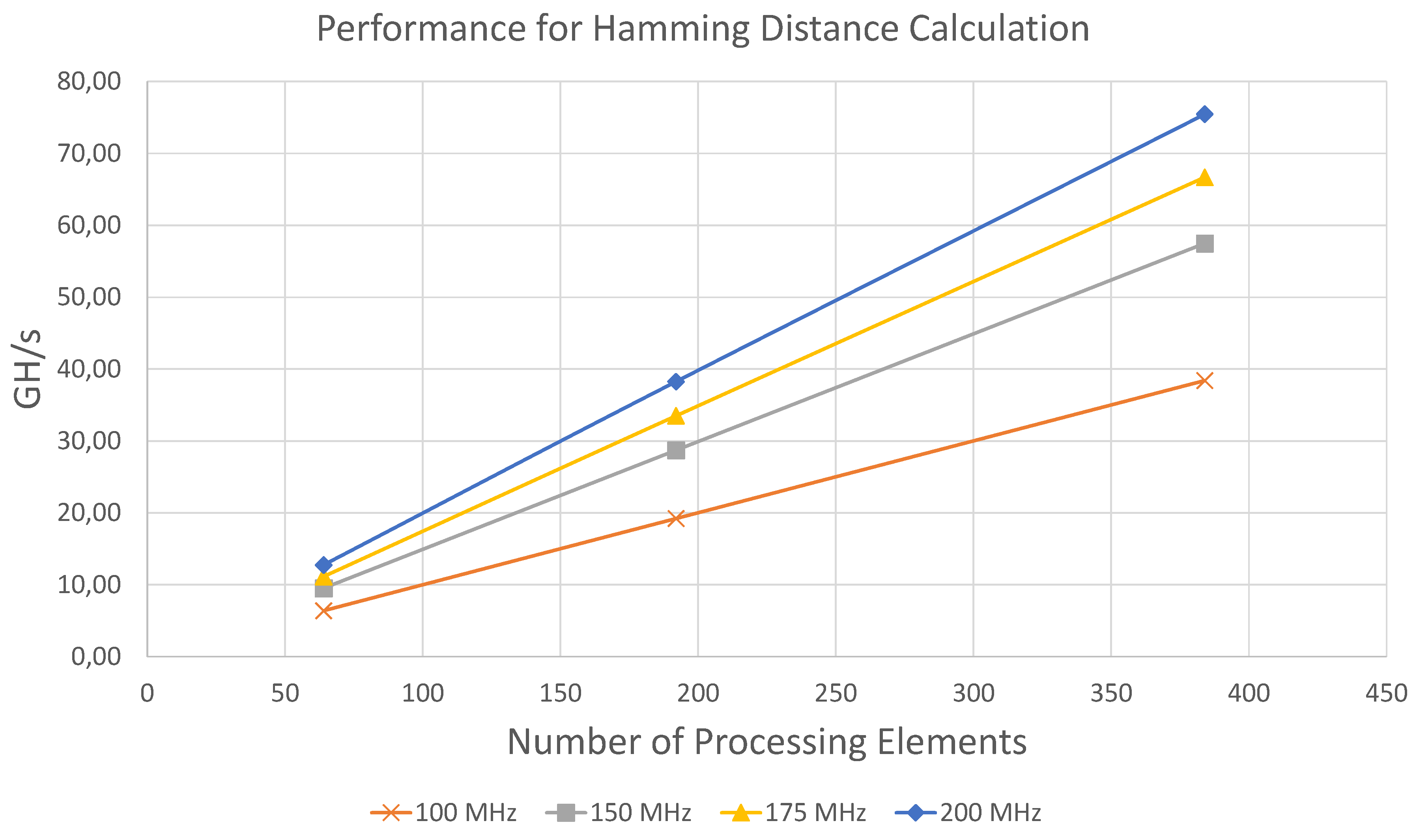
All performance measurements were conducted with the above-mentioned data set, consisting of one million static and ten million dynamic signatures. For time reasons, only configurations with 512 bit width, which are most relevant for the application under consideration, could be included. Using a threshold value of 205 about 0.00025 % (24.75 million) of all results passed the filter and were written to the DDR memory. Per iteration (streaming the dynamic signatures through all available PE) each static signature produced approximately 25 valid results. The calculation times were measured including all data transfers from and to the host, but without validation of the results, as this validation is not required during normal operation in the target application.
The achieved performance for different configurations are displayed in
Table 4 and in
Figure 6.
The results show that the performance of the architecture scales linearly in terms of the number of processing elements and the clock frequency. For all configurations the measured performance is within 98.2% to 99.99% very close to the maximum theoretically achievable throughput, which is determined by . The highest throughput in terms of compared bits per second was achieved using 384 PE at 200 MHz with 38.63 Tbit/s.
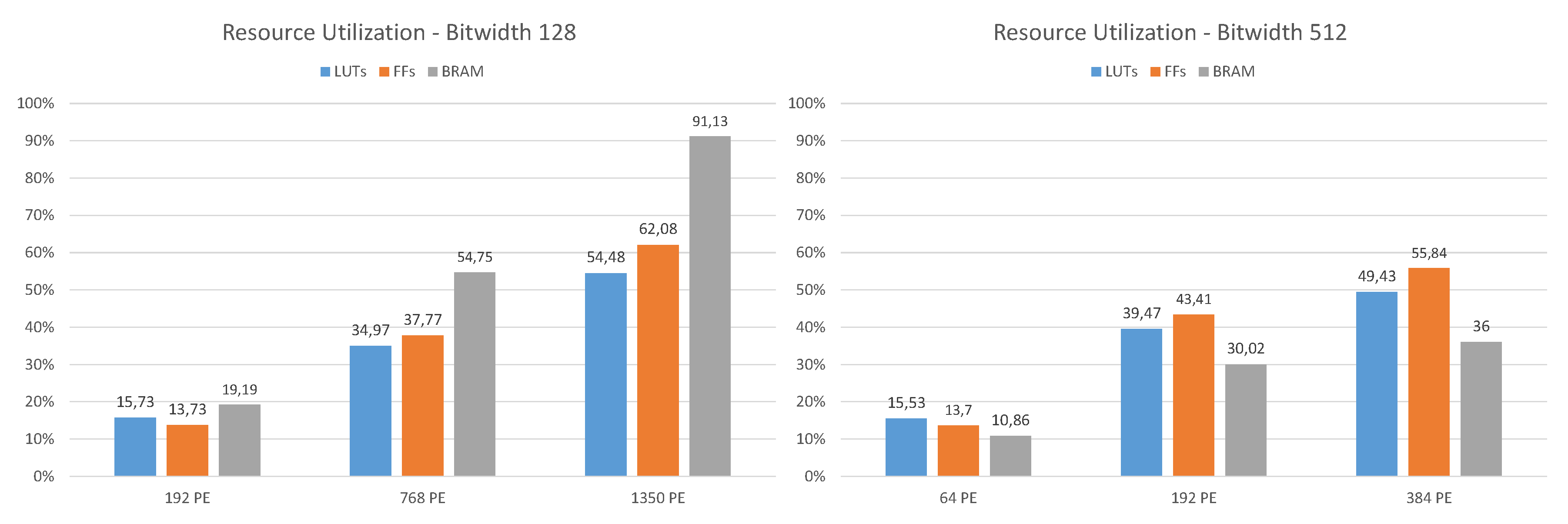
5.3. Resource Use
In
Figure 7 the resource utilization for different design configurations with 128 and 512-bit signature Hamming distance calculations at 200 MHz is shown. Typical for FPGAs, the occupied configurable logic blocks (CLBs), the basic cells, do not scale with the size of the design. The higher the FPGA utilization of a design, the denser the CLBs are packed. A configuration for 512-bit and 512 PE at a clock frequency of 150 MHz has also been synthesized. The implemented design revealed a few timing errors within the PCIe endpoint and was therefore not considered for the measurements. In this case both the LUT and FF utilization were about 65%, the BRAM usage increased to 41.2%. Especially for design configurations with a high number of PE (bit width 128, 1150 PE), it is noticeable that the available BRAMs (2160 for XCVU9P) become the limiting resource. This can be explained by the fact that the outputs of the PE containing the results are buffered via a FIFO and then further processed by the result collector, whereby these FIFOs each use one BRAM. For the examples shown here, the standard collector configuration where four results are combined in every collector unit was used.
Table 5 shows the LUT and BRAM utilizations for Hamming distance processing elements for 128-bit and 512-bit signatures. With increasing bit lengths the adder stage, which has five stages for 128-bit and seven for 512-bit, does not have a great impact on the scalability of the system. For a design with a bit width of 512 and 384 PE almost 50% of the available LUTs of the FPGA are occupied, which limits further scaling of this configuration in terms of parallelism.
Additionally, the resource utilization of central architecture components (compare
Figure 1) is depicted in
Table 6. For a moderate sized design, about 10% of LUTs, 3% of FFs and 5% of BRAM are required, leaving a significant portion of the FPGAs resources for the actual calculation units. As mentioned in
Section 4.3, more DDR memories can be used to speed up storing the results. With each DDR requiring about 1.6% of the LUTs, one DDR can be added in trade for about 17 PE of 512-bit or 85 PE of 128-bit.
As mentioned in
Section 4, the proposed architecture can easily be tailored towards the used target FPGA. This includes manual placement optimizations by splitting up one large DCU into multiple smaller DCUs. The smaller DCUs are interconnected and the dynamic data stream is passed from one to another in a daisy-chain. Not splitting the designs resulted in timing errors, especially when the required control signals had to pass SLR boundaries. An optimized design for an XCVU9P-2 FPGA uses three DCUs, matching the number of available SLRs in the FPGA.
Figure 8 shows the floorplan of a fully routed design including three DCUs, each placed in a separate SLR. Placing each DCU in its own SLR resulted in a significant reduction of timing and routing issues, thus increasing the number of possible PE. So far no benefits have been observed from using more than one DCU per SLR.
5.4. Energy Consumption
For the example design configuration with 512-bit signatures, 200 MHz and 384 PE the Vivado power estimator calculated a power usage of 24.4 W for the FPGA. The energy consumption was in the same range (
) for other configurations. Due to technical limitations it was not possible to measure the power consumption of the entire accelerator card. A reasonable estimate for the total system power usage can be calculated as depicted in Equation (
2). In the equation a power consumption of 4 W for the DDR and 9 W for the board infrastructure are assumed, additionally, an uncertainty factor of 2 W is included as well as a power supply loss factor of 0.7.
Using the performance listed in
Table 4 and the estimated power consumption of 50.7 W an energy efficiency of 1.49 GH/s/W is calculated.
6. Discussion and Future Work
A scalable streaming-based system architecture for high-throughput bit string comparisons on FPGAs has been presented. The proposed architecture can be easily adapted to the needs of the application in terms of applied distance metric, bit widths and parallelism. It is highly optimized towards FPGA architectures in general and the Xilinx Virtex UltraScale+ architecture in particular. Using 512-bit signatures and 384 PE in parallel running at 200 MHz the proposed design achieves a performance of 75.45 billion Hamming distance comparisons per second (GH/s), which is very close to the theoretical peak performance of 76.8 GH/s. The throughput of up to 38.63 TBit/s significantly outperforms all other published implementations, which focussed on single population counts for bit width between 16 and 1024, rather than optimizing for throughput and parallel processing. For example in [
30] for a 512-bit LUT-based population count running at 125 MHz a performance of 64 GBit/s was achieved, which is nearly by three orders of magnitude slower than our implementation which was measured with data transfers included. Since there were no implementations optimized for throughput, the authors created reference implementations for CPU and GPU leveraging the platforms intrinsic (CPU) and parallel programming (OpenCL). The authors FPGA-based implementation outperforms the CPU by a factor of 86 and the GPU by a factor of 5. Furthermore, when energy efficiency is considered, a reasonable estimation shows that the FPGA design (1.49 GH/s/W) is six times as efficient as the GPU implementation (224.06 MH/s/W).
The architecture presented is well suited to serve as a starting point for future research, from the perspective of developing configurable hardware systems of general utility and as a foundation for a scalable high-throughput system for biological sequence comparison. At this point, the architectural bottlenecks remain largely unknown and we have yet to investigate the scalability of the design for alternative distance metrics, and indeed to examine other domains employing the Hamming distance. In the context of binary signature-based comparison of molecular sequences, we will in future work more closely consider the nature of the data set and its relationship to the optimal signature width, with a design space exploration informed at each stage by the characteristics of the sequence data set and its encodings. There remains some possibility that for large datasets focused on a particular taxonomic group—such as the 43,000 Staphylococcus aureus genomes present in Staphopia [
37]—that the signature densities may deviate from the assumption of uniformity.
For example, it is not yet known, where the actual bottleneck is located and related to that, how well the design scales with alternative distance metrics. For this reason, active research on the architecture should be pursued, i.e., after an extended design space exploration, e.g., with various bit widths has been performed. During these extended test series, the energy consumption of the system will be measured as well. Returning our focus to the architectural components, we note that the DDR of the accelerator board delivers 512-bit data every clock cycle and is driven by a 300 MHz clock. Thus, if the design clock frequency can be increased to 300 MHz, the peak performance for 384 PE, 512-bit signature Hamming distance calculation is expected to rise to over 120 GH/s. Since it has been shown that the performance scales linearly with the number of used processing elements, it needs to be investigated, if more PE can be realized with the given FPGA resources. One possible solution might be to save LUT resources in the adder stages of the population count by combining LUT-based ternary adders and DSP slices. The number of used LUTs could also be reduced by redesigning the first stage of the hamming distance PE and combining xor and addition of two 3-bit inputs in one LUT. Furthermore, the LUTs in the following additions could be substituted by DSP-based adders. The best possible outcome would be, if both the clock frequency and the number of PE could be increased simultaneously.
Additionally, the implementation of additional distance metrics (e.g., Euclidean distance) using the presented architecture is planned. We also intend to optimize the design for further application scenarios, e.g., finding the best X-matches in a large database. For such scenarios, it might be of interest to extend the architecture with a sorting mechanism for results. It could also be worthwhile to investigate optimization strategies on other FPGAs, especially small and low-cost devices. Furthermore we would like to analyze how the scalability behaves also beyond the limits of single FPGAs in an FPGA-cluster.