Figure 1.
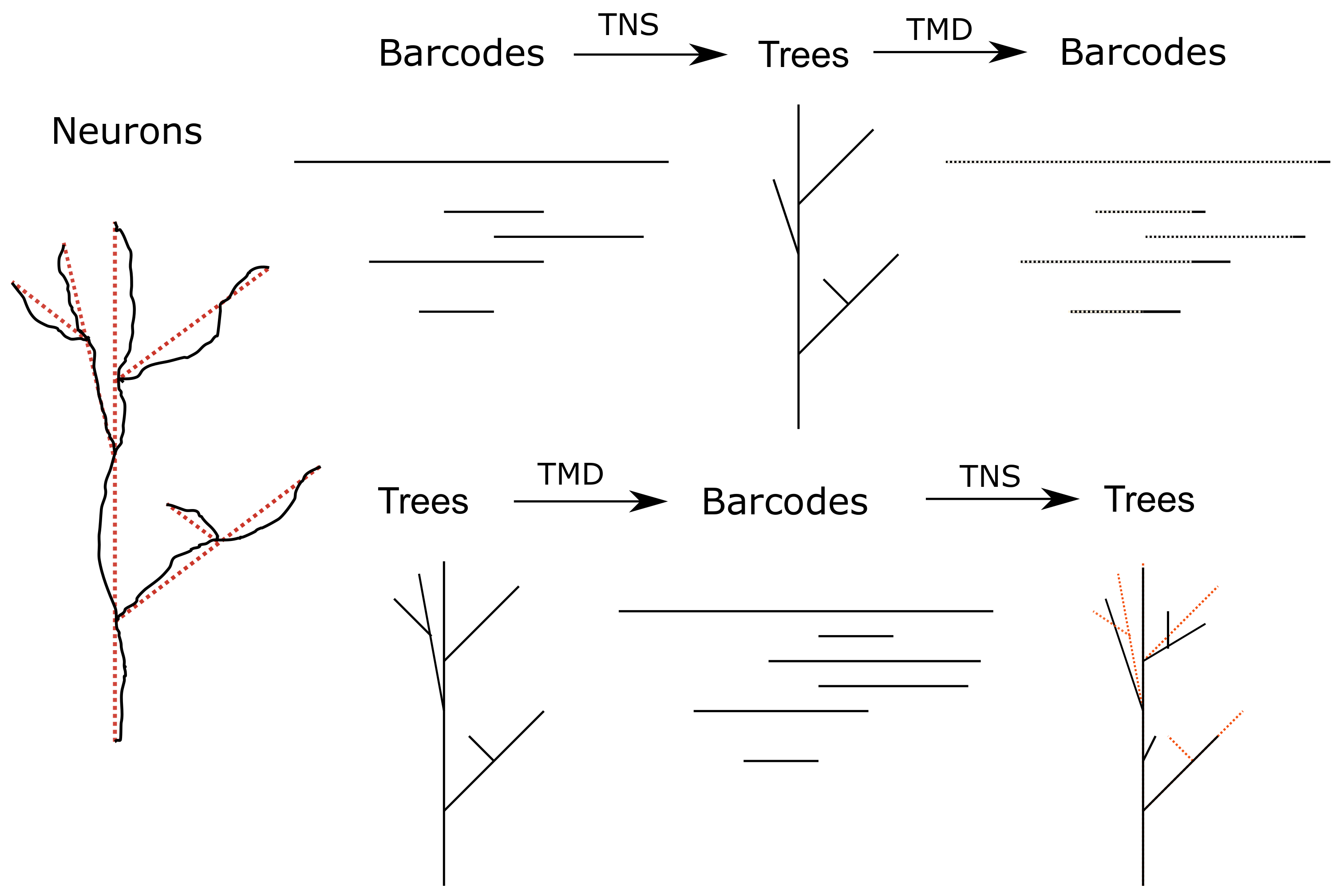
The two composites of TMD and TNS. (Left) An illustration of how a neuron (black) is modeled as a tree (dashed red lines). We describe this process and how to extract a barcode from a tree in
Section 2.3. (Top) The composite
applied to a barcode
B. The new barcode
is indicated in dashed lines on top of the barcode
B on the right. We show in
Section 4 that the barcodes
B and
will almost certainly be very similar and quantify this similarity. (Bottom) The composite
applied to a tree
T. The tree
T that we start with is indicated in dashed red lines under the new tree
. The trees
T and
can be quite different combinatorially, as seen on the right.
Figure 1.
The two composites of TMD and TNS. (Left) An illustration of how a neuron (black) is modeled as a tree (dashed red lines). We describe this process and how to extract a barcode from a tree in
Section 2.3. (Top) The composite
applied to a barcode
B. The new barcode
is indicated in dashed lines on top of the barcode
B on the right. We show in
Section 4 that the barcodes
B and
will almost certainly be very similar and quantify this similarity. (Bottom) The composite
applied to a tree
T. The tree
T that we start with is indicated in dashed red lines under the new tree
. The trees
T and
can be quite different combinatorially, as seen on the right.
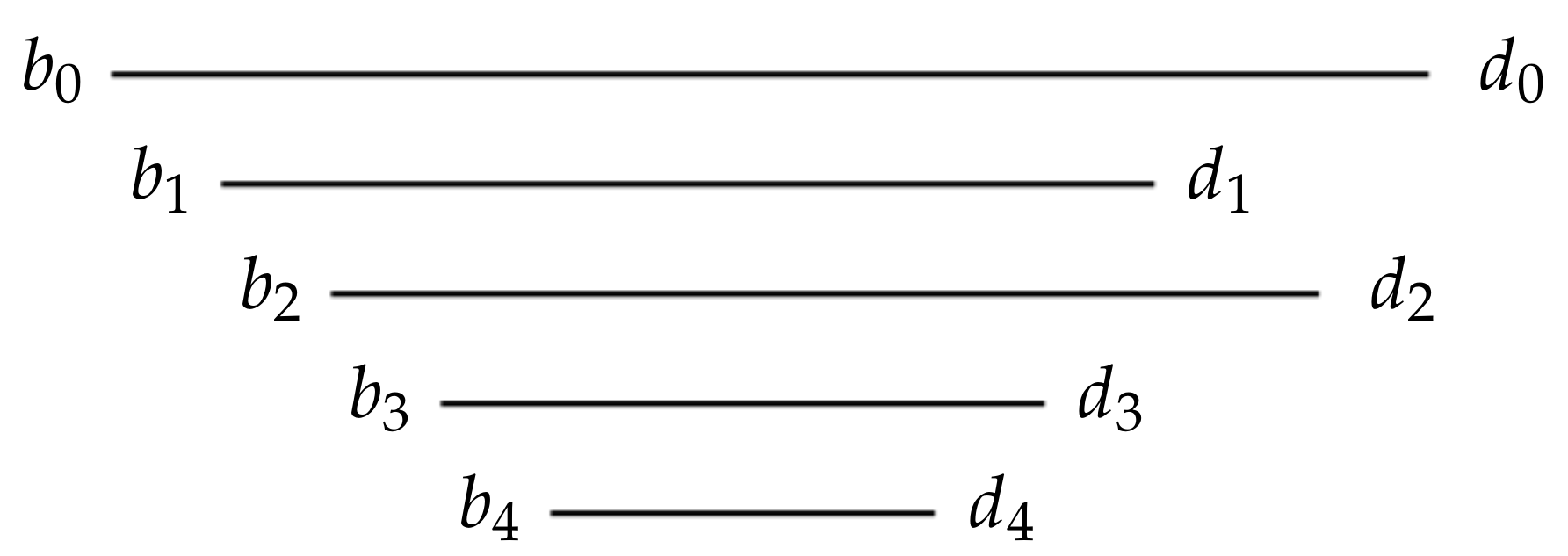
Figure 2.
A strict barcode belonging to the equivalence class . One bar contains all the others. The remaining bars are ordered by their birth times . Similarly, the deaths are ordered , leading to the notation .
Figure 2.
A strict barcode belonging to the equivalence class . One bar contains all the others. The remaining bars are ordered by their birth times . Similarly, the deaths are ordered , leading to the notation .
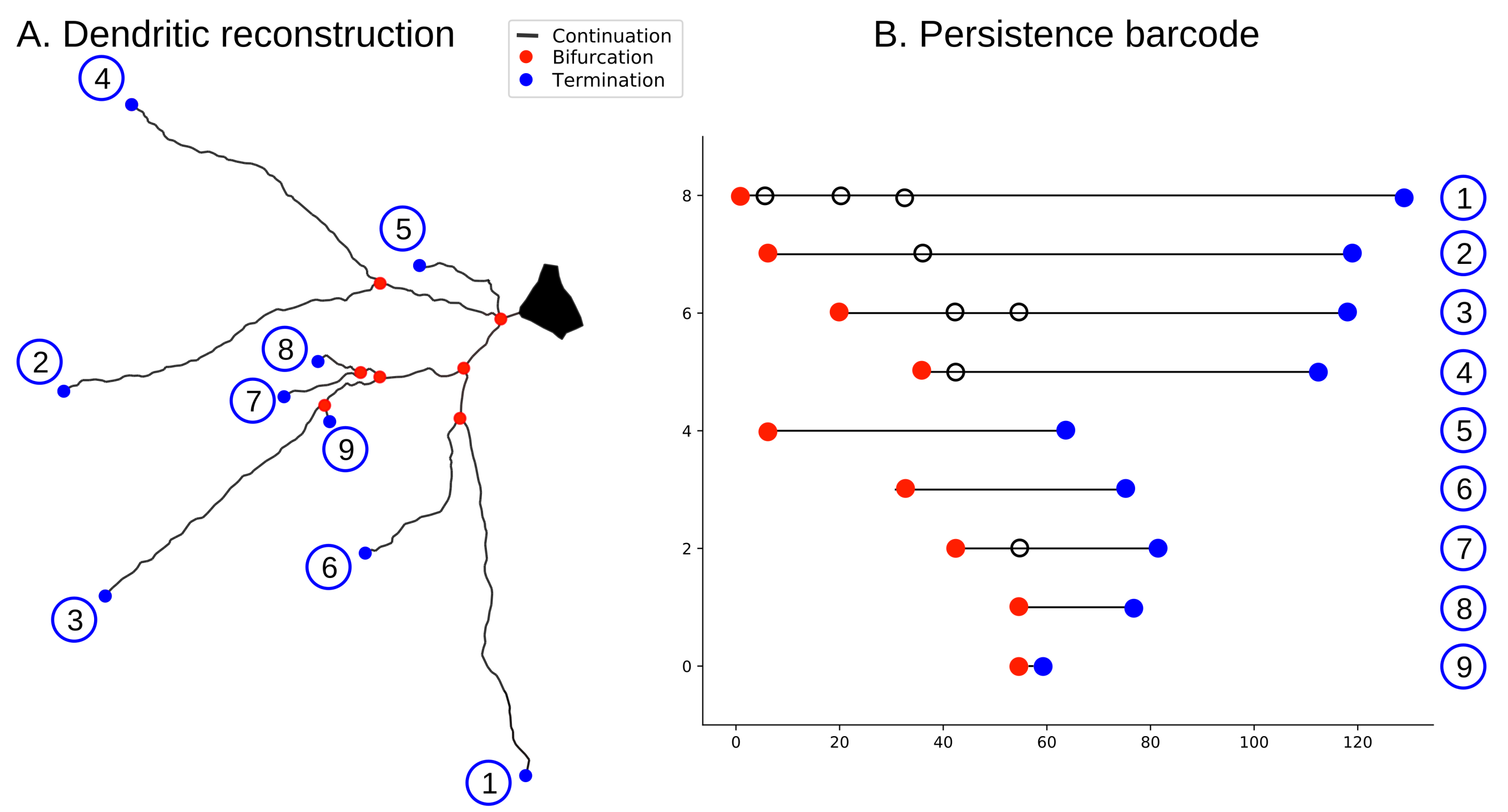
Figure 3.
The algorithm to encode a tree structure as a persistence barcode. (A) neuronal tree; (B) persistence barcode generated with TMD. Each branch in the tree (A) corresponds to a bar in the barcode (B); the circled numbers encode the correspondence between branches and bars. Terminations are shown in blue, bifurcations in red, and branches in between in black.
Figure 3.
The algorithm to encode a tree structure as a persistence barcode. (A) neuronal tree; (B) persistence barcode generated with TMD. Each branch in the tree (A) corresponds to a bar in the barcode (B); the circled numbers encode the correspondence between branches and bars. Terminations are shown in blue, bifurcations in red, and branches in between in black.
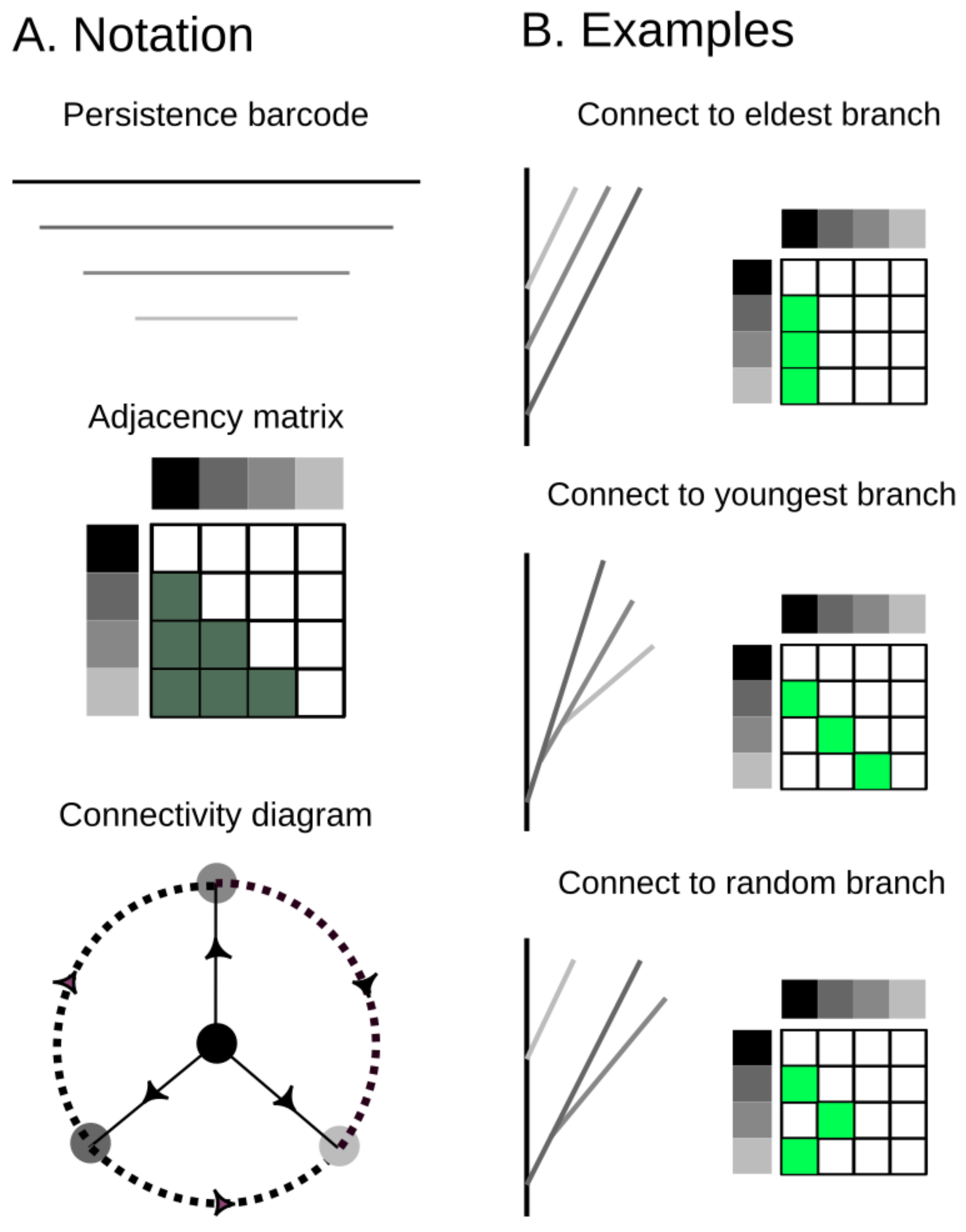
Figure 4.
A strict barcode, whose bars are ordered according to birth times (greyscale), defines a unique ordering of death times. This ordering and the Elder Rule constrain the possible combinatorial types of trees that can be realized from this barcode. (A) the notation that will be used in this paper from a barcode that corresponds to an adjacency matrix of possible connectivities. Equivalently, the possible connectivities are presented in the connectivity diagram; (B) examples of possible tree realizations from branches that connect to the longest one (top) to random (bottom).
Figure 4.
A strict barcode, whose bars are ordered according to birth times (greyscale), defines a unique ordering of death times. This ordering and the Elder Rule constrain the possible combinatorial types of trees that can be realized from this barcode. (A) the notation that will be used in this paper from a barcode that corresponds to an adjacency matrix of possible connectivities. Equivalently, the possible connectivities are presented in the connectivity diagram; (B) examples of possible tree realizations from branches that connect to the longest one (top) to random (bottom).
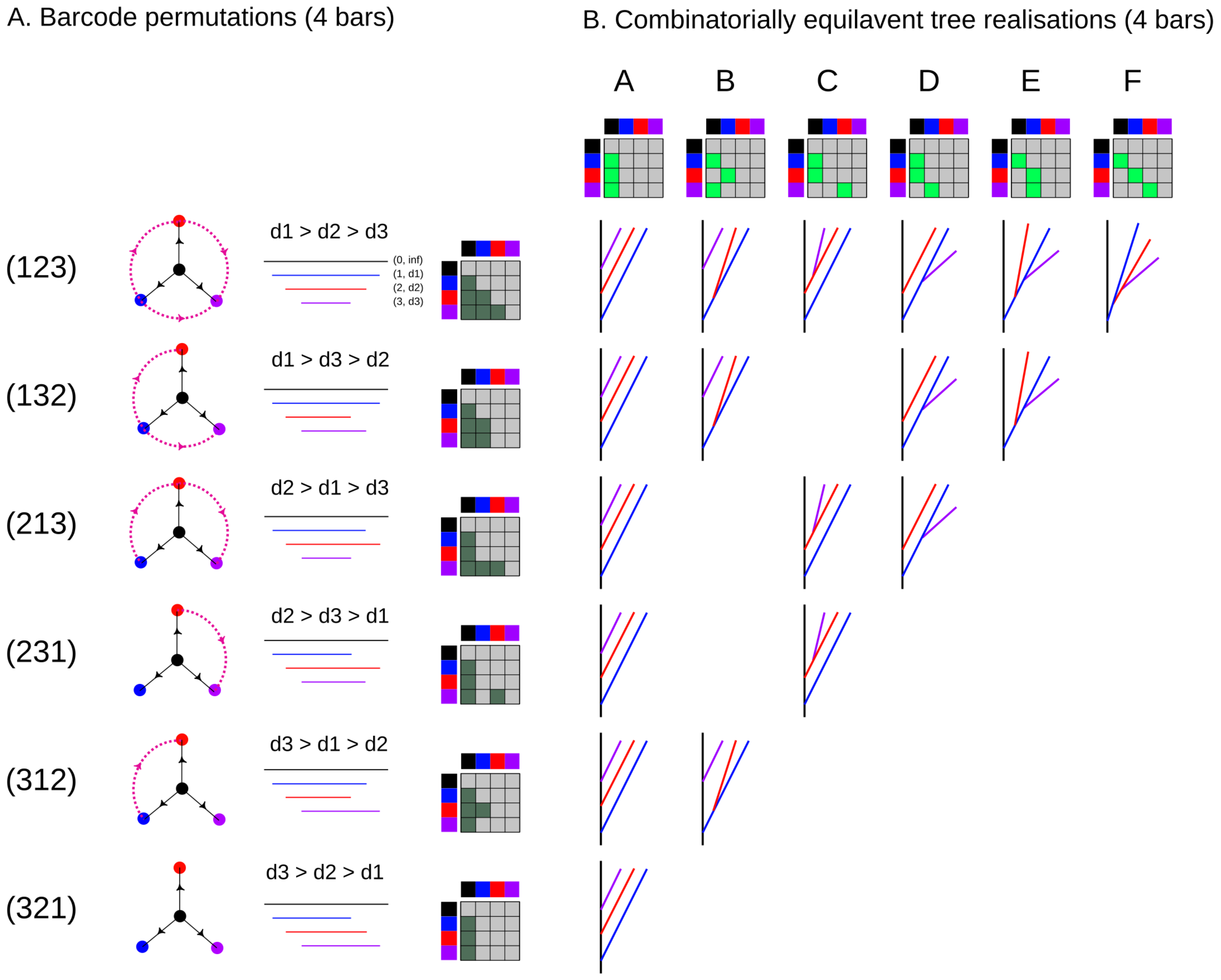
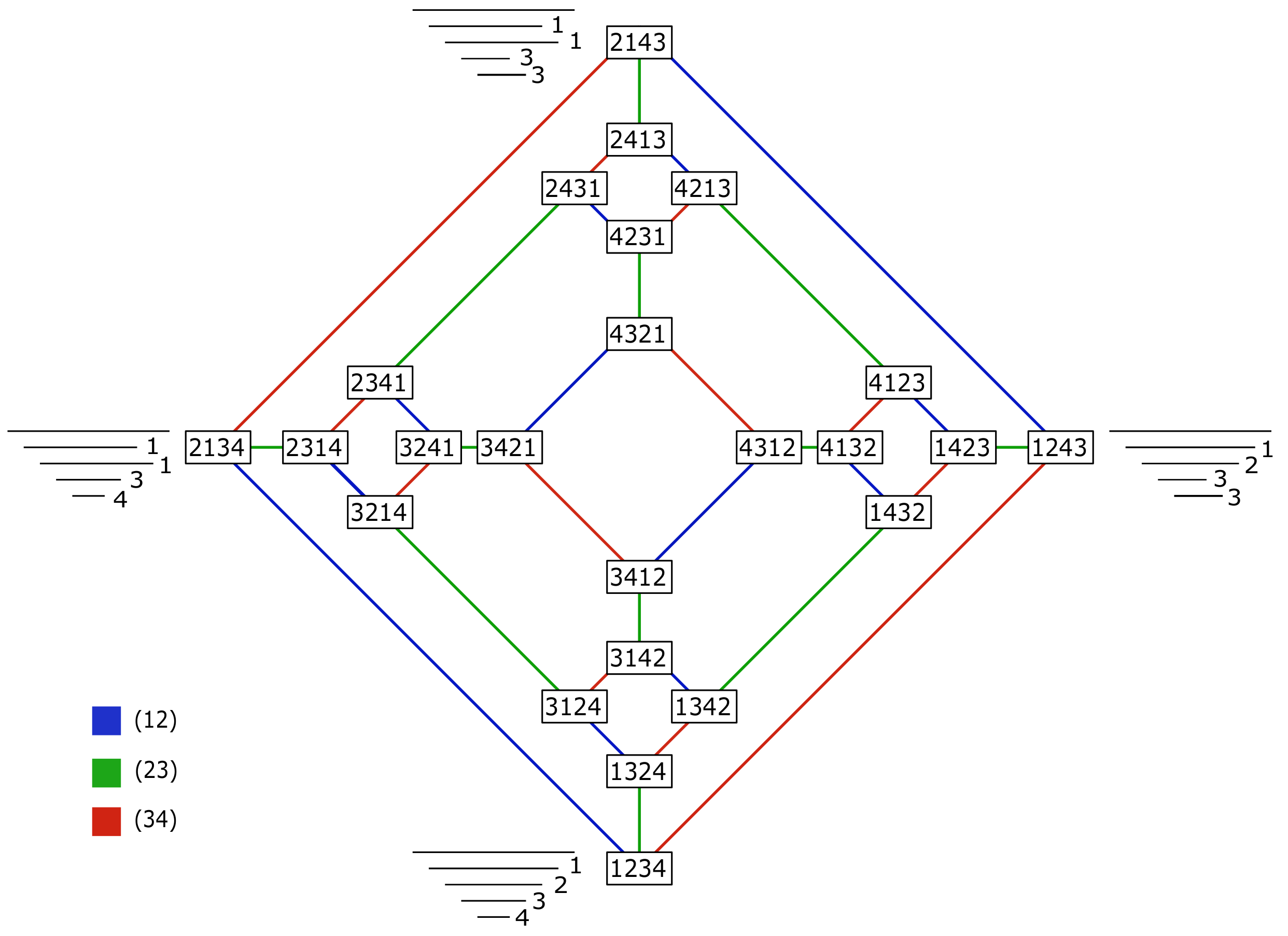
Figure 5.
Tree-realizations of all possible strict barcodes B with four bars. Each row (left) represents a possible permutation of death times for the corresponding order of bars in B, i.e., a possible TMD-type. Each barcode can be realized by a subset of all the combinatorial tree types, each represented by a column, with a corresponding adjacency matrix.
Figure 5.
Tree-realizations of all possible strict barcodes B with four bars. Each row (left) represents a possible permutation of death times for the corresponding order of bars in B, i.e., a possible TMD-type. Each barcode can be realized by a subset of all the combinatorial tree types, each represented by a column, with a corresponding adjacency matrix.
Figure 6.
The two possible moves that respect the condition of a realizable barcode. Move modifies the barcode’s ordering, whereas move does not change the order of the deaths.
Figure 6.
The two possible moves that respect the condition of a realizable barcode. Move modifies the barcode’s ordering, whereas move does not change the order of the deaths.
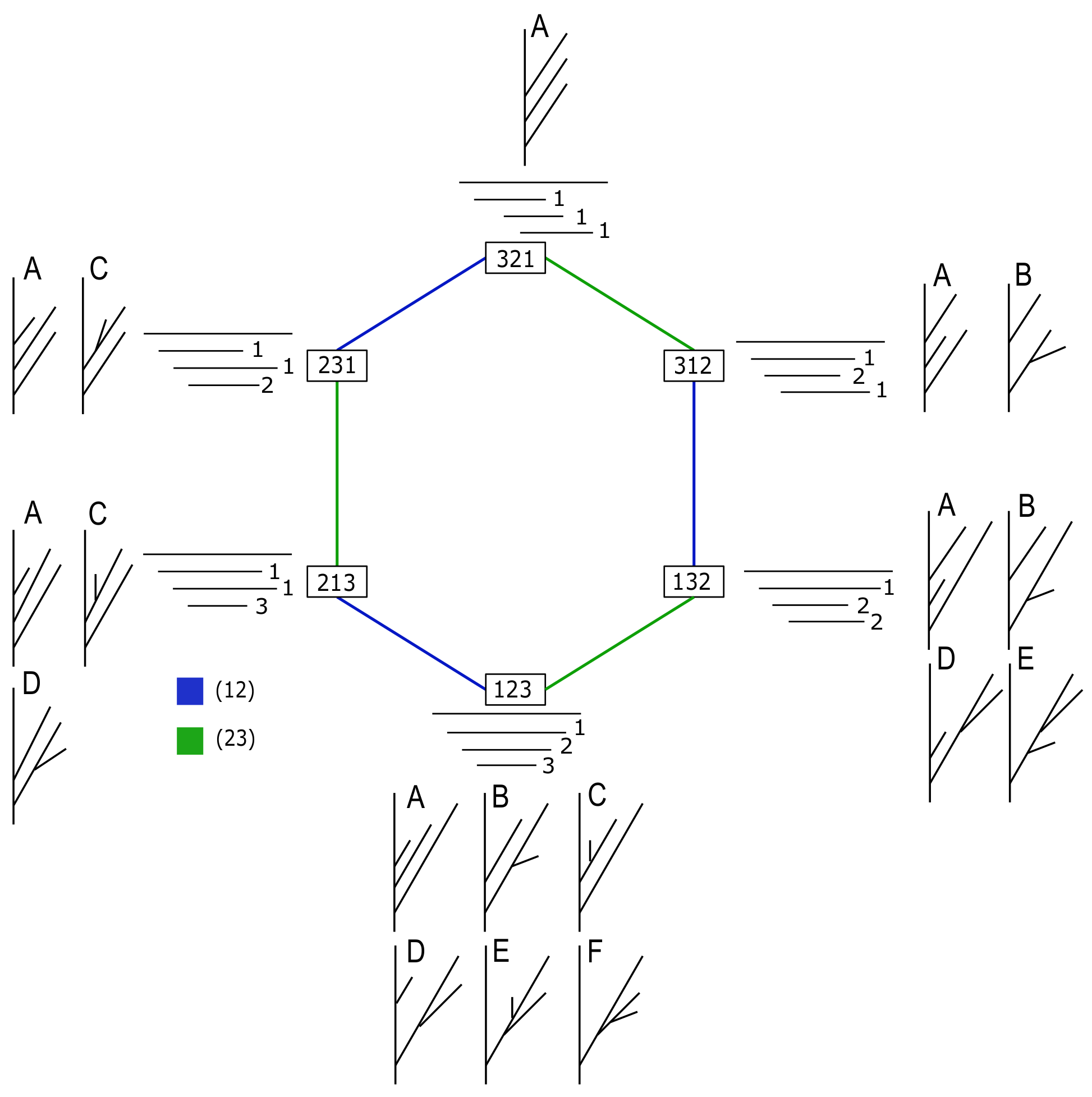
Figure 7.
A representation of the space of barcodes with four bars up to permutation equivalence class as the Cayley graph of
generated by the transpositions
and
, respectively. Each vertex is an element of the group. The edges represent the transposition to convert one end point into the other, colored by generator. The number to the right of each bar is its index. All trees
T such that
are indicated next to a barcode
B with the corresponding tree type of
Figure 5. The number of such trees can be computed using Lemma 2.
Figure 7.
A representation of the space of barcodes with four bars up to permutation equivalence class as the Cayley graph of
generated by the transpositions
and
, respectively. Each vertex is an element of the group. The edges represent the transposition to convert one end point into the other, colored by generator. The number to the right of each bar is its index. All trees
T such that
are indicated next to a barcode
B with the corresponding tree type of
Figure 5. The number of such trees can be computed using Lemma 2.
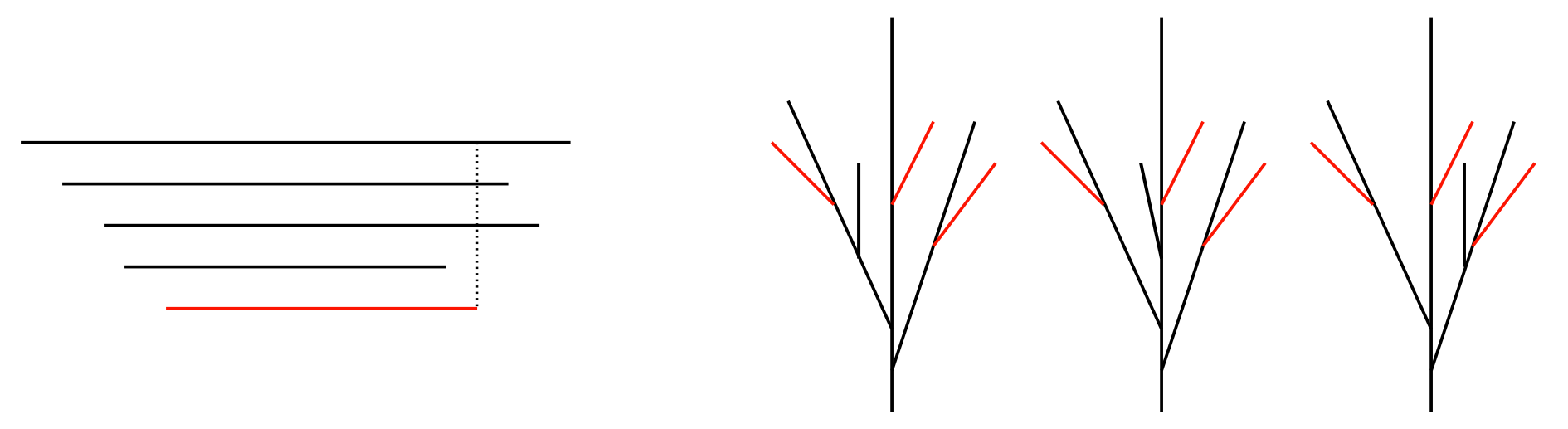
Figure 8.
A barcode B in equivalence class is shown in black. There are three possible combinatorial equivalence classes of trees whose TMD barcode is B, also represented in black. After adding the extra bar in red, we obtain a new barcode , in the equivalence class . In a tree-realization of , the branch corresponding to the red bar can be attached to any of the branches corresponding to the 0th, 1st, and 2nd bars, represented on the trees by the red branches. This leads to nine possible combinatorial equivalence classes of trees for the barcode .
Figure 8.
A barcode B in equivalence class is shown in black. There are three possible combinatorial equivalence classes of trees whose TMD barcode is B, also represented in black. After adding the extra bar in red, we obtain a new barcode , in the equivalence class . In a tree-realization of , the branch corresponding to the red bar can be attached to any of the branches corresponding to the 0th, 1st, and 2nd bars, represented on the trees by the red branches. This leads to nine possible combinatorial equivalence classes of trees for the barcode .
Figure 9.
The Cayley graph representing generated by . For the four outside elements, we provide the barcode associated with the permutation. The number next to each bar is its index.
Figure 9.
The Cayley graph representing generated by . For the four outside elements, we provide the barcode associated with the permutation. The number next to each bar is its index.
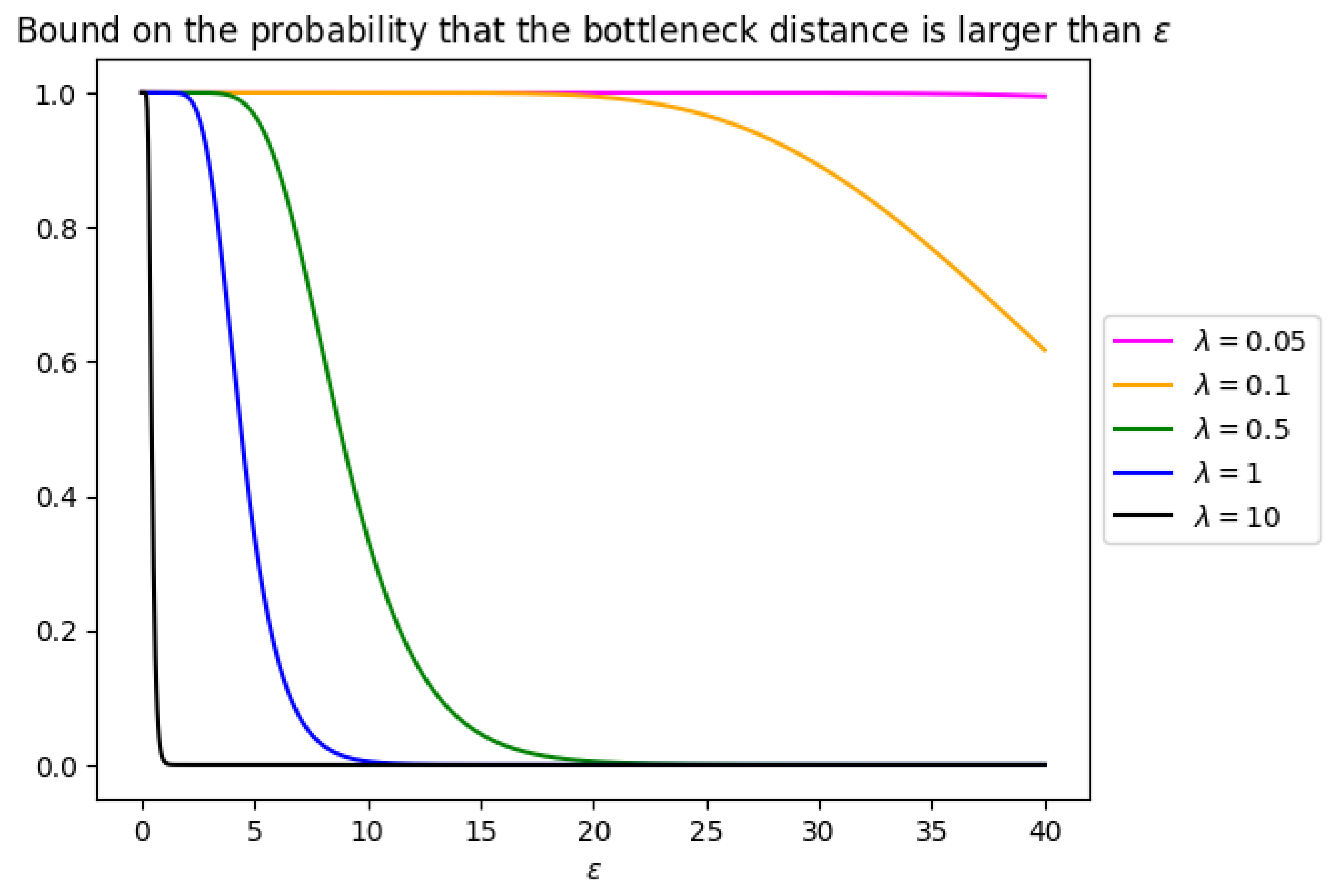
Figure 10.
Upper bound on the probability that the bottleneck distance between
B and
is larger than
(Equation (
1)) for various values of
and for
.
Figure 10.
Upper bound on the probability that the bottleneck distance between
B and
is larger than
(Equation (
1)) for various values of
and for
.
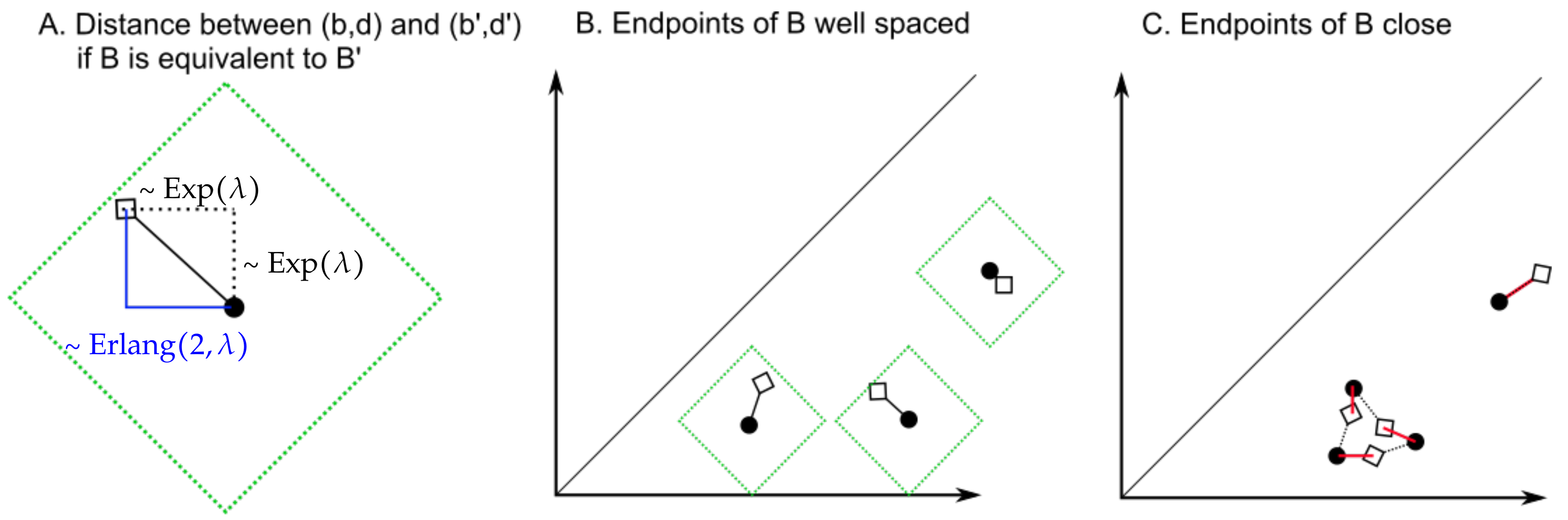
Figure 11.
(A) The -distance between the black bullet and the diamond follows an Erlang distribution. The interior of the green square defines a bound for the -distance from the black bullet that depends on the value of the parameter . (B) If the endpoints of the bars of B are sufficiently far away from each other and , then, with high probability, taking will minimize the -distance between pairs of endpoints of bars. (C) If the endpoints of B are instead close to each other, then it is more likely that , so that the optimal choice of (represented by red segments) is not the identity. The red distances do not necessarily follow exponential distributions, so the proof of Lemma 4 does not apply.
Figure 11.
(A) The -distance between the black bullet and the diamond follows an Erlang distribution. The interior of the green square defines a bound for the -distance from the black bullet that depends on the value of the parameter . (B) If the endpoints of the bars of B are sufficiently far away from each other and , then, with high probability, taking will minimize the -distance between pairs of endpoints of bars. (C) If the endpoints of B are instead close to each other, then it is more likely that , so that the optimal choice of (represented by red segments) is not the identity. The red distances do not necessarily follow exponential distributions, so the proof of Lemma 4 does not apply.
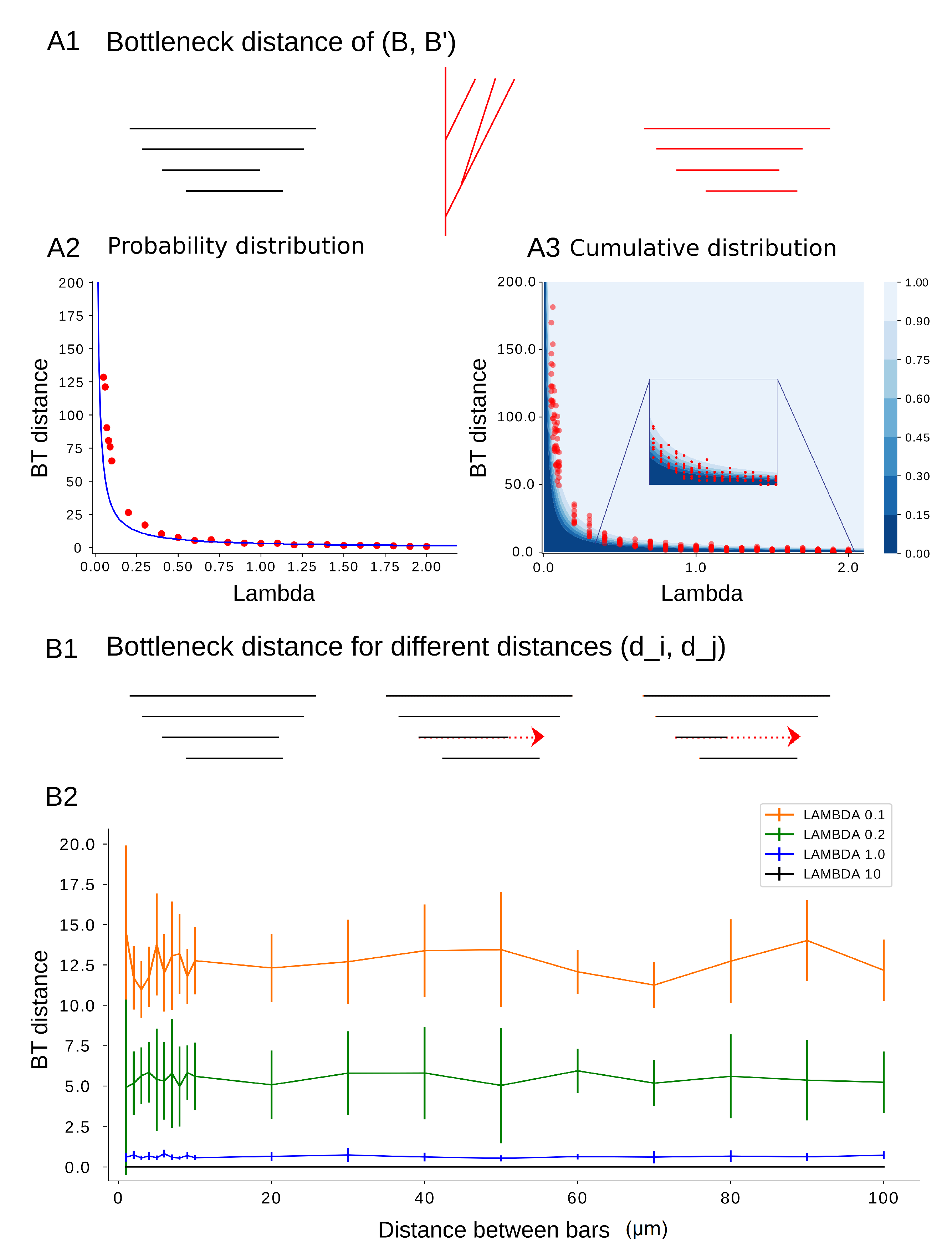
Figure 12.
(A1–A3) Bottleneck distance as a function of . We compute the bottleneck distance between an input barcode B and an output barcode for . (A1) From barcode B (in black), a tree (in red) is generated using the TNS which results in a new barcode (in red). (A2) The average bottleneck distance (red points) is compared to the expected mean of the probability distribution function found in Lemma 4 (blue curve). (A3) The bottleneck distances (red) are compared to the cumulative distribution probability for and (blue). (B1–B2) bottleneck distance between B and as a function of distances between bars in B. (B1). We consider barcodes of the same permutation type for different distances between two bars and of the initial barcode B that are consecutive in the order of deaths. (B2) For each input barcode with increasing , the distance between death times presented in x-axis, 100 synthesized barcodes are generated and the bottleneck distance between the input and output barcodes is computed (y-axis), which depends only on the value of and not on the distance between the bars.
Figure 12.
(A1–A3) Bottleneck distance as a function of . We compute the bottleneck distance between an input barcode B and an output barcode for . (A1) From barcode B (in black), a tree (in red) is generated using the TNS which results in a new barcode (in red). (A2) The average bottleneck distance (red points) is compared to the expected mean of the probability distribution function found in Lemma 4 (blue curve). (A3) The bottleneck distances (red) are compared to the cumulative distribution probability for and (blue). (B1–B2) bottleneck distance between B and as a function of distances between bars in B. (B1). We consider barcodes of the same permutation type for different distances between two bars and of the initial barcode B that are consecutive in the order of deaths. (B2) For each input barcode with increasing , the distance between death times presented in x-axis, 100 synthesized barcodes are generated and the bottleneck distance between the input and output barcodes is computed (y-axis), which depends only on the value of and not on the distance between the bars.
![Algorithms 13 00335 g012 Algorithms 13 00335 g012]()
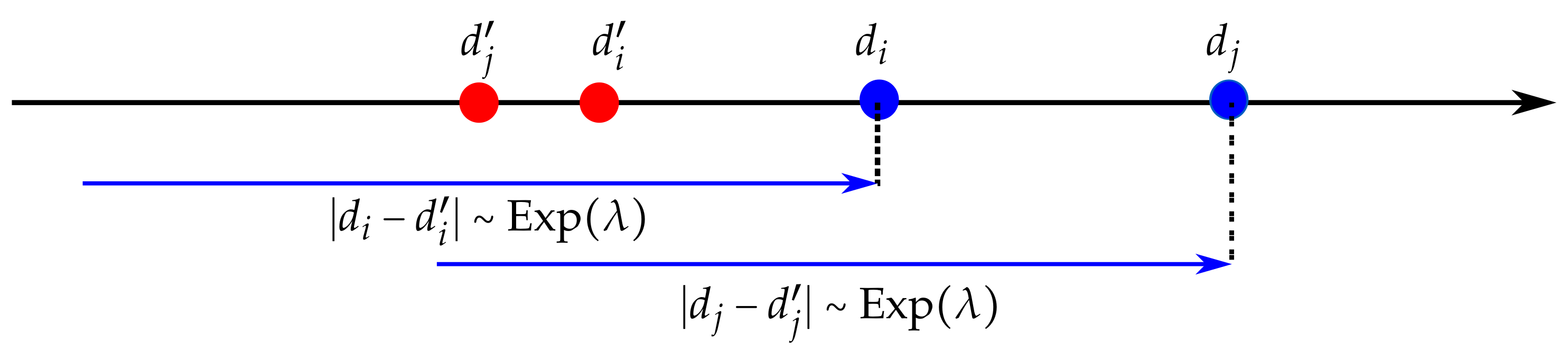
Figure 13.
We are interested in the case where when we start from . The distances and both follow an exponential law of parameter . The probability to terminate increases exponentially when approaching and , as represented by the blue arrows.
Figure 13.
We are interested in the case where when we start from . The distances and both follow an exponential law of parameter . The probability to terminate increases exponentially when approaching and , as represented by the blue arrows.
Figure 14.
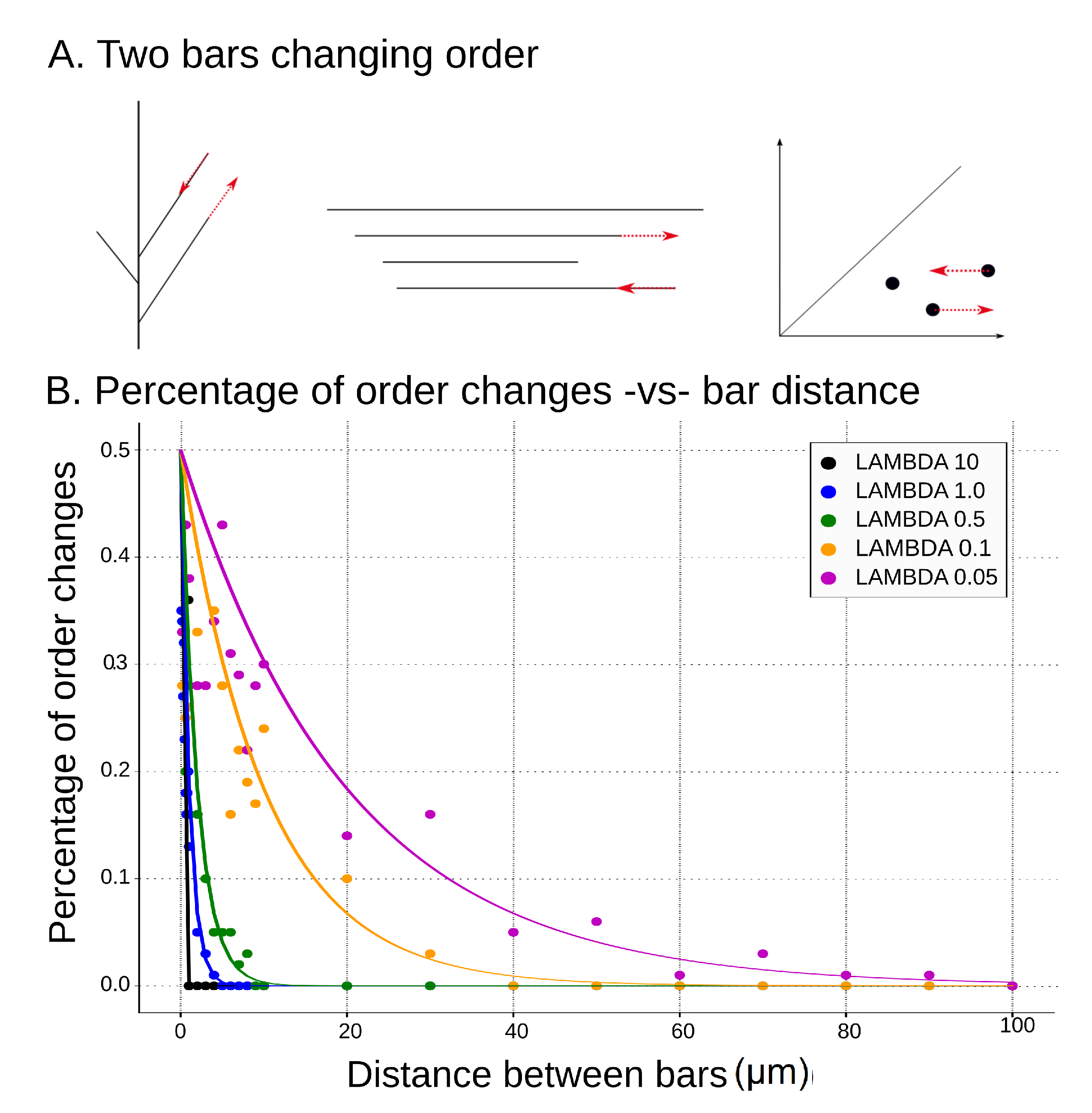
(A) Example of two bars changing order, which results in switching of classes. We show here a tree, its barcode, and the corresponding persistence diagram when two consecutive deaths switch their order. The impact of the change is illustrated by the red arrows; (B) percentage of order changes per 100 repetitions for varied distance between death times of two consecutive bars of the input barcode. Comparison of theoretical results (solid lines) to simulations (scatter plot) for different values of lambda.
Figure 14.
(A) Example of two bars changing order, which results in switching of classes. We show here a tree, its barcode, and the corresponding persistence diagram when two consecutive deaths switch their order. The impact of the change is illustrated by the red arrows; (B) percentage of order changes per 100 repetitions for varied distance between death times of two consecutive bars of the input barcode. Comparison of theoretical results (solid lines) to simulations (scatter plot) for different values of lambda.
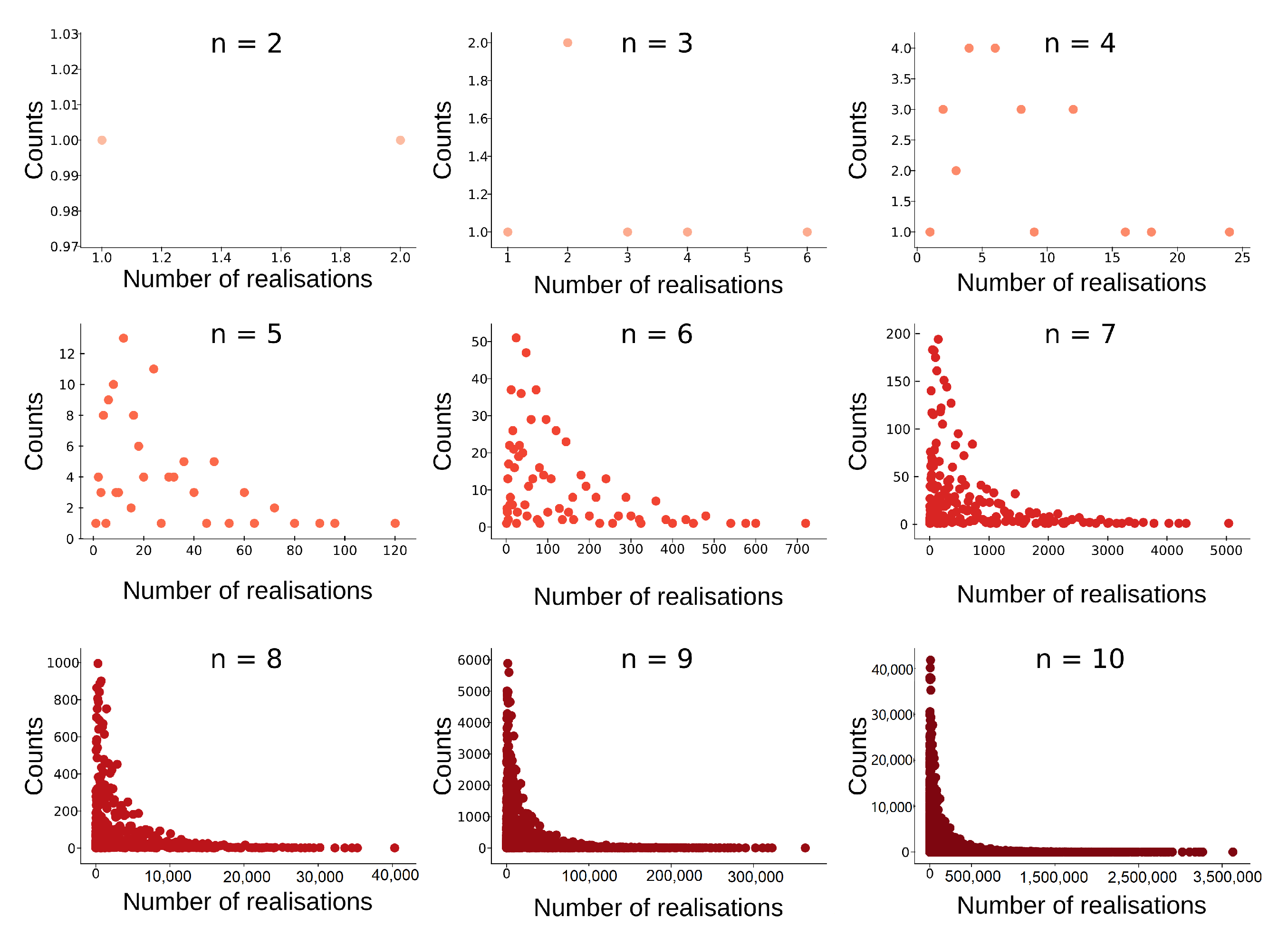
Figure 15.
Histogram of tree-realization numbers for equivalence classes of barcodes with bars (). The maximal tree-realization number for a fixed number of bars can be achieved with exactly one equivalence class that of the strictly ordered barcode.
Figure 15.
Histogram of tree-realization numbers for equivalence classes of barcodes with bars (). The maximal tree-realization number for a fixed number of bars can be achieved with exactly one equivalence class that of the strictly ordered barcode.
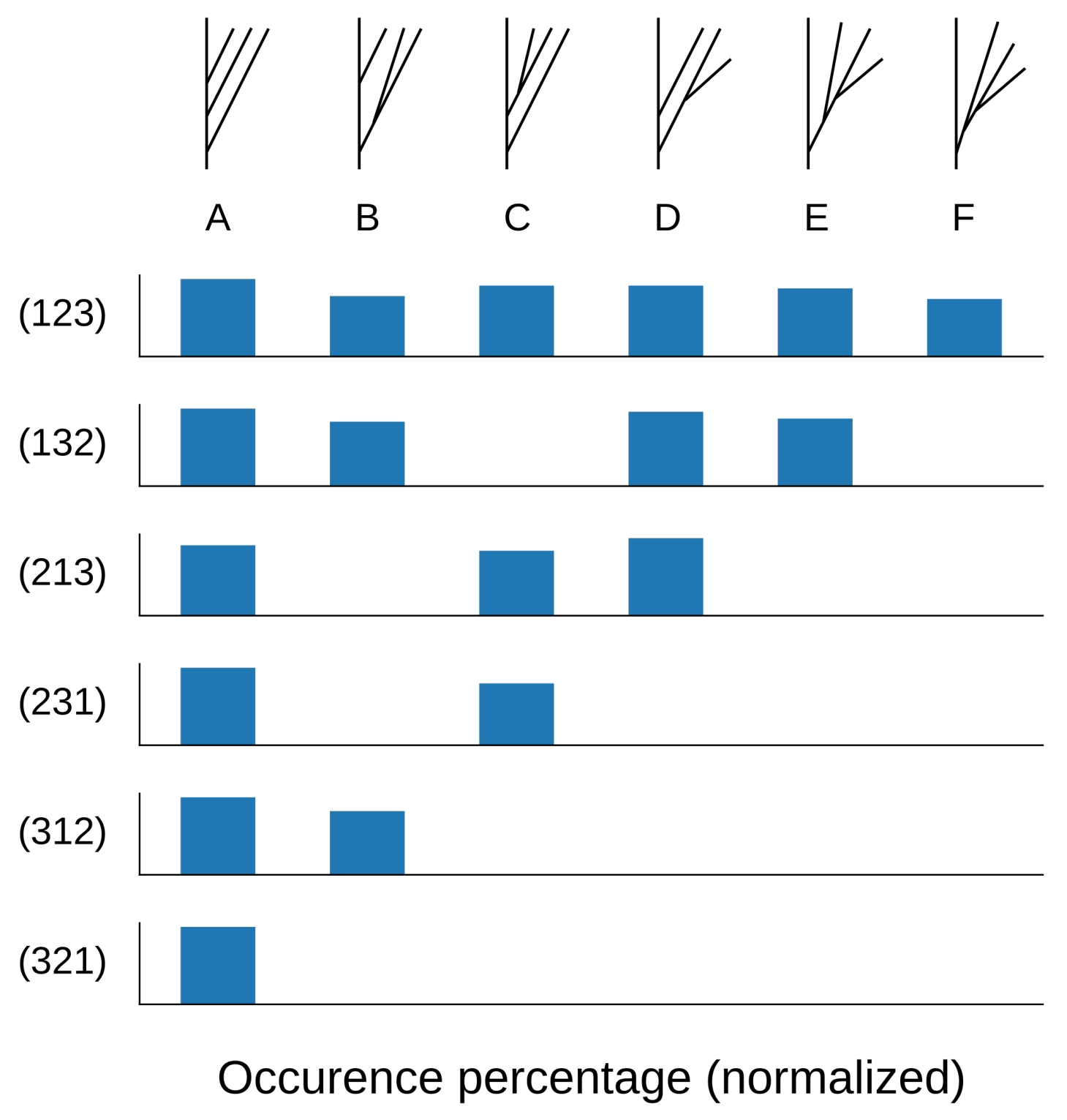
Figure 16.
Empirical distribution (percentage of 1000 trees) of synthesized geometric trees with four branches by combinatorial tree type (A–F) for a given input barcode equivalence class (rows), when . We observe that the distribution is approximately uniform.
Figure 16.
Empirical distribution (percentage of 1000 trees) of synthesized geometric trees with four branches by combinatorial tree type (A–F) for a given input barcode equivalence class (rows), when . We observe that the distribution is approximately uniform.
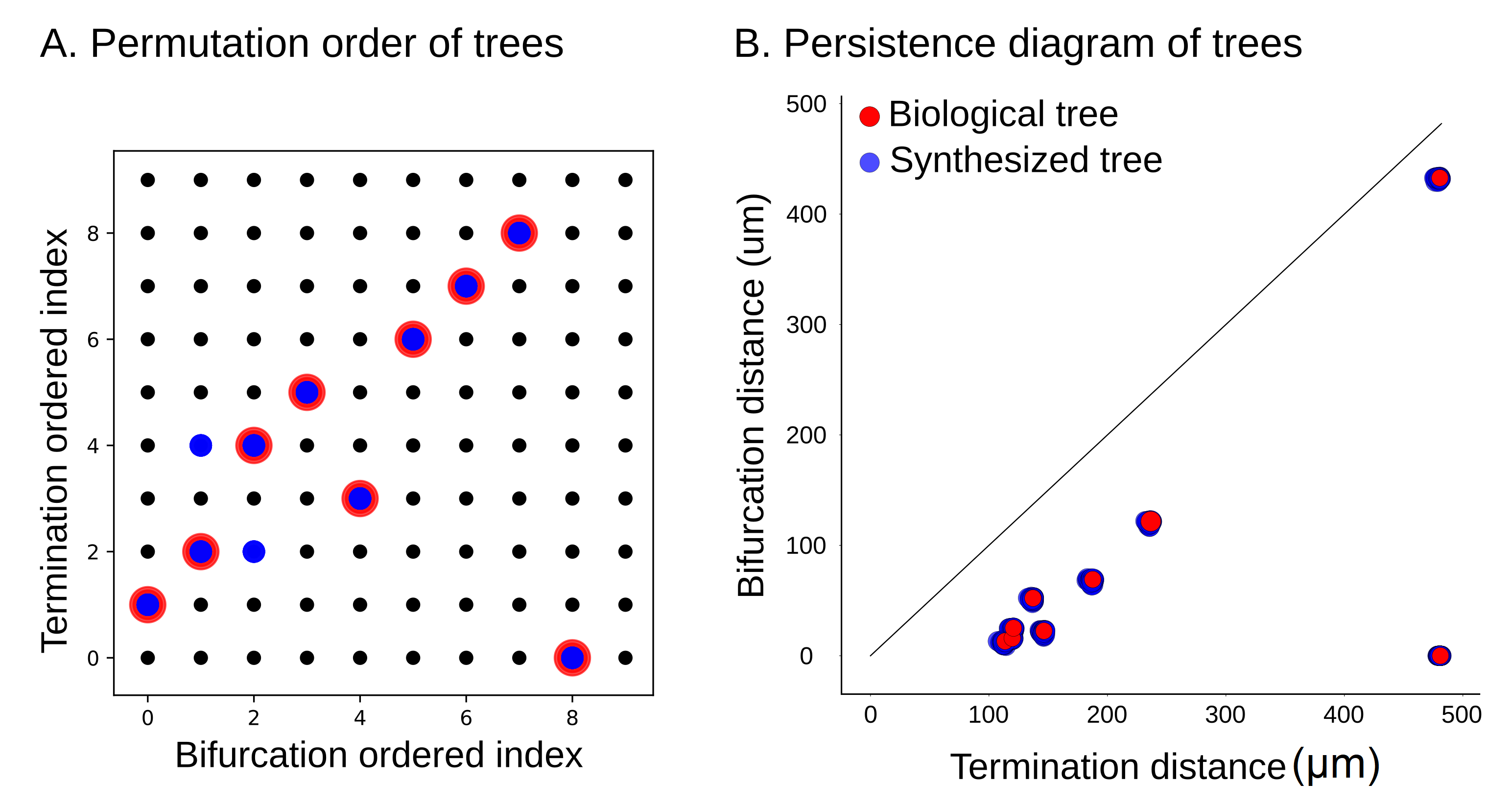
Figure 17.
Barcode-equivalence class, represented by the corresponding permutation, (A) and persistence diagram (B) of 100 synthesized cells based on a geometric tree with eight branches, extracted from a layer 4 pyramidal cell. The barcode-equivalence classes of the synthesized trees (represented by blue dots) can differ from that of the original tree due to the stochastic nature of synthesis algorithm. The persistence diagrams of the synthesized trees ((B), blue) are essentially indistinguishable from those of the original tree ((B), red).
Figure 17.
Barcode-equivalence class, represented by the corresponding permutation, (A) and persistence diagram (B) of 100 synthesized cells based on a geometric tree with eight branches, extracted from a layer 4 pyramidal cell. The barcode-equivalence classes of the synthesized trees (represented by blue dots) can differ from that of the original tree due to the stochastic nature of synthesis algorithm. The persistence diagrams of the synthesized trees ((B), blue) are essentially indistinguishable from those of the original tree ((B), red).
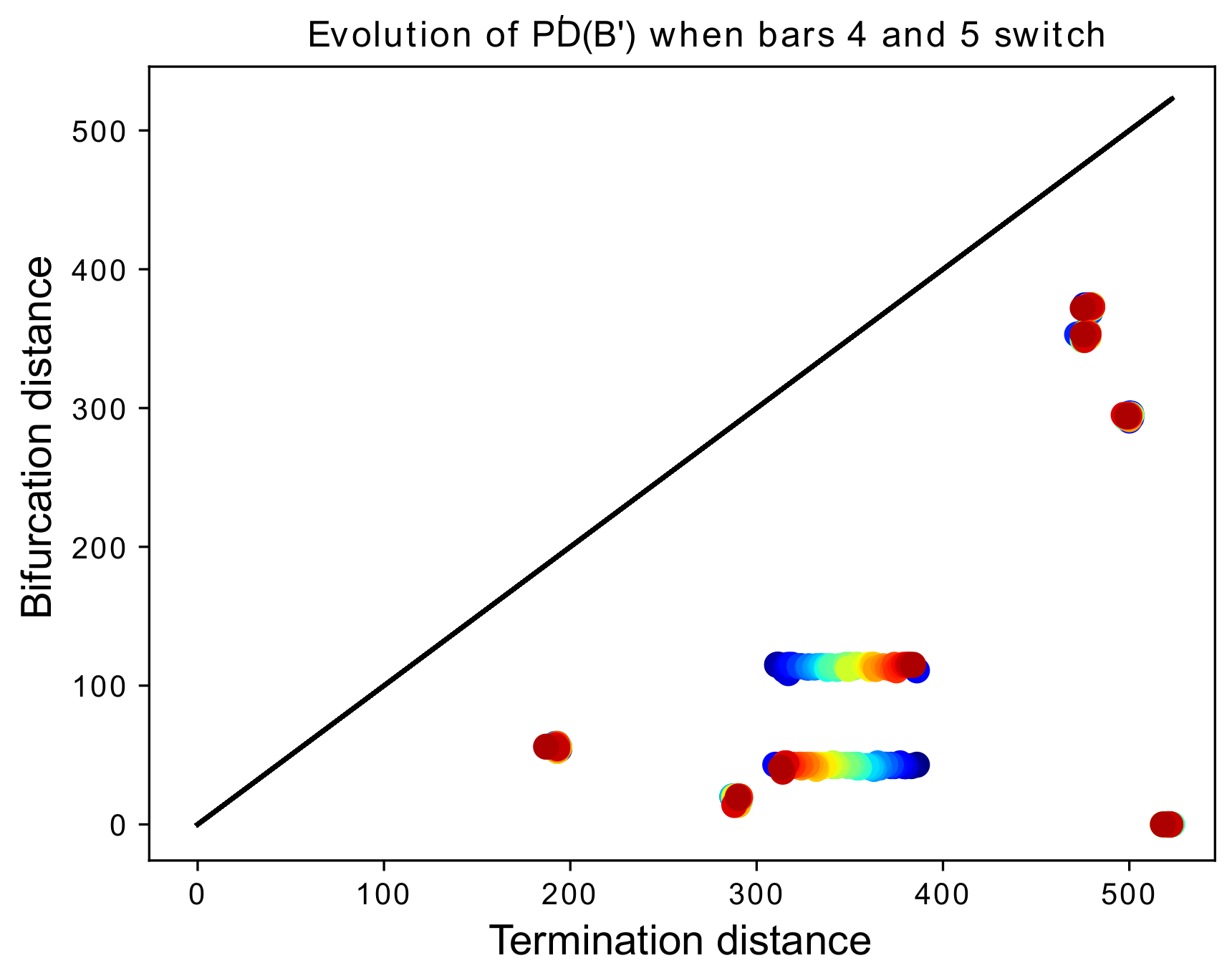
Figure 18.
We begin with a barcode with eight bars. The death times and (i.e., the 4th and 5th largest death times) are slowly switching as k increases, represented by red-shifting of the color of the points in the persistence diagram. When (in red), we have the original barcode B, and when (in blue) we obtain a barcode identical to the original, except that is replaced by and by .
Figure 18.
We begin with a barcode with eight bars. The death times and (i.e., the 4th and 5th largest death times) are slowly switching as k increases, represented by red-shifting of the color of the points in the persistence diagram. When (in red), we have the original barcode B, and when (in blue) we obtain a barcode identical to the original, except that is replaced by and by .
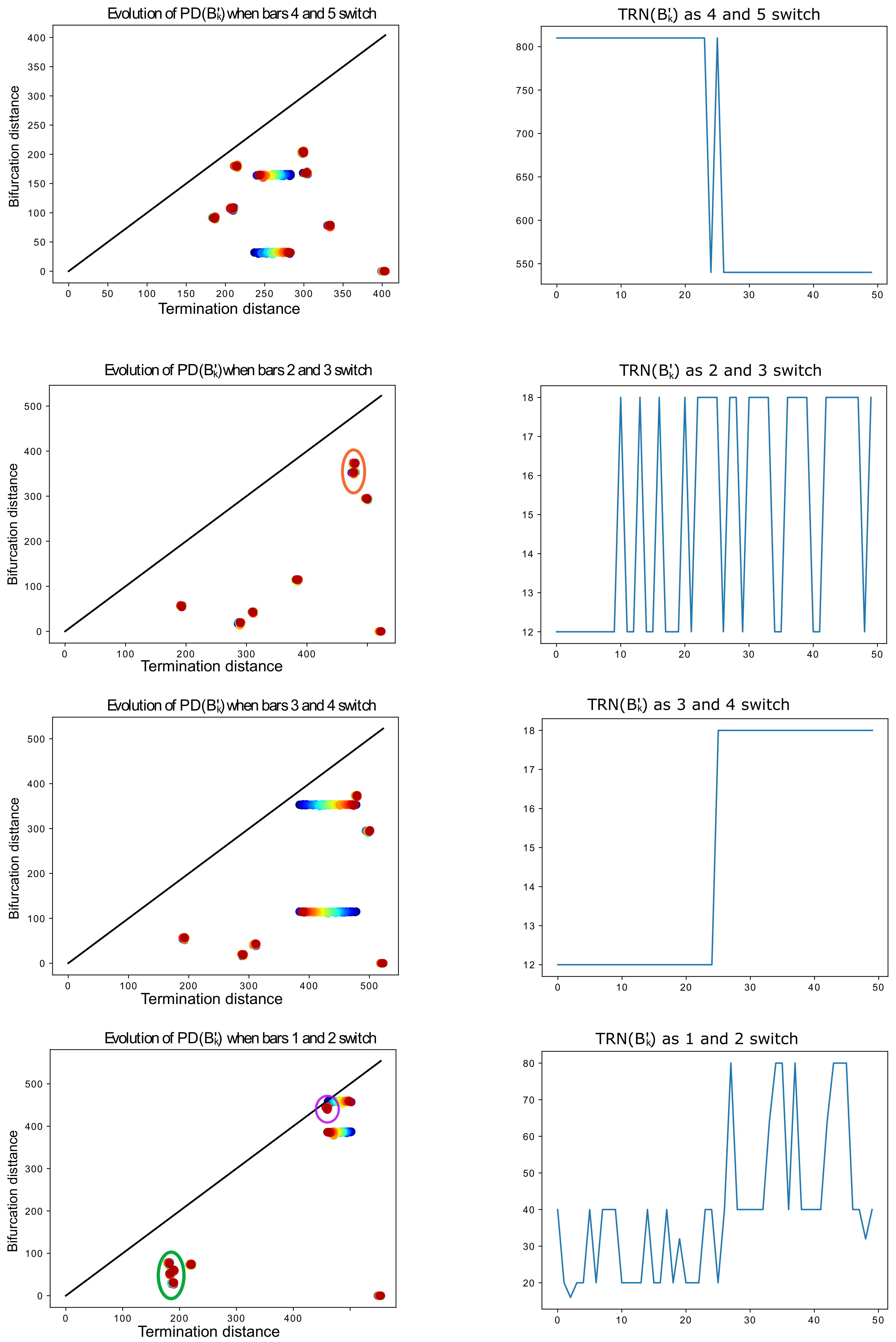
Figure 19.
On the left, evolution of
as
k increases (represented by red-shifting of the point color, from red
to blue
), for various pairs of bars. When not clear, we circle in orange the two points that switch. On the right, the corresponding evolution of the tree realization number
as
k increases. For instance, as indicated in
Table 2, the tree-realization number of
is 810 and that of
is 540. The barcodes
exhibit the behavior described in Lemma 5, except for the last row, in which death times that are too close to each other (circled in purple and green) interfere with the process. Without this interference, the tree-realization numbers should oscillate between 20 and 40. When
k gets close to 50 (blue), the death time
(largest death time) starts interfering with the third one
(circled in purple) in the tree synthesis process.
Figure 19.
On the left, evolution of
as
k increases (represented by red-shifting of the point color, from red
to blue
), for various pairs of bars. When not clear, we circle in orange the two points that switch. On the right, the corresponding evolution of the tree realization number
as
k increases. For instance, as indicated in
Table 2, the tree-realization number of
is 810 and that of
is 540. The barcodes
exhibit the behavior described in Lemma 5, except for the last row, in which death times that are too close to each other (circled in purple and green) interfere with the process. Without this interference, the tree-realization numbers should oscillate between 20 and 40. When
k gets close to 50 (blue), the death time
(largest death time) starts interfering with the third one
(circled in purple) in the tree synthesis process.
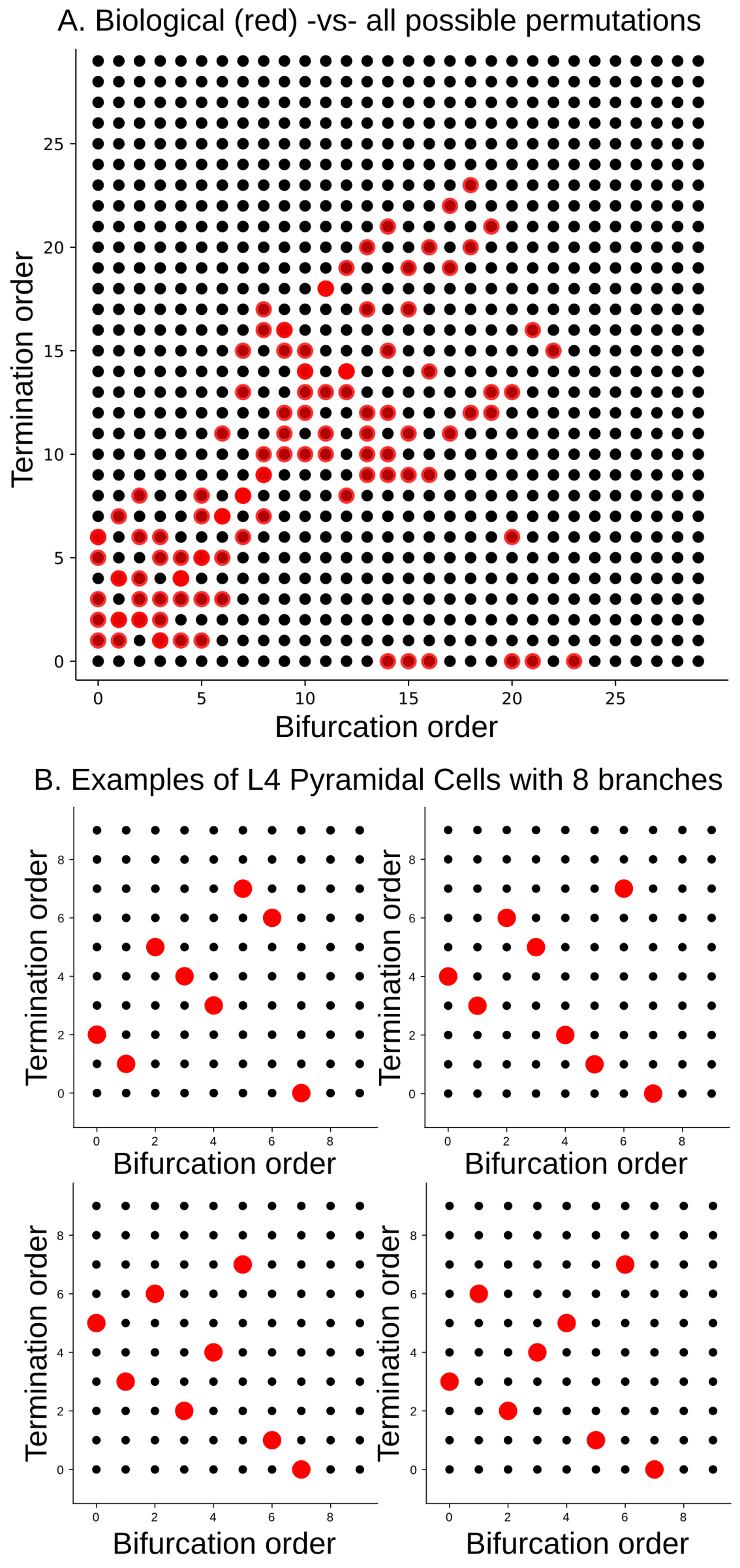
Figure 20.
(A) TMD-equivalence classes of a population of biological geometric trees with at most 30 bars (red dots), represented by their associated permutations; (B) examples of TMD-equivalence classes of individual biological geometric trees with eight branches, extracted from layer 4 pyramidal cells (red dots).
Figure 20.
(A) TMD-equivalence classes of a population of biological geometric trees with at most 30 bars (red dots), represented by their associated permutations; (B) examples of TMD-equivalence classes of individual biological geometric trees with eight branches, extracted from layer 4 pyramidal cells (red dots).
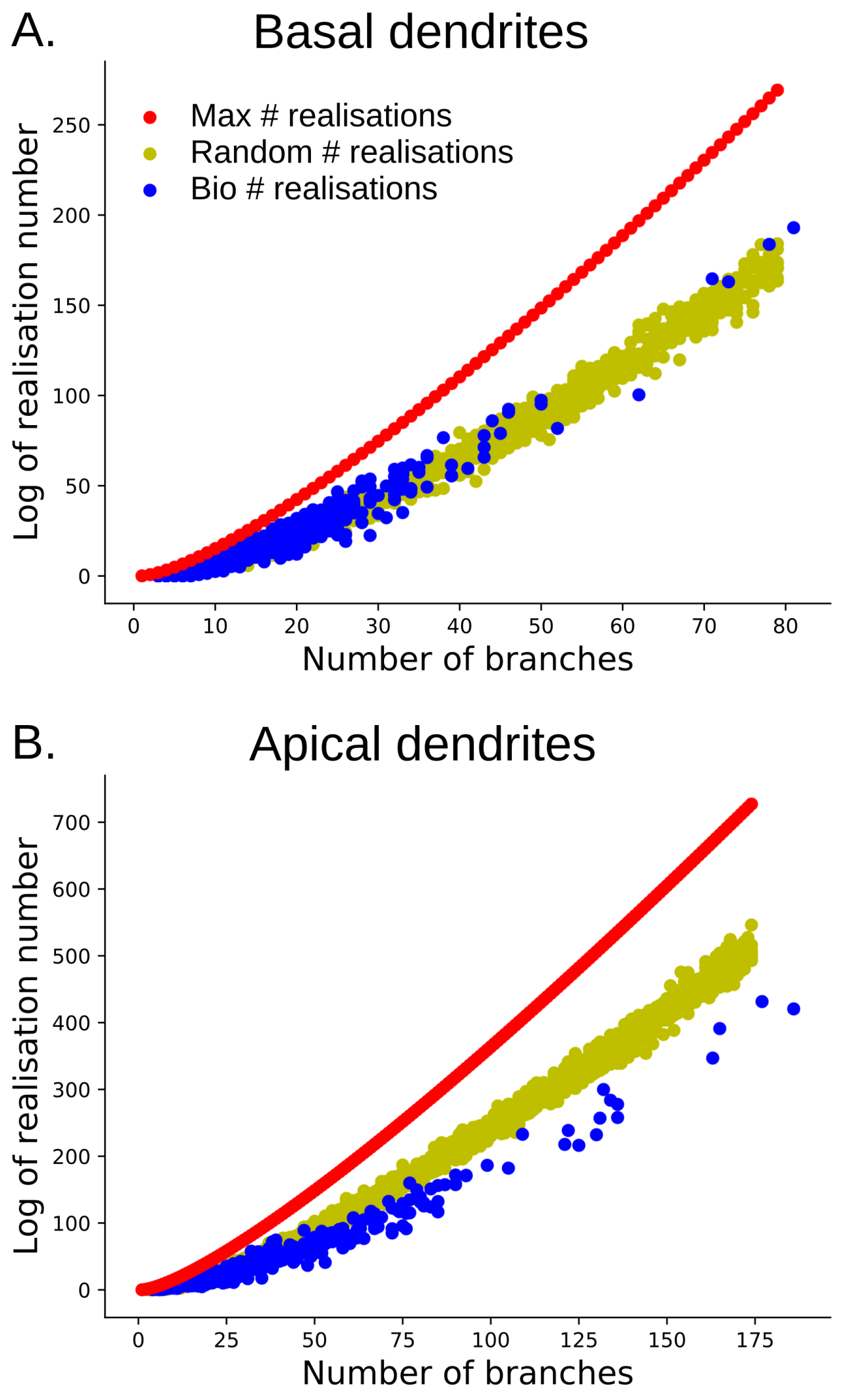
Figure 21.
The log of the tree-realization number for barcodes with varying numbers of bars. (A) the log of tree-realization number for barcodes of basal dendrites (in blue) in comparison with random barcodes (in yellow) and the maximum tree-realization number ( for bars) (in red); (B) the log of the tree-realization number for barcodes of apical dendrites (in blue) in comparison with random barcodes (in yellow) and the maximum maximum tree-realization number (in red).
Figure 21.
The log of the tree-realization number for barcodes with varying numbers of bars. (A) the log of tree-realization number for barcodes of basal dendrites (in blue) in comparison with random barcodes (in yellow) and the maximum tree-realization number ( for bars) (in red); (B) the log of the tree-realization number for barcodes of apical dendrites (in blue) in comparison with random barcodes (in yellow) and the maximum maximum tree-realization number (in red).
Table 1.
Summary and terminology of the TMD and TNS algorithms. The TMD computes the barcode of a tree from the tips of branches towards the root, whereas the TNS grows the tree in the opposite direction, from the root to the leaves.
Table 1.
Summary and terminology of the TMD and TNS algorithms. The TMD computes the barcode of a tree from the tips of branches towards the root, whereas the TNS grows the tree in the opposite direction, from the root to the leaves.
| | TMD | TNS |
|---|
| Goal | Compute the barcode of a tree based on a distance function | Grow a new tree from a barcode |
| Directionality | From leaves to root | From root to leaves |
| Domains | | |
Table 2.
For each example displayed in
Figure 19, we list the permutation type and the tree-realization number of the original barcode
B and of
, and the indices of the bars that are switched. The superscript
i in
indicates the corresponding row of
Figure 19. For example, the largest death time of barcode
is the second bar (in order of birth times), and its shortest death is the third one. When we switch the 4th and 5th (from largest to smallest) death times in
and
, the TRN changes from 810 to 540.
Table 2.
For each example displayed in
Figure 19, we list the permutation type and the tree-realization number of the original barcode
B and of
, and the indices of the bars that are switched. The superscript
i in
indicates the corresponding row of
Figure 19. For example, the largest death time of barcode
is the second bar (in order of birth times), and its shortest death is the third one. When we switch the 4th and 5th (from largest to smallest) death times in
and
, the TRN changes from 810 to 540.
| | Permutation | TRN | Bars That Switch |
|---|
| | 810 | 4 and 5 |
| | 540 | 4 and 5 |
| | 12 | 2 and 3 |
| | 18 | 2 and 3 |
| | 12 | 3 and 4 |
| | 18 | 3 and 4 |
| | 20 | 1 and 2 |
| | 40 | 1 and 2 |