Segment-Based Clustering of Hyperspectral Images Using Tree-Based Data Partitioning Structures
Abstract
1. Introduction
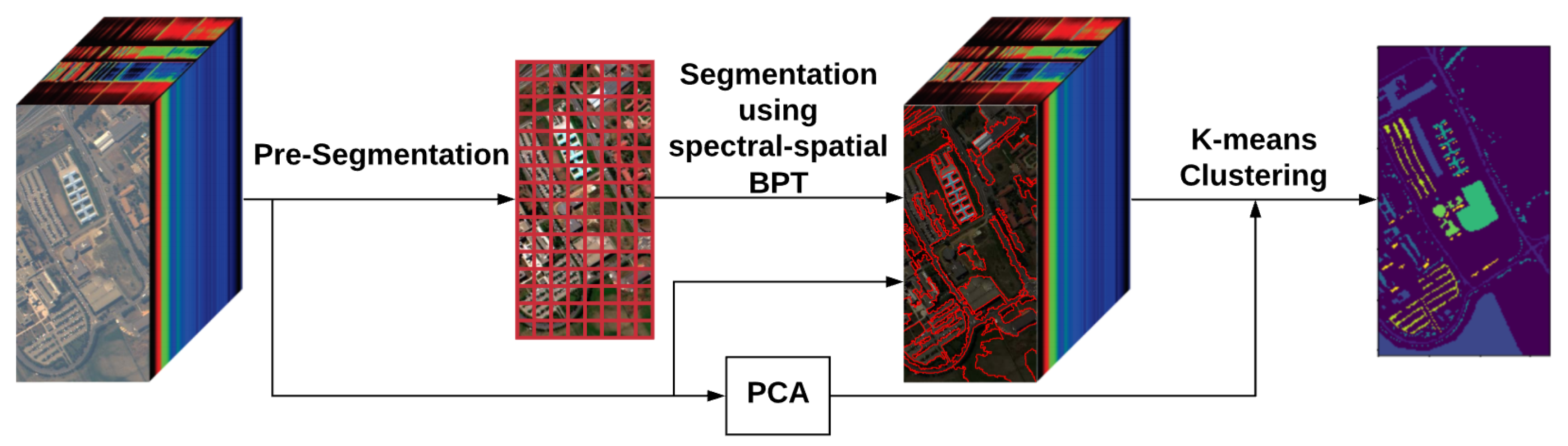
2. Methodology
2.1. Pre-Segmentation
2.2. BPT Building
2.3. BPT Pruning
2.4. K-Means Clustering
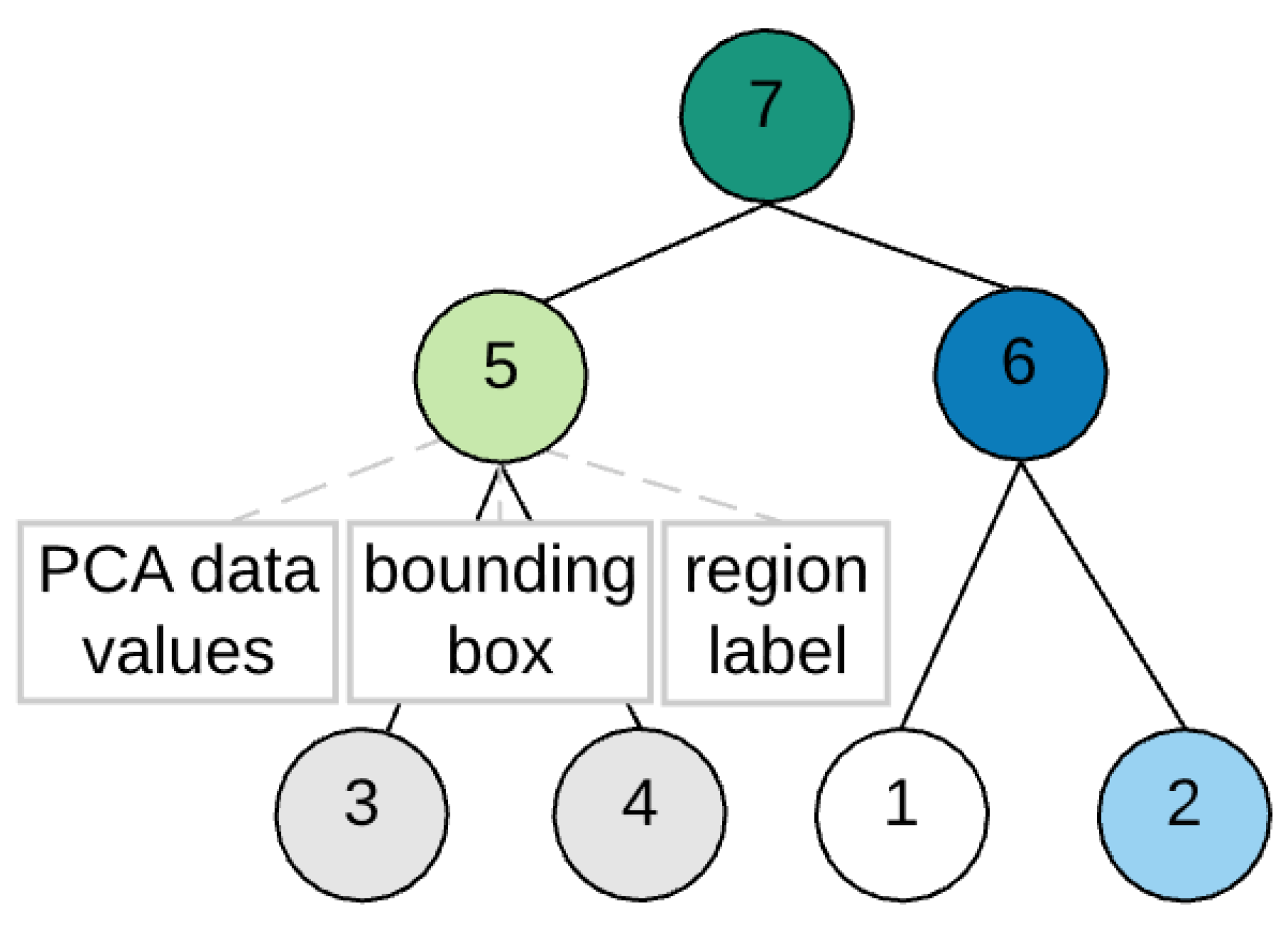
- region label: a unique region number,
- bounding box: a rectangular box formed by i and j pixel coordinates of the segmentation map with the size of the box equal to the number of pixels included in the region and
- PCA data values: a vector containing the PCA-reduced values with the pixel coordinates corresponding to the coordinates of the bounding box.
| Algorithm 1 The filtering algorithm introduced in [30]. |
function Filter (RootTree , CandidateSet U) { U← if ( is a leaf) { the closest point in U to } else{ the closest point in U to C’s midpoint for all () do if u.isFarther( then end for if () { } else{ Filter(, U) Filter(, U) } } } |
3. Results and Comparisons
- Salinas scene—collected by the 224-band AVIRIS (Airborne Visible/Infrared Imaging Spectrometer) sensor over Salinas Valley, California, and it is characterized by high spatial resolution (3.7-m pixels) and resolution 512 lines by 217 samples in the wavelength range 0.4–2.5 μm. Salinas ground truth contains 16 classes.
- Salinas-A is a subscene of Salinas image and it comprises pixels that are located within the same scene as Salinas at [samples, lines] = [591–676, 158–240]. It includes vegetables, bare soils, and vineyard fields, and its ground truth contains six classes.
- PaviaC is acquired by the ROSIS (Reflective Optics System Imaging Spectrometer) sensor over the city center of Pavia (referred as PaviaC), central Italy. The data set contains 115 spectral bands covering the wavelength ranging from 0.43 to 0.86 μm, but only 102 effective bands were used for experiments after removing low-SNR and water absorption bands [37]. The original image dimension, with the spatial resolution of 1.3 m, is used in this experiment. The data set consists of nine land cover classes.
- PaviaU is also acquired by the ROSIS senser over University of Pavia. The image is of a size of and it has a spatial resolution of 1.3 m. Similar to PaviaC, a total of 115 spectral bands were collected of which 12 spectral bands are removed due to noise and the remaining 103 bands are used for classification [37]. The ground reference image available with the data has nine land cover classes.
- Indian Pines scene was gathered by AVIRIS sensor over the Indian Pines test site in North-western Indiana and consists of pixels and 224 spectral reflectance bands in the wavelength range 0.4–2.5 × m. The scene contains two-thirds agriculture, and one-third forest or other natural perennial vegetation. There are two major dual lane highways, a rail line, low density housing, other built structures, and smaller roads. The ground truth available is divided into 16 classes.
- Samson scene is an image with pixels and 156 spectral channels covering the wavelengths from 401 nm to 889 nm. The spectral resolution is 3.13 nm. There are three target end-members in the data set, including “Rock”, “Tree”, and “Water”.
- Jasper Ridge is one of the most widely used hyperspectral image data sets, with each image of size pixels. Each pixel contains at 198 effective channels with the wavelengths ranging from 380 to 2500 nm. The spectral resolution is up to 9.46 nm. There are four end-members latent in this data set, including “Road”, “Dirt”, “Water”, and “Tree”.
- Urban scene consists of images of pixels with spatial resolution of 10 m and 210 channels with wavelengths ranging from 400 nm to 2500 nm. There are three versions of the ground truth, which contain four, five, and six end-members, respectively. In this experiment, four end-members are used, including “Asphalt”, “Grass”, “Tree”, and “Roof”.
3.1. Evaluation Metrics
- Purity is an external evaluation criterion of cluster quality. It is the most common metric for clustering results evaluation, defined as:where n denotes the number of data points in the image. The range of purity metric is , where 0 and 1 represent the lowest and highest cluster quality.
- NMI is a normalization of the mutual information score (MI), where is obtained as:, , and are the probabilities of a data point being in cluster , class , and in the intersection of and , respectively. The NMI score is defined, as follows:where and are the entropies of and C, respectively. The larger NMI value indicates higher clustering accuracy.
- OA is the number of correctly classified pixels in divided by the total number of pixels.
3.2. Parameter Settings
3.3. Effect of the Number of Regions
3.4. Effect of Number of Clusters
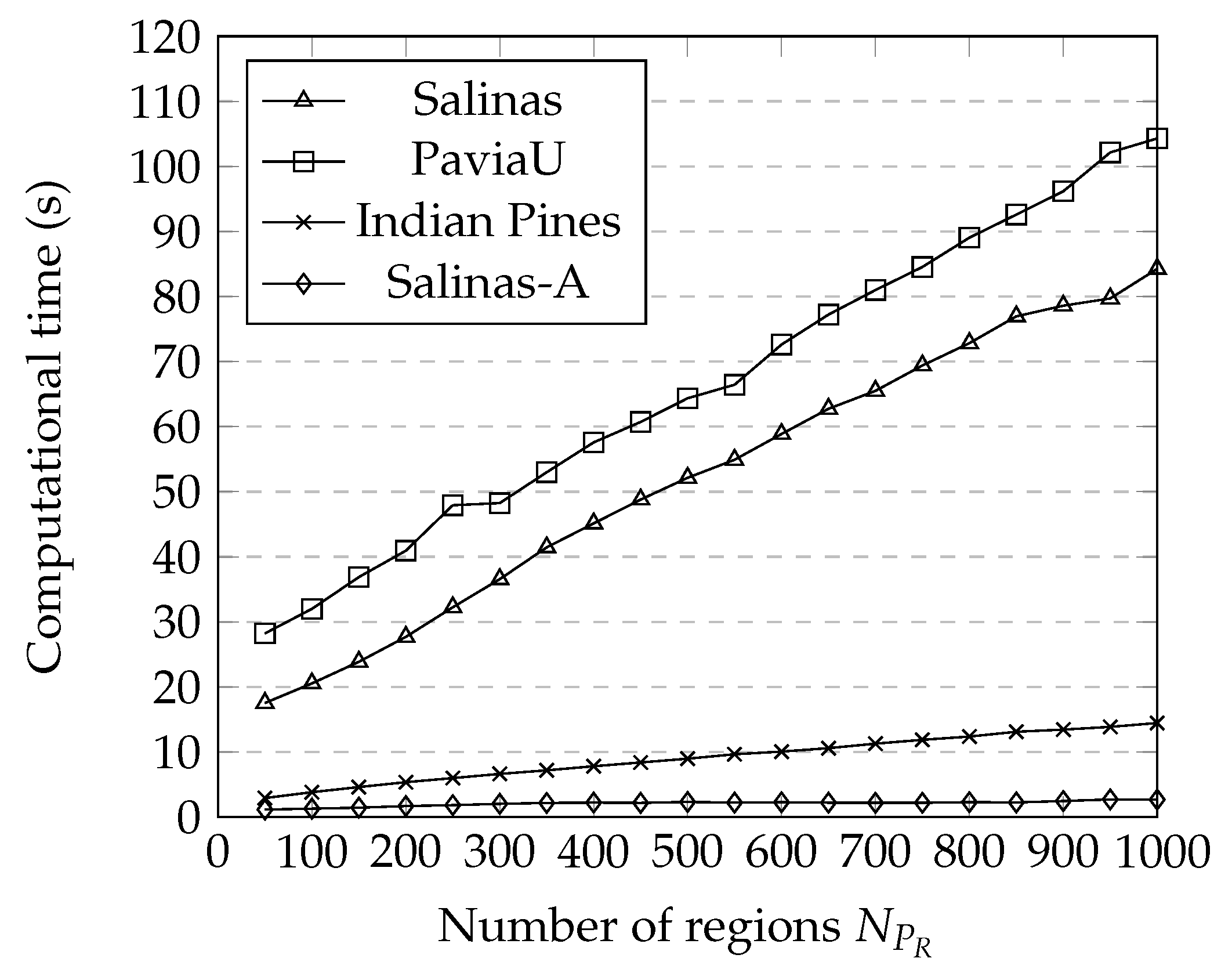
3.5. Computational Time
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kanning, M.; Siegmann, B.; Jarmer, T. Regionalization of Uncovered Agricultural Soils Based on Organic Carbon and Soil Texture Estimations. Remote Sens. 2016, 8, 927. [Google Scholar] [CrossRef]
- Heldens, W.; Heiden, U.; Esch, T.; Stein, E.; Müller, A. Can the Future EnMAP Mission Contribute to Urban Applications? A Literature Survey. Remote Sens. 2011, 3, 1817–1846. [Google Scholar] [CrossRef]
- Clark, M.; Roberts, D. Species-Level Differences in Hyperspectral Metrics among Tropical Rainforest Trees as Determined by a Tree-Based Classifier. Remote Sens. 2012, 4, 1820–1855. [Google Scholar] [CrossRef]
- Roy, S.; Krishna, G.; Dubey, S.R.; Chaudhuri, B. HybridSN: Exploring 3D-2D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar] [CrossRef]
- Signoroni, A.; Savardi, M.; Baronio, A.; Benini, S. Deep Learning Meets Hyperspectral Image Analysis: A Multidisciplinary Review. J. Imaging 2019, 5, 52. [Google Scholar] [CrossRef]
- Zhao, Y.; Yuan, Y.; Wang, Q. Fast Spectral Clustering for Unsupervised Hyperspectral Image Classification. Remote Sens. 2019, 11, 399. [Google Scholar] [CrossRef]
- Mehta, A.; Dikshit, O. Segmentation-Based Projected Clustering of Hyperspectral Images Using Mutual Nearest Neighbour. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5237–5244. [Google Scholar] [CrossRef]
- Nyasaka, D.; Wang, J.; Tinega, H. Learning Hyperspectral Feature Extraction and Classification with ResNeXt Network. arXiv 2020, arXiv:2002.02585. [Google Scholar]
- Archibald, R.; Fann, G. Feature Selection and Classification of Hyperspectral Images With Support Vector Machines. Geosci. Remote Sens. Lett. IEEE 2007, 4, 674–677. [Google Scholar] [CrossRef]
- Rasti, B.; Ghamisi, P.; Ulfarsson, M. Hyperspectral Feature Extraction Using Sparse and Smooth Low-Rank Analysis. Remote Sens. 2019, 11, 121. [Google Scholar] [CrossRef]
- Ranjan, S.; Nayak, D.; Kumar, S.; Dash, R.; Majhi, B. Hyperspectral image classification: A k-means clustering based approach. In Proceedings of the 2017 4th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 6–7 January 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Lunga, D.; Prasad, S.; Crawford, M.; Ersoy, O. Manifold-Learning-Based Feature Extraction for Classification of Hyperspectral Data: A Review of Advances in Manifold Learning. IEEE Signal Process. Mag. 2014, 31, 55–66. [Google Scholar] [CrossRef]
- Gao, L.; Zhao, B.; Jia, X.; Liao, W. Optimized Kernel Minimum Noise Fraction Transformation for Hyperspectral Image Classification. Remote Sens. 2017, 9, 548. [Google Scholar] [CrossRef]
- Bakken, S.; Orlandic, M.; Johansen, T. The effect of dimensionality reduction on signature-based target detection for hyperspectral remote sensing. In Proceedings of the CubeSats and SmallSats for Remote Sensing III, San Diego, CA, USA, 30 August 2019; p. 20. [Google Scholar] [CrossRef]
- Luo, G.; Chen, G.; Tian, L.; Qin, K.; Qian, S.E. Minimum Noise Fraction versus Principal Component Analysis as a Preprocessing Step for Hyperspectral Imagery Denoising. Can. J. Remote Sens. 2016, 42, 106–116. [Google Scholar] [CrossRef]
- Kovács, Z.; Szabo, S. An interactive tool for semi-automatic feature extraction of hyperspectral data. Open Geosci. 2016, 8. [Google Scholar] [CrossRef]
- Frassy, F.; Dalla Via, G.; Maianti, P.; Marchesi, A.; Rota Nodari, F.; Gianinetto, M. Minimum noise fraction transform for improving the classification of airborne hyperspectral data: Two case studies. In Proceedings of the 2013 5th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Gainesville, FL, USA, 26–28 June 2013. [Google Scholar] [CrossRef]
- Bachmann, C.; Ainsworth, T.; Fusina, R. Exploiting manifold geometry in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 441–454. [Google Scholar] [CrossRef]
- Mehta, A.; Dikshit, O. Segmentation-based clustering of hyperspectral images using local band selection. J. Appl. Remote Sens. 2017, 11, 015028. [Google Scholar] [CrossRef]
- Dey, V.; Zhang, Y.; Zhong, M. A review on image segmentation techniques with remote sensing perspective. In Proceedings of the ISPRS TC VII Symposium—100 Years ISPRS, Vienna, Austria, 5–7 July 2010; Volume 38. [Google Scholar]
- Tarabalka, Y.; Benediktsson, J.; Chanussot, J. Spectral—Spatial Classification of Hyperspectral Imagery Based on Partitional Clustering Techniques. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2973–2987. [Google Scholar] [CrossRef]
- Mehta, A.; Dikshit, O. Projected clustering of hyperspectral imagery using region merging. Remote Sens. Lett. 2016, 7, 721–730. [Google Scholar] [CrossRef]
- Mehta, A.; Ashapure, A.; Dikshit, O. Segmentation Based Classification of Hyperspectral Imagery Using Projected and Correlation Clustering Techniques. Geocarto Int. 2015, 31, 1–28. [Google Scholar] [CrossRef]
- Aggarwal, C.; Procopiuc, C.; Wolf, J.; Yu, P.; Park, J. Fast Algorithms for Projected Clustering. ACM Sigmod Rec. 1999, 28, 61–72. [Google Scholar] [CrossRef]
- Pavithra, M.; Parvathi, R. A survey on clustering high dimensional data techniques. Int. J. Appl. Eng. Res. 2017, 12, 2893–2899. [Google Scholar]
- Veganzones, M.; Tochon, G.; Dalla Mura, M.; Plaza, A.; Chanussot, J. Hyperspectral Image Segmentation Using a New Spectral Unmixing-Based Binary Partition Tree Representation. IEEE Trans. Image Process. Publ. IEEE Signal Process. Soc. 2014, 23. [Google Scholar] [CrossRef] [PubMed]
- Valero, S.; Salembier, P.; Chanussot, J. Hyperspectral Image Representation and Processing With Binary Partition Trees. IEEE Trans. Image Process. Publ. IEEE Signal Process. Soc. 2012, 22. [Google Scholar] [CrossRef] [PubMed]
- Tarabalka, Y.; Chanussot, J.; Benediktsson, J. Segmentation and classification of hyperspectral images using watershed transformation. Pattern Recognit. 2010, 43, 2367–2379. [Google Scholar] [CrossRef]
- Calderero, F.; Marques, F. Region Merging Techniques Using Information Theory Statistical Measures. IEEE Trans. Image Process. 2010, 19, 1567–1586. [Google Scholar] [CrossRef] [PubMed]
- Kanungo, T.; Mount, D.; Netanyahu, N.; Piatko, C.; Silverman, R.; Wu, A. An Efficient K-Means Clustering Algorithm Analysis and Implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Ahmed, M.; Seraj, R.; Islam, S. The k-means Algorithm: A Comprehensive Survey and Performance Evaluation. Electronics 2020, 9, 1295. [Google Scholar] [CrossRef]
- Valero, S.; Salembier, P.; Chanussot, J. Comparison of merging orders and pruning strategies for Binary Partition Tree in hyperspectral data. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 2565–2568. [Google Scholar] [CrossRef]
- Valero, S. Hyperspectral Image Representation and Processing with Binary Partition Trees. Ph.D. Thesis, Universitat Politècnica de Catalunya (UPC), Barcelona, Spain, 2011. [Google Scholar]
- Valero, S.; Salembier, P.; Chanussot, J.; Cuadras, C. Improved Binary Partition Tree construction for hyperspectral images: Application to object detection. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 2515–2518. [Google Scholar] [CrossRef]
- Hyperspectral Remote Sensing Scenes. 2018. Available online: http://lesun.weebly.com/hyperspectral-data-set.html (accessed on 2 September 2019).
- Hyperspectral Remote Sensing Scenes. 2018. Available online: http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes (accessed on 2 September 2019).
- Zhao, C.; Yao, X.; Huang, B. Real-Time Anomaly Detection Based on a Fast Recursive Kernel RX Algorithm. Remote Sens. 2016, 8, 1011. [Google Scholar] [CrossRef]





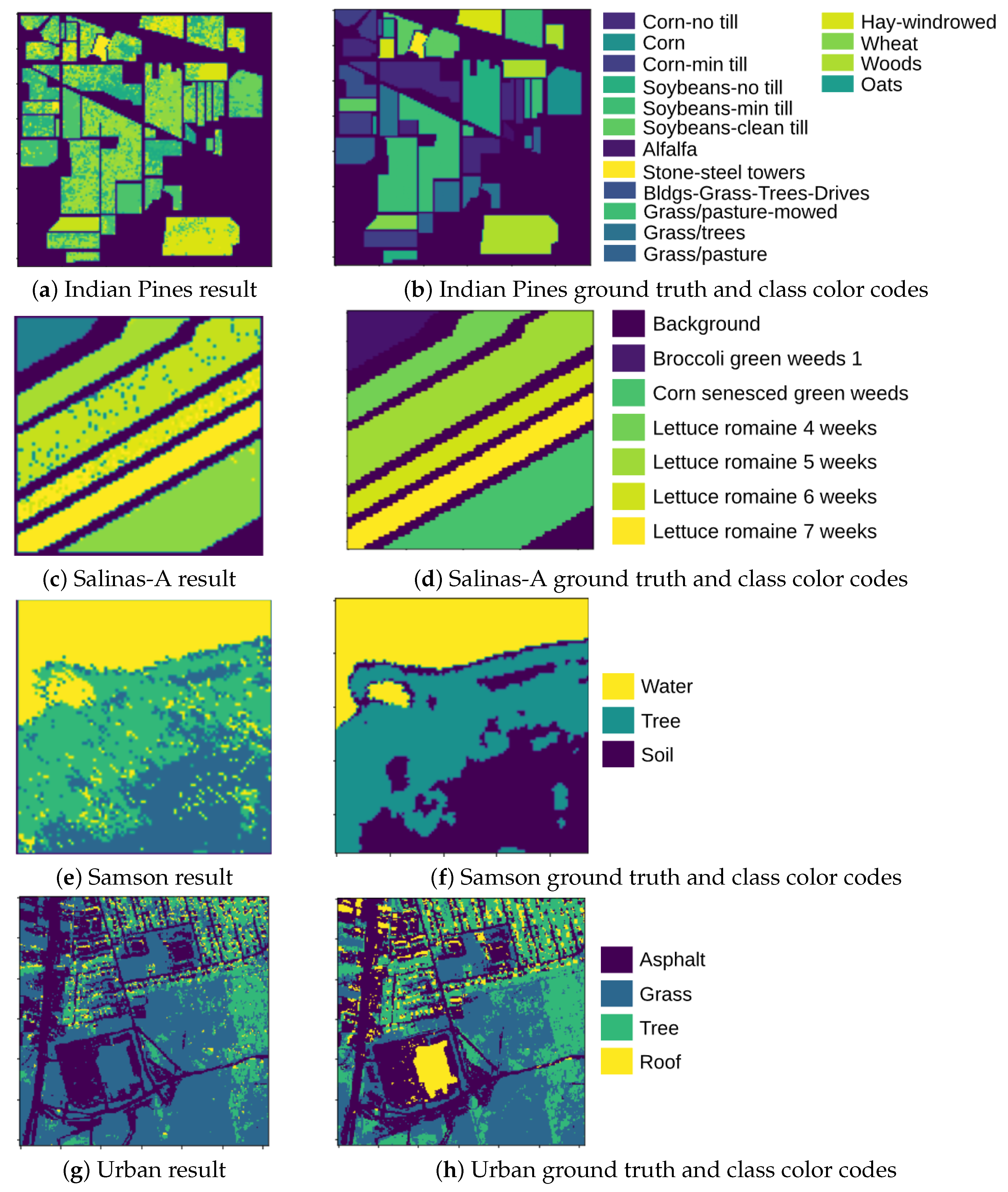
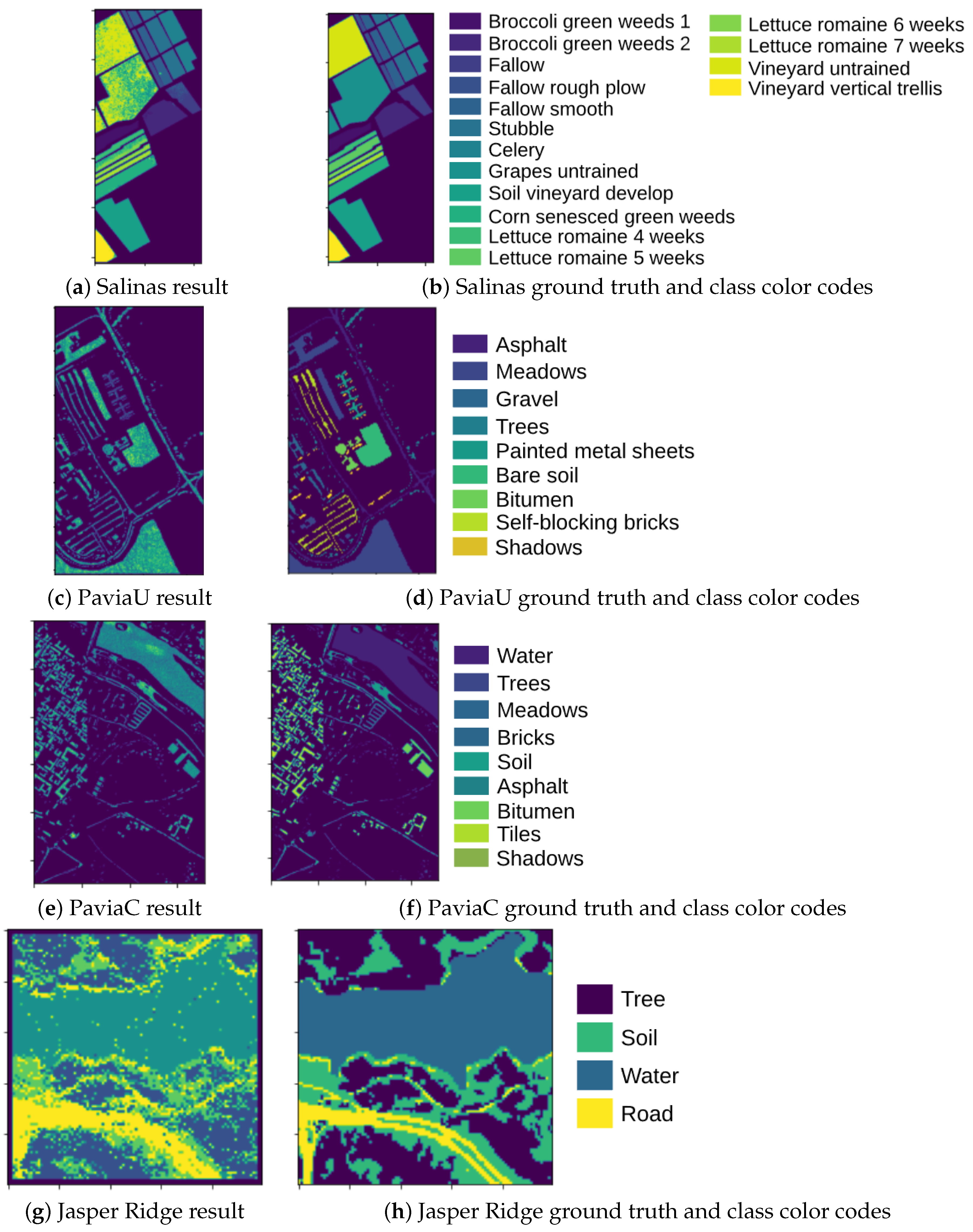
| Data Set | Number of Clusters (k) | Varying k (Steps of 2) |
|---|---|---|
| Salinas | 16 | 16 to 26 |
| PaviaU | 9 | 9 to 19 |
| Indian Pines | 16 | 16 to 26 |
| Salinas-A | 6 | 6 to 16 |
| Samson | 3 | 3 to 13 |
| Urban | 4 | 4 to 14 |
| Jasper Ridge | 4 | 4 to 14 |
| PaviaC | 9 | 9 to 19 |
| Data Set | Framework | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PCMNN [7] | FSC [6] | CLUS-BPT | |||||||||
| NMI | k | Purity | NMI | k | Purity | NMI | k | ||||
| Salinas | 0.8586 | 82.06 | 24 | 0.62 | 0.72 | 16 | 0.7638 | 0.8882 | 89.37 | 26 | 48 |
| PaviaU | 0.5654 | 57.98 | 13 | 0.61 | 0.57 | 16 | 0.6996 | 0.5806 | 82.44 | 17 | 400 |
| Indian Pines | - | - | - | 0.46 | 0.49 | 16 | 0.5758 | 0.6025 | 57.75 | 20 | 32 |
| Salinas-A | - | - | - | 0.85 | 0.81 | 6 | 0.8753 | 0.8572 | 91.22 | 6 | 6 |
| Samson | - | - | - | 0.91 | 0.75 | 3 | 0.6896 | 0.6698 | 87.93 | 3 | 6 |
| Urban | - | - | - | 0.51 | 0.33 | 4 | 0.90 | 0.3906 | 79.96 | 4 | 128 |
| Jasper Ridge | - | - | - | 0.91 | 0.76 | 4 | 0.7652 | 0.5658 | 76.73 | 4 | 32 |
| PaviaC | - | - | - | - | - | - | 0.8412 | 0.8369 | 83.97 | 9 | 150 |
| Framework | PCMNN CT(s) [7] | FSC CT(s) [6] | CLUS-BPT CT(s) | |
|---|---|---|---|---|
| Data Set | ||||
| Salinas | 134.63 | 1.62 | 7.48 | |
| PaviaU | - | 1.34 | 58.2 | |
| Indian Pines | - | 0.53 | 2.72 | |
| Salinas-A | - | 0.06 | 1.56 | |
| Samson | - | 0.10 | 1.52 | |
| Urban | - | 0.41 | 2.15 | |
| Jasper Ridge | - | 0.11 | 2.78 | |
| PaviaC | - | - | 18.26 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ismail, M.; Orlandić, M. Segment-Based Clustering of Hyperspectral Images Using Tree-Based Data Partitioning Structures. Algorithms 2020, 13, 330. https://doi.org/10.3390/a13120330
Ismail M, Orlandić M. Segment-Based Clustering of Hyperspectral Images Using Tree-Based Data Partitioning Structures. Algorithms. 2020; 13(12):330. https://doi.org/10.3390/a13120330
Chicago/Turabian StyleIsmail, Mohamed, and Milica Orlandić. 2020. "Segment-Based Clustering of Hyperspectral Images Using Tree-Based Data Partitioning Structures" Algorithms 13, no. 12: 330. https://doi.org/10.3390/a13120330
APA StyleIsmail, M., & Orlandić, M. (2020). Segment-Based Clustering of Hyperspectral Images Using Tree-Based Data Partitioning Structures. Algorithms, 13(12), 330. https://doi.org/10.3390/a13120330






