A Hybrid Metaheuristic Algorithm for the Efficient Placement of UAVs

Abstract

This work addresses the problem of using Unmanned Aerial Vehicles (UAV) to deploy a wireless aerial relay communications infrastructure for stations scattered on the ground. In our problem, every station in the network must be assigned to a single UAV, which is responsible for handling all data transfer on behalf of the stations that are assigned to it. Consequently, the placement of UAVs is key to achieving both network coverage and the maximization of the aggregate link capacities between UAVs and stations, and among the UAVs themselves. Because the complexity of this problem increases significantly with the number of stations to cover, for a given fixed number p of available UAVs, we model it as a single allocation p-hub median optimization problem, and we propose a hybrid metaheuristic algorithm to solve it. A series of numerical experiments illustrate the efficiency of the proposed algorithm against traditional optimization tools, which achieves high-quality results in very short time intervals, thus making it an attractive solution for real-world application scenarios.

1. Introduction

Unmanned Aerial Vehicles (UAV), also known as remotely piloted aircraft, were initially used in military applications. Nevertheless, with the development of various technologies in the telecommunications industry, UAVs have become more affordable and accessible to civilian and commercial applications [1]. This has eased the use and allowed for the application of multiple UAVs in singular tasks, such as traffic control, cargo transport, emergency and rescue operations, weather monitoring, among others. In these tasks, it is expected that UAVs are enabled with communication resources in order to allow the exchange of information with other agents of the environment in a bidirectional way.

The use of UAVs in emergency and unexpected circumstances, such as disaster relief and service recovery, has become a focus of study, because the deployment of terrestrial infrastructure is economically infeasible or simply not doable. Compared to a single UAV, there are several advantages to establishing and using a system with multiple UAVs, which can be enumerated as follows [2]: (i) the purchase and maintenance of several small aircrafts is cheaper than a large UAV with a size equivalent to the group formed by small ones; (ii) the use of a large UAV scarcely increases the coverage area, whereas multiple UAVs increase the scalability of the operation easily, and (iii) in the event of UAV failure, the possibility of “survival” or continuity in the execution of a multi-UAV mission is much greater than in a mission in which the failing UAV is the only executor. Naturally, the deployment of an aerial networking infrastructure formed by multiple UAVs also brings about a number of challenges and potential disadvantages if compared to the use of a single UAV. In particular, aerial multi-hop communication introduces additional delays to packet flows due to a number of factors, such as (i) the typical store-and-forward operation of UAVs when relaying packets to each other; ($ii$) the mechanisms of the medium access control (MAC) protocol in place to share the wireless channel(s) and support reliable data transfer; ($iii$) packet buffering in all UAVs; and, ($iv$) distributed user association, authentication procedures, etc. Needless to say, other issues arise that are related to trust and security of many deployed UAVs [3,4].

In this work, we look at the problem of UAV-assisted wireless communications [5], where UAVs are deployed to establish an aerial communication platform to provide wireless access for terrestrial users from the sky. In other words, the deployed UAVs do not generate their own data packets. Instead, the UAVs simply serve as aerial relays to connect users on the ground. We consider that each station is assigned to a single UAV, which is responsible for carrying data traffic to or from users assigned to other UAVs. Hence, different from recent work in the literature, where the UAV placement problem seeks to maximize the number of covered users [6,7] or to minimize the number of required UAVs [8,9], our goal is to maximize the total (sum) link capacity of the aerial communication infrastructure (considering both air-to-ground (A2G) and air-to-air (A2A) link capacities) given a fixed number of UAVs that are placed at the same (given) altitude from the ground. For that, and in line with other works [6,7,8,9,10,11], perfect user location information (ULI) is assumed. Because of such constraints, there is no minimum link rate requirement in our problem, and the provisioning of connectivity to all users is of paramount importance. In this sense, the solution we provide is best suited to application scenarios related to disaster relief, rescue operations, and provisioning of user connectivity in remote or hostile environments, for example. We recognize the UAV placement problem at hands as a typical p-hub median problem, according to which the goal is to determine the location of p “facilities” in a network of n nodes, while the total “distance” between demanding nodes and the nearest facility is minimized. Given the well-known combinatorial complexity of this problem, we propose and analyze two optimization strategies: (i) the application of CPLEX’s branch-and-cut optimizer (version 12.10.0) and (ii) the biased randomized-Iterated Local Search (BR-ILS) metaheuristic algorithm, which is capable of delivering close-to-optimal results under significant gains in computational time, with respect to the former method.

The rest of the paper is organized, as follows: Section 2 presents a review on related work; Section 3 presents the system model of the UAVs placement problem; Section 4 presents the methodology to solve the aforementioned problem; Section 5 reports the computational results; and, finally, Section 6 concludes with a summary and future research.

2. Related Work

Employing UAVs as aerial communication platforms has become a rising research topic. As mentioned before, UAV-aided wireless communications have found a wide range of applications during the last decade [12,13,14,15] and, more recently, many authors have addressed the placement problem. In particular, in [15], the authors dealt with the UAV placement problem with non-orthogonal multiple access techniques and proposed a machine learning approach in order to adjust the UAVs’ positions within the three-dimensional space, when the ground users are roaming. The Q-learning-based algorithm was applied when UAVs were moving. The authors tested two different scenarios: a single UAV case considering three users that were uniformly distributed within an area of 1 km × 1 km, and a multiple-UAV case. Unfortunately, the work did not attempt to solve the problem for large network sizes. Besides, a unified spatial analytical approach for non-orthogonal-aided UAV networks is desired, as the authors themselves pointed out. The proposed machine learning framework left some open issues such as the time it takes the algorithm to be tested and the considerable delays if the number of users is large.

In [16], the authors proposed a minimax facility location model for optimizing network delays that are caused by topological arrangements, which occur during UAV deployment in heterogeneous networks, and their mapping to a particular demand area. Instead of considering data link rates, the proposed model was aimed in the direction of the delay optimization by accurate positioning of the UAVs. The authors solved the question using entropy nets, which the authors considered to be the neural network version of decision trees. In that approach, a decision is taken while using fewer neural connections. The proposed approach was tested in a network of up to 500 users and six UAVs in an area of 10 km × 10 km. Later, the same authors proposed a similar approach to overcome the two problems, namely, the Macro Base Station decision problem and the cooperative UAV allocation problem [17]. Howeber, the proposed approach proved to be time consuming and the delays varied with an increase of the size network, since more iterations were required to localize the additional UAVs.

In [18], the authors studied the deployment of a Software Defined Network (SDN)-based UAV network, where the UAVs act as forwarding elements and the SDN controller manages the network. In particular, the issue of control overhead caused by the UAV-SDN controller communication was discussed. Here, the authors have not considered the delay due to data link rates, but, due to multi-hop communication, the UAVs are interconnected and each control packet between UAVs and the SDN controller will be transmitted multiple times. The authors proposed a scheme involving the buffering of update packets at intermediate nodes and merging of control packets to achieve a trade-off between control overhead and delay. The authors tested the proposed scheme in a network with a total of 36 UAVs deployed in an 1 km × 1 km area, with the controller being placed at some specific corner. The simulations results have shown that, as buffering time increases, the delay increases, as expected, but overhead decreases.

In [19], the authors investigated the problem of positioning UAVs in a wireless ad hoc network. They modeled the problem as a facility location problem and proposed a quadratic unconstrained binary optimization model. The main objective was to improve the connectivity at the shortest total distance and to maximize the linkage (downlink). The problem was solved using CPLEX’s branch-and-cut optimizer. Test problems of size $m=10$ to 100 for the wireless nodes, and $n=3$ to 7 for the UAVs were generated and solved. Despite the effort of the authors for solving different scenarios varying the number of users and UAVs, large networks were not considered. On the other hand, in [20], the authors proposed a relay placement mechanism in order to find the ideal location for UAVs that act as relay nodes, in order to support live video transmissions with satisfactory quality of experience to the users and improving the connectivity. The authors considered a flying ad hoc network scenario implemented on the Mobile MultiMedia Wireless Sensor Network (M3WSN) OMNeT++ framework [21] composed of 30 UAVs moving over an area of 150 m × 150 m. Although the results appear to be satisfactory in terms of maintaining network connectivity while supporting real time multimedia transmissions, the entire terrain scenario can be considered reasonably small.

In [22], the authors considered the final deployment location of an UAV facility in a three-dimensional space with the aim of reaching a balance between service quality and interference. The authors took different scenarios into account, where either each user is selfish, and prefers the UAV to be located as close to himself as possible, or not, and they proposed a strategy-proof mechanism to overcome this issue. The success of the mechanism depends on whether the users report their locations truthfully. The authors presented empirical analysis in a single UAV scenario. In [23], the authors addressed the mission assignment and location management for UAVs in a mission-critical flying ad hoc network. The authors considered a scenario where the origin node is the ground control station and the destination node is a mission-performing UAV. Thus, the model aims to find UAVs’ optimal mission assignment and locations together by maximizing the weighted sum of the communication performance and the mission performance functions. They assumed that UAVs that are not assigned to any mission are operated as relay nodes. The authors considered the communication performance as the lowest channel capacity among the links belonging to routing paths. In order to evaluate the communication performance, the authors did not consider area or coverage nor delay or data link rates, instead they considered a function in terms of the mission assignments, the locations of all nodes and the routing protocol in use. They proposed a Particle Swarm Optimization algorithm in order to solve the joint problem. A simulation scenario with 7 to 20 available UAVs and two missions was considered.

In [24], the authors dealt with the UAV placement problem in a multi-channel UAV network, in order to be resilient to any device or link capability loss. The authors modeled the problem that was based on Coulumb’s law, with users being represented as positive charges and drones as negative charges. In this model, UAVs are supposed to be attracted by users within their sensing range. By doing so, the authors focused on an initial UAV positioning in order to seek an optimal coverage. In the proposed model, the authors took into account the mean lifetime of the drones, the IEEE 802.11 communication protocol and the drones capacity. The proposal was evaluated with the help of a simulator developed by the authors, considering 500 users and up to 10 UAVs. The proposed framework was set up for particular events, such as a public gathering or a disaster situation where the network should be quickly deployed. However, the work failed to present numerical values regarding the time that is spent on finding a solution and the delay related to the data link rate.

More recently, in [25], the authors investigated the router node placement problem within a specific geographical area. The idea was to form a viable, UAV-composed, ad hoc wireless mesh network that has performance measures optimized via a rapidly exploring random trees-based algorithm. The authors proposed a model that uses network coverage as an objective function which asses the total geographical area covered by the wireless mesh network. The authors did not focus on the delay related to the data link rates but on the network connectivity; thus, they included a penalty function that evaluate how infeasible a particular solution is based on a distance measure. The authors considered three different cases consisting of 16, 32, and 200 mesh routers in areas of $32\times 32$, $64\times 64$, and 4000 m × 4000 m, respectively. The performance of the proposed algorithm was compared with two optimization techniques: Particle Swarm Optimization and covariance matrix adaptation evolution strategy; computation times at 20.1 s for large instances were presented.

Despite the efforts and methodologies that were proposed by many authors, there are still open questions that need to be answered in order to effectively solve the placement of UAVs. One concern is regarding the requirement of a more autonomous and quick response by current applications when deploying UAV networks. Another matter is related to the placement of UAVs in disaster scenarios. In such events, it is preferable to obtain solutions to UAV placement through algorithms that do not consume too much time. On the other hand, a framework for UAV networks that can be effortlessly changed to fit different network scenarios in terms of number of users and geographical area dimensions is desired. Moreover, the performance of an UAV network is usually measured in terms of network connectivity, which, in turn is focused on the distances between UAVs and users or delay due to propagation delay. However, data rate links play an important role when designing such networks and, therefore, the focus on the impact of this measure may help to design efficient placement of UAVs.

3. System Model and Problem Formulation

In this section, the problem of placing UAVs to build an aerial relay infrastructure for users scattered on the ground is modeled as a single allocation p-hub median problem [26]. The advantage of modeling the problem in this way is that we can limit the number of UAVs needed beforehand, which, in turn, can be adjusted depending of the size of the network. Moreover, by doing so, we consider UAV-ground and UAV-UAV channels. When considering these two types of channels, the UAV-aided communications exhibit several unique characteristics when compared to terrestrial communication networks [1]. In addition, we take network coverage at the expense of the overall increase in the link capacity of the network into account.

The p-hub median problem is a classic location problem in which the objective is to determine the placement of p facilities (called medians) in a graph of n nodes, that minimizes the sum of distances between each demanding node and the nearest median. Hence, the positioning of multiple UAVs as aerial relays can be regarded as a type of location problem if the individual nodes on the ground are seen as the clients (demanding nodes), while the UAVs are treated as the p medians providing a service (which, in our case, consists of relaying data packets to or from the nodes assigned to them). As previously mentioned, perfect user location information is also assumed, and all UAVs must be placed at a fixed altitude h from the terrain (also defined beforehand). Due to these constraints and conditions, no minimum data link rate requirement is imposed, and the goal is to determine the placement of UAVs in the network so that the total (sum) link capacity is maximized, while every user on the ground is assigned to only one UAV.

3.1. The p-Median Optimization Problem

We use the quadratic integer programming formulation based on the very first model proposed by O’kelly [27], which has been extensively applied to solve small to large instances of p-hub median problems. Hence, before we apply it to the UAV-assisted communications infrastructure optimization problem, we first describe its general formulation according to the key variables, cost function, and optimization constraints.

The classical p-hub median problem consists of locating p hubs from a set of n nodes in such a way that the average distance between hubs and nodes is minimized. Thus, it is assumed that there is a set N of graph nodes, with cardinality $\left|N\right|=n$, which are respectively associated with two-dimensional (2D) coordinates $(x,y)$, previously known. For every pair of users i and j, let $W_{ij}$ represent “flow units” that need to be transferred from a source node i to a destination node j across either one or two hubs only. The cost of collecting $W_{ij}$ units of flow from a source node i to a destination node j is denoted by $T_{ij}$. Given that we want to investigate whether a node i must (i) become one of the p hubs or (ii) be assigned (or not) to a given hub k, the decision variable is represented by $X_{ik}$, which is defined as

$$\begin{array}{cc}\hfill X_{ik}& =\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathrm{user}i\mathrm{is}\mathrm{assigned}\mathrm{to}\mathrm{hub}k\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

The particular case $X_{kk}=1$ means that user k has been converted into a hub. This is because the only locations that are searched to place the hubs are the positions of the users themselves. This means that, out of the n positions available, p of them will be occupied by a hub (i.e., a user will become a hub). Accordingly, the uncapacitated single allocation p-hub median problem can be formulated as follows:

$$\begin{array}{cc}\hfill \mathrm{Minimize}& {\displaystyle \sum _{i,j,k,l\in N}{W}_{ij}(T_{ik}{X}_{ik}+T_{kl}{X}_{ik}{X}_{jl}+T_{jl}{X}_{jl})}\end{array}$$

(1)

$$\begin{array}{cc}\mathrm{Subject\; to}:\hfill & {\displaystyle \sum _{k=1}^n{X}_{kk}=p,}\hfill \end{array}$$

(2)

$$\begin{array}{ccc}& {\displaystyle \sum _{k=1}^n{X}_{ik}=1,}& \hfill \forall i\in N\end{array}$$

(3)

$$\begin{array}{ccc}& X_{ik}\le X_{kk},& \hfill \forall i,k\in N\end{array}$$

(4)

$$\begin{array}{ccc}& X_{ik}\in \{0,1\},& \hfill \forall i,k\in N\end{array}$$

(5)

Equation (1) describes the cost function as the total sum transfer and transmission costs from origin user to its associated hub, between hubs, and from the destination hub to the destination user. Equation (2) gives the exact number of p hubs to be placed in the network. Equation (3) is the single allocation constraint, ensuring that the transmission from any source to user i and vice-versa, i.e., from user i to any destination node is only sent through the p-hub to which the user i is assigned. Equation (4) guarantees that a user cannot have a direct link to a node unless it is a hub, thus avoiding a direct path between origin and destination users and, finally, Equation (5) states that the decision variable must be binary (0 or 1).

The aforementioned equations summarize the problem, which is, finding the optimal locations of the p hubs (a subset of the nodes set), as well as the allocation of the remaining nodes to the hubs. This particular quadratic programming formulation has $\mathcal{O}\left(n^2\right)$ variables and it is hard to solve due to its non-convexity. Despite the possibility of conversion into a mixed integer linear program, it has been demonstrated that the linearization has $\mathcal{O}\left(n^3\right)$ variables and constraints, thus restricting the size of problems that may be solved [28,29].

3.2. System Model

In this section, we describe how we model the UAV placement problem as an uncapacitated single allocation p-hub median problem. We seek to find the locations of p UAVs that maximize the total (sum) link capacity, while ensuring that each of the n users are assigned to only one UAV, as mentioned before. Thus, because we target the application of the UAV-assisted relay infrastructure to scenarios, such as disaster relief, rescue operations, remote or hostile environments, etc., no minimum requirements are imposed on data link rates (i.e., we seek to provide the best possible data link rates under given circumstances). For that, we consider the Shannon capacity to express the maximum data rate (expressed in b/s) that can be achieved at either air-to-ground (A2G) or air-to-air (A2A) data link between two nodes i and k, i.e.,

$$\begin{array}{c}\hfill C_{ik}=B{log}_2\left(1+\frac{S_{ik}}{N}\right),\end{array}$$

(6)

where B denotes the channel bandwidth (Hz), N is the noise power within the channel bandwidth B, and $S_{ik}$ denotes the signal power received on either side of the A2G link (user i and UAV k), or in either side of the A2A link (UAV i and UAV k). In this scenario, the UAVs act as “base stations” to users on the ground, relaying data packets to or from any user assigned to it. Consequently, every transfer of data packets between a pair of users has to go through either two hops (one UAV assigned to both users) or three hops (two UAVs, each assigned to a distinct user in the pair). Additionally, the UAVs are responsible for the scheduling of all transmissions among users assigned to them, and they do so in a way that no interference occurs (i.e., all transmissions are assumed to be collision-free). Note that we are only concerned with establishing the aerial relay infrastructure by focusing on determining the optimal placement of UAVs that render the highest total (sum) rate capacity. Therefore, we do not consider flows of data packets between pairs of users, i.e., we are not concerned with data throughput in this work. This also means that signal interference due to the activity of other (distant) users or UAVs is not taken into account and, therefore, only thermal background noise is considered (assumed to be additive white Gaussian noise (AWGN)).

As far as the channel propagation model is concerned, we assume that all of the UAVs are placed at a constant altitude h from the ground (defined beforehand), and they are all in Line-of-Sight (LOS) to each other and to every other user on the ground. Consequently, the Friis path-loss propagation model is assumed [30] for both A2G and A2A channels, which means that the received signal power $S_{ik}$ (in dBm) between a node i and a node k will be given by

$$S_{ik}=P_t+G_t+G_r-20{log}_{10}\left(\frac{4\pi f_c}{c}\right)-20{log}_{10}\left(d_{ik}\right),$$

(7)

where $P_t$ is the transmit power (measured in dBm), $G_t$ and $G_r$ are the transmit and receive antenna gains, respectively (expressed in dBi), $f_c$ is the carrier frequency (in Hz), c is the speed of ligth ($3\times {10}^8$ m/s), and $d_{ik}$ is the absolute distance (or LOS distance) between node i and node k. Thus, for an A2G link, the absolute distance between user i and UAV k will be given by $d_{ik}=\sqrt{h^2+r_{ik}^2}$, where $r_{ik}$ denotes the Euclidean distance between user i’s location on the ground and the $(x,y)$ coordinates of UAV k on the ground (i.e., its projection on the ground). Likewise, because all of the UAVs are located at the same altitude h, the absolute distance between UAV i and UAV k is simply given by $d_{ik}=r_{ik}$.

We first need to note that we are not dealing with specific flows of data packets between users in order to cast the problem of placing UAVs as aerial relays to users on the ground within the framework of a p-median optimization problem, as mentioned previously. Therefore, the term $W_{ij}$ in Equation (1) simplifies to $W_{ij}=1,\forall i,j\in N$. Moreover, because the problem formulation is posed as a minimization optimization problem, we consider the inverse of each link capacity as the corresponding link cost, i.e., the time needed to transmit a bit. Therefore, we let

$$\begin{array}{cc}\hfill T_{ij}& =\frac{1}{C_{ij}}\hfill \end{array}$$

(8)

to express the link cost between node i and node j, i.e., a link either connecting a user i to an UAV j (A2G link), or an UAV i to an UAV j (A2A link).

Note that, according to the general description of the p-hub median problem, the only locations that are searched for placing the hubs are the locations of the users themselves. In our case, this means that every UAV will be placed right above a distinct user on the ground. Consequently, because all of the UAVs are located at the same altitude h, the total cost introduced by the corresponding p A2G links to users right below the UAVs are constant across all possible combination of UAV placements. For this reason, we do not need to take those costs into account. Finally, we can treat the optimization of UAV placement as a p-hub median problem after appropriate modifications to the original model presented in Equation (1), as follows

$$\begin{array}{ccccc}& \mathrm{Minimize}:\hfill & & {\displaystyle \sum _{i,j,k,l\in N}{T}_{ik}{X}_{ik}+T_{kl}{X}_{ik}{X}_{jl}+T_{jl}{X}_{jl}}\hfill & \hfill \end{array}$$

(9a)

$$\begin{array}{cccc}& \mathrm{Subject\; to}:\hfill & & \sum _{k=1}^n{X}_{kk}=p,\hfill \end{array}$$

(9b)

$$\begin{array}{cccc}& & & \sum _{k=1}^n{X}_{ik}=1,\forall i\in N\hfill \end{array}$$

(9c)

$$\begin{array}{cccc}& & & X_{ik}\le X_{kk}\forall i,k\in N\hfill \end{array}$$

(9d)

$$\begin{array}{cccc}& & & X_{ik}\in \{0,1\}\forall i,k\in N\hfill \end{array}$$

(9e)

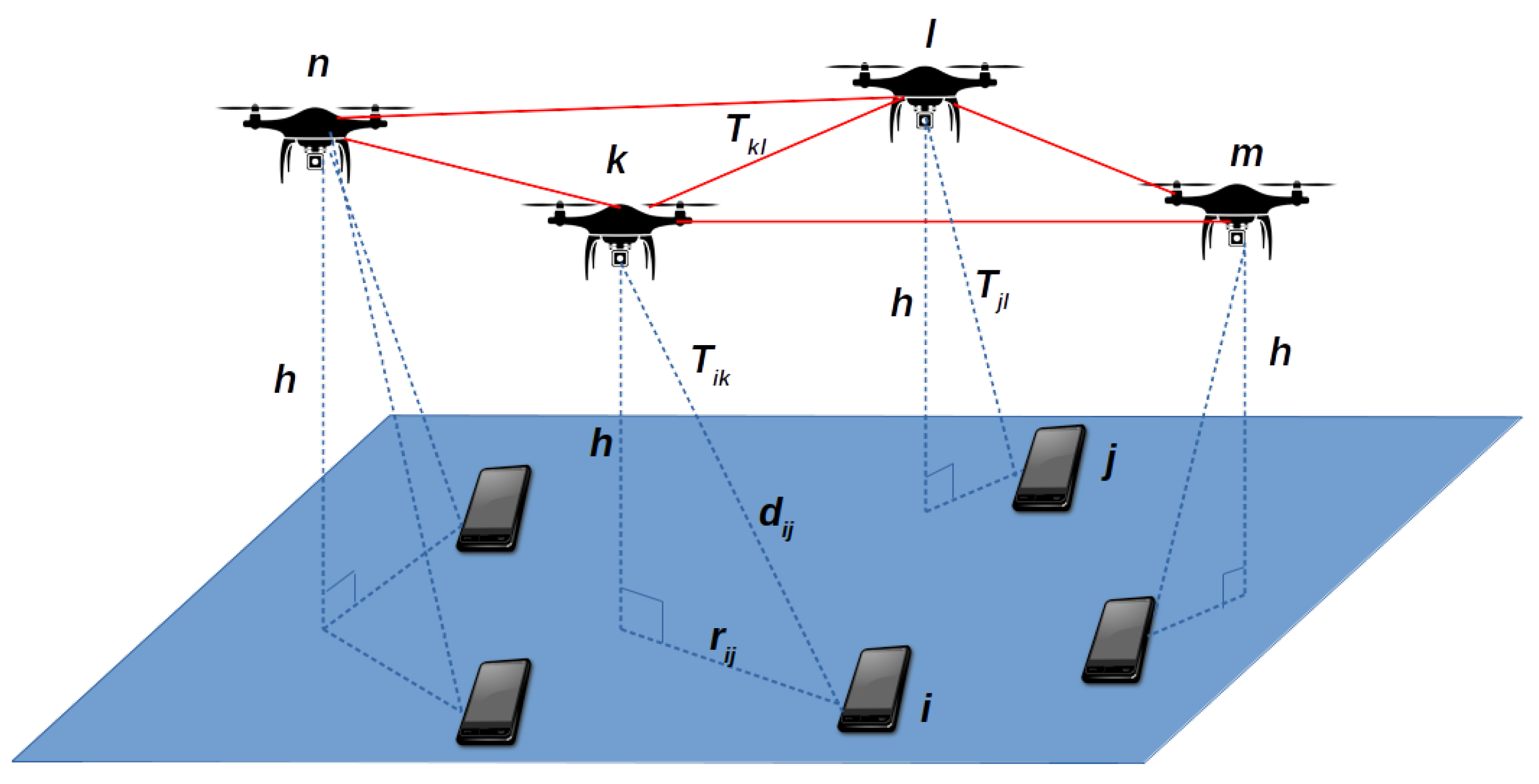
Figure 1 depicts the general network scenario of our problem. The full red lines indicate the links between UAVs, while the dashed blue lines show the links between ground users and UAVs. It also displays the key variables used in the formulation of the problem, such as the altitude h of UAVs, the LOS distances between users and UAVs (e.g., $d_{ij}$), and Euclidean distances between users and UAVs’ projections on the ground (e.g., $r_{ij}$). Figure 1 shows an example where user i can communicate with user j by using the three-hop path that contains UAV k (with link cost $T_{ik}$), UAV l (with link cost $T_{kl}$), and user j (with link cost $T_{jl}$).

The quadratic integer linear program that is posed by Equation (9a)–(9e) can be linearized and solved by well-known optimization tools, e.g., CPLEX’s branch-and-cut optimizer. Nevertheless, as discussed in Section 3.1, the problem may become intractable due to the excessive number of variables and constraints, thus, in the following, we also propose a hybrid optimization methodology integrating a biased randomized (BR) technique with the popular Iterated Local Search (ILS) algorithm, which provides further improvements for the execution time and problem size.

4. The Biased Randomized and Iterated Local Search (BR-ILS) Algorithm

The metaheuristic methodology integrates a Biased Randomized (BR) technique and the Iterated Local Search (ILS) method. The interest of applying such a hybrid strategy is due to the capacity that these techniques have for dealing with different real-world applications. It has been observed that population-based metaheuristics are predominant over single-solution ones when designing communication networks [31]. However, single-solution metaheuristics might offer some advantages over populational approaches. In particular, the ILS metaheuristic employs less parameters and might be easier to implement. By including BR within the ILS, some random choices are included, so that different outcomes at each execution of the metaheuristic are generated. Moreover, the uncapacitated single allocation p-hub median problem is a well-known NP-hard problem. Once the set of hubs is found, the sub-problem of optimal allocation of non-hub nodes to hubs is also NP-hard for $p\ge 3$ [32]. Thus, the application of a hybrid methodology seems to be an appropriate choice.

Even though exact optimization methods provide an assured convergence to the optimal solution, the computational complexity with respect to the problem size may cause severe limitations. Thus, for larger instances, an attractive possibility is the adoption of metaheuristic algorithms, which trade optimality for runtime. These methods allow the resolution of large-scale instances of a specific problem by providing satisfactory solutions in a reasonable execution time.

The ILS, which is a single solution-based method based on the Hill Climbing algorithm [33], explores a sequence of solutions that were created as perturbations of a promising candidate solution. The method finds a solution, known as current solution, and goes to a better solution by exploring the search space in steps within its neighborhood. This better solution is then used as the current solution in the next iteration. The process is repeated until a stop condition is fulfilled. In the ILS approach, the perturbations are applied to the current solution to generate neighboring solutions.

A key point of our proposed methodology is the application of BR during the iterative construction of possible solutions. In this regard, every time that the algorithm constructs a solution, the eligible elements of a feasible solution are ranked according to some criteria, and then chosen according to a skewed probability function biased towards the most promising elements. Among the candidate distributions that are to be considered are the geometric distribution and triangular descendent, among others. However, we pick the geometric distribution, because it only has one parameter ($\beta$), which is an attractive choice to be applied in our approach. It assigns higher selection probabilities to more promising solution elements instead of relying, for example, on a restricted candidate list, as some frameworks do [34,35]. This allows us to take advantage of BR features to improve the search space generated by the ILS and, thus, to complement the search [36]. The motivation for implementing hybrid algorithms is usually to obtain better performance approaches that take advantage of the properties of each individual strategy [37]. Algorithm 1 summarizes the logic behind the integration of BR into ILS; hence, named BR-ILS.

The procedure starts by generating an initial solution. The input parameters to the algorithm are: (i) the number of users n and the number of UAVs p; ($ii$) the stopping criterion, in our case, it is based on a time limit maxTime; ($iii$) the percentage $per$ of UAVs of the current solution to be changed during the perturbation stage; ($iv$) the $(x,y)$ coordinates of users coords; (v) the capacity between users capacity; and, ($vi$) the parameter $\beta$ for the geometric distribution function.

Algorithm 1 General Biased Randomized-Iterated Local Search (BR-ILS) Framework.

Require:n, p, maxTime, per, coords, capacity,$\beta$

Ensure: currentSolution ← generateSolution($n,p,$ coords, capacity, $\beta$)     ▹ BR phase 1: bestSolution ← currentSolution 2: credit ← 0 3: while stopping criteria is not met do                  ▹ ILS phase 4:     newSolution ← perturbate(currentSolution, $per$) 5:     proSolution ← localSearch(newSolution) 6:     delta ← cost(currentSolution) - cost(proSolution) 7:     if delta $\ge 0$ then 8:         credit ← delta 9:         currentSolution ← proSolution 10:         if cost(proSolution) < cost(bestSolution) then 11:            bestSolution ← proSolution 12:         end if 13:     else if -delta ≤ credit then 14:         credit ← 0 15:         currentSolution ← proSolution 16:     end if 17: end while 18: return bestSolution

Firstly, the given number p of UAVs among the positioned users are randomly chosen, using a uniform probability distribution. Let k be a candidate location for an UAV and that any user i could be assigned to k. Thus, all of the data transmitted from user i to user j (and vice-versa) has to be sent through UAV k. Accordingly, the inverse of the capacity is computed, i.e., $T_{ik}=1/C_{ik}$. Moreover, if user j is assigned to an UAV l, then the inverse of the capacity between these UAVs, $T_{kl}$, is also computed. In order to evaluate the location k as a potential placement of an UAV, we calculate $T_{ik}$ for every positioned user i in the graph, leading to a matrix whose entries are the elements $T_{ik}$. Subsequently, for each user in the graph, we add the previously selected UAVs in a list that is sorted according to $T_{ik}$. Subsequently, the BR technique is applied. In order to better illustrate how the BR works, let us compare it to the greedy randomized adaptive search procedure (GRASP) [38]. In such approach, the best element to be chosen at each stage is put into a restricted candidate list, and the element to be included in the solution is randomly selected using a uniform distribution. Contrary to GRASP, when applying BR, all of the elements are eligible to be selected at each step in the construction of a solution. Thus, at each iteration, the possible UAV candidates are taken into account.

Once the initial solution has been generated, the ILS main loop starts. Inside the loop, the current solution is perturbed in order to improve the users’ allocations obtained so far, thus generating a new solution. The perturbation occurs by removing a percentage per of the selected UAVs from the current solution. Once a percentage of the UAVs has been removed, the removed ones are replaced by newly selected UAVs; thus, the solution is reconstructed in order to generate a promising solution during this stage. In order to do that, we generate a new assignment of users to UAVs searching into the neighborhood of the current solution.

Subsequently, a local search process is carried out. By following the steps in the local search procedure, the solution approaches the closest local optima by using a neighborhood search scheme. The local search tries to improve the solution at each iteration. Thus, the procedure tries to alternate the selected UAV k with one of the remaining UAVs in the new solution at hands. Once the promising solution is generated, the cost of the solution containing the new UAV configuration is compared to the solution that contains the original UAV. Moreover, the new configuration is chosen following a credit-based system that allows for accepting a new solution, even if this offers a risk, in comparison to the solution at hands. Here, the credit is calculated as the value of the improvement obtained. Thus, the credit value can be seen as an acceptance criterion. If the promising solution improves the current solution, then the current solution is updated. Subsequently, if the promising solution also improves the best solution found so far, it is updated as well. Notice that, in this step, the total (sum) link capacity is calculated, which takes into account the links from the n users allocated to the p UAVs and the links between UAVs. At any time, the best solution found is updated and saved. The loop is executed until the time-based stopping criterion is reached. In the end, the algorithm returns the best solution. All in all, the BR-ILS is a simple and easy-to-implement procedure. As for the complexity of BR-ILS, the time spent is bounded by the predefined time limit $maxTime$. Within the while loop (line 3 of Algorithm 1), the perturbate function consists in removing a random set of UAVs and selecting another random set, this can be executed in $\mathcal{O}(n·plogp)$. The localSearch function consists in changing the assigned UAV of each user and has a complexity of $\mathcal{O}(n·p)$. Therefore, each iteration of the while loop has a total complexity of $\mathcal{O}(n·plogp)$.

5. Experimental Study

The proposed approach for the optimization aims at the efficient positioning of the UAVs in order to obtain the best possible coverage while maximizing link capacity. The proposed model was numerically analyzed for its efficiency on the basis of the parameters and configurations that are presented in this section. Test problems of size $n=\{10,20,30,50,100,200\}$ and $p=\{3,10\}$ were generated and solved. Each instance was generated spreading the nodes in a 5 km × 5 km area following a Uniform spatial distribution. For each problem, the capacity was calculated according to Equation (6) and the parameters for simulations are presented in

Table 1. Simulation Parameters.

Parameters	Description
Carrier frequency $f_c$	2 GHz
UAVs altitude h	2000 m
Transmission gain $G_t$	0 dBi
Reception gain $G_r$	0 dBi
Thermal noise power $\sigma$	−90 dBm
UAV transmission power	20 dBm
User transmission power	20 dBm
Channel bandwidth	20 MHz

. A complete list with the generated instances can be downloaded from github.com/Stephdnie/p-UAV-instances. The proposed BR-ILS algorithm was implemented while using Java^® 7SE applications. The vast amount of tools available in the standard API of Java and its objected-orientation made the development process easy. A standard personal computer was used to perform all tests, an Intel^®Core^®i7-3520M CPU @ 2.90 GHz and 12 GB RAM running the Windows^®10 operating system.

During the implementation process of the BR-ILS, some of the details that required attention were found, especially: (i) The meticulous design of the different classes so that a convenient level of coupling and cohesion was reached; (ii) The quality of the Random Number Generator to perform random choices during the exploration of the space, which impacts directly the performance of our algorithm. We used the LFSR113 from the SSJ library created by L’ecuyer et al. [39] in order to overcome this situation. This generator provides a period of $2^{113}$, compared to the period $2^{48}$ of the generator provided by the standard Java library; and ($iii$) The level of precision used to store and operate with numerical values was key to reach the fastness of the proposed BR-ILS. The necessary algorithm parameters to complete the tests were specified, as follows: the maximum time during the ILS block was set to $maxTime=900$ s; the Geometric distribution parameter $\beta$ and the percentage $per$ were randomly chosen in the interval $(0.1,0.3)$.

In the following, a complete analysis of the results is presented and, for that purpose, a test-bench that runs the BR-ILS algorithm was set for running a total of ten times, collecting information regarding the performance of the algorithm, each of them running with a different simulation seed. To assess the performance obtained, a gap is defined as the percentage difference between the (potentially) optimal solution, previously found by CPLEX, and the one found by the algorithm. In addition, run-time information is used to compare the efficiency of both methods.

Table 2. Comparison of the results that were obtained with CPLEX and BR-ILS.

Instance			CPLEX		BR-ILS
	n	p	Cost (1)	Time (s)	Cost (2)	SD	Time (s)	Gap%
	10	3	9.4373	180.50	9.4373	0.00	0.12	0.00
	20		33.6638	907.34	33.6638	0.00	0.27	0.00
Small	30		70.4836	7204.41	70.4836	0.00	0.45	0.00
	40		134.3173	7202.50	120.0516	0.00	0.70	−10.72
	50		–	–	179.2856	0.00	0.81	–
	100	10	–	–	773.9002	0.00	116.09	–
Large	200		–	–	2847.7467	0.34	476.30	–

shows a comparison of the results obtained by using both our proposed BR-ILS algorithm and the branch-and-cut algorithm, whose implementation is provided by the optimization software ILOG CPLEX Version 12.10.0 by IBM^®. This software tool was chosen due to its wide adoption among operations research community and its reliability [40]. The optimizer automatically determines smart settings for a wide range of algorithm parameters, usually resulting in optimal linear programming solution performance. However, due to restrictions that are imposed by the limited memory and CPU clock, it was necessary to manually turn off the aggregator, clique generator, the heuristic, and to set the optimizer time limit to CPXPARAM_TimeLimit = 10,000 s. With these settings, CPLEX is capable of finding optimal solutions as long as a sufficiently large timeframe is provided; otherwise, it will provide a near-optimal solution. Finally, since the branch-and-cut method is deterministic, it is executed only once per instance.

The table is organized as follows: (i) The first three columns show the size of the instances classified as Small and Large, the number of users represented with n, and the number p of UAVs to be selected; (ii) The next two columns, denoted by Cost (1) and Time give the solution found by the solver CPLEX, and the time it took to find it; (iii) The last three columns, denoted by Cost (2), SD, Time, and Gap, give the average cost of the found solutions, the standard deviation, the average run-time, and the corresponding percentage deviation (gap) with respect to the Cost (1) when applying our proposed BR-ILS metaheuristic for the aforementioned sets of generated instances. The elapsed times are shown in seconds.

Notice that, for instances that are larger than 50 users and three UAVs, the results obtained by CPLEX were not included, because the solver was not able to find a feasible solution, due to time and memory requirements. In particular, for the instance with 40 users and 3 UAVs, CPLEX finds a worse solution than the one found by BR-ILS, in a much longer time. This situation indicates that the 10,000 s timeframe allowed CPLEX to find a feasible solution, although non-optimal. Furthermore, because BR-ILS is a non-deterministic metaheuristic, it is important to note that the aforementioned results are stable, i.e., present low variability. This is indicated by the zero SD of the Cost observed for all instances, except for the $n=200,p=10$ case which, however, also presents a relatively low level of variation, i.e., just 0.34 over an average cost of 2847.7467. Thus, the results indicate a good level of stability for the method, obtaining almost identical solutions for all instances and runs. All in all, the results that are shown in Table 2 can be considered to be satisfactory, because, for most of the instances, the standard deviation as well as the computation times indicate the capacity of the BR-ILS algorithm to obtain good quality solutions in a few seconds.

For illustration purposes, Figure 2 displays the configuration of the network when the algorithm is applied for solving the instance with $n=20$ and $p=3$. Figure 2a displays the distribution of users in the area without allocating the UAVs. Figure 2b illustrates the positions of users selected as UAVs, as well as the assignments that were provided by the solution. Once our methodology is applied, the algorithm is able to find the best placement of UAVs, and the set of users assigned to the selected UAVs. The UAVs are represented with a squared symbol.

Figure 3 graphically summarizes the total inverse link capacity that was obtained when the UAVs are placed following a Naive heuristic versus the total inverse link capacity obtained when the BR-ILS algorithm is applied. The Naive heuristic consists of dividing the area in equal parts depending on the number of UAVs. In particular, for three UAVs, the area is divided into three equal subareas. Following, the centroid of each subarea is found and the UAVs are placed as close as possible to the centroid. Finally, the users in each subarea are assigned to the selected UAVs. Notice the improvement that is obtained in terms of the total cost with the adoption of the proposed methodology. On average, the total link capacity (or, similarly, the total cost) is improved by $12.24\%$ when the UAVs are placed by using BR-ILS.

6. Conclusions

In this paper, we have treated the UAV placement problem to deploy a wireless infrastructure for communications in the context of disaster relief, rescue operations, and providing user connectivity in remote or hostile environments. The UAVs serve as aerial relays to connect users on the ground, and we seek to maximize the total link capacity of the aerial communication infrastructure. The problem is recognized as a typical p-hub median problem, with a mathematical formulation developed in order to consider the air-to-ground and air-to-air propagation model.

The mixed integer linear programming formulation is optimized via the classical CPLEX branch-and-cut algorithm and via a hybrid metaheuristic, the BR-ILS. The latter is proposed in order to obtain reduced computational cost in association with optimal or close-to optimal solutions. The experimental results show that BR-ILS largely outperforms CPLEX solver for small and large-sized instances, in terms of execution time, while achieving zero gap for the instances whose optimal solution could be obtained by CPLEX. Moreover, when compared to a naive heuristic allocation strategy, the BR-ILS algorithm is able to deliver an average improvement of about 12% for the total cost when different numbers of users are uniformly scattered on the ground. Finally, it is worth mentioning that the BR-ILS algorithm is relatively simple: it has been applied to the tested instances without requiring any special fine-tuning or set-up process, which makes it an appealing tool to support the solution of the UAV placement problem.

Future work involves extending the problem formulation and experimental analysis to more diverse scenarios and parameters, considering flows of data packets between users and other wireless network setups. In fact, the formulation of the p-hub median problem allows for its extension to consider individual flows of packets between users, which is a quite useful feature of this optimization problem. This means that one can consider the actual traffic load that is imposed on each end-to-end connection established between two any users on the ground. However, to treat this problem, one needs to carefully address the impact of channel errors on packet transmissions within each link searched by the algorithm. Moreover, depending on the application scenario, the characteristics and statistics of the packet flows need to be carefully addressed, so they can be properly incorporated into the proposed framework. Furthermore, the adaptation of BR-ILS to other versions of the p-hub median problem is possible. One of the interesting variants of this problem is the capacitated version [41] and, therefore, another orientation for future research could be to consider a fixed link capacity for each UAV. Under these conditions, the mathematical model may include the capacity restrictions.