Deep Feature Learning with Manifold Embedding for Robust Image Retrieval
Abstract
1. Introduction
2. Related Work
3. Formulation and Pipeline
3.1. Formulation
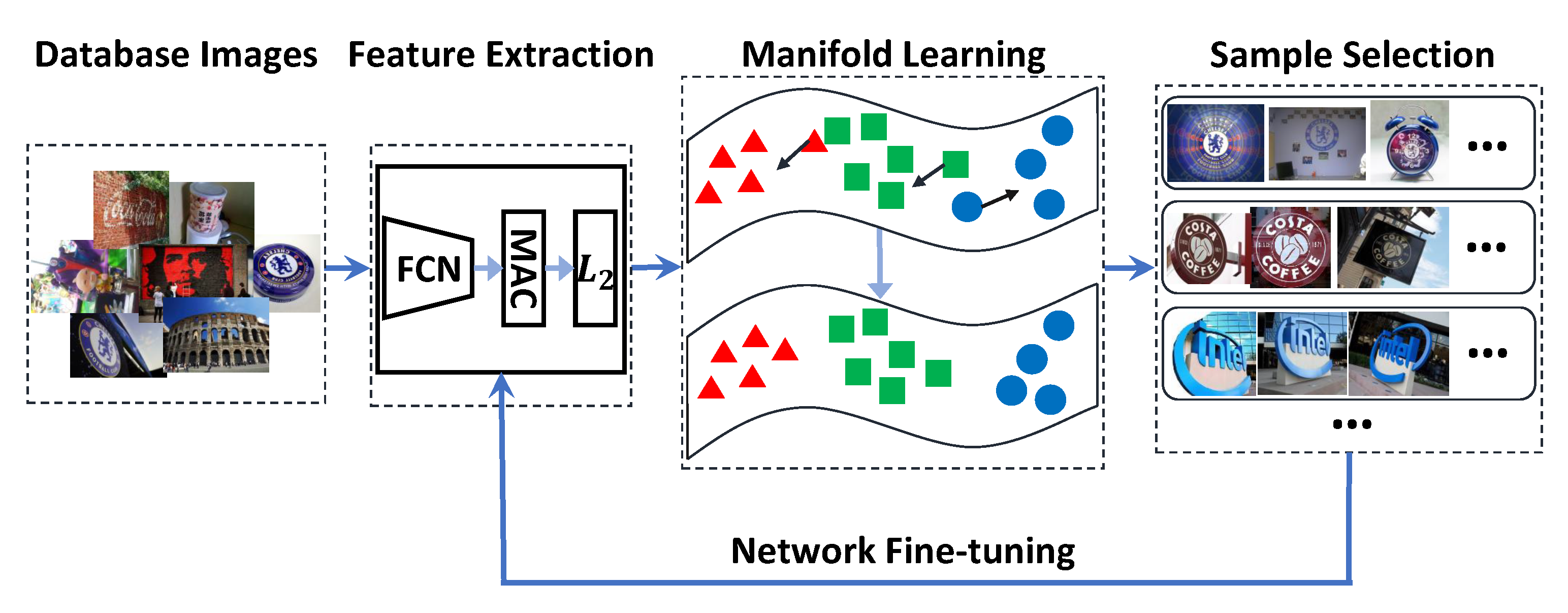
3.2. Pipeline
4. Self-Supervised Training Example Selection
4.1. MAC Image Representation
4.2. Refining Distance Metric with Manifold Learning
4.3. Training Pairs Selection
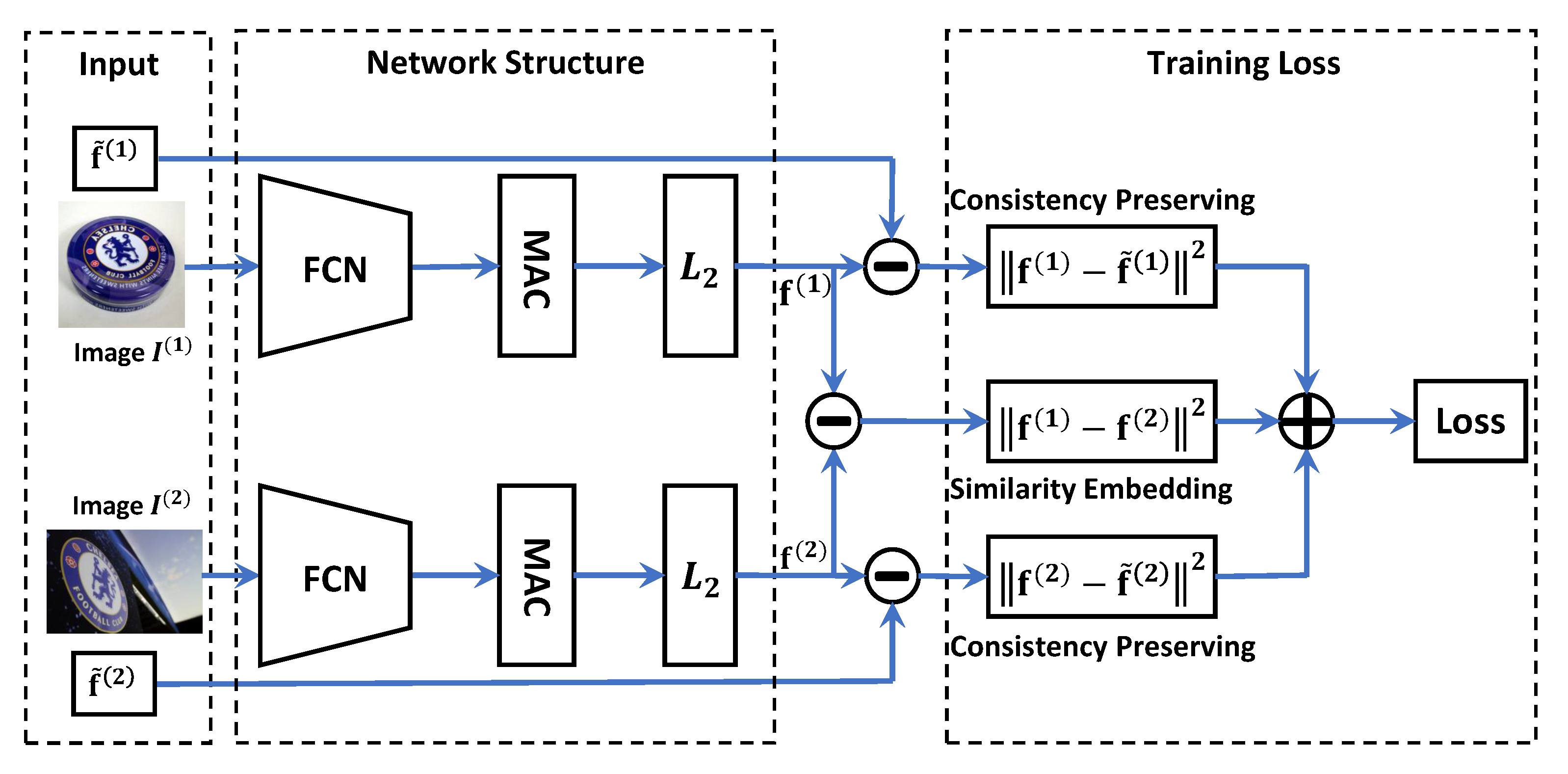
5. Siamese Feature Learning
5.1. Network Structure
5.2. Objective and Optimization
5.3. Iteratively Mining and Learning
6. Experiments
6.1. Experimental Setup
6.1.1. Datasets
6.1.2. Implementation Details
6.2. Impact of Parameters
6.2.1. Balance Factor
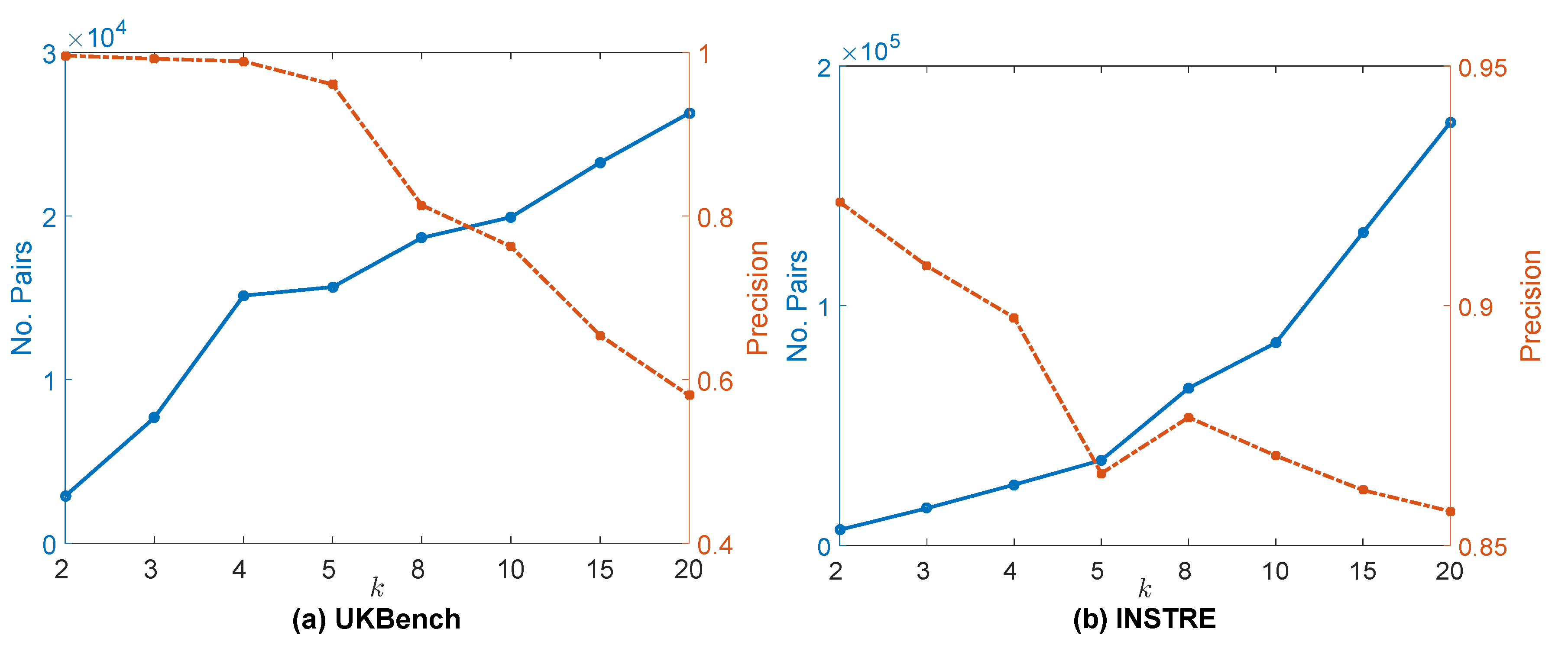
6.2.2. Impact of Nearest Neighbor Number
6.3. Evaluation and Comparison
6.3.1. Effectiveness of Manifold Learning-Based Training Example Selection
6.3.2. Effectiveness of Iteratively Mining and Training
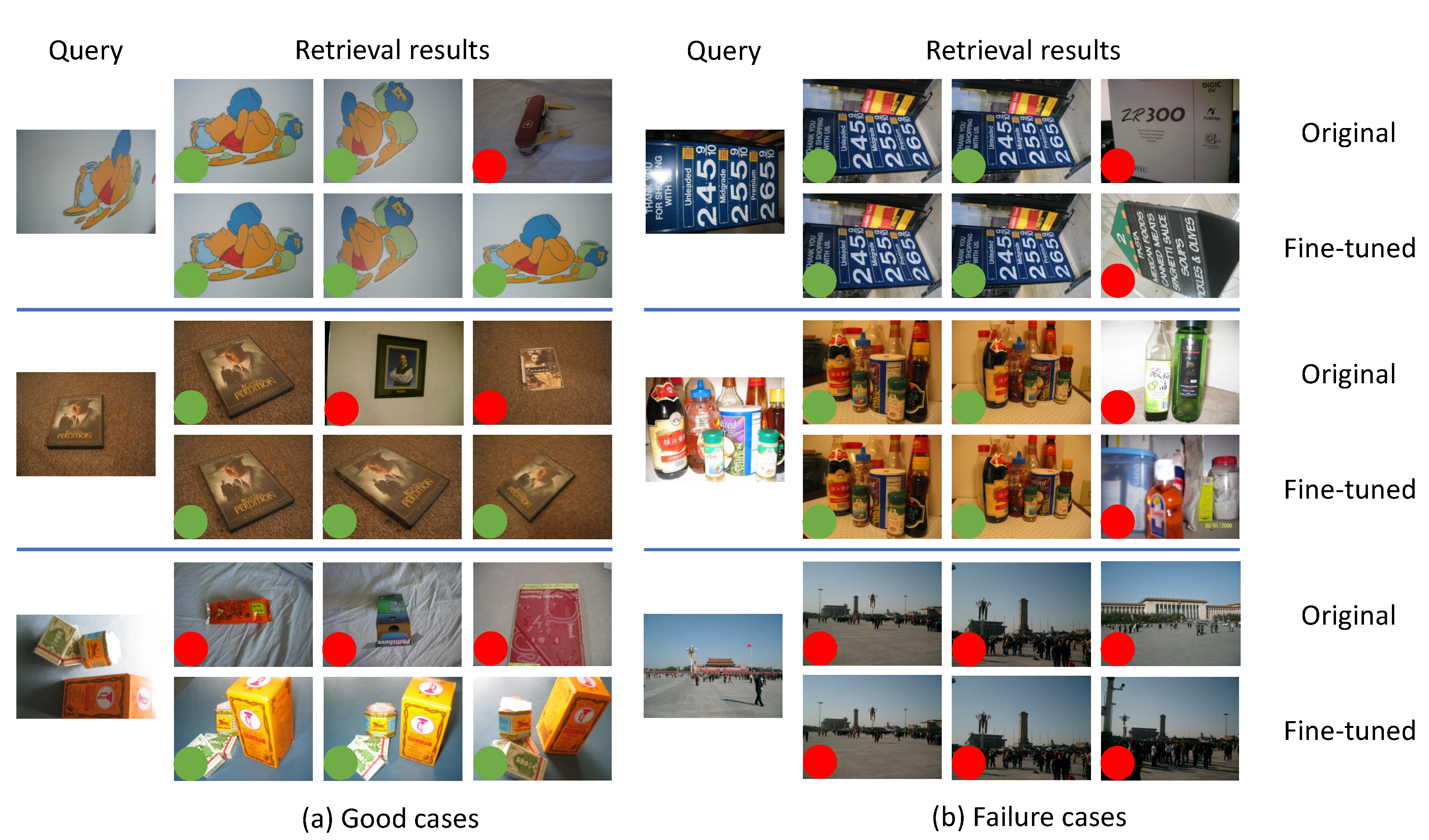
6.3.3. Performance Improvement upon Baseline
6.3.4. Comparison with the State-of-the-Art
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zheng, L.; Yang, Y.; Tian, Q. SIFT meets CNN: A decade survey of instance retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 1224–1244. [Google Scholar] [CrossRef]
- Al-Jubouri, H.A. Content-based image retrieval: Survey. J. Eng. Sustain. Dev. 2019, 23, 42–63. [Google Scholar] [CrossRef]
- Zhou, D.; Weston, J.; Gretton, A.; Bousquet, O.; Schölkopf, B. Ranking on data manifolds. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 13–18 December 2004; pp. 169–176. [Google Scholar]
- Kontschieder, P.; Donoser, M.; Bischof, H. Beyond pairwise shape similarity analysis. In Proceedings of the Asian Conference on Computer Vision (ACCV), Xi’an, China, 23–27 September 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 655–666. [Google Scholar]
- Luo, L.; Shen, C.; Zhang, C.; van den Hengel, A. Shape similarity analysis by self-tuning locally constrained mixed-diffusion. IEEE Trans. Multimed. 2013, 15, 1174–1183. [Google Scholar] [CrossRef][Green Version]
- Yang, X.; Koknar-Tezel, S.; Latecki, L.J. Locally constrained diffusion process on locally densified distance spaces with applications to shape retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 22–24 June 2009; pp. 357–364. [Google Scholar]
- Pedronette, D.C.G.; Almeida, J.; Torres, R.D.S. A scalable re-ranking method for content-based image retrieval. Inf. Sci. 2014, 265, 91–104. [Google Scholar] [CrossRef]
- Pedronette, D.C.G.; Torres, R.D.S. Image re-ranking and rank aggregation based on similarity of ranked lists. Pattern Recognit. 2013, 46, 2350–2360. [Google Scholar] [CrossRef]
- Yang, F.; Hinami, R.; Matsui, Y.; Ly, S.; Satoh, S. Efficient image retrieval via decoupling diffusion into online and offline processing. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 9087–9094. [Google Scholar]
- Zhou, J.; Liu, X.; Liu, W.; Gan, J. Image retrieval based on effective feature extraction and diffusion process. Multimed. Tools Appl. 2019, 78, 6163–6190. [Google Scholar] [CrossRef]
- Rodrigues, J.; Cristo, M.; Colonna, J.G. Deep hashing for multi-label image retrieval: A survey. Artif. Intell. Rev. 2020, 53, 5261–5307. [Google Scholar] [CrossRef]
- Bai, S.; Zhang, F.; Torr, P.H. Hypergraph convolution and hypergraph attention. Pattern Recognit. 2021, 110, 107637. [Google Scholar] [CrossRef]
- Donoser, M.; Bischof, H. Diffusion processes for retrieval revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013; pp. 1320–1327. [Google Scholar]
- Bosch, A.; Zisserman, A.; Muñoz, X. Scene classification using a hybrid generative/discriminative approach. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 712–727. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Sivic, J.; Zisserman, A. Video Google: A Text Retrieval Approach to Object Matching in Videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2003; p. 1470. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Babenko, A.; Slesarev, A.; Chigorin, A.; Lempitsky, V. Neural codes for image retrieval. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; pp. 584–599. [Google Scholar]
- Babenko, A.; Lempitsky, V. Aggregating local deep features for image retrieval. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1269–1277. [Google Scholar]
- Ng, J.Y.H.; Yang, F.; Davis, L.S. Exploiting local features from deep networks for image retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Boston, MA, USA, 7–12 June 2015; pp. 53–61. [Google Scholar]
- Gordo, A.; Almazán, J.; Revaud, J.; Larlus, D. Deep image retrieval: Learning global representations for image search. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016; pp. 241–257. [Google Scholar]
- Radenović, F.; Tolias, G.; Chum, O. CNN image retrieval learns from BoW: Unsupervised fine-tuning with hard examples. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016; pp. 3–20. [Google Scholar]
- Wan, J.; Wang, D.; Hoi, S.C.H.; Wu, P.; Zhu, J.; Zhang, Y.; Li, J. Deep learning for content-based image retrieval: A comprehensive study. In Proceedings of the ACM International Conference on Multimedia (MM), Orlando, FL, USA, 3–7 November 2014; pp. 157–166. [Google Scholar]
- Han, X.; Leung, T.; Jia, Y.; Sukthankar, R.; Berg, A.C. Matchnet: Unifying feature and metric learning for patch-based matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3279–3286. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Learning to compare image patches via convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 4353–4361. [Google Scholar]
- Cao, R.; Zhang, Q.; Zhu, J.; Li, Q.; Li, Q.; Liu, B.; Qiu, G. Enhancing remote sensing image retrieval using a triplet deep metric learning network. Int. J. Remote Sens. 2020, 41, 740–751. [Google Scholar] [CrossRef]
- Min, W.; Mei, S.; Li, Z.; Jiang, S. A Two-Stage Triplet Network Training Framework for Image Retrieval. IEEE Trans. Multimed. 2020, 22, 3128–3138. [Google Scholar] [CrossRef]
- Wiggers, K.L.; Britto, A.S.; Heutte, L.; Koerich, A.L.; Oliveira, L.S. Image retrieval and pattern spotting using siamese neural network. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Gong, Y.; Wang, L.; Guo, R.; Lazebnik, S. Multi-scale orderless pooling of deep convolutional activation features. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; pp. 392–407. [Google Scholar]
- Razavian, A.S.; Azizpour, H.; Sullivan, J.; Carlsson, S. CNN features off-the-shelf: An astounding baseline for recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Columbus, OH, USA, 23–28 June 2014; pp. 512–519. [Google Scholar]
- Jegou, H.; Perronnin, F.; Douze, M.; Sánchez, J.; Perez, P.; Schmid, C. Aggregating local image descriptors into compact codes. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1704–1716. [Google Scholar] [CrossRef]
- Tolias, G.; Sicre, R.; Jégou, H. Particular object retrieval with integral max-pooling of CNN activations. arXiv 2015, arXiv:1511.05879. [Google Scholar]
- Li, Y.; Kong, X.; Zheng, L.; Tian, Q. Exploiting Hierarchical Activations of Neural Network for Image Retrieval. In Proceedings of the ACM International Conference on Multimedia (MM), Amsterdam, The Netherlands, 15 October 2016; pp. 132–136. [Google Scholar]
- Arandjelovic, R.; Gronat, P.; Torii, A.; Pajdla, T.; Sivic, J. NetVLAD: CNN architecture for weakly supervised place recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 5297–5307. [Google Scholar]
- Bai, S.; Bai, X. Sparse contextual activation for efficient visual re-ranking. IEEE Trans. Image Process. 2016, 25, 1056–1069. [Google Scholar] [CrossRef]
- Bai, S.; Zhou, Z.; Wang, J.; Bai, X.; Latecki, L.J.; Tian, Q. Ensemble Diffusion for Retrieval. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 774–783. [Google Scholar]
- Bai, S.; Bai, X.; Tian, Q. Scalable person re-identification on supervised smoothed manifold. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 June 2017; Volume 6, p. 7. [Google Scholar]
- Iscen, A.; Tolias, G.; Avrithis, Y.; Furon, T.; Chum, O. Efficient diffusion on region manifolds: Recovering small objects with compact cnn representations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 June 2017; pp. 926–935. [Google Scholar]
- Bai, S.; Bai, X.; Tian, Q.; Latecki, L.J. Regularized Diffusion Process for Visual Retrieval. In Proceedings of the AAAI, San Francisco, CA, USA, 4–9 February 2017; pp. 3967–3973. [Google Scholar]
- Li, Y.; Kong, X.; Fu, H.; Tian, Q. Node-sensitive Graph Fusion via Topo-correlation for Image Retrieval. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 3777–3787. [Google Scholar] [CrossRef]
- Xu, J.; Wang, C.; Qi, C.; Shi, C.; Xiao, B. Iterative Manifold Embedding Layer Learned by Incomplete Data for Large-scale Image Retrieval. arXiv 2017, arXiv:1707.09862. [Google Scholar] [CrossRef]
- Iscen, A.; Tolias, G.; Avrithis, Y.; Chum, O. Mining on Manifolds: Metric Learning without Labels. arXiv 2018, arXiv:1803.11095. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Jegou, H.; Schmid, C.; Harzallah, H.; Verbeek, J. Accurate image search using the contextual dissimilarity measure. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2–11. [Google Scholar] [CrossRef] [PubMed]
- Qin, D.; Gammeter, S.; Bossard, L.; Quack, T.; Van Gool, L. Hello neighbor: Accurate object retrieval with k-reciprocal nearest neighbors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 777–784. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.-F. Imagenet: A large-scale hierarchical image database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Nister, D.; Stewenius, H. Scalable recognition with a vocabulary tree. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New York, NY, USA, 17–22 June 2006; Volume 2, pp. 2161–2168. [Google Scholar]
- Jegou, H.; Douze, M.; Schmid, C. Hamming embedding and weak geometric consistency for large scale image search. In Proceedings of the European Conference on Computer Vision (ECCV), Marseille, France, 12–18 October 2008; pp. 304–317. [Google Scholar]
- Wang, S.; Jiang, S. INSTRE: A new benchmark for instance-level object retrieval and recognition. ACM Trans. Multimed. Comput. Commun. Appl. 2015, 11, 37. [Google Scholar] [CrossRef]
- Bai, S.; Bai, X.; Tian, Q.; Latecki, L.J. Regularized Diffusion Process on Bidirectional Context for Object Retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 1213–1226. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. OSDI 2016, 16, 265–283. [Google Scholar]
- Zheng, L.; Zhao, Y.; Wang, S.; Wang, J.; Tian, Q. Good practice in CNN feature transfer. arXiv 2016, arXiv:1604.00133. [Google Scholar]
- Zhou, W.; Li, H.; Sun, J.; Tian, Q. Collaborative index embedding for image retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1154–1166. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, S.; Tian, L.; He, F.; Liu, Z.; Tian, Q. Query-adaptive late fusion for image search and person re-identification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1741–1750. [Google Scholar]
- Torii, A.; Sivic, J.; Pajdla, T.; Okutomi, M. Visual place recognition with repetitive structures. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013; pp. 883–890. [Google Scholar]
| N-S Score | Epochs | |
|---|---|---|
| 0.125 | 3.86 | 8 |
| 0.25 | 3.87 | 10 |
| 0.5 | 3.88 | 12 |
| 1 | 3.84 | 16 |
| 2 | 3.82 | 20 |
| Mining Method | Network | N-S Score |
|---|---|---|
| Baseline | VGGNet-16 | 3.77 |
| Original | VGGNet-16 | 3.84 |
| Manifold | VGGNet-16 | 3.88 |
| Baseline | ResNet-50 | 3.90 |
| Original | ResNet-50 | 3.93 |
| Manifold | ResNet-50 | 3.96 |
| Network | Baseline | 1st Iter. | 2nd Iter. | 3rd Iter. |
|---|---|---|---|---|
| VGGNet-16 | 3.77 | 3.86 | 3.88 | 3.88 |
| ResNet-50 | 3.90 | 3.95 | 3.96 | 3.96 |
| Dataset | Network | Baseline | Fine-Tuned |
|---|---|---|---|
| UKBench | VGGNet-16 | 3.77 | 3.88 |
| ResNet-50 | 3.90 | 3.96 | |
| Holidays | VGGNet-16 | 0.802 | 0.821 |
| ResNet-50 | 0.855 | 0.869 | |
| INSTRE | VGGNet-16 | 0.316 | 0.529 |
| ResNet-50 | 0.472 | 0.564 |
| Method | Network | Dims | UKBench | Holidays |
|---|---|---|---|---|
| SPoC [20] | V | 512 | 3.65 | 0.802 |
| Neural Codes [19] | FA | 4096 | 3.55 | 0.789 |
| NetVLAD [35] | FV | 256 | - | 0.821 |
| Radenović et al. [23] | FV | 512 | - | 0.825 |
| Gordo et al. [22] | FV | 512 | 3.78 | 0.864 |
| Ours | FV | 512 | 3.88 | 0.821 |
| Ours | FR | 2048 | 3.96 | 0.869 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Li, Y. Deep Feature Learning with Manifold Embedding for Robust Image Retrieval. Algorithms 2020, 13, 318. https://doi.org/10.3390/a13120318
Chen X, Li Y. Deep Feature Learning with Manifold Embedding for Robust Image Retrieval. Algorithms. 2020; 13(12):318. https://doi.org/10.3390/a13120318
Chicago/Turabian StyleChen, Xin, and Ying Li. 2020. "Deep Feature Learning with Manifold Embedding for Robust Image Retrieval" Algorithms 13, no. 12: 318. https://doi.org/10.3390/a13120318
APA StyleChen, X., & Li, Y. (2020). Deep Feature Learning with Manifold Embedding for Robust Image Retrieval. Algorithms, 13(12), 318. https://doi.org/10.3390/a13120318




