CYK Parsing over Distributed Representations
Abstract
1. Introduction
- We propose a distributed version of the CYK algorithm, called D-CYK, that works solely on the basis of distributed representations and matrix multiplication;
- We show how to implement D-CYK by means of a standard recurrent neural network.
2. Related Work
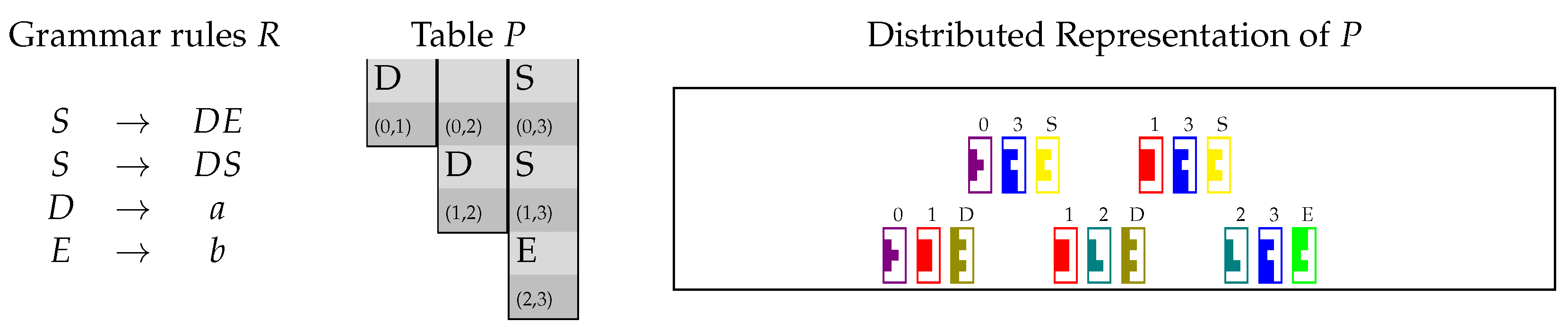
3. Preliminaries
3.1. CYK Algorithm
| Algorithm 1 CYK(string , rule set R) return table P. |
|
3.2. Distributed Representations with Holographic Reduced Representations
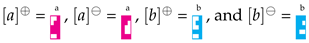 . In this way strings are sequences of pieces; for example,
. In this way strings are sequences of pieces; for example,
 encodes (equivalently, ). Then, like in Tetris, elements with complementary shapes are canceled out and removed from a sequence; for example, if
encodes (equivalently, ). Then, like in Tetris, elements with complementary shapes are canceled out and removed from a sequence; for example, if
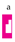 is applied to the left of
is applied to the left of
 , the result is
, the result is
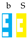 as
as
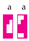 disappears. Sets of strings (sums of matrix products) are represented in boxes, as for instance:
disappears. Sets of strings (sums of matrix products) are represented in boxes, as for instance:

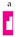 is applied to the left of the above box L, the result is the new box:
is applied to the left of the above box L, the result is the new box:

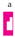 selects
selects  but not
but not 
4. The CYK Algorithm on Distributed Representations
- (i)
- the table P by means of two matrices and ;
- (ii)
- the unary rules in R by means of a matrix for each nonterminal symbol ; and
- (iii)
- the binary rules in R by means of matrices for each .
4.1. Encoding the Table P in matrices and
4.2. Encoding and Using Unary Rules
| Algorithm 2 D-CYK_unary(string , matrices ) return and |
|




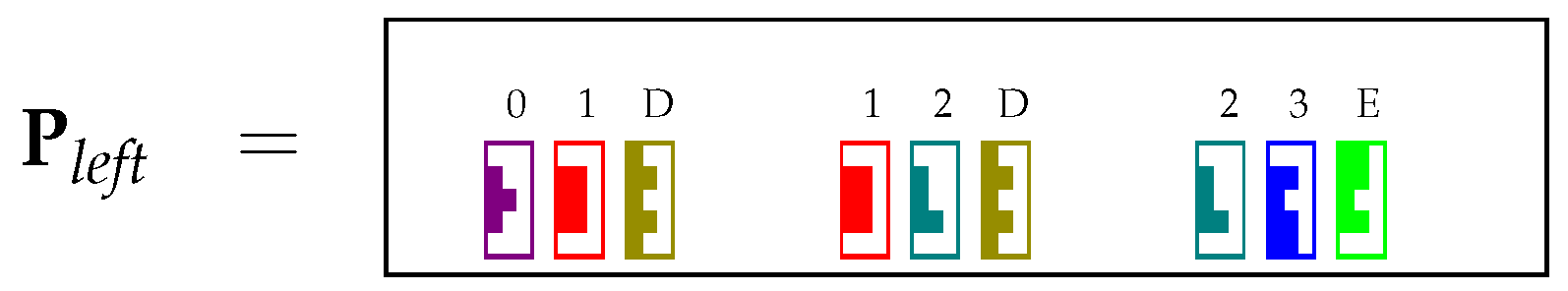

4.3. Encoding and Using Binary Rules
| Algorithm 3 D-CYK_binary(, rules for each A) return |
|



5. Interpreting D-CYK as a Recurrent Neural Network
5.1. Building Recurrent Blocks
5.2. Decoding Phase
6. Experiments
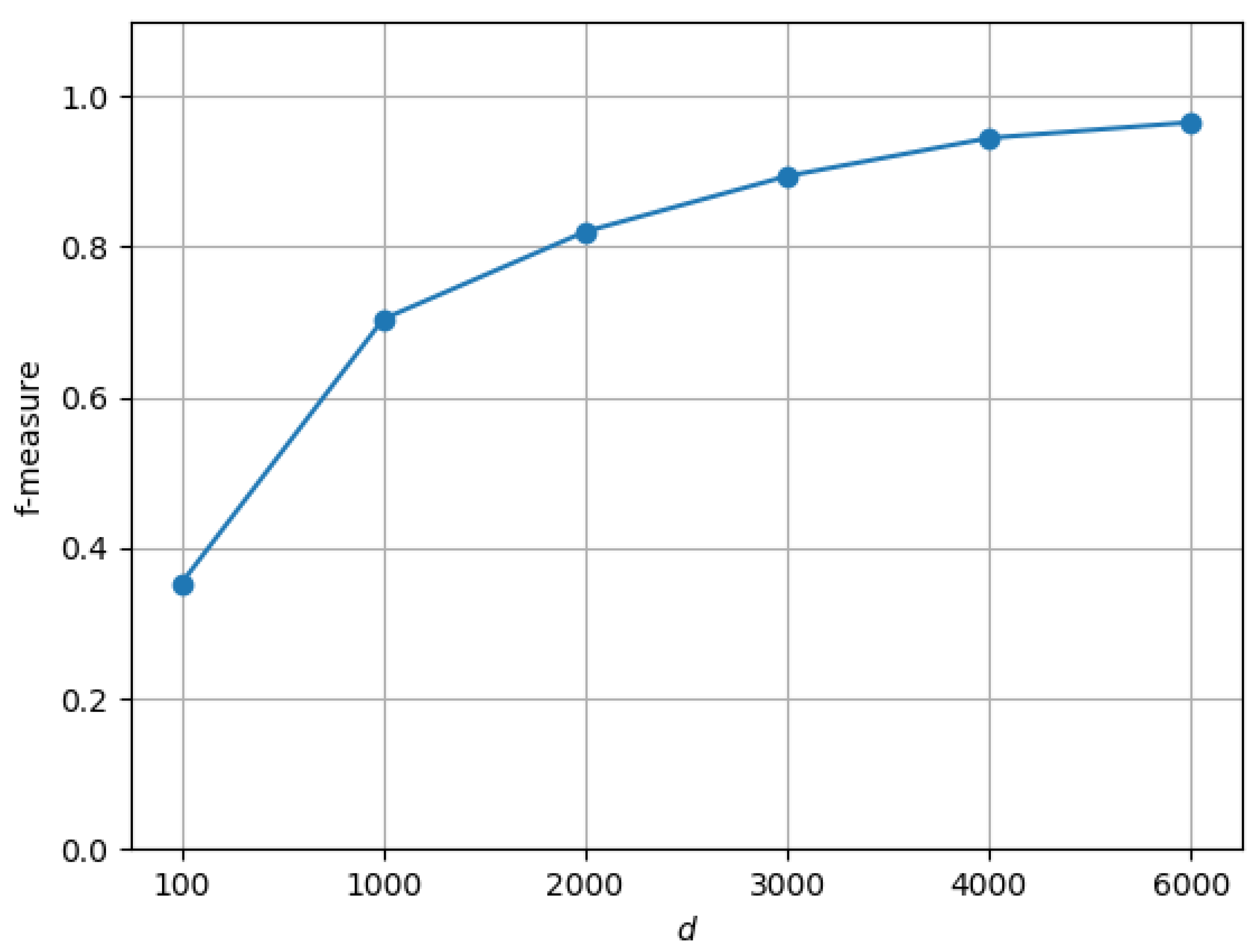
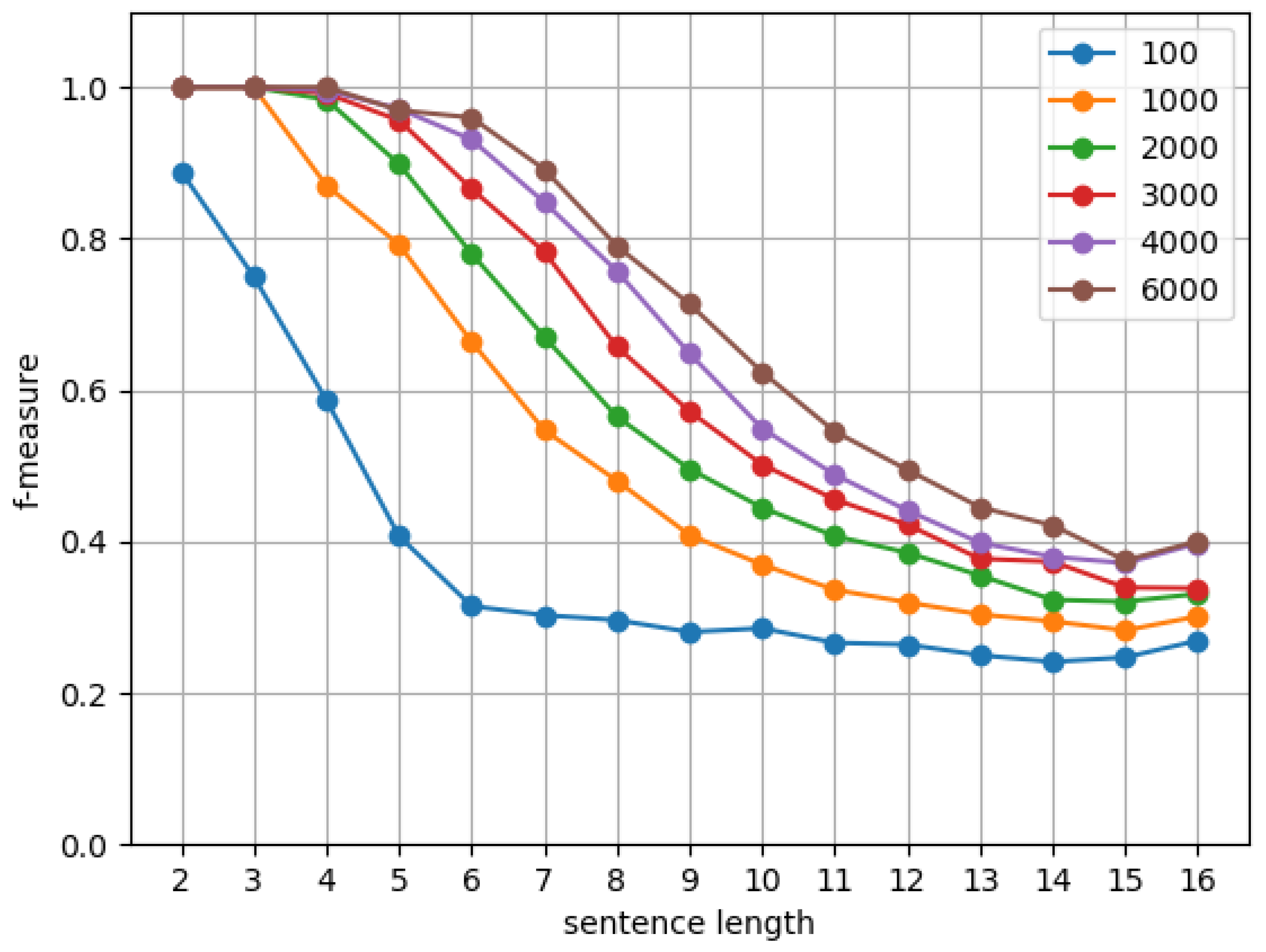
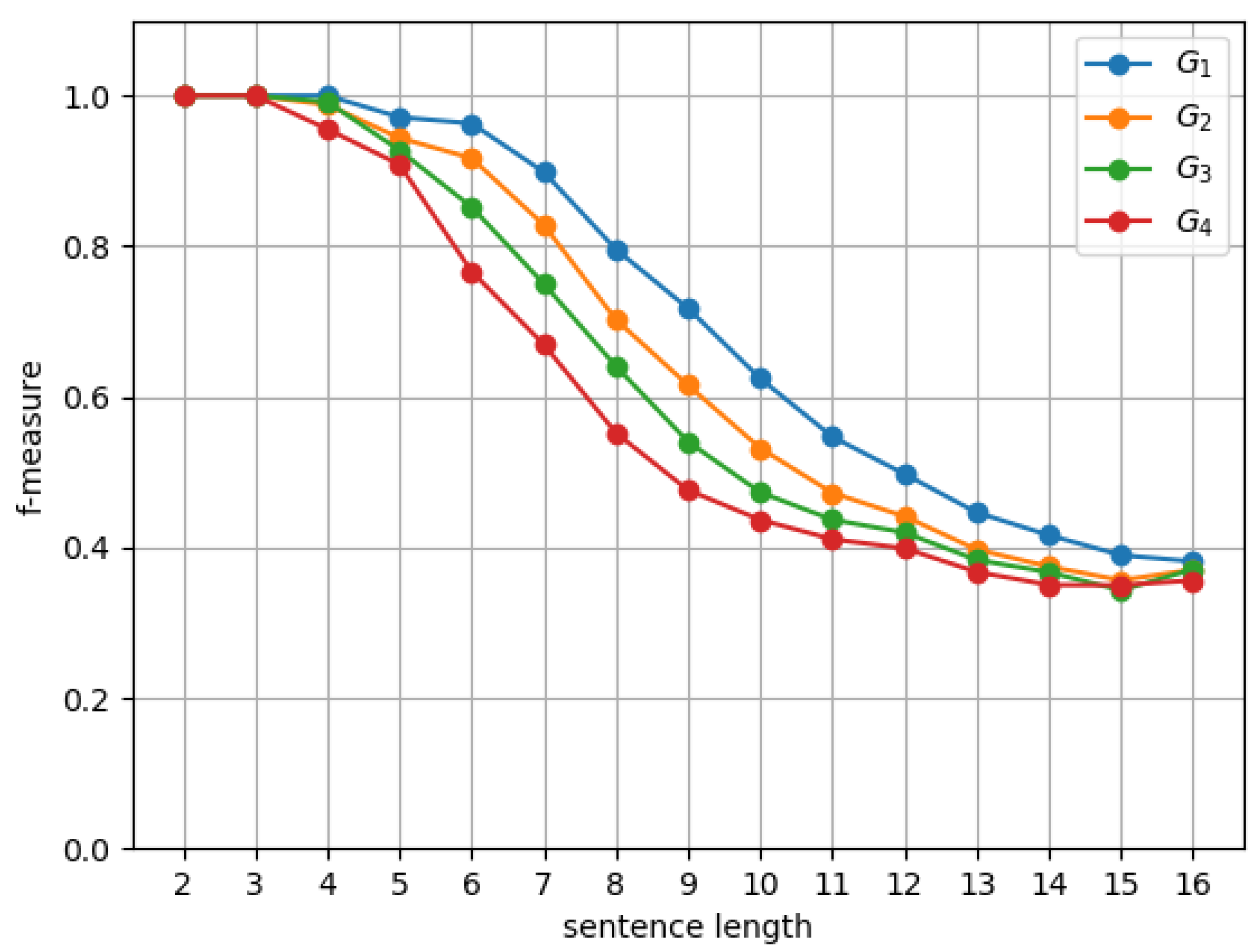
6.1. Experimental Setup
| Algorithm 4 Dec() return table P |
|
6.2. Results and Discussion
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Hopcroft, J.E.; Motwani, R.; Ullman, J.D. Introduction to Automata Theory, Languages, and Computation, 2nd ed.; Addison-Wesley: Reading, MA, USA, 2001. [Google Scholar]
- Sippu, S.; Soisalon-Soininen, E. Parsing Theory: LR(k) and LL(k) Parsing; Springer: Berlin, Germany, 1990; Volume 2. [Google Scholar]
- Aho, A.V.; Lam, M.S.; Sethi, R.; Ullman, J.D. Compilers: Principles, Techniques, and Tools, 2nd ed.; Addison-Wesley Longman Publishing Co., Inc.: Reading, MA, USA, 2006. [Google Scholar]
- Graham, S.L.; Harrison, M.A. Parsing of General Context Free Languages. In Advances in Computers; Academic Press: New York, NY, USA, 1976; Volume 14, pp. 77–185. [Google Scholar]
- Nederhof, M.; Satta, G. Theory of Parsing. In The Handbook of Computational Linguistics and Natural Language Processing; Clark, A., Fox, C., Lappin, S., Eds.; Wiley: Hoboken, NJ, USA, 2010; Chapter 4; pp. 105–130. [Google Scholar]
- Cocke, J. Programming Languages and Their Compilers: Preliminary Notes; Courant Institute of Mathematical Sciences, New York University: New York, NY, USA, 1969. [Google Scholar]
- Younger, D.H. Recognition and parsing of context-free languages in time (n3). Inf. Control 1967, 10, 189–208. [Google Scholar] [CrossRef]
- Kasami, T. An eFficient Recognition And Syntax-Analysis Algorithm For Context-Free Languages; Technical Report; Air Force Cambridge Research Lab: Bedford, MA, USA, 1965. [Google Scholar]
- Charniak, E. Statistical Language Learning, 1st ed.; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Huang, L.; Chiang, D. Better k-best Parsing. In Proceedings of the Ninth International Workshop on Parsing Technology, Association for Computational Linguistics, Vancouver, BC, Cananda, 9–10 October 2005; pp. 53–64. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Valiant, L.G. General Context-Free Recognition in Less Than Cubic Time. J. Comput. Syst. Sci. 1975, 10, 308–315. [Google Scholar] [CrossRef]
- Graham, S.L.; Harrison, M.A.; Ruzzo, W.L. An Improved Context-Free Recognizer. ACM Trans. Program. Lang. Syst. 1980, 2, 415–462. [Google Scholar] [CrossRef]
- Fanty, M.A. Context-Free Parsing with Connectionist Networks; American Institute of Physics Conference Series; American Institute of Physics: College Park, MD, USA, 1986; Volume 151, pp. 140–145. [Google Scholar] [CrossRef]
- Nijholt, A. Meta-parsing in neural networks. In Cybernetics and Systems ’90; Trappl, R., Ed.; World Scientific: Vienna, Austria, 1990; pp. 969–976. [Google Scholar]
- Earley, J. An Efficient Context-free Parsing Algorithm. Commun. ACM 1970, 13, 94–102. [Google Scholar] [CrossRef]
- Henderson, J. Inducing History Representations for Broad Coverage Statistical Parsing. In Proceedings of the 2003 Human Language Technology Conference of the North American Chapter of the Association for Computational Linguistics, Edmonton, AB, Canada, 27 May–1 June 2003; pp. 103–110. [Google Scholar]
- Chen, D.; Manning, C.D. A Fast and Accurate Dependency Parser using Neural Networks. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing, EMNLP, Doha, Qatar, 25–29 October 2014; pp. 740–750. [Google Scholar]
- Watanabe, T.; Sumita, E. Transition-based Neural Constituent Parsing. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), 26–31 July 2015; pp. 1169–1179. [Google Scholar] [CrossRef]
- Dyer, C.; Ballesteros, M.; Ling, W.; Matthews, A.; Smith, N.A. Transition-Based Dependency Parsing with Stack Long Short-Term Memory. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), Beijing, China, 26–31 July 2015; pp. 334–343. [Google Scholar] [CrossRef]
- Socher, R.; Bauer, J.; Manning, C.D.; Ng, A.Y. Parsing with Compositional Vector Grammars. In Proceedings of the 51st Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Sofia, Bulgaria, 4–9 August 2013; pp. 455–465. [Google Scholar]
- Dyer, C.; Kuncoro, A.; Ballesteros, M.; Smith, N.A. Recurrent Neural Network Grammars. In Proceedings of the NAACL HLT 2016, the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, San Diego, CA, USA, 12–17 June 2016; pp. 199–209. [Google Scholar]
- Vinyals, O.; Kaiser, L.; Koo, T.; Petrov, S.; Sutskever, I.; Hinton, G. Grammar as a Foreign Language. arXiv 2014, arXiv:1412.7449v3. [Google Scholar] [CrossRef]
- Weiss, G.; Goldberg, Y.; Yahav, E. On the Practical Computational Power of Finite Precision RNNs for Language Recognition. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers), Melbourne, Australia, 15–20 July 2018; pp. 740–745. [Google Scholar] [CrossRef]
- Suzgun, M.; Belinkov, Y.; Shieber, S.; Gehrmann, S. LSTM Networks Can Perform Dynamic Counting. In Proceedings of the Workshop on Deep Learning and Formal Languages: Building Bridges, Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 44–54. [Google Scholar] [CrossRef]
- Plate, T.A. Holographic Reduced Representations. IEEE Trans. Neural Netw. 1995, 6, 623–641. [Google Scholar] [CrossRef] [PubMed]
- Zanzotto, F.; Dell’Arciprete, L. Distributed tree kernels. In Proceedings of the International Conference on Machine Learning, Edinburgh, UK, 26 June–1 July 2012; pp. 193–200. [Google Scholar]
- Johnson, W.B.; Lindenstrauss, J. Extensions of Lipschitz mappings into a Hilbert space. Contemp. Math. 1984, 26, 189–206. [Google Scholar] [CrossRef]
- Sahlgren, M. An Introduction to Random Indexing. In Proceedings of the Methods and Applications of Semantic Indexing Workshop at the 7th International Conference on Terminology and Knowledge Engineering, Copenhagen, Denmark, 16 August 2005; pp. 1–9. [Google Scholar]
- Zhang, A.; Lipton, Z.C.; Li, M.; Smola, A.J. Dive into Deep Learning. Corwin. 2020. Available online: https://d2l.ai (accessed on 14 October 2020).
- Do, D.T.; Le, T.Q.T.; Le, N.Q.K. Using deep neural networks and biological subwords to detect protein S-sulfenylation sites. Brief. Bioinform. 2020, bbaa128. [Google Scholar] [CrossRef] [PubMed]
- Le, N.Q.K.; Yapp, E.K.Y.; Nagasundaram, N.; Yeh, H.Y. Classifying Promoters by Interpreting the Hidden Information of DNA Sequences via Deep Learning and Combination of Continuous FastText N-Grams. Front. Bioeng. Biotechnol. 2019, 7, 305. [Google Scholar] [CrossRef] [PubMed]
| Grammar | Rules | Binary |
|---|---|---|
| 8 | 5 | |
| 25 | 5 | |
| 28 | 8 | |
| 34 | 14 | |
| 41 | 21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zanzotto, F.M.; Satta, G.; Cristini, G. CYK Parsing over Distributed Representations. Algorithms 2020, 13, 262. https://doi.org/10.3390/a13100262
Zanzotto FM, Satta G, Cristini G. CYK Parsing over Distributed Representations. Algorithms. 2020; 13(10):262. https://doi.org/10.3390/a13100262
Chicago/Turabian StyleZanzotto, Fabio Massimo, Giorgio Satta, and Giordano Cristini. 2020. "CYK Parsing over Distributed Representations" Algorithms 13, no. 10: 262. https://doi.org/10.3390/a13100262
APA StyleZanzotto, F. M., Satta, G., & Cristini, G. (2020). CYK Parsing over Distributed Representations. Algorithms, 13(10), 262. https://doi.org/10.3390/a13100262






