1. Introduction
Ensemble learning combines multiple individual learners to improve the generalization performance of an individual learner [
1,
2]. It is an important and popular branch of machine learning and is widely used in attack detection [
3,
4,
5], fraud recognition [
6,
7], image recognition [
8,
9], biomedicine [
10,
11], intelligent manufacturing [
12,
13], time series analysis [
14,
15] and other fields. Ensemble learning usually involves multiple weak classifiers, such as decision trees [
16], support vector machines [
17], neural networks [
18] and
k-nearest neighbors [
19], to form a strong classifier, multiple strong classifiers [
20] or even a combination of multiple machine learners to complete the learning task. Currently, ensemble learning is regarded as the best way to solve machine learning problems [
21].
Classic ensemble learning algorithms include bagging and boosting [
22,
23]. The basic idea of bagging is that the original dataset is first repeatedly replaced with uniform random sampling to obtain sample subsets; then, different individual learners are trained on these subsets, which are finally integrated by voting. The basic idea of boosting is to select a subset from the sample set as a training set according to a uniform distribution, then run a weak classifier multiple times to give a larger distribution weight to the samples that failed to train, and finally integrate the set by weighting. Bagging and boosting are the most elegant and widely utilized ensemble strategies, Livieris et al. [
24] develop two ensemble prediction models that use these strategies for combining the predictions of multiple weight-constrained neural network classifiers. Based on bagging and boosting design philosophy, the current popular ensemble learning algorithms mainly include AdaBoost [
25], random forest (RF) [
26], gradient boosting decision tree (GBDT) [
27], and extremely randomized trees (ERTs) [
28].
To obtain good ensemble effects, individual learners should be accurate and diverse [
23]. Theoretical and experimental studies have shown that combining a set of accurate and complementary learners can improve the generalization ability of ensemble learning. The diversity between learners is an important factor affecting the generalization performance of ensemble systems. Most existing classical ensemble learning algorithms implicitly use the diversity between learners. To enhance the diversity, Rokach [
29] proposes a variety of methods, such as manipulating the inducer, manipulating the training sample, changing the target attribute representation and partitioning the search space. For example, the DECORATE algorithm [
30] adds artificial data to the training dataset to train the classifier to increase the diversity of the training data and reduce the classification error.
Although the diversity of learners is necessary for improving the ensemble effect, maximizing diversity does not result in the best generalization performance. The experimental results also show that no strong correlation exists between the accuracy of the learners and diversity. An increase in diversity actually reduces the overall accuracy [
31], as its improvement comes with the cost of reducing the accuracy of each individual classifier [
32]. Compared with the overall diversity, the accuracy of an individual learner is the main factor of the success of ensemble learning [
33]. Liu et al. [
34] introduce the diversity factor as a regular term for ensemble learning to avoid overfitting. Therefore, to improve the overall ensemble learning performance, a balance between the diversity and accuracy of the learners must be established. Under the premise of considering accuracy and diversity, Zhang et al. [
35] propose a classifier selection method based on a genetic algorithm. They integrated unsupervised clustering with a fuzzy assignment process to make full use of data patterns to improve the ensemble performance. Mao et al. [
36] propose a transformation ensemble learning framework in which the combination of multiple base learners is converted into a linear transformation of all these base learners and which constructs an optimization objective function for balancing accuracy and diversity. The alternating direction multiplier method is used to solve this problem. This method effectively improves the performance of ensemble learning.
In previous studies [
35,
36], when the ensemble learning model was built, although the objective function includes accuracy and diversity factors, the diversity factor is used as a regularization term to avoid overfitting. Nevertheless, the diversity factor considers only the prediction results of the classifier. The diversity does not express the accuracy factor that the diversity should imply, nor does it reflect how to produce an individual learner with moderate diversity. The weighted ensemble strategy is to assign a weight to the individual learner so that it can properly represent the ensemble. It has been demonstrated to be highly efficient in many real-world fields, such as biochemistry [
37], medical diagnosis [
38] and statistical modeling [
39]. In the past two decades, there has been an unprecedented development in the field of computational intelligence. Evolutionary computing and swarm intelligence have proved effective in many applications because of their flexible methods and few assumptions based on objective functions, such as deep learning [
40] and multiobjective optimization [
41,
42,
43]. Particle swarm optimization (PSO) is one among many such techniques and has been widely used in continuous/discrete function with complex structures optimization problems [
44].
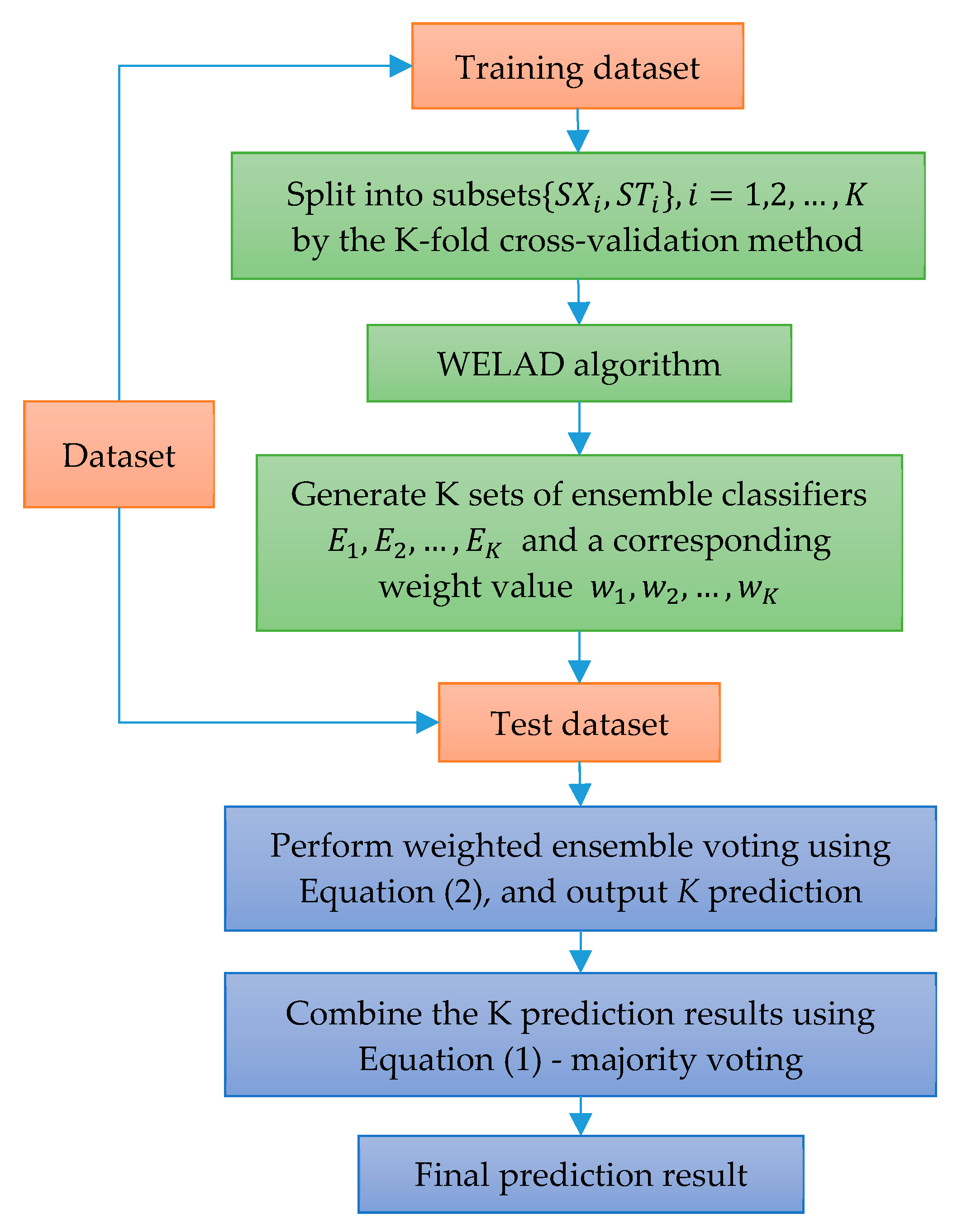
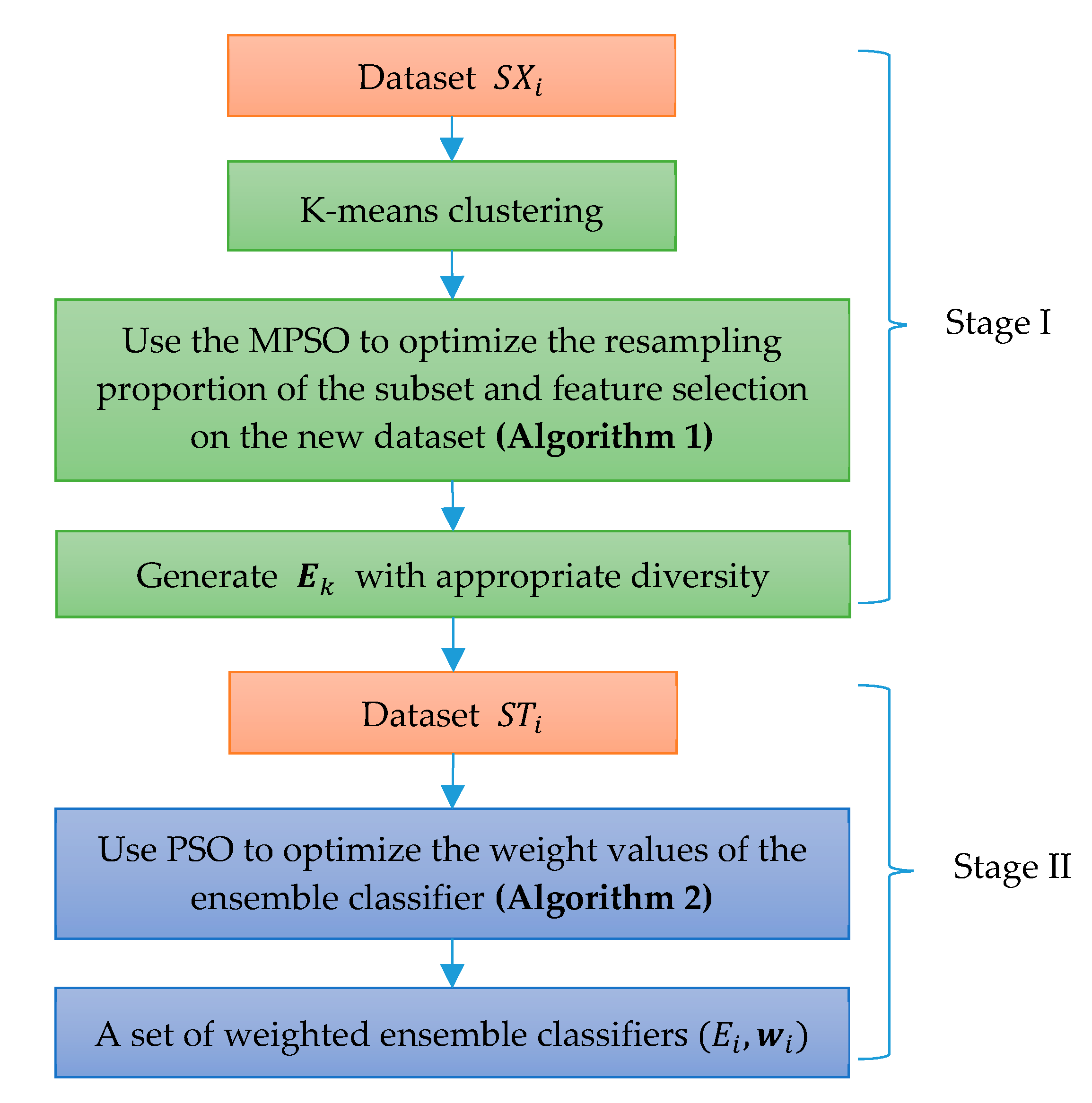
In this paper, a novel weighted ensemble learning algorithm based on diversity (WELAD) is proposed to balance the accuracy and diversity in ensemble learning. The method is divided into two stages: the first stage follows the principle of moderate diversity of individual learners to generate diversified individual learners by manipulating training samples and input features, and the diversity measure adopts the disagreement equation of the pairwise measure. This method includes the accuracy factor of the ensemble classifier and uses this value as the fitness function value of the PSO algorithm [
45] to control the iterative search process, after which a set of ensemble classifiers with appropriate accuracy and adequate diversity is obtained. In the second stage, the weighted ensemble of the classifiers is used. In the ensemble process, the optimization objective function considers both the accuracy and diversity simultaneously for ensemble learning. The diversity factor at this stage is used as a regularization term to prevent overfitting. The diversity measurement method at this stage considers only the dissimilarity in the prediction results of the ensemble classifiers. Then, the PSO algorithm is used to optimize the weight values of a set of classifiers, and finally, a weighted ensemble classifier with good generalization performance is obtained. The major distinction between the WELAD design philosophy and previous studies is in the use of ensemble classifiers with appropriate diversity as an important factor when constructing ensemble learning models. Therefore, in the first stage, when the PSO algorithm is used to search for appropriate diversified individual classifiers, the fitness function of the PSO algorithm takes into account the accuracy of the individual learner and deliberately generates the individual learner to improve the performance of the ensemble classifier.
The rest of this paper is organized as follows:
Section 2 provides the relevant theoretical background for this study, including introductions to the strategies for combining ensemble classifiers, the diversity measure and the PSO algorithm. In
Section 3, we describe the proposed WELAD approach using a two-stage PSO algorithm. We present our experimental results in
Section 4 and analyze the proposed method and the current and classic ensemble learning algorithms. Finally, in
Section 5, we provide conclusions, summarize this study and suggest future research directions.
5. Conclusions
To obtain a good ensemble performance, each individual learner that composes an ensemble classifier is required to have high accuracy and appropriate diversity. To balance the diversity and accuracy in the existing research on ensemble learning, the problem of how to generate individual learners with diversity cannot be fully reflected. In this study, a two-stage weighted ensemble learning method is proposed. When creating individual classifiers and classifiers for integration, the diversity and accuracy are considered at the same time, the corresponding adaptive function of the PSO algorithm is constructed, and the PSO algorithm is used to optimize the target model.
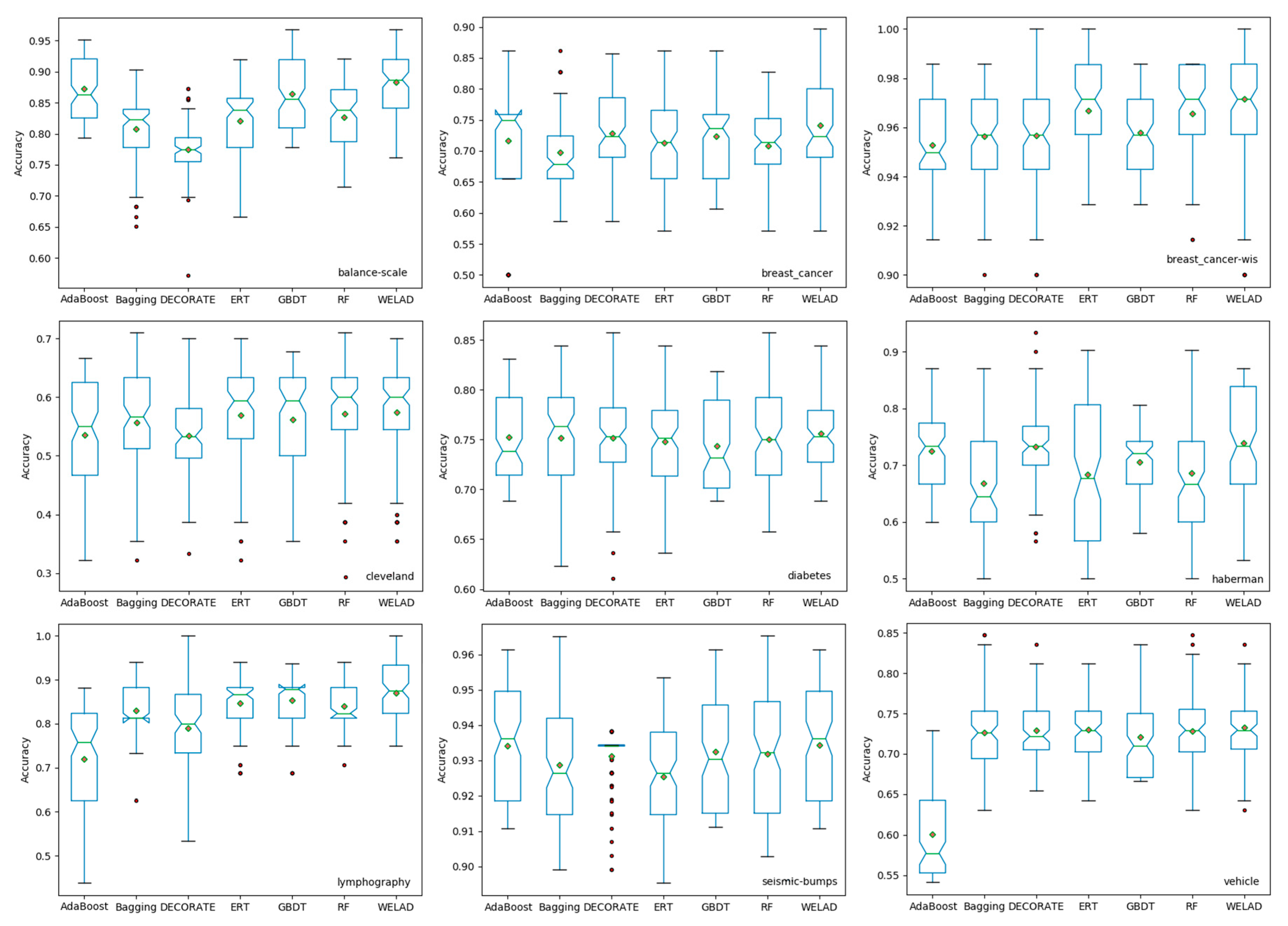
The proposed ensemble learning method is evaluated on 30 UCI datasets, and the experimental results show that the proposed method achieves the highest mean accuracy and the lowest standard deviation of the mean value, which means that the proposed method has better classification performance and stability. In subsequent work, other evolutionary optimization algorithms (i.e., differential evolution [
59]) or different swarm intelligence optimization algorithms (i.e., cuckoo search [
60] and artificial bee colony [
61]) can be used to compare whether their classification performances are different. Another ensemble model called stacking will be used [
62]. The method can also be applied to related fields, such as high-tech industry or quality medical services management.