1. Introduction
In the field of operations research, project management remains a topic of intensive research from various angles such as scheduling and resource allocation. For both cases, there exist such well-known formulations as a resource-constrained project scheduling problem (RCPSP) and a resource leveling problem (RLP). The former aims to minimize the completion time of the set of jobs with given precedence relations and the set of limited required resources. The latter deals with resource allocation with the objective to minimize the cost of resource usage. Both problems were proved to be NP-hard (see [
1] for RCPSP and [
2] for the resource leveling problem). To respond to practical requirements, these basic models undergo numerous modifications. For example, the model that optimizes the distribution of man hours for workforce or throughput on a production line was presented by Neubert and Savino [
3].
In this paper, we focus on the resource leveling problem with several practical enhancements. However, we also refer to RCPSP modeling techniques and approaches that are used for the RLP and applicable to our case. The RLP was actively studied from both the theoretical and practical sides. In the paper of Rieck and Zimmermann [
4] three basic objective function types from the existing literature were presented with properties and existing solution approaches. The first objective function type was described as a total amount of variations in resource utilization within the project duration. The second case arises when available resource utilization is exceeded; it is total (squared) overload cost. The authors also presented a total adjustment cost function, which is formed by costs arising from increasing and decreasing resource utilization. In all cases, the planning horizon was fixed with the reference that for mid-term planning usually there is a determined project deadline. There are some papers involving multi-criteria optimization techniques with attention to both project duration and resource utilization. However, RLP with a fixed deadline and the objective functions that were presented above still attracts attention: The majority of the following literature references are focused on this formulation.
From the practical side, these RLP types are found in a wide range of industries, especially in construction. For these particular cases, researchers apply different heuristics to provide good solutions. An overview of existing RLP heuristic techniques was prepared by Christodoulou et al. [
5]. We can point out recent results with references to industrial problems. For example, a meta-heuristic genetic algorithm was applied to RLP based on a construction project in the paper of Selvam and Tadepalli [
6]. Simulated annealing was also tested in the construction area by Piryonesi et al. [
7]. Li et al. [
8] implemented a genetic algorithm for the RLP with uncertain activity durations and possible overlapping. Construction area and project management usually include discrete resources such as equipment, machines, materials or manpower. Cherkaoui et al. [
9] studied a tactical level of construction and large-scale engineering planning. To achieve robust tactical planning and resource allocation, they created a proactive approach providing lower variations in project costs in case of resource capacity uncertain data. The problem was denoted as rough cut capacity planning (RCCP), but it is also similar to the classical RLP with several practical changes. The same notation was also used by Baydoun et al. [
10].
There is another point that inspires us to study and develop RLP solution methods. Energy is the main continuous resource, and the energy management problem becomes more and more crucial for any industry. According to this, the scheduling of operations with attention to careful energy consumption remains actual. Artigues et al. [
11] considered the industrial case of the energy scheduling problem for a pipe-manufacturing plant. The goal was to minimize the electricity bill, which was raised by penalties for power overrun. The two-step solution approach was proposed with a constraint programming assignment and sequencing part and an MILP scheduling and energy part. Many industrial management problems can be represented as RLP, especially if the parameters are defined and well formalized. Sometimes the energy is not the main resource. For example, for computer embedded systems it can be CPU power, and for data transfer networks it is channel capacity. An example of an optimization problem from the space industry could be found in the paper of Capelle et al. [
12]. In this practical study, the goal was to maximize a data transfer from satellites to a network of optical ground stations. While we see that this formulation is closer to an assignment problem, further research may fit in RLP formulation with satellite data buffer capacity, energy, and data transfer limits.
For the resource leveling problem, the case with variable job duration was considered by Hans, who proposed a branch and cut algorithm [
13]; furthermore, Kis developed an improved branching scheme [
14]. In these models, the precedence relations are defined on periods and job duration depends on the resources allocated to each job. The resource consumption is calculated in an aggregated way for each period. The concept of variable job duration has also been modeled in the following studies (see [
4,
15]) but with the objective of makespan minimization or balanced profile usage. Bianco et al. [
16] also considered the resource leveling problem and proposed a lower bound based on Lagrangian relaxation, and a branch and bound algorithm for the suggested model. The resource leveling model with the overload cost and overlapping of jobs with precedence relations was presented by Baydoun et al. [
10] with a focus on different overlapping rules such as overlapping after implementation of some essential predecessor part.
We follow these ideas and study the generalization of models presented by Baydoun et al. [
10] and Bianco et al. [
16]. The goal is to minimize overload cost when an extra resource amount is required beyond the available limit. In contrast to these studies, we consider a more flexible resource distribution. The main difference could be presented in the following way. In these papers, there is one decision variable (denoted as assigned workload [
10] or the fraction [
16] of activity in a period) describing the progress made by a given job in a given period, and it defines the requirement for each resource type. In our case, we enrich the model to make the allocation of resources per period independently with additional decision variables.
For example, suppose there is one job
j which requires overall one unit of resource
and two units of resource
. In the models considered by [
10,
16] the solution defines only job fractions (these models are denoted as ’aggregate fraction’ in the following). Suppose in the solution the job is implemented in two time periods with equal fractions in both periods (50%/50%). Then according to the models in the first period, we involve 0.5 units of resource
and 1 unit of resource
, and the same in the second period. The involved resource amount equals the multiplication of this decision variable and a resource amount required to carry out the job (fixed input parameter). So there exists a constant ratio between the involved renewable resource amount (or efforts made by different resources) for a given job in all periods. We point out that particular fraction values are not important. With any fraction of the job
j in any period, there will be the same ratio 0.5 between the involved resources (caused by the total required amount ratio of resource
to resource
). According to our model, it is possible to make a more flexible allocation without any fixed relations between the resources involved to complete the job in some period. For example, it is possible to involve 0.75 units of
and
units of
in the first period and the remaining 0.25 units of
and
units of
in the second period. In this solution, resources are allocated with an independent ratio: 1.5 in the first period and 0.16 in the second period.
The main contribution of this paper is in the new generalized formulation for this type of resource leveling problem. We analyze the difference between this new generalized model and aggregated fraction models from the literature, with a comparison of performance and solution quality for the same instance set. Several particular formulations of this new approach were studied. We also study the case with discrete overloading of resources, which is compliant with human resources allocation. However, we do not consider job overlapping of predecessors and successors.
The rest of the paper is organized as follows. In
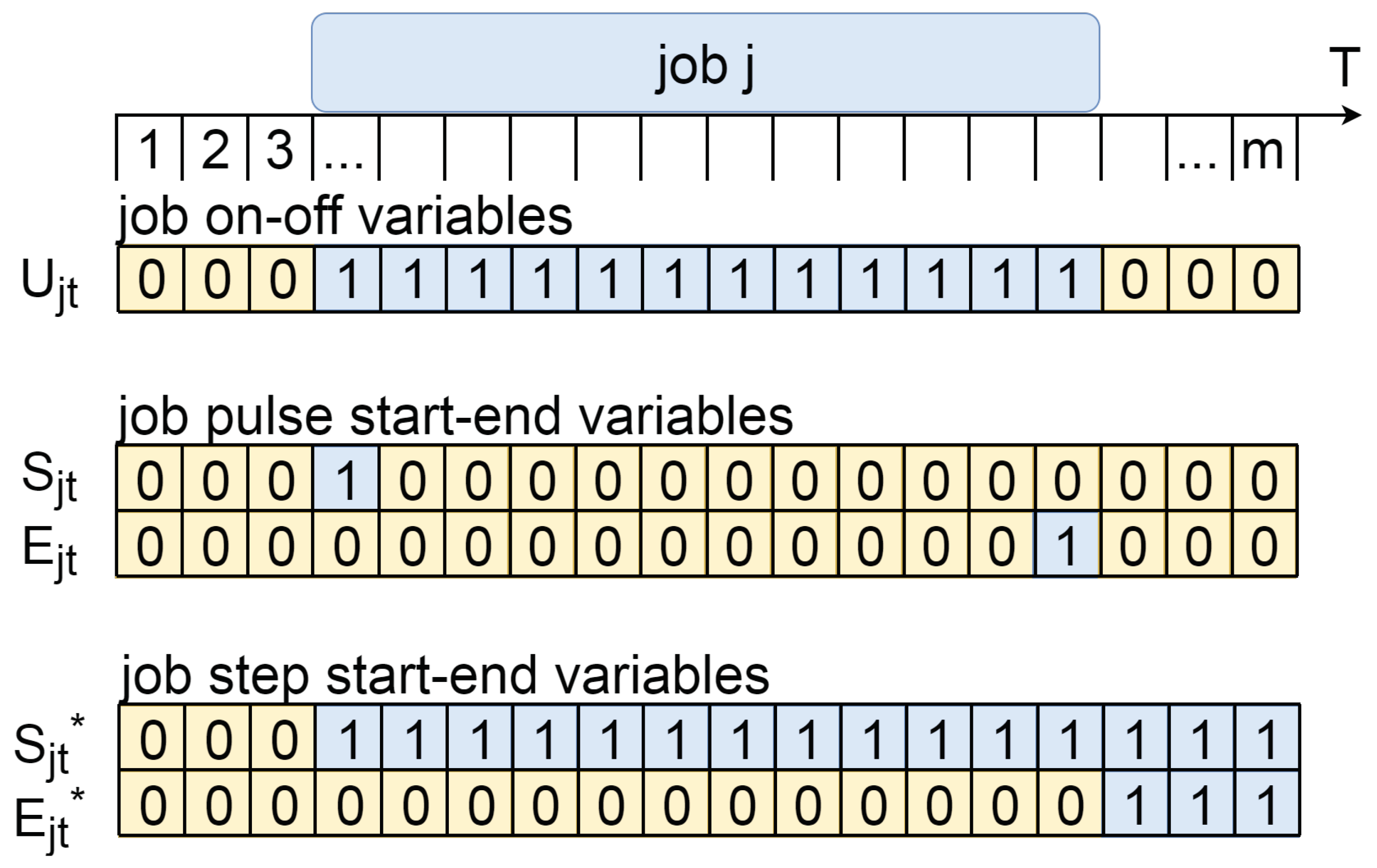
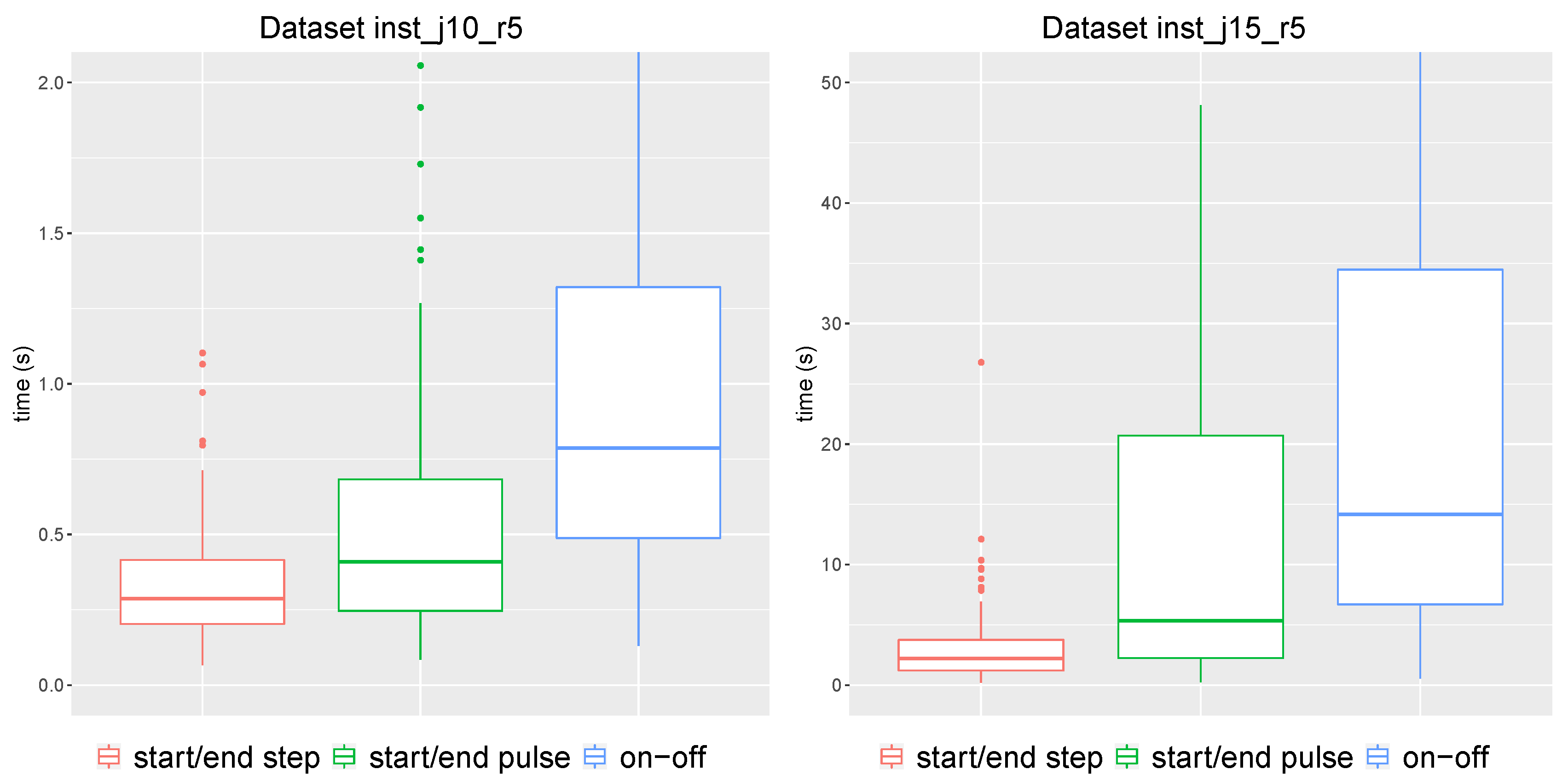
Section 2 we present the new generalized formulation idea with several modeling implementations. We consider three different formulations of scheduling constraints and decision variables. After some experiments, we choose the binary step start/end formulation of variables for scheduling constraints. In
Section 3 we describe a theoretical difference and relations between our generalized formulation and aggregated fraction and analyze the results of computational experiments.
Section 4 presents the case of the discrete overload objective function and discrete resources. After, we make some concluding remarks.
4. Discrete Resource Case
In the Objective Function (
24), continuous overloading variables are used in order to calculate the cost of extra resources. It is compliant with such continuous resources as electricity or heat. However, in practice such resources as machines or human operators can be only available in discrete units. For this case, two possible models can be used.
Firstly, decision variable
can be defined as integer with the minimal unit of each resource
. New variables
set the number of extra units used and they replace
in Objective Function (
24) and Constraint (
23):
We define this model as (discrete objective). This case can be used not only for discrete resources, but it also suits the usual practice when additional resources could be demanded in some packages, for example, the batteries.
Secondly, it is also possible to define other decision variables related to resource allocation as integers. This corresponds to the case when we have discrete resources and we allocate a discrete amount of workload to all periods. We define this model as (discrete objective and resources).
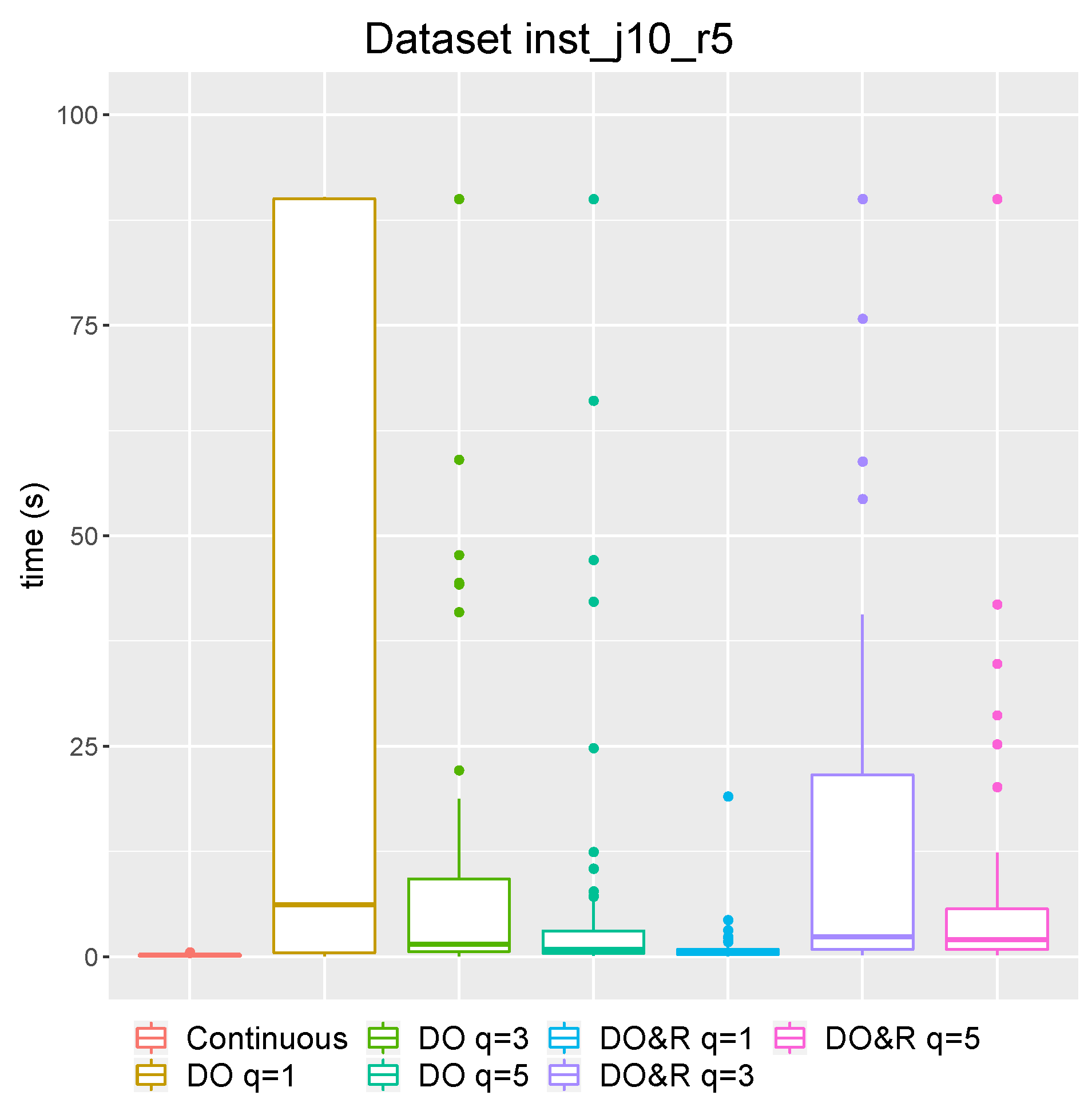
A computational experiment has been run to compare the behavior of continuous and discrete versions of the model. Seven models with different types and parameters of overload variables were considered: The original model with continuous overload variables, three versions of the discrete model with different resource unit size , , equal to 1, 3, and 5, defined as , and the same values of q for the discrete resource allocation case defined as .
Figure 4 presents the computational results for dataset
with a 90 s time limit for all models. Each column is a boxplot that aggregates the data about the solution time, defining the median, lower and upper values, and quartiles. In addition,
Table 10 provides the mean values of the objective function, solution time, and gap which was not presented in
Figure 4. Here we also compare optimal solution objective function value provided by discrete model and continuous generalized model (
), and calculate relative delta. For example, for instance
I and model
it is
As could be expected, the computation time for the discrete model is higher than for the basic continuous model. For some part of the instances, no optimal solution was reached in 90 s for the discrete model, while all the instances were solved for the basic continuous model faster than in a second. However, the information about the gap provided by the solver shows that the main issue is in the proof of optimality: All instances had a very small gap value when the time limit was reached. It is also interesting that the second model type with the discrete allocation of resources provides optimal solutions much faster than the first type . Consequently, it is possible to use these discrete models with some reasonable small gap tolerance.
5. Conclusions
In this paper, we propose a new mathematical formulation for a resource leveling problem with a variable duration of jobs. We consider the extra resource usage cost as the objective function which has to be minimized. Extra resources are required because of a lack of available resources during a fixed planning horizon with a deadline. The main idea behind this new formulation is to provide a more flexible allocation of different resources to jobs, which allows obtaining solutions with better objective function values. Moreover, we consider different models for scheduling decision variables and constraints.
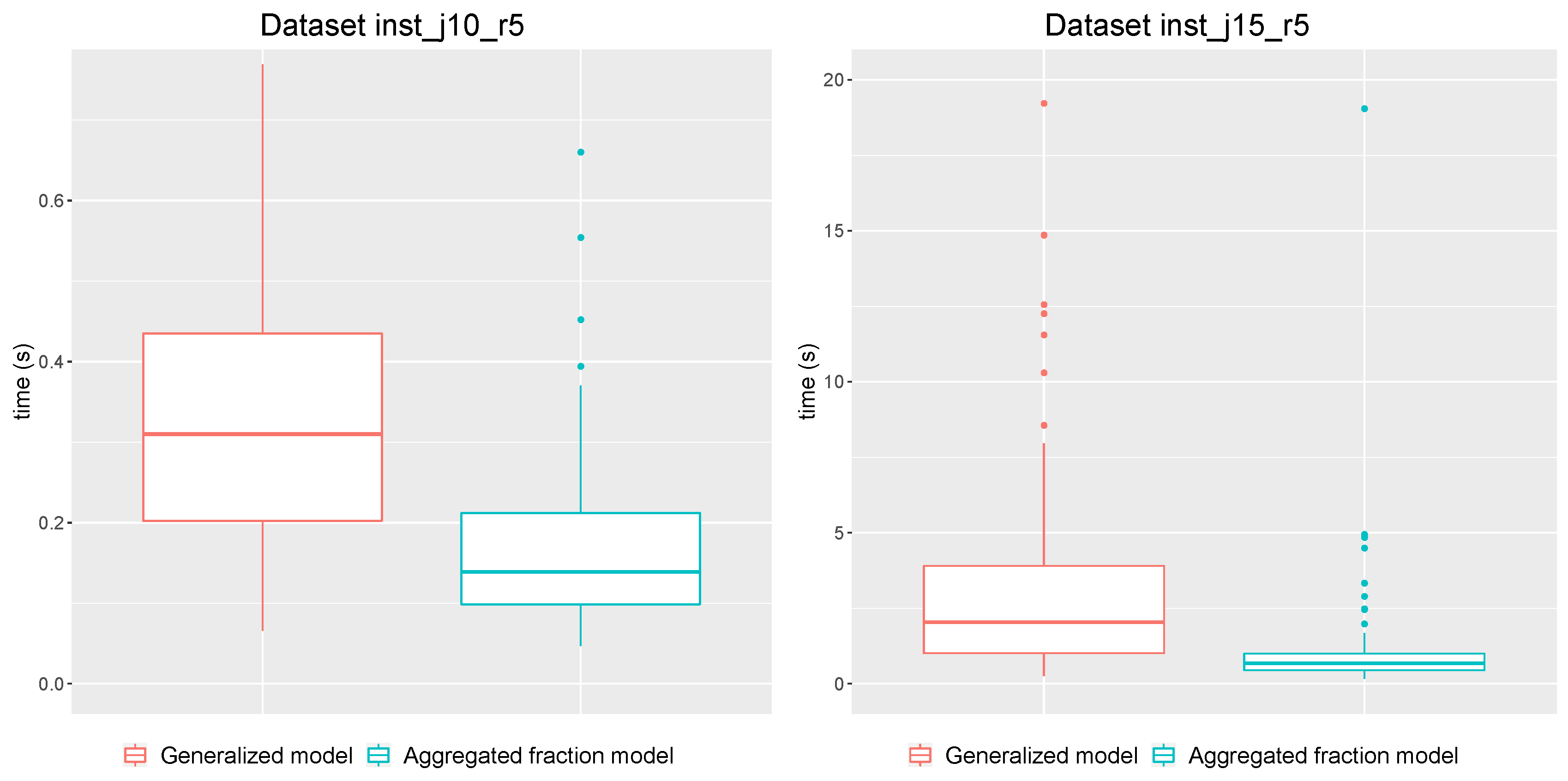
This new formulation approach is compared to other RLP formulations with overload which were found in the literature. We defined them as aggregated fraction models to underline the main difference. The numerical experiments show that, even if the generalized formulation uses more variables and constraints, it provides much better solutions. In this paper the primary goal was to present and evaluate an improvement in solution quality. We also had a secondary goal to demonstrate that our generalized model can compete with the aggregated fraction model with the same solver computational resource and time limit. We compared the proofed optimal solution of the aggregated fraction formulation with a suboptimal solution of a generalized formulation obtained at the same time. We can state that with the same solver and time limit, the generalized formulation also provides better solution quality. However, we did not test any acceleration methods for this RLP model.
There are two directions for further research. Firstly, it would be valuable to provide a theoretical estimation of the difference in the value of the objective function for the generalized and fraction-aggregated models. This would allow determining some subsets of instances with a maximum difference between solution quality. Secondly, with good perspectives in solution quality, it is reasonable to focus on model improvements and adapt existing RLP solution algorithms for the new model. This will require more tests with instances and the application of some resource leveling problem benchmark datasets for model performance comparison. Some particular real case-based problems may also inspire further steps. For example, scheduling of workforce with additional constraints such as variable experience depending on previous actions [
23].
In order to improve the solution procedure, the development of a Benders decomposition algorithm is planned for future research. Besides, approximation schemes can be quite efficient as we can estimate the objective function value difference for the discrete and the continuous resource models, which provides the estimated accuracy if the scheme is based on the continuous model.