Nearest Embedded and Embedding Self-Nested Trees
Abstract
1. Introduction
2. Preliminaries
2.1. Unordered Rooted Trees
2.2. DAG Compression
2.3. Self-Nested Trees
3. Height Profile of the Tree Structure
3.1. Definition and Complexity
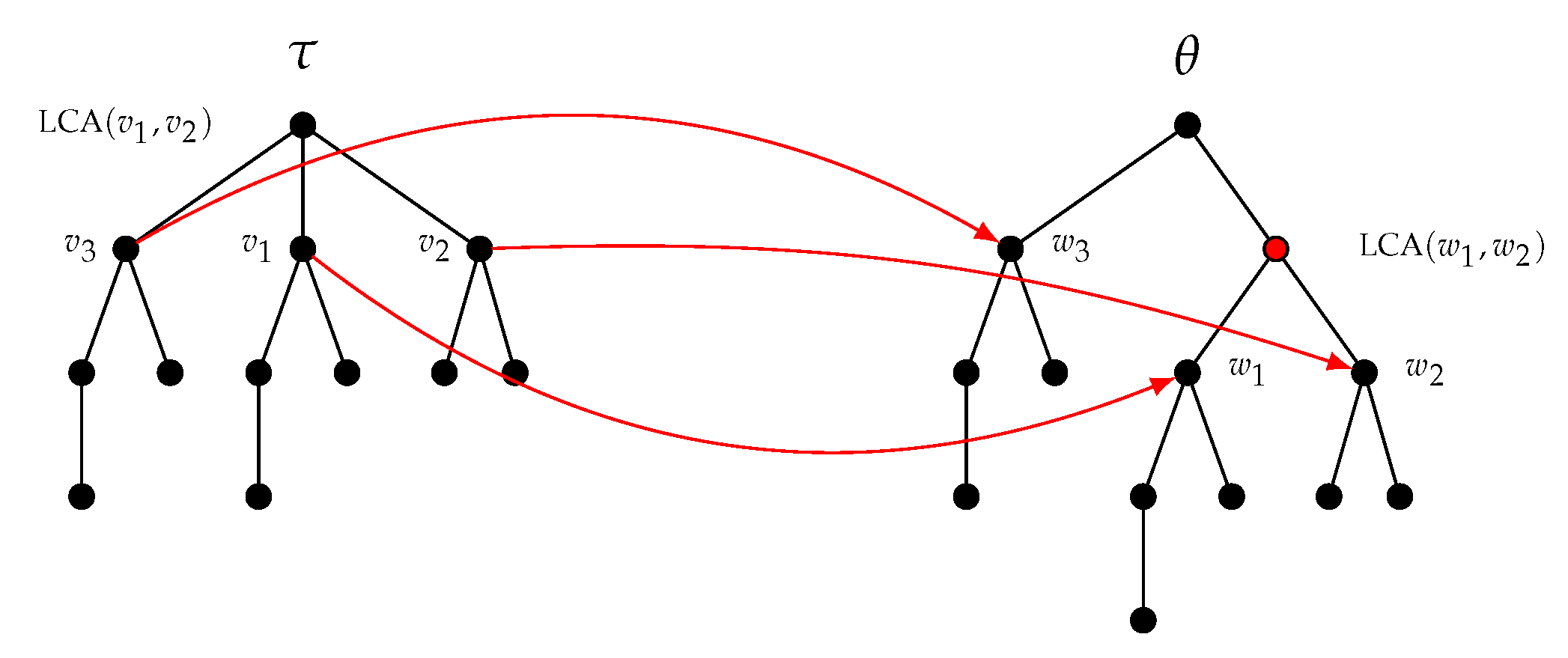
3.2. Relation with Self-Nested Trees
| Algorithm 1: Construction of a self-nested tree from its height profile. |
 |
4. Approximation Algorithms
4.1. Definitions
4.1.1. Editing Operations
4.1.2. Constrained Editing Operations
4.1.3. Preserving the Height of the Pre-Existing Nodes
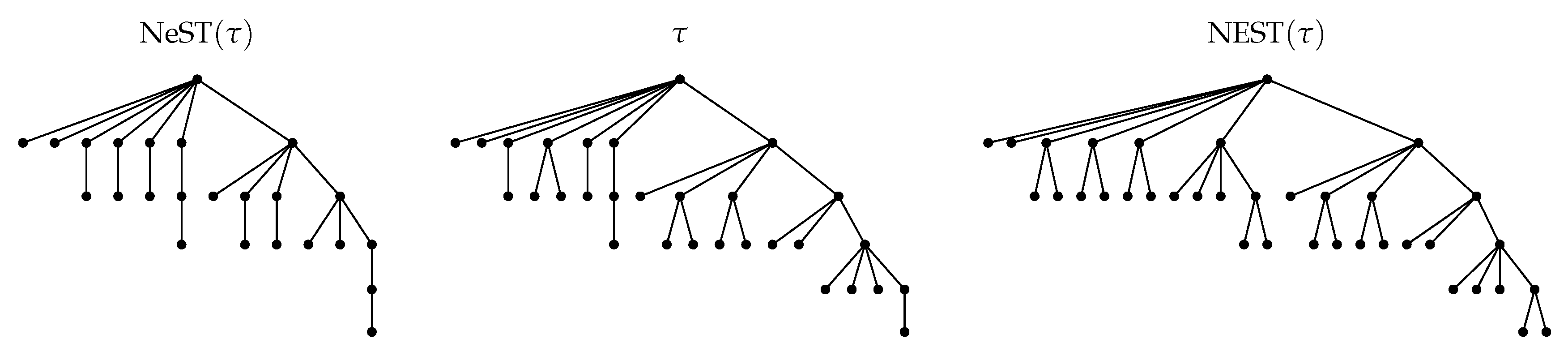
4.1.4. NEST and NeST
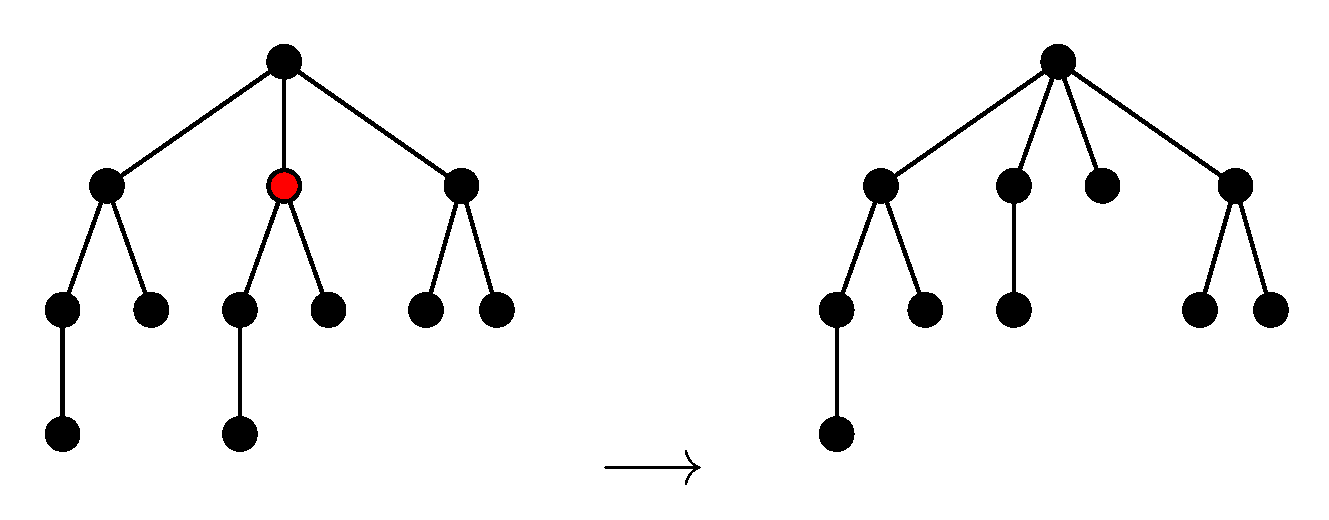
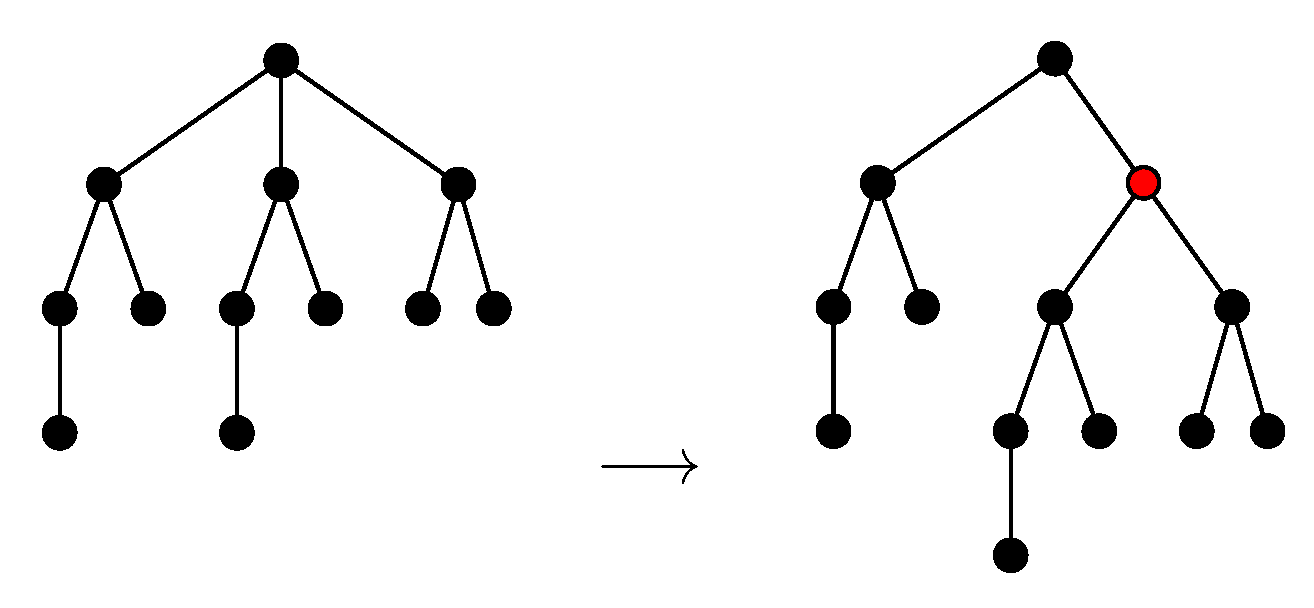
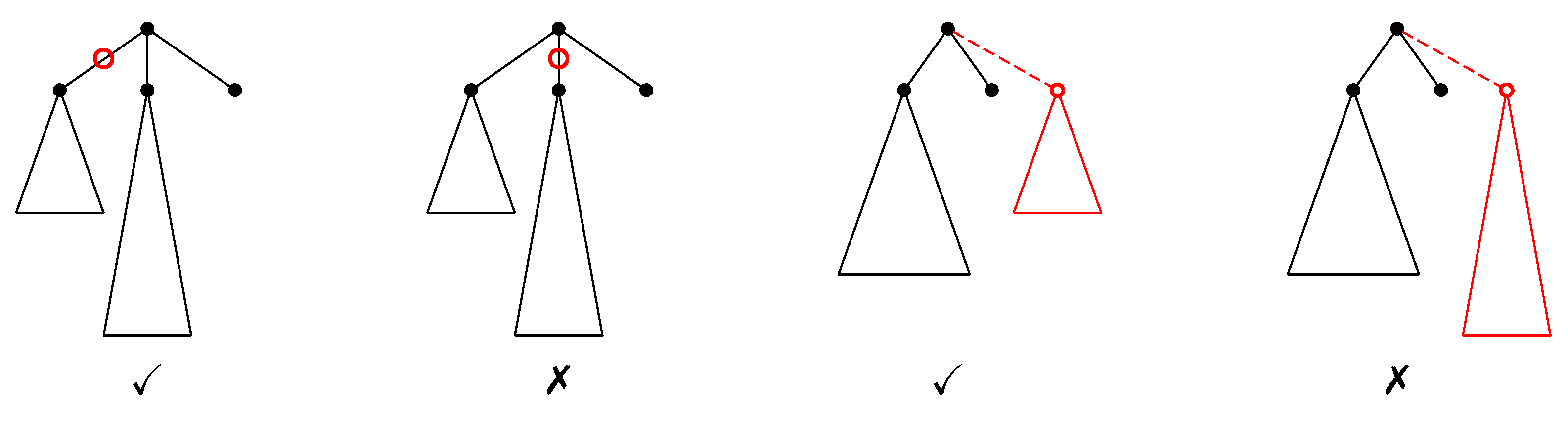
- Internal nodes (AI): adding w as a child of v making w the parent of the child c of v can be done only if .
- Subtrees (AS): adding t as a child of v can be done only if .
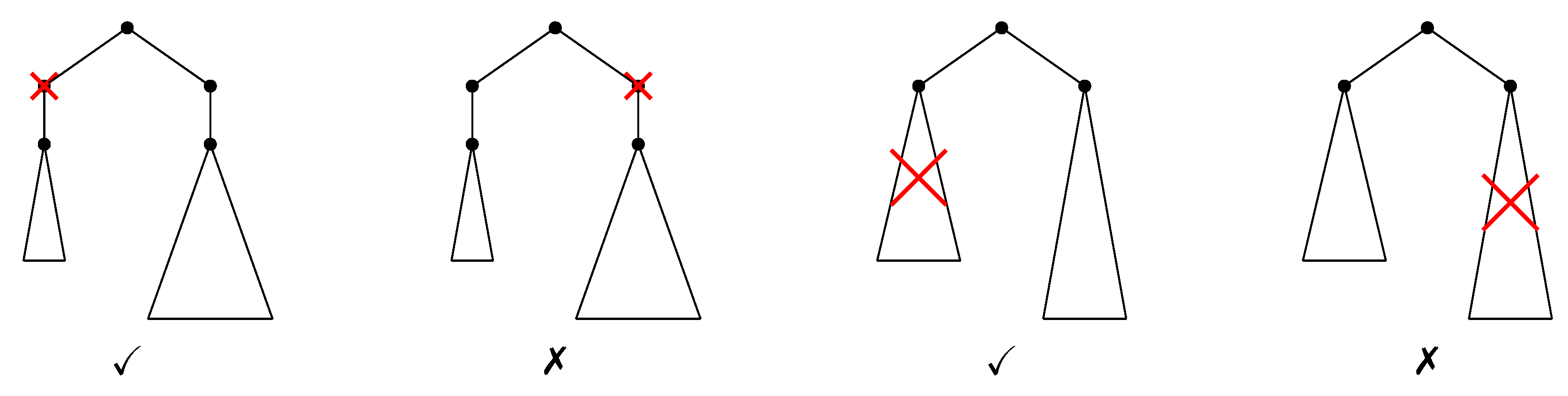
- Internal nodes (DI): deleting (making the unique child w of v a child of u) can be done only if there exists , , such that .
- Subtrees (DS): deleting the subtree , , of can be done if there exists , , such that .
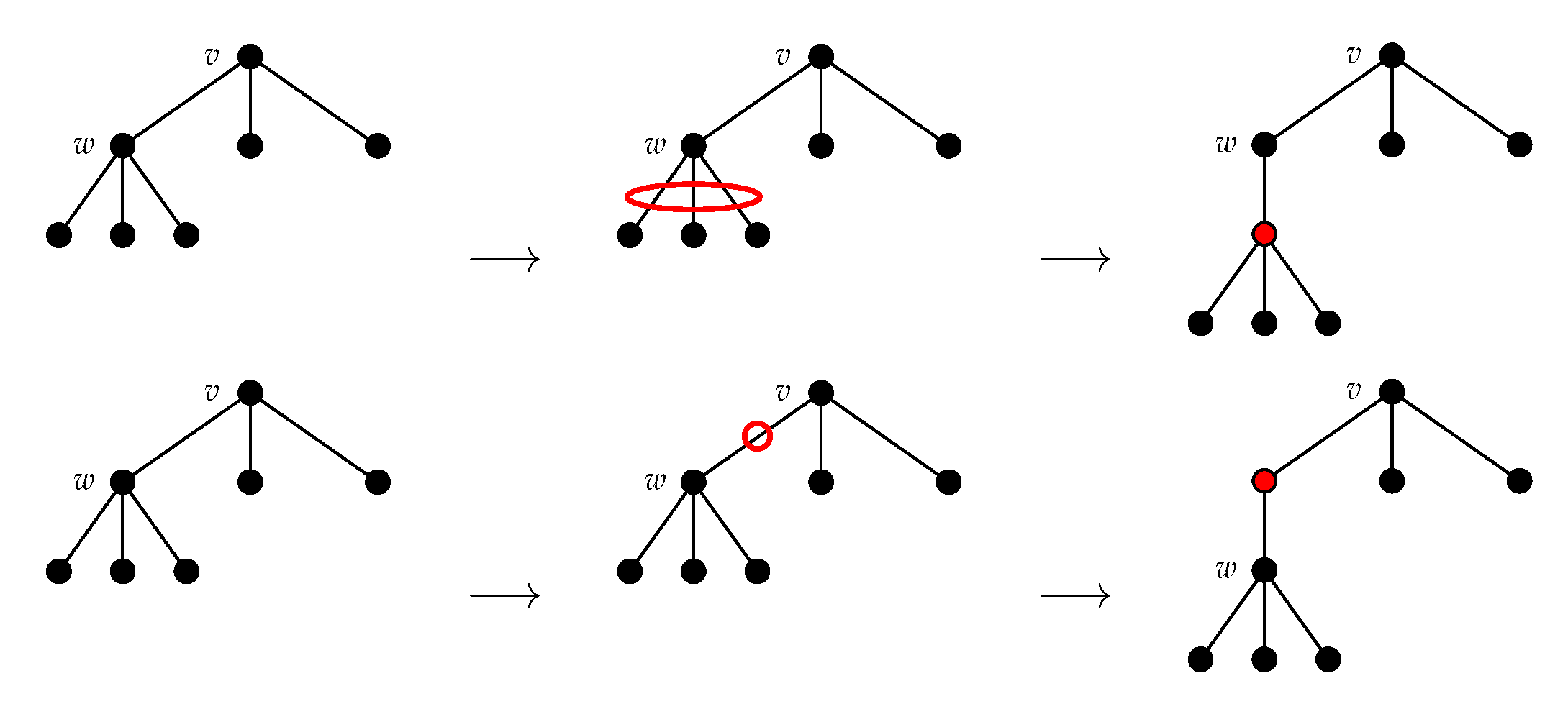
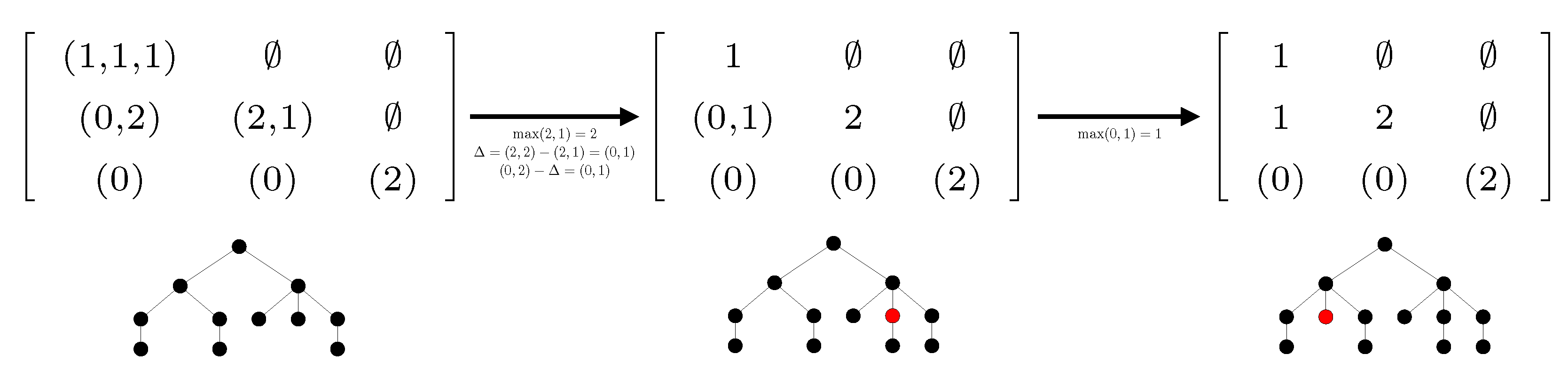
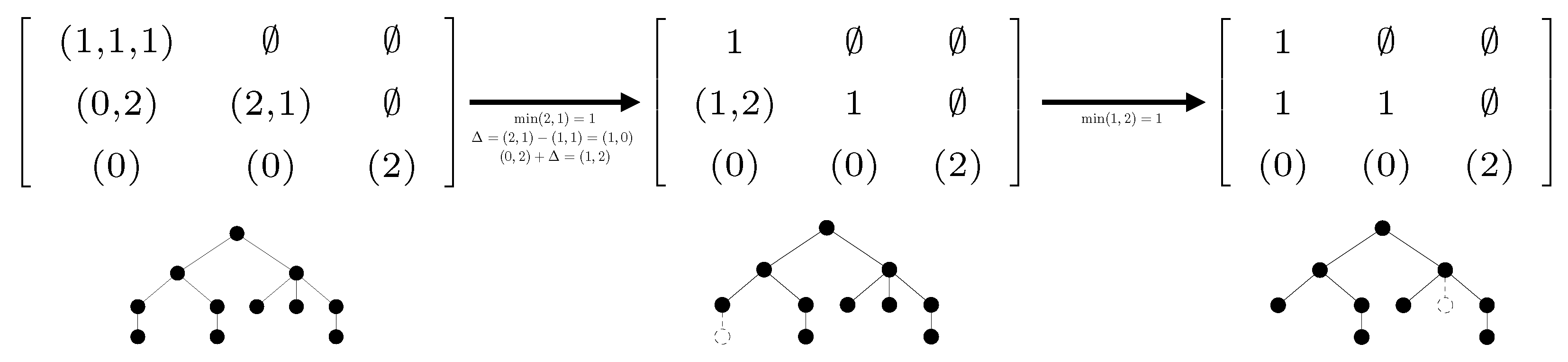
4.2. NEST Algorithm
| Algorithm 2: Construction of the nearest embedding self-nested tree. |
 |
4.3. NeST Algorithm
| Algorithm 3: Construction of the nearest embedded self-nested tree. |
 |
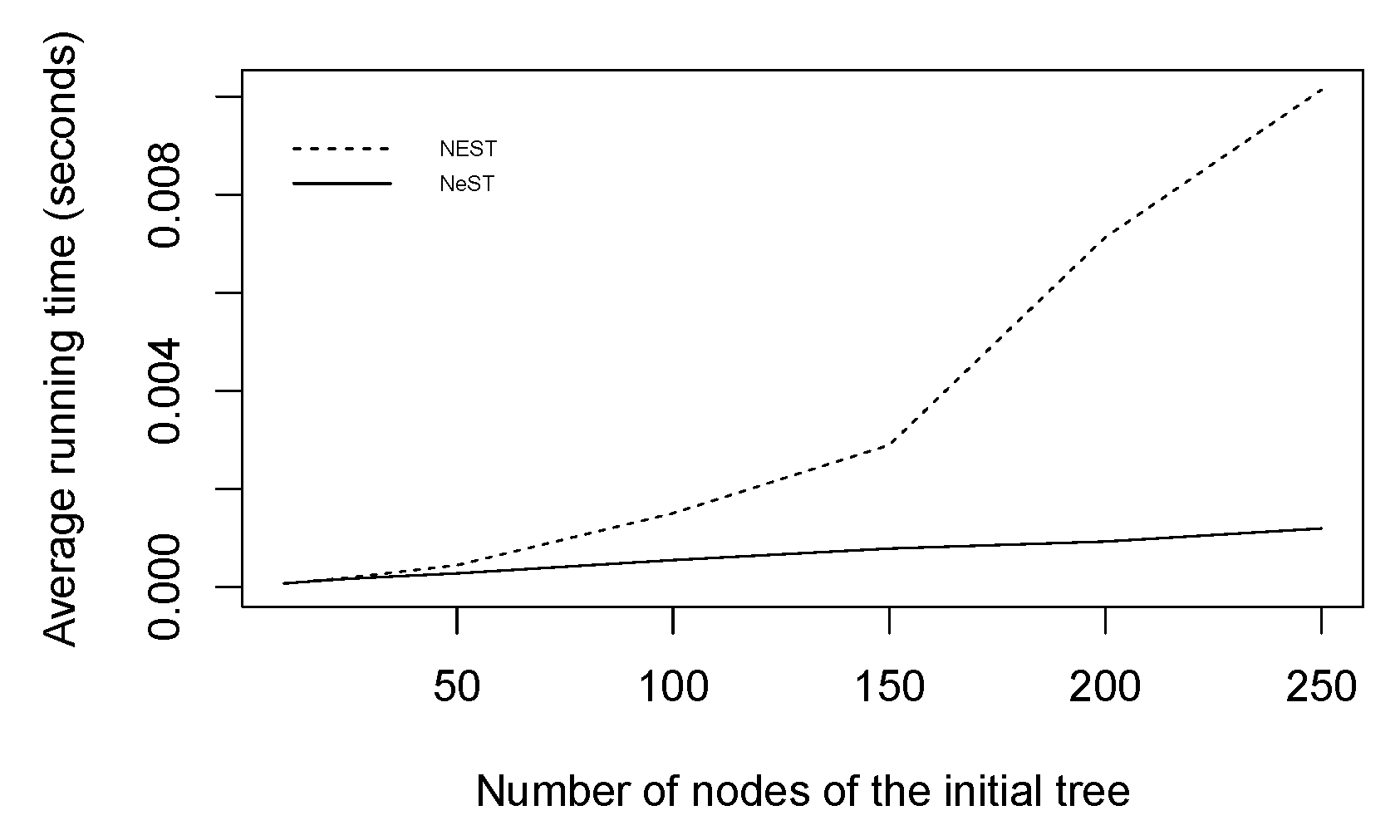
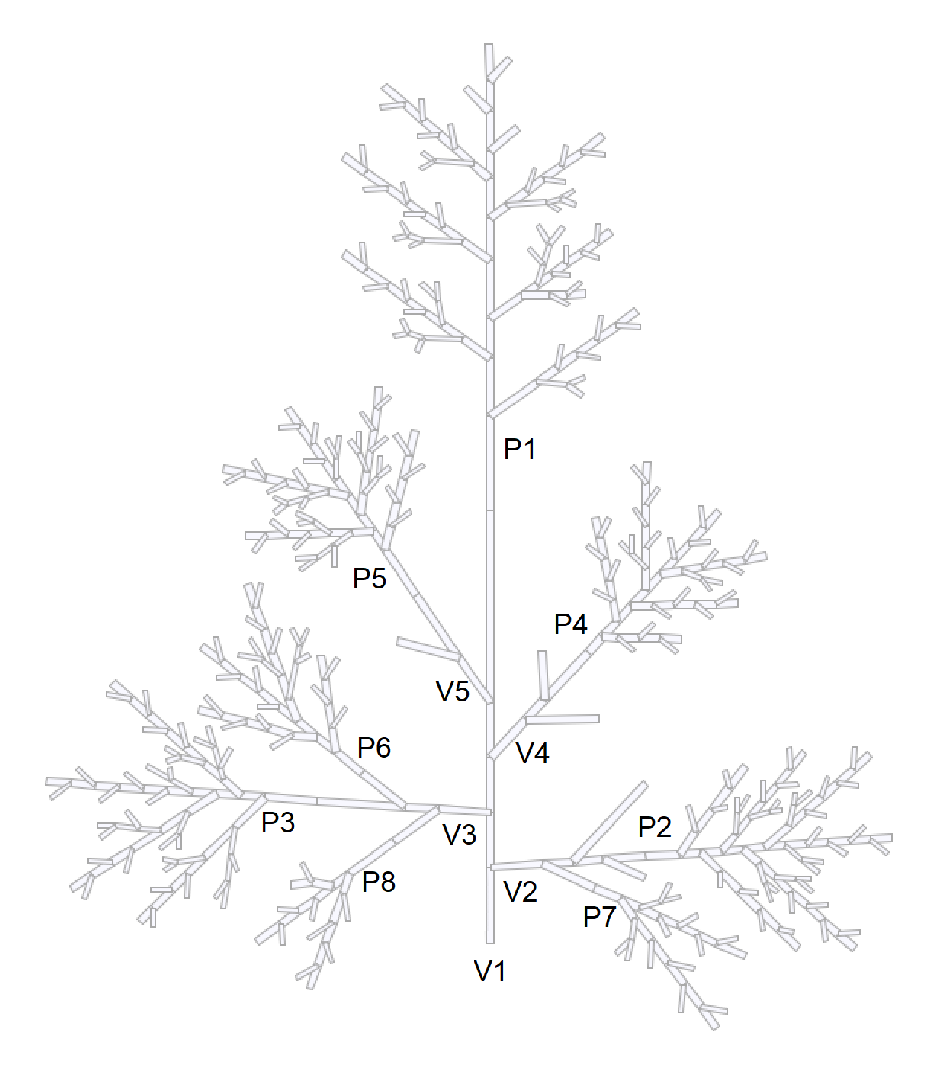
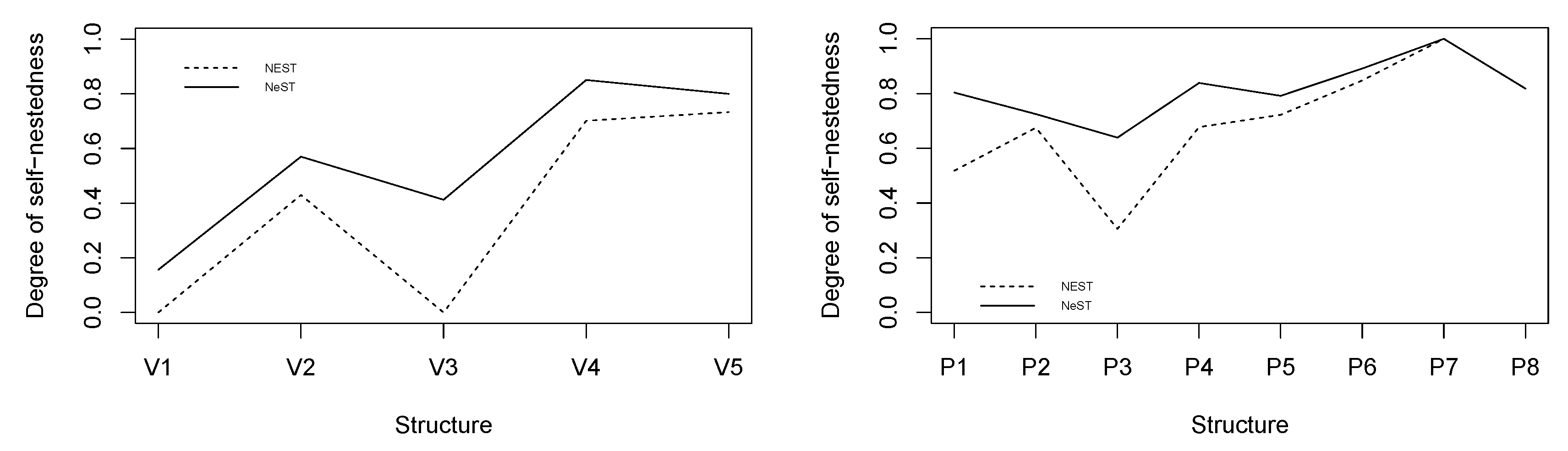
5. Numerical Illustration
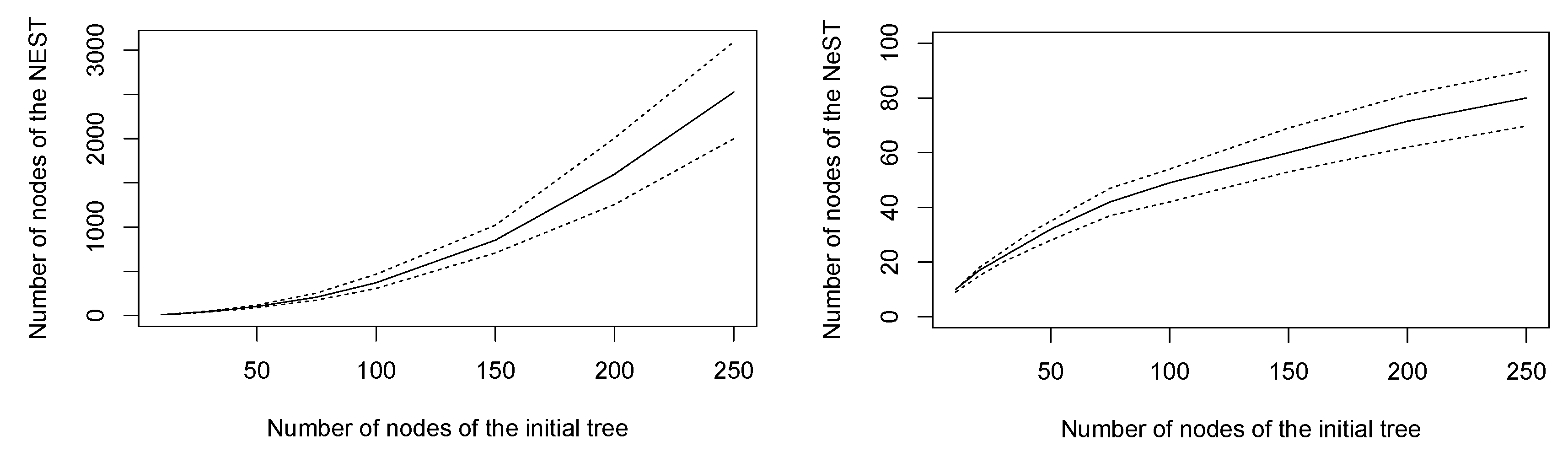
5.1. Random Trees
5.2. Structural Analysis of a Rice Panicle
6. Summary and Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
References
- Bille, P.; Gørtz, I.L.; Landau, G.M.; Weimann, O. Tree compression with top trees. Inf. Comput. 2015, 243, 166–177. [Google Scholar] [CrossRef]
- Bousquet-Mélou, M.; Lohrey, M.; Maneth, S.; Noeth, E. XML Compression via Directed Acyclic Graphs. Theory Comput. Syst. 2014, 57, 1322–1371. [Google Scholar] [CrossRef]
- Buneman, P.; Grohe, M.; Koch, C. Path Queries on Compressed XML. In Proceedings of the 29th International Conference on Very Large Data Bases, VLDB’03, Berlin, Germany, 9–12 September 2003; Volume 29, pp. 141–152. [Google Scholar]
- Frick, M.; Grohe, M.; Koch, C. Query evaluation on compressed trees. In Proceedings of the 18th Annual IEEE Symposium of Logic in Computer Science, Ottawa, ON, Canada, 22–25 June 2003; pp. 188–197. [Google Scholar]
- Godin, C.; Ferraro, P. Quantifying the degree of self-nestedness of trees. Application to the structural analysis of plants. IEEE Trans. Comput. Biol. Bioinform. 2010, 7, 688–703. [Google Scholar] [CrossRef] [PubMed]
- Busatto, G.; Lohrey, M.; Maneth, S. Efficient Memory Representation of XML Document Trees. Inf. Syst. 2008, 33, 456–474. [Google Scholar] [CrossRef]
- Lohrey, M.; Maneth, S. The Complexity of Tree Automata and XPath on Grammar-compressed Trees. Theor. Comput. Sci. 2006, 363, 196–210. [Google Scholar] [CrossRef][Green Version]
- Greenlaw, R. Subtree Isomorphism is in DLOG for Nested Trees. Int. J. Found. Comput. Sci. 1996, 7, 161–167. [Google Scholar] [CrossRef]
- Azaïs, R.; Cerutti, G.; Gemmerlé, D.; Ingels, F. treex: A Python package for manipulating rooted trees. J. Open Source Softw. 2019, 4, 1351. [Google Scholar] [CrossRef]
- Aho, A.V.; Hopcroft, J.E.; Ullman, J.D. The Design and Analysis of Computer Algorithms, 1st ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1974. [Google Scholar]
- Zhang, K. A constrained edit distance between unordered labeled trees. Algorithmica 1996, 15, 205–222. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azaïs, R. Nearest Embedded and Embedding Self-Nested Trees. Algorithms 2019, 12, 180. https://doi.org/10.3390/a12090180
Azaïs R. Nearest Embedded and Embedding Self-Nested Trees. Algorithms. 2019; 12(9):180. https://doi.org/10.3390/a12090180
Chicago/Turabian StyleAzaïs, Romain. 2019. "Nearest Embedded and Embedding Self-Nested Trees" Algorithms 12, no. 9: 180. https://doi.org/10.3390/a12090180
APA StyleAzaïs, R. (2019). Nearest Embedded and Embedding Self-Nested Trees. Algorithms, 12(9), 180. https://doi.org/10.3390/a12090180




