A FEAST Algorithm for the Linear Response Eigenvalue Problem

Abstract

In the linear response eigenvalue problem arising from quantum chemistry and physics, one needs to compute several positive eigenvalues together with the corresponding eigenvectors. For such a task, in this paper, we present a FEAST algorithm based on complex contour integration for the linear response eigenvalue problem. By simply dividing the spectrum into a collection of disjoint regions, the algorithm is able to parallelize the process of solving the linear response eigenvalue problem. The associated convergence results are established to reveal the accuracy of the approximated eigenspace. Numerical examples are presented to demonstrate the effectiveness of our proposed algorithm.

1. Introduction

In computational quantum chemistry and physics, the random phase approximation (RPA) or the Bethe–Salpeter (BS) equation describe the excitation states and absorption spectra for molecules or the surfaces of solids [1,2]. One important question in the RPA or BS equation is how to compute a few eigenpairs associated with several of the smallest positive eigenvalues of the following eigenvalue problem:

$$\mathcal{H}w=\left[\begin{array}{cc}A& B\\ -B& -A\end{array}\right]\left[\begin{array}{c}u\\ v\end{array}\right]=\lambda \left[\begin{array}{c}u\\ v\end{array}\right]=\lambda w,$$

(1)

where $A,B\in {\mathbb{R}}^{N\times N}$ are both symmetric matrices and $\left[\begin{array}{cc}A& B\\ B& A\end{array}\right]$ is positive definite [3,4,5]. Through a similarity transformation, the eigenvalue problem (1) can be equivalently transformed into:

$$Hz=\left[\begin{array}{cc}0& K\\ M& 0\end{array}\right]\left[\begin{array}{c}y\\ x\end{array}\right]=\lambda \left[\begin{array}{c}y\\ x\end{array}\right]=\lambda z,$$

(2)

where $K=A-B$ and $M=A+B$. The eigenvalue problem (2) was still referred to as the linear response eigenvalue problem (LREP) [3,6] and will be so in this paper, as well. The condition imposed upon A and B in (1) implies that both K and M are $N\times N$ real symmetric positive definite matrices. However, there are cases where one of them may be indefinite [7]. Therefore, to be consistence with [8,9,10], throughout the rest of the paper, we relax the condition on K and M to that they are symmetric and one of them is positive definite, while the other may be indefinite. There has been immense recent interest in developing new theories, efficient numerical algorithms of LREP, and the associated excitation response calculations of molecules for materials’ design in energy science [11,12,13,14,15].

From (2), we have $Kx=\lambda y$ and $My=\lambda x$, and they together lead to:

$$\begin{array}{cc}\hfill KMy& ={\lambda }^{2}y,\hfill \\ \hfill MKx& ={\lambda }^{2}x.\hfill \end{array}$$

Since $KM=K{M}^{1/2}{M}^{1/2}$ has the same eigenvalues as $M^{1/2}K{M}^{1/2}$, which is symmetric, all eigenvalues of $KM$ are real. Denote these eigenvalues by ${\omega }_i$ ($1\le i\le N$) in ascending order, i.e.,

$${\omega }_1\le {\omega }_2\le \cdots \le {\omega }_N.$$

(3)

The eigenvalues of $MK$ are ${\omega }_i$ ($1\le i\le N$), as well. Let $\iota =\sqrt{-1}$, the imaginary unit, and:

$${\lambda }_i=\left\{\begin{array}{cc}\sqrt{{\omega }_i},\hfill & \mathrm{if}{\omega }_i\ge 0,\hfill \\ \iota \sqrt{-{\omega }_i},\hfill & \mathrm{if}{\omega }_i<0.\hfill \end{array}\right.$$

(4)

The eigenvalues of H are:

$$\pm {\lambda }_i\mathrm{for}i=1,2,\dots ,N.$$

This practice of enumerating the eigenvalues of H will be used later for the much smaller projection of H, as well.

Since the dimension N is usually very large for systems of practical interest, solving LREP (2) is a very challenging problem. The iterative methods are recent efforts for computing the partial spectrum of (2), such as the locally-optimal block preconditioned 4D conjugate gradient method (LOBP4DCG) [6] and its space-extended variation [16], the block Chebyshev–Davidson method [10], as well as the generalized Lanczos-type methods [8,9]. These algorithms are all based on the so-called pair of deflating subspaces, which is a generalization of the concept of the invariant subspace in the standard eigenvalue problems. Thus, these methods can be regarded as extensions of the associated classical methods for the standard eigenvalue problem. Recently, in [17], a density-matrix-based algorithm, called FEAST, was proposed by Polizzi for the calculation of a segment of eigenvalues and their associated eigenvectors of a real symmetric or Hermitian matrix. The algorithm promises high potential for parallelism by dividing the spectrum of a matrix into an arbitrary number of nonintersecting intervals. The eigenvalues in each interval and the associated eigenvectors can be solved independently of those in the other intervals. As a result, one can compute a large number of eigenpairs at once on modern computing architectures, while typical Krylov- or Davidson-type solvers fail in this respect because they require orthogonalization of any new basis vector with respect to the previously-converged ones.

The basic idea of the FEAST algorithm is based on the contour integral function:

$$\begin{array}{c}\hfill f(\alpha )=\frac{1}{2\pi \iota }{\oint }_{\mathcal{C}}{(\mu -\alpha )}^{-1}d\mu \end{array}$$

to construct bases of particular subspaces and obtain the corresponding approximate eigenpairs by the Rayleigh–Ritz procedure where $\mathcal{C}$ is any contour enclosing the set of wanted eigenvalues. The corresponding theoretical analysis was established in [18]. In particular, it was shown that the FEAST algorithm can be understood as an accelerated subspace iteration algorithm. Due to the advantage of the FEAST algorithm in parallelism, it has been well received in the electronic structure calculations community. Additionally, the improvements and generalizations of FEAST algorithm have been active research subjects in eigenvalue problems for nearly a decade. For example, in [19], Kestyn, Polizzi, and Tang presented the FEAST eigensolver for non-Hermitian problems by using the dual subspaces for computing the left and right eigenvectors. In [20], the FEAST algorithm was developed to solve nonlinear eigenvalue problems for eigenvalues that lie in a user-defined region. Some other work for the FEAST method can be found in [21,22,23,24]. Motivated by these facts, in this paper, we will continue the effort by extending the FEAST algorithm to LREP.

The rest of the paper is organized as follows. In Section 2, some notations and preliminaries including the canonical angles of two subspaces and basic results for LREP are collected for use later. Section 3 contains our main algorithm, the implementation issue, and the corresponding convergence analysis. In Section 4, we present some numerical examples to show the numerical behavior of our algorithm. Finally, conclusions are drawn in Section 5.

2. Preliminaries

${\mathbb{R}}^{m\times n}$ is the set of all $m\times n$ real matrices. For $\mathcal{X}\subseteq {\mathbb{R}}^n$, $dim(\mathcal{X})$ is the dimension of $\mathcal{X}$. For $X\in {\mathbb{R}}^{m\times n}$, $X^T$ is its transpose and $\mathcal{R}(X)$ the column space of X, and the submatrix $X_{(:,i:j)}$ of X consists of column i to column j. $I_n$ is the $n\times n$ identity matrix or simply I if its dimension is clear from the context. For matrices or scalars $X_i$, $diag(X_1,X_2,\cdots ,X_k)$ denotes the block diagonal matrix with diagonal block $X_1,X_2,\cdots ,X_k$.

For any given symmetric and positive definite matrix $W\in {\mathbb{R}}^{N\times N}$, the W-inner product and its induced W-norm are defined by:

$${⟨x,y⟩}_W=y^{T}Wx,{\parallel x\parallel }_W=\sqrt{{⟨x,x⟩}_W}.$$

If ${⟨x,y⟩}_W=0$, then we say $x{\perp }_{W}y$ or $y{\perp }_{W}x$. The projector ${\Pi }_W$ is said to the W-orthogonal projector onto $\mathcal{X}$ if for any vector $x\in {\mathbb{R}}^N$,

$${\Pi }_{W}x\in \mathcal{X}\mathrm{and}(I-{\Pi }_W)x{\perp }_W\mathcal{X}.$$

For two subspaces $\mathcal{X},\mathcal{Y}\subseteq {\mathbb{R}}^N$ with $k=dim(\mathcal{X})\le dim(\mathcal{Y})=\ell$, let X and Y be the W-orthonormal basis matrices of subspaces $\mathcal{X}$ and $\mathcal{Y}$, respectively, i.e.,

$$X^{T}WX=I_k,\mathcal{R}(X)=\mathcal{X},\mathrm{and}{Y}^{T}WY=I_{\ell },\mathcal{R}(Y)=\mathcal{Y}.$$

Denote the singular values of $X^{T}WY$ by ${\sigma }_j$ for $1\le j\le k$ in ascending order, i.e., ${\sigma }_1\le \cdots \le {\sigma }_k$. The diagonal matrix of W-canonical angles from (If $\ell =k$, we may say that these angles are between $\mathcal{X}$ and $\mathcal{Y}$ [25].) $\mathcal{X}$ to $\mathcal{Y}$ in descending order is defined by:

$${\Theta }_W(\mathcal{X},\mathcal{Y})=diag({\theta }_W^{(1)}(\mathcal{X},\mathcal{Y}),\cdots ,{\theta }_W^{(k)}(\mathcal{X},\mathcal{Y})),$$

where ${\theta }_W^{(1)}(\mathcal{X},\mathcal{Y})\ge \cdots \ge {\theta }_W^{(k)}(\mathcal{X},\mathcal{Y})$ and:

$$0\le {\theta }_W^{(j)}(\mathcal{X},\mathcal{Y})=arccos{\sigma }_j\le \frac{\pi }{2},\mathrm{for}1\le j\le k.$$

In what follows, we sometimes place a vector or matrix in one or both arguments of ${\Theta }_W(.,.)$ with the understanding that it is about the subspace spanned by the vector or the columns of the matrix argument.

Several theoretical properties of the canonical angle and LREP have been established in [25] and [3], respectively. In particular, the following lemmas are necessary for our later developments.

Lemma 1

([9] Lemma 3.2). Let $\mathcal{X}$ and $\mathcal{Y}$ be two subspaces in ${\mathbb{R}}^N$ with equal dimension $dim(\mathcal{X})=dim(\mathcal{Y})=k$. Suppose ${\theta }_W^{(1)}(\mathcal{X},\mathcal{Y})<\pi /2$. Then, for any set $\{y_1,y_2,\cdots ,y_{k_1}\}$ of the basis vectors in $\mathcal{Y}$ where $1\le k_1\le k$, there is a set $\{x_1,x_2,\cdots ,x_{k_1}\}$ of linear independent vectors in $\mathcal{X}$ such that ${\Pi }_W{x}_j=y_j$ for $1\le j\le k_1$, where ${\Pi }_W$ is the W-orthogonal projector onto $\mathcal{Y}$.

Lemma 2

([3] Theorem 2.3). The following statements hold for any symmetric matrices $K,M\in {\mathbb{R}}^{N\times N}$ with M being positive definite.

(a) 

There exists a nonsingular $\Psi \in {\mathbb{R}}^{N\times N}$ such that:

$$K=\Psi {\Lambda }^2{\Psi }^{T}andM=\Phi {\Phi }^T,$$

where $\Lambda =diag({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_N)$, ${\lambda }_1^2\le {\lambda }_2^2\le \cdots \le {\lambda }_N^2$ and $\Phi ={\Psi }^{-T}$.

(b) 

If K is also definite, then all ${\lambda }_i>0$, and H is diagonalizable:

$$H\left[\begin{array}{cc}\Psi \Lambda & \Psi \Lambda \\ \Phi & -\Phi \end{array}\right]=\left[\begin{array}{cc}\Psi \Lambda & \Psi \Lambda \\ \Phi & -\Phi \end{array}\right]\left[\begin{array}{c}\Lambda \\ & \Lambda \end{array}\right].$$

(c) 

The eigen-decomposition of $KM$ and $MK$ is:

$$(KM)\Psi =\Psi {\Lambda }^{2}and(MK)\Phi =\Phi {\Lambda }^2,$$

respectively.

Lemma 3

([10] Lemma 2.2). Let $\mathcal{Z}$ be an invariant subspace of H and $Z={[V^T,U^T]}^T$ be the basis matrix of $\mathcal{Z}$ with both V and U having N rows, then $\mathcal{R}(MV)=\mathcal{R}(U)$.

Lemma 4

([25] Lemma 2.1). Let A and B be two symmetric matrices and $\lambda (A)$ and $\lambda (B)$ be the set of the eigenvalues of A and B, respectively. For the Sylvester equation $AY-YB=S$, if $\lambda (A)\cap \lambda (B)=⌀$, then the equation has a unique solution Y, and moreover:

$${\parallel Y\parallel }_F\le \frac{1}{\eta }{\parallel S\parallel }_F,$$

where $\eta =min|\mu -\omega |$ over all $\mu \in \lambda (A)$ and $\omega \in \lambda (B)$.

3. The FEAST Algorithm for LREP

3.1. The Main Algorithm

For LREP, suppose ${\lambda }_{{\ell }_i}$ for $i=1,\cdots ,s$ are all the wanted eigenvalues whose square are inside the circle $\mathcal{C}$ with center at c and radius r on the complex plane, as illustrated in the following Figure 1.

Figure 1. Schematic representation of the wanted eigenvalues.

Given a random matrix $Y\in {\mathbb{R}}^{N\times s}$, for any filter function $f(·)$ that serves the purpose of filtering out the unwanted eigen-directions, we have, by Lemma 2,

$$f(KM)Y=\Psi f({\Lambda }^2){\Phi }^{T}Y.$$

As we known in [10], the ideal filter for computing ${\lambda }_{{\ell }_i}$ for $i=1,\cdots ,s$ should map all s wanted eigenvalues to one and all unwanted ones to zero. For such a purpose, we also consider the filter function applied in [17], i.e.,

$$\begin{array}{c}\hfill f(\alpha )=\frac{1}{2\pi \iota }{\oint }_{\mathcal{C}}{(\mu -\alpha )}^{-1}d\mu .\end{array}$$

By Cauchy’s residue theorem [26] in complex analysis, we have:

$$\begin{array}{cc}\hfill f(KM)Y& =\Psi f({\Lambda }^2){\Phi }^{T}Y\hfill \\ \hfill & =\Psi \left(\frac{1}{2\pi \iota }{\oint }_{\mathcal{C}}{(\mu I-{\Lambda }^2)}^{-1}d\mu \right){\Phi }^{T}Y\hfill \\ \hfill & ={\Psi }_{(:,{\ell }_1:{\ell }_s)}{\Phi }_{(:,{\ell }_1:{\ell }_s)}^{T}Y.\hfill \end{array}$$

(5)

As stated in [24] [Lemma 1], the matrix ${\Phi }_{(:,{\ell }_1:{\ell }_s)}^{T}Y$, with probability one, is nonsingular if the entries of Y are random numbers from a continuous distribution and they are independent and identically distributed. Therefore, naturally, the columns of $f(KM)Y$ span the invariant subspace of $KM$ corresponding to ${\lambda }_{{\ell }_i}^2$ for $i=1,\cdots ,s$. However, it needs to calculate the contour integral. In practice, this is done by using numerical quadratures to compute this filter $f(KM)$ approximately. It is noted that ${\lambda }_{{\ell }_i}^2$ for $i=1,\cdots ,s$ are all real. Let $\mu =c+r{e}^{\iota t}$ for $0\le t\le 2\pi$. Then, we have:

$$\begin{array}{cc}\hfill \frac{1}{2\pi \iota }{\oint }_{\mathcal{C}}{(\mu I-{\Lambda }^2)}^{-1}d\mu & =\frac{r}{2\pi }{\int }_0^{2\pi }{e}^{\iota t}{\left((c+r{e}^{\iota t})I-{\Lambda }^2\right)}^{-1}dt\hfill \\ \hfill & =\frac{r}{2\pi }\left({\int }_0^{\pi }{e}^{\iota t}{(\mu I-{\Lambda }^2)}^{-1}dt+{\int }_{\pi }^{2\pi }{e}^{\iota t}{(\mu I-{\Lambda }^2)}^{-1}dt\right)\hfill \\ \hfill & =\frac{r}{2\pi }{\int }_0^{\pi }\left(e^{\iota t}{(\mu I-{\Lambda }^2)}^{-1}+\overline{e^{\iota t}}{(\overline{\mu }I-{\Lambda }^2)}^{-1}\right)dt\hfill \\ \hfill & =\frac{r}{\pi }{\int }_0^{\pi }Re\left(e^{\iota t}{(\mu I-{\Lambda }^2)}^{-1}\right)dt,\hfill \end{array}$$

where $Re()$ stands for the real part. A q-point interpolatory quadrature rule, such as the trapezoidal rule or Gauss–Legendre quadrature, leads to:

$$f(KM)Y\approx \frac{r}{\pi }\sum _{i=1}^q{\omega }_{i}Re\left(e^{\iota t_i}{({\mu }_{i}I-KM)}^{-1}Y\right),$$

(6)

where $t_i$ and ${\omega }_i$ are the quadrature nodes and weights, respectively, and ${\mu }_i=c+r{e}^{\iota t_i}$ for $1\le i\le q$. Let $V=\tilde{f}(KM)Y=\frac{r}{\pi }{\sum }_{i=1}^q{\omega }_{i}Re\left(e^{\iota t_i}{({\mu }_{i}I-KM)}^{-1}Y\right)$. Then, by (6), V is computed by solving shifted linear systems of the form:

$$({\mu }_{i}I-KM)X_i=Y,i=1,2,\cdots ,q.$$

(7)

Furthermore, for any interpolatory quadrature rule, we have by [18] that:

$$\tilde{f}(\alpha )>\frac{1}{2}\mathrm{for}|\alpha -c|<r.$$

(8)

It follows by Lemma 3 that if the columns of V span the y-component of an approximate invariant subspace of H, then the columns of $U=MV$ should span the x-component of the same approximate invariant subspace. Therefore, {$\mathcal{R}(U)$, $\mathcal{R}(V)$} is a pair of approximated deflating subspaces of H. By [3], the best approximations of ${\lambda }_{{\ell }_i}$ for $i=1,\cdots ,s$ with the pair of approximate deflating subspaces {$\mathcal{R}(U)$, $\mathcal{R}(V)$} are eigenvalues of:

$$\begin{array}{c}\hfill H_{SR}=\left[\begin{array}{cc}0& W_1^{-T}{U}^{T}KU{W}_1^{-1}\\ W_2^{-T}{V}^{T}MV{W}_2^{-1}& 0\end{array}\right],\end{array}$$

where $W_1$ and $W_2$ are two nonsingular factors of $V^{T}U=W_1^T{W}_2$. In particular, we choose $W_1=W_2=R$ where $R^{T}R$ is $V^{T}U$’s Cholesky decomposition. This leads to:

$$\begin{array}{c}\hfill H_{SR}=\left[\begin{array}{cc}0& G\\ I& 0\end{array}\right],\mathrm{where}G=R^{-T}{U}^{T}KU{R}^{-1}.\end{array}$$

Let the eigenvalues of G be ${\rho }_j^2$ in ascending order and the associated eigenvectors be $q_j$, i.e., $G{q}_j={\rho }_j^2{q}_j$ for $1\le j\le s$. Then,

$$\begin{array}{c}\hfill H_{SR}{\widehat{z}}_j={\rho }_j{\widehat{z}}_j,{\widehat{z}}_j=\left[\begin{array}{c}{\rho }_j{q}_j\\ q_j\end{array}\right].\end{array}$$

Approximating eigenpairs of H is then taken to be (${\rho }_j$, ${\tilde{z}}_j$) where:

$${\tilde{z}}_j=\left[\begin{array}{c}{\rho }_j{\tilde{\psi }}_j\\ {\tilde{\varphi }}_j\end{array}\right],{\tilde{\varphi }}_j=U{R}^{-1}{q}_j\mathrm{and}{\tilde{\psi }}_j=V{R}^{-1}{q}_j.$$

(9)

We summarize the pseudo-code of the FEAST algorithm for LREP in Algorithm 1. A few remarks regarding Algorithm 1 are in order:

Remark 1.

 

(a) In practice, we do not need to save $V_{(i)}$, $U_{(i)}$ and $G_{(i)}$ for every i in Algorithm 1. In fact, the subscript “${}_{(i)}$” is just convenience for the convergence analysis in the next subsection.

(b) Since the trapezoidal rule yields much faster decay outside $\mathcal{C}$ than the Gauss–Legendre quadrature [23], our numerical examples use the trapezoidal rule to evaluate $f(KM)Y$, i.e., in (6),

$$\begin{array}{cccc}\hfill {\mu }_i& =c+r{e}^{\iota \pi t_i},t_i=\frac{i-1}{q-1},\hfill & \hfill & for1\le i\le q,\hfill \\ \hfill {\omega }_1& =\frac{\pi }{2(q-1)},{\omega }_q=\frac{\pi }{2(q-1)},{\omega }_i=\frac{\pi }{q-1},\hfill & \hfill & for2\le i\le q-1.\hfill \end{array}$$

(c) In Algorithm 1, it usually is required to know the eigenvalue counts s inside the contour $\mathcal{C}$ in advance. In practice, s is unknown a priori, and an estimator has to be used instead. Some available methods have been proposed in [27,28] to estimate eigenvalue counts, based on stochastic evaluations of:

$$\frac{1}{2\pi \iota }{\oint }_{\mathcal{C}}trace\left({(\mu I-KM)}^{-1}\right)d\mu .$$

(d) In our numerical implementation of Algorithm 1, we monitor the convergence of a computed eigenpair $({\rho }_j,{\tilde{z}}_j)$ by its normalized relative residual norm:

$$r({\rho }_j)=\frac{\parallel H{\tilde{z}}_j-{\rho }_j{\tilde{z}}_j{\parallel }_1}{{(\parallel H\parallel }_1+|{\rho }_j|)\parallel {\tilde{z}}_j{\parallel }_1}.$$

(10)

The approximate eigenpair $({\rho }_j,{\tilde{z}}_j)$ is considered as converged when:

$${\rho }_j\in (\underline{\omega },\overline{\omega })andr({\rho }_j)<\epsilon ,$$

where $\underline{\omega }=c-r$, $\overline{\omega }=c+r$, and ε is a preset tolerance.

Algorithm 1 The FEAST algorithm for LREP.

Input: Given an initial block $Y_{(0)}\in {\mathbb{R}}^{N\times s}$. Output: Converged approximated eigenpairs $({\rho }_j,{\tilde{z}}_j)$.  1: for $i=1,2,\cdots$, until convergence do  2:  Compute $V_{(i)}=\tilde{f}(KM)Y_{(i-1)}$ by (6), and $U_{(i)}=M{V}_{(i)}$.  3:  Compute $V_{(i)}^T{U}_{(i)}=R_{(i)}^T{R}_{(i)}$, ${\tilde{U}}_{(i)}=U_{(i)}{R}_{(i)}^{-1}$, ${\tilde{V}}_{(i)}=V_{(i)}{R}_{(i)}^{-1}$, and $G_{(i)}={\tilde{U}}_{(i)}^{T}K{\tilde{U}}_{(i)}$.  4:  Compute the spectral decomposition $G_{(i)}=Q_{(i)}{\Omega }_{(i)}{Q}_{(i)}^T$ and approximate eigenpairs $({{\rho }_j}_{(i)},{{\tilde{z}}_j}_{(i)})$ where ${{\tilde{z}}_j}_{(i)}={\left[{{\rho }_j}_{(i)}{{\tilde{\psi }}_j}_{(i)}^T,{{\tilde{\varphi }}_j}_{(i)}^T\right]}^T$ by (9) for $j=1,\cdots ,s$.  5:  If convergence is not reached then go to Step 2, with $Y_{(i)}={\tilde{V}}_{(i)}{Q}_{(i)}$.  6: end for

3.2. Convergence Analysis

Without loss of generality, we suppose in this subsection:

$$\begin{array}{c}\hfill |\tilde{f}({\lambda }_{{\ell }_1}^2)|\ge \cdots \ge |\tilde{f}({\lambda }_{{\ell }_s}^2)|>|\tilde{f}({\lambda }_{{\ell }_{(s+1)}}^2)|\ge \cdots \ge |\tilde{f}({\lambda }_{{\ell }_N}^2)|,\end{array}$$

and use the following simplifying notation:

$$\begin{array}{|ll|}\hline {\Psi }_1={\Psi }_{(:,{\ell }_1:{\ell }_s)},& {\Psi }_2={\Psi }_{(:,{\ell }_{(s+1)}:{\ell }_N)},\\ {\Phi }_1={\Phi }_{(:,{\ell }_1:{\ell }_s)},& {\Phi }_2={\Phi }_{(:,{\ell }_{(s+1)}:{\ell }_N)},\\ {\Lambda }_1={\Lambda }_{({\ell }_1:{\ell }_s,{\ell }_1:{\ell }_s)},& {\Lambda }_2={\Lambda }_{({\ell }_{(s+1)}:{\ell }_N,{\ell }_{(s+1)}:{\ell }_N)},\\ {\tilde{\Psi }}_{(k)}=[{{\tilde{\psi }}_1}_{(k)},\cdots ,{{\tilde{\psi }}_s}_{(k)}],& {\tilde{\Phi }}_{(k)}=[{{\tilde{\varphi }}_1}_{(k)},\cdots ,{{\tilde{\varphi }}_s}_{(k)}].\\ \hline\end{array}$$

In Algorithm 1, for a given scalar k, naturally, we would use ${\tilde{\Psi }}_{(k)}$ as approximations to ${\Psi }_1$ and ${\tilde{\Phi }}_{(k)}$ as approximations to ${\Phi }_1$. In this subsection, we will investigate how good such approximations may be. Notice that $\tilde{f}({\Lambda }_1^2)$ is invertible since $\tilde{f}({\lambda }_{{\ell }_i}^2)>1/2$ for $i=1,\cdots ,s$ by (8).

Lemma 5.

Suppose ${\Psi }_1^{T}M{Y}_{(0)}$ is nonsingular. Then, $Y_{(i)}$ is full column rank for all i in Algorithm 1.

Proof. 

We prove this statement by induction. If ${\Psi }_1^{T}M{Y}_{(j)}$ is invertible for some j, then:

$$\begin{array}{cc}\hfill V_{(j+1)}& =\tilde{f}(KM)Y_{(j)}=\tilde{f}(KM)\Psi {\Phi }^T{Y}_{(j)}\hfill \\ \hfill & =\tilde{f}(KM)({\Psi }_1{\Phi }_1^T+{\Psi }_2{\Phi }_2^T)Y_{(j)}\hfill \\ \hfill & =\left({\Psi }_1\tilde{f}({\Lambda }_1^2){\Phi }_1^T+{\Psi }_2\tilde{f}({\Lambda }_2^2){\Phi }_2^T\right)Y_{(j)}\hfill \\ \hfill & =\left({\Psi }_1+{\Psi }_2\tilde{f}({\Lambda }_2^2){\Phi }_2^T{Y}_{(j)}{E}_{(j)}^{-1}\right)E_{(j)},\hfill \end{array}$$

where $E_{(j)}=\tilde{f}({\Lambda }_1^2){\Phi }_1^T{Y}_{(j)}=\tilde{f}({\Lambda }_1^2){\Psi }_1^{T}M{Y}_{(j)}$ is nonsingular. Thus, $V_{(j+1)}$ has full column rank. This leads to $R_{(j+1)}$ and $Q_{(j+1)}$ both being invertible. By Step 5 of Algorithm 1, we have $Y_{(j+1)}={\tilde{V}}_{(j+1)}{Q}_{(j+1)}=V_{(j+1)}{R}_{(j+1)}^{-1}{Q}_{(j+1)}$, which is also full column rank. Furthermore,

$$\begin{array}{cc}\hfill {\Psi }_1^{T}M{Y}_{(j+1)}& ={\Psi }_1^{T}M{V}_{(j+1)}{R}_{(j+1)}^{-1}{Q}_{(j+1)}\hfill \\ \hfill & ={\Psi }_1^{T}M\left({\Psi }_1+{\Psi }_2\tilde{f}({\Lambda }_2^2){\Phi }_2^T{Y}_{(j)}{E}_{(j)}^{-1}\right)E_{(j)}{R}_{(j+1)}^{-1}{Q}_{(j+1)}\hfill \\ \hfill & =E_{(j)}{R}_{(j+1)}^{-1}{Q}_{(j+1)}\hfill \end{array}$$

is nonsingular. We conclude by induction that $Y_{(i)}$ is full column rank for $i=1,2,\cdots .$ □

Theorem 1.

Suppose the condition of Lemma 5 holds. For $1\le k_1\le k_2\le s$, there exist $\widehat{Y}\in {\mathbb{R}}^{N\times ({\ell }_{k_2}-{\ell }_{k_1}+1)}$ where $\mathcal{R}(\widehat{Y})\subseteq \mathcal{R}(Y_{(0)})$ and $\widehat{X}=M\widehat{Y}$ such that, for any k,

$$\begin{array}{cc}\hfill \parallel tan{\Theta }_M({\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},V_{(k)}){\parallel }_F& \le {\left(\frac{|\tilde{f}({\lambda }_{{\ell }_{(s+1)}}^2)|}{|\tilde{f}({\lambda }_{{\ell }_{k_2}}^2)|}\right)}^k\times {\parallel tan{\Theta }_M({\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},\widehat{Y})\parallel }_F,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \parallel tan{\Theta }_{M^{-1}}({\Phi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},U_{(k)}){\parallel }_F& \le {\left(\frac{|\tilde{f}({\lambda }_{{\ell }_{(s+1)}}^2)|}{|\tilde{f}({\lambda }_{{\ell }_{k_2}}^2)|}\right)}^k\times {\parallel tan{\Theta }_{M^{-1}}({\Phi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},\widehat{X})\parallel }_F.\hfill \end{array}$$

(12)

Proof. 

We first prove:

$$\begin{array}{c}\hfill \mathcal{R}(V_{(i)})=\mathcal{R}\left({(\tilde{f}(KM))}^i{Y}_{(0)}\right),\mathrm{for}1\le i\le k,\end{array}$$

(13)

by induction. It is obviously true for $i=1$. Suppose that (13) holds for $i=j-1$. Then, there exists a nonsingular matrix $F\in {\mathbb{R}}^{s\times s}$ such that:

$$\begin{array}{c}\hfill V_{(j-1)}={\left(\tilde{f}(KM)\right)}^{j-1}{Y}_{(0)}F.\end{array}$$

Now, for $i=j\le k$, we have:

$$\begin{array}{cc}\hfill Y_{(j)}& =V_{(j-1)}{R}_{(j-1)}^{-1}{Q}_{(j-1)}\hfill \\ \hfill & ={\left(\tilde{f}(KM)\right)}^{j-1}{Y}_{(0)}F{R}_{(j-1)}^{-1}{Q}_{(j-1)},\hfill \end{array}$$

where $R_{(j-1)}$ and $Q_{(j-1)}$ are both invertible by Lemma 5. Then,

$$\begin{array}{cc}\hfill V_{(j)}=\tilde{f}(KM)Y_{(j)}& =\tilde{f}(KM){\left(\tilde{f}(KM)\right)}^{j-1}{Y}_{(0)}F{R}_{(j-1)}^{-1}{Q}_{(j-1)}\hfill \\ \hfill & ={\left(\tilde{f}(KM)\right)}^j{Y}_{(0)}F{R}_{(j-1)}^{-1}{Q}_{(j-1)}.\hfill \end{array}$$

Thus, we have $\mathcal{R}(V_{(j)})=\mathcal{R}({(\tilde{f}(KM))}^j{Y}_{(0)})$. This completes the proof of (13).

By Lemma 1, there exists $\widehat{Y}\in {\mathbb{R}}^{N\times ({\ell }_{k_2}-{\ell }_{k_1}+1)}$ where $\mathcal{R}(\widehat{Y})\subseteq \mathcal{R}(Y_{(0)})$ such that:

$${\Pi }_M\widehat{Y}={\Psi }_1{\Psi }_1^{T}M\widehat{Y}={\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},$$

(14)

where ${\Pi }_M$ is the M-orthogonal projector onto $\mathcal{R}({\Psi }_1)$. Let ${\widehat{\Lambda }}_1^2=diag({\lambda }_{{\ell }_{k_1}}^2,\cdots ,{\lambda }_{{\ell }_{k_2}}^2)$ and ${\widehat{\Psi }}_1={\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}$. Consider:

$$\begin{array}{cc}\hfill \widehat{Z}={\left(\tilde{f}(KM)\right)}^k\widehat{Y}& ={\Psi }_1{\left(\tilde{f}({\Lambda }_1^2)\right)}^k{\Phi }_1^T\widehat{Y}+{\Psi }_2{\left(\tilde{f}({\Lambda }_2^2)\right)}^k{\Phi }_2^T\widehat{Y}\hfill \\ \hfill & ={\widehat{\Psi }}_1{\left(\tilde{f}({\widehat{\Lambda }}_1^2)\right)}^k+{\Psi }_2{\left(\tilde{f}({\Lambda }_2^2)\right)}^k{\Phi }_2^T\widehat{Y}.\hfill \end{array}$$

It follows by (13) that $\mathcal{R}(\widehat{Z})\subseteq \mathcal{R}(V_{(k)})$. Therefore, we have:

$$\begin{array}{cc}\hfill \parallel tan{\Theta }_M({\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},V_{(k)}){\parallel }_F& \le \parallel tan{\Theta }_M({\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},\widehat{Z}){\parallel }_F\hfill \\ \hfill & ={∥{\Psi }_2^{T}M\widehat{Z}{({\widehat{Z}}^{T}M\widehat{Z})}^{-1/2}{\left[{\widehat{\Psi }}_1^{T}M\widehat{Z}{({\widehat{Z}}^{T}M\widehat{Z})}^{-1/2}\right]}^{-1}∥}_F\hfill \\ \hfill & ={∥{\Psi }_2^{T}M\widehat{Z}{\left({\widehat{\Psi }}_1^{T}M\widehat{Z}\right)}^{-1}∥}_F\hfill \\ \hfill & ={∥{\left(\tilde{f}({\Lambda }_2^2)\right)}^k{\Phi }_2^T\widehat{Y}{\left(\tilde{f}({\widehat{\Lambda }}_1^2)\right)}^{-k}{({\widehat{\Psi }}_1^{T}M\widehat{Y})}^{-1}∥}_F\hfill \\ \hfill & ={∥{\left(\tilde{f}({\Lambda }_2^2)\right)}^k{\Psi }_2^{T}M\widehat{Y}{\left(\tilde{f}({\widehat{\Lambda }}_1^2)\right)}^{-k}{({\widehat{\Psi }}_1^{T}M\widehat{Y})}^{-1}∥}_F\hfill \\ \hfill & \le \underset{{\ell }_{(s+1)}\le j\le N}{max}|\tilde{f}({\lambda }_j^2){|}^k\times \underset{{\ell }_{k_1}\le j\le {\ell }_{k_2}}{max}\frac{1}{|\tilde{f}({\lambda }_j^2){|}^k}\times {\parallel tan{\Theta }_M({\widehat{\Psi }}_1,\widehat{Y})\parallel }_F\hfill \\ \hfill & \le {\left(\frac{|\tilde{f}({\lambda }_{{\ell }_{(s+1)}}^2)|}{|\tilde{f}({\lambda }_{{\ell }_{k_2}}^2)|}\right)}^k\times {\parallel tan{\Theta }_M({\widehat{\Psi }}_1,\widehat{Y})\parallel }_F,\hfill \end{array}$$

which gives (11). Similarly we can prove (12). □

As we know in [29], an important quantity for the convergence properties of projection methods is the distance of the exact eigenspace from the search subspace. Theorem 1 establishes bounds on M-canonical angles from ${\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}$ to the search subspace $V_{(k)}$ and $M^{-1}$-canonical angles from ${\Phi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}$ to the search subspace $U_{(k)}$, respectively, to illustrate the effectiveness of the FEAST algorithm for LREP. As stated in [18], if the spectrum of $KM$ is distributed somewhat uniformly, then we would expect $|\tilde{f}({\lambda }_{{\ell }_{(s+1)}}^2)/\tilde{f}({\lambda }_{{\ell }_{k_2}}^2)|$ to be as small as ${10}^{-3}$. That means $\parallel tan{\Theta }_M({\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},V_{(k)}){\parallel }_F\to 0$ and $\parallel tan{\Theta }_{M^{-1}}({\Phi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},U_{(k)}){\parallel }_F\to 0$ at a rate of ${10}^{-3k}.$ Based on Theorem 1, the following theorem is obtained to bound the M-canonical angles between ${\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}$ and ${{\tilde{\Psi }}_{(k)}}_{(:,k_1:k_2)}$ and the $M^{-1}$-canonical angles between ${\Phi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}$ and ${{\tilde{\Phi }}_{(k)}}_{(:,k_1:k_2)}$, respectively.

Theorem 2.

Suppose the condition of Lemma 5 holds. Using the notations of Theorem 1, we have:

$$\begin{array}{cc}\hfill \parallel sin{\Theta }_M({\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},{{\tilde{\Psi }}_{(k)}}_{(:,k_1:k_2)}){\parallel }_F& \le \gamma \parallel tan{\Theta }_M({\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},\widehat{Y}){\parallel }_F,\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill \parallel sin{\Theta }_{M^{-1}}({\Phi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},{{\tilde{\Phi }}_{(k)}}_{(:,k_1:k_2)}){\parallel }_F& \le \gamma \parallel tan{\Theta }_{M^{-1}}({\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},\widehat{X}){\parallel }_F,\hfill \end{array}$$

(16)

where:

$$\gamma =\sqrt{1+\frac{1}{{\eta }^2}{\parallel {\Pi }_M^{V}KM(I-{\Pi }_M^V)\parallel }_2^2}{\left(\frac{|\tilde{f}({\lambda }_{{\ell }_{(s+1)}}^2)|}{|\tilde{f}({\lambda }_{{\ell }_{k_2}}^2)|}\right)}^k,\eta =\underset{\genfrac{}{}{0pt}{}{{\ell }_{k_1}\le i\le {\ell }_{k_2}}{j<k_{1}orj>k_2}}{min}|{\lambda }_i^2-{\rho }_j^2|,$$

and ${\Pi }_M^V$ is the M-orthogonal projector onto $\mathcal{R}(V_{(k)})$.

Proof. 

Let ${\tilde{Q}}_{(k)}=[{Q_{(k)}}_{(:,1:k_1)},{Q_{(k)}}_{(:,k_2:s)}]$, ${\tilde{\Omega }}_{(k)}=diag({{\Omega }_{(k)}}_{(1:k_1,1:k_1)},{{\Omega }_{(k)}}_{(k_2:s,k_2:s)})$ and ${\tilde{V}}_{(k)}^{\perp }\in {\mathbb{R}}^{N\times (N-s)}$ such that $[{\tilde{V}}_{(k)},{\tilde{V}}_{(k)}^{\perp }]$ is M-orthogonal matrix, i.e.,

$${[{\tilde{V}}_{(k)},{\tilde{V}}_{(k)}^{\perp }]}^{T}M[{\tilde{V}}_{(k)},{\tilde{V}}_{(k)}^{\perp }]=I_N.$$

Then, we can write ${\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}={\tilde{V}}_{(k)}C+{\tilde{V}}_{(k)}^{\perp }{C}^{\perp }$, where $C={\tilde{V}}_{(k)}^{T}M{\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}$ and $C^{\perp }={({\tilde{V}}_{(k)}^{\perp })}^{T}M{\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}$. Furthermore, we have:

$$\begin{array}{cc}\hfill \parallel sin{\Theta }_M({\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},V_{(k)}){\parallel }_F& =\parallel sin{\Theta }_M({\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},{\tilde{V}}_{(k)}){\parallel }_F={\parallel C^{\perp }\parallel }_F,\hfill \\ \hfill \parallel sin{\Theta }_M({\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})},{{\tilde{\Psi }}_{(k)}}_{(:,k_1:k_2)}){\parallel }_F& ={∥{\left[{\tilde{V}}_{(k)}{\tilde{Q}}_{(k)},{\tilde{V}}_{(k)}^{\perp }\right]}^{T}M{\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}∥}_F\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & =\sqrt{\parallel {\tilde{Q}}_{(k)}^T{C\parallel }_F^2+{\parallel C^{\perp }\parallel }_F^2}.\hfill \end{array}$$

(18)

Now, we turn to bound the term $\parallel {\tilde{Q}}_{(k)}^T{C\parallel }_F$. Notice that $[{\tilde{V}}_{(k)},{\tilde{V}}_{(k)}^{\perp }]{[{\tilde{V}}_{(k)},{\tilde{V}}_{(k)}^{\perp }]}^{T}M=I_N.$ It follows by Lemma 2 that:

$$KM[{\tilde{V}}_{(k)},{\tilde{V}}_{(k)}^{\perp }]{[{\tilde{V}}_{(k)},{\tilde{V}}_{(k)}^{\perp }]}^{T}M{\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}={\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}{\Lambda }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}^2.$$

(19)

Multiply (19) by ${\tilde{V}}_{(k)}^{T}M$ from the left to get:

$$\begin{array}{cc}\hfill & {\tilde{V}}_{(k)}^{T}MKM[{\tilde{V}}_{(k)},{\tilde{V}}_{(k)}^{\perp }]{[{\tilde{V}}_{(k)},{\tilde{V}}_{(k)}^{\perp }]}^{T}M{\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}={\tilde{V}}_{(k)}^{T}M{\Psi }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}{\Lambda }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}^2\hfill \\ \hfill & \Rightarrow G_{(k)}C+{\tilde{V}}_{(k)}^{T}MKM{\tilde{V}}_{(k)}^{\perp }{C}^{\perp }=C{\Lambda }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}^2\hfill \\ \hfill & \Rightarrow G_{(k)}C-C{\Lambda }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}^2=-{\tilde{V}}_{(k)}^{T}MKM{\tilde{V}}_{(k)}^{\perp }{C}^{\perp }.\hfill \end{array}$$

Furthermore, we have:

$$\begin{array}{cc}\hfill & {\tilde{Q}}_{(k)}^T{G}_{(k)}C-{\tilde{Q}}_{(k)}^{T}C{\Lambda }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}^2=-{\tilde{Q}}_{(k)}^T{\tilde{V}}_{(k)}^{T}MKM{\tilde{V}}_{(k)}^{\perp }{C}^{\perp }\hfill \\ \hfill \Rightarrow & {\tilde{\Omega }}_{(k)}{\tilde{Q}}_{(k)}^{T}C-{\tilde{Q}}_{(k)}^{T}C{\Lambda }_{(:,{\ell }_{k_1}:{\ell }_{k_2})}^2=-{\tilde{Q}}_{(k)}^T{\tilde{V}}_{(k)}^{T}MKM{\tilde{V}}_{(k)}^{\perp }{C}^{\perp }.\hfill \end{array}$$

By Lemma 4, we conclude that:

$$\begin{array}{cc}\hfill \parallel {\tilde{Q}}_{(k)}^T{C\parallel }_F& \le \frac{1}{\eta }{\parallel -{\tilde{Q}}_{(k)}^T{\tilde{V}}_{(k)}^{T}MKM{\tilde{V}}_{(k)}^{\perp }{C}^{\perp }\parallel }_F\hfill \\ \hfill & \le \frac{1}{\eta }\parallel {\tilde{V}}_{(k)}^{T}MKM{\tilde{V}}_{(k)}^{\perp }{C}^{\perp }{\parallel }_F\le \frac{1}{\eta }\parallel {\tilde{V}}_{(k)}^{T}MKM{\tilde{V}}_{(k)}^{\perp }{\parallel }_2{\parallel C^{\perp }\parallel }_F\hfill \\ \hfill & =\frac{1}{\eta }\parallel M^{1/2}{\tilde{V}}_{(k)}{\tilde{V}}_{(k)}^{T}MKM{\tilde{V}}_{(k)}^{\perp }{(V_{(k)}^{\perp })}^T{M}^{1/2}{\parallel }_2{\parallel C^{\perp }\parallel }_F\hfill \\ \hfill & =\frac{1}{\eta }\parallel {\tilde{V}}_{(k)}{\tilde{V}}_{(k)}^{T}MKM{\tilde{V}}_{(k)}^{\perp }{(V_{(k)}^{\perp })}^T{M\parallel }_2{\parallel C^{\perp }\parallel }_F\hfill \\ \hfill & =\frac{1}{\eta }\parallel {\Pi }_M^{V}KM(I-{\Pi }_M^V){\parallel }_2{\parallel C^{\perp }\parallel }_F.\hfill \end{array}$$

(20)

The inequality (15) is now a consequence of (17), (18), (20), and Theorem 1. Similarly we can prove (16). □

4. Numerical Examples

In this section, we present some numerical examples to illustrate the effectiveness of Algorithm 1 and the upper bounds in Theorem 1.

Example 1.

We first examine the upper bounds of Theorem 1. For simplicity, we consider diagonal matrices for K and M. Take $M=K=diag({\lambda }_1,\cdots ,{\lambda }_N)$ with $N=100$ where:

$${\lambda }_1=1+\eta ,{\lambda }_2=1,{\lambda }_3=1-\eta ,{\lambda }_j=\frac{N+4-j}{2N},forj=4,\cdots ,N.$$

In such a case, there are two eigenvalue clusters: $\{\pm {\lambda }_1,\pm {\lambda }_2,\pm {\lambda }_3\}$ and $\{\pm {\lambda }_4,\cdots ,\pm {\lambda }_N\}$, and $\Psi =K^{-1/2}$.

We seek the approximations associated with the first cluster $\{\pm {\lambda }_1,\pm {\lambda }_2,\pm {\lambda }_3\}$ and vary the parameter $\eta >0$ to control the tightness among eigenvalues. To make the numerical example repeatable, the initial block $Y_{(0)}$ is chosen to be:

$$Y_{(0)}=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ \frac{1}{N}& sin1& cos1\\ ⋮& ⋮& ⋮\\ \frac{N-3}{N}& sin(N-3)& cos(N-3)\end{array}\right].$$

In such a way, $Y_{(0)}$ satisfies the condition that $Y_{(0)}^{T}M{\Psi }_{(:,1:3)}$ is nonsingular. We run Algorithm 1 and check the bound for $\parallel tan{\Theta }_M({\Psi }_{(:,1:3)},V_{(k)}){\parallel }_F$ given by (11) with $k=1$ and $k=2$, respectively. In Algorithm 1, the trapezoidal rule is applied to calculate $\tilde{f}(KM)Y_{(0)}$ with the parameters $c=1$ and $r=0.2$. We compute the following factors:

$$\begin{array}{cc}\hfill {\epsilon }_1& =\parallel tan{\Theta }_M({\Psi }_{(:,1:3)},V_{(k)}){\parallel }_F,\hfill \end{array}$$

(21a)

$$\begin{array}{cc}\hfill {\epsilon }_2& ={\left(\frac{|\tilde{f}({\lambda }_4^2)|}{|\tilde{f}({\lambda }_3^2)|}\right)}^k\times {\parallel tan{\Theta }_M({\Psi }_{(:,1:3)},\widehat{Y})\parallel }_F,\hfill \end{array}$$

(21b)

in Table 1. From Table 1, we can see that, as η goes to zero, the bounds ${\epsilon }_2$ for $k=1,2$ are sharp and insensitive to η.

Table 1. ${\epsilon }_1$ together with their corresponding upper bounds ${\epsilon }_2$ of Example 1.

$\mathit{\eta }$	${\mathit{\epsilon }}_1$ (for $\mathit{k}=1$)	${\mathit{\epsilon }}_2$ ($\mathit{k}=1$)	${\mathit{\epsilon }}_1$($\mathit{k}=2$)	${\mathit{\epsilon }}_2$ ($\mathit{k}=2$)
${10}^{-1}$	$4.4772\times {10}^{-5}$	$3.6089\times {10}^{-3}$	$7.9793\times {10}^{-10}$	$2.4574\times {10}^{-6}$
${10}^{-2}$	$5.9244\times {10}^{-5}$	$3.5685\times {10}^{-3}$	$1.0762\times {10}^{-9}$	$2.3402\times {10}^{-6}$
${10}^{-3}$	$5.9128\times {10}^{-5}$	$3.5639\times {10}^{-3}$	$1.0740\times {10}^{-9}$	$2.3372\times {10}^{-6}$
${10}^{-4}$	$5.9116\times {10}^{-5}$	$3.5635\times {10}^{-3}$	$1.0738\times {10}^{-9}$	$2.3369\times {10}^{-6}$
${10}^{-5}$	$5.9115\times {10}^{-5}$	$3.5635\times {10}^{-3}$	$1.0738\times {10}^{-9}$	$2.3369\times {10}^{-6}$

Example 2.

To test the effectiveness of Algorithm 1, we chose three test problems, i.e.,test1 totest3 in Table 2, which come from the linear response analysis for Na${}_2$, Na${}_4$, and silane (SiH4) compounds, respectively [9]. The matrices K and M oftest1,test2, andtest3 are both symmetric positive definite with order $N=1862$, 2834, and 5660, respectively. We compute the eigenvalues whose square lies in the interval (${\underline{\omega }}_t$,${\overline{\omega }}_t$) for $t=1,2,3$ and the associated eigenvectors by using the MATLAB parallel pool. The interval (${\underline{\omega }}_t$,${\overline{\omega }}_t$) and their corresponding eigenvalue counts $s_t$ for $t=1,2,3$ are detailed in Table 2. All our experiments were performed on a Windows 10 (64 bit) PC-Intel(R) Core(TM) i7-6700 CPU 3.40 GHz, 16 GB of RAM using MATLAB Version 8.5 (R2015a) with machine epsilon $2.22\times {10}^{-16}$ in double precision floating point arithmetic. In demonstrating the quality of computed approximations, we calculated the normalized residual norms $r({\rho }_j)$ defined in (10) and relative eigenvalues errors:

$$\begin{array}{c}\hfill e({\rho }_j)=\frac{|{\rho }_j-{\lambda }_j|}{{\lambda }_j}\end{array}$$

for the $j\mathrm{th}$ approximation eigenvalue $({\rho }_j,{\tilde{z}}_j)$ where ${\lambda }_j$ were computed by MATLAB’s function eig on H, and considered to be the “exact” eigenvalues for testing purposes.

Table 2. Test matrices.

Problem	N	K	M	(${\underline{\mathit{\omega }}}_1$, ${\overline{\mathit{\omega }}}_1$)	${\mathit{s}}_1$	(${\underline{\mathit{\omega }}}_2$, ${\overline{\mathit{\omega }}}_2$)	${\mathit{s}}_2$	(${\underline{\mathit{\omega }}}_3$, ${\overline{\mathit{\omega }}}_3$)	${\mathit{s}}_3$
test 1	1862	Na${}_2$	Na${}_2$	(0.40,0.50)	3	(0.60,0.70)	3	(1.50,1.60)	3
test 2	2834	Na${}_4$	Na${}_4$	(0.03,0.04)	4	(0.05,0.06)	4	(0.32,0.33)	5
test 3	5660	SiH4	SiH4	(0.25,0.30)	3	(0.75,0.80)	6	(1.75,1.80)	8

In this example, we first investigated how the maximal relative eigenvalue errors and normalized residual norms, i.e., $maxe({\rho }_j)$ and $maxr({\rho }_j)$ in Table 3, respectively, changed for an increase in the number of quadrature points q in (6). We used the direct methods, such as Gaussian elimination, to solve the shifted linear systems (7) in this example. The numerical results of Algorithm 1 by running four FEAST iterations with q varying from four to nine are presented in Table 3. It is shown by Table 3 that the trapezoidal rule with 6, 7, or 8 quadrature nodes already achieved satisfactory results.

Table 3. Changes of $maxe({\rho }_j)$ and $maxr({\rho }_j)$ with the number of quadrature nodes q varying from 4 to 9.

q	TEST 1		TEST 2		TEST 3
	$\mathbf{max}\mathit{e}({\mathit{\rho }}_{\mathit{j}})$	$\mathbf{max}\mathit{r}({\mathit{\rho }}_{\mathit{j}})$	$\mathbf{max}\mathit{e}({\mathit{\rho }}_{\mathit{j}})$	$\mathbf{max}\mathit{r}({\mathit{\rho }}_{\mathit{j}})$	$\mathbf{max}\mathit{e}({\mathit{\rho }}_{\mathit{j}})$	$\mathbf{max}\mathit{r}({\mathit{\rho }}_{\mathit{j}})$
4	$1.25\times {10}^{-5}$	$7.54\times {10}^{-6}$	$2.35\times {10}^{-7}$	$6.82\times {10}^{-7}$	$1.87\times {10}^{-11}$	$7.48\times {10}^{-8}$
5	$7.08\times {10}^{-8}$	$5.69\times {10}^{-7}$	$8.13\times {10}^{-10}$	$3.99\times {10}^{-8}$	$1.26\times {10}^{-13}$	$1.07\times {10}^{-9}$
6	$5.64\times {10}^{-10}$	$5.08\times {10}^{-8}$	$4.23\times {10}^{-12}$	$2.72\times {10}^{-9}$	$1.29\times {10}^{-13}$	$1.68\times {10}^{-11}$
7	$5.39\times {10}^{-12}$	$4.97\times {10}^{-9}$	$9.53\times {10}^{-13}$	$2.01\times {10}^{-10}$	$1.29\times {10}^{-13}$	$2.71\times {10}^{-13}$
8	$9.95\times {10}^{-14}$	$5.10\times {10}^{-10}$	$9.52\times {10}^{-13}$	$1.54\times {10}^{-11}$	$1.29\times {10}^{-13}$	$4.29\times {10}^{-15}$
9	$9.93\times {10}^{-14}$	$5.37\times {10}^{-11}$	$9.52\times {10}^{-13}$	$1.21\times {10}^{-12}$	$1.29\times {10}^{-13}$	$4.00\times {10}^{-16}$

Notice that the wanted eigenvalues are inside the intervals presented in Table 2. The shift and invert strategy is usually not available for LREP since the traditional algorithms to calculate the partial spectrum of LREP, such as the methods proposed in [6,8], combined with the shift and invert strategy will lose the structure of (2).

In addition, as stated in [17], the FEAST algorithm can be cast as a direct technique in comparison to iterative Krylov subspace-type methods, because it is based on an exact mathematical derivation (5). Therefore, by dividing the whole spectrum of LREP into a number of disjoint intervals, the FEAST algorithm is able to compute all eigenvalues simultaneously on the parallel architectures. From this aspect, as [24], we compared Algorithm 1 with the MATLAB built-in function eig, which was used to compute all eigenvalues of H, and then, the target eigenvalues were selected in this example. Let the number of quadrature nodes $q=7$ and the convergence tolerance $\epsilon ={10}^{-8}$. Table 4 reports the total required CPU time in seconds of Algorithm 1 and eig fortest 1,test 2, andtest3, respectively. It is clear from Table 4 that Algorithm 1 was much faster than the MATLAB built-in function eig in this example. A similar comparison between the FEAST-type algorithms and the MATLAB built-in function eig in terms of timing can be found in [30,31].

Table 4. Comparison of Algorithm 1 and eig for CPU time in seconds.

Problem	eig	Algorithm 1
test 1	45.82	15.88
test 2	159.77	37.08
test 3	1200.71	233.12

Example 3.

As stated in Section 3, the implementation of Algorithm 1 involves solving several shifted linear systems of the form:

$$({\mu }_{i}I-KM)X_i=Y,fori=1,2,\cdots ,q.$$

Direct solvers referring to $\mathcal{O}(N^3)$ operations are prohibitively expensive in solving large-scale sparse linear systems. Iterative methods, such as Krylov subspace-type methods [32], are usually preferred for large-scale sparse linear systems. However, Krylov subspace solvers may need a large number of iterations to converge. A way to speed up the FEAST method for LREP is to terminate the iterative solvers for linear systems before full convergence is reached. Therefore, in this example, we investigated the effect of the accuracy in the solution of linear systems on the relative eigenvalues errors and normalized residual norms. The linear systems were solved column-by-column by running GMRES [33] until:

$$\frac{\parallel Y_{(:,j)}-({\mu }_{i}I-KM){X_i}_{(:,j)}{\parallel }_2}{\parallel Y_{(:,j)}{\parallel }_2}\le {\epsilon }_{lin}.$$

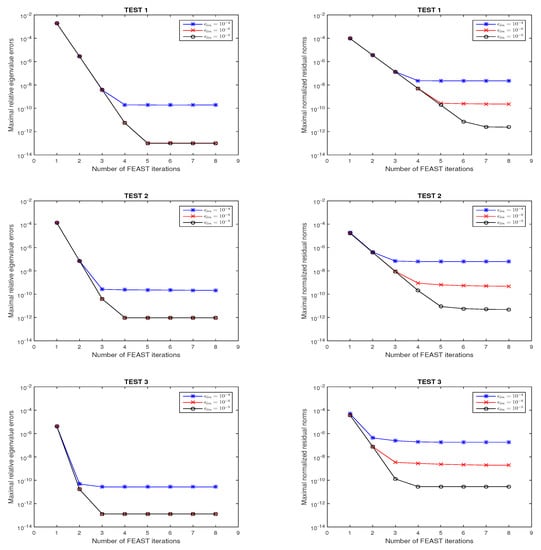
Figure 2 plots the maximal relative eigenvalues errors and normalized residual norms of Algorithm 1 with $q=7$ in solvingtest 1,test 2, andtest 3with ${\epsilon }_{lin}={10}^{-4}$, ${10}^{-6}$, and ${10}^{-8}$. It is revealed by Figure 2 that the accuracy from the solution of the linear systems translated to the accuracy of the eigenpairs obtained by the FEAST algorithm for LREP; that is to say, higher accuracy in solving linear systems leads to better numerical performance in Algorithm 1. In particular, for a rather large ${\epsilon }_{lin}$, such as ${\epsilon }_{lin}={10}^{-4}$, it is hard to obtain satisfactory normalized residual norms in this example.

Figure 2. Convergence behavior of Algorithm 1 for test 1, test 2, and test 3 with ${\epsilon }_{lin}={10}^{-4}$, ${10}^{-6}$, and ${10}^{-8}$, respectively.

5. Conclusions

In this paper, we proposed a FEAST algorithm, i.e., Algorithm 1, for the linear response eigenvalue problem (LREP). The algorithm can effectively calculate the eigenvectors associated with eigenvalues that are located inside some preset intervals. Compared with other methods for LREP, the attractive computational advantage of Algorithm 1 is that it is easily parallelizable. We implemented numerical examples by using the MATLAB parallel pool to compute the eigenpairs in each interval independently of the eigenpairs in the other interval. The corresponding numerical results demonstrated that Algorithm 1 was fast and could achieve high accuracy. In addition, theoretical convergence results for eigenspace approximations of Algorithm 1 were established in Theorems 1 and 2. These theoretical bounds revealed the accuracy of the approximations of eigenspace. Numerical examples showed that the bounds provided by Theorem 1 were sharp.

Notice that the main computational tasks in Algorithm 1 consisted of solving q independent shifted linear systems with s right-hand sides. Meanwhile, as described above, the relative residual bounds in the solution of the inner shifted linear systems were translated almost one-to-one into the residuals of the approximate eigenpairs. Therefore, the subjects of further study include the acceleration of solving shifted linear systems on parallel architectures and theoretical analysis on how the accuracy of the inexact solvers in solving shifted linear systems interacts with the convergence behavior of the FEAST algorithm. In addition, while the algorithm in this paper is for real symmetric K and M, it is also available for the case of Hermitian K and M, simply by replacing all $\mathbb{R}$ by $\mathbb{C}$ (the set of complex numbers) and each matrix/vector transpose by the complex conjugate and transpose.