1. Introduction
In recent years, due to internet’s universal spread and social media’s extensive use, the amount of disposable information continuously grows in an exponential rate. As a result, the need for compact and efficient information representations has never been more significant. Among the rest, information networks can undoubtedly be considered as one of the most prominent data representations that harmonically combines different aspects of information in the same entity. Inevitably, data graphs have widespread application in various scientific fields such as chemistry, biology, sociology, computer science, and digital marketing. Regarding the social media case, the information can conveniently be expressed as graph where each user is represented as a vertex and any kind of social interaction, such as “friendship”, “following”, “retweeting”, “sharing”, etc., as an edge. The size of real-world graphs have outreached the millions or even billions of scalable inter-connected vertices making social networks one of the most flourishing sources of information nowadays.
Due to the expanded application of information networks in a wide range of contemporary problems, such as customer segmentation, epidemiology, social phenomena analysis, network summarization, political influence evolution, criminal identification, tissue/organ detection, etc.; network analysis has attracted great scientific interest and become a very intriguing research area.
One of the most controversial but doubtlessly important issue in network analysis is community detection, which aims to identify groups of network elements, also known as communities, based on a well-defined similarity measure that acts correspondingly to a pattern recognition mechanism for clustering vertices to subsets [
1,
2]. The necessity of community detection, as clearly stated in [
3], lies under the deeper understanding of the subjacent hierarchy structure that can consequently lead to the extraction of advantageous insights regarding graph’s dynamic processes such as the network evolution and the implicit interactions among unrelated vertices unfolding.
Even if there is not a generally accepted definition for what a community is [
1,
4], its concept can be intuitively perceived as the subset of vertices which intra-cluster connectivity, that is the number of edges connecting vertices belonging to the same community, is dense and the corresponding inter-cluster connectivity, that is the number of edges connecting the community vertices with the rest of the graph, is sparse. Specifically, a set of vertices is generally expected to form a meaningful community when its intra-cluster density is considerably larger and its inter-cluster density is markedly smaller than the average link density of the original graph [
2]. However, as it is strongly underlined in [
5], the optimal community detection is achieved not by minimizing the inter-cluster, or by maximizing the intra-cluster connectivity of the generated structure, but rather when the final inter-cluster or intra-cluster connectivity is less or comparatively more than the expected. In other words, a good graph division would not merely be the one in which the number of connections between communities is minimized, but rather the one in which there are fewer inter-connection edges than expected. This is the abstraction that has practically made community detection one of the most conceptually challenging and computationally demanding network analysis topics.
There are copious algorithms and methods that have already been published to detect the underlying community structure, the great majority of which initially tried to leverage the graph’s topological properties. From similarity measures calculation such as shortest paths extraction [
6] and centrality betweenness maximization [
7], to random-walk betweenness maximization, cuts [
1] and geodesic edge betweenness [
4], to name but a few, the network connectivity acted principally as the basic criterion for performing the division of a network to communities. It is worth mentioning that due to community detection’s extensive application in diverse research fields, such as physics and discrete mathematics, many alternatives influenced by different scientific backgrounds have also been published with the most impressive among them engaging linear algebra techniques [
1,
4], Markov chains theory [
1] or elementary circuit analysis theory [
1].
Due to the great diversity of the proposed approaches, the introduction of a general, well interpretable and unanimously agreed criterion, responsible for evaluating the quality of the generated community structure has been more than fundamental in any case. Hence, the modularity function [
8] has primarily been defined as the quality measure for assessing the generated community structure [
1] and has secondly served as the stopping criterion in the repetitive process cases. Among the profuse amount of modularity measures defined, the one introduced by Girvan and Newman [
8] is broadly considered as the state-of-the-art in community detection and unquestionably its performance serves as standard.
Along with the network structure oriented approaches, there is plenty of research that enhance the above-mentioned similarity measures with different information modalities, such as the node associated attributes intrinsically included. In particular, based on the homophily concept, which is the natural human tendency for interacting with peers of similar interests and characteristics [
9], it is more than obvious that a valuable community should be the group of associated vertices that besides being more densely intra-connected, should also have various distinctive node attributes in common [
3]. Thus, plentiful hybrid methods [
3,
7,
10,
11,
12,
13,
14,
15,
16,
17] have been published to uncover communities, leveraging not only the vertices associations but also the inherent node attribute information.
Nevertheless, as it is already proven in [
18], there is no algorithm that can be universally applied and optimally export the subjacent network structure for any possible real-world network, since on one hand, the classic community detection methods and algorithms are not only of high polynomial degree in the size of vertices and edges but also substantially unscalable, while on the other hand, the hybrid approaches obligingly require superlative statistical network analysis. Thereafter, the application on real-world data networks of the existing methods, both classic and hybrid, has practically proven infeasible. Albeit the obvious over-demanding resources requirements in both cases, the outcome of the classic approaches might also be considered comparably inaccurate, since in the case of social media graphs, the network topology-oriented methods deliberately neglect critical modalities of information inherently included, such as the user content information.
Therefore, the introduction of a novel, distributed community detection methodology that combines the topological properties with the integral user profile information seems to be assuredly prosperous. Specifically, in the proposed approach the network structure, expressed by the loose similarity and the local edge betweenness that is a properly modified, in terms of scalability and efficiency, Girvan–Newman edge betweenness measure, along with the user profile information in the form of node attribute vectors are ably combined to unveil the subjacent community structure. This is the actual purpose of this work, for which the experimentation with various real-world social networks workably verified that the proposed methodology is profoundly promising, extremely scalable and adequately efficient.
The remainder of this manuscript is organized as follows:
Section 2 presents the existing community detection bibliography;
Section 3 comprehensively analyzes the proposed methodology and its implementation;
Section 4 describes the experimentation process and assess its outcome; and
Section 5 outline the conclusions and propose the future goals of this research work.
2. Background
Due to community detection’s significant importance and its widespread application in various scientific sectors, affluent graph clustering algorithms and network community extraction methods have been introduced to tackle this computationally demanding and conceptually challenging problem. The profuse amount of research can roughly be distinguished to either classic or hybrid approaches regarding the type of information employed to disclose the graph’s subjacent community structure.
Principally, the classic approaches are iterative processes that traditionally rely on either the elementary network topology properties [
1,
2,
3,
4,
5,
19,
20,
21] or the user content information [
4,
11,
12,
13]. The major drawbacks of those approaches are on one hand, the heavy computational demands that require the repetitive recalculation of a global similarity measure, which can implicitly be interpreted as the repetitive traversing over the entire network for each vertex calculation, and on the other hand the inaccurate generated hierarchy structure due to the lack of social information context consideration, in the case of network topology oriented approaches.
On the contrary, the more sophisticated hybrid methods [
7,
13,
14,
15,
16,
17,
18,
22,
23,
24,
25,
26,
27,
28] try to combine all the intrinsic information modalities by defining either global probabilistic inference-based models or global heuristic measure-based models to unveil the underlying communities. Even if their generated outcome is considered more accurate and further qualitative comparing to the respective of classic algorithms, since all the different information aspects are taken into account, their application is limited to particularly small networks due to the exhaustive statistical analysis required.
2.1. Classic Methods
2.1.1. Network Topology Oriented
Based on concepts introduced for general network analysis [
1,
2,
4], this category include algorithms that without any question can be considered as the standards in community detection and graph partitioning. By plainly focusing on the topological properties of the graph and regarding the processing strategy applied, these basic methods can subsequently be categorized to divisive, agglomerative or transformation.
The divisive algorithms apply an iterative but straightforward top-down processing strategy which ultimate scope is to identify and remove all the edges that inter-connect the underlying communities. Initially, the whole network is considered a single community. At each iteration step, the set of edges that meet certain well-defined similarity criteria is recognized as the set of interconnection edges that are ultimately removed from the network. Until reaching a certain point of stability, where the modularity measure is fully satisfied and the edge removal is no longer required, the similarity calculation and therefore the edge removal step is repeatedly performed [
2]. The most popular, in terms of concept and implementation simplicity, is the one introduced by Girvan–Newman [
8], in which the removal criterion is based on the number of the shortest paths running along each edge, also known as edge betweenness. Due to its algorithmic clarity, the Girvan–Newman algorithm’s performance serves as one of the community detection standards. There are many alternatives proposed depending on different modularity concepts, such as geodesic edge betweenness [
1], cuts [
4], maximum-flow betweenness and random-walk edge betweenness [
5,
19] which nevertheless are way more complex and far more computationally demanding comparing to Girvan–Newman [
8]. However, it is worth pointing out that the fast greedy modularity optimization method proposed by Clauset, Newman and Moore [
1], which is basically a Girvan–Newman [
8] optimized implementation, manages to reduce the overall complexity and thus can be practically applied on large information networks having similarly good community performance.
In contrast to divisive, the agglomerative algorithms are bottom-up approaches that initially consider singletons, which is the case where each vertex is considered a distinct community. At each iteration step, the scope is to merge the existing level communities and compose meta-communities that would serve as future iterations’ communities. The merging criterion engage a universally applied similarity measure that is exhaustively calculated over all the existing communities in order to generate the upper level hierarchy structure and so forth, up to the point of ideally ending up to a single community matching the whole graph [
1]. The most prevalent agglomerative algorithm, is the one introduced by Blondel [
1] that ingeniously contrasts the intra-connection and the inter-connection densities of the generated communities during each iteration step, with the original graph’s average density in order to decide for the formation of the next level meta-communities. There are plenteous alternatives [
4,
21] using radically different similarity measures and modularity functions comparing to the respective introduced by Blondel, such as Infomap [
3], Simulated Annealing [
4], External optimization [
1], Generative Models [
4] and Label Propagation Methods [
3] that add alternative perspectives on the agglomerative community detection process.
Finally, inspired by different scientific domains, such as physics and linear algebra, it is noteworthy that there are many proposed approaches aiming to transform the original network structure to different information representations. The introduced transformations intent to tackle the inherent community detection complexity by projecting the initial information network to different dimensions and applying simple solutions from different research fields. Among those, the most representative are:
The Spectral Clustering [
1], where each node is properly expressed as the combination of the connectivity matrix eigenvectors. This way the community detection problem is transformed to a data mining clustering problem;
The Genetic Algorithms [
2,
14,
15,
16,
17], which are particularly repetitive meta-heuristics inspired by the theory of natural evolution;
The Markov chain and random walks [
4], where the modularity measure considers the respective to each node eigenvectors corresponding to second eigenvalue of the transition matrix of a random walk; and
The Current-Flow Edge Betweenness [
1], which considers the graph as a resistor network for which the centrality of each edge is calculated using the Kirchhoff’s equation.
2.1.2. User Content Oriented
Due to the homophily [
9,
11], which is the immanent human tendency where individuals tend to get associated with similar peers, the application of community detection in social graphs can alternatively be translated as the identification and the classification of the underlying social contexts [
1]. Without any doubt, the community detection concept is inherently interwoven with the complex user profile information that cannot be explicitly presented with any other kind of network objects association. Thereafter, there are many approaches proposed [
4,
11,
13] which are specifically designed for social network analysis that strive to reveal the subjacent communities by solely depending on the user content information.
The majority of the existing user content oriented methods are, to the best of our knowledge, based on the concept of the Homophilic FCA (Formal Concept Analysis) [
11,
13], which is a special case of the original FCA (Formal Concept Analysis) [
11]. Homophilic FCA endeavor to form groups of vertices by searching for potential semantic relationships between network objects that are either explicitly or implicitly connected and share similar social interests. Bear in mind that the original FCA is the knowledge extraction method that follows the notion of the Galois lattice hierarchy [
11] detection concept where the existing network connections are believed to imply intention to linking rather than actual linking between network objects.
2.2. Hybrid Approaches
The real-world social networks natively include two different information modalities, the network topology structure and the user content information that could both be used for the identification of meaningful, in terms of social context, communities. The methods and algorithms that make the valid assumption that the community extraction process should be determined by the combination and not merely by either the network connectivity structure or the node attribute information are classified as hybrids and can consequently be divided to probabilistic inference-based models and heuristic measure-based models.
The probabilistic inference-based models are practically mixed probabilistic generative models that combine the network topology and the user content information in order to infer the potential subjacent network hierarchy. The most considerable representatives are the CESNA (Community extraction from Edge Structure and Node Attributes) [
13] and its alternatives [
9,
27,
29], the BAGC (Bayesian Attributed Graph Clustering) [
30], the GBAGC (Generalized Bayesian Attributed Graph Clustering) [
26] and Metacode [
28]. Generally, those methods try to infer the probable generated community distribution by combining the network linking generation and the node attribute classification. However, even if those approaches seem prosperous in terms of efficiency, as it is underlined in [
7], they are not only deeply sensitive to the initial values and the corresponding input data type representations but also require exhaustive statistical analysis of the network topology properties for the model definition.
The heuristic measure-based models consider the topological properties and the content attributes of each social graph node as input to a heuristic function which outcome determines the posterior community structure. The most significant heuristic measure-based representatives include, but not limited, to models that:
Handle the network connectivity information, expressed in vectors, as part of each corresponding user node information [
22,
23,
31];
Construct content edges by selecting the top K neighbors of each vertex using the node attribute information contained [
10,
13];
Optimize a unified objective function [
24,
32]; and
Leverage the well-known Swarm Intelligence methods such as BA (Bat Algorithm) [
14,
17], FA (Firefly Algorithm) [
14,
16] and PeSOA (Penguins Search Optimization) [
15] to define bio-inspired metaheuristics schemes that use the evolution mechanisms to proceed to the detection of underlying communities.
Those hybrid approaches have been pragmatically proven [
10,
13,
15,
17,
24] to generate more qualitative community hierarchy structures to the classic approaches’ outcome. However, they have shown strong limitations performance-wise, regarding the size of the networks that are capable of handling, and sensitivity regarding the processing type of the information, especially regarding the binary and the categorical data types [
7].
3. Proposed Methodology
Due to the social networks rapid growth, the need for eminently efficient and highly scalable methodologies, capable of leveraging all included information modalities, have become very critical. Thus, a novel, distributed community detection methodology is introduced, based on the following intuitive assumptions:
The nodes belonging in the same community are more likely to share common user content attributes, according to the homophily concept [
9,
11,
13];
The nodes would be assigned to the community where most of their neighbors belong, following the Label Propagation Method concept [
3,
10], and the notion of the high intra-connection density prerequisite of Infomap [
3]; and
The merrier shortest paths that an edge engages, the more probable is to act as interconnection edge between distinct communities, according the Girvan–Newman’s [
8] edge betweenness similarity measure.
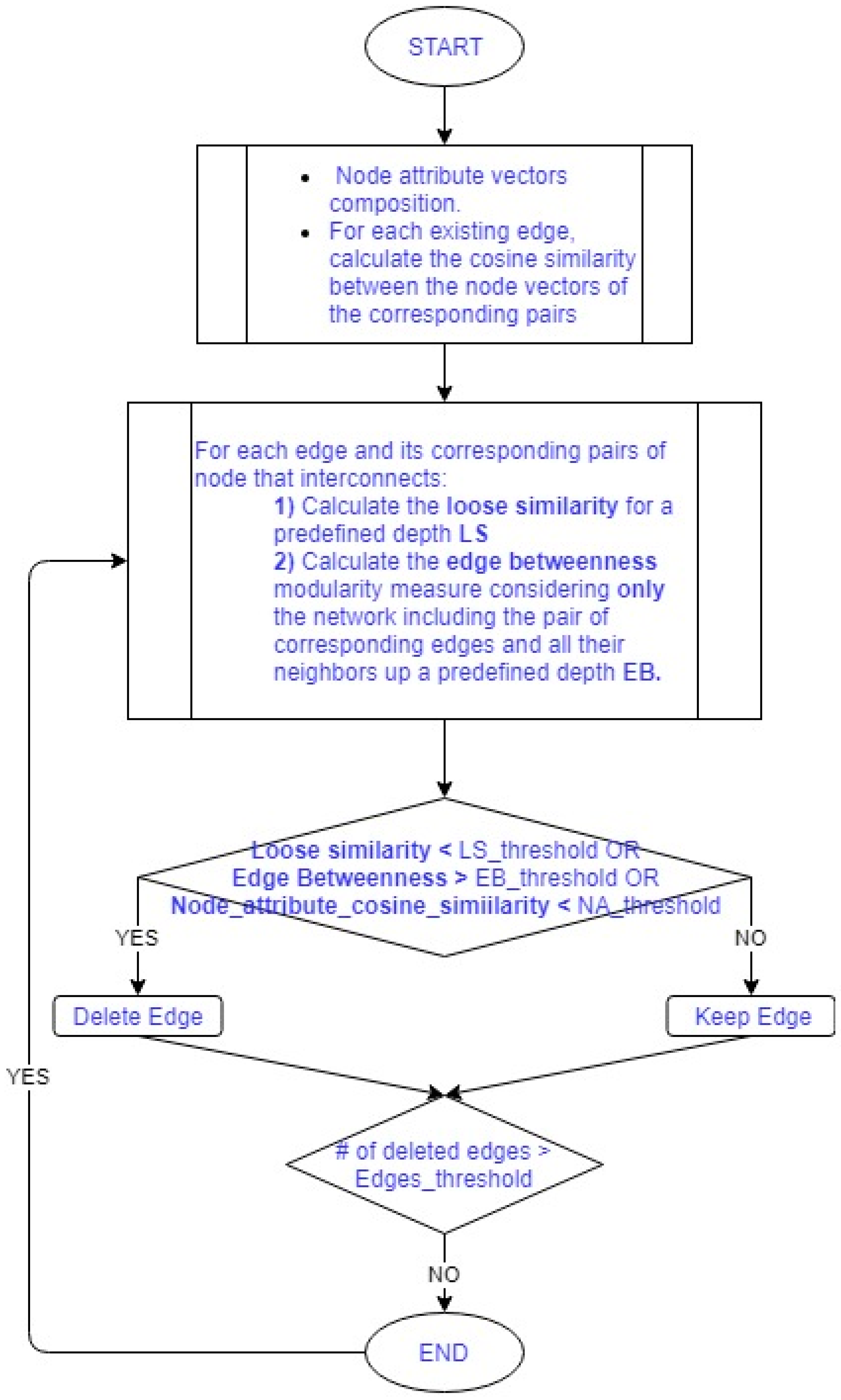
The proposed methodology is an iterative, divisive community detection process that combines the network topology features of loose similarity and local edge betweenness measure, along with the user content information in order to remove the inter-connection edges and thus unravel the subjacent community structure. Even if this iterative process might sound computationally over-demanding, its application is certainly not prohibitive, since it can be safely concluded from the experimentation results that the aforementioned measures are that well-informative and highly representative, so merely few iterations are required to converge to the final community hierarchy at any case.
As shown in
Figure 1, initially the preprocessing step takes place. During this phase, the node attribute vectors are constructed regarding each node’s intrinsic user content information provided. Then, the cosine similarity [
33] calculation between the corresponding vectors of each associated pair of nodes is performed. This calculation can naturally be performed in a distributed fashion and from this point on this similarity metric can be considered as one of the corresponding edge’s intrinsic properties.
Subsequently, the iteration step is performed. Based on the local clustering concept introduced in [
1,
4] and by aligning to the previously defined assumptions, it is more than obvious that the network topology properties of each edge are primarily benefited by their immediate neighbors rather than the whole graph. Therefore, by limiting the network topology measures to the knowledge of the up to a certain depth direct neighbors, both the qualitative clustering and the processing efficiency is ensured. Thus, the network topology properties are expressed as neighbor depth measures where:
Regarding an imminent pair of nodes and each of their corresponding sets of distinct k-depth neighbor nodes, the k-depth loose similarity is the fraction of common over the union’s total number of nodes. It should be underlined, that both sets might include nodes having depth less or equal to k, since a common node might be at a different depth for each impeding node; and
The l-depth local edge betweenness of an edge, is the total number of shortest paths that this edge engages focusing on the subgraph containing the up to the l-depth neighbors of its imminent pair of nodes. The difference between the local edge betweenness and the original edge betweenness defined in [
8], is that in the latter, the entire graph should be taken under consideration whereas in the proposed methodology this calculation is applied only in an emphatically smaller subgraph, since the repetitive calculation of all possible shortest paths on real-world social networks is considered impossible.
So forth, the LS-th depth loose similarity and the EB-th local edge betweenness measures are calculated in each iteration step for each of the existing edges. Empirically, after carefully evaluating the overall performance for the various experiments conducted and presented in the following section, both loose similarity and local edge betweenness depths have been practically proven to be strongly related to the social graph’s diameter, where specifically not deeper than the eighth depth neighbors were required at the worst case. It is worth pointing out, that both the local network topology properties calculations can inherently performed in a distributed fashion.
Then, the inter-connection label assignment for each of the existing edges occurs. Specifically, an edge would be considered inter-connected should at least one of the following cases occur:
The corresponding LS-th depth loose similarity is less than a predefined LS threshold;
The corresponding EB-th depth local edge betweenness measure is more than a predefined EB threshold; and
The corresponding node attribute cosine similarity is less than a predefined NA threshold.
If no edge removal is applied or fewer edges than a certain threshold are removed, the community extraction process is terminated and the generated structure at this point is considered final. Otherwise, the iteration step is re-executed. At this point, it should be noted that the network topology related need to be recalculated at each iteration step. It is more than obvious that after an edge removal occurs, the already calculated LS-th depth loose similarity and EB-th depth local edge betweenness measures are no longer reflect the true network structure. Therefore, in order to proceed to meaningful and qualitative network division, the network topology measures recalculation is considered mandatory.
Indisputably, in terms of efficiency and scalability, the application of a classic modularity measure that would require the repetitive process of the entire network is considered impracticable. Hence, the values of the above-mentioned thresholds play a substantially vital role to the methodology’s overall performance, affecting at the same time the number of iterations needed to converge to the final communities’ hierarchy and the general quality of the generated community structure.
Finally, even if the loose similarity implementation is consider trivial, the edge betweenness generally calculated with high polynomial solutions, outreaching the cubic bound in the average case. Fortunately, new algorithms and techniques have yet been proposed to speed up the edge betweenness calculation process [
6,
34,
35]. Specifically, by using the fast matrix multiplication technique described in [
6], the local edge betweenness calculation has been achieved in O (m × n) complexity running time in the worst case, where n and m factors denote the number of vertices and edges of the corresponding LS-depth subgraph.
4. Experiments
To assess the proposed methodology, both its execution characteristics along with the quality of the generated community structures are compared, in terms of objectivity, against the NetworkX’s implementations of the Girvan–Newman’s [
8,
36] and the Clauset–Newman–Moore [
1,
37] algorithms that generally serve as standards in the divisive community detection case. Thus, the overall performance for each the aforementioned approaches was contrasted on the thoroughly analyzed social graphs shown in
Table 1.
At this point, it should be emphasized that the over-demanding Girvan–Newman [
36] and Clauset–Newman–Moore [
37] NetworkX implementations has set strong hardware restrictions, limiting thusly the experimentation process to merely small social networks.
All the experiments were conducted in an eight node Spark 2.3.2 cluster, with 4 GBs of RAM and two virtual cores per node. The execution parameters for which the proposed methodology had the best community performance [
43] are shown in
Table 2.
Even if it seems rather pointless to compare a classic implementation with one that is completely distributed and thus extremely scalable, as presented in
Table 3, it should be highlighted that not only the execution time improvement percentage outreaches the 85% and 32% in the average case for the Girvan–Newman [
8] and the Clauset–Newman–Moore [
1] case, respectively, but also that as the number of edges of the analyzed social graph increases, the performance of the distributed proposed methodology is not proportionately affected.
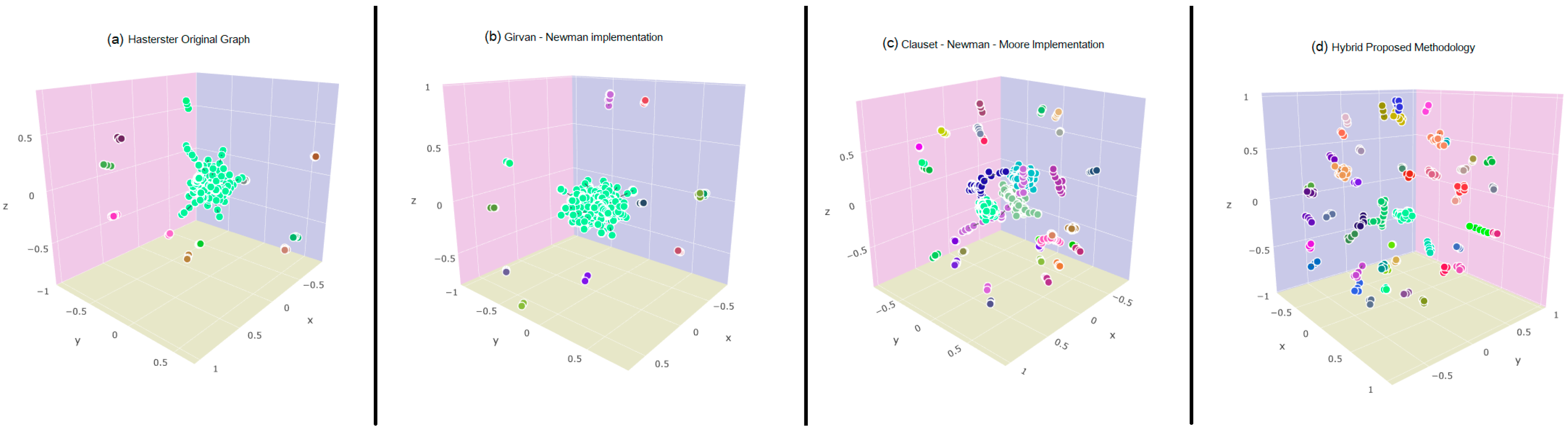
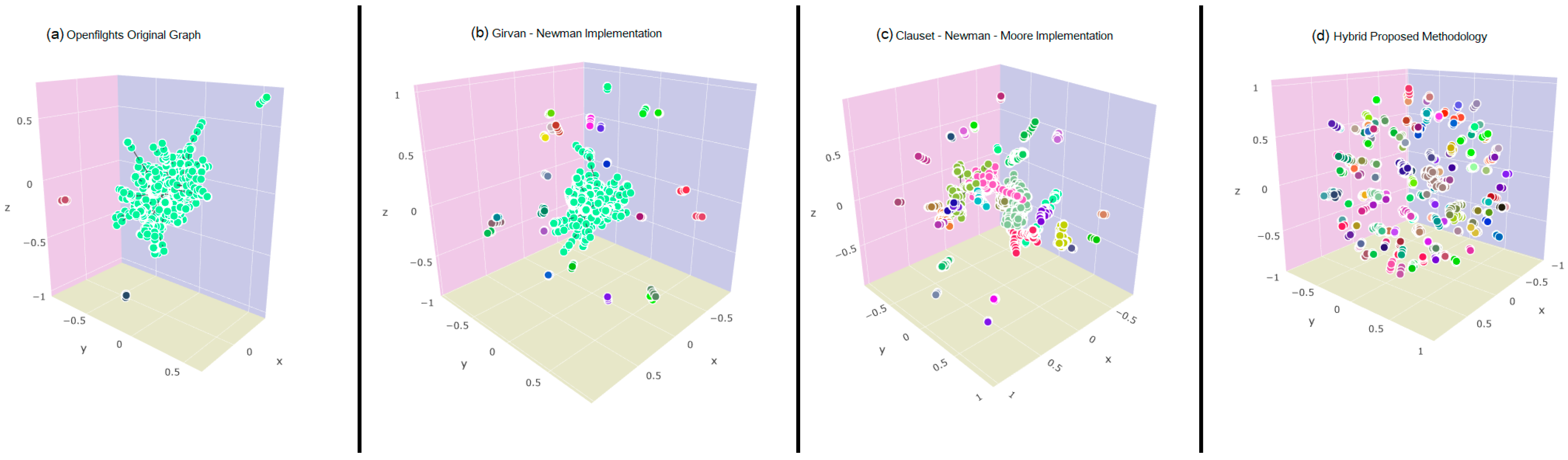
Additionally, in order to visually assess the generated community structures for each of the compared methods, the following graphical representations,
Figure 2 and
Figure 3, show the returned community hierarchy structures for the Hamsterster and the Openflights information networks cases. As presented, in the aforementioned figures, the proposed methodology generates a much more segmented community structure comparing to the respective of the classic Girvan–Newman [
8] and the Clauset–Newman–Moore [
1] approaches. In other words, the proposed methodology tends to generate numerous, compact communities, while the classic approach find difficulties in dividing densely intra-connected but contextually unrelated network elements.
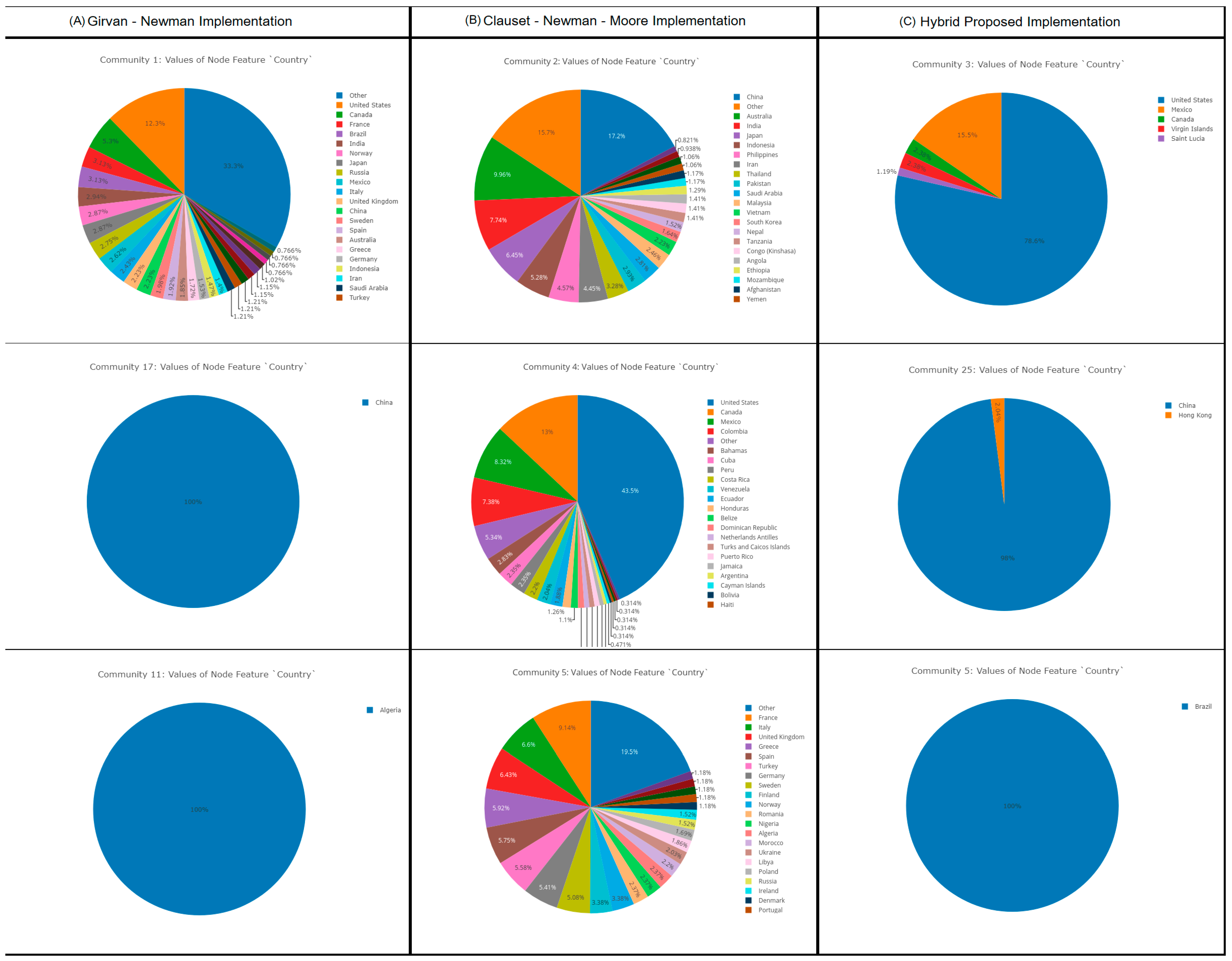
Specifically, regarding the Openflights information network [
39], where along with the name of each “country” involved, the geographic coordinates where also considered as part of the node attributes information, the consistency of the attribute relativeness is strongly assured. Since, after thoroughly analyzing the “country” node attribute distribution for the three largest communities returned per each community detection algorithm applied, as presented in
Figure 4, the proposed methodology returned communities that not only have surprisingly relevant user content characteristics but also are in the truly correct order regarding the total number of flights. In particular, the first community is the one that groups the flights of the “United States”, “Mexico”, “Canada”, “Virgin Islands”, and “Saint Lucia” to the truly largest community, then the flights to “China” and “Hong Kong” are correctly grouped together and finally all the flights from “Brazil” form the truly third largest flights community. On the contrary, both Girvan–Newman [
8] and Clauset–Newman–Moore [
1] algorithms outcome unrelated, in terms of social context information, communities. This is a very critical conclusion, since due to the homophily related assumption initially made, it is a mandatory community detection quality that the proposed methodology should be attributed with.
Finally, two network topology measures can also cross-validate the efficiency of the proposed methodology’s generated community structure, against the corresponding of the Girvan–Newman’s [
8] and the Clauset–Newman–Moore [
1]. The average generated community density [
44], and the average generated community performance [
43], which is the ratio of the number of intra-community edges plus the community non-edges with the total number of potential edges.
As shown in
Table 4, the proposed methodology tend to generate communities of similar density with the respective of Girvan–Newman [
8] and Clauset–Newman–Moore [
1] in the average case. This practically proves that despite the fact that the proposed methodology generates a much more segmented community structure, it successfully retains all the intra-connection edges as the community detection’s standards.
Finally, as shown in
Table 5, the proposed methodology constantly manages to achieve slightly better community performance than the divisive community detection baselines. This practically means, that the proposed methodology better isolates the generated communities in the average case, comparing to the respective average community performance of the Girvan–Newman [
8] and the Clauset–Newman–Moore [
1] algorithms that is truly consistent with the more segmented generated community structure returned.